Inter-granular and Intra-granular Crack Behavior in Mg Bicrystal of [$1\overline{2 }10$] Symmetric Tilt Grain Boundary: LEFM Prediction and Atomic Simulation

Abstract

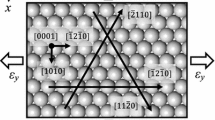
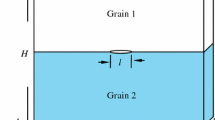
The grain boundary (GB) influences crack propagation, and the intrinsic brittleness/ductility of GB may be related to the interfacial structures. This work examined the effects of [$1\overline{2 }10$] symmetrical tilting grain boundary (STGB) on the crack behaviors in bicrystal Mg to investigate the fracture mechanisms of hexagonal close-packed Mg. The [$1\overline{2}10$] STGB bicrystal Mg models were constructed via the molecular dynamics method, and the cleavage/emission crack-tip behaviors of pre-existing inter-granular and intra-granular cracks under Mode I crack-tip stress intensity loading at T = 0 K were first studied using anisotropic linear elastic fracture mechanics and atomic simulations. For inter-granular cracks, the crack-tip behaviors depend on the intrinsic brittleness/ductility of the [$1\overline{2 }10$] STGB. The crack at the brittle GB and the nucleated voids around the crack tip cause crack propagation via void growth and coalescence. The crack tip at the ductile GB was blunted by dislocation emission around the crack tip. The results show that by introducing ductile [$1\overline{2 }10$] STGB, the crack-tip can be blunted, and the GB fracture can be prevented in Mg. For intra-granular cracks, the brittle crack tip cleaved along its cleavage plane, and the crack tip showed cleavage/emission competitive behaviors due to the influences of GB stress. The stress field of the crack-tip induced the migration of [$1\overline{2 }10$] STGB. Both the cleavage and emission behaviors were observed at the crack tip with very close critical stress intensity for Griffith cleavage (K_Ic) and dislocation emission (K_Ie).

Appendix A: LEFM Analysis of Crack-Tip Behaviors in Anisotropic Media

Considering the plane strain and infinitesimal deformation (i.e., ${u}_{k,3}=0,\;{\epsilon }_{33}=0$), the components of displacement, stress, strain, and stiffness tensor are denoted as ${u}_{i},{\sigma }_{ij},{\epsilon }_{ij}=\left({u}_{i,j}+{u}_{j,i}\right)/2,$ and ${C}_{ijkl}.$ The comma in subscript denotes partial differentiation with respect to the coordinate system. Under these assumptions, the stress field around the crack tip is given by

$${\left[{\sigma }_{11}, {\sigma }_{21}, {\sigma }_{31}\right]}^{T}=-\frac{{K}_{\text{I}}}{\sqrt{2\pi r}}\text{Re}\left\{B\langle \frac{{\nu }_{\alpha }}{\sqrt{\text{cos}\theta +{\nu }_{\alpha }\text{sin}\theta }}\rangle {B}^{-1}\right\}$$

(A1)

$${\left[{\sigma }_{12}, {\sigma }_{22}, {\sigma }_{32}\right]}^{T}=-\frac{{K}_{I}}{\sqrt{2\pi r}}\text{Re}\left\{B\langle \frac{{\nu }_{\alpha }}{\sqrt{\text{cos}\theta +{\nu }_{\alpha }\text{sin}\theta }}\rangle {B}^{-1}\right\}$$

(A2)

The displacement field around the crack tip is given by

$$u={K}_{I}\sqrt{\frac{2r}{\pi }}\text{Re}\left\{A\langle \sqrt{\text{cos}\theta +{\nu }_{\alpha }\text{sin}\theta }\rangle {B}^{-1}\right\}$$

(A3)

where A, B, and $\nu$ satisfy the following eigenvalue equation

$$N\left[\begin{array}{l}A\\ B\end{array}\right]=\nu \left[\begin{array}{l}A\\ B\end{array}\right]$$

(A4)

In Eq. [A4], $A=\left[{a}_{1}, {a}_{2},{a}_{3}\right]$ and $B=\left[{b}_{1}, {b}_{2},{b}_{3}\right]$ are the complex matrices composed of eigenvectors a and b, $\nu =\langle {\nu }_{\alpha }\rangle =\text{diag}\left[{\nu }_{\alpha }\right]$ eigenvaluedefined in the Stroh formalism, and N is the fundamental elasticity matrix defined as

$$N=\left[\begin{array}{l}{N}_{1} {N}_{2}\\ {N}_{3}{ N}_{1}^{\text{T}}\end{array}\right]$$

(A5)

with

$${N}_{1}=-{T}^{-1}{R}^{\text{T}},{N}_{2}={T}^{-1}, {N}_{3}={T}^{-1}{R}^{\text{T}}-Q$$

(A6)

and

$$Q=\left[\begin{array}{l}{C}_{11} {C}_{16} {C}_{15} \\ {C}_{16} {C}_{66} {C}_{56}\\ {C}_{15} {C}_{56} {C}_{55}\end{array}\right], \quad R=\left[\begin{array}{l}{C}_{16} {C}_{12} {C}_{14}\\ {C}_{66} {C}_{26} {C}_{46}\\ {C}_{56} {C}_{25} {C}_{45}\end{array}\right],\quad T=\left[\begin{array}{l}{C}_{66} {C}_{26} {C}_{46}\\ {C}_{26} {C}_{22} {C}_{24}\\ {C}_{46} {C}_{24} {C}_{44}\end{array}\right]$$

(A7)

In Eq. [A7], ${C}_{ij}$ is the component of the materials stiffness tensor.

The SIF is defined as

$$K={\left[{K}_{\text{II}}, {K}_{\text{I}},{K}_{\text{III}}\right]}^{\text{T}}=\sqrt{\pi a}{\sigma }^{\text{applied}}$$

(A8)

For a semi-infinite and atomically sharp crack in a homogeneous medium or materials interface with a non-oscillatory linear elastic solution, the strain energy release rate G concerning crack propagation is defined as

$$G=\frac{1}{2}{K}^{T}\Lambda K,$$

(A9)

where $\Lambda$ is the Stroh energy tensor for a crack in a homogeneous medium and materials interface that is given as

$$\Lambda =\left\{\begin{array}{ll} \frac{1}{2}Re\left(iA{B}^{-1}\right) & \quad for \;homogeneous \;medium \\ \frac{1}{4}Re\left(i{A}_{1}{B}_{1}^{-1}\right)+\frac{1}{4}Re\left(i{A}_{2}{B}_{2}^{-1}\right) & \quad at \;materials\;interface\end{array}\right.$$

(A10)

For a crack in a homogeneous medium and material interface the strain energy release rate G under Mode I loadings is given as

$$G=\left\{\begin{array}{ll}{2\gamma }_{\text{s}}, & \quad for\; homogeneous\; medium\\ {2\gamma }_{\text{s}}-{\gamma }_{\text{i}}, & \quad at \;materials\; interface \end{array},\right.$$

(A11)

where ${\gamma }_{\text{s}}$ is the average surface energy of the cleavage plane and ${\gamma }_{\text{i}}$ is the interfacial energy.

The critical SIF for Griffith cleavage is then given as

$${K}_{\text{Ic}}=\left\{\begin{array}{ll}\sqrt{{2\gamma }_{\text{s}}{\Lambda }_{22}^{-1}}, & \quad for\; homogeneous\; medium \\ \sqrt{\left({2\gamma }_{\text{s}}-{\gamma }_{\text{i}}\right){\Lambda }_{22}^{-1}}, & \quad at\; materials\; interface\end{array},\right.$$

(A12)

The critical SIF for dislocation nucleation at a crack-tip can be obtained based on the extended anisotropic elasticity theories of Rice, which is given as

$${K}_{\text{Ie}}=\sqrt{{G}_{\text{Ie}}o\left(\phi ,\theta \right)}/{F}_{12}\left(\theta \right),$$

(A13)

where $\theta$ is the angle between the crack plane and the slip plane, $\phi$ is the angle between the dislocation burgers vector and the crack front direction of the slip plane (as shown in Figure 3(b)), ${G}_{\text{Ie}}$ is the critical energy release rate for dislocation nucleation, and ${F}_{12}\left(\theta \right)$ is a geometrical factor given as

$${\frac{{K}_{I}}{\sqrt{2\pi r}}}{F}_{12}\left(\theta \right)=\left({\sigma }_{22}-{\sigma }_{11}\right)\text{sin}\theta \text{cos}\theta +{\sigma }_{12}\left({\text{cos}}^{2}\theta -{\text{sin}}^{2}\theta \right)$$

(A14)

$o\left(\phi ,\theta \right)$ is an elasticity coefficient and is given as

$$\text{o}\left(\phi ,\uptheta \right)={s}_{i}\left(\phi \right){\Lambda }_{ij}^{{\theta }^{-1}}{s}_{j}\left(\phi \right),$$

(A15)

where $s\left(\phi \right)$ is the slip vector in constrained path approximation that is given as

$$s\left(\phi \right)=\left(\text{cos}\phi ,0,\text{sin}\phi \right)$$

(A16)

and

$${\Lambda }_{ij}^{\left(\theta \right)}={\Omega }_{ik}{\Lambda }_{kl}{\Omega }_{lj}$$

(A17)

In Eq. [A13], Ω is the rotation matrix and is given as

$$\Omega =\left[\begin{array}{lll}\cos\theta & \quad - \sin\theta & \quad 0\\ \sin\theta & \quad \cos\theta & \quad0\\ 0& \quad 0 & \quad1\end{array}\right]$$

(A18)

The critical energy release rate for dislocation nucleation is given by Andric et al. as

$${G}_{\text{Ie}}=\left\{\begin{array}{ll} 0.145{\gamma }_{\text{s,e}}+0.5{\gamma }_{\text{usf}}, & \quad {\gamma }_{\text{s,e}}>3.45{\gamma }_{\text{usf}} \\ {\gamma }_{\text{usf}},& \quad {\gamma }_{\text{s,e}}<3.45{\gamma }_{\text{usf}}\end{array}\right.$$

(A19)

where ${\gamma }_{\text{s,e}}$ is the surface energy of the emission plane, and ${\gamma }_{\text{usf}}$ is the unstable stacking fault energy of the slip plane. Then the competition between emission and cleavage at the crack-tip can be estimated, i.e. ${K}_{\text{Ie}}<{K}_{\text{Ic}}$ showing emission precedes cleavage, and ${K}_{\text{Ic}}<{K}_{\text{Ie}}$ showing cleavage precedes emission.