On the Rate Dependence of Precipitate Formation and Dissolution in a Nickel-Base Superalloy

Abstract

The temporal dependence of $\gamma '$ dissolution in the polycrystalline Ni-base superalloy RR1000 has been studied with implications to thermo-mechanical processing. A resistivity-based method using an electro-thermal mechanical testing (ETMT), which overcomes the drawbacks associated with other approaches, such as calorimetry, dilatometry, and diffraction, has been used to explore the effect of transient and isothermal thermal cycles. This is supplemented by DICTRA numerical models that simulate the diffusion within the $\gamma$ phase up to the $\gamma /\gamma '$ interface. It is demonstrated that dissolution is affected by heating rate as well as the precipitate size. Below a threshold heating rate of $\sim$0.1 ${^\circ }$C s$^{-1}$, the dissolution kinetics are marginally affected, however, is sensitive to microstructure. The role of precipitate size during dissolution is governed by diffusion flux in the $\gamma$ phase at the $\gamma /\gamma '$ interface, which is inversely proportional to size. It is argued that numerical simulations that predict constitutional liquation during rapid heating by altering the width of the computation domain to match the average precipitate size of the $\gamma '$ population will yield inaccurate predictions. The influence of the heating rate on the nucleation undercooling, during subsequent cooling, has also been addressed. With increasing heating rates, the local $\gamma '$ solvus temperature is shifted to progressively higher temperatures. Unless complete dissolution of $\gamma '$ occurs prior to subsequent cooling, erroneous interpretations of nucleation undercooling can arise.

1 Introduction

The high-temperature creep strength of Ni-base superalloys required for the harsh operating conditions of the turbine in jet engines is endowed by the microstructure comprising a dispersion of L1$_2$ ordered $\gamma '$ precipitates, which are coherent with the A1 $\gamma$ matrix.^[1] The optimum properties are conferred by the size and volume fraction of the precipitates, which are determined by heat treatments following processing. For solidification processing routes, micro-segregation leads to a range in $\gamma '$ size across the dendrite cross-section. Following homogenization in the single $\gamma$ phase field after dissolution of $\gamma '$ and subsequent primary/secondary aging at sub-solvus temperatures, a near cuboidal $\gamma '$ population is obtained.^[2] For the thermo-mechanical processing route, however, the $\gamma '$ population is tailored after forging via a super-solvus or sub-solvus heat treatment. The former approach is beneficial for slower crack dwell growth and creep resistance, but at the expense of reduced tensile strength and low-cycle fatigue properties.^[3]

There has been extensive study, both experimental as well as numerical simulations of $\gamma '$ precipitation kinetics, where cooling rate plays a key role. At low cooling rates, a multi-modal precipitate distribution results, while a uni-modal population is observed for high cooling rates and has been shown to be related to driving forces for nucleation and growth.^{[4,5,6,7,8,9]} The different populations are associated not only with different undercooling, but also different compositions.^[10,11] Studies have also been carried out to assess changes in composition within the $\gamma$ phase during subsequent aging, where the composition evolves towards the equilibrium thermodynamic value.^[12,13] However, a key aspect that is often neglected relates to the dissolution of $\gamma '$ during heating. It is known that several parameters play a role in the dissolution of $\gamma '$ precipitates including the temperature of the heat treatment,^{[14,15,16,17]} elemental distribution,^[18] the precipitate size, and its distribution.^[15,41] Small $\gamma '$ precipitates are also vulnerable to dissolution during Ostwald ripening while the alloy is subjected to elevated temperatures.^[19] Other factors including the dislocation density and the presence of residual elastic strains are also considered to influence the dissolution behavior.^[20]

A study that monitors the heating behavior from samples cooled previously at different rates or alternatively during successive thermal cycles, where equilibrium conditions are not prevalent, is highly desirable. Of industrial relevance is the microstructure evolution during billet manufacture (hot extrusion or a combination of press and radial forging) prior to close die/isothermal forging which includes heat up/cooling cycles before hot work. It has been shown that an incoherent intergranular $\gamma '$ population will occur at sub-solvus temperature deformation, if dynamic recrystallization (DRX) is not complete before cooling.^[21]

The most commonly adopted method for studying phase transformations is calorimetry. It is more conventional to use calorimetry-based approaches in solid/liquid phase transitions, where the change in enthalpy is primarily dictated by latent heat through fraction solidified/melted and to a lesser extent by change in heat capacity from solid-state transitions.^[7,22,23] Dilatometry is also limited by its measurement sensitivity, which is unlikely to detect a small volume change associated with $\gamma '$ precipitation or dissolution.^[24] A more novel method, which overcomes such potential drawbacks, is based on electrical resistivity. A notable advantage is an appreciable difference in intrinsic resistivity between the $\gamma$ and $\gamma '$ phases, but also the ability to impose more rapid heating/cooling rates $\sim$50 $^\circ$C s$^{-1}$, using miniature specimens, where this approach is adopted.^[25,26,27] This method has been used to study phase transformations previously, although attempts at using this for a quantitative calculation of the $\gamma '$ fraction have been based on empiricism, rather than a systematic analysis.^[26] Based on these salient features, this study aims to develop a quantitative approach for calculating the $\gamma '$ fraction using electrical resistivity and identifying the method constraints. Further, this method will be tested by quantifying the dependence of $\gamma '$ dissolution kinetics with implications to particle size, local solvus from prior thermal cycling and heating rate. Such insights are key as they aid understanding of nucleation undercooling related to property-controlling multi-modal $\gamma '$ populations. For representative purposes, a Ni-base alloy, RR1000 (nominal composition in Table I), which is used in rotor discs will be used in this study, although it must be emphasized that the method is generic in nature.

Table I Nominal Composition (Wt Pct) of the Ni-Base Superalloy, RR1000^[1]

2 Experimental and Numerical Modeling Methods

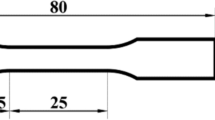
The starting material was a pancake of RR1000, which was produced using the powder metallurgy (PM) and billet forging route. This involved powder synthesis by gas atomization, compaction via hot isostatic pressing (HIP) then extrusion to produce a billet. Thereafter, the billet was isothermally forged (closed die forging) and heat treated below the solvus temperature (sub-solvus). The heat treatment comprises solutioning at $\sim$1120$^\circ$C for 4 hours followed by fan-assisted cooling then aging at 760$^\circ$C for 16 hours before air cooling. All samples were obtained from the same billet, from which test pieces of geometry 2 $\times$1$\times$40 mm$^3$ were electro-discharge machined.

An electro-thermal miniature testing (ETMT) apparatus developed at the National Physical Laboratory (NPL) was used to subject samples to thermal cycles while measuring resistance during the tests. More details of the experimental set-up can be obtained from References 26,27, through 28. RR1000 samples were subjected to a range of thermal cycles, summarized in Table II. The samples tested here explored a range of heating and cooling rates, as well as repeated thermal cycles, to explore the resultant dissolution and precipitation behavior in the presence of different $\gamma '$ populations (based on thermal history).

Room temperature resistivities were measured in a dedicated rig as current is passed through a standard resistor in series with the sample. This was used to establish uncertainties in room temperature values, needed at the start of any ETMT test. Here, a constant current of 1 A was applied to the test piece in both directions to obtain a mean value of the voltage drop, measured with a digital voltmeter, over a length of 4.2 mm. The value of resistivity was calculated from the cross-sectional area of the test piece and the length over which voltage was measured. The resistance was measured as a function of temperature within the central gauge region, typically 2.75 to 3 mm in length for Ni alloys, where the temperature profile is approximately uniform (± 5 $^\circ$C).^[29,30] Heating was through the application of a direct current (DC) from a dedicated 8 V/200 A power supply. If there is an endo/exothermic reaction resulting in absorption/evolution of heat, the system adjusts the current to maintain the specified thermal profile. Current and voltage measurements have estimated uncertainties of less than 0.1 pct, and the measured resistance resolution is ± 0.002 m$\Omega$ (standard deviation ±0.001 m$\Omega$).^[30] The observed uncertainty in resistivity, however, measured from sample to sample variation was about 1 pct, arising from the manual dimension measurements made. During heating, the sample gauge length will increase, though this is small and therefore no correction is needed (estimated from the strain increase: $\varepsilon = \alpha \Delta T \approx 0.02$ when $\Delta T = 1300\,{^\circ }$C and the thermal expansion coefficient, $\alpha \approx 15 \times 10^{-6}$ $^\circ$C$^{-1}$). The temperature resolution, determined by the Pt/Pt-13 pct Rh thermocouple, was less than 1 $^{\circ }$C at 1300$^\circ$C. The thermocouple wires were initially welded together to form a bead of about 0.5 mm in diameter and then spot welded to the center of the samples, so as to not generate any additional potential difference. All experiments were conducted under zero load, omitting thermal stresses, and under a stream of Ar to prevent oxidation at elevated temperatures. The resolution of the measured displacements of the ETMT grips is $\sim$0.1 $\upmu$m.

Table II Heating and Cooling Experiments

Scanning electron microscopy (SEM) analysis was undertaken on a Versa 3D FEG-SEM (FEI) equipped with a synergy Xmax$^\mathrm{{N}}$ 80 EDS detector and Symmetry 2 EBSD camera. Energy-dispersive spectra (EDS) maps and images were collected at 10 kV. The maps were collected with a nominal magnification of $\times 10$ k (horizontal field width 42.8 $\upmu$m) and with a pixel dwell time of 1 millisecond. Combined EDS/electron back-scatter diffraction (EBSD) data were collected at 20 kV and the current was adjusted so that the EDS had an input count rate between 200 and 250 kilo counts per second. Maps were collected with a step size of 0.1 ${\upmu }$m and a collection speed of 250 Hz. Data were collected using Aztec 5.0 software and processed using Aztec Crystal 2.0 (both packages from Oxford Instruments).

The finite difference software, DICTRA, which calculates diffusion fluxes and leading to phase interface movement using the CALPHAD approach was used for simulating the heating rate dependence of $\gamma '$ dissolution.^[31] This modeling type is ideal for tracking the $\gamma /\gamma '$ interface, which can simulate the effect of the prior thermal history and heating rate on $\gamma '$ dissolution kinetics. The model assumes interfacial equilibrium, where all the Gibbs free energy is dissipated through far-field solute diffusion with no energy loss from friction/irreversible processes at the interface. While mean field models such as PrecipiCalc,^[32] as previously demonstrated on RR1000^[33] and a model quaternary Ni-based system,^[13] can be used to quantify the dissolution kinetics based on an initial precipitate distribution size and volume fraction, here the preference is to use a simple front tracking model in 1D, such as DICTRA, since the principal aim is to demonstrate trends in dissolution kinetics that were measured in the experiments. Within the modeled domain, the $\gamma '$ precipitate is permitted to grow from one fixed end. The $\gamma '$ volume fraction is not calculated in DICTRA, however, using a 1D domain the change in $\gamma '$ length is used to qualitatively compare against observed experimental trends. For computing simplicity and efficiency, a quaternary pseudo-RR1000 alloy was used, where the concentrations of Al, Ti, and Ta correspond to the nominal chemistry of these elements in RR1000 (Table I) and the balance comprised of Ni. Two heating/cooling rates were used in the simulations, 1 ${^\circ }$C s$^{-1}$ and 30 ${^\circ }$C s$^{-1}$. The simulations were conducted from 900 K (627 $^\circ$C), below which diffusion during cooling is negligible, and the sub-solvus temperature 1200 K (927 $^\circ$C). A sub-solvus temperature was required at the start of the simulation as the calculations are diffusion-base and nucleation is not included. The simulation domain was 100 nm.

Only three solute species in this multi-component system were considered, owing to problems with the stability of the numerical scheme on convergence with increasing number of solute elements. Accordingly, the most potent $\gamma '$ forming elements from RR1000 have been included in the simulation. While it would be possible to replace these elements or include more, it is argued that this will not affect the overall trends, since only qualitative comparisons are made in this study.

3 Results

3.1 Resistivity Changes with Temperature During Heating and Cooling

The change in resistivity with temperature during heating and cooling for samples S1A and S1B (Table II) is presented in Figure 1(a). The heating rate (0.1 ${^\circ }$C s$^{-1}$) is similar to that used in calorimetry, but cooling rates differ by two orders of magnitude. In both cases, the upper bound temperature (1170$^{\circ }$C) exceeds the reported solvus, which is $\sim$1150$^{\circ }$C, as deduced from calorimetry.^[34] The heating rate of 5 ${^\circ }$C s$^{-1}$ is used between room temperature and 800$^{\circ }$C as diffusion is limited within this range.^[35] Above this temperature, the following observations are made:

• (a) The heating and cooling resistivity curves significantly differ, with larger deviations seen when the cooling rate is increased.

• (b) The onset of dissolution of $\gamma '$ on heating commences at $\sim$850$^{\circ }$C, which corresponds to the maxima in the resistivity curve. This can be attributed to the higher resistivity of $\gamma '$ compared to $\gamma$,^[26,27,30] which results in a net reduction of sample resistivity as the $\gamma '$ phase is dissolved.

• (c) A plateau in the heating curve is reached at $\sim$1160$^{\circ }$C, corresponding to the complete dissolution of $\gamma '$. Henceforth, this will be termed as the “local” solvus to distinguish this from the thermodynamic (equilibrium) solvus, which is 1145$^{\circ }$C.

• (d) As the sample cools, an increase in resistivity is not seen until $\sim$1095$^{\circ }$C and indicates the onset of nucleation of $\gamma '$ on cooling.

• (e) The overlap between the heating and cooling resistivity curves initially occurs at $\sim$1050$^{\circ }$C for S1A, but at 1010$^{\circ }$C for S1B. This overlap prevails during cooling until $\sim$820$^{\circ }$C for S1A and $\sim$905$^{\circ }$C for S1B. Cooling further sees an increasing offset between the heating and cooling curves, which is larger for higher cooling rates.

Fig. 1

Change in resistivity with temperature for sample S1A (a) and sample S1B (b) during heating and cooling (Table II): Both samples were heated at 5 ${^\circ }$C s$^{-1}$ to a super-solvus temperature before cooling at initial cooling rates of 0.1 ${^\circ }$C s$^{-1}$ for S1A (a) and 30 ${^\circ }$C s$^{-1}$ for S1B (b)

Linking these observations to the microstructure, the following nomenclature is used to describe the different distributions of $\gamma '$: (i) Primary intergranular $\gamma '$ precipitates are found at grain boundaries following thermo-mechanical deformation and exist after sub-solvus heat treatment.^[21] (ii) Secondary $\gamma '$ are those which have formed during cooling, and can comprise both intergranular and intragranular populations. Intergranular $\gamma '$ are coherent precipitates at the grain boundaries, while intragranular $\gamma '$ precipitates are coherent and within $\gamma$ grains. (iii) Tertiary $\gamma '$ are intragranular precipitates usually formed at lower temperatures than the secondary $\gamma '$ distribution.

From Figures 1(a) and (b), it can be concluded that the nucleation of $\gamma '$ occurs at a large undercooling (65 ${^\circ }$C, calculated with respect to the local solvus). However, the nucleation undercooling must be calculated with respect to the equilibrium solvus. An additional consideration in polycrystalline alloys is that a bimodal $\gamma '$ population is often observed and hence the undercooling is also dependent on the respective population.

Fig. 2

Change in resistivity with temperature for sample S4 and sample S5 during heating and cooling (Table II)

If nucleation of a $\gamma '$ population is to be considered, the volume fraction of any prior un-dissolved population is important, since it affects the solute supersaturation. Since a temporal dependence of $\gamma '$ dissolution exists, both dissolution as well as the $\gamma '$ nucleation were investigated at higher heating rates, but at temperatures below the local solvus. Accordingly, a change in resistivity with temperature during heating and cooling for S4 and S5 (Table II) is presented in Figure 2. The following observations can be made:

(f) The offset between the resistivity on heating and cooling increases with rate is accompanied by a greater resistivity at room temperature for higher heating/cooling rates.

(g) Heating/Cooling rate: The change in resistivity is similar for both heating rates and the small offset of $\sim$7 n$\Omega$m between the curves in Figure  2 arises from a similar offset existing at room temperature. A slightly higher finish temperature was attained for the higher heating rate (S5). From the shape of the resistivity curves, it is concluded that the $\gamma '$ dissolution kinetics must be similar between 10 and 30 ${^\circ }$C s$^{-1}$ but differs when the rate is decreased significantly to 0.1 ${^\circ }$C s$^{-1}$, as in Figure 1. On cooling, the onset of rapid $\gamma '$ precipitation is observed at $\sim$1047$^{\circ }$C for 30 ${^\circ }$C s$^{-1}$ and $\sim$1040$^{\circ }$C for 10 ${^\circ }$C s$^{-1}$.

In addition to the intrinsic resistivity of $\gamma$ and $\gamma '$ phases, the precipitate size will also contribute to the total resistivity. Since the starting microstructure is identical for all experiments (homogenized), the precipitate size distribution that develops during subsequent cooling will be affected by the cooling rate. This aspect is investigated in S2 (Table II), where following the heating/cooling cycle, as in S1B, an additional isothermal hold of 10 mins at 800$^{\circ }$C was introduced before rapidly cooling to room temperature. The thermal cycle subjected to this sample is shown in Figure 3.

Fig. 3

Thermal cycle subjected to sample S2, noting the first heating stage reaches a super-solvus temperature

Figure 4(a) plots the resistivity with temperature over the thermal cycles, while Figure 4(b) plots the change in resistivity during an isothermal hold. As observed for S1B, there exists an offset of $\sim$75 n$\Omega$m between heating and cooling resistivity at room temperature after the 1$^\mathrm{st}$ heating/cooling cycle. Also, the resistivity in the 2$^\mathrm{nd}$ heating curve follows that of the 1$^\mathrm{st}$ cooling curve. During the isothermal hold, a steady decrease in resistivity of $\sim$10 n$\Omega$m is observed. The grip displacement was also recorded, shown in Figure 4(c). This is a measurement from the length of the sample. Figure 4(d) focuses on the isothermal hold period, shown to be near-constant with time. During heating of these specimens, the resistance initially increases with a $\gamma$ + $\gamma '$ mixture, but when $\gamma '$ begins to dissolve, the resistance decreases. This accounts for the small loss in linearity above $\sim$650 $^\circ$C, when dissolution will initially commence. However, it is not possible to calculate this amount, since the $\gamma '$ fraction, calculated using Eqn. A2, is based on an overall change in resistance which is governed by the dissolution of $\gamma '$ (via phase transformation), rather than the temperature effect. Hence, the lower temperature threshold in this calculation corresponds to the maxima of the resistance vs temperature curve, which is $\sim$800 $^\circ$C. As the change in resistivity within this temperature range is small (15 n$\Omega$m), this has a small effect on the calculated volume fraction. It is assumed that dissolution is dominant beyond the maxima in the resistance curve at $\sim$800$^\circ$C.

Fig. 4

Change in resistivity as well as grip displacement with temperature for S2 (Table II): These are shown for the full thermal cycle (a) and (c), and during the isothermal hold (b) and (d)

3.2 Dissolution/Precipitation of $\gamma '$ During Heating/Cooling

3.2.1 Calculation of precipitate fraction using resistivity

The $\gamma '$ phase fraction is calculated by extrapolating the resistivity of the $\gamma$ and $\gamma '$ phases from the solvus to lower temperatures. This approach is similar to enthalpy-based calculations, where both solid (below solidus) and liquid (above liquidus) heat capacities are extrapolated to a given temperature to calculate the fraction solid/liquid from the measured enthalpy following the rule of mixtures.^[36] Enthalpy-based approaches are most suitable for phase changes where the latent heat is evolved. However, in solid-state phase transformations, where latent heat is absent, a resistivity-based method is ideal. Here, the resistivity of the $\gamma$ phase can be determined above the $\gamma '$ solvus temperature when only a single phase exists; the resistivity of $\gamma$ is extrapolated at temperatures below the $\gamma '$ solvus. The variation in the resistivity of $\gamma '$ with temperature and composition is taken from thermodynamic calculations within JMatProTM^[37] using the NiData database. Further details are described in the Appendix.

The rate of $\gamma '$ dissolution with temperature has a temporal dependence. Accordingly, Figure 5(a) presents the evolution of $\gamma '$ fraction with temperature for a range of heating rates, where the starting microstructure corresponds to the homogenized condition. For sample S3, only the 1$^\mathrm{st}$ heating rate is shown in Figure 5(a), as this corresponds to the same pedigree as S1(A/B/C), S4, and S5 in Table II. The evolution of $\gamma '$ during cooling for the cooling rate of 0.1 ${^\circ }$C s$^{-1}$ is shown in Figure 5(b). In addition to the role of heating rate, the precipitate size can also play an effect on dissolution kinetics, as exists for constitutional liquation.^[38,39,40] For an assessment of precipitate size on the rate of dissolution, it is necessary to have samples with differing $\gamma '$ size-populations of equal $\gamma '$ volume fraction. This has been addressed using S3 (Table II) over five successive heating/cooling cycles. In each case, a heating rate of 1 ${^\circ }$C s$^{-1}$ is used, but cooling rates of 1, 0.1, 10, and 0.05 ${^\circ }$C s$^{-1}$ were used prior to the 2$^\mathrm{nd}$, 3$^\mathrm{rd}$, 4$^\mathrm{th}$ , and 5$^\mathrm{th}$ heating runs, respectively. Figure 5(c) shows the evolution of fraction $\gamma '$ during heating as a function of temperature.

As the sample is heated, a rate dependence of dissolution kinetics is observed with heating rate. A higher heating rate slows the $\gamma '$ dissolution rate compared with a lower heating rate. A marked difference is observed between 0.1  and 1 ${^\circ }$C s$^{-1}$, while the difference is smaller for heating rates exceeding 1 up to 30 ${^\circ }$C s$^{-1}$. The remnant $\gamma '$ fraction in S4 and S5 is $\sim$0.11. For a heating rates greater than 1 ${^\circ }$C s$^{-1}$, the dissolution kinetics is retarded above $\sim$1100$^{\circ }$C, as in Figure 5(a), while in the case of Figure 5(c) for a given heating rate of 1 ${^\circ }$C s$^{-1}$, a marked decrease in dissolution kinetics above 1100$^{\circ }$C is observed in the 1$^\mathrm{st}$ heating run. For cooling rates between $\sim$[0.1-1]  ${^\circ }$C s$^{-1}$, the difference in local solvus during subsequent heating for a fixed heating rate is small, i.e., 2$^\mathrm{nd}$ heating (1$^\mathrm{st}$ cooling at 1 ${^\circ }$C s$^{-1}$), 3$^\mathrm{rd}$ heating (2$^\mathrm{nd}$ cooling at 1 ${^\circ }$C s$^{-1}$), and 5$^\mathrm{th}$ heating rate (4$^\mathrm{th}$ cooling at 0.05 ${^\circ }$C s$^{-1}$). A marked difference in solvus is obtained for a large difference in prior cooling rates, e.g., a lower solvus of $\sim$36 $^\circ$C is observed for a prior cooling rate of 10 ${^\circ }$C s$^{-1}$, compared with prior cooling rates of [0.1-1] ${^\circ }$C s$^{-1}$. For a similar heating rate, a marked increase in local solvus of $\sim$60 $^\circ$C is observed during the 1st heating run compared with 2$^\mathrm{nd}$ heating run, which clearly accounts for the role of the prior microstructure. During cooling, following an initial undercooling before nucleation, rapid growth of $\gamma '$ occurs. The heating and cooling curves superimpose below $\sim$1040$^{\circ }$C, as in Figure 5(b).

Fig. 5

Evolution of $\gamma '$ fraction with temperature over a range of heating rates and given cooling rate: (a) During heating for S1(A/B/C), S2 (1st heating rate), S4, and S5, (b) During cooling for S1A and (c) During heating over three successive heating runs for S2 (all heating rates of 1 $^\circ$C$^{-1}$ from 800$^{\circ }$C to 1210$^{\circ }$C, but variable cooling rates)

Fig. 6

Starting microstructure (forged and sub-solvus heat treated) and heat treated conditions of samples S1B, S4, and S4 are shown in columns (a–d), respectively. The rows show the corresponding (i) back-scattered electron image, (ii) EDS map of Cr, and (iii) EDS map of Ti

3.2.2 Measurement of precipitate fraction using image analysis

In the starting condition, the $\gamma '$ distribution comprises primary/secondary intergranular and secondary/tertiary intragranular populations. This is observed in the back-scattered electron image (BEI) in Figure 6(ai), where intergranular $\gamma '$ appears in gray, while intragranular precipitates appear as ‘mottled’ within the $\gamma$ grains and is corroborated by Cr and Ti EDS maps in Figures 6(aii) and (aiii), respectively. Examining S1B, there is an absence of intergranular $\gamma '$, which is corroborated by the BEI, as well as Ti- and Cr-derived EDS maps presented in Figures 6(bi) through (biii), respectively. Figures 6(c) and (d) refers to S4 and S5. In both cases, the BEI in Figures 6(ci) and (di) shows un-dissolved intergranular $\gamma '$. The Ti EDS map in (iii) highlight the Ti-rich carbides. The Cr maps show segregation to the $\gamma$ phase, contrary to Ti and Al.

The starting microstructure is further characterized in Figure 7; the Cr EDS map is overlaid with a grain boundary distribution map, which differentiates between high and low misorientations, calculated from EBSD measurements. The $\gamma '$ is observed here in regions of low Cr; the precipitates visible in this map are the intergranular primary $\gamma '$, which are located on grain boundaries. The grain boundaries are superimposed, denoted as a black line for a high-angle grain boundary ($>10^\circ$) or a gray line for a low-angle boundary ($\le 10^\circ$). The primary $\gamma '$ forms a coherent interface with the $\gamma$ grain into which it is growing, as evident by the absence of a high-angle boundary at their shared interface. The initially incoherent primary intergranular population nucleated at grain boundaries/triple points during deformation at high strain rates, when dynamic recrystallization is incomplete, has been transformed into a coherent population following sub-solvus heat treatment (as reported previously^[21]).

Fig. 7

Overlay of Cr-derived EDS map of the starting microstructure with grain boundary distribution map, calculated from electron back-scattered diffraction (EBSD) measurements

A comparison of the calculated $\gamma '$ fraction is next made with a microscopic measurement of a quenched sample. This approach is based on reliably delineating $\gamma '$ precipitates existing at the moment of quench, from those that grow during subsequent rapid cooling. This a formidable task if only a unimodal population exists in the starting microstructure, owing to the similarity in morphology of the intragranular secondary/tertiary $\gamma '$ population. One method of delineation is based on retaining the intergranular (primary/secondary) $\gamma '$ population in the starting microstructure and heating to temperatures where this is the only remnant population. The distinctly different morphology to the intragranular populations, and the added advantage of being intergranular, makes it easier to track the evolution of these precipitates. For precipitate volume fraction measurements, etched sections are used. Figure 8(a) shows a BEI corresponding to S4, which contains undissolved bright intergranular $\gamma '$. However, owing to the lower cooling rate used ($\sim$10 ${^\circ }$C s$^{-1}$), the re-precipitated secondary/tertiary intragranular population is coarse. This is unlike the case of S5 in Figure 8(b) where due to the higher cooling rate ($\sim$30 ${^\circ }$C s$^{-1}$) at the end of the isothermal hold, the re-precipitated intragranular population is extremely fine and cannot be resolved during image analysis. To overcome the issue in S4, different thresholds were applied on precipitate sizes for filtering the intragranular population. Sample S4 was observed to have volume fractions of 0.25, 0.22, 0.16 when filtered to diameters $< 400$ nm, $< 500$ nm & $< 800$ nm, respectively. Less scatter was observed in the S5 sample which had volume fractions of 0.12, 0.11, & 0.11 for the filtered diameters $< 400$ nm, $< 500$ nm & $< 800$ nm, respectively. For further details of the imaging processing methods adopted here, please refer to the electronic supplementary material. Owing to the regularity of the shape factor, it is appropriate to consider that area fractions to be equivalent to volume fraction.

Fig. 8

Back-scattered electron images for etched samples S4 (a) and S5 (b)

3.3 Modelling of Precipitate Dissolution During Heating Using DICTRA

Fig. 9

Parameters of mobility (a) and chemical potential (b) obtained in the DICTRA simulations conducted on the quaternary pseudo-RR1000 Ni-Al-Ti-Ta alloy

The finite difference software, DICTRA, was used for simulating the heating rate dependence of $\gamma '$ dissolution. For the quaternary pseudo-RR1000 Ni-Al-Ti-Ta alloy, the calculated mobility of each element in $\gamma$ and the chemical potential are shown in Figure 9. DICTRA results are presented in Figure 10 and are as follows: (a–d) cooling (1 ${^\circ }$C s$^{-1}$ and 10 ${^\circ }$C s$^{-1}$), (e–h) cooling at 1 ${^\circ }$C s$^{-1}$ followed by heating at 1 ${^\circ }$C s$^{-1}$ and 30 ${^\circ }$C s$^{-1}$ and (i–l) cooling at 30 ${^\circ }$C s$^{-1}$ followed by heating at 1 ${^\circ }$C s$^{-1}$ and 30 ${^\circ }$C s$^{-1}$. Each pane of results comprises temperatures versus time, Al concentration vs distance and interface position. During cooling, an increasing concentration gradient is observed with increasing cooling rate (smaller diffusion distance). Consequently, the far-field Al concentration approaches the nominal concentration in Table I for 30 ${^\circ }$C s$^{-1}$, unlike for the lower cooling rate, 1 ${^\circ }$C s$^{-1}$. There is a depletion in $\gamma '$ partitioning elements, such as Al, which is observed in the $\gamma$ phase at the interface. As the $\gamma '$ grows during cooling, Al is transported from $\gamma$ to the $\gamma$/$\gamma '$ interface (diffusion is neglected in $\gamma '$). The advancement of the $\gamma$/$\gamma '$ interface into $\gamma$ (growth of $\gamma '$) is $\sim$ three-fold higher for the lower versus higher cooling rates. The stalling of the interface after $\sim$200 s ($\sim$530 $^\circ$C) must be related to some numerical instability relating to diffusion being significantly reduced. When diffusion retards $\gamma '$ growth, the existing Al supersaturation leads to a second nucleation burst, giving rise to a secondary $\gamma '$ population.^[4,8] However, this aspect is not considered in DICTRA simulations, where only diffusion controlled growth is present and nucleation neglected. It is noted that the $\gamma$/$\gamma '$ interface for these simulations is assumed to be planar; it is known that an alternative spherical interface will affect the predicted velocity of a growing precipitate, as shown in the classical Whelan model.^[41] While interfacial position with time predictions may differ slightly based on the selected interface character, the qualitative trends nor conclusions of this work will change. During subsequent heating, $\gamma '$ dissolution is accompanied by a reversal in the shape of the Al concentration gradient, as Al is now transported from the $\gamma$/$\gamma '$ interface to $\gamma$. Until the reversal of the gradient occurs, the $\gamma$/$\gamma '$ interface advances into $\gamma$ (growth of $\gamma '$). Based on the final position of the interface at the end of heating, a near-equilibrium fraction $\gamma '$ is attained for the cooling/heating rate of 1 ${^\circ }$C s$^{-1}$. However, the greatest deviation from the equilibrium fraction is observed for a cooling rate of 1 ${^\circ }$C s$^{-1}$ followed by heating rate of 30 ${^\circ }$C s$^{-1}$. It is noted that irrespective of the prior cooling rate, a subsequent heating rate of 1 ${^\circ }$C s$^{-1}$ results in a $\gamma '$ volume fraction closer to the equilibrium value.

Fig. 10

Simulations of cooling and subsequent heating for heating/cooling rates of 1 ${^\circ }$C s$^{-1}$ and 30 ${^\circ }$C s$^{-1}$. Each pane of results comprises, temperature vs time, Al concentration vs distance and interface position. The simulation domain is taken as 100 nm, (a-d) cooling (1 ${^\circ }$C s$^{-1}$ and 10 ${^\circ }$C s$^{-1}$), (e-h) cooling at 1 ${^\circ }$C s$^{-1}$ followed by heating at 1 ${^\circ }$C s$^{-1}$ and 30 ${^\circ }$C s$^{-1}$ and (i - l) cooling at 30 ${^\circ }$C s$^{-1}$ followed by heating at 1 ${^\circ }$C s$^{-1}$ and 30 ${^\circ }$C s$^{-1}$

4 Discussion

4.1 Differences Between Heating and Cooling Resistivity Curves

The offset between the heating and cooling resistivity curves during heating and cooling is related to the intrinsic resistivity of the two phases, where the intrinsic resistivity of $\gamma '$ is greater than $\gamma$.^[26,27,30] During initial cooling, if complete dissolution of $\gamma '$ had occurred during prior heating, the initial lower resistivity during cooling would have arisen from undercooling effects (evident for S1A, S1B, and S1C). However, when complete dissolution of $\gamma '$ had not occurred during heating and the $\gamma '$ fraction was greater than the equilibrium fraction, then continued dissolution would occur prior to precipitation during cooling. This would be accompanied by a lower resistivity during initial cooling (S4 and S5). The initial decrease in resistivity during cooling can therefore be accounted for by these arguments. As the samples cool to lower temperatures, when rates are high, the increasingly higher resistivity below $\sim$900$^{\circ }$C compared with heating cannot be assigned to a higher $\gamma '$ fraction during cooling. This is because precipitation kinetics is governed by solid-state diffusion within $\gamma$ and is retarded at higher cooling rates. For higher cooling rates, this will then result in a lower $\gamma '$ fraction, at a given temperature, compared with that existing during heating. This must result in a lower resistivity during cooling. However, this is contrary to the experimental measurements in Figures 1 through 3. Clearly, another factor needs to be considered to account for this anomaly.

The overall resistivity is not only governed by the intrinsic resistivity of a phase, but is also affected by precipitate size and therefore the $\gamma$/$\gamma '$ interfacial area. This is specifically observed in additively manufactured specimens, where cooling rates are rapid ($\sim$100 ${^\circ }$C s$^{-1}$) and the $\gamma '$ size is $\sim$5 nm.^[44] It is noted that factors influence the electrical resistivity, such as the dislocation density,^[42] though this consideration was not needed in the present study as samples were not deformed. The room temperature resistivity in the as-built condition is $\sim$ [100–150] n$\Omega$m greater than measurements during subsequent thermal cycling (heating up to the solvus temperature and cooling back to room temperature at typically < 30 ${^\circ }$C s$^{-1}$), where the $\gamma '$ size is at least ten-fold greater on thermal cycling compared with the as-built condition.^[43] This difference in resistivity indicates that the small $\gamma '$ size, and hence a large $\gamma$/$\gamma '$ interfacial area, was a key contributor. In addition to the intrinsic resistivity of a phase, there are other contributions to the measured resistance, such as changing solute profile at the $\gamma$/$\gamma '$ interface, noting these factors possess a temporal dependence. Some aspects of this can be corroborated, as in a simple experiment (S2 in Table II), where during a short isothermal hold, the change in resistivity can be traced. It is emphasized that during an extended isothermal hold, there will be further changes in resistivity, but this is of lesser relevance to the current analysis.

A progressive decrease in resistivity is accompanied by a constant grip displacement, indicating a constant $\gamma '$ volume fraction, as expected during coarsening. Notably, this only affects the calculation of $\gamma '$ during cooling. There exists a maximum cooling rate where the offset between the heating and cooling resistivity curves is least. In the experiments shown here, this critical cooling rate is $\sim$1 ${^\circ }$C s$^{-1}$ and a minimum $\gamma '$ fraction of $\sim$0.35, as in Figure 5(a), at $\sim$900$^{\circ }$C. In lieu of this, calculations for the $\gamma '$ evolution during cooling are only attempted for the 0.1 ${^\circ }$C s$^{-1}$ cooling rate. This has a lower impact on the calculation of dissolution kinetics on heating. As emphasized, the role of a fine precipitate size on resistivity during heating is only dominant for nanometre size precipitates and when the precipitate fraction is far less that the equilibrium volume fraction. This state is analogous to the material pedigree of an as-built condition following additive manufacturing. As corroborated in Figure 4(b), the decrease in resistivity during an isothermal hold for 10 mins at 800$^\circ$C is only $\sim$10 n$\Omega$m and will be even smaller during a continuous heating experiment. If can therefore be concluded that the dissolution kinetics of $\gamma '$ are minimally impacted for the starting precipitate size and heating rates in this study.

4.2 Kinetics of $\gamma '$ Dissolution During Heating

4.2.1 Heating Rate

The dissolution of $\gamma '$ during heating is governed by solid-state diffusion and therefore by the heating rate. In a fine-grained microstructure, the solvus is defined by the complete dissolution of the intergranular $\gamma '$, which is the last to dissolve, given that this population is the first to nucleate during cooling. For a heating rate of 0.1 ${^\circ }$C s$^{-1}$, the local solvus is $\sim$1145$^{\circ }$C and was experimentally corroborated by the near-absence of the intergranular $\gamma '$ in the quenched microstructure in Figures 6(di) and (diii). These results are consistent with calorimetric studies, which report a similar solvus for typical heating rates of $\sim$ [5 -10] ${^\circ }$C min$^{-1}$ for RR1000.^[2] Beyond $\sim$1145$^{\circ }$C, the resistivity is near-constant up to $\sim$1162$^{\circ }$C. Thereafter, the increase in the resistivity is consistent with the temperature dependence of resistivity of $\gamma$ phase up to the onset of incipient melting, which occurs at $\sim$1235$^{\circ }$C. The near-constant resistivity indicates that a short-range concentration profile exists within the $\gamma$ phase, in the vicinity of the finally dissolving precipitates. A similar result has been reported in numerical simulations of $\gamma '$ dissolution, where an Al-rich concentration gradient exists in the $\gamma$ phase in the vicinity of dissolved $\gamma '$.^[40] The dissolution of $\gamma '$ during heating follows the expected trend where the rate of dissolution decreases with increasing heating rate, since it is governed by diffusion in the $\gamma$ phase. However, in the DICTRA simulations of the pseudo-RR1000 superalloy, a heating/cooling rate of 1 ${^\circ }$C s$^{-1}$ results in a near-equilibrium $\gamma '$ fraction. This indicates that as the sample is heated (immediately after cooling at 1 ${^\circ }$C s$^{-1}$), only a very small amount of initial precipitation occurs, i.e., the $\gamma$/$\gamma '$ interface initially migrates $\sim$2 $\upmu$m into the $\gamma$ phase before dissolution occurs, as in Figures 10(e) and (h). However, a time dependence is observed experimentally; a marked increase in local solvus of $\sim$38 $^\circ$C is observed for the heating rate of 1 ${^\circ }$C s$^{-1}$ compared with 0.1 ${^\circ }$C s$^{-1}$, as in Figure 5(a).

The emphasis in this study was to understand the implications of prior thermal history and heating rate on $\gamma '$ dissolution by tracking the $\gamma /\gamma '$ interface and to show how the solute gradient ahead of the interface is dictated by the prior thermal history. This is complementary to other approaches, such as the methods described by Semiatin et al.^[45] It can be concluded that the resistivity-based method is an effective method for calculating the dissolution kinetics of $\gamma '$ over a wide range of heating rates, which in the absence of latent heat makes use of resistivity, which is markedly different in $\gamma$ and $\gamma '$. This is a viable alternative to more traditional methods based on calorimetry, dilatometry, or diffraction.^{[22,23,24,25,46]}

4.2.2 Precipitate Size

The role of prior thermal history (precipitate size) and heating rate during the dissolution kinetics of $\gamma '$, referring to the experimental results presented in Figure 5(c) are rationalized here. In addition to the role of heating rate, the precipitate size is intimately related to the formation sequence of the different $\gamma '$ populations during cooling.^[4,6,8,25] This has been also investigated using numerical simulations with DICTRA, showing that the $\gamma '$ dissolution rate is inversely proportional to the square of the precipitate size.^[40] In the present study, this aspect has been experimentally evaluated in S3 (Table II). Using the same heating rate (1 ${^\circ }$C s$^{-1}$) and using prior different cooling cycles [0.05 ${^\circ }$C s$^{-1}$ to 10 ${^\circ }$C s$^{-1}$], the temporal dependence of dissolution for a range in precipitate size distributions was quantitatively assessed. In all cases, complete $\gamma '$ dissolution occurred at the end of the heating run. The starting condition for the 1$^\mathrm{st}$ heating cycle was sub-solvus heat treated with a minimum concentration gradient at the $\gamma$/$\gamma '$ interface. This has been independently confirmed in previous studies using APT.^[11,13] The populations are characterized by a difference in Al and Cr concentrations, expected as these populations nucleate at different temperatures during cooling. A dissolution temperature range must exist for the different populations during subsequent heating or different solvus temperatures for these populations.

The markedly higher local solvus in the 1$^\mathrm{st}$ heating run compared to all other heating runs can be attributed to the higher local solvus temperature of the existing intergranular population, which is prominent in the 1$^\mathrm{st}$ heating run, since it corresponds to primary $\gamma '$ following thermo-mechanical deformation and subsequent sub-solvus heat treatment. The occurrence of secondary intergranular $\gamma '$ following cooling through the solvus temperature is lower compared to the initial primary population, and is known to depend on the cooling rate.^[21] However, another possible explanation also exists. Unlike in the heat treated case, during continuous cooling since diffusion within the $\gamma$ phase is almost absent below $\sim$700$^{\circ }$C,^[35] a diffusion distance determined by a concentration profile exists in the $\gamma$ phase at the $\gamma$/$\gamma '$ interface. This was shown in the concentration profile for Al, in Figures 10(a) through (d). During any subsequent heating cycle, dissolution of the $\gamma '$ phase requires a reversal in the shape of the Al gradient, such that now Al must be transported from the $\gamma$/$\gamma '$ interface to $\gamma$ and will initially retard the dissolution kinetics compared with the heat-treated case. It is not possible to ascertain the relative contributions of size with implications to the local solvus or the existing of a concentration gradient at the $\gamma$/$\gamma '$ interface during continuous cooling, unless one of these features is constant. If the local solvus is constant for a given population, then the role of size can be unambiguously considered. This is specifically seen in the case of the 2$^\mathrm{nd}$ - 5$^\mathrm{th}$ heating cycle in Figure 5(c), where nucleation of $\gamma '$ during prior cooling occurred at $\sim$[1095 - 1100]$^{\circ }$C.

A shallower concentration gradient exists in the $\gamma$ phase ahead of the $\gamma$/$\gamma '$ interface (representing a larger diffusion distance) for lower cooling rates, as in Figures 10(a) through (d) and consequently, the initial dissolution kinetics must be accelerated, as predicted in the simulations in Figures 10(e) through (l). However, the reverse is observed in Figure 5(c), indicating more rapid dissolution for the prior cooling rate of $\sim$10 ${^\circ }$C s$^{-1}$ resulting in a smaller $\gamma '$ size, compared with cooling rates between $\sim$[0.05 - 1] ${^\circ }$C s$^{-1}$. In summary, dissolution of $\gamma '$ commences when Al diffuses from the $\gamma /\gamma '$ interface into the $\gamma$ phase. This is governed by the interfacial concentration of Al, which increases with temperature. When at lower prior cooling rates (1 $^\circ$C/s), a larger $\gamma '$ length in Figure 10(h) and large diffusion distance in Figure 10(e) is seen. Higher prior cooling rates (30 $^\circ$C/s) result in a shorter $\gamma '$ length in Figure 10(l) and smaller diffusion distance in Figure 10(k). On subsequent heating, dissolution commences readily, leading to a decreasing $\gamma '$ length in Figure 10(h). However, a larger length $\gamma '$ exists before heating and, hence, taking a longer time for dissolution. Initial $\gamma '$ precipitation occurs on heating (increasing $\gamma '$ length), before the solute flux curve reverses in shape, leading to $\gamma '$ dissolution (decreasing $\gamma '$ length) in Figure 10(l). The converse is observed here with a lower length $\gamma '$ present before heating.

One possibility for the dependence of $\gamma '$ size on dissolution is by considering the role of diffusion within the $\gamma '$ phase itself, which is neglected in the simulations. If diffusion occurs within the $\gamma '$ phase, then a larger size precipitate will decrease the extent of back-diffusion within the phase, retarding the dissolution kinetics. Despite the inter-diffusion coefficient for Ni$_3$Al is comparable to the $\gamma$ phase in Ni-base alloys and Ni-Al-Cr between $\sim$[1000-1100]$^{\circ }$C (typically, $\sim [10^{-15}-10^{-14}]$ m$^2$ s$^{-1}$), diffusion in Ni$_3$Al can be ignored owing to near-stoichiometry.^[47,48] Another commonly adopted approach in accounting for the rate dependence of $\gamma '$ dissolution on size is through the treatment of constitutional liquation.^[40] In numerical simulations, the implications of precipitate size on $\gamma '$ dissolution are considered solely by the size of the domain itself ($\sim$50 nm for tertiary, $\sim$300 nm for secondary, and $\sim$2000 nm for primary)^[40,49] and dissolution is tracked by the movement of the $\gamma$/$\gamma '$ interface. Dissolution is completed when the domain is entirely comprised of $\gamma$ phase, which for a given heating rate occurs faster for a smaller domain (determined by the $\gamma '$ population being considered). However, this rationale cannot account for the difference in dissolution of $\gamma '$ corresponding to the 1$^\mathrm{st}$ and 2$^\mathrm{nd}$ heating cycles in Figure 5(c), where a similar heating rate of 1 ${^\circ }$C s$^{-1}$ was used. If diffusion within $\gamma '$ is ignored and when interfacial equilibrium holds, as for small Peclet numbers,^[50] the temporal dependence of $\gamma '$ dissolution will be solely dependent on diffusion within the $\gamma$ phase. The only explanation for the accelerated dissolution kinetics for the higher prior cooling rate is related to the increase in solute flux. However, the present simulations were carried out in a 1D domain. For a more accurate calculation of dissolution kinetics, it is important to incorporate the precipitate size (R), since the dissolution rate will be inversely proportional to some power of R, i.e., $\propto (1/R)^{n}$.

While arguments based on the local solvus dictated by nucleation undercooling during prior cooling can be used to account for the slower dissolution kinetics of intergranular $\gamma '$, a temporal dependence for the secondary population will also exist. In this case, the size effect in dissolution is dictated primarily by the solute flux at the $\gamma$/$\gamma '$ interface, which is inversely proportional to the precipitate size. Experimental confirmation of this phenomenon is provided in observations of constitutional liquation, where localized melting of intragranular $\gamma '$, as opposed to only intergranular $\gamma '$ has also been reported for high heating rates.^[38,39]

4.2.3 Implications to Undercooling for $\gamma '$ Precipitation

From the preceding sections, the dissolution of $\gamma '$ is dependent on the following: (i) heating rate and (ii) precipitate size distribution dictated by prior thermal history. The equilibrium solvus temperature on the other hand is a thermodynamic quantity and is independent of the aforementioned factors. In the presence of intergranular $\gamma '$, for the lowest heating rate (0.1 ${^\circ }$C s$^{-1}$), the local solvus temperature is $\sim$1145$^{\circ }$C. If the assumption is made that 0.1 ${^\circ }$C s$^{-1}$ is the maximum heating rate below which temporal dependence in $\gamma '$ dissolution is negligible, then $\sim$1145$^{\circ }$C can be defined as the equilibrium solvus. For $\gamma '$ precipitation the undercooling is calculated with respect to the equilibrium solvus temperature. Following complete dissolution of $\gamma '$ at $\sim$1145$^{\circ }$C, during subsequent cooling the onset of nucleation of $\gamma '$ was observed at $\sim$1095$^{\circ }$C and this temperature is independent of cooling rates between [0.1 - 30] ${^\circ }$C s$^{-1}$. It would appear, therefore, that the undercooling for the initial $\gamma '$ population is $\sim$50 $^\circ$C. It is not possible to ascertain a minimum threshold precipitate fraction, when a measurable change in resistance can be recorded, affecting the undercooling measurement. A similar situation prevails in calorimetry or dilatometry, involving solid-state phase transformations. Only when latent heat evolves (melting/freezing), it becomes easier to measure undercooling more accurately, owing to recalescence. Further, the undercooling is dependent on the population that forms; this study has been restricted to secondary inter/intragranular $\gamma '$. On this basis, an “apparent” undercooling 50 $^\circ$C is given, but is an underestimate.

Table III Volume Free Energy, ${\varvec{\mathrm{\Delta } }}{\varvec{G}}_{\varvec{\mathrm{v}}}$, and Critical Radius, $R^*$, of the Embryo for Nucleation as a Function of Undercooling Following

First, undercooling determines the critical embryo size beyond which the growth of the nucleated phase occurs. The variation in the constrained lattice parameter for $\gamma '$ between room temperature and 1000$^{\circ }$C is $\sim$3.59 Å and $\sim$3.65 Å, respectively, for RR1000 and also for a range of Ni-base alloys.^[46,51] The free energy change per unit volume (${\mathrm{\Delta }} {G}_{\mathrm{v}}$) required for nucleation can be calculated from the tangent method using the molar free energy vs composition diagram, but for Ni$_3$Al, it can be approximated as $\sim$ [4 - 6] $\mathrm{\Delta } T$ (J mol$^{-1}$).^[23] The range in molar volume between 1000$^{\circ }$C and 1200$^{\circ }$C varies between $7.2 \times 10^{-6}$ - $7.2 \times 10^{-6}$ m$^3$.^[37] The interfacial energy, ${\gamma} _{\mathrm{int}}$, is taken for that of a coherent interface, $\sim$0.025 J m$^{-2}$,^[13] while the contribution of elastic misfit energy is neglected, given coherency. Therefore, for a range of undercoolings from $\sim$ 5 - 150 $^\circ$C, the critical embryo size, $R^*=2 (\gamma _{\mathrm{int}}/\Delta G_{\mathrm{v}} )$, can be calculated and is given in Table III.

The critical embryo size changes by an order of magnitude with undercooling. Also, the critical embryo size must be greater than the lattice parameter and from Table III it follows that the maximum undercooling possible for nucleation of any $\gamma '$ population is $\sim$150 $^\circ$C. Nucleation undercooling is dependent on $\Delta G_{\mathrm{v}}$, which is calculated at the composition of $\gamma$ phase at a given temperature. In the case of the first population, this corresponds to the nominal composition, $C_0$. However, in the case of subsequent populations, it is always with respect to the composition of $\gamma$ phase at that temperature. It is reasonable to conclude that higher levels of undercooling, $\sim$150 $^\circ$C are pertinent for the formation of the tertiary $\gamma '$ populations. These values are comparable to modelling results using PrecipiCalc for a Ni-Al-Cr-Ta model alloy, where undercoolings for the first and second populations range between $\sim$30 $^\circ$C and $\sim$200 $^\circ$C, respectively.^[13] This range of undercooling also imposes caution while deducing the nucleation of latter populations from the cooling resistivity curve, where the change in morphology of $\gamma '$ at large fractions affects the shape of the resistivity curve; an observation also reported in Reference 25.

Second, the magnitude of undercooling can be lowered (increase in nucleation rate through an increase in active nucleation sites), if the ${\mathrm{\Delta }} {G}_{\mathrm{v}}$ term can be increased through an increase in remnant strain energy. One way of engendering this is through prior deformation, where an increased dislocation density and triple points act as favorable nucleation sites and a recent study has adequately demonstrated this in RR1000.^[21] Following high strain rate deformation at 1100 $^{\circ }$C (strain rates of 0.1 s$^{-1}$, 1 s$^{-1}$ , and 10 s$^{-1}$ up to a nominal strain of $\sim$1), on subsequent heating to $\sim$1170$^{\circ }$C and isothermal hold (complete dissolution of $\gamma '$), an increasing $\gamma '$ fraction with strain rate was observed on cooling at 0.01 ${^\circ }$C s$^{-1}$ up to 1100$^{\circ }$C prior to quenching. Since dynamic recrystallization was incomplete at high strain rates, a preponderance of secondary intergranular $\gamma '$ was observed (area fraction $\sim$0.08-0.11) at 1100$^{\circ }$C, which indicates a lower undercooling compared with the intragranular population.

Third, it has been reported that nucleation undercooling increases with cooling rates (up to $\sim$2 ${^\circ }$C s$^{-1}$) with reports of nucleation undercoolings up to $\sim$85 $^\circ$C.^[7,23] A key observation from the preceding discussion is that if prior higher heating rates are used, then complete dissolution of $\gamma '$ is shifted to higher temperatures. In the absence of complete dissolution, during subsequent cooling, initial precipitation kinetics of $\gamma '$ is significantly retarded (S4 and S5), as explained in the preceding sections. The onset of an increase in resistivity is shifted to lower temperatures with increasing un-dissolved $\gamma '$, as in Figure 2(a) and (b). If this temperature is erroneously considered the onset of nucleation, an incorrect interpretation can be made regarding the rate dependence of nucleation undercooling. Considering other alloys, undercoolings of $\sim$ 20 $^\circ$C and 85 $^\circ$C were reported for low ($\sim$10 $^\circ$C/min) and high ($\sim$ 20 $^\circ$C/min) cooling rates in the alloy AD730.^[7] For a typical cooling rate of $\sim$ 15 $^\circ$C/min, nucleation undercoolings of $\sim$ [50 - 60] $^\circ$C were reported in case of IN100 and another low solvus high refractory alloy (LSHR). Differences can arise from the influence of the prior heating rate and the initial precipitate size. For higher heating rates, the dissolution of $\gamma '$ shifts to higher temperatures and on cooling, initial precipitation is retarded, which can be erroneously interpreted. This has been demonstrated in case of S4 and S5 in Table II. Differences in the measured undercoolings are also dependent on the sensitivity and accuracy of the measurement methods; the resistivity-based method adopted in this study has been shown to be a viable approach.

5 Conclusions

• 1. The resistivity-based method can be used to experimentally measure the evolution of $\gamma '$ over a wide range of heating/cooling rates and overcomes drawbacks from other techniques including calorimetry and dilatometry. A limitation of the method arises during calculation of the $\gamma '$ fraction during cooling, as the resistivity is influenced by very small precipitates at higher fractions ($\sim$0.35).

• 2. The rate of $\gamma '$ dissolution decreases with increasing heating rate and a marked difference occurs between 0.1 ${^\circ }$C s$^{-1}$ and 1 ${^\circ }$C s$^{-1}$. The dissolution kinetics is only marginally affected by heating rates between [1-30] ${^\circ }$C s$^{-1}$.

• 3. The initial microstructure also plays a key role in the dissolution kinetics during heating. It is shown that the local solvus temperature dictated from prior cooling affects the rate of dissolution when a primary intergranular population is present, as in a fine-grained alloy. The role of precipitate size in dissolution primarily arises through the diffusion flux in $\gamma$ phase at the $\gamma$/$\gamma '$ interface, which is inversely proportional to size, in the case of secondary populations. Numerical simulations that treat the precipitate size by altering the size of the computation domain do not capture this crucial aspect.

• 4. Some possible errors in deducing nucleation undercooling have been addressed. It is shown that for higher heating rates the local solvus is shifted to significantly higher temperatures compared with the thermodynamic solvus. Unless complete dissolution of $\gamma '$ occurs prior to cooling, erroneous interpretations of nucleation undercooling can arise.

Appendix

The resistivity of the $\gamma$ phase was determined using S1C (Table II), where the sample was heated beyond the incipient melting temperature. The change in resistivity with temperature is plotted in Figure A1. The variation in resistivity with temperature follows the pattern in Figures 1 and 2. The onset of the linear region beyond $\sim$1162$^{\circ }$C up to the onset of incipient melting ($\sim$1235$^{\circ }$C) was taken as the resistivity of $\gamma$ phase. A best-fit linear fit yields the temperature dependence of the resistivity of $\gamma$ phase, $\rho _{\gamma }$ in n$\Omega$m is:

Fig. A1

Change in resistivity with temperature for S1C (Table II) beyond incipient melting. Heating at 5 $^\circ$C s$^{-1}$ up to 800$^{\circ }$C followed by 0.1 $^{\circ }$C s$^{-1}$ up to 1170$^{\circ }$C. Cooling at 0.1,$^{\circ }$C s$^{-1}$ up to 800$^{\circ }$C and then at 5 $^{\circ }$C s$^{-1}$ to room temperature

$$\begin{aligned} \rho _{\gamma } = 0.1004 T +1302.5 \end{aligned},$$

(A1)

where T is temperature in $^{\circ }$C. The gradient in Eq. 1 agrees well with the thermodynamic database value ($\sim$ 0.07), NiData using a commercial program, JMatProTM.^[31] Since the starting microstructure is homogenized, the $\gamma '$ fraction at room temperature corresponds to the equilibrium fraction, which is $\sim$0.42 in the case of RR1000.^[31] Assuming that the resistivity of the alloy is comprised of a weighted fraction of the individual $\gamma$ and $\gamma$ phases:

$$\begin{aligned} V_{\gamma '} = \frac{\rho - \rho _{\gamma }}{\rho _{\gamma '} - \rho _{\gamma }} \end{aligned},$$

(A2)

where $V_{\gamma '}$ is the volume fraction of $\gamma$. At RT, $V_{\gamma '}$ is 0.42 and from $\rho$ and $\rho _{\gamma }$, using Eq. 2, $\rho _{\gamma '}$ can be calculated. From JMatProTM, the resistivity gradient of $\gamma '$ with temperature is $\sim$0.2929, and therefore, the resistivity of $\gamma '$ is given by

$$\begin{aligned} \rho _{\gamma '} = 0.2929 T+1750.2. \end{aligned}$$

(A3)

In summary, the $\gamma '$ volume fraction with temperature is calculated using a weighted average measurement, as in Eq. A2. Intrinsic resistivities of $\gamma$ and $\gamma '$ with temperature are therefore needed, i.e., Eqs. A1 and A3. As there is no way of obtaining the intrinsic resistivity of $\gamma '$ with temperature, the values are provided by NiData, but that of the $\gamma$ phase is obtained by extrapolating the resistivity of the $\gamma$ phase above the $\gamma '$ solvus to lower temperatures (Figure A1). It is observed that the slope of the variation in the $\gamma$ resistivity with temperature matches the extrapolation and therefore is a good validation of the model.