1 Introduction

Annealing twins are known since long[1] to be very common in Face-Centered Cubic (FCC) metals and alloys with low-to-medium stacking fault energy, but, quite surprisingly, the exact mechanisms by which they appear and evolve during thermomechanical processing remain poorly understood. One reason might be that the term annealing twins is too general, and actually covers different types of twins arising by distinct mechanisms. As pointed out already 70 years ago, annealing twin formation is a process that accompanies grain boundary migration.[2] But there are several mechanisms by which grain boundaries may migrate during annealing, the two main ones being (i) the migration of a recrystallization front driven by the consumption of the energy stored in the form of defects (mostly dislocations) induced by plastic deformation, and (ii) the migration of a grain boundary to reduce its curvature or to adopt a lower energy plane, within the so-called grain growth regime, with no stored energy involved.

In his early paper, Burke[2] reported that annealing twins are prominent after recrystallization and that «the twins found in coarse grained metals are all formed after recrystallization is complete». Regarding the abundancy of annealing twins, the amount of stored energy and the relative energy of twin boundaries compared to random boundaries have been pointed out as the main controlling factors by Charnock and Nutting,[3] who gathered data from different materials. The low energy of twin boundaries is indeed the established reason why they can be formed and kept in the microstructure while grains evolve.

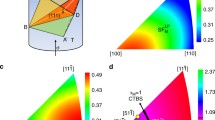
Since their first observations, twins in FCC materials have motivated constant efforts within the physical metallurgy community to elucidate the question of their formation. The interest has been renewed and amplified with the emergence of the Grain Boundary Engineering (GBE) concept by which some properties of a given material can be improved by controlling the grain boundary network.[4,5,6,7] Most of published GBE works actually aim at controlling the amount and connectivity of twin boundaries and other special boundaries arising from the intersection of the latter. Noteworthy within this context, not only the fraction and misorientation of the different types of boundaries matter, but their plane,[8,9] their network, and their connectivity must also be taken into account.[10] Considering the interfacial plane, two types of twin boundaries must be distinguished: coherent twin boundaries lying in the {111} plane that contains the mirror symmetry element relating the two adjacent crystal lattices, and incoherent twin boundaries lying in any other plane. Both the coherent and incoherent twin boundaries are characterized by the same misorientation of the two crystal lattices, 60 deg 〈111〉 or a mirror symmetry by the {111} plane perpendicular to the latter 〈111〉 rotation axis. Such twin-related crystal lattices have one-third of their atomic positions in common, which means that this twin relationship also corresponds to a Σ = 3 Coincident Site Lattice (CSL). Only the inclination of the interface plane differs between coherent and incoherent twin boundaries. This difference is of utmost importance when considering the interfacial properties like energy or mobility, as will be shown later.

Beyond GBE, twins and twin boundaries are defects of interest for optimizing technological materials because they may impact, positively or negatively, many different properties. Table I summarizes few of the published works on the influence of twin boundaries on properties (mostly focusing on Ni base superalloys for the sake of consistency and conciseness). Because in many papers dealing with GBE, twin boundaries are not quantified separately from the other low Σ index CSL boundaries, Table I in fact gathers information on the influence of either twin boundaries only or CSL boundaries with Σ ≤ 27. CSL boundaries with Σ ≤ 27, often referred to as “special boundaries” in the GBE literature, include Σ = 3 twin boundaries, Σ = 9 and Σ = 27 that arise from multiple twinning and intersection Σ = 3 twin boundaries, and Σ = 1 CSL boundaries, also called Low misorientation Angle Grain Boundaries (LAGBs).

Table I Influence of Twin or Σ ≤ 27 CSL Boundaries on Properties (Literature Survey Focused on Ni and Ni Base Superalloys)
Full size table

From the literature survey of Table I, it turns out that the effect of twin boundaries, and more generally of low-Σ CSL boundaries, is beneficial in situations involving interfacial diffusion of chemical species and chemical reactions (intergranular corrosion/oxidation, hydrogen embrittlement). On the other hand, the role of twin boundaries can be much more ambiguous when dealing with mechanical properties. The most striking example is that of fatigue resistance where, on the one hand, long coherent twin boundaries have clearly been identified as preferential nucleation sites for cracks, but on the other hand a higher fraction of special boundaries seems to decrease the crack growth rate. The statement widely spread in the literature that GBE leads to an improvement of properties can actually not be considered as a general statement, and should be specified whenever used.

It must be emphasized at this point that changing the grain boundary network can rarely be done with keeping all other microstructure parameters constant. For example, the grain size, or the distribution of second phase particles, or the shape of general boundaries can be changed. This point is never pointed out, but GBE routes generally make boundaries tortuous, with a very possible effect on crack propagation rate. Thus, the effects observed on some properties could also be due to those latter side changes and therefore be only indirectly related to the grain boundary network.[22,27,30]

A better understanding of the twin formation mechanisms is definitely needed to account for the relationships between twins and all other microstructure features and untangle the complex relationships between microstructure and properties. Noteworthy twin formation does not only result from, but also participates to microstructure evolution mechanisms. For example, the appearance of a twin at a moving boundary locally changes its misorientation and, in turn, its energy and mobility. In this way, twin formation can notably participate to recrystallization mechanisms[31,32] and to texture randomization as multiple twinning leads to a wide range of orientations.[33] Twin boundaries have been reported also to slow down the grain growth process, in a Ag-8Au-3Pd alloy[34] or high manganese steels.[35,36] The effect has also been observed in large-scale molecular dynamics simulations of grain growth in nanocrystalline nickel.[37] It is worth noting that only small amounts of low-mobility boundaries are enough to end up with a significant effect on the coarsening kinetics of the polycrystal, as shown in nickel by both mesoscale grain growth models and molecular dynamics.[38]

This paper addresses the formation and evolution of twin boundaries during thermomechanical processing of FCC metals and alloys, viewed at the mesoscale and from several perspectives. First the twin formation mechanisms which have been proposed through the years are summarized and commented in Section II. Section III presents the experimental methods and parameters used for quantifying twins and their networks and morphologies. Then it will be confirmed in Section IV that annealing twins are mostly formed during recrystallization and it will be shown in Section V that twins can greatly evolve after their formation. The possibility of controlling twin amounts by thermomechanical processing will be discussed in Section VI in light of the information presented in the former sections. Finally, the state of the art of models and simulation tools able to account for the existence of twins will be presented in Section VII.

2 Proposed Twin Formation Mechanisms

The mechanisms proposed until then to explain how twins can form along a moving grain boundary have been reviewed in 1984 by Meyers and McCowan.[39] There were four mechanisms referred to as (i) growth accident, (ii) grain encounter, (iii) coalescence of stacking fault packets nucleating at grain boundaries, and iv) grain boundary dissociation.

The growth accident theory has been originally proposed by Carpenter and Tamura[1] and was developed later by Burke[2] and by Fullman and Fisher.[40] The growth accident mechanism, according to which twins form on grain boundary portions that are macroscopically parallel to {111}, or on {111} facets,[2] is schematized on Figure 1(a). A first twin boundary (thick red line) is formed while the grain boundaries are moving towards their curvature center (white arrows) and is stable if the net interfacial energy balance is negative (grain boundary segments with lower interfacial energy are schematized by thinner black lines). This mechanism can then be repeated to form a parallel-sided twin, a configuration often observed experimentally, and which also occurs with a relatively high frequency in molecular dynamics simulation of grain growth.[41] Actually, if the first twinning event leads to a favorable change in grain boundary energies, the second one should have the opposite effect and would be unstable; there is thus an issue with the proposed stability argument, unless the formation of the second twin boundary occurs as another neighbor grain with a suitable orientation has been encountered. An alternative explanation could be that twin formation allows for relaxation of some kind of internal stresses, the nature of which remains to be identified.[41]

Fig. 1
figure 1

Schematic representation of the proposed models for annealing twin formation by (a) the original growth accident model (scheme adapted from Ref. [39]), (b) the atomistic variant of the growth accident model proposed by Gleiter (adapted from Ref. [42]), (c) the coalescence of stacking fault packets (adapted from Ref. [39]), (d) grain boundary dissociation (adapted from Ref. [39]). (e) Alternative evolution of the twin “popped-out” in (d) (Color figure online)

Full size image

Some 20 years later, Gleiter revisited the growth accident model by considering the {111} faceted nature of the grain boundaries and their migration by lateral ledge motion.[42] Figure 1(b) schematizes a white grain growing and consuming a gray grain. The thick black line is the grain boundary that moves upwards (white arrow) while atoms are added on the left and/or right ledges or while a new {111} plane nucleates on top of the upper one. The A, B, and C lines stand for compact {111} planes stacked following the ABC sequence representative for the FCC lattice. If the ledge movement or the nucleation of a new atomic plane creates a stacking fault, with atoms in position B instead of A on Figure 1(b), Gleiter’s model considers the twin to be formed, but actually only a stacking fault has been created at this stage. It could turn into a twin (with the red C plane as twin boundary mirror plane) if the next plane to be nucleated is of type A, or be a simple intrinsic stacking fault if the next plane is of C type. Noteworthy to make Gleiter’s version of the growth accident model work, the grain boundary has to migrate in the opposite direction to its center of curvature, which can occur during recrystallization but usually not during grain growth (except at triple junctions). With concave boundary instead of a convex one, any stacking fault would be terminated by Shockley partial dislocations (see Figure 12 of Reference 43), with an associated energetic cost.

The grain encounter mechanism[44] has a rather explicit name: two grains with orientations related to each other by a 60 deg 〈111〉 rotation come into contact as they grow in a polycrystal and then form a twin boundary. This is quite similar to what has been called “stimulation theory” by Burgers[45,46]: in this former model, one of the two grains was supposed to be smaller and expand after meeting its twin and forming the twin boundary. The grain encounter mechanism cannot explain the twin frequencies observed experimentally, this can be ruled out by simple probability calculations. In a randomly textured material, assuming that all grains have the same size and 14 neighbors and admitting a deviation of 9 deg from the perfect twin relationship, the probability that two grains are twin related is only 1.4 pct.[47] Furthermore, even if the consideration of non-random crystallographic texture can increase this number, the grain encounter mechanism could hardly explain the existence of multiple twin boundaries in a grain. During recrystallization, because of the complex 3D shape of recrystallized grains, the formation of twin boundaries by encountering of twin-related crystallites is nevertheless observed quite often in 2D sections.[43]

Another mechanism is the formation of a twin by coalescence of stacking fault packets formed at migrating recrystallization front which has been observed by TEM.[48] On Figure 1(c), the dashed lines stand for stacking faults, and are terminated by Shockley partial dislocations (upside down red T symbols). The recrystallization front (thick black line) is moving leftwards (white arrow). Because partial dislocations do not pile up right on top of each other to minimize their energy, the right end of the formed twin has been drawn inclined, different from Meyers original figure. Another difference is the decrease in boundary energy (symbolized with a thinner black line) which has been pointed out in the original work of Dash and Brown[49] as the driving force for twin formation.

Later on, Mahajan et al. proposed a somewhat similar mechanism,[47] but with a finer description of the grain boundary structure, and referring to the formation of Shockley partial loops at {111} steps of grain boundaries. Both Meyers and McCowan[39] and Mahajan[49] consider that, once formed, the twin can expand by the migration of the recrystallization front (leftwards on Figure 1(c)) but also by the migration of the non-coherent end segments moving to the right. The nature of driving force for making the non-coherent segments move in the opposite direction to the grain boundary is nevertheless unclear. This movement increases the coherent twin boundary area. Even though the latter has low energy, the interfacial energy balance is positive, small but positive, and thus unfavorable. The movement of the non-coherent segment could possibly result from an applied external stress field, or from internal stresses which would make the partial dislocations glide, but without stress, the reason for their movement remains unclear to the authors.

In the grain boundary dissociation or “pop-out” model originally proposed in Reference 50 and schematized on Figure 1(d), the initiating process is the emission of partial dislocations from grain boundary ledges and the boundary (thick black line) dissociates to form a coherent twin terminated by a non-coherent segment (red), and the misorientation of the boundary is changed so that the energy balance is negative (segment of lower energy, thinner black line), hence favorable. With these regards, the grain boundary dissociation mechanism has similarities with the latter “Shockley partial loops” mechanism but here grain boundary migration is not required to form the twin. The decomposition of a relatively immobile low-energy boundary has indeed been observed by TEM in the Inconel 600 Nickel base superalloy by Kumar et al.[51]

Leaving the grain encounter model apart, the mechanisms described above fall into two categories, those by which the twin is formed by atom addition at wrong sites onto {111} grain boundary facets (Figures 1(a) and (b)), and those involving the emission of Shockley partial dislocations at grain boundary ledges/steps as an initiation process. In both kinds of mechanisms, the grain boundary structure is evoked, suggesting that the probability of forming twins should be related to the frequency of {111} facets/terraces and steps/ledges, which in turn depends on the macroscopic grain boundary plane and on local curvature. Topological information available at the mesoscopic scale sounds thus relevant to discuss and better understand the mechanisms at play at finer scales.

Any situation where the boundary is tortuous should increase the probability of finding a suitable configuration to form a twin somewhere along the boundary. Recrystallization fronts are usually very tortuous because of the heterogeneity of the stored energy field that provides the driving force for their migration.[52] The stored energy field is influenced by the amount of macroscopic strain applied and also by other parameters like the initial grain size. The twin density obtained after recrystallization in pure nickel has indeed been shown to be correlated with the recrystallization front tortuosity,[53] varying with the amount of prior strain applied and with the initial grain size. Another phenomenon that can distort a grain boundary is its interaction with second phase particles (referred to as Smith Zener pinning).[54,55] And a high frequency of twin boundaries in contact with second phase particles has indeed been observed in Nickel base superalloys.[55,56,57]

Other factors, like solute atom segregation or temperature known to affect the microscopic and atomic structure of grain boundaries (notably via the roughening/de-faceting transition[58,59,60,61,62,63]), may have a consequence on the frequency of twin formation. For example, Pande and Imam found a drastic decrease in twin density when doping nickel with 200 ppm boron.[64] Low frequency of twins is also typical of solidification structures,[65] which could possibly be related to grain boundaries being non-faceted at high temperatures. Regarding these two (interdependent) factors, one should also keep in mind that they also affect the relative energy of the twin boundaries compared to general grain boundaries, which is another possible reason for their effect on the amounts of twins created.

In addition, as a concluding remark on the proposed mechanisms for annealing twin formation, one should point out that mostly coherent twin boundaries are addressed in the literature. Definitely, much remains to be discovered and understood about twin formation in general and the formation of incoherent twins would deserve more specific attention. The stability argument, by which twin formation is driven by the reduction of the total interfacial energy, would probably be very questionable concerning incoherent twin boundaries since they have much higher energy compared to coherent ones (see Section V). On the other hand, for twins formed during recrystallization, not only the interfacial energies but also the consumed stored energy should be taken into account in the energetic balance. Stored energy being usually by far higher than interfacial energy, its reduction as the recrystallization front migrates could easily compensate for the creation of a twin boundary, be it coherent or incoherent.

3 Experimental (Mesoscale) Methods for Quantifying Twins, Their Networks, and Morphologies

Coherent twins can easily be recognized in 2D sections of polycrystals as straight intragranular interfaces. Early works based on optical observations could already provide relevant pieces of information to propose formation mechanisms, as discussed in Section II. Nowadays, Electron BackScattered Diffraction (EBSD) which provides crystal orientation maps is routinely used in physical metallurgy labs. Within an EBSD map, twin boundaries can be detected based on their misorientation. Because of the orientation measurement accuracy of the technique (typically half a degree with conventional experimental setups), a tolerance must be admitted in the twin detection procedure. The angular tolerance proposed by Brandon[66] is the most commonly used and is physically grounded since it considers a maximum density of geometrically necessary dislocations which can be admitted in the boundary before it completely loses its particular nature. This tolerance \( \omega \) applies to any CSL boundary, and is adapted to the degree of coincidence:

$$ \omega = \theta_{\text{HAGB}} \cdot {\sum}^{ - 1/2} $$
(1)

Considering high misorientation angle grain boundaries (HAGBs) to be characterized by a minimum disorientation θHAGB of 15 deg,[67] Brandon’s tolerance angle for Σ = 3 twin boundaries is 8.66 deg. This is the maximum admitted deviation angle between a measured boundary misorientation and the theoretical one, 60 deg 〈111〉, to consider the current boundary as a twin boundary. Actually, other—more restrictive—tolerance limits have been proposed through the years (listed in Reference 68) and could be used for studying annealing twins since it has been proven that most of them are very close to the ideal misorientation of 60 deg 〈111〉, typically within less than a degree.[69] In case the material has been deformed after the formation of the twins, the tolerance should nevertheless be chosen large enough to account for the deviation from the perfect twin relationship as a result of dislocation storage near/in the boundary.[20]

Grain boundary traces can also be analyzed on orientation maps, so that the consistency of the trace with a {111} plane can be checked for any twin boundary segment. This way, incoherent twins and possibly coherent ones can be distinguished.[70] Grain boundary trace analysis can also be made in two perpendicular sections to unambiguously determine the grain boundary plane,[71,72,73] and definitely confirm the coherent nature of a given twin boundary.

For quantifying twin boundaries in a 2D section of a microstructure, several parameters can be used, among which

  • NG, the number of twin boundaries per grain:

    $$ N_{\text{G}} = \frac{{N_{\text{cr}} - N_{\text{gr}} }}{{N_{\text{gr}} }}, $$
    (2)

    where Ngr is the number of grains delimited by HAGBs (twin boundaries excluded) and Ncr is the number of crystallites delimited by either HAGBs or twin boundaries.

  • NL, the number of twin boundaries per unit length, often referred to as the twin boundary density[74]:

    $$ N_{L} = \frac{{N_{\text{tb}} }}{L}, $$
    (3)

    where Ntb is the number of twin boundaries intercepted by a straight line of length L

  • LA, the length of twin boundaries per unit area:

    $$ L_{A} = \frac{{L_{\text{tb}} }}{A} $$
    (4)

    where Ltb is the total length of twin boundaries detected in an area A; it is stereologically related[75] to NL by

    $$ L_{A} = N_{L} .\frac{\pi }{2} $$
    (5)

  • FL, the length fraction of twin boundaries among all grain boundaries

    $$ F_{L} = \frac{{L_{\text{tb}} }}{{L_{\text{tb}} + L_{\text{HAGB}} }}, $$
    (6)

    where LHAGB is the total length of HAGBs (twin boundaries excluded) detected in the same area A

  • FN, the number fraction of twin boundaries among all grain boundaries

    $$ F_{N} = \frac{{N_{\text{tb}} }}{{N_{\text{tb}} + N_{\text{HAGB}} }}, $$
    (7)

    where NHAGB is the number of HAGBs (twin boundaries excluded) intercepted by the same straight line of length L.

Depending on the discussed issue, the most relevant parameter must be chosen, as they are not all equivalent. To illustrate this point, Figure 2 shows the quantification results obtained with three different parameters for the same set of microstructures (Inconel 718 superalloy, in the solution state, after annealing at different temperatures, with or without deformation prior to annealing). The full symbols refer to microstructures free of stored energy and the open ones correspond to the microstructures which have been deformed before annealing. The difference between both types of experiments will be further commented in Section III (more material processing details will be given there), but for now, let us focus on the different twin boundary quantification parameters and how they relate to each other. Figure 2(a) shows that the length of twin boundaries per unit area can vary much (here multiplied by 6) while the length fraction remains more or less the same. This is typically the case when grains and their twins grow homothetically, the length of boundaries per unit area decreases while the proportion of twin and grain boundaries is constant. Figure 2(b) shows a slight increase in length fraction as the number of twin boundaries per grain increases. This sounds logical since in the ideal case where the grains would keep the same size (i.e., same length of HAGBs per unit area), any added twin would increase both the number of twin boundaries per grains and the twin boundary length fraction. In the case of real microstructures, the dependence is not so easy to be inferred as the grain size is usually not constant, with a direct consequence on the length of HAGBs per unit area and measured length fractions. Finally, Figure 2(c) illustrates that the number of twin boundaries per grain and the length of twin boundaries per unit area do not correlate well with each other either. This is mostly due to the shape of twins and their boundaries which can vary very much depending on the thermomechanical history (see Section III), from flat perfectly coherent interfaces crossing the whole grain to highly tortuous twin interfaces mostly made of incoherent segments.

Fig. 2
figure 2

Comparisons among twin boundary quantification results from the same set of microstructures. Brandon’s tolerance[66] has been applied to detect Σ = 3 boundaries. Length fraction vs length per unit area (a) and vs number of twin boundaries per grain (b). Number of twin boundaries per grain vs length per unit area (c). The material was solution treated Inconel 718 submitted to annealing at different temperatures, with (open symbols) or without (full symbols) deformation applied prior to annealing

Full size image

Twin boundary quantification is thus not that straightforward and the best quantification parameter to be used depends very much on the context. Even though the length fraction has been used many times, to measure the efficiency of GBE processing routes for example, it has the major drawback of being very sensitive to the grain size, and should thus be avoided whenever possible. The number of twin boundaries per grain sounds better suited when discussing twin nucleation and the number of times a twin appeared as the grain was growing. On the other hand, the length of twin boundaries per unit area or the number of twins per unit length are probably better guides for discussing crack propagation issues for example.

Moreover, because twins, notably when arising from GBE routes, can form complex interconnected networks,[51,76] quantifying their number or length might not be sufficient, and additional parameters must be defined to characterize the boundary network itself; for example, Betti numbers can be used for that purpose.[77] To account not only for the boundary misorientations but also for the grain boundary planes, a stereological approach has been developed at Carnegie Mellon University to assess the five-parameter grain boundary character statistical distributions.[78,79] But then, topology is lost. To get the grain boundary plane of each singular boundary, 3D characterization techniques are required.

The first descriptions of the 3D shape of annealing twins were based on serial sectioning by mechanical polishing combined with optical microscopy.[39,81] Then, EBSD was used to get richer crystallographic information from each section, obtained after either mechanical polishing again[82] or ion milling in a dual-beam microscope (FIB-SEM).[80,83] The use of ion milling improved drastically the spatial resolution of the 3D data sets along the sectioning direction (let us call it Z), but to the detriment of the scanned volume, and thus of the statistical relevancy. It is worth mentioning that the recently developed Plasma-Xe+FIB technology considerably reduced this drawback,[80] with achievable volumes typically up to 100 µm wide (instead of 10 µm with conventional Ga+FIB systems) and potentially no loss in spatial resolution. Also to address this major drawback of 3D EBSD characterization in a FIB-SEM, a prototype called Tribeam microscope has been setup at UCSB with a femtosecond laser added onto a FIB-SEM to allow for material ablation, which is now available in a commercial version.[84,85,86] 3D data acquisition using the Tribeam system is 4 to 6 orders of magnitude faster compared to that achievable with a Ga+FIB-SEM. The scanned volumes are in the range of several hundreds of µm wide, with still a reasonable resolution in the Z direction (sub µm range). All 3D techniques listed above are destructive; they are thus not suited for in situ or sequential experiments aiming at following the evolution of a given region of interest. Only techniques based on X-ray diffraction enable that.

The High-Energy X-ray Diffraction Microscopy (HEDM)[12,80,87,88] is extremely powerful but requires a synchrotron source and is thus hardly accessible. It has recently been adapted in the form of lab equipment, under the name of LabDCT for laboratory diffraction contrast tomography.[89] With measurable volumes in the range of a few mm wide[90] and a better angular resolution than conventional EBSD (~0.05 to 0.1 deg),[89,90] LabDCT is very likely to spread over labs in the coming years and will be very useful to go further in the understanding of grain boundary networks, provided that the spatial resolution (that is for now in the range of 20 µm) will be further improved.[91]

4 Annealing Twins Formed During Recrystallization vs Grain Growth

Figure 3 compares typical microstructures obtained after static recrystallization and after grain growth. Those are from the same series used for building Figure 2 and next Figure 4. The material is the Inconel 718 nickel base superalloy. It has preliminary been submitted to hot deformation at a supersolvus temperature, with cooling after deformation fast enough to avoid precipitation of second phases. Apart from the unavoidable presence of few insoluble carbide and carbonitride particles, the material can then be considered as being single phased. Its microstructure was equiaxed with an average grain size of about 10 µm and it was free of stored energy, as the cooling rate was chosen slow enough to let the remnant hot-deformation stored energy be consumed through post-dynamic recrystallization. Samples were subsequently submitted either directly to heat treatments at different temperatures to make the grains grow under capillarity driving forces, or to cold deformation followed by a heat treatment to proceed to static recrystallization, driven by the consumption of the stored energy.

Fig. 3
figure 3

EBSD map of single-phase Inconel 718 microstructures where only Σ = 3 twin boundaries, Σ = 9 CSL boundaries CSL, and grain boundaries (with a disorientation of at least 5 deg) are plotted red, green, and black, respectively. Brandon’s tolerance[66] has been applied to Σ = 3 and Σ = 9 boundaries. (a) and (b) After grain growth. (c) and (d) After static recrystallization (Color figure online)

Full size image
Fig. 4
figure 4

(a) Σ = 3 twin boundary density (length per unit area) and (b) number of twin boundaries per grain as a function of the average grain size (AGS) in Inconel 718 microstructures arising from recrystallization (empty and gray-filled symbols) or from grain growth (full black symbols). Black lines on (a) are power laws fitted onto the recrystallization (LA = 2372.9 AGS−0.88; R2 = 0.926) and on the grain growth data (LA = 598.9 AGS−0.76; R2 = 0.972)

Full size image

The microstructures of Figure 3 have been selected to have similar grain sizes, which is important to discuss the amounts of twins created under both regimes. Since they form as the grains develop, a higher number of twins can be expected in larger grains. The recrystallized microstructure of Figures 3(c) and (d) has been obtained by 10 pct deformation by cold torsion and 10 minutes annealing at 1010 °C, leading to an average recrystallized grain size of 34.1 µm. The grain growth heat treatment of Figures 3(a) and (b) has been adjusted to achieve a similar average grain size, 35.4 µm, obtained after 10 minutes at 1050 °C. It is obvious that the annealing twins arising from recrystallization are very different from those after grain growth, as already pointed out by Meyers and McCowan some 35 years ago.[39] In the recrystallized microstructure, both the overall density of twin boundaries and the proportion of incoherent ones are much higher as compared to the microstructure after grain growth. After grain growth, most of the twins are coherent, with straight boundary traces most of the time crossing the whole grain. The terms recrystallization twins and grain growth twins would provide a more accurate depiction of these distinct configurations, rather than general application of the term of annealing twins.

Figure 4 shows data from the same series of Inconel 718 experiments and relates the twin density and the number of twin boundaries per grain to the grain size. Black symbols refer to grain growth microstructures; black disks are from simple heat treatments; black diamonds are from experiments where, even though it has been deformed, the material has not recrystallized during the subsequent annealing at 985 °C and has thus been attributed a full black symbol. All other symbols refer to samples which recrystallized during annealing (10 minutes at 1010 °C) after cold deformation, either in torsion or compression, to different levels of strain, and for few of them varying also the initial microstructure.

The most striking output of this figure is the clear dependence of the Σ = 3 twin density (here measured as LA) to the average grain size, for both the recrystallization and the grain growth regimes, and the clear difference between both regimes. Recrystallization leads to much higher twin densities than grain growth for a given grain size. Noteworthy, the recrystallization data are also more scattered than the grain growth ones, and this scattering is even more pronounced when considering the number of twin boundaries per grain (Figure 4(b)) instead of the twin boundary density (Figure 4(a)). This scatter could not simply be related to the deformation conditions which have been varied to get these data: torsion vs compression, amount of strain (in the range 5 to 15 pct) and initial microstructure. The amount of twins in a recrystallized microstructure can definitely be varied a lot for a given material, but the exact mechanisms behind that remain to be clarified. The number of twin boundaries per grain on Figure 4(b) is three to four times higher after recrystallization as compared to after grain growth. Moreover, the number of twin boundaries per grain seems to increase with increasing recrystallized grain size but stays constant along with grain growth, which is consistent with early observations reported by Burke in 1950.[2]

The number of twins per grain increasing with grain size during recrystallization also clearly arose from experiments performed on pure nickel where the correlation was established by microstructure analyses at different stages of the recrystallization process (Figure 9 of Reference 53). This work also showed that, for a given initial grain size and by comparing samples compressed to 30 and 60 pct height reduction, the amounts of twins created in the recrystallizing grains primarily depend on the applied strain level. Each of the two deformed states was recrystallized at two different temperatures (350 °C and 450 °C) and led to the same microstructure, i.e., same grain size and same twin density, independent from the recrystallization temperature, and thus from the recrystallization rate. Recrystallization took about 10 times longer at the lower temperature, with no visible effect on the final recrystallized microstructure. This result questions the widely spread idea that the probability of forming twins would depend on the velocity of the moving boundary.[49] To the authors best knowledge, the effect of the grain boundary (or here recrystallization front) velocity has never been demonstrated unambiguously and would deserve dedicated research.

On the other hand, the number of twins per grain staying constant during grain growth (and independently from the annealing temperature within the applied temperature range of Figure 4) suggest that no new twin is formed, or only very few ones, during the capillarity-driven grain boundary motion process. This could be confirmed thanks to the 3D-HEDM technique, on a pure nickel sample submitted to successive annealing steps to make the grains grow.[92] Only a few twin nucleation events could be detected, always along grain boundary triple junctions and in configurations leading to a reduction of the interfacial energy, consistently with the growth accident theory schematized on Figure 1(a). It is worth noticing that the probability of finding somewhere in the microstructure a grain boundary junction fulfilling the energetic requirements must be dependent on crystallographic texture.[40] An increase in twin boundary fraction was reported with increasing grain size of α-brass[93] and explained by the same Fullman and Fisher theory, but the samples had been submitted to cold deformation before being annealed, it is therefore possible that the observed correlation is inherited from the recrystallization stage and not from the grain growth process. Moreover, as mentioned in Section II, the use of boundary length fractions can be misleading when comparing microstructures with different grain sizes. On the other hand, an increase in twin boundary fraction during static recrystallization followed by a decrease in the grain growth regime has been reported in the alloy 825 by Bai et al.[94] which is fully consistent with the above discussion on pure nickel data.

To complete the discussion of the twin configurations observed in recrystallized microstructures (such as that of Figures 3(c) and (d)) and those typical for grain growth (Figures 3(a) and (b)), a series of annealing steps and EBSD analyses has been performed using a heating stage in the SEM chamber.[95,96] The evolution of a region of interest is shown in Figure 5.

Fig. 5
figure 5

Recrystallization and grain growth in the 304L steel, followed using an in-SEM chamber heating stage and EBSD mapping in between each annealing step. The initial sample was obtained by quenching after hot compression, at the onset of dynamic recrystallization. It was then annealed at temperature at 1000 °C except for the first steps where temperature was a little bit reduced to slow down the recrystallization process. (a) through (j) are snapshots at different stages indicated on the temperature–time plot. Grain boundaries (>10 deg) are plotted black, Σ = 3 and Σ = 9 CSL boundaries (within the tolerance of Brandon’s criterion[66]) are plotted red and green, respectively. Background gray level goes brighter and brighter with decreasing the Kernel Average Misorientation (range 0 to 5 deg) (Color figure online)

Full size image

The material is 304L austenitic steel, it was initially in hot-deformed and quenched state, with very little dynamically recrystallized fraction (few small recrystallized grains visible at former grain boundaries on Figures 5(a) and (b)). All along the annealing steps, recrystallization progressively consumes the deformed grains (regions appearing darker as they have higher dislocation densities and thus higher intragranular misorientations). Once the deformed matrix has been completely consumed (near steps (e), (f)), grains keep growing driven by capillarity forces. This series is consistent with what has been seen on Figure 3: (i) many twins and a great amount of incoherent ones are produced as the recrystallized grains develop, and (ii) grain growth tends to keep mainly coherent ones. Thanks to the observation of the same area after each annealing step, the microstructure appears to gradually change between both configurations typical for recrystallization and for grain growth. Most of the twins present after grain growth have been originally formed during recrystallization, consistent with Burke’s quote given in the introduction.[2] A few of them seem to appear during grain growth, notably near triple junctions, which would be consistent with both the early growth accident theory,[1,2,40] and with the recent previously quoted 3D-HEDM results.[92] On the other hand, in the present experiments, it could also be due to a 2D section artifact (twins formed in a recrystallizing grain below the surface which only appear when the grain has grown enough to reach it). Meanwhile, many twins disappear at the observed surface, by different mechanisms which will be discussed in more detail in Section V, and not only because their host grain is being consumed by the neighbors.

5 Evolution of Pre-existing Twins

Figure 6 shows an EBSD map series of a 304L steel sample submitted to successive annealing steps near 950 °C in the SEM chamber (same device and same material as in Figure 5). Figure 6(a) was taken just after full recrystallization (similar to step (f) of Figure 5) and the following maps show how twin and grain boundaries evolve in the early stages of grain growth. Two black crosses have been placed as fixed landmarks to help visualize which boundaries are moving and which are not.

Fig. 6
figure 6

Grain growth after static recrystallization in the 304L steel, followed using an in-SEM chamber heating stage and EBSD mapping in between each annealing step. The initial sample was hot deformed and then annealed near to 950 °C to complete static recrystallization (a) and then further annealed for different times to make grains grow: (b) 10 s, (c) 20 s, (d) 30 s, and (e) 50 s, cumulated times. Grain boundaries with a disorientation higher than 10 deg are plotted black, Σ = 3 and Σ = 9 CSL boundaries (within the tolerance of Brandon’s criterion[66]) are plotted red and green, respectively (Color figure online)

Full size image

Straight (thus most likely coherent) twin boundaries are very stable, staying immobile throughout the annealing series (typical example encircled on top of Figure 6(a)). The reason for that is obvious, considering their very low energy and mobility.[97,98] It has been demonstrated that the grain boundary character distribution measured after extended grain growth in different FCC metals is inversely correlated with the grain boundary energy,[99,100,101] and that those lying in {111} planes are predominant.[79] The coherent twin boundaries, once formed, are kept and expand as their hosting grain is growing because there is very little thermodynamic driving force to make them disappear owing to their low energy. Even if submitted to a driving force of some kind, they would hardly move because of their low mobility. But Monte Carlo and phase field simulations of grain growth with grain boundary energy dependent on misorientation suggested that energy matters more than mobility in the evolution of the grain boundary population.[102] In the sequence shown in Figure 6, the only situations where coherent twin boundaries disappear are when they belong to a grain being consumed by a neighbor, or when they are associated to an incoherent segment that moves.

Contrary to coherent segments, incoherent twin boundaries formed previously are indeed observed to move inside the growing grains. They move in the direction of their curvature center and either adopt a stable configuration (upwards single arrow), or vanish in a grain boundary (downwards single arrow), or collapse and disappear (double arrow). There is no wonder that incoherent twin boundaries behave so differently compared to coherent ones. The energy of coherent twin boundaries is only 2 to 5 pct that of HAGBs, while incoherent twin boundaries have a roughly 10 times higher energy as compared to coherent ones (Table II). The energy of incoherent twin boundaries is very much dependent on their plane inclination, so that some incoherent twin boundaries have energy values close to that of HAGBs.

Table II Interfacial Energy Values for FCC Metals, from Literature
Full size table

The difference in energy between coherent and incoherent twin boundaries directly derives from the energy dependence on grain boundary inclination that is known for long[104] and came also out from ab initio calculations.[97] Because of the energy anisotropy of Σ = 3 twin boundaries, they tend to adopt particular crystallographic planes, the coherent {111} of course, but beyond them, other planes of relatively low energies (notably {112} or close to it).[40,105,106,107,108] It is worth noticing that the structure of incoherent twin boundaries is particular in the sense that they are composed of Shockley partial dislocations in successive {111} planes. The elastic distortion fields associated with individual dislocations that interact with each other, and the energy of individual dislocations is minimized when they pile up in particular planes, notably {112} at 45 deg from their gliding plane; 45 deg is the angle between (111) and \( (1\bar{1}2) \).

The mobility of Σ = 3 twin boundaries also depends very much on their plane inclination.[109] Molecular dynamics simulations showed that mobility increases with deviation from {111}.[110] This result is noticeably consistent with the boundary migration mechanisms by step motion, the step density increasing with the deviation from {111}. Remarkably, incoherent twin boundaries have higher mobility (one order of magnitude) as compared to general HAGBs[98]; this makes them be kind of an exception since low mobility usually goes along with low energy (e.g., for coherent Σ = 3 twin boundaries and for LAGBs). The high mobility of incoherent twin boundaries is consistent with their dislocation-based nature, as they may migrate through collective glide of the partial dislocations.[108] In the experiment of Figure 6, they obviously move under thermal activation, driven by their curvature or possibly by their interaction with the free surface, but they can also move under the action of an applied stress as shown by in situ TEM indentation testing of nano-twinned copper films by Wang et al.[111] It seems likely that the high degree of elastic anisotropy across twin boundaries could provide a driving force for their motion.

On the other hand, triple arrows in Figure 6(d) show how an incoherent segment can be formed when two crystallites of the same twin variant born at different places of a given matrix crystal (here at triple junctions next to each other) expand and meet each other as the whole grain is growing. This scenario made based on 2D observations would deserve further confirmation in 3D, but nevertheless provides a quite clear picture of a possible reason why so many incoherent twin boundaries are formed during recrystallization. A recrystallization front is tortuous, the same twin variant of a recrystallizing grain can form at different places and produce incoherent segments later when the twin crystallites merge with each other. The quadruple arrow is another example of twin coalescence accompanied with the formation of incoherent segments as the grain is growing (black boundary moving leftwards). Similar processes but involving crystallites of different twin variants lead to the formation Σ = 9 CSL boundaries.[112]

To end with the description of the different types of events visible on Figure 6, the area encircled at the bottom of Figure 6(c) highlights the stability of configurations involving the boundaries of several twin variants within a grain. Let us remind here that two of the four possible Σ = 3 twin variants within a grain form a Σ = 9 boundary (plotted green on Figures 5 and 6) as they meet. Another example of the stability of systems made of several twin variants can be found in the grain at the top of Figures 5(d) through (j).

6 How to Control Twin Amounts in Thermomechanical Processing?

One motivation to control the amount of twin boundaries in a microstructure could be for the sake of GBE, and then the referred goal is to build up a network of special boundaries as dense and interconnected as possible. Controlling the formation and evolution of twin boundaries is the main mean for achieving this goal.[8,10]

The whole literature on GBE converges towards cyclic processes, where the material must be slightly deformed and then annealed for short time. The main mechanism promoted at each cycle of such a route is Strain-Induced grain Boundary Migration (SIBM), the strain level must be low, below that required for nucleation of recrystallized grains. The process itself is also called “strain annealing” and must be regarded as a recrystallization mechanism since it is driven by the consumption of stored energy. The formation of twins by boundary decomposition mechanisms has been reported to be predominant under such conditions, in copper and several nickel base superalloys.[51] Some level of strain is required to initiate grain boundary migration/decomposition and thus the formation of twins during the subsequent annealing. Interestingly enough, Burke already noticed in 1950[2] that «deformations too slight to cause recrystallization resulted also in the appearance of many detached twins», where the term recrystallization should probably be understood as nucleation of new recrystallized grains. Once the stored energy has been consumed, another deformation cycle is required to revive the process during the next annealing. The migration of the incoherent twin boundaries under the stress applied during deformation or the remnant internal stresses are likely to provide a driving force to meet other twin boundaries and form stable configurations which will contribute to the build-up of an interconnected network of low-CSL boundaries.

Li and Tin[113] confirmed, in Inconel 600 alloy, that strain annealing and dynamic recovery promote the formation of twin boundaries and showed that recrystallization (both static and dynamic) mostly generate random grain boundaries to the detriment of special ones. Indeed, if recrystallization nucleation is activated, then new grains form and consume the deformed matrix and its twins. Increasing strain above the threshold required for nucleation of new grains increases the nucleation density, leads to smaller recrystallized grains, lower number of twins per grain (since the latter is decreasing with the recrystallized grain size) and thus no chance to form an interconnected special boundary network. Another reason to apply a limited strain at each cycle is that the twin boundaries accumulate dislocations during deformation,[20,21] and could lose their twin character.

The annealing stage of a GBE process should not be too long either, because after some time the strain energy is consumed, the boundaries stop moving, and new twins cannot nucleate any longer, but on the other hand incoherent twin segments can keep moving (as shown in Figure 6) and make the twin density decrease. It is also very obvious, notably from the results shown in the present paper, that the material should never enter the grain growth regime, otherwise many incoherent twins would be lost.

It is worth noticing that the mechanism to be promoted for the sake of GBE has strong similarities to that leading to the appearance of overgrown grains in nickel base superalloys when low levels of stored energy are involved. Those are recrystallized grains characterized by a high density of twins, which grow from sparse nuclei,[114] driven by the consumption of stored energy.[115,116,117]

Now comes the opposite question: how, or is it possible, to get rid of twins by thermomechanical processing? The motivation could be to avoid the presence of large flat coherent boundaries which have been shown to be preferential fatigue crack nucleation sites.[11,12,13,18] It sounds difficult, since twins form naturally in high density during recrystallization. On the other hand, grain growth leads to much lower densities since only few twins form under this grain boundary migration regime, and incoherent boundaries tend to disappear from the growing grains thanks to their migration. But the twin boundaries left after grain growth are mainly long flat coherent ones, which is detrimental with regard to fatigue crack nucleation. One route to be explored could be to go for recrystallization at very high temperatures, relying on the grain boundary energy anisotropy diminishing[118] and grain boundary roughening, but then short exposure times would be required to avoid getting too large grains, and there is little chance that the difference in energy between twin and grain boundaries would be small enough that twins would not be favored any longer. It could be worth checking also what would be the effect of applying an electric current since it has been shown that recrystallization and grain growth kinetics under Joule effect heating are different from those under radiative heating.[119] To date, it nevertheless sounds rather challenging to imagine processing routes which could suppress twins, without changing the chemical composition of the material to tune interfacial energies and grain boundary structures. Coming back to the example of nickel-based superalloys, increasing the cobalt content has been shown to decrease the stacking fault energy of the FCC Ni base matrix (40.1 ± 1.2 mJ.m−2, 33.3 ± 0.9 mJ.m−2 and 24.9 ± 0.5 mJ.m−2 in alloys with 5, 15 and 23 wt pct Co, respectively[120]). Higher twin densities can thus be reasonably expected in Ni base superalloys with higher Co contents.[121] The recrystallized microstructures shown in the two latter references, for alloys with 23 wt pct Co, nevertheless do not seem to exhibit particularly high twin densities compared to alloys with lower or no Co content (e.g., Inconel 718, Figure 3), or compared to pure Ni which has a 3 to 5 times higher stacking fault energy (Table II). To the authors best knowledge, literature is still missing from a rigorous comparison of twin densities in alloys of different composition and stacking fault energy, at the same grain size and at the same stage of recrystallization/grain growth processes.

7 State of the Art of Mesoscopic Models and Simulations Accounting for Twins

The notion of models or simulations accounting for twins gives rise to a large panel from very simple to deeply complex methodologies. Of course, the simple models (phenomenological ones) are usually easy to be used but have very limited predictive power (often limited to the experimental data used for their calibration). The more complex ones tend to cover a much larger range of validity with accuracy but generally require large and complex calculations. Moreover, modeling of twins could be discussed at the scale of one interface (micro) or at the polycrystal scale (meso) and with regard to different mechanisms and aspects (modeling of twins appearance, interactions between twins, description/definition of twin boundary properties as mobility and energy, impact of the twins on the global grain boundary network evolution during recrystallization or grain growth, etc.). Some of these topics, largely discussed in literature, are briefly summarized in the following. Due to the restrictions in length and time scales, microscale simulations, such as those based on molecular dynamics[41,97,98,122,123] are, generally speaking, scarcely usable to discuss the behavior of an important number of twins or grains. Then, the focus is on mesoscopic approaches.

Most mean field models proposed so far aim at describing twin boundary frequencies as a function of grain size. Both Gleiter’s and Pande’s approaches are consistent with the growth accident model and gave rise to two well-known equations for twin density prediction. In Gleiter’s works, an atomistic view of the twin interface, following the mechanism described by Fullman and Fisher,[40] combined with classical nucleation modeling leads to an expression for the twin formation probability P, defined as the ratio between the frequencies of nuclei with twin orientation and with the original matrix orientation, to quantify annealing twin formation. The first version of this probability function[42] and the ad hoc parameters are given in Eq. [8] and Table III. It must be highlighted that if all parameters of Eq. [8] have physical meanings, their determination for a given material is difficult, which mitigates the direct applicability of Gleiter’s model. However, interesting discussions have emerged from this formalism, like the dependence on twin density on temperature as discussed in Reference 124.

Table III Parameters in the Mathematical Formulation of Gleiter’s Model, Eq. [8]
Full size table
$$ P = e^{{\frac{{\left( {\gamma_{t} + \gamma_{ik}^{t} - \gamma_{ab} } \right)\left( {Q - kT\ln \left( {\frac{\Delta G^\circ }{kT}} \right)} \right)}}{{\left( {\gamma_{t} + \gamma_{ik}^{t} - \gamma_{ab} + \frac{{\pi \varepsilon^{2} h^{2} }}{{kT\ln \left( {\frac{\Delta G^\circ }{kT}} \right) - Q}}} \right)kT}}}} $$
(8)

Pande et al. proposed another mathematical model[74,125] to predict annealing twin density evolution during grain growth and provided an atomistic model, also based on the growth accident theory, afterwards[49] as a theoretical basis of this pseudo-empirical model. In this approach, since annealing twin nucleation and growth occurs during the motion of grain boundaries, the twin density is assumed to be totally linked to the grain size. More precisely, it is assumed that the increase in twin boundary number per grain is proportional to the product of the driving force and the resulting increase in grain size. Derived for the grain growth regime, i.e., with a driving force inversely proportional to the grain size, the latter assumption leads to a mathematical equation of the same form as the originally proposed one[74] to predict the twin density (NL, i.e., the number of twins intercepts per unit length) as a function of the mean grain size (D):

$$ N_{L} = K\gamma \frac{1}{D}\ln \left( {\frac{D}{{D_{0} }}} \right), $$
(9)

with \( K \) a constant, \( \gamma \) the grain boundary energy and \( D_{0} \) the minimum grain size for annealing twin formation. It must be emphasized that this model was shown to be consistent with a large amount of published experimental data.[3,42,126] Two limitations can nevertheless be raised concerning Pande’s model and these experiment vs model comparisons. First, the parameters \( K \) and \( D_{0} \) have no real physical meaning and can thus be seen as fitting parameters. Second, the comparisons are usually made on log–log scale plots, which strongly smoothes any possible deviation between the model and the experimental data.

None of Gleiter’s and Pande’s models accounts for the experimental observation that almost no twins are formed within the grain growth regime. To fill this gap and rely on the observation that the number of twins per grain on the contrary remains constant, mostly determined by the number of twins present in the largest grains at the end of recrystallization (i.e., those intended to grow during grain growth), another model has been proposed by Jin et al.[127] Derived from the classical Hillert’s grain growth mean field model, a mean field approach with only one fitting parameter, taking into account grain size classes and their evolution, was proposed in this work and shown to be able to predict the evolution of twin density as a function of the mean grain size in the Inconel 718 nickel base superalloy submitted to grain growth annealing.

A major drawback of the above-described mean field approaches is that topology is not described. Given the complex shapes of twins and of multiply twinned grains, full field approaches appear much better relevant.

At the mesoscopic scale, the terminology full field is classically used to describe numerical methods where the local behavior of the grain boundary network, i.e., the polycrystal topology, is taken into account in the simulations comparatively to mean field models where statistical quantities are discussed.

In an early attempt, Gerstman et al.[128,129] proposed a method for inserting twins in a 2D microstructure made of hexagon-shaped grains. A grain is randomly chosen, a portion of the grain is assigned the twin orientation, and the twin boundary is constructed. The obvious limitations of the approach are its 2D nature and the non-realistic grain shape it is based on. Coherent twin boundaries have then been inserted in a 3D polycrystal with better realistic grain shapes,[130] but in this work incoherent twin boundaries could still not be handled. Accounting for the complexity of twin topologies requires more advanced numerical frameworks to simulate twin formation and their evolution along with the overall microstructure evolution.

The numerical simulation of the behavior of different grain boundaries is multiscaled. As already mentioned, some works concentrate on the atomistic aspect of the behavior and formation of twin boundaries, while others concentrate at a mesoscopic level in order to predict the microstructural evolution of grain boundary networks. It is interesting to highlight that, as in microscopic approaches,[97,123] the way the twin boundaries are numerically taken into account in mesoscopic full field approaches is usually related to their energetics.

At the mesoscopic scale, the grain boundary can be parameterized by five macroscopic crystalline parameters: two defining the boundary plane unit normal vector and three for describing the misorientation between the neighboring grains. The main challenge in the study of grain boundary motion is the dependence of intrinsic grain boundary properties such as energy and mobility on these multiple structural parameters. Moreover, defining the energy and mobility of a crystalline interface experimentally[99,131] or numerically[97,98] is by far not straightforward.

In a full field context, simulations can be performed using probabilistic Monte Carlo Potts (MC),[132] Celullar Automata (CA),[133,134] MultiPhase Field (MPF),[135,136,137] Front-Tracking or Vertex[138,139], or Level Set (LS) models.[140,141,142,143] These numerical methods are currently used and developed by many researchers[144] and regularly compared for particular metallurgical mechanisms.[138,145,146] Of course, all the mentioned models have their own strengths and weaknesses. Probabilistic voxel-based approaches such as MC and some CA formulations are very popular. These models consider uniform grids composed of cells to model microstructure and stochastic laws to predict the motion of interfaces. These simulations are efficient in terms of computational cost and the scalability is excellent. On the other hand, deterministic approaches, based on the resolution of partial differential equations, are generally more accurate in the description of the involved physical mechanisms although they are numerically more expensive. For instance, front-tracking or vertex approaches are based on an explicit description of interfaces in terms of vertices. Interface motion is imposed at each increment by computing the velocity of a set of points. A major difficulty of these approaches is related to the complexity of handling all the possible topological events, such as disappearance and appearance of new grains, which is not straightforward, especially in 3D. Other deterministic approaches, also called front-capturing approaches, avoid these topological problems since they are based on an implicit description of the interfaces: the MPF and the LS methods. The major limitation of these two methods is generally the computational cost when used in a finite element (FE) framework. When dealing with anisotropy of grain boundary properties, which is an absolute requirement for handling twin boundaries, all these methods present, at this time, important limitations.

Indeed, if several full field studies of recrystallization and/or grain growth have been carried out with non-uniform grain boundary energy,[147,148,149] it must be highlighted the difficulties concerning a clear description of the grain boundary energy and accounting for its successive derivatives which have an impact on the capillarity driving pressure remain an unsolved issue in the state of the art.

Several anisotropic full field grain growth frameworks also exist based on LS and MPF approaches.[145,150,151,152,153,154,155,156,157,158] Of particular note is the relatively new MPF formulation used in,[143] which allows for both the definition of heterogeneous grain boundary energies and mobilities, and the MPF method applied in,[151] which shows very interesting results when considering microstructures made of grain boundaries of two types. However, both formulations suffer from inherent numerical instabilities when increasing the heterogeneity of the system. Concerning the LS method, Elsey et al.[156] define a grain boundary energy “per grain” and then use an ad hoc averaging operation to define the energy at the interface between two grains. They then solve the grain growth problem isotropically using the highest grain boundary energy, followed by a mathematical procedure to correct the evolution of the grain boundary network to take into account the presence of multiple boundary energies. This approach was also studied and validated in Reference 145. However, this framework is almost exclusively geometric and a seemingly arbitrary junction energy must be defined at the triple junctions in order to obtain the correct behavior of the system. Hallberg et al.[154] used another method which imposes isogonic point triple junctions and solves curvature-driven grain growth for heterogeneous grain boundary energies. Other very recent work from the same group[155] goes so far as to simulate on regular grids the full anisotropic case (misorientation and inclination-dependent grain boundary energy) using a LS formulation close to the one proposed in Reference 157 in FE context. In Reference 158 the formulation proposed in Reference 157 is applied to 2D single-phase polycrystals to explore the sensitivity of this numerical framework to variations in its numerical parameters as well as the effect that different grain boundary energy functions can have on the development of a material microstructure.

Overall, a reasonable questioning can still emerge from all the cited literature concerning the dependence of the grain boundary energy to the inclination of the boundary as well as the misorientation rotation axis. For example, the impact of the torque terms generated by inclination-dependent grain boundary energies is systematically neglected. As such, supplemental terms depending on both the boundary energy and the boundary geometry should probably be developed and integrated in the existing full field formulations in the coming years to aspire to a fully anisotropic formulation for grain growth enabling to describe properly coherent or incoherent twin interfaces.[159]

Another interesting topic which remains to be explored in full field simulations is the development of nucleation criteria for modeling the appearance of annealing twins during recrystallization. Studying the impact of the recrystallized front tortuosity suggested in Reference 53 will require full field simulations notably able to make a recrystallization front migrate in a stored energy field that can be heterogeneous at the intragranular scale. This by itself constitutes a numerical challenge.[160]

8 Conclusions

This paper summarizes the different mechanisms proposed for explaining the formation of annealing twins and emphasizes differences between those formed during recrystallization and those left in the microstructure after grain growth. The literature usually focusses on the formation of coherent twins, with the reduction in interfacial energy as a driving force. Not much has been proposed to explain the formation of incoherent twin boundaries and for them the latter energetic argument would be questionable since they have energies much higher than coherent ones and sometimes close that of general high-angle grain boundaries. Incoherent twin boundaries are in great proportions in recrystallized microstructures and almost absent after grain growth, notably because, owing to their high mobility, they move and vanish from the growing grains. On the other hand, very few twins are formed during grain growth under capillarity forces. The difference in twin topologies after recrystallization and after grain growth is such that it would justify calling them recrystallization twins and grain growth twins instead of referring to annealing twins as a whole.

The knowledge gained on twin formation and their evolution during thermomechanical processing allows for understanding why the works on grain boundary engineering converged to processing routes by cycling slight deformation and short annealing. The development of large multiply twinned domains with a density of interconnected twin boundaries is achieved by promoting strain-induced boundary migration (SIBM). Twins are formed along the tortuous migrating boundaries, and with a large fraction of incoherent segments arising from the coalescence of several twin crystallites of the same variant. Incoherent segments are highly mobile, both under thermal activation and under stress, which is likely to contribute to the formation of the targeted interconnected network of low-CSL boundaries. Once the stored energy has been consumed during annealing, another deformation and annealing cycle is required to revive the process. For the sake of GBE, nucleation of new recrystallized grains should be avoided since their growth would consume some of the formerly formed twins and related boundary network.

To validate mechanisms and to be able to generate digital microstructures with realistic twin topologies, further improvements are still required in modeling and simulation tools for microstructure evolution. Progresses have notably been made to account for the dependence of grain boundary energy on misorientation and inclination in recrystallization and grain growth models, but the description of this dependence itself still lacks from a general formulation. Numerical simulations will be a precious tool in the near future to revisit the proposed twin formation mechanisms and validate or invalidate them with regard to the resulting 3D topologies.