Modeling of Ti-W Solidification Microstructures Under Additive Manufacturing Conditions

Abstract

Additive manufacturing (AM) processes have many benefits for the fabrication of alloy parts, including the potential for greater microstructural control and targeted properties than traditional metallurgy processes. To accelerate utilization of this process to produce such parts, an effective computational modeling approach to identify the relationships between material and process parameters, microstructure, and part properties is essential. Development of such a model requires accounting for the many factors in play during this process, including laser absorption, material addition and melting, fluid flow, various modes of heat transport, and solidification. In this paper, we start with a more modest goal, to create a multiscale model for a specific AM process, Laser Engineered Net Shaping (LENS™), which couples a continuum-level description of a simplified beam melting problem (coupling heat absorption, heat transport, and fluid flow) with a Lattice Boltzmann-cellular automata (LB-CA) microscale model of combined fluid flow, solute transport, and solidification. We apply this model to a binary Ti-5.5 wt pct W alloy and compare calculated quantities, such as dendrite arm spacing, with experimental results reported in a companion paper.

1 Introduction

The Laser Engineered Net Shaping (LENS™) Process is an additive manufacturing (AM) technique for the fabrication of metallic parts, originally developed at Sandia National Laboratories in the 1990s. Parts are built in a layer-by-layer fashion as powder is injected into a melt pool created by a focused laser beam, which is moved in a specific pattern to build the desired part. LENS™ and other energy deposition-based AM processes have gathered interest because of their potential for producing parts with advantageous microstructural features,[1] unique structures,[2] and/or improved mechanical properties.[3] Additional abilities of such deposition processes include building of compositionally or functionally graded parts,[4] fully dense parts, and use in part repair.[5] Parts made from titanium alloys in particular, owing to its low density, high strength, and corrosion resistance, have the potential to be produced via LENS™ for applications ranging from biomedical to aerospace.[6] One of the biggest challenges in the use of AM processes is, however, the details of the relationships between processing parameters and the properties of the final part. While extensive research has been done in modeling of the molten pool and microstructure produced in welding operations, different process parameters, material properties, and forces acting on the molten pool in laser and electron beam-based deposition processes necessitate model extensions for AM conditions. The development of such a model for a given additive process is aided by a detailed understanding of similarities and differences between welding and AM conditions, and how the conditions affect development of the microstructure in the solidified material. The purpose of this paper is to present the first step in the development of a multiscale computational model of AM processes, with the goal of predicting details of the as-solidified microstructures and properties in metallic alloys. We focus on the LENS™ process for a specific alloy system.

There is a wide range of physical phenomena occurring during the deposition and rapid solidification of alloys created via LENS™ and similar beam-based deposition processes. As the laser is moved across the sample, a melt pool is created that involves not only the melted powder feedstock but also previously deposited layers. Heat transport through various modes in solid, liquid, and gas are important in determining the temperature field and molten pool dimensions.[7] Owing to the inherent asymmetry of the beam melting problem (particularly when beam motion is accounted for), there will be a significant location dependence of the thermal gradient and cooling rate; these temperature fields play a large role in initial microstructure formation and thus on the properties of the final part. Much of our detailed understanding of these fields come from applications of the finite element method (FEM), which has been used extensively to model them.[8,9,10,11,12,13] For solidification in the LENS™ process in particular, Hofmeister[8] used a combination of thermal imaging and finite element modeling to estimate cooling rates and thermal gradients in the molten pool for various sets of process parameters. Similarly, Wang and Felicelli[10] used a 2D finite element model to calculate temperature as a function of time in different regions of the molten pool for the deposition of a thin plate structure with a moving beam, a work later expanded to 3D by the same authors.[11]

While the role of fluid transport is sometimes neglected in the calculation of these temperature fields, the melt pool created in beam-based melting problems is highly dynamic.[14] Large temperature gradients, capillary forces, and Marangoni convection play important roles in its evolution as well as in the evolution of the corresponding temperature fields.[15,16] For example, the role of Marangoni convection in welding has been studied extensively[17,18,19] and several FEM-based models of coupled fluid and heat transport in weld pools that include Marangoni and buoyancy forces have been developed.[20,21,22] Such models typically used multi-layer meshes and solved the incompressible Navier–Stokes equations for fluid flow in the melt pool. Later models expanded on this work to include material addition, with the corresponding forces on the molten pool arising from powder injection.[23,24,25] More recently, Wei et al.[26] modeled a beam-based melting and solidification problem with fluid flow, heat transport, and solidification in order to study the effects of epitaxy on the grain growth and texture of multiple deposited layers. Acharya et al.[27] modeled a similar problem for scanning laser epitaxy use in part repair, investigating the role of process parameters and fluid transport on solidification conditions. Additionally, Morville et al.[28] used COMSOL Multiphysics^® to simulate the fluid flow, melting, and transient temperature conditions encountered during direct laser metal deposition. Another approach has been based on the use of the Lattice Boltzmann method (LB), which is an attractive method for solving this particular fluid transport problem (relative to Navier–Stokes algorithms) because of its ease of handling complex geometries,[29,30] ease of modeling the changing boundary conditions found in solidification[31,32] and its ability to model coupled fluid, heat, and solute transport problems.[7,31,33] Additionally, the method is computationally efficient and easily parallelized.[34,35] Körner et al.[7,36] used a thermal Lattice Boltzmann model for the combined heat transport, fluid flow, and phase change problem, for Ti-6Al-4V in a powder bed-based AM process.

The initial solidification is highly dependent on the temperature field and is important to the development of the as-solidified microstructure. By influencing the gas–liquid interface along with local cooling rates and thermal gradients, fluid flow can influence microstructural changes such the formation of stray grains,[37] the orientation of grains at the solidification front,[38] and the development of porosity and surface roughness.[39] Calculated thermal gradient G and solidification rate R values from either mathematical models or heat transport FEM-based models (with and without consideration of fluid flow) can be used to empirically determine microstructural quantities such as dendrite arm spacing,[40] or map pairs of G and R into zones of “columnar,” “equiaxed,” and “mixed” grain morphology.[41,42,43]

Cellular automata (CA) models of solidification, first developed by Rappaz and Gandin,[44] have successfully been coupled with process-scale models to simulate grain growth[43,45] as well as the growth of dendritic colonies within grains.[46] The CA used by Yin and Felicelli,[46] originally developed by Beltran-Sanchez and Stefanescu[47] based on the work of Rappaz, has been used to successfully model binary alloy solidification by others as well.[48,49,50] It has also been expanded into 3D and used for ternary alloy growth.[51] The coupled LB-CA model has recently been applied to model combined fluid flow, solute transport, and solidification problems for binary and ternary alloy systems.[33,52,53,54,55,56,57,58] Use of a CA for solidification has the advantage of computational efficiency over alternative approaches, such as the phase field method, but discretization error and grid effects are significant drawbacks. Corrections to minimize the grid effects that tend to occur in such models have been proposed[59,60,61] and utilized by many solidification models. Combinations of the phase field and cellular automata methods can be used to model multiscale solidification as well; for example, Tan and Shin[62] considers solidification of both grains (using a CA) and dendritic colonies (using phase field) in 2D at the appropriate length and time scales.

The present work uses a multiscale approach to model microstructure in a binary alloy (Ti-5.5 wt pct W) system, which was chosen because of its the potential for significant grain growth restriction based on its phase diagram.[63] We employed the commercial software package COMSOL Multiphysics^® to model the macroscale process as a simplified beam melting problem, considering the effects of fluid flow, heat transport, and temperature-dependent materials properties. At the microscale, information passed from COMSOL simulations is used to determine initial conditions, thermal gradients, cooling rates, and fluid flow velocities to be passed to a LB-CA model. The focus of this paper is on the application of the LB-CA model to the combined fluid flow, solute transport, and solidification for domains within the COMSOL-simulated LENS melt pool. In Section II, we present background information on solidification that motivates our choice of the model, which is described in Section III. Results are summarized in Section IV and comparisons to experiment are given in Section V, accompanied by a discussion of the validity of the model. Section VI presents conclusions and needs for future work.

2 Background

The development of the as-solidified microstructure in beam-based solidification processes depends on the temperature field, particularly the local thermal gradient G and cooling rate $\dot{T}$, as well as materials properties of the solidifying alloy. Assuming that the rate of heat transport in the solid is much faster than that of the liquid and that the thermal gradient ahead of the interface is very large, there will be a positive temperature gradient ahead of the solidification front and the latent heat released on solidification will be conducted back through the solid. This situation leads to constrained growth as described by Kurz and Fischer,[64] with a negligible thermal component to the undercooling ahead of the front. For binary alloy growth of an alloy with composition C ₀, these conditions lead to the development of a solutal boundary layer arising from the difference in liquidus and solidus composition at a given undercooling relative to the initial composition’s liquidus temperature $T_{L}^{{C_{0} }}$. The difference between the local temperature in the melt and the liquidus temperature at the local solute concentration is referred to as the constitutional undercooling. Perturbations of the originally planar interface can more effectively conduct away this boundary layer than a planar boundary and, provided a region of constitutional undercooling exists ahead of the solidification front, the planar interface will break down into long cells as the perturbations grow into the undercooled liquid. The surfaces of these cells may in turn become unstable and break down into secondary and/or ternary arms, depending on the solidification conditions.[65]

The radii of the perturbations that form cells or dendrites are limited by the solid–liquid surface energy, which serves to locally depress the liquidus temperature and works against solidification in regions of high curvature. We can represent this effect in a model by including an interfacial component to the total undercooling. The dendrite tip radius represents a balance (for a given set of conditions) between a sharp tip (which can most effectively conduct away the solutal boundary layer being formed in its wake) and a blunt tip (which has less solid–liquid interfacial area). Given the rapid rates of solidification in beam melting processes, the process of planar front breakdown and development of cells and dendrites is very common. In the case of the Ti-W system with low solute concentration (see Figure 1(a) for its phase diagram,[66]), the solute partition coefficient k, which describes the ratio of the liquidus to the solidus slope, is greater than 1; the equilibrium concentration of solute at a given undercooling for the solid phase will be larger than that for the liquid phase. Therefore, as the solid grows and absorbs solute, the solutal boundary layer will be depleted of solute relative to the initial alloy concentration. The region of the phase diagram focused on in this paper is such that the liquidus and solidus curves can be approximated as linear, as shown in Figure 1(b).

Fig. 1

(a) The equilibrium phase diagram for the Ti-W system. As a beta-isomorphous element, W exhibits mutual solubility with the high-temperature BCC phase of Ti. This combined with the large melting point difference between the two elements leads to a large range of temperatures over which solidification occurs. The alpha HCP phase appears at low temperatures. (b) The region of interest in the phase diagram for the solidification problem (highlighted in (A) with blue). Over this relatively narrow range of temperature and dilute W concentrations, the equilibrium liquidus and solidus are approximated as linear (Color figure online)

As detailed by Rappaz and Gandin,[44] the solidification morphologies depend on the interplay between the local thermal gradient G and cooling rate. For the planar front to become unstable and break down into cells, G must be small enough for development of the region of constitutional undercooling ahead of the front and the solidification rate must be fast enough such that the more efficient solute diffusion around the perturbation tips overcomes the interfacial energy penalty of their curvatures, allowing them to grow into cells rather than melting back into the liquid. At even faster solidification rates (large $\dot{T}$) and smaller G, the surfaces of the cells themselves are unstable and a columnar dendritic microstructure is formed. At the fastest solidification rates and smallest G, nucleation in the undercooled zone dominates over growth of the original grains and a transition to an equiaxed dendritic microstructure occurs. Kurz and Fischer[64] detail the typical ranges of G and $\dot{T}$ values in binary alloy solidification that leads to different morphologies. Additionally, the cells and dendrites that form tend to be finer with increasing cooling rate.[64,67,68] Solidification during the LENS™ process occurs under locally high cooling rates and large thermal gradients; experimental and modeling work on LENS™ in Hofmeister et al.[8] shows G on order of 10⁵ K/m and $\dot{T}$ between 10³ and 10⁴ K/s, with the larger values closer to the melt pool bottom. The multiscale model of LENS™ solidification in Yin and Felicelli[46] yielded similar values, while the solidification maps by Bontha et al.[42] show thermal gradients and solidification velocities on par with or larger than those in the previous works. These conditions would be expected to heavily favor planar interface breakdown and the development of cells and dendrites,[65] and experimental work on rapid solidification of β-Ti alloys has shown the dominant microstructural feature to be long columnar dendritic grains and/or cellular structures heavily textured with the 〈001〉 directions aligned with the heat flow direction.[69,70,71] While these large thermal gradients typically give rise to a strong dendritic or cellular microstructure, reduction in G and $\dot{T}$ near the top of the melt pool may give rise to mixed columnar and equiaxed structure.[42] As shown later, the current model is capable of simulating all of these morphologies (cellular, dendritic, and equiaxed) under appropriate conditions.

While the primary driver in the development of solidification microstructures are the effects described above, there are other phenomenon that must also be taken into account to best model molten pool development and solidification in the LENS™ process. Specifically, the effects of epitaxial growth[26] as well as the movement of the laser beam[9,13,72] can have a significant effect on the dendrite orientations. Epitaxial growth leads to preferred initial growth in prescribed directions, which may not align with the large thermal gradients. The moving beam leads to an anisotropic melt pool where G and $\dot{T}$ vary significantly based on melt pool location.[73,74] Reheating and remelting of previous layers, the different conditions encountered in each layer, and solid-state phase transformations in previously deposited layers will also play roles in microstructural development.[1] While these factors are not fully accounted for in the present work, the basic formalism described next is capable of modeling these effects.

3 Approach

Owing to the different physical phenomena at varied length and time scales of this problem, as described above, a multiscale approach is needed. In the long term, our goal is to couple fluid flow, heat flow, and solute transport to a solidification model to more completely describe the process. In this paper, we focus on a first step toward this goal: the coupling of a microscale model of solidification with a continuum-level simulation of the melt pool, which will provide boundary conditions for the microscale. At the continuum scale, the commercial software package COMSOL Multiphysics^® is used to model heat absorption with heat and fluid transport for a simplified beam melting problem. At the microscale, a LB-CA model simulates solute and fluid transport during solidification.

3.1 Process Modeling

The sets of conservation equations for energy, momentum, and mass equations are coupled and solved in two dimensions using the fluid flow and heat transfer modules of COMSOL Multiphysics^®. The fluid flow module accounts for buoyancy and the Marangoni effect assuming laminar flow and a Newtonian fluid, while the heat transport module considers conduction, convection, and radiation as modes of transport. Linear variation of surface tension with temperature through the thermocapillary coefficient γ, as well as temperature-dependent model input values for density, thermal conductivity, and heat capacity for both liquid and solid β Ti-5.5 wt pct W are considered in the model. They are estimated as described in Section IV. The Marangoni effect was incorporated in a similar manner as in the COMSOL simulations of Morville et al.,[28] being modeled with the relation $\eta \partial \varvec{u}/\partial y = \gamma \partial T/\partial x$, in which η is the dynamic viscosity of the fluid (equivalent to the kinematic viscosity multiplied by the fluid density), $\partial \varvec{u}/\partial y$ is the variation in fluid velocity in the direction perpendicular to the free surface, and ∂T/∂x is the temperature gradient along the free surface.[75]

Three values of the beam power were used in the COMSOL simulations: 183 W, 259 W, and 367 W (referred to from this point on as “low,” “middle,” and, “high”). The beam diameter was 500 μm for each power, with a Gaussian distribution of energy. The model simulates a stationary beam melting problem, with a fixed molten pool geometry (estimated based on SEM images) that is varied as a function of input power.[63] Owing to these assumptions, calculated values for temperature and fluid flow fields are used here only to estimate the thermal gradients, cooling rates, and fluid flow fields at short times near the melt pool walls after turning off the energy source. These estimated values will serve as initial and boundary conditions for the microscale fluid flow and solidification model, detailed in Sections III–B and III–C.

3.2 The Lattice Boltzmann Method

The Lattice Boltzmann Method (LBM), an evolution of the lattice gas cellular automata, provides an alternative to solving the full Navier–Stokes equations in fluid dynamics problems.[29,76] LBM models the fluid as a series of fictitious fluid particle distribution functions $f_{i} (\varvec{x},t)$ at each grid point $\varvec{x}$ and time t, which removes the noise inherent to the particle-based lattice gas model.[29,77] Being based on both microscale particle behavior while satisfying mesoscale conservation and evolution equations for fluid, the LBM provides a way to bridge the two scales[78,79] and has accurately simulated benchmark fluid flow problems (e.g., Couette flow).[29,76,80] In the two-dimensional applications described here, an LBM time step consists of solving the discrete Boltzmann equation for the distribution functions on a square lattice via successive collision and propagation steps. In the present work, the D2Q9 lattice is used (see Figure 2). A second set of distribution functions, represented by $g_{i} (\varvec{x},t)$, is used to model the distribution of solute. These distribution functions undergo collision and propagation steps on the same LB lattice as the fluid and are coupled to the fluid particle distribution functions through the macroscopic velocity u. The details of the LBM to solve coupled fluid and solute transport problems are well documented in the literature[52,53,54,55,56] and are shown briefly in the Appendix. The LBM for fluid and solute transport was verified by Zhou for several coupled fluid and solute transport problems in 1D and 2D.[81] We note that the LBM is also capable of simulating turbulent flow, though it typically requires very fine grids and/or alternations to some of the equations.[29]

Fig. 2

The D2Q9 lattice used in the Lattice Boltzmann model. The velocities are denoted by the vectors e _i with the magnitudes given in Eq. [A1]

Coupled transport of fluid flow, heat, and solute would not be possible to simulate accurately in the present model for molten titanium alloys, which is limited to a single grid spacing and time step, owing to the disparate rates of heat and solute transport. The thermal Lattice Boltzmann method for coupled heat and incompressible fluid flow fields has been used previously to simulate convection problems[29,82,84,84] and been coupled to cellular automata (CA) to simulate the solid–liquid phase change for pure materials.[7,31,32,36,79] If it is assumed that the fluid is incompressible, viscous heat dissipation is negligible, and no work is done by the external pressure, an additional set of distribution functions can be introduced to the model for heat transport. These are analogous to those for solute (the heat is advected as a passive scalar), but include a heat diffusivity, internal energy density, and a heat source term in place of solute diffusivity, concentration, and the solute source term, respectively. The inclusion of temperature-dependent force terms for effects such as capillarity, wetting, or buoyancy allows the coupling of the energy evolution equations into those for fluid.[7,85] Use of the thermal Lattice Boltzmann method with a second set of distribution functions to model the internal energy density has been shown to agree with analytical solutions for natural convection, lid-driven convection in square cavities, and other benchmark fluid dynamics problems.[78,82,85,86]

Though the present work is focused on microstructure evolution and not the process-scale melt pool dynamics, we are exploring such a model for consideration of the coupled fluid flow and heat transport problem at the appropriate scale. This approach has a notable advantage over the present COMSOL model in that it enables direct tracking of the solid–liquid interface, allowing for direct coupling to the microstructure evolution model.

3.3 Cellular Automata (CA) for Solidification

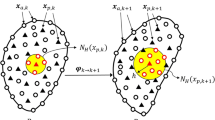
In our approach, solidification of an initially liquid domain is calculated on the same grid and at the same time step as the LBM calculations. Three cell types are considered: solid, liquid, and interface. Solid cells act as impenetrable boundaries for the fluid flow, while fluid flow is allowed within interface cells. Liquid cells cannot directly border a solid cell—a layer of interface cells is always present. Once an interface cell has completely solidified, it is changed to solid and neighboring liquid cells become new interface cells. As in the original CA of Rappaz, the amount of solidification in an interface cell over a given time step is calculated as a function of the local undercooling.[44] In this CA, however, the calculation is not given by an analytical function of solidification velocity with undercooling but rather by assuming that the driving force for free energy is dominated by local interface kinetics. The driving free energy, G _K , is proportional to an interfacial velocity V for the cell. The fundamental equations for these quantities are[87]

$$ \frac{{\Delta G_{K} }}{{RT_{I} }} = \frac{{\left( {1 - k^{\text{eq}} } \right)}}{{m_{L}^{\text{eq}} }} \left( {T_{m}^{\text{Ti}} + m_{L}^{\text{eq}} C_{L} - T_{I} } \right) $$

(1)

and

$$ V = fV_{0} \left( {\frac{{ - \Delta G_{K} }}{{RT_{I} }}} \right) $$

(2)

in which R is the gas constant, T _I is the local interface temperature in the cell (determined via the macroscale temperature fields as functions of time), and C _L the local solute concentration in the cell (as calculated via LBM). $T_{m}^{\text{Ti}}$, k ^eq, and m ^eq _L are the melting point of pure solvent (titanium here), the equilibrium liquidus slope, and the equilibrium solute partition coefficient, respectively, as determined from the phase diagram (Figure 1). The parameters m ^eq _L and k ^eq are assumed to be constant with low solute concentrations, as indicated in Figure 1(b). The change in solid fraction Δf _s is related to the interface velocity V, Δx, Δt, and the angle $\varPhi$ between the interface normal and the grid axis direction via

$$ \Delta f_{s} = \frac{V\Delta \cos \left( \varphi \right)\Delta t}{\Delta x} $$

(3)

This equation for ΔG _K can be rewritten in terms of the local equilibrium solute concentrations $C_{L}^{\text{eq}}$ and $C_{S}^{\text{eq}}$ as

$$ \frac{{\Delta G_{K} }}{{RT_{I} }} = C_{S}^{\text{eq}} - C_{L}^{\text{eq}} + C_{L} (1 - k^{\text{eq}} ) $$

(4)

These equilibrium concentrations, in turn, are functions of the cell’s local temperature and the phase diagram, as described below. An additional term, related to the local interface curvature $\kappa$ (calculated via the algorithm given in Beltran-Sanchez and Stefanescu,[88]) Gibbs–Thomson coefficient $\varGamma$, and a function characterizing the crystal anisotropy (the function for a crystal with fourfold symmetry used by Jelinek et al.[35] is used here) is added to the expression for $C_{L}^{\text{eq}}$to account for the local depression of the liquidus arising from the solid–liquid interfacial energy,

$$ C_{L}^{\text{eq}} = \frac{{T_{I} - T_{m}^{\text{Ti}} }}{{m_{L}^{\text{eq}} }} + \frac{{\kappa \varGamma \left( {1 - \delta \cos (4(\phi - \theta )} \right)}}{{m_{L}^{\text{eq}} }} $$

(5)

in which $\theta$ is a given grain’s “preferred” orientation, and $\delta$ a coefficient characterizing the surface energy anisotropy. The solute concentration of the solid formed is given by

$$ C_{S}^{eq} = k^{eq} C_{L}^{eq} $$

(6)

If a non-zero change in solid fraction is calculated, the appropriate amount of solute must be added or withdrawn from the cell via the LBM solute distribution functions. This is calculated by solving the solute balance in the cell; note that if f _s approaches or reaches 1, the solute must instead be added or removed from cells that still contain appreciable liquid.

$$ S = \frac{{\Delta f_{s} (C_{L} - C_{S}^{\text{eq}} )}}{{1 - f_{s} - \Delta f_{s} }} $$

(7)

If $k^{\text{eq}}$ > 1 (as in the case of the Ti-W system), there is an additional constraint that solidification cannot occur if the amount of withdrawn solute leads to a subzero concentration. To reduce the deleterious effects of grid anisotropy on the growing colonies, the approach taken by Zhan et al.[61] is used in which solidification of “clusters” of cells are evolved in tandem, effectively expanding the local neighborhood of the solidification from the typical Moore or Von Neumann neighborhoods and allowing the colonies that are misaligned with the grid to maintain their preferred orientations.

To account for nucleation of new grains, a probabilistic approach, similar to that of Rappaz, is taken in which the change in local undercooling over a given amount of time is related to the probability that nucleation has occurred in the cell. If the probability is larger than a randomly generated number, a new grain is nucleated. The equation used for the density of nuclei as a function of undercooling, as well as the equation for the nucleation probability, is described in more detail in Yin and Felicelli.[46] However, for the COMSOL simulations of LENS solidification at the melt pool wall, the thermal gradient is large enough that such nucleation did not occur at a rate comparable to that of columnar growth from epitaxial colonies at the wall. The resultant microstructures are thus dominated by the growth of epitaxial dendrites nucleated along the boundary.

4 Results and Discussion

Because of sparse thermochemical data on the Ti-W system, many of the materials constants had to be approximated. For the estimation of specific heat, density, and viscosity as functions of temperature as required for COMSOL, the values for a different molten titanium system with more available data (Ti-6Al-4V) were used. The assumption is that such properties for the Ti-5.5W system would be similar, which is reasonable if the material is treated as homogenous continuum as in the COMSOL simulations. For the solidification model, reasonable values from the previous solidification models or order-of-magnitude estimates were made when parameters were unknown for the Ti-5.5W system. The constants used in the solidification model and sources for the values and/or equations used to obtain them are described in Table I, along with temperature-dependent equations for Ti-6Al-4V properties. Please see Figure 1(b) for definitions of the parameters used to characterize the phase diagram. The phase diagram and solidification model in general are performed using mole fraction of W; the results are converted to weight percent of W for the figures. All solidification model results used the Ti-W phase diagram, though for the multiscale simulations, the temperature and fluid flow data are from COMSOL results for Ti-6Al-4V.

Table I Parameters Used in the Macro- and Microscale Models

4.1 Model Examples

To test the solidification model, the thermal gradient G was held constant at 100,000 K/m and cooling rate Ṫ varied to examine dendrite tip undercooling as a function of tip velocity. The mesh size was set to 0.4 μm, and the time step to 0.64 μs. For each Ṫ, the model was run until the rate of advance of the tip was near the steady state Ṫ/G (adding rows to the simulations as necessary), at which the interface temperature was determined. Due to discretization, these temperatures and velocities were not exactly constant and error bars are included to account for the uncertainty in the exact values. At larger Ṫ, the steady-state dendrite tip velocities are larger and a corresponding larger driving force for solidification is necessary to maintain the steady state. Since this requires a larger undercooling, the tip temperature decreases with increasing cooling rate as shown in Figure 3, which shows the same trends as the analytical model of Kurz, Giovanola, and Trivedi for constrained alloy growth.[89] However, the present work used different equations, model parameters, and was limited to two dimensions, so the exact dependence of tip velocity and undercooling achieved here and that calculated by the analytical model is not directly comparable. For many solidification velocities, somewhat smaller undercooling is needed to achieve the same dendrite tip velocity here relative to the analytical prediction. This suggests that the choices for f and V ₀ in Eq. [2] may be large, leading to a small overestimation of local solidification rates

Fig. 3

The present model prediction for the dendrite tip velocity–undercooling relationship of a single Ti-5.5 weight percent dendrite at steady state during constrained solidification. At larger solidification velocities, a larger undercooling relative to the equilibrium liquidus temperature for Ti-5.5W is necessary to drive solidification. The thermal gradient was held at 100,000 K/m for all data points

To validate the combined solute transport, solidification, and fluid flow model, we compared the case of a single nuclei growing in a melt at constant undercooling (20 K below $T_{L}^{{C_{0} }}$) with and without fluid flow. The mesh size was set to 0.4 μm and the time step to 0.64 μs, with a 301 by 301 grid and 40,000 total times steps of simulation time. The left, top, and bottom boundaries were held at constant solute concentration C ₀. The right boundary is held at a constant concentration gradient to mimic the fact that the domain is semi-infinite and at some point far away from the dendrite, there is no concentration gradient. A constant velocity boundary condition on the left boundary maintained a fluid flow field from left to right, diverging to the left of the growing dendrite and converging on its right. In Figure 4, we compare a growing dendrite for the case without fluid flow (a) and that with fluid flow (b). In the figure, we see that fluid flow has a clear impact on the dendrite symmetry; the arm growing opposite the direction of the fluid flow has solute supplied to it via the fluid flowing from the left boundary, and the solute-depleted boundary region that formed as the solid grew was advected away by the flow. Thus, the arm growing opposite the direction of the fluid flow grows more rapidly than the other arms. The opposite arm has its growth stunted, as the solute-depleted region tends to build up near the convergence region of the fluid. The arms transverse to the direction of flow grew somewhat faster as well, though not nearly as much as the arm opposite the flow direction. This effect is confirmed by other similar LB-CA models for dendritic growth in binary alloys.[52,53,55]

Fig. 4

Solidification of a single dendrite in a melt of constant undercooling (20 K below the liquidus temperature for Ti-5.5W) after 0.0256 s. (a) In the absence of fluid flow, solute transport is limited to diffusion. The dendrite is symmetrical as the dendrite arms grow into the liquid. (b) With fluid driven at 0.001 m/s from left to right, solute transport via both diffusion and advection alters the symmetry of (A) as the arms grow at different rates depending on their orientation relative to the fluid flow direction. The color bar corresponds to the concentration of W in wt pct

4.2 Microstructure Simulation

In this section, we investigate the variety of microstructures the present model is capable of simulating. At relatively small thermal gradients and solidification velocities, nucleation of new grains ahead of the primary solidification front becomes significant. Homogeneous nucleation of new grains is modeled as a Gaussian process that is a function of undercooling and is characterized by three parameters[46,90]: the maximum nucleation density N _max, the mean nucleation undercooling ΔT _N , and the standard deviation of the nucleation distribution T. These parameters are typically unknown and difficult to predict, particularly when heterogeneous nucleation sites are activated much more easily.[91] They are often roughly estimated; for example,[90] used ΔT _N = 5 K, ΔT = 0.5 K, and N _max = 10¹² m⁻³ for Al-3 wt pct Cu.[92] used a Gaussian distribution for both surface and volume nucleation of Al-7 wt pct Si, placing ΔT _N at 10 K. Experimental observations by Basak and Das[93] estimated ΔT _N to be near 0.2 ΔT _m in a pure metal. In the present calculations, the ΔT _N and ΔT _σ values from Boettinger[91] and N _max of 5 × 10¹² m⁻³ were used. As shown by Dong and Lee,[90] the choice of parameters will have a significant impact on the location of the columnar to equiaxed transition within the solidification maps in Bontha et al.[42,65] Unmelted particles and other melt inhomogeneities, which are particularly an issue with high melting point alloying additions such as tungsten, would be expected to play a significant role in nucleation and will be addressed in future work with a process model that consider such factors.

To model epitaxial growth of multiple dendritic colonies, liquid domains were initialized with the bottom wall 5 K below $T_{L}^{{C_{0} }}$. Heterogeneous nucleation sites covering this wall are all initially active, with randomly chosen solid fractions and orientations near or aligned with the heat flow direction. Domains were chosen to have constant G and V (where $V = {\raise0.7ex\hbox{${\dot{T}}$} \!\mathord{\left/ {\vphantom {{\dot{T}} G}}\right.\kern-0pt} \!\lower0.7ex\hbox{$G$}}$). With V = 0.0002 m/s and G = 50,000 K/m, a relatively coarse columnar dendritic microstructure results (as shown in Figure 5(a)). At a faster solidification rate (V = 0.001 m/s) and the same thermal gradient, a transition to a microstructure dominated by grains nucleated ahead of the initial columnar dendritic front is observed (see Figure 5(b)). There were no exact values for V or G at which this transition occurs, rather a gradual trend toward nucleated grains dominating the microstructure over the epitaxial columnar grains as G was reduced and V increased. This observation is on par with that observed by Dong and Lee[90] in directional solidification modeling. Under the conditions encountered in AM processes, this columnar to equiaxed transition may occur near the top of the molten pool in the latter stages of solidification. However, owing to the limitations of the present macroscale model, the present work is limited to the early-stage solidification near the molten pool bottom. The more rapid solidification rate and larger thermal gradient near the molten pool walls lead to finer columnar dendrites as shown in Figure 5(c), or cellular structures as shown in Figure 5(d). Nucleation at the small length scale of these structures did not occur in the model. Growth of both cells and dendrites under AM conditions has been observed experimentally,[93] and the transition from dendrites to cells at fast cooling rates has been modeled via CA previously.[46]

Fig. 5

Variations of microstructure depending on solidification conditions. (a) represents coarse columnar dendrites (cooling rate 10 K/s, thermal gradient 50,000 K/m) and (b) A mixture of columnar and equiaxed dendrites nucleated from the bulk liquid (cooling rate 50 K/s, thermal gradient 50,000 K/m). Under the more rapid solidification conditions and larger thermal gradients as would typically be encountered in the LENS process, more fine columnar dendrites as in (c) (cooling rate 2500 K/s, thermal gradient 250,000 K/m) and columnar cells as in (d) (cooling rate 4000 K/s, thermal gradient 250,000 K/m) would be more typical. The color bar corresponds to the concentration of W in wt pct

4.3 Multiscale Modeling of LENS Microstructure

The COMSOL simulations for Ti-6Al-4V, despite using three different values for power (183 W (“low”), 259 W (“middle”), and 367 W (“high”)) and melt pool size, yielded the same general fluid flow pattern as shown in Figure 6. The general pattern of the flow consists of two large convection cells on the left and right sides of the melt pool, with some more minor fluid flow in the central portion of the melt pool just below the energy source. The formation of similar convection patterns, with two main cells driven by surface forces and slower fluid flow below the region of energy absorption, has been seen in two-dimensional models of welding and AM processes and arises primarily from the Marangoni effect.[18,23,27,28] The size and relative velocity of the fluid within these convection cells were observed to have significantly larger surface velocity at higher beam powers because of the larger thermal gradients present under those conditions. For the microstructure results presented here, we consider two regions at the melt pool walls that are aligned with the maximum temperature gradients (the 0.1 mm squares highlighted in Figure 6 for the low-power case). The analogous regions to those of Figure 6 are used for simulation of the solidification for the each of the three power levels, though the exact X and Y coordinates will vary as the size of the melt pool changes with beam power. For region “A,” just underneath the large convection cell, the fluid flow is parallel to the wall. To model this region, the fluid is initialized everywhere to the COMSOL value for the magnitude of the fluid flow in the region for the given power. Since there is additional solidification occurring on both sides of this location, periodic boundary conditions are used for the LB fluid flow, solute flow, and the solidification CA. The top boundary is held at a fluid velocity in the positive X direction from COMSOL. Immediately above region “B,” fluid flow is perpendicular to the interface, diverging to the left and right near the wall. For this region, the top boundary is held at a constant velocity in the negative Y direction as determined with COMSOL, while the left and right boundaries are subject to zero velocity gradient conditions to allow the fluid to flow out either side. The left and right boundaries are also subject to a zero-concentration gradient boundary condition. In both cases, the top boundary is held at a constant concentration C ₀, providing a source of solute for the growing solid. The solidification at other regions along the solidification boundary was not modeled here.

Fig. 6

COMSOL simulation results for temperature (a) (in K) and fluid velocity magnitude (b) (in m/s) under conditions representative of the LENS process. The black outline represents the fixed molten pool geometry considered. Due to the effects of the strong Marangoni convection, the temperature field is not symmetric about the region where beam absorption occurred. This leads to significant differences in thermal gradient and fluid flow pattern in Domain A, represented by the red square, and Domain B, represented by the blue square (Color figure online)

While the local thermal gradients and cooling rates vary as a function of laser power for a given location, they also vary strongly from the effects of convection in the melt pool. Because of the large convection cell, the thermal gradients ahead of the solidification front at location “A” are small relative to the rest of the molten pool. The cooling rates are also relatively slow as heat from the top of the melt pool is advected into this region by the fluid flow from the adjacent cell. At location “B,” the thermal gradient is very large as a result of the heat being advected downward and the fast heat conduction out through the solid. The cooling rate is initially slow owing to the latent heat release and the advected heat from above, but as the Marangoni convection weakens following shutoff of the heat source, more rapid cooling occurs. As shown in the table below, the expected trend of decreasing thermal gradient and cooling rate with increasing laser power generally holds for location “A,” but at location “B” the slowest cooling rate occurs for the middle power. At higher powers, increased fluid flow advects heat toward the sides and away from the bottom melt pool wall.

Using the temperatures predicted by COMSOL at multiple times following shutoff of the power source, we approximated the temperature as a function of time at the tops and bottoms of the two solidification regions following laser shutoff. It was observed that for all three input powers and both domains, cooling started slowly (generally in the first 0.02 seconds) and then tended to occur at a constant rate. The thermal gradient was at its largest at the time of laser shutoff, then tending to decrease or remain constant. For this reason, parabolic functions were fit to the first 0.02 seconds for the top and bottom temperatures, and linear functions after the 0.02 second mark. It was assumed that the temperature gradients over these small domains are linear, and cells between the top and bottom walls were assigned temperatures interpolated from the two wall values depending on their relative locations in the domain. Figure 7 shows an example of these functions for the low-power case in region “A.”

Fig. 7

Local temperature as a function of time following energy source shutoff at the bottom (solid line) and top (dashed line) of Domain A for the COMSOL simulation performed at low power. The thermal gradient and cooling rate across the domain depend on position and time

The modeled microstructures for region A under the low, middle, and high powers (along with the total time taken for 37.5 and 97.5 pct domain solidification) are shown in Figure 8. Chosen values for the length and time scales in the model were Δx = 2.857 × 10⁻⁷ m and Δt = 3.2543 × 10⁻⁷ seconds. As expected, the time to solidification increased with increasing power because of the decrease in cooling rate and corresponding decrease in steady-state dendrite tip velocity. With the decreased cooling rate, the solute concentrations within the dendrites increased as well; the smaller tip velocities required smaller local undercooling values, which correspond to higher values for C ^eq_S . A finer microstructure (smaller dendrite arm spacing) was formed in the low-power case relative to the middle and high powers—another function of cooling rate. Relative to “control” simulations with no fluid transport and solute transport in the liquid by diffusion only, there was negligible differences in solidification time, dendrite arm spacing, or concentration profiles in the liquid and solid, largely because there is little to no vertical movement of the fluid, and the horizontal movement of the fluid with the periodic boundary condition does not effectively mix the solutal boundary layer ahead of the solid. This condition is somewhat similar to that encountered by the tips perpendicular to the direction of the fluid flow in the example in Figure 4. In addition, the velocity at the solidification front itself tends toward zero as it was driven from the top boundary rather than from the sides. As a result, the region of fluid that is moving fast enough to effectively mix the solute is always ahead of, not at, the solidification front.

Fig. 8

Model results for solute concentration profile in Domain A microstructure. Arrows represent fluid velocity, for cells that have not completely solidified. At partial domain solidification (a-c), more time is needed to reach the same solidification threshold with increasing input power. At complete domain solidification (d-f), this is again true; it is also seen that a larger solute concentration in the dendrite arms is present as well with increasing input power. The color bar corresponds to the concentration of W in wt pct

The domain B microstructures at 99 pct solidification are shown in Figure 9 alongside their control counterparts that included no fluid transport. Chosen values for length and time scales were x = 2.55 × 10⁻⁷ m and t = 2.60 × 10⁻⁷ s in these calculations, which results in the same relaxation parameters for fluid and solute as those in domain A. These structures are more significantly affected by the fluid flow as it is initially flowing toward the front, which leads to a scenario similar to that of the dendrite tip facing the fluid flow shown in Figure 4; solute is supplied to the front by the incoming solute-rich fluid as the solidification process consumes it. For the low-power case, the fluid flow is not strong enough to have an effect and for the high-power case, the local undercooling near steady-state is already near the equilibrium solidus value. Under this condition, adding more solute will not increase the driving force. Because of this effect and the relatively small fluid velocity, the difference between the low-power microstructure and its control counterpart is small and only visible at the domain bottom (corresponding to early solidification, prior to reaching larger undercooling values). The 99 pct solidification threshold is reached at approximately the same time for calculations with and without fluid flow. The high-power case, with its faster fluid flow, shows a larger region near the bases of the dendrites with larger concentration than its control counterpart. However, it too has the majority of solidification taking place near the limit of constitutional undercooling and the 99 pct threshold is reached only slightly faster with the inclusion of fluid flow. The middle power, with the slowest solidification rate, is examined more closely at three different times in the solidification process in Figure 10. The fluid, initially moving in the direction of the front, is pushed back as it begins to advance and forced out the side. The fluid goes from a primarily vertical flow to more horizontal, and the fluid flow at the wall tends toward zero. However, the time period in which the fluid flow was supplying solute from the constant concentration top boundary to the front was long enough that a significant difference in early solidification rate and solid concentration is seen.

Fig. 9

Model results for solute concentration profile in Domain B microstructure. (a-c) represent the microstructure without fluid flow for the low, middle, and high power, while (d-f) represent the microstructure with fluid flow at the same power. The most notable difference is the tendency for more solute to get incorporated into the dendrite arms, as fluid from the top boundary is driven toward the solidification front allowing some mixing of the solutal boundary layer. The color bar corresponds to the concentration of W in wt pct

Fig. 10

Solute concentration profile for Domain B at the middle input power. (a-c) represent the solute concentration field as well as the fluid velocity field for various times, while (d-f) represent the same times on a control run done in the absence of fluid flow. The early solidification occurs faster and at higher solute concentrations with fluid flow, as it allows mixing of the solutal boundary layer with the addition of relatively solute-rich fluid from the top boundary. The color bar corresponds to the concentration of W in wt pct

4.4 Comparison to Experiment

By plotting solute (W) concentration at the tops of the dendrite arms, and dividing the domain width by the number of concentration peaks, the primary dendrite arm spacing for each domain and power can be calculated. The results are shown in Tables II and III with an example given in Figure 11(a). In general, the arm spacing tended to be smaller for Domain B, which was to be expected as the cooling rates in that position of the melt pool tended to be larger .

Table II Thermal Parameters from the Macroscale Simulations

Table III Predicted Dendrite arm Spacing Under Different AM Processing Conditions

Fig. 11

(a) Variation in solute concentration as a function of X position in the domain, for three different Y positions in the modeled microstructure for Domain B. The peaks represent dendrite arms, while the valleys represent the solute-depleted interdendritic liquid, allowing an estimate of primary dendrite arm spacing. As the dendritic front advances, the solute concentration within the dendrite arms decreases as the local temperature decreases and the solidification front approaches a steady-state velocity. (b) EDS results on a Ti-5.5W as-deposited sample fabricated via LENS, showing a similar concentration profile at the same length scale.[63]

The spacing, as is often the case,[90]) was non-uniform, making the calculation of primary dendrite arm spacing subject to some statistical error. Values of the estimated model parameters, such as the Gibbs–Thomson and diffusion coefficient, would be expected to alter the dendrite radii as well as the spacing, though variation of these parameters was not considered in the present work. Comparing Domain B arm spacing values to those from Domain B control runs with no fluid flow yielded little to no distinct differences, though some variation did occur. Since fluid flow seemed to only have an effect on the very early stages of solidification, any differences in spacing would likely be negligible closer to the tops of the domains as steady state is approached; the “extra” or “missing” arms would either coalesce or form later on.

Figure 11(a) shows the solidified concentration profile from Domain B at high power for three Y positions. Closer to the bottom of the domain (light gray line), the solid concentration of W within the dendrite arms was large as the early solidification occurred at higher temperature and therefore higher solute concentration. As solidification proceeded, the solidification front approached a steady-state undercooling close to the constitutional limit (e.g., the concentration within the dendrite arms approached C ₀).

The simulated concentration fluctuations can be compared to experimental data of the concentration variation of W collected by EDS, as described in Mendoza et al.[63] and shown in Figure 11(b). The experimental concentration profile showed variations in solute concentration with periodicity that is quite close to what we predict in the simulations (about 7 µm). While the predicted magnitudes in the concentration profile are quite close to the experimental W concentrations, there are uncertainties that hinder the direct comparison between the two results, both from inadequacies in the model and in our ability to identify whether the simulated and experimental data correspond to the same location in the melt pool, i.e., that the solidification has the same thermodynamic and flow conditions. The potential errors in the modeling are many. In addition to the specific solidification model, the present work does not account for the impingement of dendrites in one domain on those in another as the beam moves and the grains grow. The dendritic colonies in the fastest growing grains could dominate the sample’s volume and be most likely to show up on an EDS line scan; we simply selected two random domains and modeled the solidification conditions and microstructures, not necessarily the ones in the most favorable positions for growth. The present model also does not account for the deposition of new material, building of multiple layers, the energy source motion, and is limited to the COMSOL approximation of steady-state molten pool conditions. While location-dependent values of thermal gradient and cooling rate were observed in the simulated melt pool, these additional factors are also sources of large variation of thermal conditions within real molten pools in AM processes. To fully understand the variation of thermal conditions within a molten pool under a given set of process parameters, the relative importance of all of these factors would need to be accounted for. A more complex process model, such as a thermal Lattice Boltzmann model accounting for the moving beam and tracking of the solid–liquid interface, coupled to a model of the impingement of grains during solidification, would be necessary to more accurately model the solute concentration values within the dendritic colonies. These caveats aside, however, we are quite encouraged at the ability of the LB-CA model to predict the behavior of AM dendritic microstructures.

5 Conclusions and Future Work

The current microscale LB-CA model was able to reproduce realistic columnar dendritic and cellular microstructures under the conditions expected in LENS solidification based on COMSOL simulation results. The correct general trends in solidification rate and morphology were achieved with variation of solidification conditions. The results of the COMSOL process-scale simulations show that convection in the melt may play a significant role in the temperature gradients and cooling rates that develop; the solidification at different locations within this molten pool would be occurring under vastly different temperatures and fluid flow fields. The LB-CA modeled microscale solidification with fluid flow based on the COMSOL results, from which it was shown that fluid flow parallel to the interface fails to effectively mix the solutal boundary layer and approaches zero at the wall, leading to a negligible effect on solidification. Fluid flow in select locations in which the fluid is brought in from the center of the melt pool may lead to locally increased solidification rate and concentration variations arising from more effective mixing of the solutal boundary layer. However, fluid flow from the center of the melt pool also brings in heat, which may slow the solidification rate and negate this effect. The primary effect of fluid flow appeared to be in its alterations to the local thermal gradients and cooling rates in the melt pool, which in turn alter local solidification behavior. The fluid flow tended not to have a direct impact on the solute transport, as its orientation was generally parallel to the primary solidification front.

Comparison of the modeled dendritic colonies to EDS line scan results on the same alloy shows that the predicted primary dendrite arm spacing of 5-15 μm is accurate, though the EDS values of solute concentration within the dendrite arms and interdendritic regions are not an exact match with the model as it did not account for several processes (such as solid-state diffusion in reheated layers) that are known to occur. To further build on this work, a process-scale model that explicitly tracks the interface and can directly pass temperature fields to the microscale model is needed, which would allow for the solidification problem to be modeled more accurately and for a larger region of the melt pool. A concurrent multiscale model, in which the solidification model and process-scale heat and fluid transport model interact in a concurrent way, would be expected to improve the accuracy and variety of conditions that can be modeled. Modeling the solidification of grains instead of the individual dendrites has been shown to be feasible for AM processes[76] and would provide information that is likely to have a larger impact on the understanding of the mechanical properties of produced parts. Other potential future steps include expansion of the model to 3D, inclusion of multiple layer deposition and effects of epitaxy, deviation from local equilibrium compositions and phases, along with inhomogeneities in the melt such as unmelted particles. In short, while the present results are an important first step, there is much yet to accomplish before having a truly predictive AM process model.

Appendix: Lattice Boltzmann Method Details

For the D2Q9 lattice as shown in Figure 2, the fluid density distribution function $f_{i} ({\mathbf{x}},{\text{t}})$at each lattice site at position $\varvec{x}$ and time t has 9 components. The corresponding unit vectors for velocity are given as follows:

$$ e_{i} = \left\{ {\begin{array}{*{20}l} {(0,0)} &\quad {i = 1} \\ {( \pm c,0)} &\quad {i = 2,3,4,5} \\ {( \pm c, \pm c)} &\quad {i = 6,7,8,9} \\ \end{array} } \right. $$

(A1)

where c is the lattice speed $\Delta x/\Delta t$. We use a square lattice with constant lattice spacing Δx and time step Δt. These distribution functions, over a given time step, undergo successive collision and propagation steps. During the propagation step, the particle distributions located at position Δx at time t are moved to position $\varvec{x} + \varvec{e}_{\varvec{i}}$ at time $t + \Delta{t}$ by

$$ f_{i}^{in} \left( {\varvec{x} + \varvec{e}_{\varvec{i}} , t + \Delta t} \right) = f_{i}^{out} \left( {\varvec{x}, t} \right) $$

(A2)

in which the distribution at an arbitrary site moving in the i direction moves to the next lattice site in that direction. Superscripts “in” and “out” refer to the functions going into and out of the collisions at time t, respectively. A key assumption to the LBM is that during the collision step, the fluid at each site evolves toward its equilibrium distribution, i.e.,

$$ f_{i}^{\text{out}} \left( {\varvec{x}_{\varvec{i}} , t} \right) = f_{i}^{\text{in}} \left( {\varvec{x}, t} \right) + \frac{1}{{\tau_{f} }}\left( { f_{i}^{\text{eq}} \left( {\varvec{x}, t} \right) - f_{i}^{\text{in}} \left( {\varvec{x}, t} \right)} \right) $$

(A3)

in which the equilibrium distribution is given by

$$ f_{i}^{\text{eq}} \left( {\varvec{x}, t} \right) = \omega_{i} \rho \left( {1 + \frac{{{\mathbf{e}}_{i} \cdot \varvec{u}}}{{c_{s}^{2} }} + \frac{{(\varvec{e}_{i} \cdot \varvec{u})^{2} }}{{2c_{s}^{4} }} - \frac{{\varvec{u}^{2} }}{{2c_{s}^{2} }}} \right) $$

(A4)

The effects of the flow in each direction of the distribution functions are weighted by

$$ \varvec{\omega}_{i} = \left\{ {\begin{array}{*{20}c} {{\raise0.7ex\hbox{$4$} \!\mathord{\left/ {\vphantom {4 9}}\right.\kern-0pt} \!\lower0.7ex\hbox{$9$}}} & {i = 1} \\ {{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 9}}\right.\kern-0pt} \!\lower0.7ex\hbox{$9$}} } & {i = 2, 3, 4, 5} \\ {{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {36}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${36}$}}} & {i = 6, 7, 8, 9} \\ \end{array} } \right. $$

(A5)

Here, the commonly used BGK approximation replaces the collision operator as a single relaxation time τ _f for fluid, which is related to the viscosity ν as follows:

$$ \tau_{f} = 3 + \frac{1}{2} $$

(A6)

In these equations, c ²_s is the speed of sound, given by c ²/3. At each lattice site, conservation of mass and momentum give the macroscopic fluid density ρ and velocity u, given by

$$ \rho = \mathop \sum \limits_{i} f_{i} $$

(A7)

and

$$ \varvec{u} = \frac{1}{\rho }\mathop \sum \limits_{i} \varvec{e}_{\varvec{i}} f_{i}, $$

(A8)

respectively. We note that if the next lattice site contains no fluid, the directions of the distribution functions are reversed such that they will “bounce back” into the liquid on the next time step.

As the method approximates an incompressible Newtonian flow, these equations are only accurate for Mach numbers much less than 1 (the Mach number here is defined as $|\varvec{u}|/c_{s}$). Körner et al.[7] We note that a body force term F _i could be added to the collision equation to simulate the effects of an external force, such as buoyancy or surface tension,[7,77] which is not considered in the model shown here.

As shown in the previous work, analogous collision and propagation equations can be solved for solute transport coupled to the fluid flow via the fluid velocity $\varvec{u}$. The solute transport problem is solved on the same lattice with the same time step as the fluid flow, characterized by solute distribution functions $g_{i} ({\mathbf{x}},{\text{t}})$ that collide and propagate on the same grid as the fluid. It is assumed that these functions are passively advected by the fluid; they are coupled to the fluid flow problem via the velocity $\varvec{u}$ at each grid point, but do not in turn affect the fluid flow field. The collision and propagation equations for solute are

$$ g_{i}^{\text{in}} \left( {\varvec{x} + \varvec{e}_{\varvec{i}} , t + \Delta t} \right) = g_{i}^{\text{out}} \left( {\varvec{x}, t} \right) $$

(A9)

and

$$ g_{i}^{\text{out}} \left( {\varvec{x}_{\varvec{i}} , t} \right) = g_{i}^{\text{in}} \left( {\varvec{x}, t} \right) + \frac{1}{{\tau_{s} }}\left( {g_{i}^{\text{eq}} \left( {\varvec{x}, t} \right) - g_{i}^{\text{in}} \left( {\varvec{x}, t} \right)} \right) + \omega_{i} S $$

(A10)

respectively. In Eq. [17], S is a term representing the change in the liquid’s solute concentration over the time step (calculated as a function of the solidification process, as described below). The equations for the equilibrium solute distribution functions and solute relaxation parameter are given by

$$ g_{i}^{eq} \left( {\varvec{x}, t} \right) = \omega_{i} \rho \left( 1 + \frac{{{\mathbf{e}}_{i} \cdot \varvec{u}}}{{c_{s}^{2} }}\right) $$

(A11)

and

$$ \tau_{s} = 3{\text{D}} + \frac{1}{2} $$

(A12)

The solute diffusivity “D” is considered to vary as a function of temperature; therefore, the relaxation parameter will vary slightly among different locations in the simulation domain. The macroscopic solute concentration at a given point is calculated as

$$ C = \mathop \sum \limits_{i} g_{i} $$

(A13)

If the velocity field is set to zero everywhere, purely diffusive solute transport can be considered, while if the solute diffusivity is very small, τ_S approaches 1/2 (very slow relaxation toward equilibrium) and purely advective solute transport can be modeled.[99] By performing the collision and propagation steps consecutively for both fluid and solute, the coupled transport of both quantities can be modeled.

Although the present work does not use the thermal Lattice Boltzmann method, if it is assumed that the heat is passively advected by the fluid, the equations for coupled heat and fluid transport are very similar to those of fluid and solute transport. A gravity-buoyancy force term may be introduced into the fluid collision equation using the Boussinesq approximation that density is a linear function of temperature in the force term, though the fluid is still considered incompressible with constant properties elsewhere in the model.[78] Such a body force would have the basic form

$$ F_{i} = 3w_{i} \varvec{e}_{i} \varvec{g}\beta (T - T_{0} ) $$

(A14)

in which $\varvec{g}$ is a dimensionless vector representing gravity, $\beta$ is a coefficient of thermal expansion, T is a local temperature (calculated from the internal energy distribution functions), and T ₀ a reference temperature. Note that this would drive fluid with a temperature less than T ₀ downward from gravitational forces, while fluid above T ₀ would have a force in the opposite direction. This temperature-dependent force term couples the fluid flow field to the temperature field, and the fluid velocity $\varvec{u}$ in turn exerts influence on the equilibrium energy distribution at each grid point as it did for the solute distribution. To model AM processes via the thermal Lattice Boltzmann method, capillary and thermocapillary forces at the liquid–gas interface would be necessary as well.