Abstract
Press-hardened boron steel has been utilized in anti-intrusion systems in automobiles, providing high strength and weight-saving potential through gage reduction. Boron steel spot welds exhibit a soft heat-affected zone which is surrounded by a hard nugget and outlying base material. This soft zone reduces the strength of the weld and makes it susceptible to failure. Additionally, different welding regimes lead to significantly different hardness distributions, making failure prediction difficult. Boron steel sheets, welded with fixed and adaptive schedules, were characterized. These are the first experimentally determined residual stress distributions for boron steel resistance spot welds which have been reported. Residual strains were measured using neutron diffraction, and the hardness distributions were measured on the same welds. Additionally, similar measurements were performed on spot welded DP600 steel as a reference material. A correspondence between residual stress and hardness profiles was observed for all welds. A significant difference in material properties was observed between the fixed schedule and adaptively welded boron steel samples, which could potentially lead to a difference in failure loads between the two boron steel welds.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Press-hardened boron steel (22MnB5) is classed as an ultra-high-strength steel (UHSS) consisting of a significant proportion of martensite, with an ultimate tensile strength (UTS) of up to 1500 MPa.[1] The steel has been utilized in the automotive industry in structural and anti-intrusion components such as B-pillars, bumper reinforcements, roof, and side rails.[1,2,3] The main attraction of using martensitic steels is the weight reduction, achieved through gage reduction, and increased passenger safety it provides.
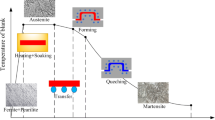
Boron steel in its as-delivered form consists of ferritic-pearlitic microstructure.[4,5] The as-delivered steel is usually austenitized at 1173 K and 1223 K (900 °C and 950 °C) for 5 to 10 minutes[5,6,7] and then quenched and formed in a single step in a die. Due to the high strength, press-hardened boron steel exhibits poor cold formability compared to other steel grades;[2] hence, a hot forming process is used to produce the martensitic phase transformation and desired part shape in one step.
As mentioned, boron steel has found an important application in the automotive industry. A major joining method in the automotive industry is resistance spot welding, with several thousand welds made on a single car. During spot welding, the weld and surrounding material are exposed to a wide range of temperatures, from the melting point at the weld center to ambient temperature in the base material (BM). As a consequence, the resistance spot weld (RSW) exhibits varying microstructures with corresponding varying material properties. The area directly underneath the electrodes at the sheet–sheet interface experiences the highest temperature, where the metal exceeds melting temperature and rapidly solidifies upon cooling (due to the water-cooled electrodes), leaving a hard weld nugget. A decreasing temperature gradient extends outward from this area (in the length as well as thickness direction), resulting in altered microstructures, known as the Heat-Affected Zone (HAZ). Particularly for boron steel RSWs, there is a steep gradient of material properties in the HAZ.[8]
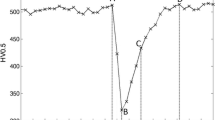
RSWs of the UHSS steel family exhibit unique hardness profiles compared with lower strength grade steels. The RSWs are characterized with high hardness values in the nugget and outlying BM, and a sudden drop in the area between these regions, as indicated in Figure 1. The cause for this sudden drop has been established to be due to tempering of the parent martensitic microstructure.[9,10,11]
Hardness profile of press-hardened boron steel spot weld with schematic of RSW work-piece. Adapted from Ref. [8]
The microstructural differences between the HAZ and nugget/BM are an influencing factor on failure; however, the location of the HAZ plays an important role as well.[12] The sharp notch tip of a spot weld, located at the weld nugget edge where the sheets start to separate, may cause a stress concentration when the weld is loaded. The difference in material properties between the HAZ and nugget/BM may enhance the stress concentration.[12] Therefore, it is crucial to characterize the gradients of material properties that occur through a spot weld.
Traditionally, spot welds are produced with a fixed weld schedule, utilizing a fixed amperage for a set amount of time. This type of weld schedule is usually established for a specific steel type and thickness range. A recent development is adaptively controlled welding. Such a system continually adjusts the weld current and time in reference to a master resistance curve. This master curve is calculated from previously stored current, voltage, and resistance values of known acceptable welds. The current and time are therefore continuously adjusted to keep the parameters as close as possible to the master curve, resulting in consistently acceptable welds.[13]
Predicting failure of press-hardened boron steel welds presents a unique challenge. While welds in non-martensitic materials exhibit a gradual decline in hardness from the nugget to the BM, martensitic welds show a soft HAZ surrounded by a hard nugget and outlying BM. It is this mechanical mismatch between the hard nugget/BM and soft HAZ which causes the HAZ to be a critical area, with reduced mechanical properties.[14] Additionally, the rapid heating and cooling cycles experienced by the steel could potentially lead to significant induced residual stresses, which could affect the loading response of the weld. In order to understand failure of the welds, it is critical to understand the material property variation caused by welding, such as the induced residual stress and microstructural gradients. This paper attempts to characterize the aforementioned properties to improve understanding of boron steel spot weld failure.
1.1 Experimental Methods for Measuring Residual Strain
To ensure correlation between hardness and residual strain, measurements must be performed on the same spot weld. Therefore, a non-destructive method of measuring residual strains is sought, whereafter the weld will be sectioned for hardness testing.
Non-destructive residual strain measurement methods include electron, X-ray, and neutron diffraction. Due to the strong interaction between electrical charges, electrons have a very small penetration depth in heavy (large atomic number) materials; hence, the technique is more suited for measuring very thin samples (<100 nm).[15] Neutrons and high-energy synchrotron X-rays have similar penetration depths, in the order of tens of millimeters.[16] With similar penetration depths, the choice between neutron and synchrotron X-ray diffraction comes down to the geometry over which measurements are made, known as the gage volume shape. Due to the diffraction angle being ~90 deg for neutron diffraction, one obtains a near cubic gage volume. Compared to neutron diffraction, the low scattering angles (~10 deg) used in synchrotron X-ray scattering lead to a very elongated gage volume.[17] In the 1.5-mm-thin automotive gage welded joints used in this project, the elongated gage volume would lead to averaging of both the top and bottom layers, leading to spatial resolution deterioration and difficulty in obtaining residual strains. Thus, the neutron diffraction technique was selected. For an introduction to residual strain measurement techniques through neutron diffraction, the reader is referred to the excellent work by Hutchings et al.[16]
1.2 Determination of Strain-Free Reference Parameter
The measurements of the internal strains, and hence the residual stresses, are based on a comparison of the measured lattice plane spacing with a reference value (d 0 or sin θ 0). During welding, temperature gradients extend out from the point of highest temperature and cause changes in solute content and microstructural gradients, which may cause a steep variation in the d 0 spacing. Hence, it is not recommended to use a single global reference parameter for welded specimens. Indeed, the estimation of a reference is the biggest challenge for scattering methods in welds.
It is possible to relieve a region from the constraint of the surrounding macroscopic stress field, and thereby measure d 0. An example of such a technique is extracting a reference comb from the weld under investigation through electrical discharge machining (EDM). It is assumed that the teeth of the comb are made free from the constraint of the surrounding material and are essentially strain-relieved regions.[18] The teeth may be more closely spaced in regions where it is expected that steep gradients in residual strain may occur. It has been shown, however, that significant variations occur in the direction parallel to the length of the teeth.[18] Therefore, when using combs to obtain the reference parameter, it is recommended to measure as close to the teeth ends as possible. Multiple measurements of the teeth ends are also recommended for more accurate reference estimates.
If the comb method is to be applied to the work presented in this paper, a comb would have to be machined out after the initial neutron diffraction experiments and re-measured at a later date. Experimental time to measure combs was not afforded for this work, and hence the comb method was not employed. Additionally, it is very difficult to embed the gage volume in the sample.
An elegant alternative solution to finding the d 0 distribution is assuming a state of plane stress in the work-piece. A common assumption for thin welded plates, as is the case for the work-pieces investigated in this paper, is a state of plane stress.[19,20,21,22] Using this plane-stress assumption, a d 0 (or sin θ 0) value is applied at each measurement location to force the normal stress to zero. The in-plane stresses, calculated with the same d 0 value, are thus corrected. It is possible that there may be some through-thickness stresses present (for example, from the electrode tip during cooling); however, given the plate thickness (1.5 mm) compared to the in-plane dimensions (40 × 120 mm) of the work-piece, a plane stress assumption is reasonable. As will be shown later, the d 0 distribution will also give an indication of microstructural changes (or pseudo-strain) through the weld.
1.3 Relationship Between Hardness and Residual Stress
Hardness measurements of the investigated welds were used as an additional tool to understand the residual stress distributions of the welds. During the welding process, the initial microstructure of the steel work-piece will transform when heated and cooled. These phase changes, linked to changes in crystal structure, are associated with transformation strains.[15] These transformations may be regarded as modes of deformation, with the surrounding matrix phase accommodating the transformation product.
Transformations may occur in two ways. The first is the displacive mechanism, where the new structure is produced through a deformation of the parent microstructure and may be associated with martensite. The second is the reconstructive mechanism, involving diffusion of atoms leading to a volume change. This mechanism may be associated with ferrite. The displacement occurring from a martensitic transformation may cause the surrounding material to be under additional compressive stress. The ferrite phase, which is softer than the martensitic phase, will hence deform plastically. Compressive stresses can thus be accommodated.
The measured hardness values give an indication of changing microstructures and hence may indicate how the residual stresses have been accommodated.
2 Experimental Method
2.1 Materials
The material, designated as 22MnB5, was supplied by Tata Steel as 1.5-mm-thick unhardened steel sheets. The hot forming process was performed at WMG on a 500 tonne Enefco press with matched tooling faces. The process was performed in accordance with Mohr.[2] The as-delivered boron steel was coated with a 20-μm-thick layer of protective zinc, which prevents oxidation of the steel during press hardening.[7] It has been shown, however, that the subsequent zinc oxides have detrimental effects on the final welds;[23] hence, the layer of oxides was removed through sand blasting after the hot forming stage, as is the typical industry practice.
Spot welds were also produced on 1.5-mm-thick galvanized DP600 steel sheets, also supplied by Tata Steel. DP600 is a dual-phase steel consisting of ferrite and 15 to 20 pct martensite.[24,25] The coating was not removed before spot welding, due to the fact that heat treatment of DP600 was not necessary and hence oxides were not present. Again, this is in accordance with industry practice. The DP600 steel is well documented and provides a ready source from which to verify experimental results. The steel provided valuable insight in relation to the neutron diffraction experiments, due to its martensite content and the effect of the ferrite phase.
2.2 Producing Spot Welds
Spot welding was performed with a Matuschek[26] welding control system and ARO[27] servo-controlled spot welding gun. For the boron steel, two spot weld configurations were utilized: one with fixed welding parameters and another welded through adaptive control. The fixed weld schedule was obtained from an automotive OEM, which was specifically developed, and optimized, for welding boron steel. This schedule consisted of two pulses; the first pulse at a set current and time, with a short “off-time,” followed directly by a second pulse consisting of higher current and longer weld time.
For the adaptive welding trials, the master resistance curve was created by producing spot welds at increasing current and weld times until expulsion. Once expulsion is reached, the control system stores the recorded values and uses the master curve as a boundary for the welding parameters.
It was decided that exposing the DP600 steel to similar fixed welding parameters to the boron steel would aid in making comparisons between the two, as the two steel types are exposed to the same current for the same amount of time and are the same thickness.
Before proceeding to residual strain measurements, peel testing was performed on sacrificial parts to ensure button pull-out failure occurred consistently. It was also checked that the weld nugget diameters conformed to the automotive standard of 4 to 5√t,[28] where t is the sheet thickness. The tests were performed to the ISO 10447:2007 specification.[29]
2.3 Residual Strain Measurement
Residual strain distributions were determined using non-destructive neutron diffraction at the SALSA (Strain Analyzer for Large-Scale Applications) beam line at the Institut Laue-Langevin (ILL), Grenoble.[30] Three perpendicular strain measurements were made along the radial, hoop, and axial directions, as shown in Figure 2. The radial and hoop directions are in the sheet plane and the axial direction is out-of-plane. The residual strains were mapped, and the residual stresses were subsequently calculated as a function of position from the weld center. Measurements were taken on the 211 plane, as recommended by the ISO 21432:2005 standard.[31] The 211 plane peak was found at 89.1 deg.
Radial collimators were used as the defining optics on both incident and diffracted beams, effectively creating a sampling gage volume of 1.2 × 1.2 × 2 mm3. Due to the allocated beam time, residual strain measurements were taken at 1 mm intervals. The scan line was taken at depths corresponding to the sheet mid-plane at 0.75 mm above and below the sheet–sheet interface, shown as the green line in Figure 3. Due to the sampling gage volume, an average strain through the sheet thickness was measured per measurement point. The measured residual strain and hardness results for both the top and bottom plates showed similar values and distributions; hence, only the results for the top plate are shown in this paper.
The collimator setup gave the beam a triangular intensity shape function with a full width at half maximum (FWHM) of approximately 0.6 mm at the point of focus.[32] The measured diffracted peaks were fitted using a flat background and Gaussian peak shape using the LAMP (Large Array Manipulation Program) software.[33]
2.4 Hardness Measurements
After performing the residual strain measurements, the measured welds were sectioned in half using a Buehler IsoMet 4000 linear precision saw. The sectioned samples were then mounted in a thermosetting resin using a Buehler SimpliMet hot mounting press. The mounted samples were subsequently polished, using a final stage 3 μm diamond suspension polishing liquid. All samples were etched with 2 pct Nital. Hardness measurements were performed on a Wilson Hardness Tukon 1202 hardness tester with a motorized stage. Hardness tests were performed in accordance with BS EN ISO 6507-1:1998.[34] A Vickers indenter tip was used with a load of 0.5 kgf (or equivalently 4.9 N).
Three line scans were performed on the upper plate, at 0.55, 0.75, and 0.95 mm from the sheet–sheet interface, as illustrated in Figure 3. The three weld configurations (fixed schedule boron, adaptively welded boron, and DP600) were welded with 1.5-mm-thick sheets; hence, the chosen measurement lines are distributed equally through the upper sheet thickness in all work-pieces. The different schedules will give varying weld sizes; however, utilizing the chosen scan lines will mean that comparisons may be made in reference to the known sheet thickness.
It was previously stated that it is crucial to characterize the gradients of material properties through the RSWs. Hardness measurements were taken at intervals of 0.2 mm, giving a clear view of material gradients. For the neutron diffraction data, the 1 mm spacing between measurement points along with the gage volume averaging will give a coarser view of the material gradients. Due to the allocated beam time, this was the highest resolution afforded.
3 Results and Discussion
3.1 Hardness
Figure 4 shows the hardness distributions of the fixed schedule boron steel weld taken at 0.55 mm (red line), 0.75 mm (green line), and 0.95 mm (blue line) above the sheet–sheet interface. The figure indicates that there is relatively little difference in hardness through the thickness of the sheet for the fixed schedule weld.
Figure 5 shows the hardness distribution of the adaptively welded boron steel. A significant difference in hardness can be seen through the thickness of the sheet, specifically in the area of the nugget. Due to the shallow nugget, a reduced amount of martensite is present in the upper portion of the top sheet. Additionally, a soft HAZ region may have developed in the upper portion.
The bottom measurement line, traveling directly through the weld nugget, shows the highest hardness values. This is to be expected, as the nugget is mainly composed of martensite. The middle and top lines exhibit reduced hardness values due to the heat-treated area at the nugget periphery. Due to the nature of constant weld parameter adjustment associated with adaptive welding, the area surrounding the nugget may have undergone multiple heating and cooling cycles, leading to the heat-treated area. Beyond the central nugget region, the 3 hardness lines converge to approximately 475HV at ±4 mm and then show a reduced hardness in the HAZ. In both cases, the dip in hardness correlates to the edge of the HAZ in the images.
Figure 6 shows the hardness distribution of the DP600 welded with a fixed schedule. As with the fixed schedule boron steel weld, the DP600 weld exhibits little variation through the sheet thickness. The fact that both fixed schedule welds show such constant hardness indicates that the adaptive welding schedule is responsible for significant hardness variation through the sheet thickness.
An interesting point to note is that even though both the boron steel and DP600 welds experienced cooling rates sufficient to form martensite, the DP600 nugget hardness is approximately 100 HV lower than the fixed schedule boron steel nugget and the bottom measurement line of the adaptive schedule boron steel weld (which runs fully through the nugget). This can be understood, in part, by the carbon content of the steels, with an increase in carbon content leading to an increase in hardness.[35] Of course, different alloying elements and austenite grain size will also have an effect on the hardness.
For the steels used in this work, the boron steel has a carbon content of 0.23 wt pct and DP600 has a content of 0.1 wt pct. Martensite is a supersaturated solution of carbon in ferritic iron, having a tetragonal structure, with the degree of tetragonality increasing with carbon content. The effect of this will later be discussed in the peak broadening results.
3.2 Measured Residual Strains
The residual strains in Figures 7 through 9 were estimated using a single strain-free reference parameter for all three directions. However, it must be noted that this global reference parameter does not take account of microstructure changes along the work-piece length. Therefore, the strains presented in this section are solely the measured strains without corrections applied. The data will be corrected in the next section through the plane-stress assumption. The presented results are not compared to one another, as they need further processing to be able to make comparative judgements. It must also be noted that the measurements do not take into account any existing strains induced during prior processing (cold rolling or hot forming).
Measured residual strains of boron steel welded with fixed schedule. Adapted from Ref. [36]
Measured residual strains of DP600 welded through fixed weld schedule. Adapted from Ref. [36]
The global reference parameter was taken as the average of the three directions at the furthest measurement location from the weld center, where it was assumed the residual stresses tend to zero. This is a common “far-field” method, where it is assumed d 0 does not vary. In Figure 7, it can be seen that there are some fluctuations in strains at 14 mm from the weld center, and the strains have not yet converged to a zero value. This is, however, the first approximation to a strain-free parameter with the data available. The same principle was applied to the strains in Figure 8 (adaptively welded boron steel) and Figure 9 (fixed schedule DP600).
For the fixed schedule boron steel weld, it can be seen that the strain in the hoop direction is the largest in tension, with peak values of 1400 × 10−6 ε at approximately 4 mm from the weld center. There is a significant drop to −1200 × 10−6 ε in compression outside the weld at 8 mm. The radial and hoop strains are in tension in the nugget and HAZ (between approximately −5 to 5 mm from the weld center), whereas the axial strain is completely in compression.
The strain distribution for the adaptively welded boron steel is shown in Figure 8. A clear transition in the strain gradients can be seen in the HAZ at approximately 6 mm from the weld center, with a peak strain in the hoop direction of approximately 1500 × 10−6 ε.
The measured residual strain distribution of the DP600 weld is shown in Figure 9. The weld exhibits a smoother varying strain distribution. This distribution corresponds well to the hardness distribution shown previously. The weld exhibits a peak strain in the weld center of approximately 1300 × 10−6 ε.
3.3 Plane-Stress Correction
In order to first calculate the residual stresses, a valid strain-free reference (d 0) is required, as indicated previously in equation 2. Although far-field values are commonly used for the d 0 value, microstructural changes, as a result of welding, are known to lead to a variation in the d 0 value across the weld.[16,21] In such cases, a global reference d 0 value cannot be assumed;[16] hence, it is necessary to obtain the distribution of d 0 as a function of distance from the weld center for accurate strain calculations.
As previously discussed, a common assumption for thin geometries is that the normal (out-of-plane) stress is zero throughout the weld.[19,20,21,22] Using this plane-stress assumption, a d 0 value is applied at each measurement location to force the normal stress to zero. The in-plane stresses, calculated with the same d 0 value, are thus corrected.
The changing d 0 value can readily be expressed as an “offset” to the measured strain. The “offset” is known as the pseudo-strain and is applied to correct for the varying microstructure. The pseudo-strain may be used as an indicator of the magnitude of the microstructural changes expressed as strain. Figure 10 shows the pseudo-strain distribution for the fixed schedule boron steel weld, stemming from the application of the plane-stress assumption. Figures 11 and 12 show the pseudo-strain distributions for the adaptively welded boron steel and DP600, respectively. The hardness distribution of the welds is included in each figure to highlight the similar profile between the two distributions. A similar relation between hardness and pseudo-strain was found in other works.[21]
Figure 12 shows a pseudo-strain difference of approximately 800 × 10−6 between the hard nugget and relatively soft BM of the DP600 work-piece. This is to be expected, as both regions have undergone significantly different processing routes, leading to different microstructures.
In Figure 10, the boron steel nugget and BM exhibit similar hardness values, indicating similar microstructures; however, there is a pseudo-strain difference of approximately 500 × 10−6. A possible explanation for this difference is the way in which the nugget and BM were heated and quenched. In the press-hardening operation, previously described in Section II–A, the steel was austenitized at 1223 K (950 °C) and experienced a quench rate of approximately 100 K/s at full press closure, measured through a thermocouple.[8] The peak temperature experienced by the boron steel nugget was approximated by simulating the fixed welding schedule through SORPAS,[37] a dedicated resistance spot welding finite element package. The results indicated that the nugget experienced a peak temperature of approximately 2273 K (2000 °C) and a cooling rate of approximately 140 K/s.
These differences in peak temperature and cooling rates indicate that, although both the nugget and BM exhibit similar hardness values, the martensite has formed in a different morphology, leading to a difference in pseudo-strain values. A similar conclusion may also be made of Figure 11, for the adaptively welded boron steel.
3.4 Calculated Residual Stresses
Figure 13 shows the residual stress distribution for the fixed schedule boron steel weld calculated with the plane-stress assumption applied. Additionally, the hardness distribution is overlaid. Figure 14 shows the same information for the adaptive control-welded boron steel weld and Figure 15 for the DP600 fixed schedule weld. Note that the axial stress is not shown, as it is necessarily zero.
The fixed schedule boron steel weld and surrounding HAZ experience a tensile stress which decreases to a balancing area of compressive stress in the base material. The tensile stresses are manifested due to the melted nugget contracting and cooling during welding. The HAZ area has also experienced elevated temperatures and subsequently contracted during cooling, leading to a tensile stress. A clear symmetry can be seen about the weld center, both in terms of residual stress and hardness. A sudden drop in hardness correlated with an increase in residual stress values can be seen in the HAZ (approximately 4 to 5 mm from the weld center). Stress in the hoop direction reaches a peak of ~450 MPa at approximately 4 mm and decreases into negative values through the HAZ and BM. The radial direction stress reaches a peak of ~280 MPa at approximately 5 mm and follows a similar path into the negative stress region as the hoop stress, although with a less steep gradient.
The calculated residual stress distribution of the adaptively welded boron steel weld is shown in Figure 14. Again, a peak in stress can be seen in the HAZ, with the hoop stress being dominant. As one moves from the HAZ into the base material, the hoop stress changes from a tensile to a compressive state. The radial stress, however, remains tensile for a much greater distance compared to the fixed schedule RSW.
The adaptively controlled boron steel weld exhibits a very different residual stress distribution to the fixed schedule boron steel weld. This difference is most likely due to the different heating and cooling regimes associated with the different welding parameters of the fixed and adaptive schedules. The effect of these different welding parameters is evidenced in the hardness distributions presented in Figures 4 and 5. As stated previously, microstructural transformations may be associated with strains due to the crystal structure transformations. The hardness distribution of the adaptive weld, shown in Figure 5, exhibited a clear hardness gradient through the sheet thickness. The difference in strain distributions may therefore also be associated with the sampling gage volume averaging the microstructural gradients of the adaptive weld. This is in contrast to the relatively unvarying microstructural gradients of the fixed schedule weld, shown previously in Figure 4.
The residual stress distribution of the DP600 weld is shown in Figure 15. The nugget and surrounding HAZ experience tensile stresses, leading to compressive stresses into the base material. The hoop and radial directions exhibit similar stress levels, with the hoop stresses being slightly higher. As with the boron steel welds, a correlation between hardness and residual stress is presented. It is interesting to note that both boron steel welds and the DP600 weld exhibit residual stress values of approximately 200 MPa in the weld center, although DP600 does not show the tensile peak. Considering that all welds have a martensitic weld center, this value may be partly associated with the formation of martensite upon cooling.
3.5 Peak Broadening
The measured diffraction peak may broaden or contract due to changes in crystal structure. This change can be measured by the FWHM of the Gaussian curve. The FWHM can be used to investigate the effect that different microstructures have on the diffraction pattern, and will in turn be used to infer the microstructural variation as a function of the distance from the weld center. As mentioned previously, the sudden decrease in hardness in the HAZ has been suggested to be due to martensite tempering. During the tempering process, martensite will precipitate carbon in the form of carbide phases and at the same time will lose some tetragonality and tend toward a body-centered cubic (bcc) shape. As tempering progresses, the martensite matrix loses all tetragonality and transforms to ferrite and cementite, which nucleates at the grain boundaries.[38]
In their respective investigations of dual-phase steels, Filippone[39] and Woo[40] stated that there exists an overlap in diffraction patterns of ferrite and martensite, due to the similar crystal structures and lattice parameters of the two phases. It was also shown that martensite has an inherently broader peak, due to the increased tetragonality of the crystal structure compared to the ferrite crystal structure.[39]
A correlation between FWHM and hardness for the fixed schedule boron steel weld can be seen in Figure 16. From the hardness distribution, it seems that the BM starts from approximately 6 mm from the weld center, where the hardness levels out to a stable value. However, the FWHM distributions reach a stable value at approximately 8 mm. Therefore, the region beyond 8 mm from the weld center can be used as a reference FWHM value for martensite. The difference between the FWHM and hardness in the zone of rapid microstructural change may be due to the smearing effect resulting from the neutron beam sampling volume.
The weld nugget region (from −3 to 3 mm) consists mainly of martensite. However, there are small microstructural changes in the thickness direction from the nugget border to the face of the top plate, as shown previously in Figure 4. This means that the region from the nugget center to the face of the top plate is not as homogeneous as the same region in the BM. This difference is illustrated by the greater degree of variation in FWHM observed in the weld region. Nevertheless, the effect of martensite is evident in the weld and BM, with both exhibiting higher FWHM values than the HAZ. There is a difference of approximately 0.1 deg between the nugget and BM. This correlates well to the difference in pseudo-strain previously described in section 3.3 and lends verification that the difference in heating and cooling that the nugget and BM experienced has led to a different martensite morphology between the two regions.
The sudden drop in FWHM (at approximately 4 mm), coupled with an equally severe drop in hardness, indicates a move away from the martensitic microstructure towards a softer phase with a reduced tetragonality, likely tempered martensite. As discussed previously, tempering of martensite has the effect of lowering the tetragonality of the phase.[41] The reduced hardness is a strong indicator of tempering. Indeed, other authors have identified the soft HAZ microstructure in boron steel welds to be tempered martensite.[9,10,11]
The spot weld created through adaptively controlled welding also shows correlation between hardness and FWHM in Figure 17. Due to the size of the granularity of the neutron measurement, the measured change in FWHM at 2.5 and −2.5 mm does not correlate precisely to the sharp change in hardness at the same distances.
The boron steel welds created through the fixed and adaptive weld schedules show different FWHM and hardness values in the HAZ with respect to each other. The lower values, both in terms of FWHM and hardness, for the adaptively controlled weld indicate that the steel has been tempered to a greater degree than the fixed schedule weld.
As stated previously, tempered martensite is associated with ferrite formation. It was also mentioned that the DP600 BM contains ferritic microstructure. Hence, the FWHM results of the DP600 BM are used to investigate the degree of tempering which has occurred in the adaptively welded boron steel. Figure 18 shows that the DP600 BM exhibits a FWHM value of 0.5 deg, which may be attributed to a significant proportion of ferrite. The FWHM value of the adaptively welded boron steel HAZ exhibits a similarly low value of approximately 0.6 deg. These two similar figures suggest that martensite tempering has occurred, with associated ferrite formation.
In the previous section, it was established that the DP600 nugget exhibited a hardness value of 100 HV lower than the boron steel nuggets. This is due to a reduced tetragonality of the martensite phase due to a lower carbon content in the DP600 steel. The FWHM results lend further verification to this observation, where the DP600 nugget center shows a FWHM value of 0.27 deg less than the boron steel weld center.
4 Conclusions
To the authors′ knowledge, experimentally determined residual stresses in spot welded boron steel have not been previously reported. Residual strains were measured in three weld configurations (fixed schedule, adaptively welded boron steel, and fixed schedule DP600). To overcome the inherent microstructural variation which results from welding, residual stress values were calculated using a plane-stress assumption. Due to the neutron beam sampling volume, all measured values represent an effective average over a volume of approximately 2.8 mm3. All welds exhibited a tensile stress in the weld nugget due to the molten nugget cooling and contracting at the end of the weld cycle. In all cases, the base material near the HAZ exhibited compressive residual stresses, so that equilibrium may be achieved in the work-piece.
It was observed that the nugget and BM of the fixed schedule boron weld exhibited different pseudo-strain values from each other. This indicates that, although the processing route of each part was sufficient to lead to martensite formation, a different morphology may have developed. The difference in FWHM of the same regions lends further verification to this.
The boron steel and DP600 welds exhibited interesting correlations between residual stress and hardness distributions. The DP600 weld showed a flat residual stress profile across the nugget with a smooth decrease into the base material. The fixed schedule boron steel weld, however, showed peaks on the HAZ periphery and a decreased residual stress value in the weld center. The reduced hardness in the HAZ, in conjunction with peaks in residual stress, indicates that this is an area exhibiting extreme variation of properties and will make a significant contribution to the overall loading response of the weld.
An unexpected difference between the fixed and adaptive schedule boron steel welds was observed, in terms of hardness, residual stress, and FWHM. This most likely stems from the difference in heat inputs during the different welding schedules. The adaptively welded work-piece exhibited a thin nugget, causing various through-thickness weld regions to superimpose on the final results. This shows how sensitive boron steel is to the welding process and opens up possible further research to optimize the spot welding process for best performance.
Compared to the DP600 weld, the fixed schedule boron steel weld exhibited sharper material property gradients in the HAZ. Even greater variations were seen in the adaptively welded boron steel sample, with a sudden drop in hardness at the nugget periphery and another drop in the HAZ. As mentioned previously, the sharp notch tip of a spot weld may cause a stress concentration when the weld is loaded and the difference in material properties between the HAZ and nugget/BM may enhance the stress concentration.[12] Taking this into consideration, it is likely that a different stress gradient will develop during loading in the adaptive weld than in the fixed schedule weld and the resulting stress gradient may be enhanced to different degrees, leading to different failure loads.
This work forms part of a project on fracture prediction of spot welded boron steel. Further areas which will be reported in the future will be on extracting HAZ mechanical properties through physical simulation and finite element simulation of quasi-static loading of boron steel welds.
References
A. Bardelcik, M.J. Worswick, S. Winkler, and M.A. Wells, Int. J. Impact Eng., 2012. 50: pp 49-62.
D. Mohr and F. Ebnoether, Int. J. Solids Struct., 2009. 46: pp 3535-47.
M. Naderi, L. Durrenberger, A. Molinari, and W. Bleck, J. Mater. Sci. Eng. A, 2007. 478(1): pp 130-39.
M. Naderi, Saeed-Akbari A., and W. Bleck, J. Mater. Sci. Eng. A, 2007. 487: pp 445-455
M. Merklein and J. Lechler, J. Mater. Process. Technol., 2006. 177(1): pp 452-55.
R. Mohan Iyengar, B. Fedewa, Y.W. Wang, D.F. Maatz Jr., and R.L. Hughes: SAE Technical Paper, 2008. 2008-01-0857.
H. Karbasian and A.E. Tekkaya, J. Mater. Process. Technol., 2010. 210(15): pp 2103-18.
N.D. Raath: Ph.D. Thesis, University of Warwick, 2014.
Yu, Y., C. Wang, S. Chen, and Z. Lu, Adv. Mater. Res., 2011. 339: pp 375-78.
Choi, H.S., G.H. Park, W.S. Lim, and B.M. Kim, J. Mech. Sci. Technol., 2011. 25: pp 1543-50.
Kong, J.P., T.K. Han, K.G. Chin, B.G. Park, and C.Y. Kang, Mater. Des., 2013. 54(1): pp 598-609.
Lienert T, Siewert T, Babu S, Acoff V (2011) ASM Handbook Volume 6A Welding Fundamentals and Processes. ASM International, Russell
J. Larsson: in AWST-2011, 2011. Belik.
S. Sommer: LS Dyna forum, Ulm, 2012, vol. 1: pp 1–10.
Withers, P.J. and H.K.D.H. Bhadeshia, Mater. Sci. Technol., 2001. 17(4): pp 366-75.
Hutchings MT, Withers PJ, Holden TM, Lorentzen T, Introduction to the characterization of residual stress by neutron diffraction. 2005, CRC Press, Boca Raton, pp 4-5.
J. Altenkirch: Ph.D. Thesis, University of Manchester, 2009.
Hughes, D.J., M.N. James, D.G. Hattingh, and P.J. Webster, J. Neutron Res. 2003. 11(4): pp 289-93.
Staron, P., M. Kocak, S. Williams, and A. Wescott, Phys. B 2004. 350(1): pp E491-E93.
Allen, A.J., M.T. Hutchings, C.G. Windsor, and C. Andeani, Adv. Phys., 1985. 34(4): pp 445-73.
Hughes, D.J., E. Koukovini-Platia, and E.L. Heeley, Fusion Eng. Des., 2014. 89(1): pp 104-08.
Florea, R.S., C.R. Hubbard, K.N. Solanki, D.J. Bammann, W.R. Whittington, and E.B. Marin, J. Mater. Process. Technol., 2012. 212(11): pp 2358-70.
Ji, C.W., I. Jo, H. Lee, I.D. Choi, Y. do Kim, and Y.D. Park, J. Mech. Sci. Technol., 2014. 28(11): pp 4761-69.
Avramovic-Cingara, G., Y. Ososkov, M.K. Jain, and D.S. Wilkinson, Mater. Sci. Eng., 2009. 516(1): pp 7-16.
Matya, M. and X.Q. Gayden, Weld. J., 2005. 84(11): pp 172-82.
Matuschek Messtechnik GmbH, http://www.matuschek.de/index_en.htm. Accessed 29 July 2016.
ARO Technologies, http://www.arotechnologies.com/en-GB. Accessed 29 July 2016.
den Uijl, N., T. Okada, T. Moolevliet, A. Mennes, E. van den Aa, M. Uchihara, S. Smith, H. Nishibata, T. van der Veldt, and K. Fukui, Weld. World, 2012. 56(8): pp 51-63.
British Standards Institute: BS EN ISO 10447:2007. British Standards, 2007.
Hughes, D.J., G. Bruno, T. Pirling, and P.J. Withers, Neutron News, 2006. 17(3): pp 28-32.
British Standards Institute: ISO/TS 21432:2005. British Standards, 2005.
Pirling, T., G. Bruno, and P.J. Withers, J. Mater. Sci. Eng. A, 2006. 437(1): pp 139-44.
LAMP, the Large Array Manipulation Program. http://www.ill.eu/data_treat/lamp/the-lamp-book/. Accessed 19 October 2016.
British Standards Institute: BS EN ISO 6507-1:1998. British Standards, 1998.
Krauss, G., Mater. Sci. Eng. A, 1999. 273(1): pp 40-57.
Raath, N.D., D.J. Hughes, D. Norman, I. McGregor, and R. Dashwood, Characterization of Minerals, Metals, and Materials. 2013, Wiley: San Antonio, pp 481-90.
SORPAS User Manual 7.0. 2007: SWANTEC Software and Engineering ApS.
Reed Hill, R.E. and R. Abbaschian, Physical metallurgy principles. 1973, Van Nostrand, NewYork. pp 733-39.
Filippone, R., J. Root, P. Jacques, and S. Yue, ISIJ, 2002. 42(3): pp 304-09.
Woo, W., V.T. Em, E.Y. Kim, S.H. Han, Y.S. Han, and S.H. Choi, Acta Mater., 2012. 60(20): pp 6972-81.
Honeycombe, R.W.K. and H.K.D.H. Bhadeshia, Steels Microstructure and Properties. 2011, Butterworth-Heinemann, Oxford. pp 184-93.
Acknowledgments
The authors would like to thank Tata Steel, WMG, and the EPSRC for funding this work. The authors would also like to thank the ILL for allocating beam and experimental support. The authors also thank Ellen van den Aa, Guido Hensen, Martin Thornton, Thilo Pirling, Darren Stewardson, Martyn Wilkinson, David Cooper, Darren Grant, Stefan Kousoulas, Carl Lobjoit, and Zachary Parkinson.
Author information
Authors and Affiliations
Corresponding author
Additional information
Manuscript submitted October 14, 2016.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Raath, N.D., Norman, D., McGregor, I. et al. Effect of Weld Schedule on the Residual Stress Distribution of Boron Steel Spot Welds. Metall Mater Trans A 48, 2900–2914 (2017). https://doi.org/10.1007/s11661-017-4079-9
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11661-017-4079-9