Abstract
The linear friction welding (LFW) process is finding increasing use as a manufacturing technology for the production of titanium alloy Ti-6Al-4V aerospace components. Computational models give an insight into the process, however, there is limited experimental data that can be used for either modeling inputs or validation. To address this problem, a design of experiments approach was used to investigate the influence of the LFW process inputs on various outputs for experimental Ti-6Al-4V welds. The finite element analysis software DEFORM was also used in conjunction with the experimental findings to investigate the heating of the workpieces. Key findings showed that the average interface force and coefficient of friction during each phase of the process were insensitive to the rubbing velocity; the coefficient of friction was not coulombic and varied between 0.3 and 1.3 depending on the process conditions; and the interface of the workpieces reached a temperature of approximately approximately 1273 K (1000 °C) at the end of phase 1. This work has enabled a greater insight into the underlying process physics and will aid future modeling investigations.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Linear friction welding (LFW) is a solid-state welding process that is used to manufacture high-performance aerospace components,[1,2] with the titanium alloy Ti-6Al-4V being commonly used.[2–4] The process has many advantages over traditional fusion welding methods, including excellent mechanical properties, avoidance of melting, and very low defect rates.
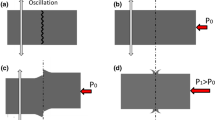
During LFW, one workpiece is oscillated relative to another whilse under a large applied force, as shown in Figure 1. The process is said to occur over four phases:[3,5,6]
-
Phase 1—Initial phase. During this phase asperity contact exists between the two surfaces to be joined and heat is generated due to friction—see Figure 1(a). The asperities soften and deform, increasing the true area of contact between the workpieces. Negligible axial shortening (burn-off) in the direction perpendicular to oscillation is observed during this phase.
-
Phase 2—Transition phase. During this phase the material plasticizes, so the true area of contact increases to 100 pct of the cross-sectional area—see Figure 1(b). The heat conducts back from the interface plasticizing more material and the burn-off begins to register due to viscous material expulsion.
-
Phase 3—Equilibrium phase. During this phase the interface force, thermal profile, and the rate of burn-off reach a quasi-steady-state condition. Significant burn-off occurs through the rapid expulsion of the plasticized material.
-
Phase 4—Deceleration phase. Once the burn-off reaches the pre-set value, the relative motion is ramped down and the workpieces are aligned. In some applications, an additional forging force may also be applied.
To understand how the process works, researchers have studied the evolution of the process forces with time,[5,6] used computational models to predict the temperature and deformation,[1,7–10] and have examined the weld microstructures.[4,8,11,12] Computational models are particularly useful as they provide a means of predicting what happens at the weld interface in the rapidly evolving process. However, the models are limited by a lack of data[13]—in particular, the interface force, friction coefficient, and steady-state burn-off rate as a function of the process inputs for the different phases of a weld. This paper addresses these issues using a systematic design of experiments to determine the effects of the process inputs on the average values of these outputs for the different phases of the process for Ti-6Al-4V linear friction welds. Finally, to understand the reason for the transition from phase 1 to phase 2, thermal models were used to predict the temperature at the interface between the two workpieces at the end of phase 1. These values were then related to the material flow behavior.
2 Methodology
2.1 Experimental
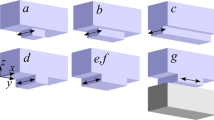
The experiments used workpieces with dimensions of 40 × 20 × 60 mm3 with oscillation taking place in the 40-mm length direction, as shown in Figure 2(a). The Ti-6Al-4V parent material had a bimodal alpha-beta microstructure, as shown in Figure 2(b). Prior to welding, the workpieces were cleaned with acetone.
Design Expert V.7, a design of experiments (DOE) software package, was used to identify a range of experiments for a regression model. To keep the number of experiments low, the inputs that had the largest effect on the outputs were investigated: amplitude, A, frequency, f, applied force, F a, and the burn-off, B o.[2,4] Although the amplitude and frequency were considered as two individual process inputs in this paper, they are sometimes combined into a single input term called the average rubbing velocity, v r, which Addison[14] defines as:
The experiments were completed using the FW34 LFW machine at TWI, Cambridge. The operating window for the combination of frequency, amplitude, and applied force that can be used with this machine is illustrated in Figure 2(d). The final input, the burn-off, was adjusted between 1 and 3 mm because previous studies[2,4] indicated that this critically affected whether the interface oxides were removed. These inputs were entered into the DOE software to generate a range of experimental conditions for a D-optimal regression analysis. The forging force in phase 4 remained the same as the applied force previously used. The remaining process inputs: ramp up time, oscillation decay time, and forging time were kept constant and had values of 0.1, 0.1, and 10 seconds, respectively.
The experimental design was specified to include enough experiments to account for a quadratic relationship between the inputs and outputs, since this behavior has been observed in the literature.[4,14] Some of the experiments were repeated to test the variance giving 25 experimental conditions for the DOE analysis, which are listed (welds 1 to 25) in Table I. In addition, four experiments were completed using thermocouples (welds 26 to 29). To insert the k-type thermocouples, several workpieces had four 1.2 mm diameter holes drilled through them perpendicularly to the oscillation direction and parallel to the direction of the applied force at the positions shown in Figure 2(c). To position the thermocouples at distances of 0.3, 1, 2.5, and 4.5 mm from the weld interface, a plug was placed into the holes at the interface end of the workpiece. The thermocouple wire was inserted through the opposite end until it made contact with the plug, the thermocouples where then fixed into position using an epoxy resin.
Metallographic specimens were produced from the experiments (welds 1 to 25) in Table I. The welds were sectioned 45 deg to the direction of oscillation and parallel to the applied force. The sectioned samples were placed into a hot resin, and then ground down using the following grit silicon carbide papers: 240, 1200, 2500, and 4000. After grinding, the sectioned samples were polished using colloidal silica polish on a micro-cloth and etched using hydrofluoric acid. The metallographic samples were viewed under a refractive microscope to determine the microstructure of the weld interface and to see if any surface impurities could be observed.
2.2 Analysis of the Force and Displacement History
High-speed data acquisition systems were used to measure the oscillator position, x 1, in-plane force, F in, axial position (the displacement perpendicular to the direction of oscillation), and the applied force, F a—see schematic diagram in Figure 3 for definitions. The axial position was used to estimate the burn-off history.
To determine the force at the interface of the two workpieces and the energy input, the data were analyzed in a similar way to that described in Ofem et al.[6] The analysis assumed:
-
Friction from the bearings on the oscillating tool was negligible.
-
Movement of the samples in the tooling was negligible.
From the schematic diagram in Figure 3, the instrumentation between the oscillating chuck and hydraulic cylinder records the in-plane force, F in. This does not represent the force at the weld interface, F int, due to the effects of momentum acting on the workpiece and tooling. Summing the forces on the chuck in the vertical direction enables the weld interface force, F int, to be determined
where M is the mass of the chuck and workpiece (approximately 280 kg) and a is the acceleration. The force convention is shown in Figure 3. Note that while F in is positive downwards, F int is positive upwards.
The acceleration may be calculated using numerical differentiation or if sinusoidal displacement is assumed the acceleration may be calculated from
where t is the time, ω is the angular frequency, and x 1 is the displacement. Equation [3] is less susceptible to noise when compared to the numerical differentiation method.[6] Since the motion of the workpieces in these experiments was sinusoidal, Eq. [3] was used for the analyses presented in this paper.
The average interface force generated over a phase, F pa, was divided by the applied force to determine the average dynamic friction coefficient μ:
The total energy inputted to the weld interface, E x, may then be estimated by integrating the power with respect to time
where T is the total duration of the weld and v is the velocity.
To determine the average power input for one of the phases, the energy input for that phase was divided by the phase duration. Finally, the burn-off rate during phase 3 was determined by calculating the gradient of the line where the burn-off reached steady state.
2.3 Regression Analysis
An “analysis of variance” (ANOVA) was conducted using Design Expert V.7. This identified which inputs and input interactions were statistically important for mathematically modeling the process outputs of interest. The statistically insignificant factors were then removed from the equations. Several statistical criteria were considered when reducing the factors. These are listed below, and the reader is referred to the cited text for further explanation:[15]
-
R-squared (R 2): The percentage of variation in the data explained by the regression model.
-
Adjusted R-squared (Adj R 2): As for R 2 but adjusted for the number of factors in the model.
-
Predicted R-squared (Prd R 2): A measure of the percentage of variation for new data explained by the model.
-
Adequate precision (Ad. Pr): This is the signal to noise ratio and compares the range of the predicted values at the design points to the average prediction error.
-
P-Values (P–V): This helps the user determining which input factors are of significance. The smaller the value, the better with values equal to or lower than 0.05 being statistically significant. The overall value for the equation describes how significant it is.
2.4 Thermal Modeling
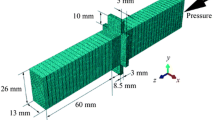
To understand the condition of the material at the transition between phase 1 and 2, a 2D thermal model of phase 1 was created using the DEFORM finite element analysis (FEA) software. Grujicic et al.[8] demonstrated that there is very little variation in the thermal profile in the through-thickness direction, allowing the process to be modeled with a 2D model oriented in the direction of oscillation. As shown in Figure 4, the tooling extended to within 5 mm of the interface as occurred in the experiments. Temperature-dependent thermal conductivity, specific heat, and emissivity data from the DEFORM software’s library were used; the convective heat transfer coefficient was assumed[1] to be 10 W/(m2 K); and the conductive heat transfer coefficient with the tooling was assumed [1] to be of 10,000 W/(m2 K). The temperature of the environment was assumed to be 293 K (20 °C). A uniform mesh size of 0.5 mm was used across the 2D model.
The heat from the LFW process was applied with a uniform heat flux (Q) across most of the workpiece interface which was linearly reduced to 50 pct of this value, an amplitude (A) away from the edge as shown in Figure 4. The reduction at the edges was due to the sinusoidal movement of the workpieces—the point at the corner is only in contact with the other workpiece 50 pct of the time. The heat flux was determined using two methods: Method 1 used the power input calculated from the force and displacement history and Eq. [5]; and Method 2 used the average power input for phase 1 derived from the statistical analysis. The thermal profiles were predicted along the center line of the weld in the direction perpendicular to oscillation and then compared against the thermocouple measurements. A comparison of these methods enabled validation of the statistical data generated with the DOE.
3 Results and Discussion
3.1 Weld Appearance and Microstructure
Regardless of the process inputs used, the macrostructures of the Ti-6Al-4V linear friction welds were similar in appearance in the fact that they had several distinct zones—a weld center zone (WCZ), a thermo-mechanically affected zone (TMAZ), and the parent material—and were surrounded by the expelled interface material (flash). These characteristics are typical of Ti-6Al-4V linear friction welds.[2,4,8,11,13] The different zones are displayed in Figure 5(a). The WCZ which many authors suggest experiences significant recrystallization,[4,8,11,13] was found to have either a widmanstatten and/or martensitic microstructure, as shown in Figures 5(b) and (c), respectively. The WCZ was then followed by a TMAZ. The material in this region had been deformed mechanically and affected by the heat from the welding process but did not appear to have undergone any significant recrystallization due to the original grains of the parent material being present. The remainder of the workpieces consisted of the initial parent material, as previously shown in Figure 2(b).
Worthy of note, the welds that had only experienced a small amount of burn-off, i.e., approximately 1 mm, had surface impurities, such as oxides, along the weld interface, as shown in Figure 5(d). Future work may do well to consider how the process inputs influence the removal of these impurities as they can affect the properties[4] and possibly the life of a weld.[1]
3.2 Force Histories
A plot of the force history for a typical weld is shown in Figure 6(a). Typically the in-plane force started out with a relatively low value during phase 1, before increasing to a maximum during phase 2 and then reducing a little and stabilising during phase 3. This is typical of most Ti-6AL-4V linear friction welds.[5] For two of the welds, the force histories were enlarged so that the force variation over a single cycle during phase 3 could be viewed, which is shown in Figure 6(b) for a low rubbing velocity weld and Figure 6(c) for a high rubbing velocity weld. The two responses are remarkably different. Firstly, the magnitude of the component caused by acceleration (M.a) is much greater for the high rubbing velocity weld due to the high accelerations. Secondly, the variation of the interface force over a cycle differed: for the low rubbing velocity weld, the force reached a peak value shortly after the workpieces changed direction and was then relatively uniform until the workpieces changed direction again. This behavior is similar to that reported in Ofem et al.[6] who claimed that this was due to forging of the workpieces at the end of each stroke due to the higher pressure caused by the smaller interfacial area. This shortening then resulted in ‘ploughing’ as the workpieces were brought back together. Once fully aligned ‘ploughing’ ceases and the interface force decreases. For the high rubbing velocity weld, there was no initial peak—the interface force increased continuously until the workpiece changes in direction. It is unclear that whether the ‘ploughing’ mechanism was active or not. There were fewer data points recorded over a cycle due to the higher frequency which made it more difficult to view the point to point variation. In addition, for high rubbing velocities, the component of the force due to acceleration was a much larger proportion of the total force, which may have increased the error in the calculated interface force. These phenomena were independent of the applied force.
Force history displaying: (a) the phases, in-plane force, applied force and burn-off for the weld made with a frequency of 42.1 Hz, an amplitude of 2.4 mm an applied force of 32 kN and a burn-off of 2 mm (Note that Phase 0 is the time one of the workpieces was oscillated in free space prior to contact with the other); in-plane and interface forces as a function of time for (b) a low rubbing velocity (120 mm/s) at 100 kN and (c) a high rubbing velocity (540 mm/s) at 100 kN welds
3.3 Regression Analysis
The results from the statistical tests performed on the final models are displayed in Table II. Much of the variability within the results is accounted for with the exception being the welding time for phase 2 due to the short duration of this phase.
The equations for the process outputs are listed below (these are listed so that other researchers may use them for modeling input and/or validation data):
Although the frequency and amplitude are two separate process inputs, the regression analysis demonstrated that it was acceptable to consider them as a single input—an average rubbing velocity—as varying either while keeping the average rubbing velocity constant had relatively little influence on the results (Although it should be emphasised that this result may only be applicable to Ti-6Al-4V for the process input range investigated). To illustrate this, the steady-state burn-off rate is plotted as a function of the frequency and average rubbing velocity in Figure 7(a). Therefore, all subsequent regression analysis plots are displayed as a function of the average rubbing velocity. Figure 7(b) shows how the burn-off rate was affected by the combination of rubbing velocity and applied force: it increased with both. The amount of burn-off had no effect on this value.
The results from the regression analysis for the average welding time, power, interface force, and coefficient of friction for the three main phases are displayed in Figure 8. Phase 4 was very short in duration and was ignored.
From Figure 8(a), the parameter that had the greatest effect on the duration of each of the phases was the rubbing velocity. The duration was inversely related to the rubbing velocity, power, and burn-off rate. This is because the higher rubbing velocities increased the rate of heat generation, enabling the material to heat, and plasticize more rapidly (reducing the duration of phases 1 and 2). In addition, the higher rubbing velocities reduced the duration of phase 3 due to an increased rate of material expulsion. Although not shown the duration of phase 3 varied linearly with the amount of burn-off. In fact, with the exception of the duration of phase 3, the burn-off input had no influence on the results in Figure 8 and is, therefore, not included.
The results for the power in Figure 8(b) show that increasing the rubbing velocity increases the power input to the weld for all phases. The power input for phase 1 was generally the lowest of the three and was greatly affected by the applied force. The power input for phases 2 and 3 was greater and showed less dependence on the applied force.
Both the interface force and coefficient of friction were largely independent of the rubbing velocity: being mainly influenced by the phase and applied force, as shown in Figure 8(c) and (d). This result was not anticipated and has not been reported elsewhere. To understand why this may have occurred, this result is compared with the flow stress vs. temperature and strain rate data for this alloy which is reproduced in Figure 9. As the rubbing velocity is increased so is the strain rate,[1] which increases the required flow stress. The increased rubbing velocity also increases the heat input (see Figure 8(b)), which, due to the relatively low thermal conductivity of titanium, can increase the interface temperature,[1] thus reducing the required flow stress. The net result appears to be a cancelation of the two effects, resulting in minimal change of the average interface force required to maintain oscillation.
Ti-6Al-4V flow stress data as a function of temperature and strain rate at a strain of 4 (reproduced from Turner et al.[1])
The average interface force increases with the applied force, as shown in Figure 8(c). For phase 1, this is due to more of the asperities at the interface of the workpieces being “squashed” onto each other, increasing the true surface contact area, which increases the friction force.[16,17] For phases 2 and 3, this is probably due to the rate of expulsion of the viscous material from the interface. For a comparable rubbing velocity, a decrease in the applied force decreases the rate of material expulsion, see Figure 7(b), causing less high temperature material to be removed from the joint. Consequently, the extra heat from the remaining material is combined with the heat generated from the viscous plastic deformation during the next cycle of oscillation, thus resulting in a higher interface temperature which reduces the material flow strength and the required interface force to maintain oscillatory motion. This theory is supported by experimental investigations completed by Romero et al.,[11] who compared the microstructures of Ti-6Al-4V linear friction welds and concluded that the interface temperature reduces considerably when welds are produced with higher applied forces. Modeling work by Turner et al.[1,7] also supports this view.
The coefficient of friction is obviously strongly linked to the interface force. This parameter has been reported because of its common use in process models.[8–10] The average value was relatively insensitive to the rubbing velocity, however, with the lower forces it ranged between about 0.8 and 1.3, depending on the phase; while at the higher forces it was consistently around 0.4. Due to the big difference in the results in phase 1, and the fact that an adhesion of the materials occurs in phases 2 and 3, it is highly unlikely that coulombic friction is occurring at any point during the LFW process. Therefore, coulombic modeling—even during phase 1—for the LFW process is highly questionable.
Finally there appears to be an advantage in using high rubbing velocities to minimise the overall energy input to a weld—see Figure 10. This is a consequence of the higher power input and shorter duration of these welds.
3.4 Thermal Profiles at the End of the Initial Phase (Phase 1)
Figure 11 displays thermal profiles at the end of phase 1 for four different process input combinations. As stated earlier, the heat flux was determined from the force and displacement history (Method 1) and the statistical analysis (Method 2). The temperatures recorded at the interface at the end of phase 1 ranged between 1213 K (940 °C) and 1333 K (1060 °C), with an average of approximately 1273 K (1000 °C) across all the process conditions. It is well known that the beta-transus temperature for titanium is around 1273 K[4,11] (1000 °C) and as seen in Figure 9, there is a significant reduction in the flow stress at this temperature. This lower flow stress likely allows for adhesion between the two materials and facilitates extrusion of the hot metal from the weld region. Hence this explains why the transition from phase 1 to phase 2 is associated with this temperature.
A comparison of the modeled thermal profiles and experimental measurements for different average rubbing velocities, Vr, and applied forces, Fa, predicted at the end of phase 1. The modeled thermal profiles were estimated using: the heat flux calculated from the force and displacement history (Method 1), and the heat flux calculated from the statistical analysis (Method 2)
There was good agreement between the two methods for estimating the heat input and the experimental thermocouple recordings. An increase in the rubbing velocity and/or applied force increased the gradient of the thermal profile, concentrating the heat close to the weld interface. As stated in the previous section, the high rubbing velocity welds generate more power and take a much shorter time. Therefore, there is little time for the heat to conduct into the bulk material which is why the thickness of the highly heated region is reduced.
4 Conclusions
The main findings from this work are:
-
1.
The design of experiments technique allowed formulas for describing the burn-off rate, duration, weld power, interface force, friction coefficient, and process energy to be determined for a range of process inputs and the different process phases. These results provide input and validation data for Ti-6Al-4V LFW process models.
-
2.
The outputs were primarily dependent on the average rubbing velocity and applied force. Adjusting the frequency and/or amplitude while keeping the average rubbing velocity constant had little effect on the outputs.
-
3.
The microstructure at the weld interface can consist of either Widmanstatten and/or Martensite.
-
4.
The interface force increased with the applied force but was largely insensitive to the rubbing velocity for all phases of the process.
-
5.
The energy required to produce a weld is reduced with higher rubbing velocities and applied forces due to the process taking less time.
-
6.
The thermal profiles predicted at the end of phase 1 indicated that irrespective of the process inputs the temperature at the interface was around 1273 K (1000 °C), which corresponds to the beta-transus temperature for Ti-6Al-4V.
References
Turner, R., Gebelin, J.-C., Ward, R. M. & Reed, R. C. Linear Friction Welding of Ti–6Al–4V: Modelling and Validation. Acta Materialia 59, 3792–3803 (2011).
A.C. Addison: Report—894/2008. Granta 44, 2008.
Vairis, A. & Frost, M. On the Extrusion Stage of Linear Friction Welding of Ti 6Al 4V. Materials Science and Engineering A 271, 477–484 (1999).
Wanjara, P. & Jahazi, M. Linear Friction Welding of Ti-6Al-4V: Processing, Microstructure, and Mechanical-Property Inter-Relationships. Metallurgical and Materials Transactions A 36A, 2149–2164 (2005).
Vairis, A. & Frost, M. High Frequency Linear Friction Welding of a Titanium Alloy. Wear 217, 117–131 (1998).
Ofem, U. U., Colegrove, P. A., Addison, A. & Russell, M. J. Energy and Force Analysis of Linear Friction Welds in Medium Carbon Steel. Science and Technology of Welding and Joining 15, 479–485 (2010).
Turner, R., Ward, R. M., March, R. & Reed, R. C. The Magnitude and Origin of Residual Stress in Ti-6Al-4V Linear Friction Welds: An Investigation by Validated Numerical Modeling. Metallurgical and Materials Transactions B 43B, 186–197 (2011).
Grujicic, M., Arakere, G., Pandurangan, B., Yen, C. F. & Cheeseman, B. A. Process Modeling of Ti-6Al-4V Linear Friction Welding (LFW). Journal of Materials Engineering and Performance 21, 2011–2023 (2011).
Tao, J., Zhang, T., Liu, P., Li, J. & Mang, Y. Numerical Computation of a Linear Friction Welding Process. Materials Science Forum 575 -578, 811–815 (2008).
Vairis, A. & Frost, M. Modelling the Linear Friction Welding of Titanium Blocks. Materials Science and Engineering A 292, 8–17 (2000).
Romero, J., Attallah, M. M., Preuss, M., Karadge, M. & Bray, S. E. Effect of the Forging Pressure on the Microstructure and Residual Stress Development in Ti–6Al–4V Linear Friction Welds. Acta Materialia 57, 5582–5592 (2009).
A. Chamanfar, M. Jahazi, J. Gholipour, P. Wanjara, and S. Yue: Metall. Mater. Trans. A, 2013, vol. 44A, pp. 4230–38.
I. Bhamji, M. Preuss, P.L. Threadgill, and A.C. Addison. Mater. Sci. Technol., 2011, vol. 27, pp. 2–12.
A.C Addison: TWI Industrial Members Report—961/2010. Main 44, 2010.
D.C. Montgomery: Design and Analysis of Experiments. John Wiley and Sons Inc., Hoboken, 2000, pp. 60–125.
B. Bhushan: Introduction to Tribology. Wiley, New York, 2002, 99, 199, 560.
F.P. Bowden and D. Tabor. The Friction and Lubrication of Solids. Oxford University Press, New York, 1950, p. 10.
Acknowledgments
The authors would like to thank the Engineering and Physical Sciences Research Council (EPSRC), the Boeing Company and The Welding Institute (TWI) for funding the research presented in this paper. In addition, the advice and comments provided Mr. David R. Bolser of the Boeing Company was greatly appreciated.
Author information
Authors and Affiliations
Corresponding author
Additional information
Manuscript submitted April 5, 2014.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution License which permits any use, distribution, and reproduction in any medium, provided the original author(s) and the source are credited.
About this article
Cite this article
McAndrew, A.R., Colegrove, P.A., Addison, A.C. et al. Energy and Force Analysis of Ti-6Al-4V Linear Friction Welds for Computational Modeling Input and Validation Data. Metall Mater Trans A 45, 6118–6128 (2014). https://doi.org/10.1007/s11661-014-2575-8
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11661-014-2575-8