1 Introduction

The aim of modern thermomechanical processing technologies is to achieve both high strength and ductility of the steel product. The combination of desired properties can be achieved by optimizing the chemical composition of the steel and/or by suitable thermomechanical processing. As a rule, the development of fine microstructure is a prerequisite for obtaining high strength combined with good ductility in majority of constructional steels, specifically in HSLA grades. However, producers of thin gage products face another challenge, which is the necessity of finish rolling in γ + α region. In this case, the texture development may cause a problem for the mechanical properties of products, e.g., impact toughness.

The concept of AHSS steels was built on another approach in which the amount of ferrite, bainite, martensite, and eventually retained austenite plays a crucial role in achieving a proper balance between strength and ductility.[1,2] In addition, the morphology and mechanical stability of these constituents are very important for properties and crash worthiness. Specifically, this refers to retained austenite whose stability is affected by the carbon segregation.

Required relation between volume fractions of ferrite and martensite, which is crucial for the quality of steel,[1–3] is obtained through applying special cooling paths during laminar cooling after hot rolling or continuous annealing after cold rolling. The latter process was investigated in the earlier work.[4] The laminar cooling was considered in this paper. This is a complex process, therefore, physical and numerical simulations are particularly needed in design of manufacturing of DP steel products. Efficiency of numerical simulations in a support for technology design depends on the accuracy of models and their capability to reproduce properly physical phenomena occurring in the industrial process. Problem of a selection of an adequate model for a particular application, as well as problem of identification of model parameters, are crucial for the efficiency and effectiveness of simulations. Therefore, the objectives of the paper were twofold. Physical simulations of hot plastic deformation and heat treatment were performed and used to identify and validate models. Validated models were applied to simulate the manufacturing of DP steel strips by hot rolling and laminar cooling.

2 Numerical Models

Two numerical models of various complexities and various predictive capabilities are proposed in the paper. The first one is based on the Avrami equation[5] with the main coefficient introduces as a function of temperature. The second model is based on the cellular automata method (CA). Both models are implemented in the FE code, which simulates temperature distribution in the workpiece at the macroscale. Transfer of data between the models is introduced and multiscale approach is formulated. The CA model is computationally more demanding and still cannot find direct application in industrial conditions, but on the other side it can provide new quality of obtained data not achievable by conventional models.

2.1 FE Model for Hot Strip Rolling and Laminar Cooling

Thermal–mechanical–microstructural model is used in the simulations. Finite element method is applied in the thermal and mechanical parts. The solution assumes that the material obeys Huber-Mises yield criterion and associated Levy–Mises flow rule. The velocity field is calculated by searching for a minimum of the functional. This is a well-known approach and detailed description of the FE code is given in Reference 6. The Hansel and Spittel equation[7] was selected as the flow stress model in the Levy–Mises flow rule:

$$ \sigma_{p} = A\varepsilon^{B} \exp \left( {C\varepsilon } \right)\dot{\varepsilon }^{D} \exp \left( {ET} \right), $$
(1)

where \( \varepsilon \) is the strain, \( \dot{\varepsilon } \) is the strain rate, T is the temperature in °C, A to E are the material parameters.

The mechanical part is coupled with the finite element solution of the Fourier heat transfer equation:

$$ \nabla \cdot \left( {k\nabla T} \right) + Q = c_{p} \rho \frac{\partial T}{\partial t}, $$
(2)

where k is the conductivity, Q is the heat generation rate due to deformation work and due to transformation, c p is the specific heat, ρ is the density, T is the temperature in °C, and t is the time.

The FE solution of Eq. [2] is used in simulation of temperature changes during both continuous rolling and cooling after rolling. The following boundary condition is applied:

$$ k\nabla T = h_{\text{c}} \left( {T_{\text{a}} - T} \right), $$
(3)

where h c is the heat transfer coefficient and T a is the ambient temperature.

The ambient temperature is either temperature of the air or temperature of the roll or temperature of the water, depending on the conditions of cooling. Heat transfer coefficient for air is calculated from typical convention-radiation equation. Heat transfer coefficient for the contact with the roll is assumed 50 kW/m2K. Heat transfer coefficient for water cooling depends on the amount of water and on the pressure and is calculated using equation proposed in Reference 8. The FE solution is coupled with the microstructure evolution model described in Section II–B and with the phase transformation model described in Sections III–C, III–D, respectively. In consequence, simulations of microstructure evolution accounting for current, local temperatures calculated along the flow lines are possible.

2.2 Microstructure Evolution Model

Microstructure evolution model is based on the equations proposed by Sellars[9]:

$$ X = 1 - \exp \left[ { - b_{1} \left( {\frac{t}{{t_{0.5} }}} \right)^{{b_{2} }} } \right] $$
(4)
$$ t_{0.5} = b_{3} \varepsilon_{i}^{{b_{4} }} \dot{\varepsilon }^{{b_{5} }} D_{0}^{{b_{6} }} \exp \left( {\frac{{Q_{\text{RX}} }}{{R\hat{T}}}} \right) $$
(5)
$$ D_{\text{RX}} = b_{7} \varepsilon^{{b_{8} }} \dot{\varepsilon }^{{b_{9} }} D_{0}^{{b_{10} }} \exp \left( {\frac{{Q_{\text{DX}} }}{{R\hat{T}}}} \right) $$
(6)
$$ D_{\gamma }^{{b_{11} }} = D_{\text{RX}}^{{b_{11} }} + b_{12} t\exp \left( { - \frac{{Q_{\text{GROWTH}} }}{{R\hat{T}}}} \right), $$
(7)

where X is the recrystallized volume fraction, t 0.5 is the time for 50 pct recrystallization, ε i is the effective strain, D 0 is the grain size prior to deformation, R is the gas constant, D RX is the recrystallized grain size, D γ is the grain size after growth, \( \hat{T} \) is the temperature in K, and b 1 to b 12 are the material coefficients.

Coefficients in the model were determined in Section III–D. Microstructure evolution equations were solved along the flow lines in the rolling process using current, local values of strains, strain rates, and temperatures calculated by the FE code. The distribution of the grain size along the thickness of the strip was determined.

2.3 Phase Transformation Model Based on the Avrami Equation

Since control of the structural components, volume fraction and morphology are crucial in the DP steels,[10,11] and phase transformations model is the most important part of the present work. Avrami equation is the basis of the first proposed model:

$$ X = 1 - \exp \left( { - kt^{n} } \right), $$
(8)

where X is the volume fraction of a new phase, k and n are the model parameters, t is the time.

Theoretical considerations show that constant value of n in Eq. [8] can be used. On contrary, the coefficient k must vary with temperature in a way linked to the form of a transformation C curve of the TTT diagram. A modified Gaussian function, which was proposed in Reference 12, was selected for the ferritic transformation:

$$ k = k_{ \hbox{max} } \exp \left[ { - \left( {\frac{{T - T_{\text{nose}} }}{{a_{7} }}} \right)^{{a_{8} }} } \right] $$
(9)

In the equations below, which complete the phase transformation model, parameters are introduced as a with number in subscript. These parameters are subject of identification in the following part of the paper. In Eq. [9], k max = a 5/D γ is the maximum value of k, T nose = A e3 + 400/D γ  − a 6 is a temperature position of the nose of the Gaussian function, where D γ is austenite grain size. Coefficient a 7 is proportional to the nose width thickness at mid height and a 8 is related to the sharpness of the curve. Investigation performed in Reference 13 has shown that following equations describe well coefficient k respectively in pearlitic (k p) and bainitic (k b) transformations:

$$ k_{\text{p}} = \frac{{a_{14} }}{{D_{\gamma }^{{a_{16} }} }}\exp \left( {a_{13} - a_{12} T_{100} } \right) $$
(10)
$$ k_{\text{b}} = a_{23} \left( {a_{22} - a_{21} T_{100} } \right), $$
(11)

where T 100 = T/100, °C.

The incubation time in the case of the ferritic transformation is negligible for lean chemical composition of a steel. Incubation time is introduced for bainitic (τ b) and pearlitic (τ p) transformations:

$$ \tau_{\text{P}} = \frac{{a_{9} }}{{\left( {Ae_{1} - T} \right)^{{a_{11} }} }}\exp \left( {\frac{{a_{10} \times 10^{3} }}{{R\hat{T}}}} \right) $$
(12)
$$ \tau_{\text{b}} = \frac{{a_{17} k_{\text{b}} }}{{\left( {B_{\text{s}} - T} \right)^{{a_{19} }} }}\exp \left( {\frac{{a_{18} \times 10^{3} }}{{R\hat{T}}}} \right), $$
(13)

where T is the temperature in °C, \( \hat{T} \) is the temperature in K.

Start temperatures for the bainitic and martensitic transformations are functions of chemical composition:

$$ B_{\text{s}} [^\circ {\text{C}}] = a_{20} - 425[{\text{C}}] - 42.5[{\text{Mn}}] - 31.5[{\text{Ni}}] $$
(14)
$$ M_{\text{s}} [^\circ {\text{C}}] = a_{26} - a_{27} C_{\gamma }, $$
(15)

where C γ is the carbon concentration in the remaining austenite.

Fraction of austenite, which transforms into martensite, is calculated according to the Koistinen and Marburger model[14]:

$$ F_{\text{m}} = \left\{ {1 - \exp \left[ { - 0.011\left( {M_{\text{s}} - T} \right)} \right]} \right\}\left( {1 - F_{\text{f}} - F_{\text{p}} - F_{\text{b}} } \right) $$
(16)

where F f, F p, and F b is the fraction of ferrite, pearlite, and bainite with respect to the whole volume of material, T is the temperature in °C.

Coefficient n in Eq. [8] has numbers a 4, a 15, and a 24 for ferritic, pearlitic, and bainitic transformations, respectively. Thus, the model contains 23 coefficients. According to the procedure developed by the Authors, these model coefficients are identified using inverse analysis for the data derived from the dilatometric tests described in Section III–D.

2.4 CA Model for Phase Transformations

The main idea of the cellular automata technique is to divide a specific part of the material into one-, two-, or three-dimensional space of finite cells. Each cell is characterized be a state and contains values of internal variables (q). Each cell is surrounded by neighbors, which additionally affect one another according to rules of interactions (transition rules). They are based on the knowledge defined, while studying a particular physical phenomenon and they control changes of the state of cells, according to the general relation:

$$ \varUpsilon_{i}^{t + 1} = \left\{ {\begin{array}{*{20}c} {{\text{new}}\;{\text{state}}\;{\text{if}}\left( \varLambda \right)} \\ {\varUpsilon_{i}^{t} } \\ \end{array} } \right., $$
(17)

where t is the time step.

Λ = Λ(\( \varUpsilon_{i}^{t} \), \( \varUpsilon_{j}^{t} \), q, p) is a logical function, which defines a new state of the cell i on the basis of the state of the cell i and the neighboring cells j in the previous time step (t) and on the basis of the values of internal (q) and external variables (p), Y j is the state of the jth cell, j ∈ N(i), N(i) is the surrounding of the ith cell. The cell can be in three different states: ferrite (α), austenite (γ), and ferrite–austenite (α/γ). The last state is used to describe CA cells located at the interface between austenite and ferrite grains. Internal variables in the model are the ferrite volume fraction, the carbon concentration, the growth length l of the ferrite cell into the ferrite–austenite cell, and the growth velocity v of an interface cell. The temperature is the external variable.

Details of the applications of the CA model to simulate phase transformations can be found in References 15, 16 and Authors’ approaches covering transformations during heating and cooling of DP steels are described in References 17, 18. Since the transition rules control the cells behavior during calculations (i.e., during the cooling process), they have to be based on the knowledge regarding two main mechanisms: nucleation and subsequent growth of the ferrite grains. The nucleation mechanism is a stochastic process. To replicate this character, at the beginning of each time step a number of nuclei N nuc is calculated in a probabilistic manner. Additionally, the locations of the grain nuclei are generated randomly along the grain boundaries. When a cell is selected as a nuclei, the state of this cell changes from austenite (γ) to ferrite (α) and all the neighboring cells of the ferrite (α) change their state to ferrite–austenite (α/γ), see Reference 17 for details.

After the nucleus appears in the CA space, the growth of the ferrite phase is calculated in the following steps. However, nucleation process continues and new nuclei may occur during the entire CA simulation until the end of transformation. The transition rules describing growth of ferrite grains are designed to replicate experimental observations of mechanisms responsible for this process. The velocity of the γ/α interface was assumed to be a product of the mobility M and the driving force for interface migration F: \( v = MF \). The mobility of the γ/α interface is described by

$$ M = M_{0} D\left( T \right), $$
(18)

where M 0 is the mobility coefficient, T is the temperature in °C, and D is the diffusion coefficient.

The driving force for the phase transformation is defined as follows:

$$ F = F_{\text{chem}} + F_{\text{mech}} $$
(19)

where F chem and F mech are the chemical and mechanical driving force, respectively.

The influence of the F mech was neglected in the present model. The chemical force is due to differences in the chemical potentials of iron atom in austenite and ferrite phases at the interface:

$$ F_{\text{chem}} = \mu_{\text{Fe}}^{\gamma } - \mu_{\text{Fe}}^{\alpha } , $$
(20)

where \( \mu_{\text{Fe}}^{\gamma } ,\mu_{\text{Fe}}^{\alpha } \) is the chemical potential of iron atom in austenite and ferrite phases, respectively.

Knowing the interface velocity, a growth length is calculated in the current time step t. The growth length \( l_{i,j}^{i} \) of the ferrite cell with index (i) toward a ferrite–austenite neighboring cell with index (j) is described as References 15:

$$ l_{i}^{t} = \int\limits_{{t_{0} }}^{t} {v_{i} {\text{d}}t} , $$
(21)

where t 0 is the time when the CA cell (i) changed into the ferrite state, and v i is the growth velocity of the CA cell (i).

The ferrite volume fraction in the CA cell (i) calculated as a result of the growth is

$$ X_{i}^{t} = \sum\limits_{1}^{{N_{\text{neigh}} }} {x_{j}^{t} } = \sum\limits_{1}^{{N_{\text{neigh}} }} {\frac{{l_{j}^{t} }}{{L_{\text{CA}} }}}, $$
(22)

where X i is the total ferrite volume fraction in the CA cell (i), as a contribution x j from all the neighboring ferrite cells, L CA is the dimension of a CA cell in the space.

Based on these calculations, the transition rule in Eq. [17] is defined as follows [17]:

$$ \varLambda_{1} = \varUpsilon_{i}^{t} = \alpha /\gamma \wedge F_{i}^{t} > F_{\text{cr}} $$
(23)
$$ \varLambda_{2} = \varUpsilon_{j}^{t} = \gamma \wedge \varUpsilon_{i}^{t} = \alpha $$
(24)
$$ {\text{If}}\left( {\varLambda_{1} } \right)\;{\text{then}}\;Y_{j}^{t} = \alpha \quad {\text{If}}\left( {\varLambda_{2} } \right)\;{\text{then}}\;Y_{j}^{t} = \gamma /\alpha $$
(25)

The CA cell changes the state from γ/α into α when ferrite volume fraction F in the cell exceeds the critical value F cr. Otherwise, the cell remains in the γ/α state. When the cell changes its state to α, all the neighboring cells in the γ state change their states into the γ/α state. When a change in the cell state occurs, the corresponding carbon concentration changes according to the FeC diagram. In the present model, the carbon concentration in the γ CA cells increases uniformly, because the diffusion problem was not considered directly. The effect of diffusion is indirectly accounted for by relation of the phase boundary mobility on the diffusion coefficient in Eq. [18].

3 Identification of the Models

There are several coefficients in the models described in Section II. These coefficients were identified using inverse analysis of experimental tests. In the case of the phase transformation model, inverse analysis was preceded by the sensitivity analysis (SA).

3.1 Sensitivity Analysis

Any model can be identified using the inverse approach described in the next section. Identification was successful for the flow stress model and microstructure evolution model, see Section IV–D. However, due to a large number of coefficients in the phase transformation model, the problem of effectiveness of the optimization techniques has to be considered before the inverse analysis is performed. Uniqueness of the solution should be discussed as well. Some light on the solution of these problems can be put by performing the sensitivity analysis of the output of the model with respect to the coefficients in this model. The SA method deals with the question which factors of the physical model or computer simulation are really significant. Various aspects of applications of the sensitivity analysis in engineering were discussed in References 19, 20 and the sensitivity analysis of the phase transformation models was presented in References 20. Basic principles of the SA algorithm used in the present work are described briefly below. The screening method, derived from Morris Design (MD) algorithm, was used. In the algorithm, the term of parameter main effect is introduced and it is determined by computing a number of elementary effects at different points in the input space and next estimated by mean value and standard deviation. The elementary effect of the ith parameter at a given point a in the domain Ω is defined as

$$ \varsigma_{i} ({\mathbf{a}}) = \left| {\frac{{d(a_{1} , \ldots ,a_{i - 1} ,a_{i} + \Delta ,a_{i + 1} , \ldots ,a_{k} ) - d({\mathbf{a}})}}{\Delta }} \right|, $$
(26)

where d is the one of the outputs of the model. Vector a is any point from Ω region such that the perturbed point a + Δ is still in Ω. To compare elementary effects for various parameters, the parameter domain is rescaled to the interval [0,1].

A finite distribution F i of elementary effects for each parameter x i is obtained by sampling a in \( \varOmega \). The distribution F i is next described by the mean value. A mean characterizes the sensitivity of the model output with respect to ith parameter and is called sensitivity index of ith parameter. A high sensitivity index indicates that the parameter is important and it substantially influences the output.

The MD algorithm was performed for all parameters of the conventional phase transformation model. This procedure was not applied to the CA model, as in this case a smaller number of coefficients have to be identified, namely six in comparison to 23. The conventional model output was either start and end temperatures of transformations or volume fractions of phases after cooling. The sensitivity of the output with respect to the coefficients a in the model was determined for various cooling rates in the range from 0.02 to 500 °C/s.

The sensitivity indices calculated with respect to all outputs of the phase transformation model are shown in Figure 1. The model outputs were the transformation start and end temperatures for each phase and the volume fractions of phases. Coefficients with negligible influence (a 12-a 16) are not presented in this figure. Similar results for the volume fractions of the structural constituents are shown in Figure 2 and again coefficients with the negligible influence (a 12-a 16) are disregarded. The coefficients with low influence on the output receive small weights in the optimization, which allows for a decrease of the computing time.

Fig. 1
figure 1

Sensitivities of the transformation start and end temperatures with respect to the coefficients in the model (FS, ferrite start; PS, pearlite start; BS, bainite start; MS, martensite start)

Full size image
Fig. 2
figure 2

Sensitivities of the volume fraction of structural components with respect to the coefficients in the model (F, ferrite; P, pearlite; B, bainite; M, martensite)

Full size image

It was observed that, as far as the temperatures of start and end of transformations are considered, coefficients a 4-a 8 control the ferritic and the pearlitic transformations, coefficients a 17-a 24 control the bainitic transformation, and coefficients a 20 and a 26 control the start temperature for the martensitic transformation. There are some cross relations, but the sensitivities of one transformation with respect to the coefficients of the model of another transformation are small.

Analysis of sensitivity indices for the volume fraction of the structural constituents with respect to the coefficients in the phase transformations model shows that these relations are more complex than those observed for the temperatures. Beyond this, the sensitivity indices are much higher. Coefficient a 20 has a significant influence on volume fractions of all structural components. Since the sum of volume fractions has to be equal to 1, each coefficient influences at least two structural constituents. Coefficient a 20 has particularly strong influence on the volume fractions of ferrite, bainite, and martensite. The sensitivity index is in this case about three times higher than the average value for the remaining coefficients. Coefficients a 9-a 11, a 17-a 19, a 22, and a 27 show no or very low influence on the volume fractions of the structural components.

3.2 Inverse Algorithm

Identification was performed for all models presented in the paper. The models contain coefficients, which are grouped in the vector x. The values of these coefficients are different for different steels. Inverse method allows for fast and efficient determination of components of the vector x. Basic principles of this method are described in a number of publications, see for example.[21] Mathematical model of an arbitrary process can be written as follows:

$$ {\mathbf{d}} = F({\mathbf{x}},{\mathbf{p}}), $$
(27)

where \( {\mathbf{d}} = \{ d_{1} , \ldots ,d_{r} \} \) is the vector of output parameters measured in the test, \( {\mathbf{x}} = \{ x_{1} , \ldots ,x_{l} \} \) is the vector of coefficients in the model, \( {\mathbf{p}} = (p_{1} , \ldots ,p_{k} \} \) is the vector of process parameters.

When vectors p and x are known, the solution of the problem [27] is called a direct problem. Inverse problem of [27] is defined as determination of the components of the vector x for known vectors d and p. When the problem is linear, the inverse function can be found and the problem can be often solved analytically. For the models in the present work, these relations are nonlinear and the problem is transformed to an optimization task. Thus, the objective of the inverse analysis is determination of the optimum components of the vector x by searching for the minimum, with respect to x, of the objective function defined as a square root error between measured and calculated components of the vector d:

$$ \varPhi ({\mathbf{x}},{\mathbf{p}}) = \sum\limits_{i = 1}^{n} {\beta_{i} [{\mathbf{d}}_{i}^{\text{c}} ({\mathbf{x}},{\mathbf{p}}_{i} )} - {\mathbf{d}}_{i}^{\text{m}} ]^{2} $$
(28)

where \( {\mathbf{d}}_{i}^{\text{m}} \), \( {\mathbf{d}}_{i}^{\text{c}} \) is the vectors containing measured and calculated values of output parameters, respectively, β i is the weights of the points, (i = 1…n), and n is the number of measurements.

3.3 Multicomponent Systems Managing Trough Thermodynamics Predictions

The assumed objectives of numerical modeling are twofold. The first is calculation of phase transformation diagrams on the basis of thermodynamic models. The second is application of numerical methods to modeling phenomena occurring during transient phase transformations. The former approach is discussed in this section.

In order to fulfill the mechanical properties requirements, modern alloys have to be based on complex multicomponent systems which, as a first approximation, can be dealt with thermodynamics methods. Experimentally determined phase diagrams are usually available for binary systems only and, to limited extent, for ternary systems. The thermodynamic properties controlling driving forces for phase transformations, boundary conditions, and kinetic parameters are functions of temperature and chemical composition. Computational approach has emerged and established over last 30 years as the efficient way of studying complex systems. In this paper, CALculation of PHAse Diagrams (CALPHAD) method was applied to generate the data for modeling phase transformations.

The CALPHAD method is based on the fact that a phase diagram is a representation of the thermodynamic properties of a system. If the thermodynamic properties are known, it is possible to calculate the multicomponent phase diagrams and to solve a number of a different material dependent engineering problems. Some of them may be very complex because they involve all possible interactions occurring in a system composed of ten to twenty alloying elements. Experimental solution of this problem is costly and requires significantly longer times than if it is solved by numerical simulations using such tools as for example Thermo-Calc, DICTRA, JMatPro, FactSage, Pandat, and MTDATA.

The developed model is valid for any multiphase steel but all experiments were performed for the DP steel with the chemical composition given in Table II. The ThermoCalc software was used to provide the equilibrium characteristics of the investigated steel. By fitting the simple temperature functions to the calculated values, the set of equations was obtained for the carbon concentration at the phase boundaries:

$$ \begin{aligned} C_{\gamma \beta } & = - 0. 9 4 { + 0} . 0 0 2 2 8T \\ C_{\gamma \alpha } & = 4. 5 7- 0. 0 0 5 4 1 2T \\ \end{aligned} $$
(29)
$$ \begin{aligned} C_{\alpha } & = - 0.05869 + 0.0003827T - 8.288688 \times 10^{ - 7} T^{2} + 5.997 \times 10^{ - 10} T^{3} \quad {\text{for}}\quad T \le 910\,{\text{K}}\,(637\,^\circ {\text{C)}} \\ C_{\alpha } & = - 0.0208533 + 0.000102818T - 9.36396 \times 10^{ - 8} T^{2} \quad {\text{for}}\quad T > 910\,{\text{K}}\,(637\,^\circ {\text{C)}} \\ \end{aligned} $$
(30)

where C γα is the carbon content in austenite at the γ-α phase boundary, C γβ is the carbon content in austenite at the γ-cementite phase boundary, and C α is the carbon content in ferrite.

Equilibrium temperatures A e1 and A e3 calculated by the ThermoCalc software were 1002.2 K and 1100.6 K (729.2 °C and 827.6 °C), respectively. The equilibrium parameters are the boundary conditions for the transient models for preheated ferrite or undercooled austenite.

4 Experiments

The objective of the experiments was supplying data for validation of the models. Three sets of experiments were performed:

  • Plastometric tests, which supplied data for identification of the rheological model.

  • Stress relaxation tests, which supplied data for identification of the microstructure restoration model.

  • Dilatometric tests, which supplied data for identification of the phase transformation model.

Results of these tests are presented in this chapter.

4.1 Selection of the Material

As opposed to HSLA steels, the mechanical properties of AHSS grades are shaped through combination of proper fractions of phase constituents, their morphology, and mechanical behavior. Major and minor constituents of AHSS are specified in Table I. In the present paper, the analysis is constrained to the dual-phase (DP) steel with the chemical composition given in Table II.

Table I Major and Minor Constituents of AHSS
Full size table
Table II Chemical Composition of the Investigated DP Steel, Wt Pct
Full size table

Structure of the DP steels is composed of ductile ferrite and hard martensite. Volume fraction of martensite F m in majority of products does not exceed 30 pct. Such phase composition and second phase morphology give high strength and ductility of products. Soft matrix (ferrite) contributes to ductility of the steel. Deformation of this structure leads to strain concentration in ferrite, which gives good hardening characteristic in comparison with HSLA steels. Two-phase structure of DP steel strips is obtained by control of the ferritic transformation. In general, accelerated cooling is applied to the temperature of maximum rate of ferritic transformation. After that, material is subject to slow cooling in air to obtain required fraction of ferrite, i.e., around 70 to 80 pct. Accelerated cooling is applied again and then the remaining austenite is transformed into martensite or martensite/bainite complexes. This controlled cooling is applied either during laminar cooling after hot rolling (for thicker strips) or during the continuous annealing (for thinner strips). In the latter process, the strip is heated to the intercritical range of temperatures and, in consequence, the amounts of intercritical ferrite and transformed ferrite during cooling can be distinguished. The present paper is focused on the former process. Practical realization of the thermal cycle during industrial laminar cooling is difficult. Therefore, application of numerical simulations to design the cooling schedule for DP steels is presented in the work.

4.2 Two-Phase Microstructures

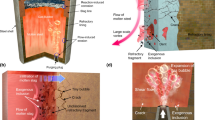
Various experimental techniques are used to investigate multiphase microstructures. Among them techniques for microstructure examination, such as light microscopy, X-ray diffraction, transmission electron microscopy (TEM), and scanning electron microscopy (SEM) have gained recognition as powerful tools for microstructure examination. Substantial progress has been recently made in the field of advanced steels, largely due to high resolution scanning electron microscope (FEG-SEM), electron backscattering diffraction (EBSD), and image classification.[22] These techniques reveal many structural features and they supplied information, which allowed building new generation of multiscale models of phase transformations. Selected examples of the performed analysis of the two-phase microstructure are shown below. Typical DP steel microstructure is presented in Figure 3. The color metallography by etching with LePera and Klemm reagents was used to distinguish the phase constituents. Characterization of microstructure of DP steel with FEG_SEM, including EBSD phase mapping, image quality map, and distribution of retained austenite, is shown in Figure 4. The micrograph in Figure 4b shows that the sample contains small content of retained austenite, which is in agreement with Klemm etching in Figure 3(b). Using IQ distribution, one may estimate the fraction of microstructural constituents in the analyzed area (Figure 4f).

Fig. 3
figure 3

Characterization with FEG_SEM of microstructure of DP steel after the physical simulation in Gleeble 3800 simulator, etched in LePera reagent (a) and etched in Klemm reagent (b)

Full size image
Fig. 4
figure 4figure 4

Characterization of microstructure of DP steel with FEG_SEM: EBSD phase mapping (a), image quality map (b), distribution of retained austenite (c), IQ map (d), distribution of IQ (e), deconvolution of the total IQ distribution assuming that it represents the superposition of IQ for ferrite, bainite, and martensite (f)

Full size image

4.3 Plastometric Tests and Stress Relaxation Tests

As mentioned, the focus of the paper is on phase transformations in the DP steels. However, since the state of the microstructure after hot rolling is important for modeling phase transformation, the finishing train of the hot strip mill was included in the analysis. Two sets of experiments were performed to develop models for the hot rolling process. The first was plastometric tests performed on the Gleeble 3800 simulator for identification of the flow stress model.

The samples measuring ϕ10 × 12 mm were compressed to the strain of 1 at temperatures 1123 K to 1503 K (850 °C to 1230 °C) and strain rates 0.1 to 30 s−1. Loads and temperatures were monitored during the tests. Inverse algorithm described in Section III–B[21] with x = {A, B, C, D, E}T was used. The following values of coefficients in Eq. [1] were obtained in the present work: A = 3255.3, B = 0.196, C = −0.283, D = 0.119, E = −0.003.

The second set of experiments was performed for identification of the microstructure evolution model. Stress relaxation tests were performed on the Gleeble 3800 simulator following the idea described in Reference 23. This method is well known and the results only are given below. Inverse algorithm described in Section III–B with x = {b 1-b 12, Q RX, Q DX, Q GROWTH}T was used. The coefficients in equations describing recrystallization and grain growth, which were determined on the basis of the stress relaxation tests, are given in Table III.

Table III Coefficients in Microstructure Evolution Eqs. [4] to [7] Determined for the DP Steel with Chemical Composition in Table II
Full size table

4.4 Dilatometric Tests and Identification of the Phase Transformation Models

Tests performed for identification of the phase transformation models were conducted with dilatometer DIL 805, which is capable of deforming the sample prior to cooling. In this case, the samples were cylindrical, having dimensions of ϕ4 × 7 mm. The tubular samples, ϕ4/2 × 10 mm, were used for experiments not involving deformation.

Measurements \( {\mathbf{d}}_{i}^{\text{m}} \) were obtained from the dilatometric tests at constant cooling rates. Components \( {\mathbf{d}}_{i}^{\text{c}} \) were calculated using the model of the direct problem, which was described in Section II–C. Identification of parameters of the phase transformation model was performed by the solution of the inverse problem using algorithm in Section III–B with x = a, see Reference 24 for details. Measuring the start and end temperatures for transformation and volume fractions of phases after cooling to room temperature was used as d m in the inverse analysis. Thus, in the particular case of phase transformations, the objective function [28] was defined as

$$ \varPhi ({\mathbf{x}},{\mathbf{p}}) = \sqrt {\frac{1}{n}\sum\limits_{i = 1}^{n} {\left( {\frac{{T_{{i{\text{m}}}} - T_{{i{\text{c}}}} }}{{T_{{i{\text{m}}}} }}} \right)^{2} + \frac{1}{k}\sum\limits_{i = 1}^{k} {\left( {\frac{{X_{{i{\text{m}}}} - X_{{i{\text{c}}}} }}{{X_{{i{\text{m}}}} }}} \right)^{2} } } } , $$
(31)

where T im and T ic is the measured and calculated start and end temperatures of phase transformations, °C, n is the number of temperature measurements, X im and X ic is the measured and calculated volume fractions of phases at room temperatures, and k is the number of measurements of volume fractions of phases.

Inverse analysis with the objective function [31] gave the values of the coefficients a in Table IV. Comparison of predicted and calculated CCT diagrams is shown in Figure 5(a), where A is the austenite, F is the ferrite, P is the pearlite, B is the bainite, and M is the martensite. Similar comparison for the volume fractions of the structural components is shown in Figure 5(b).

Table IV Coefficients in the Phase Transformation Model Obtained from the Inverse Analysis for the DP Steel with the Chemical Composition in Table I
Full size table
Fig. 5
figure 5

Comparison of the CCT diagrams (a) and volume fractions of structural components (b) obtained from measurements (filled symbols) and calculated by the model with the coefficients in Table IV (open symbols)

Full size image

The results of dilatometric tests were also used for identification of the CA model. Due to long computing times, four cooling rates were selected for identification purposes (Figure 6). This range was carefully selected to match industrial cooling conditions. It is seen that good agreement between measurements and predictions by the CA model was obtained.

Fig. 6
figure 6

Comparison of the CCT diagrams measured (filled symbols) and calculated by the CA model (open symbols) surrounded by corresponding morphology of microstructure. Bright grains represent ferrite and dark grains represent hard constituents P + B + M

Full size image

4.5 Physical Simulations

Physical simulation of the dual phase microstructure development was performed using the dilatometer DIL 805. The samples were heated to 1273 K (1000 °C), maintained at this temperature for 30 seconds, and cooled with three different thermal cycles, which are presented in Figure 7. The objective was to compare phase composition after these cycles. Calculated changes in the carbon concentration and obtained volume fractions on the basis of conventional and cellular automata based models are shown in Figures 8 and 9, respectively.

Fig. 7
figure 7

Thermal cycles used in physical simulations

Full size image
Fig. 8
figure 8

Changes of carbon concentration in the austenite during the 3 cooling cycles obtained from (a) conventional and (b) cellular automata models

Full size image
Fig. 9
figure 9

Volume fractions of phases after the 3 cooling cycles obtained from (a) conventional and (b) cellular automata models

Full size image

Obtained CA results are in agreement with those predicted by the conventional phase transformation model. The main difference is related with shorter incubation time forecasted by the CA model (Figure 8(b)). At this stage of development, the CA model predicts only ferritic transformation. Thus, depending on the cooling conditions, the remaining phase called hard constituent may be pearlite, bainite, or martensite. Both conventional and CA models predict phase transformation kinetics and volume fractions. However, the conventional model does not provide corresponding microstructure morphologies, which can be provided by the cellular automata (see Figure 6). This is the main advantage of the latter model. Comparison between numerical and experimental microstructure morphologies is presented in Figure 10.

Fig. 10
figure 10

Comparison between numerical (left) and experimental (right) microstructure morphologies after thermal cycles (a) I, (b) II and (c) III

Full size image

Analysis of the micrographs in Figure 10 allowed estimation of volume fractions. For the cycle I about 80 pct of the ferrite and 10 to 15 pct of the pearlite and traces of the bainite. For the cycles II and III observations are similar, about 80 pct of the ferrite is present in the microstructure, the rest is martensite and traces of the pearlite and the bainite. These observations agree with the CA model predictions from Figure 9. It can be concluded that cycle III gives the microstructure, which is the closest to the DP steel standard.

As presented, the CA model can significantly reduce amount of experimental investigation needed to obtain images of appropriate microstructure morphologies. Additionally, when the microstructure is in the digital form a quick qualitative and quantitative assessment can be performed, e.g., volume fraction calculation, average grain sizes, skeletonization, phase boundary length, etc., as presented in Figure 11.

Fig. 11
figure 11

Example of additional analyses that can be made on the basis of data from the CA model (a, b) skeletons of martensite and ferrite, respectively, (c, d) phase boundaries, (e, f) phase internal grain boundaries. Results for the thermal cycle I

Full size image

Quantitative comparison between results obtained for the investigated cooling cycles is given in Table V. As it is seen, obtained data are in good agreement with the experimental findings, what proves good predictive capabilities of the developed CA model. Degree of skeletonization for ferrite phase (M α ) and hard constituent (M β ) was defined as

$$ M_{\alpha } = \frac{{L_{\alpha } }}{\sum L }\quad M_{\beta } = \frac{{L_{\beta } }}{\sum L }, $$
(32)

where L α , L β is the skeletons length of ferrite phase and hard constituent, respectively.

Table V Quantitative Comparison of Results Obtained for Investigated Cooling Cycles
Full size table

5 Simulation of the Hot Rolling and Laminar Cooling

5.1 Hot Rolling

The developed models were applied to simulate the manufacturing process for the DP steel. Forces and austenite grain size changes during hot rolling in the 6th stand of the finishing train were calculated, see Reference 13 for the details of the process. These were typical hot rolling simulations and the results are not presented here. The objective was to evaluate the sensitivity of the DP microstructure with respect to the rolling parameters (entry temperature, reduction in passes, rolling velocity). Earlier analysis[25] has shown that the austenite grain size D γ is the only one parameter, which directly influences volume fractions of phases after laminar cooling. Although its influence on the volume fractions of bainite and martensite is small, it was considered in the next work.[26] It was shown that the finishing rolling temperature T f has also indirect influence on volume fractions of phases. Therefore, only those independent variables in rolling, which have the influence on T f and D γ were considered and the results are presented in Reference 26. In the present work, the finishing rolling temperature T f and the austenite grain size D γ were considered as independent variables in simulations of the laminar cooling process.

5.2 Laminar Cooling

An arbitrary laminar cooling system composed of two sections was considered. There were 40 boxes in each section and the length of each box was 1 m. Sections were divided into 12 zones of three types: intensive zone, normal zone, and trimming zone. Distance between the sections was 20 m. Schematic illustration of this laminar cooling system is shown in Figure 12. Number of boxes in each zone is given in the figure, as well as in Table VI. Maximum water flux in various zones is also given in Table VI. Maximum heat transfer coefficient for the laminar water cooling was calculated on the basis of equation proposed in Reference 8. This heat transfer coefficient was decreased proportionally to the water flux decrease.

Fig. 12
figure 12

Schematic illustration of the laminar cooling system for steel strips

Full size image
Table VI Number of Boxes and Maximum Water Flux in Each Zone of the Laminar Cooling (I, intensive; N, normal, T, trimming)
Full size table

The developed model was applied to simulate phase transformations during laminar cooling. Rolling velocity in the last stand v, strip thickness h, and finishing rolling temperature T f have been considered as independent variables. The objective of simulations was to design the cooling technology, which gives the required volume fractions of phases. Selected simulations with the objective to obtain 23 pct of hard constituents (martensite and bainite) and minimum of bainite in the steel were performed. Three cases are presented: case A with v = 7.5 m/s and h = 4 mm, case B with v = 7.5 m/s and h = 3 mm, and case C with v = 6 m/s and h = 3 mm. Finishing rolling temperature was 1153 K (880 °C) in all cases. Water flux in all zones for the three cooling cycles is given in Table VII. Figure 13(a) shows temperature changes calculated for the three cases. Figures 13(b) through (d) show kinetics of transformations for cases A, B, and C, respectively. Calculated volume fractions of phases are shown in Figure 14(a). The model calculates also changes the average carbon concentration in the austenite, which is presented in Figure 14(b). There are slight differences between the cooling cycles, but the average carbon concentration at the beginning of martensitic transformation is similar about 0.42.

Table VII Water Flux (m3/h) in Each Zone of the Laminar Cooling for the Cycles A, B, and C
Full size table
Fig. 13
figure 13

Temperatures calculated for the three considered cycles (a) and kinetics of transformations for h = 4 mm, v = 7.5 m/s (b), h = 3 mm, v = 7.5 m/s (c), h = 3 mm, v = 6 m/s (d)

Full size image
Fig. 14
figure 14

Calculated volume fractions of phases (a) and changes of the average carbon concentration in the austenite (b) for the three investigated cooling cycles

Full size image

Analysis of results in Figures 13 and 14 shows that developed model allows to design the cooling schedule, which gives required phase composition of the steel. Accuracy of the design of the cooling parameters can be improved by an application of the optimization methods, which will be the objective of future works. Performed simulations have shown that for thicker strips and larger velocity, the considered laminar cooling system is not efficient enough to avoid bainite in steel. Presented above numerical system, which can be used under industrial manufacturing conditions, is the main outcome from the research presented within the paper.

6 Conclusions

A set of microstructure evolution models were proposed in the paper. Physical simulations were used to identify and verify these models. The following conclusions were drawn:

  1. 1.

    Verification confirmed good predictive capabilities of developed models for phase transformations. Conventional model based on the Avrami equation predicts volume fractions for a wide range of cooling rates. CA model predicts detailed images of the microstructure, which replicates properly morphologies observed in the experiment.

  2. 2.

    Conventional model, when combined with the FE code for temperature calculations, is efficient in the design of laminar cooling technology. It was shown that the setup of the laminar cooling system, which gives required volume fractions of phases, can be selected for various thicknesses of the strip and rolling velocity.

  3. 3.

    CA model supplies extensive information regarding microstructure of the product. Such parameters as volume fractions of phases, average grain sizes and distribution of grain sizes, morphology of phases, skeletonization, and phase boundary length can be calculated.

  4. 4.

    Computing times for the multiscale Avrami + FE model are few orders of magnitude smaller than for the CA + FE model. Therefore, the former can be used for the optimization of the process, while the latter should be rather applied to scientific research on material behavior during heat treatment of DP steels.