1 Introduction

The properties of steels are highly sensitive to and predominantly controlled by their chemical composition and microstructure. For the production practice of steels, two kinds of alloying components, substitutional (i.e., Mn, Co, Ni, and Cr) and interstitial (i.e., C and N) elements, can be distinguished for manipulation of the final microstructure in order to optimize the mechanical, physical, and chemical properties. The microstructure of hot-rolled steel grades, for example, is essentially formed during the austenite (γ) to ferrite (α) phase transformation. So, the γ → α transformation in steels has been investigated extensively from both a technological point of view and a fundamental scientific point of view.[1–9]

In general, the γ → α phase transformation of steels comprises three overlapping mechanisms: nucleation, growth, and impingement. Upon nucleation, a new interface is generated that separates the product ferrite phase from the parent austenite phase. This interface migrates into the surrounding parent phase during the subsequent growth, and the migration rate of the interface principally is determined by the diffusion of alloying elements away from the interface and/or the mobility of the interface.[1,4–7] The thus formed microstructure is influenced by the impingement of the growing ferritic particles. Hence, occurrence of various nucleation and growth mechanisms would bring diversity in the prevailing γ → α transformation mechanism and thereby the resulting microstructure (i.e., a transition from interfaced-controlled to diffusion-controlled growth in isothermal annealing,[10,11] as well as a transition from diffusion-controlled to interface-controlled growth in isochronal annealing,[12] were observed during the γ → α transformation in ultra-low carbon Fe-C alloys).

Very recently, abnormal γ → α transformation behavior in pure iron and substitutionally alloyed Fe-Co alloys characterized by the occurrence of more than one maximum in the transformation rate as a function of transformed fraction and transition from diffusion-controlled to interface-controlled growth in ultra-low-carbon Fe-C alloy was recognized for the first time, with the aid of high-resolution dilatometry and differential thermal analysis.[13–15] Microscopic evidence and kinetic analysis on the basis of phase-transformation models demonstrated that the occurrence of the abnormal transformation part can be explained by a repeated (i.e., autocatalytic) nucleation ahead of the migrating γ/α interface and that in pure iron and the investigated substitutional iron-based alloys the entire γ → α transformation can be considered as a partitionless, massive transformation, i.e., occurring without any redistribution of the alloying element.[13–15] In the case of the ultra-low-carbon Fe-C alloy, it could be shown that at a moderated slow cooling rate (5 Kmin−1), the transformation rate curve exhibits a multiply peaked nature, the effect of which was shown to be due to a transition from diffusion-controlled growth to interface-controlled growth.[15]

Against the preceding background investigation of the influence of the other interstitial alloying component, nitrogen, which, for the same highly dilute composition, is known to diffuse slower than carbon in austenite, and which is of technological importance, i.e., for adjusting the surface performance,[16] is interesting. It was found in previous research[17] on Fe-0.96 at. pct Si-(20 to 3000 atom ppm) N that the transformation is shifted to lower temperature and is slowed down upon increasing the nitrogen content, and that substantial long-range diffusion of nitrogen would occur.

In this article, the isochronal-transformation characteristics of an ultra-low-nitrogen Fe-based alloy, Fe-0.005 at. pct N, have been systematically investigated by means of high-resolution dilatometric measurements. The thus obtained data of relative length change have been adopted for the determination of the kinetic parameters of the investigated γ → α transformation. In addition, microscopic analyses of the transformed specimens were performed.

2 Experimental Details

2.1 Alloy Production

Bulk Fe (with an impurity of carbon of 0.0014 at. pct C (Table I) for composition data) and a Fe-0.24 at. pct N master alloy prepared by a gas-nitriding process[18] were used for the preparation of alloys. The melting process was carried out in a vacuum inductive-melting furnace, and the molten alloy was cast in a copper mold.

Table I Chemical Composition of the Iron Used (Provided by Aldrich Chemical Company)
Full size table

The as-cast ingots of 7 mm in diameter were hammered down to rods of 6 mm in diameter. In order to achieve a homogeneous distribution of the alloying element, the rod was sealed in a quartz container filled with argon gas at 3 × 104 Pa, annealed at 1473 K for 100 hours, and cooled down to the ambient temperature within the furnace. The composition of the specimens was determined by inductively coupled plasma–optical emission spectrometry (ICP-OES). The nitrogen concentration, as measured both before and after the dilatometric measurements, of the investigated ultra-low-nitrogen Fe-N specimens is 0.0052 at. pct (Table II).

Table II Chemical Composition of the Investigated Ultra-Low-Nitrogen Fe-N Alloys as Determined by ICP-OES (Composition Uncertainty is Approximately 0.0009 Atomic Percent)
Full size table

The as-cast rods were machined from the cylindrical rod by a lathe into dilatometric specimens with a diameter of 5 mm and length of 10 mm. Fresh specimens were used for each dilatometric measurement cycle to ensure that for each measurement the specimen had the same initial microstructure and thermal/mechanical history.

2.2 Dilatometric Measurement

A Bähr DIL 802 differential dilatometer (Bähr Thermoanalyse GmbH, Hüllhorst, Germany) was used to record the length change of the samples. With this instrument, the length difference between the sample and an inert reference sample was measured, which resulted in a resolution of approximately ±10 nm (specimen length of approximately 10 mm). The measurements were performed under flowing high-purity argon (approximately 7.0 Lh−1) to protect the specimens from oxidation. The obtained differential dilatometry length-change signal was calibrated using the known thermal expansion of a standard single-crystal sapphire specimen, and the absolute temperature was calibrated by the Curie temperature of pure iron.[19]

2.3 Temperature Program

The applied annealing treatment cycle in the dilatometric experiments was in general as follows. The specimen was heated from room temperature to 1273 K with a (programmed) rate of 20 Kmin−1 and kept at this temperature only for 3 minutes (in order to avoid the loss of nitrogen at the high temperature). It was then cooled continuously with (programmed) rates of 5, 10, and 15 Kmin−1 to 373 K.

It has to be pointed out that the cooling rate of the sample for dilatometer measurements is somewhat smaller than the programmed cooling rate of the furnace. Table III presents a comparison of the programmed and actual cooling rates of the sample during the γ → α transformation.

Table III Comparison of the Programmed and the Actual Cooling Rates around the Explored γ → α Transformation during the Dilatometric Measurements of Fe-0.005 At. Pct N Alloy (Unit: Kmin− 1)
Full size table

2.4 Microstructural Analysis

2.4.1 Grain-size determination

The ferrite grain sizes of the fully transformed specimens (after the dilatometric experiments) were analyzed by light microscopical analysis. The grain boundaries were revealed by etching with a 2.5 vol pct Nital solution. The line-intercept method[20] was employed in three different directions in order to determine the mean grain size. The line-intercept method results in a grain-size value, which underestimates the true grain size. The true average of all grain diameters of the ferrite was thus assessed by multiplying the obtained intercept length by a factor of 1.5.[20] The grain-size distribution was obtained by dividing the number of grains in a certain range of the true grain diameter by the total number of measured grains.

2.4.2 Texture analysis

The orientation relationships of the (adjacent) (sub)grains in the annealed dilatometric specimens were determined by application of orientation imaging microscopy (OIM) employing a scanning electron microscope (LEO 438VP, LEO Electron Microscopy Ltd., Cambridge, England) equipped with a device for recording electron back scattered diffraction patterns leading to so-called Kikuchi patterns (TSL, OIM 2.6 for data acquisition and evaluation). This technique allows the measuring of crystal orientations with a resolution of 1 deg at a lateral spatial resolution of 0.3 μm.[21]

3 Isochronal γ → α Transformation Characteristics In fe-0.005 At. Pct N

3.1 Dilatometric Measurements

3.1.1 Thermal expansion behavior

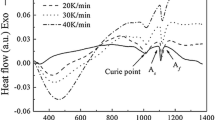
The recorded relative length change of the investigated interstitial Fe-0.005 at. pct N specimen with a heating rate of 20 Kmin−1 and a cooling rate of 10 Kmin−1, respectively, during one heat treatment cycle as described in Section II–C, is shown in Figure 1(a). During continuous heating, the specimen expands before the onset of the α → γ transformation; the transformation is associated with a length contraction. After completion of the transformation, the normal thermal expansion and contraction of austenite occurs upon continued heating and subsequent cooling. After completion of the γ → α transformation upon cooling, associated with length increase, the normal thermal contraction of ferrite can be observed upon continued cooling.

Fig. 1
figure 1

(a) Measured relative length changes of an Fe-0.005 at. pct N specimen during continuous heating (20 Kmin−1) from room temperature to 1223 K and subsequent continuous cooling (10 Kmin−1) interrupted by an isothermal annealing at 1223 K for 3 min and (b) enlargement of the high-temperature part of (a) on cooling

Full size image

The transformation upon heating is associated with the (inhomogeneous) build up of the α/γ misfit deformation energy. After completion of the α → γ phase transformation upon heating, this misfit-strain energy relaxes, which corresponds with length reduction on top of the length increase due to thermal expansion (arrow B in Figure 1(a)). Therefore, the slope of the recorded length change of austenite upon continued heating after the α → γ transformation is not constant. After holding at 1223 K for 3 minutes, the misfit-strain energy has fully relaxed. Then, upon subsequent cooling, only normal contraction of austenite occurs, and the correspondingly recorded dilation data reflect (only) the thermal linear contraction of austenite.

As pointed out by Richter and Mülheims[22], the small length change of the specimen (less than 0.1 μm for a specimen length of approximately 10 mm) after one complete measurement cycle, i.e., including one α → γ transformation and one γ → α transformation, is not accompanied by a density change of the sample: the growth of the product phase during the phase transformation is not completely isotropic. Because the kinetic analysis is based on the relative change in length during the phase transformation, the fractions of γ and α phase can be calculated from the data of relative length change ( \( \frac{{\Delta L}} {{L_{0} }} \) where L 0 is the initial specimen length and ΔL is the length change) during the (nonisothermal) transformation as described by Li et al.[23]

It has also to be noted the ferromagnetic-paramagnetic transition temperature (Curie temperature), indicated by the dashed arrows in Figure 1(a), associated with a sudden change in the recorded length-change curves, has been adopted for the temperature calibration.[19] Further, it is observed that a slight change in slope, marked by A, occurs in the recorded length-change curve at approximately 680 K. This instrumental effect is caused by a radial temperature gradient in the sample due to the heating from the surrounding furnace. Above 750 K (the transformation occurs at approximately 1160 K), the sample exhibits a uniform temperature and a constant expansion coefficient (outside the region of the magnetic transition). The effect is observed for a high heating rate (20 Kmin−1) as programmed to avoid possible loss of nitrogen during the heating described in Section II–C. For the cooling rate of 10 Kmin−1, such a phenomenon did not occur in the measured curve (Figure 1(a)).

The high-temperature part of the relative length changes of the Fe-0.005 at. pct N specimen upon cooling is shown in Figure 1(b). Clearly, the γ → α transformation shows an abnormal change of length (indicated by the arrow in Figure 1(b)). The effect occurs for all applied cooling rates (Figure 2).

Fig. 2
figure 2

The ferrite fraction, f α , as a function of temperature T, calculated from isochronal dilatometric measurements of different fresh Fe-0.005 at. pct N specimens (i.e., having the same thermal and mechanical history) subjected to cooling from the austenite-phase field at rates of 5, 10, and 15 Kmin−1

Full size image

3.2 Ferrite fraction and ferrite formation rate

The dilation behavior of different fresh Fe-0.005 at. pct N specimens was investigated for different cooling rates (5, 10, and 15 Kmin−1)Footnote 1. The development of the ferrite fraction, f α , determined in the preceding the length-change data is shown as a function of temperature in Figure 2. The curves of f α , for 5, 10, and 15 Kmin−1 are more or less parallel to each other. The higher the applied cooling rates, the lower the onset temperature of the γ → α transformation.

The variation of the austenite-ferrite transformation behavior is particularly evident by closely inspecting the transformation rate, \( {df_{\alpha } } \mathord{\left/ {\vphantom {{df_{\alpha } } {dt}}} \right. \kern-\nulldelimiterspace} {dt} \) (\( {dT} \mathord{\left/ {\vphantom {{dT} {dt}}} \right. \kern-\nulldelimiterspace} {dt} \) is known and constant). The corresponding results for \( {df_{\alpha } } \mathord{\left/ {\vphantom {{df_{\alpha } } {dt}}} \right. \kern-\nulldelimiterspace} {dt} \) are shown as a function of the transformation temperature, T (Figure 3(a)) and as function of the ferrite fraction, f α (Figure 3(b)). It is important to note that the observed fluctuations of \( {df_{\alpha } } \mathord{\left/ {\vphantom {{df_{\alpha } } {dt}}} \right. \kern-\nulldelimiterspace} {dt} \) (of relative value of approximately 10−1 (Figure 3)) are much larger than the relative error of ±1 × 10−3 in f α due to the accuracy of the length change data of approximately ±10 nm. The following observations can be made.

  1. (a)

    Abnormal transformation behavior, characterized by the occurrence of two maxima in the transformation rate curve, was detected for all applied cooling rates in the Fe-0.005 at. pct N specimens.

  2. (b)

    The value of \( {df_{\alpha } } \mathord{\left/ {\vphantom {{df_{\alpha } } {dt}}} \right. \kern-\nulldelimiterspace} {dt} \) in the range of the first peak (abnormal transformation) increases strongly with increasing the applied cooling rate. The range of the first peak ends at approximately f α  = 0.13 (Figure 3(b)), which also represents the start of the last, main maximum (normal transformation).

  3. (c)

    The value of \( {df_{\alpha } } \mathord{\left/ {\vphantom {{df_{\alpha } } {dt}}} \right. \kern-\nulldelimiterspace} {dt} \) in the range of the last, main maximum (normal transformation) increases slightly with increasing applied cooling rate.

The preceding observation for the transformation behavior for the γ → α transformation in the Fe-0.005 at. pct N alloy resembles the abnormal transformation behavior observed for pure iron (and the substitutional iron-based Fe-Co alloy) and contrasts with the transformation behavior observed for the ultra-low-carbon Fe-C, as discussed in Section IV–B.

Fig. 3
figure 3

The ferrite transformation rate, df α /dt, as a function of (a) temperature, T, (b) ferrite fraction, f α , of the investigated Fe-0.005 at. pct N alloy for applied cooling rates of 5, 10, and 15 Kmin−1

Full size image

3.3 Microstructural Analysis

The microstructure of the explored Fe-0.005 at. pct N specimens after completed γ → α transformation with an applied cooling rate of 10 Kmin−1 is shown in the micrograph of Figure 4. The ferrite produced by the γ → α transformation is composed of irregular, equaxed grains; many subgrains have formed along the original grain boundaries of a large austenite grain as discussed in Section V–B–2.

Fig. 4
figure 4

Ferrite grain morphology of Fe-0.005 at. pct N alloy after completed γ → α transformation (cooling rate of 10 Kmin−1). Light optical micrograph; applied etchant: 2.5 vol pct Nital solution

Full size image

An example of the crystallographic orientation variation in the ferrite microstructure and, therefore, the grain morphology of the completely transformed ultra-low-nitrogen Fe-N alloy is shown in the OIM micrograph of Figure 5. The austenite grain-size distribution before the γ → α transformation in the case of an abnormal α → γ → α transformation could be approximately distinguished and estimated by the final ferrite grains exhibiting large-angle boundaries representing orientation differences larger than 15 deg, a result obtained from OIM measurements (thick black lines in Figure 5). This austenite grain-size distribution is monomodal and corresponds to the initial ferrite grain-size distribution also regarding the average grain size (Figure 6). Subgrains separated by small-angle boundaries with differences in orientation from 2 to 5 deg can be discerned by image contrast. Evidently, many subgrains have formed, mainly along the grain boundaries of the large (initially) austenite grains.

Fig. 5
figure 5

High-angle grain boundaries (thick, black lines) and small-angle grain boundaries between subgrains (thin, gray lines) in the investigated Fe-0.005 at. pct N alloy after completed transformation (cooling rate of 10 Kmin−1)

Full size image
Fig. 6
figure 6

Comparison of the grain-size distributions of the original ferrite, of the austenite (represented by the ferrite grains after the transformation exhibiting orientation differences larger than 15 deg), and of the transformed (final) ferrite, of the investigated Fe-0.005 at. pct N alloy for an applied cooling rate of 10 Kmin−1

Full size image

Grain-size measurements of the Fe-0.005 at. pct N alloys after the γ → α transformations and cooling to room temperature were performed by taking a series of parallel optical cross-sectional images according to the method discussed in Section II–D. The etched cross sections (Figure 4) reveal both the original austenite (high angle according to the OIM analysis (Figure 5)) grain boundaries and subgrain (low angle according to the OIM analysis (Figure 5)) boundaries. The average ferrite-grain diameters measurements have been collected in Table IV as a function of the applied cooling rate. It follows that the average ferrite-grain diameter of Fe-0.005 at. pct N decreases with an increase of the applied cooling rate from 5 to 15 Kmin−1: the average grain size decreases from 219 to 145 μm. Note that the initial grain size of the Fe-0.005 at. pct N specimen before annealing is approximately 253 μm, which indicates a form of grain refinement due to the γ → α transformation under different cooling rates. Grain-size distributions of the Fe-0.005 at. pct N specimens, after completed γ → α transformation and as measured at room temperature, were determined by the method discussed in Section II–D–1. The grain-size distributions are shown in Figure 7 for the various cooling rates. Evidently, a bimodal distribution of the grain-size results for all cooling rates applied, which is not induced by a possible prior bimodal austenite grain-size distribution, as a monomodal grain-size distribution was present, as discussed in Section V–B–2 (Figure 6).

Table IV Measured Ferrite Grain Size, d α , and the Corresponding Estimated Nucleus Density N * (\( N^{*} = d^{{ - 3}}_{\alpha } \) Unit: m− 3) of the Investigated Fe-0.005 At. Pct N Alloy for Applied Cooling Rates of 5, 10, and 15 Kmin− 1
Full size table
Fig. 7
figure 7

The ferrite grain-size distribution of the investigated Fe-0.005 at. pct N alloy for applied cooling rates of 5, 10, and 15 Kmin−1 after completed transformation

Full size image

4 Transformation Mechanism

4.1 Onset Temperature

The chemical Gibbs energies of the austenite and ferrite of the investigated interstitial Fe-N alloy system, \( G^{\gamma }_{{{\text{Fe - N}}}} \) and \( G^{\alpha }_{{{\text{Fe - N}}}} \), can be evaluated as a function of transformation temperature, T, and nitrogen concentration, using the data given by Wriedt.[24] The so-called T 0 temperature, where the Gibbs energy of the metastable γ phase equals that of the metastable α phase for the same nitrogen concentration, was calculated as a function of nitrogen concentration. Thus, the determined T 0 line is given in the partial phase diagram of the Fe-N system of Figure 8.

Fig. 8
figure 8

Partial phase diagrams of Fe-X (X = C and N). The vertical dash-dotted lines indicate the interstitial solute concentrations (0.0052 at. pct N and 0.0108 at. pct C) and the dotted lines indicate the \( T^{{{\text{Fe - N}}}}_{{\text{0}}} \)and \( T^{{{\text{Fe - C}}}}_{{\text{0}}} \) lines

Full size image

The experimentally determined onset temperatures, T onset, for the γ → α transformation in the ultra-low-nitrogen Fe-N alloy specimens have been given for all applied cooling rates in Table V. It follows that the onset transformation temperatures for all applied cooling rates are located in the single α-phase field; the onset temperature decreases with increasing the applied cooling rate. This transformation is accordingly interface controlled. It was recently demonstrated by phase-field simulations and using available diffusional mobilities that solute drag effects can occur for binary Fe-based alloys below the T 0 line and above the α-solvus line.[6] Below this α-solvus line, the transformation is massive, and the driving force (Gibbs energy difference) is used to move the interface and is not dissipated by diffusion of solutes to the interface and through the interface. All measured onset temperatures of the investigated α → γ transformations of Fe-0.005 at. pct N are below the α-solvus line, and thus solute drag is not expected to play a role.

Table V Onset Temperature, T onset, for the γ → α Transformation of the Investigated Fe-0.005 At. Pct N Specimens Subjected to Different Applied Cooling Rates
Full size table

4.2 Comparison with the γ → α Transformation in Pure Iron and Fe-C

Very recently, an abnormal γ → α transformation behavior (i.e., multiple transformation-rate maxima) was observed for pure iron and substitutional iron-based alloys,[13–15] and an unusual transition from diffusion-controlled to interface-controlled growth was observed for the ultra-low-carbon Fe-C alloy.[12] A direct comparison among pure iron (Figure 9(a)), ultra-low-carbon Fe-C alloy (Figure 9(b)), and ultra-low-nitrogen Fe-N alloy (Figure 3(b)) immediately reveals a similarity of transformation kinetics for Fe-0.005 at. pct N and pure iron (this statement also holds for the substitutional iron-based alloys), and an apparently different kinetic behavior for ultra-low-carbon Fe-C alloy as follows:

  1. (a)

    The number of additional rate maxima in the first part of the transformation does not depend on cooling rate for pure iron and ultra-low-nitrogen Fe-N alloy, whereas for Fe-0.01 at. pct C alloy, the number of additional rate maxima decreases with the increasing cooling rate.

  2. (b)

    For pure iron and ultra-low-nitrogen Fe-N alloy, the additional rate maxima occur at approximately the same value of the degree of transformation and increase with the increasing cooling rate. This does not hold for Fe-0.01 at. pct C alloy.

  3. (c)

    The onset transformation temperatures for pure iron and ultra-low-nitrogen Fe-N alloy are located in the single α-phase field, whereas the onset transformation temperatures (for the diffusion-controlled growth part) in ultra-low-carbon Fe-C alloy are located between the T 0 temperature and the solvus temperature of ferrite (Figure 8).

The difference in γ → α transformation behavior between the ultra-low interstitial Fe-N and Fe-C alloys can be understood as follows. (a) The solvus line in the partial phase diagram of Fe-C lies at distinctly lower temperatures, and the T 0 line lies at distinctly higher temperatures, than holds for Fe-N, for the same amount of interstitial content (Figure 8). Thus, upon cooling with the same rate from the austenite-phase field, the Fe-C alloy spends more time (below T 0) in the α-γ two-phase field than the Fe-N alloy with the same interstitial content. (b) Moreover, for the ranges of (ultra-low) interstitial content and temperature concerned, it always holds that the diffusion coefficient of carbon in austenite is more than a factor of 2 larger than the diffusion coefficient of nitrogen in austenite (Figure 10; diffusion coefficients calculated from data taken from Saker et al.[25] and Magee[26]). Both factors, (a) and (b), make it likely that the transition from diffusion-controlled to interface-controlled is much more probable to occur in Fe-C alloy than in Fe-N alloy.

Fig. 9
figure 9

The ferrite transformation rate, \( {df_{\alpha } } \mathord{\left/ {\vphantom {{df_{\alpha } } {dt}}} \right. \kern-\nulldelimiterspace} {dt} \), as a function of ferrite fraction, f α , of (a) pure iron for applied cooling rates of 5, 10, 15 Kmin−1,[14] and 20 Kmin−1,[12] (b) Fe-0.01 at. pct C alloy for applied cooling rates of 5, 10, 15, and 20 Kmin−1[14] (Fig. 3(b) for Fe-0.005 at. pct N)

Full size image
Fig. 10
figure 10

The diffusion coefficient for the interstitial elements (nitrogen and carbon) in austenite as a function of temperature for the composition range up to approximately 0.01 at. pct. The subscripts indicate the solute concentrations

Full size image

5 Kinetic Analysis Of The Isochronal γ → α Transformation In Fe-0.005 At. Pct N

5.1 Later (Main), Normal Transformation Stage

5.1.1 Phase-transformation model

A general model of phase-transformation kinetics can be proposed on the basis of a modular constitution of nucleation, growth, and impingement processes.[27–29] The first step of this approach involves the calculation of the volume of all growing particles, assuming that all grains never stop growing and that new grains hypothetically nucleate also in the transformed material; extended transformation fraction, i.e., at this stage, “hard impingement,” is ignored. In the next step, the extended transformed fraction is corrected for hard impingement of the growing particles, and the corresponding real transformed fraction is obtained.

Based on site saturation, interface-controlled growth, and an impingement model that is an intermediate of the cases of ideally randomly and of ideally periodically dispersed growing particles (f α = tanh (x e ) with x e as the extended transformed fraction), the phase transformation model can be given as follows:[15,28]

$$ \frac{{df_{\alpha } }} {{dt}} = 3(N^{*} g)^{{\frac{1} {3}}} (1 - f^{2}_{\alpha } )v_{\alpha } \text{arctan h} ^{{\frac{2} {3}}} (f_{\alpha } ) $$
(1)

where v α is the migration velocity of the γ/α interface, g is a geometrical factorFootnote 2 (for cubic growth, g = 1; for spherical growth, \( g = {4\pi } \mathord{\left/ {\vphantom {{4\pi } 3}} \right. \kern-\nulldelimiterspace} 3 \)), and N * is the number of nuclei per unit volume.

Hence, for a known number density of nuclei per unit volume (N *) and a known value of g, the interface-migration velocity (v α ) can be determined as a function of temperature, time, or transformed fraction by using data of f α and \( {df_{\alpha } } \mathord{\left/ {\vphantom {{df_{\alpha } } {dx_{e} }}} \right. \kern-\nulldelimiterspace} {dx_{e} } \), as obtained from the isochronal measurements.

In the case of anisotropically growing particles (including thin ferrite films), the time interval that particles, nucleated randomly or nonrandomly, can grow, before blocking by other particles occurs, is on average smaller than in the case of isotropic growth. These effects have been studied quantitatively by Monte Carlo simulations.[31] A simple phenomenological approach accounting for these (hard) impingement effects has been proposed by Starink[32] and Kooi.[33] An anisotropic growth of the nucleus can be considered by this approach,[30] introducing for \( {df_{\alpha } } \mathord{\left/ {\vphantom {{df_{\alpha } } {dx_{e} }}} \right. \kern-\nulldelimiterspace} {dx_{e} } \) the expression \( \frac{{df_{\alpha } }} {{dx_{e} }} = (1 - f_{\alpha } )^{\xi } \). This leads (for strongly anisotropic growth; ξ = 2) to only a small increase of the obtained interface-migration velocity in the later part of the γ-α transformation. Furthermore, it is noted that in all our investigated nonisothermal γ → α transformations of binary Fe-based alloys,[13,15] a filmlike growth of the α phase was not observed. Further, considering a nonrandom nuclei distribution[30] leads to an even smaller change in the interface velocity for the γ → α transformation of Fe-0.005 at. pct N.

5.1.2 Determination of interface-migration velocity

The nucleus density can be estimated by the number of final (product phase) grains, assuming (implicitly) that (only) one nucleus is the origin of each grain. Thus, \( N^{ * } = d^{{ - 3}}_{\alpha } \), where d α is grain size of the product phase. The accordingly estimated value for the initial nucleus density may be an underestimate of the real nucleus density due to possible grain coarsening at higher temperatures during the cooling after the γ → α transformation. Evidently, because N * occurs in Eq. [1] with exponent 1/3, an experimental error in the nucleus density does not strongly influence the calculated values for the velocity of interface migration. In this article, all initial nucleus-density values were estimated from the product ferrite grain size (Table IV).

Adopting the nucleus density, estimated by the averaged ferritic grain size (Table IV) and using the measured experimental data for f α and \( {df_{\alpha } } \mathord{\left/ {\vphantom {{df_{\alpha } } {dt}}} \right. \kern-\nulldelimiterspace} {dt} \) in the range of the later main transformation stage (i.e.,, 0.13 < f α  < 1), the interface-migration velocity was calculated as a function of the progress of transformation (Figure 11). It follows that the interface velocity is practically constant during the transformation. It was also found that the interface-migration velocity is practically independent of the cooling rate (Table VI). Therefore, adopting a constant interface-migration velocity, a definitive fitting of the model to simultaneously the data obtained for all cooling rates was performed. A fit of reasonable quality has been obtained (Figure 12), and thus the obtained interface-migration velocity is 1.96 × 10−6 ms−1.

Fig. 11
figure 11

The interface-migration velocity, v α , as a function of the ferrite fraction, f α, for the investigated Fe-0.005 at. pct N alloy, the Fe-0.01 at. pct C alloy,[14] and pure iron[12] for an applied cooling rate of 20 Kmin−1

Full size image
Table VI The γ-α Interface-Migration Velocity, v α (Unit: ms− 1), as Determined for the Investigated Fe-0.005 At. Pct N Alloy Subjected to Different Applied Cooling Rates
Full size table
Fig. 12
figure 12

The measured and calculated transformation rate, \( {df_{\alpha } } \mathord{\left/ {\vphantom {{df_{\alpha } } {dt}}} \right. \kern-\nulldelimiterspace} {dt} \), as a function of ferrite fraction, f α , of the investigated Fe-0.005 at. pct N alloy for applied cooling rates of 5, 10, and 15 Kmin−1; the smooth curves represent the calculated results for constant interface velocity according to Eq. [1] for the main (normal) part of the transformation

Full size image

From the preceding results, it follows that the value of the interface-migration velocity is practically constant during the entire transformation temperature range of the investigated Fe-0.005 at. pct N specimens for the applied cooling rates from 5 to 15 Kmin−1 (Figure 11), which corresponds well with the results obtained recently for the γ → α transformation in pure iron[14] and substitutional Fe-1.79 at. pct Co alloy.[15] The value of the interface-migration velocity for the γ → α transformation of Fe-0.005 at. pct N is smaller than for pure iron:[14] 1.96 × 10−6 ms−1 vs 3.91 × 10−6 ms−1 and slightly larger than for Fe-0.01 at. pct C:[12] 1.96 × 10−6 ms−1 vs 1.61 × 10−6 ms−1 (Figure 11; note that if diffusion control would prevail for the γ → α transformation in Fe-N, then an interface velocity smaller than for Fe-C could be expected because the diffusion coefficient of nitrogen in γ-Fe is smaller than of carbon in γ-Fe; Figure 10).

The observed fluctuations in v α are much larger than the experimental accuracy, as can be demonstrated as follows. The accuracy of the length change data is approximately ±10 nm as discussed in Section II–B, which causes a relative error of ±3 × 10−4 in the value determined for the ferrite fraction. This uncertainly in f α introduces a relative error of ±1 × 10−3 for the interface velocity calculated according to Eq. [1], which is much smaller than the observed fluctuations (of relative value 1 × 10−1) of v α (Figure 11). The observed fluctuations of v α may correspond to a succession of periods of acceleration and deceleration in the interface-migration process (due to the accumulation and relaxation, i.e., by the vacancy diffusion,[34] of stress), in correspondence with observations by in-situ transmission electron microscopy analysis,[35] recognizing that the interface density in these large-grained specimens is small such that insufficient averaging occurs for the recorded dilatometric signal.

5.1.3 Interface mobility and transformation strain

The growth velocity of the migrating interface can be given by the following equation:[27]

$$ v = M( - \Delta G) $$
(2a)

with

$$ M = M_{0} \exp {\left( { - \frac{Q} {{{\text{R}}T}}} \right)} $$
(2b)

where M is the interface mobility, Q is the activation energy, and \( - \Delta G \equiv \Delta G_{\alpha } - \Delta G_{\gamma } \) denotes the driving force for the α → γ transformation. This equation holds in particular for small undercooling (−ΔG γα small compared to RT).[30]

Data for the interface mobility, M(T) (Eq. [2b]), are experimentally hardly available. With known values for the driving force and the interface-migration velocity, the interface mobility can be calculated. Mobility data obtained in this way for the grain growth of pure iron (ferrite) (M = 0.035 exp (−147,000/RT) m4 J−1 s−1 = 4.9 × 103 exp (−147,000/RT) mmolJ−1 s−1)[36] were adopted for the kinetic analyses in our previous publications.[14,15,28] These values reflect the intrinsic mobility of an α/α interface: no phase change takes place upon grain growth; the chemical driving force is zero; the elastic and plastic accommodation energy can be neglected; and the only driving force is the (decrease of) interface energy. The mobility values for α/α and γ/α interfaces were discussed recently,[37] and it was stated that there is a strong indication from the evaluated γ/α mobilities (determined by assuming only the difference in chemical Gibbs energy as driving force) that the γ/α mobility is much lower than that of the α/α interface boundaries, which is also stated in Gamsjäger et al.,[38] Wits et al.,[39] and Krielaart and van der Zwaag.[40] However, the effect of transformation-strain energy on the interface mobility was ignored in these works.

An estimate of the γ/α mobility, obtained in the way adopted by Hillert and Höglund,[37] Gamsjäger et al.,[38] Wits et al.,[39] and Krielaart and van der Zwaag[40] can be obtained, as well as from our experimentally determined transformed fraction for the massive γ/α transformation of pure iron (samples C and D, with the small grain size[14]).

The combination of Eq. [1] with Eq. [2b] results in the following equation:

$$ \frac{{df_{\alpha } }} {{dt}} = 3(N^{*} g)^{{\frac{1} {3}}} (1 - f^{2}_{\alpha } )M_{0} \exp {\text{ }}\left(\frac{{ - Q}} {{{\text{R}}T}}\right)( - \Delta G^{{{\text{chem}}}}_{{\alpha \gamma }} )\text{arctan\,h} ^{{\frac{2} {3}}} (f_{\alpha } ) $$
(3)

The preceding equation can be used to determine M 0 values by fittings adopting the nucleus density as estimated from the measured grain size and by using the experimental data of ferrite fraction and ferrite-transformation rate. The temperature dependence of the chemical driving force (\( - \Delta G^{{{\text{chem}}}}_{{\alpha \gamma }} \)) of pure iron at atmospheric pressure was evaluated according to Scientific Group Thermodata Europe (SGTE).[41] The magnetic model given by Hillert and Jarl[42] was adopted to evaluate the magnetic contribution to the ferrite Gibbs energy. M 0 was taken as the fitting parameter for the normal, main maximum in the explored γ → α phase transformation-rate curve of pure iron; the activation energy of M was assumed to be the same as that for the grain growth of ferrite. A comparison of the experimental and fitted ferrite fractions can be made as function of the transformation temperature in Figure 13. The obtained M 0 values are 1.4 (C), and 1.3 (D) mmolJ−1 s−1. As a result, an average value is obtained for M 0 for the γ/α interface in pure iron: approximately 1.35 mmolJ−1 s−1, also much lower than for the α/α interface.

Fig. 13
figure 13

Comparison of the experimental and fitted values for the ferrite fraction (f α ) as function of transformation temperature (T) in pure iron of different grain sizes: (a) sample C and (b) sample D in Ref. 14 (applied cooling rate of 10 Kmin−1)

Full size image

However, it should be emphasized in particular that the effect of the occurring unknown elastic and plastic accommodation energies (not recognized in Eq. [3]) for the γ/α transformation of pure iron now are implicitly incorporated in the previously obtained value for M 0. This may simply explain the difference, as discussed by Hillert and Höglund,[37] of such calculated M 0 values for γ/α and α/α interfaces.

The transformation energy does have a direct implication for the resulting growth velocity. The (negative of the) driving force for the explored γ → α transformation can be written as follows:[14,15,28]

$$ \Delta G_{{\alpha \gamma }} (T,f_{\alpha } ) = \Delta G^{{{\text{chem}}}}_{{\alpha \gamma }} (T) + {\left[ {\Delta G^{{{\text{def}}}}_{{\alpha \gamma }} (f_{\alpha } ) + \Delta G^{{{\text{int}}}}_{{\alpha \gamma }} (f_{\alpha } )} \right]} $$
(4)

where \( \Delta G^{{{\text{chem}}}}_{{\alpha \gamma }} \)is the molar chemical Gibbs energy difference of the ferrite and austenite, \( \Delta G^{{{\text{def}}}}_{{\alpha \gamma }} \) is the summation of molar elastic and plastic accommodation energies resulting from the crystalline strain induced to accommodate the volume misfit of ferrite and austenite, and \( \Delta G^{{{\text{int}}}}_{{\alpha \gamma }} \) is the molar free energy of the γ/α interface. The chemical driving force depends on temperature, and not on the fraction transformed, because the transformation is partitionless. Both \( \Delta G^{{{\text{def}}}}_{{\alpha \gamma }} \) and \( \Delta G^{{{\text{int}}}}_{{\alpha \gamma }} \)depend primarily on the fraction transformed (f α ) (and not directly on temperature). The driving force (−ΔG αγ ) consists of a negative term (\( \Delta G^{{{\text{chem}}}}_{{\alpha \gamma }} \)), which favors the transformation, and two positive terms (\( \Delta G^{{{\text{def}}}}_{{\alpha \gamma }} \) and \( \Delta G^{{{\text{int}}}}_{{\alpha \gamma }} \)), which counteract the transformation. The term, \( \Delta G^{{{\text{int}}}}_{{\alpha \gamma }} \), can be neglected for the determination of transformation-strain energy.[14,15,28]

In the research,[14,15,28] the transformation-strain energy, \( \Delta G^{{{\text{def}}}}_{{\alpha \gamma }} \), has been determined from the calculated interface-migration velocity and the mobility data of the α/α interface. It turns out that the obtained transformation-strain energy (\( \Delta G^{{{\text{def}}}}_{{\alpha \gamma }} \)) is nearly as large as the chemical driving force (\( \Delta G^{{{\text{chem}}}}_{{\alpha \gamma }} \)). Of course, this result depends on the value adopted for M 0. One may propose to apply the much lower estimate for M 0 derived above for the γ/α transformation in pure iron, ignoring the role of transformation-strain energies. For example, such a calculation has been performed for the normal transformation of the Fe-1.79 at. pct Co alloy[15] (Figure 14). The then determined deformation energy is approximately 10 Jmol−1. A similar kinetic analysis for data of Fe-1.89 at. pct Mn[15] results in considerably larger values (approximately 60 to 90 Jmol−1). The transformation-strain energy appears to vary largely for different alloy systems. Although largely different M 0 values (different by a factor of 103) have now been used, the difference in transformation-strain energy is only a factor of 3. Hence, as follows from the use of a M 0 value for the γ/α interface, as calculated ignoring the contribution of strain energy (considered in this article as a conceptual flaw), in any case the previously calculation demonstrated that the role of transformation strain on the kinetics of the γ/α transformation cannot be ignored.

Fig. 14
figure 14

The calculated sum of elastic and plastic accommodation energy and interface energy as a function of ferrite fraction (f α ) during the normal γ → α transformation of Fe-1.79 at. pct Co alloy (cooling rate of 10 Kmin−1) by adopting different M 0 (unit: mmolJ−1 s−1) values

Full size image

5.2 First Abnormal Transformation Stage

5.2.1 Phase transformation model

The γ → α transformation is accompanied by an increase of a considerable amount of volume misfit-strain energy. Thus, it is likely that the volume misfit-strain energy largely influences the transformation kinetics. A growing ferrite grain induces strain and defects in the surrounding austenite. This deformed austenite, immediately in front of the growing ferrite, may allow easier nucleation of ferrite than undeformed austenite. Thus, occurrence of repeated nucleation[13,14] (i.e., autocatalytic nucleation) provides a possible explanation for the occurrence of additional rate maxima in the beginning of the transformation and can explain the occurrence of the abnormal transformation. The burst of nucleation sites in deformed austenite in front of the growing ferrite leads to a sudden increase in the transformation rate, and the following sharp drop of the transformation rate can only correspond to a decrease of activated nuclei. This argument is supported by the measured grain size after the transformation: this measured grain size is definitely larger than the value that could be estimated by the nucleus density of active nuclei during the abnormal stage, supposing that all activated nuclei grow until the end of the transformation.

The occurrence of autocatalytic nucleation, as described in Section V–A–1, implies that the kinetic model used to describe the normal transformation kinetics cannot be applied in the case of abnormal transformation kinetics because site saturation does not hold for abnormal transformation kinetics: time-dependent nucleation has to be incorporated in the phase-transformation model. The repeated nucleation of ferrite in front of the migrating γ-α interface during the first stage of transformation, where abnormal kinetics occurs, may be described by a variation of the number of nucleation sites of the type, pf α , with p as the autocatalytic factor.[26,43]

The decrease of activated nuclei leads to the introduction of a correction factor in the expression for the nucleation density that depends on the degree of transformation and that, in first order approximation, may be taken as (\( \frac{{f_{{tr}} - f_{\alpha } }} {{f_{{tr}} - f_{{st}} }} \)), where f st and f tr denote the degrees of transformation at the start and finish of the nucleation “burst” concerned, respectively.

Thus, the nuclei number for the first peak in the \( {df_{\alpha } } \mathord{\left/ {\vphantom {{df_{\alpha } } {dt}}} \right. \kern-\nulldelimiterspace} {dt} \) curve (abnormal transformation part) of ultra-low-nitrogen Fe-N specimens considered here can be expressed as follows:

$$ N = N^{*} \delta (\tau - 0) + p(f_{\alpha } - f_{{st}} )\frac{{(f_{{tr}} - f_{\alpha } )}} {{(f_{{tr}} - f_{{st}} )}} $$
(5)

where N * is the initial nucleus density (contribution due to site saturation; as estimated from the measured ferrite grain size (Table IV)).

Following a treatment analogous to the one given for pure iron by Liu et al.,[14] the following equation is obtained:

$$ \arctan {\text{h}}(f_{\alpha } ) = v^{3}_{\alpha } {\left[ {N^{*} t^{3} + \frac{{ap}} {{f_{{tr}} - f_{{st}} }}{\int\limits_0^t {\frac{{df_{\alpha } }} {{d\tau }}(f_{{tr}} - 2f_{\alpha } )(t - \tau )^{3} d\tau } }} \right]} $$
(6)

with a = 1 for \( f_{\alpha } \in [f_{{st}} ,f_{{tr}} ] \) and a = 0 for \( f_{\alpha }\,\notin\,[f_{{st}} ,f_{{tr}} ] \).

5.2.2 Determination of the autocatalytic factor

Using the known data of df α /dt and f α in the range of 0 < f α  < 0.13, as determined by isochronal dilatometric measurements (Figure 3), of the initial nucleus density (N *) given by the value estimated from the measured grain sizes (Table IV) and of v α (=1.96 × 10−6 ms−1), as determined from the kinetic analysis of normal transformation (Section V–A–2), the autocatalytic factors (p) operating in the abnormal transformation stage of the Fe-0.005 at. pct N specimens were determined for all cooling rates by fitting Eq. [6] to the experimental data for \( {df_{\alpha } } \mathord{\left/ {\vphantom {{df_{\alpha } } {dt}}} \right. \kern-\nulldelimiterspace} {dt} \) and f α as a function of time. The thus obtained autocatalytic factors of the investigated Fe-0.005 at. pct N are presented in Table VII.

Table VII Autocatalytic Factors (p Unit: m− 3) as Determined from the First Maxima of the Ferrite Transformation Rate Occurring during the First, Abnormal Part of the γ → α Transformation of the Investigated Fe-0.005 At. Pct N Alloy for Applied Cooling Rates of 5, 10, and 15 Kmin− 1
Full size table

The values of the autocatalytic factor (p) for the first, abnormal transformation stage are approximately 1014 m−3 for all applied cooling rates. These autocatalytic factors are approximately one order of magnitude smaller than that in pure iron[14] and approximately three orders of magnitude smaller than those (approximately 1017 m−3) typical for the martensitic transformation of steels.[44] The autocatalytic factors for the first maximum of the transformation rate increase with the increasing cooling rate.

It is likely that the large grains shown in the microstructure of Fe-0.005 at. pct N specimen after experiencing the γ → α transformation indicate the initial austenite grains (Figures 4 and 5). Many subgrains could be observed in the ferrite grains, which may be indicative of the additional nuclei which had formed by autocatalytic nucleation. This could be consistent with the observed bimodal nature of the grain-size distribution found for (all) transformed Fe-0.005 at. pct N specimens. It can be expected that the higher the determined autocatalytic factor, the smaller the resulting ferrite grain size. Indeed, this corresponds with the experimental observations (Tables IV and VII).

The increase of the autocatalytic factor with cooling rate can be described as follows: at a higher cooling rate, the transformation starts at a lower temperature (Figure 2). Accordingly, the chemical driving force is correspondingly larger. Therefore, more misfit-strain energy can be accommodated before the net driving force becomes zero. Consequently, the autocatalytic effect increases with cooling rate.

6 Conclusions

  1. 1.

    Abnormal transformation kinetics, characterized by the presence of two maxima in the transformation-rate curve, were recognized upon isochronal austenite-ferrite transformation of an ultra-low-nitrogen (0.005 at. pct N) interstitial Fe-N alloy.

  2. 2.

    The entire γ → α transformation for the ultra-low-nitrogen interstitial Fe-N alloy takes place in the single α-phase region, which indicates that diffusion of nitrogen across and/or away from the migrating γ/α interface does not play a role in the kinetics: a massive transformation occurs.

  3. 3.

    The main (later), normal transformation stage can be well described by a phase-transformation model assuming site saturation, interface-controlled growth, and an appropriate impingement correction. By adopting the nucleus density estimated by the measured ferritic grain size of the transformed specimens, it is found that the migration velocity of the γ/α interface is approximately constant and does not depend on the cooling rate during the transformation. Its value is compatible with the partitionless nature of the γ → α transformation.

  4. 4.

    Different mobility values have a relatively small effect on the quantification of the transformation strain.

  5. 5.

    The abnormal part of the transformation can be ascribed to autocatalytic nucleation of ferritic grains in advance of the migrating γ/α interface, which is caused by the accommodation of the (austenite-ferrite) misfit-strain energy. The determined autocatalytic factor increases with the increasing cooling rate, as a consequence of the larger amount of misfit-strain energy that can be accommodated at lower temperatures before the net driving force becomes zero.

  6. 6.

    Comparison of the ultra-low-nitrogen Fe-N and ultra-low-carbon Fe-C alloys indicates that the γ → α transformation in Fe-N is likely to be of a massive nature, whereas this transformation can show a transition from diffusion controlled to interface controlled in Fe-C because for Fe-C both the solvus temperature is lower and the diffusion coefficient of the interstitial component in austenite is larger.