Model-based clustering using a new multivariate skew distribution

Abstract

Quite often real data exhibit non-normal features, such as asymmetry and heavy tails, and present a latent group structure. In this paper, we first propose the multivariate skew shifted exponential normal distribution that can account for these non-normal characteristics. Then, we use this distribution in a finite mixture modeling framework. An EM algorithm is illustrated for maximum-likelihood parameter estimation. We provide a simulation study that compares the fitting performance of our model with those of several alternative models. The comparison is also conducted on a real dataset concerning the log returns of four cryptocurrencies.

1 Introduction

Finite mixture models are an important tool for the statistical modeling and analysis of many kinds of data. Because of their flexibility, finite mixture models can be used as a clustering technique or as a mathematical device for obtaining a tractable form of analysis for unmanageable data distributions (Titterington et al. 1985). Historically, the multivariate normal mixture (MN-M) model has been the most popular among researchers and practitioners given its mathematical tractability and usefulness in various application domains (McNicholas 2016). Nevertheless, for many real phenomena, such a model does not provide an adequate fit to the data, and more general models are required. For example, to accommodate outliers in the data, symmetric heavy-tailed distributions are often considered for the mixture components, since they can manage the thickness of the tails by using one or a few additional parameters. By focusing on multivariate data analyses, as we will do throughout this paper, examples of symmetric heavy-tailed mixtures can be found in Peel and McLachlan (2000), Sun et al. (2010), Andrews et al. (2011), McNicholas and Subedi (2012), Dang et al. (2015), Bagnato et al. (2017), Tomarchio et al. (2022) and Tong and Tortora (2022).

A further deviation from the normality assumption of the mixture components arises when the data involve observations whose distribution is asymmetric. In these cases, the choice of mixture components that are capable of modeling asymmetry can provide a better fit. In the multivariate literature, several mixtures of skew distributions have been proposed in the past few decades. Without making an exhaustive summary of the literature (see Lee and McLachlan 2022 for such an overview), we can mention the finite mixture models based on the multivariate skew normal (MSN) and skew-t (MST) distributions, in their various characterizations, proposed by Arellano-Valle et al. (2008), Lin (2009), Lin (2010), Frühwirth-Schnatter and Pyne (2010), Cabral et al. (2012), Vrbik and McNicholas (2014) and Lee and McLachlan (2016). Two other skew mixture models are those presented by Cabral et al. (2012) and based on the multivariate skew contaminated normal (MSCN) and skew slash (MSS) distributions. In McNicholas et al. (2013) and McNicholas et al. (2017), the multivariate variance gamma (MVG) distribution is used for model-based clustering via skew mixture models. Another flexible skew mixture model is provided by Browne and McNicholas (2015), who consider the multivariate generalized hyperbolic (MGH) distribution for the mixture components.

In this paper, we expand the multivariate literature devoted to asymmetric data modeling. Specifically, we introduce the multivariate skew shifted exponential normal (MSSEN) distribution, asymmetric generalization of the multivariate shifted exponential normal (MSEN) distribution introduced by Punzo and Bagnato (2020). Compared to its symmetric counterpart, the MSSEN has an additional parameter vector that accounts for the modelization asymmetric data. From a technical point of view, the MSSEN distribution can be obtained via the well-known normal mean-variance mixture model (McNeil et al. 2015) when a convenient shifted exponential distribution is used for the mixing random variable. We show that the probability density function (pdf) of the proposed distribution has a closed-form expression. The use of the MSSEN distribution within the finite mixture model paradigm is then illustrated. Thus, in the fashion of Lin et al. (2007), Karlis and Santourian (2009), and Browne and McNicholas (2015), the present paper aims to add to the richness of non-normal model-based clustering approaches an alternative mixture model that is easily applicable to data having skewed and heavy-tailed subpopulations. Indeed, different shapes of the scatter can produce the same level of skewness and kurtosis, as measured by classical indexes. The existing multivariate skewed heavy-tailed distributions can often reach all the levels of these indexes, by working with the tailedness and skewness parameters, but with a reference to a particular shape. So, for real data, it is important to have a variety of models that can provide different possibilities for these shapes. Furthermore, the proposed model has convenient closed-form expressions for estimating its parameter at the M-step of the EM algorithm (Dempster et al. 1977), differently from other well-established mixture models, making its implementation and application easier.

The rest of the paper is organized as follows. In Sect. 2, we first present the definition and properties of the MSSEN distribution together with the introduction of the MSSEN mixture (MSSEN-M) model for clustering purposes. Also, an EM algorithm (Dempster et al. 1977) is described for maximum likelihood parameter estimation. In Sect. 3, we first compare the fitting behavior of the MSSEN-M model with those of well-established alternatives on simulated data. Then, an analysis of a real dataset concerning the log returns of four cryptocurrencies is conducted. Finally, some concluding remarks are done in Sect. 4.

2 Methodology

Herein, we present the MSSEN distribution (Sect. 2.1), its use within the mixture model paradigm (Sect. 2.2), and the EM algorithm for maximum likelihood parameter estimation (Sect. 2.3).

2.1 Multivariate skew shifted exponential normal distribution

Definition 1

A random vector $\varvec{X}\in R^d$ is said to have a multivariate skew shifted exponential normal (MSSEN) distribution with location parameter $\varvec{\xi }\in R^d$, $d\times d$ scale matrix $\varvec{\Sigma }$, asymmetry parameter $\varvec{\gamma }\in R^d$, and tailedness parameter $\theta > 0$, in symbols $\varvec{X}\sim \mathcal {SSEN}_d\left( \varvec{\xi },\varvec{\Sigma },\varvec{\gamma },\theta \right)$, if its pdf is given by

$$\begin{aligned} f_{\tiny {\text {MSSEN}}}\left( \varvec{x};\varvec{\xi },\varvec{\Sigma },\varvec{\gamma },\theta \right)&= c \frac{\exp \left[ \left( \varvec{x}-\varvec{\xi }\right) ' \varvec{\Sigma }^{-1} \varvec{\gamma }\right] }{\left[ \delta \left( \varvec{x};\varvec{\xi },\varvec{\Sigma }\right) +2\theta \right] ^{\frac{d+2}{4}}} \nonumber \\&\quad \times L_{\frac{d}{2}+1}\left( \sqrt{\left[ \delta \left( \varvec{x};\varvec{\xi },\varvec{\Sigma }\right) +2\theta \right] \varvec{\gamma }' \varvec{\Sigma }^{-1} \varvec{\gamma }},\sqrt{\frac{\delta \left( \varvec{x};\varvec{\xi },\varvec{\Sigma }\right) +2\theta }{\varvec{\gamma }' \varvec{\Sigma }^{-1} \varvec{\gamma }}}\right) . \end{aligned}$$

(1)

In (1), $\delta \left( \varvec{x};\varvec{\xi },\varvec{\Sigma }\right) =\left( \varvec{x}-\varvec{\xi }\right) '\varvec{\Sigma }^{-1}\left( \varvec{x}-\varvec{\xi }\right)$ is the squared Mahalanobis distance between $\varvec{x}$ and $\varvec{\xi }$ (with $\varvec{\Sigma }$ as covariance matrix), c is a normalizing constant given by

$$\begin{aligned} c=\frac{2\theta \exp \left( \theta \right) \left( \varvec{\gamma }' \varvec{\Sigma }^{-1} \varvec{\gamma }\right) ^\frac{d+2}{4}}{ \left( 2\pi \right) ^{\frac{d}{2}} \left| \varvec{\Sigma }\right| ^{\frac{1}{2}}}, \end{aligned}$$

with $\left| \cdot \right|$ denoting the determinant, and

$$\begin{aligned} L_{\lambda }\left( x,z \right) = \frac{1}{2} \int _{z}^\infty t^{\lambda -1} \exp \left[ -\frac{x}{2} \left( \frac{1}{t}+t\right) \right] dt \end{aligned}$$

(2)

is the incomplete Bessel function defined by Terras (1981), see also Agrest et al. (1971). Note that, when $z=0$, the function in (2) reduces to $K_{\lambda }\left( x\right)$, i.e. to the modified Bessel function of the third order; for details see Abramowitz and Stegun (1965) and Watson (1995).

To facilitate parameter interpretation, we show the effects of varying $\varvec{\gamma }$, the other parameters kept fixed, in the bivariate case ($d=2$). This information is reported via the contour levels of the MSSEN pdf in Fig. 1, where $\varvec{\gamma }=(3,3)'$ on the left, $\varvec{\gamma }=(5,5)'$ in the center, and $\varvec{\gamma }=(7,7)'$ on the right. The values of the other parameters are $\varvec{\xi }=(0,0)', \varvec{\Sigma }=\varvec{I}_2$, and $\theta =0.5$, being $\varvec{I}_2$ the $2 \times 2$ identity matrix. As we note, the asymmetry of the pdf increases as $\varvec{\gamma }$ grows.

Fig. 1

Contour levels of the MSSEN pdf, in the bivariate case, for different values of $\varvec{\gamma }$ (i.e., $\varvec{\gamma }=(3,3)'$ on the left, $\varvec{\gamma }=(5,5)'$ in the center, $\varvec{\gamma }=(7,7)'$ on the right), keeping fixed the other parameters (i.e., $\varvec{\xi }=(0,0)', \varvec{\Sigma }=\varvec{I}_2$, and $\theta =0.5$)

Similarly, we report in Fig. 2 the effect of varying $\theta$, the other parameters kept fixed, in the bivariate case ($d=2$). The subplots refer to $\theta =1$ (on the left), $\theta =0.5$ (in the center), and $\theta =0.1$ (on the right). The values of the other parameters are $\varvec{\xi }=(0,0)', \varvec{\Sigma }=\varvec{I}_2$, and $\gamma =(2,2)'$. As we see, the peakedness of the pdf grows when $\theta$ decreases. This has implications for the tail behavior by the fact that large values of $\theta$ imply light tails, whereas smaller values of $\theta$ lead to heavier tails.

Fig. 2

Contour levels of the MSSEN pdf, in the bivariate case, for different values of $\theta$ (i.e., $\theta =1$ on the left, $\theta =0.5$ in the center, $\theta =0.1$ on the right), keeping fixed the other parameters (i.e., $\varvec{\xi }=(0,0)', \varvec{\Sigma }=\varvec{I}_2$, and $\gamma =(2,2)'$)

2.1.1 Representations

A more direct interpretation of $\varvec{X}\sim \mathcal {SSEN}_d\left( \varvec{\xi },\varvec{\Sigma },\varvec{\gamma },\theta \right)$ can be given by its hierarchical representation as

$$\begin{aligned} \begin{array}{rcl} W &{} \sim &{} \mathcal{S}\mathcal{E}\left( \theta \right) , \\ \varvec{X}|W=w &{} \sim &{} \mathcal {N}_{d}(\varvec{\xi }+ \varvec{\gamma }/w,\varvec{\Sigma }/w), \end{array} \end{aligned}$$

(3)

where $\mathcal{S}\mathcal{E}\left( \theta \right)$ denotes a shifted exponential distribution on $\left( 1,\infty \right)$, with rate parameter $\theta >0$ and pdf $f_{\text {SE}}\left( w;\theta \right) =\theta \exp \left[ -\theta \left( w-1\right) \right]$, and $\mathcal {N}_{d}\left( \cdot \right)$ denotes a d-variate normal distribution. This alternative way to see the MSSEN distribution is useful for random number generation and for the implementation of the EM algorithm (see Sect. 2.3). Moreover, $\varvec{X}\sim \mathcal {SSEN}_d\left( \varvec{\xi },\varvec{\Sigma },\varvec{\gamma },\theta \right)$ has the following normal mean-variance mixture representation

$$\begin{aligned} \varvec{X}= \varvec{\xi }+ \frac{1}{W}\varvec{\gamma }+ \frac{1}{\sqrt{W}} \varvec{\Lambda }\varvec{Z}, \end{aligned}$$

(4)

where $W \sim \mathcal{S}\mathcal{E}\left( \theta \right)$, $\varvec{\Lambda }$ is a $d \times d$ matrix such that $\varvec{\Lambda }\varvec{\Lambda }' = \varvec{\Sigma }$, and $\varvec{Z}\sim \mathcal {N}_d\left( \varvec{0}_d,\varvec{I}_d\right)$ is independent of W, being $\varvec{0}_d$ and $\varvec{I}_d$ the vector of zeros and the $d \times d$ identity matrix, respectively; see, e.g., McNeil et al. (2015).

2.1.2 Moments

Thanks to the representation given in (4), and by the well-known results illustrated in McNeil et al. (2015), it is possible to show that the mean and covariance matrix for $\varvec{X}\sim \mathcal {SSEN}_d\left( \varvec{\xi },\varvec{\Sigma },\varvec{\gamma },\theta \right)$ are respectively given by

$$\begin{aligned} \varvec{\mu }&:= \text {E}\left( \varvec{X}\right) =\varvec{\xi }+ s\left( \theta \right) \varvec{\gamma } \end{aligned}$$

(5)

$$\begin{aligned} \varvec{\Phi }&:= \text {Cov}\left( \varvec{X}\right) = s\left( \theta \right) \varvec{\Sigma }+ \left\{ \theta - s\left( \theta \right) \left[ \theta + s\left( \theta \right) \right] \right\} \varvec{\gamma }\varvec{\gamma }', \end{aligned}$$

(6)

where

$$\begin{aligned} s\left( \theta \right) =\displaystyle \theta \exp \left( \theta \right) \varphi _{-1}(\theta ) \end{aligned}$$

and

$$\begin{aligned} \varphi _{m}(z)= & {} E_{-m}\left( z\right) \nonumber \\= & {} \int _{1}^{\infty } t^{m} \exp (-z t) dt \nonumber \\= & {} z^{-(m+1)}\Gamma \left( m+1,z \right) \end{aligned}$$

(7)

is the Misra function (Misra 1940), generalized form of the exponential integral function $E_n\left( z\right) = \int _{1}^\infty t^{-n} \exp (-zt) dt$ (Abramowitz and Stegun 1965).

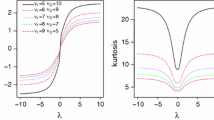
To illustrate the behavior of skewness and kurtosis coefficients and their relation with the parameters $\varvec{\gamma }$ and $\theta$, we examine the univariate case ($d=1$) and we use the notation $X \sim \mathcal {SSEN}_1\left( \xi ,\sigma ^2,\gamma ,\theta \right)$. These coefficients are respectively given by

$$\begin{aligned} \text {Skew}\left( X\right)= & {} \frac{m_3 - 3m_1 m_2 + 2 m_1^3}{\left( m_2-m_1^2\right) ^{\frac{3}{2}}}, \end{aligned}$$

(8)

$$\begin{aligned} \text {Kurt}\left( X\right)= & {} \frac{m_4- 4m_1 m_3 + 6m_1^2 m_2 - 3 m_1^4}{\left( m_2-m_1^2\right) ^{2}} -3, \end{aligned}$$

(9)

where

$$\begin{aligned} m_1= & {} \text {E}\left( X\right) = \xi + \gamma \text {E}\left( \frac{1}{W}\right) , \\ m_2= & {} \text {E}\left( X^2\right) = \xi ^2 + \left( 2\gamma \xi + \sigma ^2 \right) \text {E}\left( \frac{1}{W}\right) , \\ m_3= & {} \text {E}\left( X^3\right) = \xi ^3 + 3 \left( \gamma \xi + \sigma ^2\right) \left[ \xi \text {E}\left( \frac{1}{W}\right) + \gamma \text {E}\left( \frac{1}{W^2}\right) \right] + \gamma ^3 \text {E}\left( \frac{1}{W^3}\right) ,\\ m_4= & {} \text {E}\left( X^4\right) = \xi ^4 + 2\left( 2\gamma \xi + 3\sigma ^2\right) \left[ \xi ^2 \text {E}\left( \frac{1}{W}\right) + \gamma ^2 \text {E}\left( \frac{1}{W^3}\right) \right] + \\{} & {} \quad \quad \quad + 3\left( 2\gamma ^2 \xi + 4\gamma \xi \sigma ^2 + \sigma ^2 \right) \text {E}\left( \frac{1}{W^2}\right) + \gamma ^4 \text {E}\left( \frac{1}{W^4}\right) , \end{aligned}$$

with

$$\begin{aligned} \text {E}\left( \frac{1}{W^r}\right) = \theta \exp \left( \theta \right) E_{r}\left( \theta \right) . \end{aligned}$$

Fig. 3

Examples of behavior of $\text {Skew}\left( X\right)$ (on the left) and $\text {Kurt}\left( X\right)$ (on the right), as functions of $\gamma$, at various levels of $\theta$ for univariate SSEN distribution, given $\xi =0$ and $\sigma ^2=1$

Figure 3 shows some examples of $\text {Skew}\left( X\right)$ and $\text {Kurt}\left( X\right)$, as a function of $\gamma$, for some values of $\theta$ ($\xi =0$ and $\sigma ^2=1$). From Fig. 3a we realize that, as $\theta$ decreases, the range of possible values of $\text {Skew}\left( X\right)$ increases. Moreover, the skewness is zero when $\gamma = 0$, and this happens regardless of $\theta$. From Fig. 3b we note that $\gamma$ kept fixed, the lower the value $\theta$, the higher the kurtosis. Moreover, as $\theta$ increases, the kurtosis tends to zero regardless of $\gamma$. The behaviors of skewness and kurtosis shown in Fig. 3 are very similar to those for the asymmetric Laplace scale mixture models proposed by Punzo and Bagnato (2022).

2.1.3 Comparison with other skewed distributions

By focusing on the skewed distributions mentioned in Sect. 1, we begin to distinguish them according to whether or not they have heavier-than-normal tails. In particular, it is well-known that the MSN distribution, despite the existence of several formulations (see Lee and McLachlan 2013b), is not well-suited for modeling data showing heavier tails than the normal ones (Azzalini 2013). In such cases, it is necessary to adopt more flexible distributions, such as the MST (in its varying configurations; see Lee and McLachlan, 2013b), MSCN, MSS, MVG, MVGH, or our MSSEN, which have specific parameters controlling the heaviness of the tails.

Another aspect to consider is the definiteness of the moments, which is dependent on the values assumed by the parameters for certain distributions. For example, the moments of MST and MSS distributions are defined only when the tailedness parameters are greater than certain thresholds (see, e.g., Wang and Genton 2006; Dávila et al. 2018). These thresholds act as an obstacle to obtaining values that would result in heavier tails, thereby limiting the tail flexibility of these distributions. On the contrary, the MSSEN and other skewed distributions being considered do not encounter this issue, as their moments always exist. Moments calculation have important implications in many applied fields, such as economics and finance (Rachev et al. 2010; McNeil et al. 2015).

The considered skewed distributions also require different computational efforts for estimating their parameters. We remand this discussion to Sect. 2.2.1, where they are compared within a mixture model setting.

2.2 Finite mixtures of MSSEN distributions

For a d-variate random vector $\varvec{X}$, the pdf of the MSSEN mixture (MSSEN-M) model with k components can be written as

$$\begin{aligned} f_{\tiny {\text {MSSEN-M}}}\left( \varvec{x};\varvec{\Psi }\right) =\sum _{j=1}^k\pi _j f_{\tiny {\text {MSSEN}}}\left( \varvec{x}; \varvec{\Omega }_j\right) , \end{aligned}$$

(10)

where $\pi _j$ is the mixing proportion of the jth component, with $\pi _j>0$ and $\sum _{j=1}^k\pi _j=1$, $f_{\tiny {\text {MSSEN}}}\left( \varvec{x}; \varvec{\Omega }_j\right)$ is the pdf defined in (1) of the jth component with parameters $\varvec{\Omega }_j=\left\{ \varvec{\xi }_j,\varvec{\Sigma }_j,\varvec{\gamma }_j,\theta _{j}\right\}$, and $\varvec{\Psi }=\left\{ \left( \pi _j,\varvec{\Omega }_j\right) ; j=1,\ldots ,k\right\}$ contains all of the parameters of the mixture. Model in (10), being able to account for heterogeneity and non-normal features, such as asymmetry and heavy tails in each mixture component, constitutes a promising alternative to the existing skew mixture models.

2.2.1 Comparison with other skewed mixtures

As introduced in Sect. 1, different mixture models with asymmetric components have been proposed in the multivariate literature. First of all, we report that the features presented in Sect. 2.1.3 for the single skewed distributions directly apply to the corresponding mixture models. Here, we want to add some computational differences among them.

We start by considering the MSS mixture (MSS-M) model for which, as discussed by Prates et al. (2013), the updating expressions for all the parameters in the EM-based algorithm are not in closed form. Particularly, Monte Carlo integration may be employed, making this model the most computationally intensive to be estimated among those considered. The situation improves when the MST mixture (MST-M), MVG mixture (MVG-M), MSCN mixture (MSCN-M), and MGH mixture (MGH-M) models are considered, given that for these models only the tailedness parameters must be numerically estimated (Browne and McNicholas 2015; Prates et al. 2013; Gallaugher et al. 2022b). Anyway, estimating the tailedness parameters accurately can be a challenging task, such as in the case of the MGH-M model (Aas and Hobæk Haff 2005; Browne and McNicholas 2015). On the other hand, the MSSEN-M model is the only heavy-tailed (among those considered) having a simple closed-form expression also for the update of the tailedness parameter (refer to Sect. 2.3), making it computationally the most efficient.

A last note can be reported in terms of parsimony. Specifically, the MSN-M model is the most parsimonious (due to the lack of the tailedness parameter), whereas the MSCN-M and MGH-M models are the most parametrized (since they have two parameters, for each group, controlling the tail behavior).

2.3 Maximum likelihood: application of the EM algorithm

A standard approach to estimating the parameters of a mixture model is the maximum likelihood (ML), commonly implemented via the expectation-maximization (EM) algorithm. Let $\left\{ \varvec{X}_i, i=1,\ldots ,n\right\}$ be a sample of n independent observations from model (10). In the EM algorithm framework, such a sample is treated as incomplete. The complete-data are $\left\{ \left( \varvec{X}_i,\varvec{z}_i, w_i\right) ; i=1,\ldots ,n \right\}$, where $\varvec{z}_i=(z_{i1},\dots ,z_{ik})'$ so that $z_{ij}=1$ if observation i belongs to group j and $z_{ij}=0$ otherwise. By saying that $\varvec{Z}_i$, the random counterpart of $\varvec{z}_i$, follows a multinomial distribution consisting of one draw from k categories with probabilities $\varvec{\pi }=\left( \pi _1,\ldots ,\pi _k\right) '$, say $\mathcal {M}_k\left( \varvec{\pi }\right)$, the hierarchical representation mentioned in (3) for the single distribution can be generalized to the corresponding mixture model as

$$\begin{aligned} \varvec{Z}_i&\sim \mathcal {M}_k\left( \varvec{\pi }\right) \nonumber \\ W_{ij}&\sim \mathcal{S}\mathcal{E}\left( \theta _j\right) \nonumber \\ \varvec{X}_{i}|W_{ij}=w_{ij}&\sim \mathcal {N}_d(\varvec{\xi }_j + \varvec{\gamma }_j/w_{ij} , \varvec{\Sigma }_j/w_{ij}), \end{aligned}$$

(11)

where $W_{ij} :=W_{i}|z_{ij}=1$. Because of this conditional structure, the complete-data log-likelihood function can be written as

$$\begin{aligned} \ell _{c}\left( \varvec{\Psi }\right) = \ell _{1c}\left( \varvec{\pi }\right) +\ell _{2c}\left( \varvec{\Xi }\right) +\ell _{3c}\left( \varvec{\theta }\right) , \end{aligned}$$

(12)

where

$$\begin{aligned} \ell _{1c}\left( \varvec{\pi }\right) = \sum _{i=1}^{n}\sum _{j=1}^{k} z_{ij} \ln \left( \pi _j\right) , \end{aligned}$$

(13)

$$\begin{aligned} \ell _{2c}\left( \varvec{\Xi }\right) =&\sum _{i=1}^{n}\sum _{j=1}^{k} z_{ij} \left[ -\frac{d}{2}\ln \left( 2\pi \right) +\frac{d}{2}\ln \left( w_{ij}\right) -\frac{1}{2}\ln |\varvec{\Sigma }_j|-\frac{w_{ij}\delta _j\left( \varvec{x}_i;\varvec{\xi }_j,\varvec{\Sigma }_j\right) }{2}+ \right. \nonumber \\&+ \frac{1}{2} \left. \left( \varvec{x}_i-\varvec{\xi }_j\right) '\varvec{\Sigma }_j^{-1}\varvec{\gamma }_j + \frac{1}{2} \varvec{\gamma }_j'\varvec{\Sigma }_j^{-1}\left( \varvec{x}_i-\varvec{\xi }_j\right) - \frac{1}{2w_{ij}} \varvec{\gamma }_j'\varvec{\Sigma }_j^{-1}\varvec{\gamma }_j \right] , \end{aligned}$$

(14)

with $\varvec{\Xi }=\left\{ \left( \varvec{\xi }_j,\varvec{\Sigma }_j,\varvec{\gamma }_j\right) ; j=1,\ldots ,k\right\}$, and

$$\begin{aligned} \ell _{3c}\left( \varvec{\theta }\right) = \sum _{i=1}^{n}\sum _{j=1}^{k} z_{ij} \left[ \ln \left( \theta _j\right) -\theta _j \left( w_{ij}-1\right) \right] , \end{aligned}$$

(15)

with $\varvec{\theta }=\left\{ \theta _j, j=1,\ldots ,k\right\}$.

Working on $\ell _{c}\left( \varvec{\Psi }\right)$ in (12), the EM algorithm iterates between two steps, one E-step, and one M-step, until convergence. These steps are outlined below. As for the notation, the parameters marked with one dot correspond to the updates at the previous iteration while those marked with two dots represent the updates at the current iteration.

E-Step

The E-step requires the calculation of

$$\begin{aligned} Q\left( \varvec{\Psi }|\dot{\varvec{\Psi }}\right) = Q_1\left( \varvec{\pi }|\dot{\varvec{\Psi }}\right) + Q_2\left( \varvec{\Xi }|\dot{\varvec{\Psi }}\right) + Q_3\left( \varvec{\theta }|\dot{\varvec{\Psi }}\right) , \end{aligned}$$

(16)

the conditional expectation of $l_c\left( \varvec{\Psi }\right)$ given the observed data and using the current fit $\dot{\varvec{\Psi }}$ for $\varvec{\Psi }$. In (16) the three terms on the right-hand side are ordered as the three terms on the right-hand side of (12).

To compute $Q\left( \varvec{\Psi }|\dot{\varvec{\Psi }}\right)$ we need to replace any function $g\left( Z_{ij}\right)$ and $m\left( W_{ij}\right)$ of the latent variables which arise in (13)–(15) by $E_{\dot{\varvec{\Psi }}}\left[ g\left( Z_{ij}\right) |\varvec{X}_i=\varvec{x}_i\right]$ and $E_{\dot{\varvec{\Psi }}}\left[ m\left( W_{ij}\right) |\varvec{X}_i=\varvec{x}_i\right]$, respectively, where the expectations are taken using the current fit $\dot{\varvec{\Psi }}$ for $\varvec{\Psi }$, $i=1,\ldots ,n$ and $j=1,\ldots ,k$.

As concerns $Z_{ij}$, it is included in all the Eqs. (13)–(15) but always via the identity function, namely $g(z)=z$; therefore

$$\begin{aligned} \ddot{z}_{ij}:=\text {E}_{ \dot{\varvec{\Psi }}}\left( Z_{ij}|\varvec{x}_{i}\right) = \frac{\dot{\pi }_j f_{\tiny {\text {MSSEN}}}\left( \varvec{x}_i;\dot{\varvec{\Omega }}_j\right) }{\sum _{h=1}^k\dot{\pi }_h f_{\tiny {\text {MSSEN}}}\left( \varvec{x}_i;\dot{\varvec{\Omega }}_h\right) }, \end{aligned}$$

which corresponds to the posterior probability that the unlabeled observation $\varvec{x}_i$ belongs to the jth component of the mixture.

Regarding $W_{ij}$, it is only included in the Eqs. (14) and (15) and the functions involved are $m_1(w)=w$, $m_2(w)=1/w$, $m_3(w)=\ln (w)$. Of these, only $m_1$ and $m_2$ need to be taken into account because $m_3$ in (14) is not related to the parameters. To calculate the expectations of $m_1$ and $m_2$ we first note that the pdf of $W_{ij}|\varvec{X}_i=\varvec{x}_i$ satisfies

$$\begin{aligned} f\left( w_{ij}|\varvec{x}_i;\varvec{\Omega }_j\right)\propto & {} f\left( w_{ij},\varvec{x}_i;\varvec{\Omega }_j\right) \nonumber \\\propto & {} w_{ij}^{\frac{d}{2}} \exp \left[ - \frac{\varvec{\gamma }_j'\varvec{\Sigma }_j^{-1}\varvec{\gamma }_j}{2w_{ij}} - \frac{\delta \left( \varvec{x}_i;\varvec{\xi }_j,\varvec{\Sigma }_j\right) }{2} w_{ij} \right] \nonumber \\&\quad \times \exp \left( -\theta _j w_{ij}\right) \mathbbm {1}_{\left( 1,\infty \right) }\left( w_{ij}\right) \nonumber \\\propto & {} f_{\tiny {\text {LTGIG}}}\left( w_{ij};\frac{d}{2}+1,\varvec{\gamma }_j'\varvec{\Sigma }_j^{-1}\varvec{\gamma }_j, \delta \left( \varvec{x}_i;\varvec{\xi }_j,\varvec{\Sigma }_j\right) +2\theta _j,1 \right) , \quad \end{aligned}$$

where $\mathbbm {1}_{A}\left( \cdot \right)$ is the indicator function on the set A and $f_{\tiny {\text {LTGIG}}}$ is the pdf of a left truncated generalized inverse Gaussian distribution, which is defined in Appendix A of this manuscript. This means that

$$\begin{aligned} W_{ij}|\varvec{X}_i=\varvec{x}_i \sim \mathcal {LTGIG}_{\left( 1,\infty \right) }\left( \frac{d}{2}+1,\varvec{\gamma }_j'\varvec{\Sigma }_j^{-1}\varvec{\gamma }_j,\delta \left( \varvec{x}_i;\varvec{\xi }_j,\varvec{\Sigma }_j\right) +2\theta _j\right) . \end{aligned}$$

From Eq. (A2) we can derive the following results

$$\begin{aligned} \ddot{u}_{ij}:=\;&\text {E}_{ \dot{\varvec{\Psi }}}\left( W_{ij}|\varvec{X}_i=\varvec{x}_i\right) \nonumber \\ =&\sqrt{\frac{\dot{\varvec{\gamma }}_j'\dot{\varvec{\Sigma }}_j^{-1}\dot{\varvec{\gamma }}_j}{\left[ \delta \left( \varvec{x}_i;\dot{\varvec{\xi }}_j,\dot{\varvec{\Sigma }}_j\right) +2\dot{\theta }_j\right] }} \nonumber \\ & \times\frac{ L_{\frac{d}{2}+2}\left( \sqrt{\dot{\varvec{\gamma }}_j'\dot{\varvec{\Sigma }}_j^{-1}\dot{\varvec{\gamma }}_j\left[ \delta \left( \varvec{x}_i;\dot{\varvec{\xi }}_j,\dot{\varvec{\Sigma }}_j\right) +2\dot{\theta }_j\right] },\sqrt{\frac{\delta \left( \varvec{x}_i;\dot{\varvec{\xi }}_j,\dot{\varvec{\Sigma }}_j\right) +2\dot{\theta }_j}{\dot{\varvec{\gamma }}_j'\dot{\varvec{\Sigma }}_j^{-1}\dot{\varvec{\gamma }}_j}}\right) }{ L_{\frac{d}{2}+1}\left( \sqrt{\dot{\varvec{\gamma }}_j'\dot{\varvec{\Sigma }}_j^{-1}\dot{\varvec{\gamma }}_j\left[ \delta \left( \varvec{x}_i;\dot{\varvec{\xi }}_j,\dot{\varvec{\Sigma }}_j\right) +2\dot{\theta }_j\right] },\sqrt{\frac{\delta \left( \varvec{x}_i;\dot{\varvec{\xi }}_j,\dot{\varvec{\Sigma }}_j\right) +2\dot{\theta }_j}{\dot{\varvec{\gamma }}_j'\dot{\varvec{\Sigma }}_j^{-1}\dot{\varvec{\gamma }}_j}}\right) }, \end{aligned}$$

$$\begin{aligned} \ddot{v}_{ij}:=\;&\text {E}_{ \dot{\varvec{\Psi }}}\left( W_{ij}^{-1}|\varvec{X}_i=\varvec{x}_i\right) \nonumber \\ =&\sqrt{\frac{\left[ \delta \left( \varvec{x}_i;\dot{\varvec{\xi }}_j,\dot{\varvec{\Sigma }}_j\right) +2\dot{\theta }_j\right] }{\dot{\varvec{\gamma }}_j'\dot{\varvec{\Sigma }}_j^{-1}\dot{\varvec{\gamma }}_j}} \nonumber \\ & \times \frac{ L_{\frac{d}{2}}\left( \sqrt{\dot{\varvec{\gamma }}_j'\dot{\varvec{\Sigma }}_j^{-1}\dot{\varvec{\gamma }}_j\left[ \delta \left( \varvec{x}_i;\dot{\varvec{\xi }}_j,\dot{\varvec{\Sigma }}_j\right) +2\dot{\theta }_j\right] }, \sqrt{\frac{\delta \left( \varvec{x}_i;\dot{\varvec{\xi }}_j,\dot{\varvec{\Sigma }}_j\right) +2\dot{\theta }_j}{\dot{\varvec{\gamma }}_j'\dot{\varvec{\Sigma }}_j^{-1}\dot{\varvec{\gamma }}_j}} \right) }{ L_{\frac{d}{2}+1}\left( \sqrt{\dot{\varvec{\gamma }}_j'\dot{\varvec{\Sigma }}_j^{-1}\dot{\varvec{\gamma }}_j\left[ \delta \left( \varvec{x}_i;\dot{\varvec{\xi }}_j,\dot{\varvec{\Sigma }}_j\right) +2\dot{\theta }_j\right] }, \sqrt{\frac{\delta \left( \varvec{x}_i;\dot{\varvec{\xi }}_j,\dot{\varvec{\Sigma }}_j\right) +2\dot{\theta }_j}{\dot{\varvec{\gamma }}_j'\dot{\varvec{\Sigma }}_j^{-1}\dot{\varvec{\gamma }}_j}} \right) }.\end{aligned}$$

M-Step

The M-step requires the calculation of $\ddot{\varvec{\Psi }}$ that maximizes $Q\left( \varvec{\Psi }|\dot{\varvec{\Psi }}\right)$ in (16). Simple algebra yields the following updates

$$\begin{aligned} \ddot{\pi }_j= & {} \frac{1}{n}\sum\nolimits _{i=1}^n \ddot{z}_{ij}, \quad \ddot{\varvec{\gamma }}_j =\frac{\displaystyle \frac{1}{n_j}\sum\nolimits _{i=1}^n \ddot{z}_{ij} \ddot{u}_{ij} \left( \bar{\varvec{x}}_j - \varvec{x}_i \right) }{\bar{u}_{j}\bar{v}_{j}-1}, \quad \ddot{\varvec{\xi }}_j = \frac{\displaystyle \frac{1}{n_j}\sum\nolimits _{i=1}^n \ddot{z}_{ij} \ddot{u}_{ij} \varvec{x}_i - \ddot{\varvec{\gamma }}_j}{\bar{u}_{j}}, \\ \ddot{\varvec{\Sigma }}_j= & {} \frac{1}{n_j}\sum\nolimits _{i=1}^n \ddot{z}_{ij} \ddot{u}_{ij} \left( \varvec{x}_i-\ddot{\varvec{\xi }}_j\right) \left( \varvec{x}_i-\ddot{\varvec{\xi }}_j\right) ' - \left( \bar{\varvec{x}}_j-\ddot{\varvec{\xi }}_j\right) \ddot{\varvec{\gamma }}' - \ddot{\varvec{\gamma }} \left( \bar{\varvec{x}}_j-\ddot{\varvec{\xi }}_j\right) ' + \bar{v}_j \ddot{\varvec{\gamma }} \ddot{\varvec{\gamma }}', \\ \ddot{\theta }_j= & {} \frac{\sum \nolimits _{i=1}^n \ddot{z}_{ij}}{\sum \nolimits _{i=1}^n \ddot{z}_{ij}\left( \ddot{u}_{ij}-1\right) }, \end{aligned}$$

where $n_j=\sum _{i=1}^n \ddot{z}_{ij}$, $\bar{u}_j = (1/n_j) \sum _{i=1}^n \ddot{z}_{ij} \ddot{u}_{ij}$, $\bar{v}_j = (1/n_j) \sum _{i=1}^n \ddot{z}_{ij} \ddot{v}_{ij}$, and $\bar{\varvec{x}}_j= (1/n_j) \sum _{i=1}^n \ddot{z}_{ij} \varvec{x}_i$, $j=1,\ldots ,k$.

Interestingly, closed-form expressions are provided for all the mixture parameters, differently from the many other well-established skewed mixture models (refer to the contributions reported in Sect. 1 and comments made in Sect. 2.2.1).

2.3.1 Some notes on the initialization strategy

To start the EM algorithm, we adopt the following two-step procedure:

• 1. partition the sample into k groups using the k-means clustering algorithm (Hartigan and Wong 1979). Note that, the best solution over 25 runs of the k-means algorithm is considered.

• 2. Based on the obtained classification, compute the weighted sample mean, covariance, and skewness to initialize $\varvec{\xi }_j$, $\varvec{\Sigma }_j$, and $\varvec{\gamma }_j$, $j=1,\ldots ,k$, respectively. The tailedness parameter $\theta _j, j=1,\ldots ,k$, is set equal to 1, i.e. an intermediate value between near-normality and heavy-tails. The mixture weights $\pi _j, j=1,\ldots ,k$, are initialized by the proportion of points classified in each group.

Closely related initialization strategies have been largely adopted in the model-based clustering literature (see Basso et al. 2010; Prates et al. 2013; Lee and McLachlan 2014; Wei et al. 2019, for some examples).

3 Data analyses

In this section, we compare the performance of our proposed model with those of several reference finite mixture models. In detail, all the models are fitted to simulated data, in Sect. 3.1, and to a real dataset concerning the log returns of four cryptocurrencies, in Sect. 3.2. All the analyses are conducted via the R statistical software.

3.1 A simulation study

In this study, we consider two scenarios that differ according to the direction of the asymmetry present in the data. In particular, in Scenario A the groups show positive asymmetry, whereas in Scenario B they have negative asymmetry. For each scenario, we generate samples of size $n=200$ from the bivariate standard normal distribution, i.e. $\varvec{X}\sim \mathcal {N}_2\left( \varvec{0}_2,\varvec{I}_2\right)$. Then, for the samples to be used in Scenario A, we apply the transformation $x+\exp \left( \eta x\right) ,$ whereas for the samples to be considered in Scenario B we use the transformation $-x-\exp \left( \eta x\right) ,$ being x the generic coordinate of $\varvec{x}$. For each sample, half of the observations are selected and shifted in the bi-dimensional space by adding (subtracting) a constant $c=10$ to each of their transformed values in Scenario A (Scenario B), thus leading to two separate clusters. In the transformations above, $\eta >0$ can be used to control the levels of asymmetry and kurtosis of the samples. Specifically, as $\eta$ grows, both quantities roughly increase. Herein, we let $\eta$ be the sequence of values from 0.80 to 1.40, with increments of 0.10 and, for each value of $\eta$, we consider 500 samples. The transformation used in Scenario A has been recently considered by Gallaugher et al. (2022). Examples of generated datasets for the two scenarios are illustrated in Fig. 4.

Fig. 4

Examples of generated datasets for the two scenarios. For each scenario, three growing examples of $\eta$ are provided: $\eta =0.8$ (left), $\eta =1.1$ (center), and $\eta =1.4$ (right)

On each generated dataset, we fit our MSSEN-M model together with 9 other mixture models; all the models are fitted with $k=2$ components. In the following, we provide the detailed list of the considered models along with the R functions and packages used to fit them to the data:

• the MN-M, MSN-M, MT-M, MST-M, MSCN-M, and MSS-M models are fitted via the smsn.search() function of the mixsmsn package (Prates et al. 2013);

• the MGH-M and MVG-M models are fitted via the ghpcm() function of the mixture package (Pocuca et al. 2021);

• the MSEN-M model is fitted via the Mixt.fit() function of the SenTinMixt package (Tomarchio et al. 2021).

Note that, in the list above, the acronyms MT-M and MSEN-M refer to the multivariate t and multivariate shifted exponential normal mixtures, respectively.

The fitting performances of the considered models are now analyzed. First of all, for each $\eta$ we can obtain 500 model rankings based on the BIC in each scenario. Thus, we compute the average among these rankings to obtain an overall measure of the goodness of fit of each model, and we report such information in Fig. 5 for Scenario A, and in Fig. 6 for Scenario B.

Fig. 5

Scenario A: average rankings based on the BIC for the considered models over the 500 simulated datasets at each value of $\eta$

Fig. 6

Scenario B: average rankings based on the BIC for the considered models over the 500 simulated datasets at each value of $\eta$

It is evident that, regardless of the considered scenario, the patterns illustrated are substantially the same. In both scenarios, by starting from the bottom, we immediately note that, regardless of the value of $\eta$, the MN-M model provides the worst fitting because it is not able to account for both asymmetry and heavy tails. Then, we roughly have three groups of models. The models in the first group are the MSN-M, MT-M, and MSEN-M models. They are ranked, on average, from the 6th to the 9th position, and are only partially able to account for the features of the generated data. The models in the second group are the MGH-M and MSCN-M models, namely the most parametrized among the considered mixture models. These models are capable of modeling both asymmetry and heavy tails. Nevertheless, the higher number of parameters causes an increase in the penalty term of the BIC, with a consequent negative effect on the fitting results. However, both models seem to improve their performance as $\eta$ grows, suggesting that the extra flexibility granted by the additional parameters allows for better accommodation of the higher levels of asymmetry and kurtosis in the data (Browne and McNicholas 2015). The models in the third group generally cover, on average, the first four average positions. It is possible to note that the MVG-M model, which initially provides the best average fit, deteriorates their performance when $\eta$ increases. The MSS-M and MST-M models follow a similar pattern to each other and seem to provide a good (but not the best) fit of the data regardless of the $\eta$ value considered. On the contrary, we notice an interesting pattern related to our MSSEN-M model. Indeed, for values of $\eta$ ranging from 1.00 to 1.30, it has the best average ranking. Specifically, the average ranking smoothly increases until $\eta =1.20$, a value from which it slowly begins to decrease and converge to that of the other three models. Therefore, we have identified a range of possible values of $\eta$, i.e. data structures, for which the MSSEN-M model yields better average fitting results than the other mixture models. More in general, if we would compute for each model the global ranking over all the $\eta$ values, the MSSEN-M model would have the highest average ranking.

From another perspective, since when working with real data we might be interested only in the best fitting model, we now count how many times, over the 500 datasets for each $\eta$, every model produces the best BIC value. This information is reported in Fig. 7 for Scenario A and in Fig. 8 for Scenario B. The patterns reported are similar between the scenarios and roughly mimic those previously discussed. By focusing only on the MSSEN-M, we notice that, for values of $\eta$ ranging from 1.00 to 1.30, our model is considered the best one with the highest frequency.

Fig. 7

Scenario A: number of times for which each model provides the best BIC over the 500 simulated datasets at each value of $\eta$

Fig. 8

Scenario B: number of times for which each model provides the best BIC over the 500 simulated datasets at each value of $\eta$

To summarize, the message of this simulation study is to show that the proposed MSSEN-M model can be useful in modeling asymmetric and heavy-tailed data. Clearly, there cannot be a model that fits all types of asymmetry and heavy-tailed data better than others. Thus, our suggestion is to add our proposal to the list of candidate models to be fitted.

3.2 A real data illustration

Here, we analyze a cryptocurrency dataset. After a brief description of the background and the analyzed data in Sect. 3.2.1, we provide details on model fitting and comparison in Sect. 3.2.2. Then, we discuss the obtained results in Sect. 3.2.3.

3.2.1 Background and data description

After more than a decade of existence, the interest in the world of cryptocurrencies has exploded and cryptocurrencies are now an important class of financial assets. As such, the modelization of the log returns distribution constitutes an important aspect of analysis. Relatedly, it has been well-documented that the cryptocurrency log returns distribution presents deviation from normality both in terms of asymmetry and heavy tails (Zhang et al. 2018; Hu et al. 2019; de Melo et al. 2020). However, the majority of contributions focus on a separate (i.e. univariate) modelization of each cryptocurrency log returns distribution (see, e.g. Chu et al. 2015; Chan et al. 2017; Szczygielski et al. 2020; Punzo and Bagnato 2021, 2022), despite a multivariate analysis considering the interdependencies among cryptocurrencies would offer more complete financial information (Ji et al. 2019; Shi et al. 2020; Candila 2021).

Herein, we consider the daily adjusted close prices of the following four cryptocurrencies: DigiByte (DGB-EUR), LBRY Credits (LBC-EUR), Vexanium (VEX-EUR), and Curecoin (CURE-EUR). The data were downloaded from https://finance.yahoo.com/cryptocurrencies. All prices are in Euro. The period of analysis for the data goes from 18 September 2019 to 09 October 2021 and, as regularly done in the literature, returns are estimated by taking logarithmic differences. Thus, we have a 4-dimensional dataset with $n=752$ observations.

3.2.2 Model fitting and comparison

On these data, we fitted our MSSEN-M model, as well as the other mixture models discussed in Sect. 3.1, for $k\in \left\{ 1,2,3,4\right\}$. For each model, the BIC is used to select k, and a final ranking based on the models’ BIC values is drawn up to assess the overall best-fitting one.

Furthermore, for each model whose k has been selected by the BIC, we compute the value-at-risk (VaR). The VaR is a commonly used financial risk management tool for measuring the risk of investment losses. Here, we implement the approach used by Soltyk and Gupta (2011) and Lee and McLachlan (2013a) for the analysis of stock returns via finite mixtures of multivariate distributions. Specifically, for a portfolio of d assets log returns $X_1,\ldots ,X_d$, let $X_R=\sum _{h=1}^d X_h$ be the aggregate (or total asset) log-return. Then, the VaR is defined as the negative of the largest value of $x_\alpha$ satisfying

$$\begin{aligned} \Pr \left\{ X_R<x_\alpha \right\} \le \alpha , \end{aligned}$$

where $\alpha$ is the significance level, that in our case will be set to $\alpha =0.05$. Notice that the negative sign mentioned above ensures that the VaR is a positive value, i.e. a positive amount of loss. A large sample of size $n=100{,}000$ is generated from each of the fitted models, and the VaR estimates are obtained by taking the appropriate quantile of the simulated total asset return samples. We draw up a ranking also for the VaR, which is now based on the absolute difference between the empirical VaR and that estimated by each model.

Finally, to evaluate the accuracy of the estimated VaR values, we implement the backtesting procedure proposed by Kupiec (1995), which is one of the most common statistical tests available for this purpose. In detail, this test examines, under the null hypothesis, if the proportion of violations given by $\hat{\rho }=v/n$, where v denotes the number of log returns exceeding the estimated VaR, is statistically different from the one expected ($\alpha$). This test can be performed via the VaRTest() function of the rugarch package (Ghalanos 2020).

3.2.3 Results

Table 1 contains the results for the considered models. As we note, the overall best-fitting model is the MSSEN-M with $k=2$. It is interesting to see that in both the MN-M and MSN-M models the BIC selects $k=4$ groups in the data and they provide the worst fit among the considered models. This might be caused by the componentwise tails which are not thick enough to model the data. Furthermore, we also find that on only two occasions (MST-M and MSS-M) $k=1$ is detected.

Table 1 Number of groups k, the value of the BIC and corresponding ranking for the considered models

In terms of VaR, the empirical value is 31.03 and, in the fashion of Tomarchio and Punzo (2020), a ranking is introduced in order to simplify the reading, based on the percentage difference with respect to the empirical VaR; the lower the difference, the better the position in the ranking. The corresponding backtesting results are also provided in the last column. We see that the MSSEN-M model provides the most accurate estimate, closely followed by the MVG-M and MSEN-M models. The goodness of these VaRs is also supported by the corresponding backtesting p-values since they are the only ones for which the null hypothesis is not rejected. Overall, we also notice a certain degree of variability among the VaR estimates, as often happens in risk management when a battery of models is considered (see, e.g., Eling 2012; Bakar et al. 2015; Tomarchio and Punzo 2020). In particular, the MGH-M provides a very high VaR, emphasizing that it is more extreme in the tails than required for this dataset, thus overestimating the empirical VaR.

Fig. 9

Pairwise plots (on the lower triangle) for the cryptocurrency dataset. Colors refer to the classification estimated by the best MSSEN-M model. Histograms concerning each variable are also displayed in the main diagonal

Figure 9 reports the pairwise plot of the cryptocurrency dataset, with colors according to the classification estimated by the 2-component MSSEN-M. As we can note from many of the subplots, the two groups have roughly the same center but show different degrees of correlation. This is confirmed by the following estimated mean vectors and correlation matrices (the latter labeled as $\varvec{R}(\cdot )$) of the two groups, obtained starting from (5) and (6), respectively:

$$\begin{aligned}\varvec{\mu }_1=(-0.96, 1.96, -0.55, 2.83)', \quad \varvec{\mu }_2=(0.88, -0.79, 0.39, -1.35)',\\\varvec{R}(\varvec{\Phi }_1)= \begin{bmatrix} 1.00 &{} 0.21 &{} 0.48 &{} 0.18 \\ 0.21 &{} 1.00 &{} 0.14 &{} 0.08 \\ 0.48 &{} 0.14 &{} 1.00 &{} 0.14 \\ 0.18 &{} 0.08 &{} 0.14 &{} 1.00 \end{bmatrix} \quad \text {and} \quad \varvec{R}(\varvec{\Phi }_2)= \begin{bmatrix} 1.00 &{} 0.49 &{} 0.42 &{} 0.35 \\ 0.49 &{} 1.00 &{} 0.34 &{} 0.30 \\ 0.42 &{} 0.34 &{} 1.00 &{} 0.21 \\ 0.35 &{} 0.30 &{} 0.21 &{} 1.00 \end{bmatrix}. \end{aligned}$$

From the analysis of the means, we note how both groups are approximately centered around zero and that, for a given cryptocurrency, the sign between the two groups is opposite. Specifically, it appears that in group 1 the average log returns related to the DGB-EUR and VEX-EUR cryptocurrencies are negative compared to those of group 2. Conversely, the average log returns related to the LBC-EUR and CURE-EUR cryptocurrencies in group 1 are positive compared to those in group 2. Thus, it appears that the two groups identify two possible diversified portfolios, each of which combines (in the opposite way) positive and negative log returns of the considered cryptocurrencies.

By analyzing the correlation matrices, we see that, with the exclusion of one occasion, the correlations in the second group are regularly higher than those in the first group. Thus, the detected classification seems to distinguish between two different types of co-movements between the cryptocurrencies. This information would be lost if a single multivariate distribution would be fitted to the data, as commonly done in the cryptocurrency literature.

The estimated asymmetry parameters for the two groups are:

$$\begin{aligned} \varvec{\gamma }_1=(-1.80, 5.92, -0.23, 25.96)', \quad \varvec{\gamma }_2=(6.60, -3.36, 9.49, -10.55)'. \end{aligned}$$

We see that, in both groups, there is a notable deviation from the symmetric case (i.e. $\varvec{\gamma }=\varvec{0}$, refer to Sect. 2). Similarly to the means, the asymmetric behavior is, for a given cryptocurrency, of opposite sign between the two groups.

Finally, we report the estimated tailedness parameters for the two groups: $\theta _1=0.14$ and $\theta _2=0.05$. These values are very close to 0, suggesting a leptokurtic behavior for the pdfs of both groups.

4 Conclusions

In this article, we introduced the multivariate skew shifted exponential normal (MSSEN) distribution, an asymmetric generalization of the multivariate shifted exponential normal distribution. Because of its flexibility, we can account for typical non-normal deviations present in the data, such as asymmetry and heavy tails. Features and moments of the MSSEN distribution have been investigated, and some differences with respect to well-established distributions have been evidenced. Furthermore, we used the MSSEN distribution within the finite mixture model paradigm, thus producing the MSSEN mixture (MSSEN-M) model. An EM algorithm for maximum likelihood parameter estimation of our MSSEN-M model has been illustrated and, differently from many existing alternative models, it has closed-form expressions for all the parameter updates. As concerns the results of the presented simulation study, we showed that the proposed model can perform better than other mixture models, and we have identified possible data structures supporting this result. We have also investigated a real dataset concerning the log returns of four cryptocurrencies. The results show a better fit for our model as well as a more precise risk estimation. Furthermore, the detected classification seems to distinguish between two different types of co-movements between the cryptocurrencies, which would be lost if a single multivariate distribution would be fitted to the data, as commonly done in the cryptocurrency literature.

Appendix A: Left truncated generalized inverse Gaussian distribution

Before presenting the left truncated generalized inverse Gaussian distribution (LTGIG), we report details about the generalized inverse Gaussian (GIG) distribution. Specifically, the random variable V has a GIG distribution, in symbols $V \sim \mathcal {GIG}\left( \lambda ,\chi ,\psi \right)$, if its pdf is

$$\begin{aligned} f_{\tiny {\text {GIG}}}\left( v;\lambda ,\chi ,\psi \right) = \frac{\left( \psi /\chi \right) ^{\frac{\lambda }{2}}v^{\lambda -1}}{2 K_\lambda \left( \sqrt{\psi \chi }\right) } \exp \left\{ - \frac{\chi }{2v} -\frac{\psi }{2} v \right\} , \qquad v>0, \end{aligned}$$

where the parameters satisfy $\chi >0$, $\psi \ge 0$ if $\lambda <0$; $\chi >0$, $\psi >0$ if $\lambda =0$; and $\chi \ge 0$, $\psi >0$ if $\lambda >0$. The GIG distribution was introduced by Good (1953) and has several special cases as, for example, the gamma ($\chi =0$, $\lambda >0$) and the inverse Gaussian ($\lambda =-1/2$) distributions.

That said, the random variable W has a LTGIG distribution on the interval $(a,\infty )$, with $a>0$, in symbols $W \sim \mathcal {LTGIG}_a\left( \lambda ,\chi ,\psi \right)$, if its pdf is

$$\begin{aligned} f_{\tiny {\text {LTGIG}}}\left( w;\lambda ,\chi ,\psi ,a\right)&= A^{-1} f_{\tiny {\text {GIG}}}\left( w;\lambda ,\chi ,\psi \right) \mathbbm {1}_{\left( a,\infty \right) }\left( w\right) \nonumber \\&= \frac{\left( \psi /\chi \right) ^{\frac{\lambda }{2}}w^{\lambda -1}}{2 L_{\lambda }\left( \sqrt{\chi \psi }, a\right) } \exp \left\{ - \frac{\chi }{2w} -\frac{\psi }{2} w \right\} , \qquad a<w<\infty, \end{aligned}$$

(A1)

where

$$\begin{aligned} A= \int _a^\infty f_{\text {GIG}}\left( t;\lambda ,\chi ,\psi \right) dt. \end{aligned}$$

It is straightforward to prove that

$$\begin{aligned} \text {E} \left( W^r\right) = \left( \frac{\chi }{\psi }\right) ^{\frac{r}{2}} \frac{ L_{\lambda +r}\left( \sqrt{\chi \psi },a\right) }{ L_{\lambda }\left( \sqrt{\chi \psi }, a\right) }, \end{aligned}$$

(A2)

with $r\in \mathbb {Z}$.