Co-clustering contaminated data: a robust model-based approach

Abstract

The exploration and analysis of large high-dimensional data sets calls for well-thought techniques to extract the salient information from the data, such as co-clustering. Latent block models cast co-clustering in a probabilistic framework that extends finite mixture models to the two-way setting. Real-world data sets often contain anomalies which could be of interest per se and may make the results provided by standard, non-robust procedures unreliable. Also estimation of latent block models can be heavily affected by contaminated data. We propose an algorithm to compute robust estimates for latent block models. Experiments on both simulated and real data show that our method is able to resist high levels of contamination and can provide additional insight into the data by highlighting possible anomalies.

1 Introduction

The increasing availability of high-dimensional and sparse data calls for more efficient exploratory and pre-processing techniques. One such method is co-clustering, which provides a more effective way of grouping observations and features compared to the application of standard clustering on rows and columns independently, following what is sometimes called a tandem approach. Just like there is no comprehensive definition of clustering as a learning task, this can also be said for co-clustering. Generically speaking, by co-clustering (also called block clustering, two-way partitioning, or biclustering, especially in biostatistics) one refers to any procedure that aims at simultaneously clustering the rows and columns of a data matrix. The actual objective of these procedures varies, depending on the desired properties of the resulting co-clusters, the type of data, possible hypotheses about the generating process and so on.

One of the earliest contributions is the so-called direct clustering, proposed by Hartigan (1972), a method that looks for a hierarchical block partitioning of a data matrix through a greedy algorithm. Since then, many different approaches have been proposed. Following ideas popularised by (Breiman 2001), these approaches can be roughly divided into two categories: algorithmic approaches, focusing on the optimisation of some criterion, and model-based approaches, which postulate the existence of a partially unknown generating process and translate co-clustering into a model estimation task. For a more comprehensive overview of this field we refer for instance to Madeira and Oliveira (2004), Govaert and Nadif (2014), Brault and Lomet (2015) and Biernacki et al. (2022).

Historically, from a practical point of view, the development of co-clustering has been motivated by information extraction tasks, such as the analysis of vote patterns (Hartigan 1972), text mining (Dhillon 2001; Dhillon et al. 2003; Ailem et al. 2015, 2017), microarray data analysis (Cheng and Church 2000) and customer segmentation and recommendation systems (Shan and Banerjee 2008), among others. Besides its usefulness in mining tasks, co-clustering also offers a compressed representation of the data, making it interesting as an exploratory and variable selection technique for high-dimensional data. Moreover, unlike a tandem approach, co-clustering takes into account the dependency between rows and columns, providing a meaningful description of the groups of observations in terms of the corresponding groups of variables, and vice versa. Finally, even if the focus is on one-way grouping, in some cases co-clustering could be preferred to ordinary clustering, especially when dealing with high-dimensional data.

In addition to high dimensionality and sparsity, it is often the case that real-world data contain outliers. This is particularly problematic as larger amounts of data are available, since a manual check becomes unfeasible. For this reason, robust statistical methods are concerned with the automatic detection of outliers and the immunisation of estimation procedures against contamination.

Despite the interest in co-clustering and its many applications, up to now there exist only very few robust procedures in this field. In this paper we propose a novel robust approach to model-based co-clustering, which extends to this domain the idea of impartial trimming introduced in Cuesta-Albertos et al. (1997). The proposed approach is general and can be applied to different use cases. In more detail, we introduce row- and column-wise impartial trimming in the estimation of Latent Block Models (Govaert and Nadif 2003) and show the performance of the resulting robust procedures on simulated and real data.

The rest of the article is organised as follows. In Sect. 2 we introduce the necessary background information on Latent Block Models and make the case for the development of robust methods. In Sect. 3 we present our proposal and an algorithm for its computation. The results of experiments on simulated data are presented in Sect. 4 while Sect. 5 contains real data applications. Finally, in Sect. 6 we draw some conclusions and discuss possible future work.

2 Latent block models

Among model-based approaches, the class of Latent Block Models (LBMs), first proposed in Govaert and Nadif (2003), has become rather popular, extending finite mixture models to the two-way case. Similarly to how clustering benefits from an approach based on finite mixture models, co-clustering via LBMs can rely on well defined probabilistic foundations. LBMs allow for flexibility in modelling different types of data (continuous, contingency, categorical or binary data), as well as for the interpretability of the parameters of the model itself.

2.1 Definition and model assumptions

First, we summarise the assumptions underlying LBMs:

• Co-clusters (or blocks) are assumed to be defined by the Cartesian product of row and column partitions. Therefore, every element $X_{ij}$ of the data matrix X is assumed to belong to exactly one of such blocks.

• The sets of row labels $\lbrace Z_{i} \rbrace _{i=1}^n$ and column labels $\lbrace W_{j} \rbrace _{j=1}^p$ are assumed to be independent from one another.

• Row (resp. column) labels are are also independent and are identically distributed, following a categorical distribution.

• Conditionally on the labels $\lbrace Z_{i} \rbrace _{i=1}^n$ and $\lbrace W_{j} \rbrace _{j=1}^p$, the elements of the matrix $X_{i,j}$ are assumed to be independent and to have a conditional distribution defined by $f(x \vert \lambda _{k,l})$, where $\lambda _{k,l}$ are parameters specific to the co-cluster identified by the pair of indices (k, l). f is either a discrete or absolutely continuous probability density function (p.d.f.).

Starting from these assumptions, it is possible to write the incomplete-data likelihood of a general LBM in the following form:

$$\begin{aligned} L(\pmb {\vartheta } \vert X) = \sum _{(Z, W) \in {\mathcal {Z}}\times {\mathcal {W}}}\prod _{i,k}\pi _k^{z_{ik}} \prod _{j,l}\rho _l^{w_{jl}} \prod _{i,j,k,l}f(x_{ij}\vert \pmb {\lambda }_{kl})^{z_{ik} w_{jl}}, \end{aligned}$$

(1)

where:

• X is an n-by-p matrix with elements $x_{ij}$ taking values in a set $S \subseteq {\mathbb {R}}$, e.g., $S = {\mathbb {R}}$, $S = {\mathbb {N}}$, $S = \lbrace 0, 1 \rbrace$.

• The indices i and j refer to the rows and columns of X, respectively, and therefore $i \in [n]:= \lbrace 1, 2, \ldots , n \rbrace$ and $j \in [p]$.

• The indices k and l refer to the row and column partitions of size g and m, respectively, and therefore $k \in [g]$ and $l \in [m]$.

• ${\mathcal {Z}}$ is the set of all n-by-g binary matrices with row sums equal to 1, i.e., ${\mathcal {Z}} = \big \lbrace Z \in \lbrace 0, 1\rbrace ^{n \times g} \,:\, \sum _k z_{i,k}=1 \,\forall i \big \rbrace$. To denote that the i-th row of X belongs to row-cluster k we write interchangeably $z_{i,k}=1$ or $z_i=k$. Clearly if row i does not belong to row-cluster k then $z_{i,k}=0$. Analogous notation and assumptions apply to ${\mathcal {W}}$ and the matrix W of binary column labels, replacing n by p and g by m.

• $\pmb {\pi } = \lbrace \pi _k \rbrace _{k}$ is the vector of the mixing proportions for the row partition and belongs to the g-dimensional standard simplex, i.e., $\pmb {\pi }$ is in $[0,1]^g$ for all k and $\sum _k \pi _k = 1$. Analogous notation and assumptions apply to the column mixing proportions $\pmb {\rho } = \lbrace \rho _l \rbrace _{l}$, mutatis mutandis.

• $\Lambda = \lbrace \pmb {\lambda }_{kl} \rbrace _{kl}$ is the collection of the block parameters. Depending on the distribution chosen to model the data, the parameters $\pmb {\lambda }_{kl}$ can be either scalars or vectors. In the former case $\Lambda$ is a matrix.

• $\pmb {\vartheta } = (\text {vec}(\Lambda ),\pmb {\pi }, \pmb {\rho })$ is the vector of all the model parameters.

• f is a p.d.f. (discrete or absolutely continuous) with support in S.

The choice of the distribution f depends on the type of data one wants to model. Common choices are: Normal distribution for continuous data, Poisson distribution for counting data, Multinomial distribution for categorical data, and Bernoulli distribution for binary data. In principle, any other reasonable distribution could be used, which makes the LBM framework quite flexible.

Other model specifications are also possible, including constraints on the parameters and parsimonious versions of the ‘full’ models. For instance, one can assume equal mixing proportions, equal block variances in the Normal LBM, a block diagonal structure with sparse non-diagonal blocks in the Poisson LBM, etc.

Finally, in the case of Poisson LBMs, the addition of row and column effects is common. In this case, the block distributions $f(X_{ij}\vert \pmb {\lambda }_{kl})$ are replaced by $f(X_{ij}\vert \mu _{i}\nu _{j}\pmb {\lambda }_{kl})$, where $\mu _{i}$ and $\nu _{j}$ are the row and column effects and are estimated by $\sum _{j}x_{ij}$ and $\sum _{i}x_{ij}$, respectively. We can refer to this more complex model as ‘normalised’ Poisson LBM, in contrast to the ‘unnormalised’ Poisson LBM which does not include row and column effects.

2.2 Model estimation

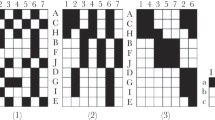
It is well known that, due to the dependence structure of the model, estimation of LBMs via the Expectation-Maximisation (EM) algorithm (Dempster et al. 1977) is unfeasible. More specifically, the expectation step is problematic since the joint row-column class posteriors ${\mathbb {P}}(Z_i,W_j\vert X,\pmb {\vartheta })$ should be estimated, but the class labels $Z_i$ and $W_j$ are not independent given the observed data X, as can be deduced from Fig. 1. For this reason, two main alternative approaches have been proposed. On one hand there is the Variational EM (VEM) algorithm, which is still in the Maximum Likelihood (ML) estimation framework, but in which the likelihood function (1) is replaced by a variational lower bound (Govaert and Nadif 2005, 2008). On the other hand, we have a block version of the Classification EM (CEM) algorithm, which lives in the Classification ML framework. That is, it aims at optimising the complete-data or classification likelihood given by (2) instead of (1) (Celeux and Govaert 1991; Govaert and Nadif 2003):

$$\begin{aligned} L_C(\pmb {\vartheta }, Z, W \vert X) = \prod _{i,k}\pi _k^{z_{ik}} \prod _{j,l}\rho _l^{w_{jl}} \prod _{i,j,k,l}f(x_{ij}\vert \pmb {\lambda }_{kl})^{z_{ik} w_{jl}}. \end{aligned}$$

(2)

Other optimisation schemes include SEM-Gibbs (an adaptation of Stochastic EM to block VEM) and V-Bayes, a Bayesian version of VEM (Keribin et al. 2015).

For convenience, we reproduce in Algorithm 1 the Block CEM algorithm, abbreviated as BCEM. Note that $\delta _x(y)$ denotes the Kronecker delta of y at x, that is, the indicator function of $\lbrace x \rbrace$ defined on the integers.

Fig. 1

Representation of the dependence structure of a general LBM as a Bayesian network. The $X_{ij}$’s are the observed elements of the data matrix, the $Z_i$’s and $W_j$’s are the unobserved row and column labels, $\pmb {\pi }$, $\pmb {\rho }$ and $\Lambda$ are the row mixing proportions, the column mixing proportions and the block parameters, respectively

The actual update rule of the parameter estimates $\hat{\pmb {\vartheta }}$ will of course depend on the distribution f. In all cases, we assume that $\hat{\pmb {\vartheta }}$ maximises the likelihood of the model given the partitions. For the most common choices of f explicit formulae for computing $\hat{\pmb {\vartheta }}$ are available (see Govaert and Nadif (2014)).

Since the objective function of the algorithm is the classification likelihood, convergence to a stationary point can be tested by checking whether $\log L_C^{t+1} - \log L_C^{t} \le \varepsilon$, where $\log L_C^{t}$ denotes the classification log-likelihood at iteration t and $\varepsilon$ is a desired tolerance.

In this paper, we focus on an extension of the BCEM algorithm, so we do not present in detail other alternatives, which can be found for instance in Govaert and Nadif (2014). However, note that the structure of BVEM, SEM-Gibbs and V-Bayes is very similar to that of Algorithm 1, with differences in the E steps for the former two and in the E and M steps for the latter algorithm.

Finally, we highlight the fact that in principle neither the incomplete nor the complete-data likelihood have to be bounded. For instance, consider a Gaussian LBM. In this case, if the cells in one block–say (k, l)–are constant, and thus equal to the block’s mean, then the likelihood is unbounded, as can easily be seen from (1) by replacing f with a univariate Gaussian p.d.f. and letting $\sigma ^2_{kl} \rightarrow 0^+$. Therefore, (classification) maximum likelihood estimation may be an ill-posed problem. We do not address this issue here, but an approach similar to that proposed in García-Escudero et al. (2008), which introduces a restriction factor controlling parameter constraints in the context of finite Gaussian mixtures, may be considered.

2.3 Co-clustering and robustness

In general co-clustering procedures are not robust, that is, they can break down even with a small fraction of contaminated data. For instance, Farcomeni (2009) considered the cellwise replacement finite-sample breakdown point of the estimates of the centroid matrix M (i.e., the matrix whose elements are the co-cluster centroids), given by

$$\begin{aligned} \varepsilon ^{cell}_{np} (M,X) = \frac{1}{np} \min \Bigg \lbrace o: \sup _{X_o} \Vert {M(X) - M(X_o)} \Vert = \infty \Bigg \rbrace , \end{aligned}$$

(3)

where o is the number of elements of X replaced by outliers and $X_o$ is the data matrix obtained after such replacement. In the cited work it is shown that for double k-means $\varepsilon ^{cell}_{np} (M,X) \le 1/{np}$ which means that even one single entry, placed far enough from the corresponding co-cluster centroid, can completely spoil the estimates.

It is easy to see that the same holds if we consider co-clustering through LBMs. To fix ideas, consider the Gaussian LBM for continuous data. Given the partition matrices Z and W, the estimates for the means of the block densities can be obtained analytically by solving the corresponding Maximum Likelihood equations and are given by

$$\begin{aligned} M_{kl}(X) = \frac{\sum _{ij}z_{ik} x_{ij} w_{jl}}{\sum _i z_{ik} \sum _j w_{jl}} \end{aligned}$$

(4)

(see for instance Govaert and Nadif (2014)). Clearly, if we take perturbed matrices of the form $X_o = (\delta _{i=i', j=j'}x + (1-\delta _{i=i', j=j'}) x_{ij})_{ij}$ (that is, matrices where we replace the element $(i',j')$ of the original matrix X with some $x\in {\mathbb {R}}$), supposing $z_{i'l'}=1$ and $w_{j'k'}=1$ from (4) we obtain that

$$\begin{aligned} (M(X) - M(X_o))_{kl} = \frac{x_{i'j'} - x}{\sum _i z_{ik'} \sum _j w_{jl'}} \delta _{k=k', l=l'}, \end{aligned}$$

and thus

$$\begin{aligned} \begin{aligned} \sup _{X_o} \Vert {M(X) - M(X_o)} \Vert&\ge \sup _{X_o} \Vert {(M(X) - M(X_o)){\textbf{e}}_{l'}} \Vert \\&= \lim _{x \rightarrow \infty } {\bigg |{\frac{x_{i'j'} - x}{\sum _i z_{ik'} \sum _j w_{jl'}}}\bigg |} = \infty , \end{aligned} \end{aligned}$$

where with a slight abuse of notation $\Vert {\cdot } \Vert$ denotes both the vector norm and its induced operator norm. In the inequality we have used the definition of operator norm $\Vert {T} \Vert =\sup _{\mathbf {\Vert {v} \Vert =1}} \Vert {T{\textbf{v}}} \Vert$, and ${\textbf{e}}_{l'}$ is the standard base vector with $l'$-th non-zero component. It immediately follows from (3) that for co-clustering with the Gaussian LBM it also holds that $\varepsilon ^{cell}_{np} (M,X) = {1}/{np}$. This is not surprising, since (4) is simply the arithmetic mean of the elements of X belonging to block (k, l). The same conclusions directly apply to the unnormalised Poisson LBM as well, since also in this case block means are estimated as in (4).

For the normalised Poisson LBM, the situation is slightly different, but we can see how outliers can spoil estimation also in this case. The standard estimates in this model are given by

$$\begin{aligned} M_{kl}(X) = \frac{\sum _{ij}z_{ik} x_{ij} w_{jl}}{\sum _i z_{ik}{\hat{\mu }}_i \sum _j w_{jl}{\hat{\nu }}_j}, \end{aligned}$$

with

$$\begin{aligned} {\hat{\mu }}_i = \sum _j x_{ij}, \quad {\hat{\nu }}_j = \sum _i x_{ij} \end{aligned}$$

(see for instance Govaert and Nadif (2014)). Considering the same type of contamination as above, we now have

$$\begin{aligned} \begin{aligned}&\inf _{X_o} M_{k'l'}(X_o) \\&= \lim _{x \rightarrow \infty } \frac{x + \sum _{i \not = i', j\not = j'}z_{ik'} x_{ij} w_{jl'}}{(x + \sum _{i \not = i', j\not = j'} z_{ik'}x_{ij}) (x + \sum _{i \not = i', j\not = j'} w_{jl'}x_{ij})} = 0. \end{aligned} \end{aligned}$$

(5)

Since in this model the block parameters are parameters of Poisson distributions, we must have $M \in (0, +\infty )^{g \times m} =: \Theta$, but (5) shows that M can pushed be arbitrarily close to the boundary $\partial \Theta$ by contaminating only one cell. Therefore, considering the more general definition of replacement finite-sample breakdown point given for example in Maronna et al. (2006), we conclude that also in this case $\varepsilon ^{cell}_{np} (M,X) = 1/{np}$.

In spite of this, so far robustness received little attention in this field. Some robust approaches have been proposed in the algorithmic setting, for example for double k-means (Farcomeni 2009) or fuzzy double k-means (Ferraro and Vichi 2015), which extend the ideas of trimming and concentration steps to the two-way case. In the model-based setting, the addition of noise column clusters was proposed in Laclau and Brault (2019) for categorical data, and Selosse et al. (2020) for count data with a specific purpose related to text mining via co-clustering. The latter two works, however, do not aim at providing robust methods in the sense that is usually implied in the statistical literature: essentially, they both design a model that accounts for noise by confining it in an ad-hoc group, without really dealing with the concept of outlier or anomaly, nor addressing the problem of break down of the estimators.

Considering that co-clustering can be especially useful on large data sets–which are more likely to contain anomalies–and that the latent block model represents a unifying and well founded probabilistic framework for co-clustering, we believe that the lack of a general approach to robustness is an important gap to be filled.

3 A robust model-based approach

We propose to extend the idea of impartial trimming to co-clustering via LBMs. First developed for the specific case of k-means clustering (Cuesta-Albertos et al. 1997) and then further extended to finite Gaussian mixtures (García-Escudero et al. 2008), in the case of standard ‘one-way’ clustering, impartial trimming consists in trimming those observations that have the lowest class posterior probabilities.

More concretely, in the case of CEM estimation for finite mixture models, in each iteration one leaves out the observations $\pmb {x}_i$ for which $d_{ik} = \pi _{k}f(\pmb {x}_i \vert \pmb {\lambda }_k)$ is below the threshold $d_{\lceil \alpha n \rceil k}$, where $\alpha$ is the trimming level (i.e., the proportion of observations to discard) and k is the mixture component to which $\pmb {x}_i$ is assigned.

3.1 The model

We consider LBMs as introduced in Sect. 2 with the addition of contamination. Let S and T contain the row and column indices of the contaminated cells. We can express the likelihood of the model in the following form (cf. García-Escudero et al. (2008)):

$$\begin{aligned} \begin{aligned} L'(\pmb {\vartheta } \vert X)&= \Bigg [ \sum _{(Z, W) \in {\mathcal {Z}}\times {\mathcal {W}}}\prod _{i \in S,k}\pi _k^{z_{ik}} \prod _{j\in T,l}\rho _l^{w_{jl}} \prod _{i\in S,j\in T,k,l}f(x_{ij}\vert \pmb {\lambda }_{kl})^{z_{ik} w_{jl}} \Bigg ] \cdot \\&\cdot \Bigg [ \prod _{(i,j) \not \in S\times T} g_{ij}(x_{ij}) \Bigg ], \end{aligned} \end{aligned}$$

(6)

where the $g_{ij}$’s denote the (unknown) density functions of the contaminated elements $x_{ij}$.

Given the likelihood function (6) and two trimming levels $\alpha _1$ and $\alpha _2$, one would want to solve the optimisation problem

$$\begin{aligned} \max _{S, T} \max _{\pmb {\vartheta } \in \Theta } L'(\pmb {\vartheta } \vert X), \end{aligned}$$

(7)

where S is a subset of [n] and T is a subset of [p], with cardinalities $\# S = n - \lceil \alpha _1 n \rceil$, $\# T = p - \lceil \alpha _2 p \rceil$. Note that if $\alpha _1 = \alpha _2 = 0$ we recover the original LBM. Since obtaining an exact solution to (7) is a computationally intractable problem, we propose a method that, at least empirically, seems to provide reasonable approximate solutions.

3.2 Estimation

As mentioned in Sect. 2.2 estimation is not so straightforward with LBMs. In the following we take the point of view of Classification Maximum Likelihood Estimation (Celeux and Govaert 1991) and build on the BCEM algorithm presented above (Algorithm 1), that first appeared in Govaert and Nadif (2003).

Our objective is to maximise the trimmed version of the classification likelihood (2), that is, to find

$$\begin{aligned} \max _{S, T} \max _{Z, W, \pmb {\vartheta }} \prod _{i \in S,k}\pi _k^{z_{ik}} \prod _{j\in T,l}\rho _l^{w_{jl}} \prod _{i\in S,j\in T,k,l}f(x_{ij}\vert \pmb {\lambda }_{kl})^{z_{ik} w_{jl}}, \end{aligned}$$

where the sets S and T are defined above. This can be equivalently stated as

$$\begin{aligned} \max _{(Z, W) \in {\mathcal {Z}}' \times {\mathcal {W}}', \pmb {\vartheta }} \prod _{i,k}\pi _k^{z_{ik}} \prod _{j,l}\rho _l^{w_{jl}} \prod _{i,j,k,l}f(x_{ij}\vert \pmb {\lambda }_{kl})^{z_{ik} w_{jl}}, \end{aligned}$$

(8)

where the partition matrix ${\mathcal {Z}}'$ is now constrained to have a proportion $\alpha _1$ of its rows empty, that is, ${\mathcal {Z}}'= \big \lbrace Z \in \lbrace 0, 1\rbrace ^{n \times g} \,:\, \sum _k z_{ik} \in \lbrace 0, 1 \rbrace \,\forall i, \, \sum _{ik}z_{ik} = n - \lceil \alpha _1 n \rceil \big \rbrace$, and analogously for ${\mathcal {W}}'$ with a proportion $\alpha _2$.

The proposed estimation procedure extends the BCEM algorithm by including a trimming step based on the concept of impartial trimming, that can be performed on the rows and on the columns. We refer to our trimmed version of the algorithm as Trimmed Block CEM (TBCEM). The pseudocode is presented in Algorithm 2.

Since the rest of the algorithm is identical to BCEM, we focus on the trimming step. To fix ideas, consider for instance trimming of the rows. Since we wish to mark as outliers those observations that conform the least to the rest of the data according to the model, we consider the following quantities to discriminate between the rows and to perform trimming:

$$\begin{aligned} s_{ik} = {\pi _k}\prod _{jl}f(x_{ij}\vert \pmb {\lambda }_{kl})^{w_{jl}} \, \propto \, {\mathbb {P}}(Z_{ik}=1 \vert X, W, \pmb {\vartheta }), \end{aligned}$$

(9)

where we have used the fact that

$$\begin{aligned} \begin{aligned} {\mathbb {P}}(Z_{ik}=1 \vert X, W, \pmb {\vartheta })&= \frac{{\mathbb {P}}(X_i \vert Z_{ik}=1, W, \pmb {\vartheta }) {\mathbb {P}}(Z_{ik}=1 \vert W, \pmb {\vartheta })}{{\mathbb {P}}(X_i \vert W, \pmb {\vartheta })} \\&= \frac{{\mathbb {P}}(X_i \vert Z_{ik}=1, W, \pmb {\vartheta }) {\mathbb {P}}(Z_{ik}=1 \vert \pmb {\vartheta })}{{\mathbb {P}}(X_i \vert W, \pmb {\vartheta })} \\&= \frac{{\pi _k}\prod _{jl}f(x_{ij}\vert \pmb {\lambda }_{kl})^{w_{jl}}}{\sum _{k}{\pi _k}\prod _{jl}f(x_{ij}\vert \pmb {\lambda }_{kl})^{w_{jl}}}. \end{aligned} \end{aligned}$$

Now, following the Maximum A Posteriori (MAP) principle, we assign row i to the class $k^*(i)$ that maximises $s_{ik}$, that is, we set $z_{ik} = 1$ if $k=k^*(i)$ and $z_{ik} = 0$ otherwise, where $k^*(i) = {{\,\mathrm{arg\,max}\,}}_k s_{ik} = {{\,\mathrm{arg\,max}\,}}_k \log s_{ik}$. At this point, to perform trimming, we select the $\alpha _1$-quantile of $\lbrace s^*_{i} \rbrace _i$, $s^*_{(\lceil \alpha _1 n \rceil )}$, where $s^*_{i} = s_{ik^*(i)}$. The $\lceil \alpha _1 n \rceil$ rows i for which $s^*_{i} \le s^*_{(\lceil \alpha _1 n \rceil )}$ are marked as outliers, since they have a low likelihood for all groups compared to the others, and so for these rows we set $z_{ik} = 0$ for all k. In this way, they are excluded and do not contribute to the estimation of the model parameters. The non-outlying rows are classified as explained above and their assignments are left untouched.

Analogously, to classify and trim the columns we use

$$\begin{aligned} t_{jl} = {\rho _l}\prod _{ik}f(x_{ij}\vert \pmb {\lambda }_{kl})^{z_{ik}} \, \propto \, {\mathbb {P}}(W_{jl}=1 \vert X, Z, \pmb {\vartheta }) \end{aligned}$$

(10)

and perform the same steps as above.

To conclude this paragraph, we observe that when f is Gaussian and we impose the constraints $\pi _k = \pi$, $\rho _k = \rho$ and $\sigma ^2_{kl} = \sigma ^2$, Algorithm 2 reduces to the Trimmed Double k-means algorithm presented in Farcomeni (2009). In particular, concerning the classification and trimming steps, in this case we have

$$\begin{aligned} \log {s}_{ik} = \log {\pi } - \frac{1}{2} \sum _{jl} {w}_{jl} \bigg ( \log ({\sigma }^2) + \frac{(x_{ij} - {\mu }_{kl})^2}{{\sigma }^2} \bigg ). \end{aligned}$$

Hence,

$$\begin{aligned} {{\,\mathrm{arg\,max}\,}}_k {s}_{ik} = {{\,\mathrm{arg\,min}\,}}_k \sum _{jl} {w}_{jl} {(x_{ij} - {\mu }_{kl})^2}, \end{aligned}$$

and similarly for the columns. Therefore, the concentration steps of Trimmed Double k-means and the impartial trimming steps of TBCEM coincide. It is easy to verify that also the M step of TBCEM and the computation of the centroid matrix in Trimmed Double k-means are identical in this case.

3.3 Theoretical properties

Here we discuss the convergence of the proposed algorithm, the existence of a solution to the optimisation problem and the robustness properties of the method.

3.3.1 Convergence

We start by proving the following result on the monotonicity of the iterations.

Proposition 1

Each iteration of Algorithm 2 does not decrease the classification log-likelihood of the model.

Proof

One iteration of the algorithm consists of three alternated optimisation steps: two Expectation-Classification steps (on the rows and on the columns) and one Maximisation step.

Consider the EC-step on the rows. Since we are maximising $\log L_C$ with respect to Z, we can regard the term $\sum _{jl} w_{jl}\log \rho _l$ as a constant $c = c(W, \pmb {\rho })$ and write

$$\begin{aligned} \log L_C&= \sum _{ik}z_{ik} \bigg (\log \pi _k + \sum _{jl} w_{jl} \log f(x_{ij}\vert \pmb {\lambda }_{kl})\bigg ) + c \\&= \sum _{ik}z_{ik} s_{ik} + c. \end{aligned}$$

(11)

For every i, we find $k^*(i) = {{\,\mathrm{arg\,max}\,}}_k s_{ik}$ and, for the indices i corresponding to the largest $n - \lceil \alpha _1 n \rceil$ $s_{ik}$’s, we set $z_{ik} = \delta _{k^*(i)}(k)$. The remaining $\lceil \alpha _1 n \rceil$ rows are not assigned to any row partition, that is, if $i'$ is one of such rows, we set $z_{i'k}=0$ for all k. Therefore, at every step, in Equation (11) the $z_{ik}$’s are chosen so that the contribution from the $s_{ik}$’s is maximised under the classification and trimming constraints.

The same argument applies, mutatis mutandis, to the EC-step on the columns.

Finally, by definition of the M-step, the parameters $\pmb {\vartheta }$ are estimated precisely as the ${{\,\mathrm{arg\,max}\,}}$ of $\log L_C$ given the partitions. Therefore, also this step cannot decrease the objective function. $\hfill\square$

From Proposition 1, it immediately follows that the algorithm is guaranteed to converge provided that the classification log-likelihood of the model is bounded from above.

Corollary 1

If $\log L_C$ is bounded from above, Algorithm 2 converges in a finite number of iterations.

Proof

Denote by $\ell ^t$ the value of $\log L_C$ at iteration t. By Proposition 1 the sequence of reals $\lbrace \ell ^t \rbrace _{t > 0}$ is monotone, therefore boundedness is a necessary and sufficient condition for its convergence.

The last part of the claim follows from the fact that the number of possible partitions is finite. $\hfill\square$

The boundedness assumption of Corollary 1 is in general data-dependent, unless the likelihood admits an upper bound for any X. We can show that this is the case for discrete block densities and also for a constrained version of the Normal LBM. This implies convergence of the algorithm independently of the data.

Proposition 2

We consider two cases.

• i. If the block density f is discrete, then $L_c$ is bounded from above in $\pmb {\vartheta }$, uniformly in X.

• ii. If the block density f is normal and it holds that

  $$\begin{aligned} \frac{\sigma _{\max }}{\sigma _{\min }} \le c, \quad c > 0 \end{aligned}$$

  (C1)

  (where $\sigma _{\max } = \max _{kl}\sigma _{kl}$, $\sigma _{\min } = \min _{kl}\sigma _{kl}$) and

  $$\begin{aligned} \# \textrm{supp} \, {\mathbb {P}}_{np} > gm + \lceil n \alpha _1 \rceil + \lceil p \alpha _2 \rceil - \lceil n \alpha _1 \rceil \lceil p \alpha _2 \rceil \end{aligned}$$

  (C2)

  (that is, the empirical measure ${\mathbb {P}}_{np}$ does not concentrate on gm points or less after trimming), then $L_c$ is bounded from above in $\pmb {\vartheta }$, for any X.

By combining Proposition 2 with Corollary 1, it follows in both cases that Algorithm 2 converges in a finite number of iterations under the conditions of Proposition 2.

Proof

In the discrete case we can bound uniformly in x the pmf, for any parameter values, simply by noting that $f(x_{ij}\vert \pmb {\lambda }_{kl})$ is a probability and thus bounded between 0 and 1.

The boundedness of f automatically implies the boundedness from above of the objective function (2).

As for the Gaussian case, f blows up only when $\sigma \rightarrow 0$ and $x = \mu$. We show that (C1) and (C2) prevent that this causes the likelihood to diverge. For notational simplicity we drop the double indices and write $\sigma _k$ to indicate the k-th component of the vectorised version of the block variances matrix. Assume that $\sigma _{k'} \rightarrow 0$ for some $k'$. The constraint (C1) implies that $\sigma _{k} \rightarrow 0$ for all k. Now, it is not difficult to see that, when $\sigma \rightarrow 0$, $f(\mu \vert \mu , \sigma )$ diverges like $1/\sigma$, while if $x \ne \mu$ it holds that $f(x \vert \mu , \sigma ) \in o(\sigma ^q)$, for any $q>0$ (see for instance Coretto and Hennig (2017)). Thanks to (C2), it is assured that there exists an x that does not coincide with any of the means $\mu _k$. Therefore (2) contains at least a factor that vanishes faster than any polynomial, and so the whole likelihood converges to 0. $\hfill\square$

We note that in general, without conditions (C1) and (C2), we cannot be sure of the likelihood boundedness in the normal case. While (C2) can be easily verified, enforcing (C1) would require an additional step in the algorithm. However, Biernacki et al. (2022) showed by a combinatorial argument that spurious solutions (i.e., configurations corresponding to unbounded or extremely large likelihood values) are unlikely to be observed in co-clustering. Finally, also note that trimmed double k-means corresponds to the case where $c=1$ in (C1) and the mixing proportions are also constrained to be equal.

For the sake of clarity, we stress the fact that the stationary point found by the algorithm is not necessarily an optimum, as has been extensively discussed in the literature (see for instance Redner and Walker (1984)). The addition of trimming of course does not change this fact.

Moreover, the problems of empty blocks and spurious solutions may both occur in (trimmed) co-clustering. In more detail, it has been argued by Biernacki et al. (2022) that the former is expected to be considerably more frequent in the two-way case compared to standard clustering, since the number of model configurations leading to at least one empty group is substantially higher. On the other hand, as mentioned above, the emergence of degenerate or spurious solutions is unlikely in co-clustering.

In the numerical implementation of our method, we run the algorithm with several random initialisations and keep only those initialisations that do not lead to configurations with empty blocks. The number of initialisations can be specified by the user, who also has the possibility to restart the method until a solution with non-empty blocks is found. This brute-force approach is reasonable when the number of groups is not too high (not more than $\approx 20$ blocks) and in our experiments it performed sufficiently well. In other scenarios, a more adequate initialisation strategy or a different algorithm may alleviate the issue of empty blocks and spurious solutions.

3.3.2 Existence

We can build on the results of Proposition 2 to prove the existence of a solution at the empirical distribution. The spirit of the proof is similar to that of Proposition 2 in García-Escudero et al. (2008) and Theorem 4 in Coretto and Hennig (2017).

Proposition 3

Consider one of the two following cases:

• i. The block density f is Poisson;

• ii. The block density f is normal and (C1) and (C2) hold.

Then there exists a $\pmb {\vartheta }^*$ that solves (8).

Proof

First, let us consider the log likelihood ${\mathcal {L}}_c$ at the empirical distribution

$$\begin{aligned} {\mathcal {L}}_c(\pmb {\vartheta }) = \sum _{ik}z_{ik}\log (\pi _k) + \sum _{jl}w_{jl}\log (\rho _l) + \sum _{ijkl}z_{ik}w_{jl} \log f(x_{ij} \vert \pmb {\lambda }_{kl}) \end{aligned}$$

(12)

where it is understood that $z_{ik} = z_{k}({\textbf{x}}_i, \pmb {\vartheta })$ and similarly for $w_{jl}$ (it suffices to redefine the labels as functions of $\pmb {\vartheta })$ that perform the optimal assignment according to the MAP principle, as seen for instance in Subsection 3.2 and in García-Escudero et al. (2008)). It is straightforward to see that

$$\begin{aligned} M:= \sup _{\pmb {\vartheta }} {\mathcal {L}}_c > -\infty . \end{aligned}$$

(13)

For instance, in the normal case take $\pmb {\vartheta }$ such that $\pi _k = 1/g$ for all k, $\rho _l = 1/m$ for all l, $\mu _{kl} = 0$ and $\sigma _{kl} = 1$ for all k, l. It is easy to see that the same holds in the Poisson case. We already know from Proposition 2 that $M < + \infty$ as well.

We will show that any maximising sequence $\{ \pmb {\vartheta }_t \}_{t=0}^{\infty }$ in the space of parameters (satisfying constraints (C1) and (C2) in the normal case) must be contained in a compact set.

[Normal case] Consider $\{ \pmb {\vartheta }_t \}$ such that $\exists k'$ so that $\sigma _{k'} \rightarrow +\infty$. By (C1) it follows that $\sigma _{k} \rightarrow +\infty$ for all k. It is then clear that all block densities $f(x \vert \mu _k, \sigma _k)$ go to zero for any x and $\mu _k$, therefore ${\mathcal {L}}_c \rightarrow -\infty$ for any $\pmb {\pi }$, $\pmb {\rho }$ and $\pmb {\mu }$.

In the proof of Proposition 2 we have already shown that if instead $\sigma _{k'} \rightarrow 0$ for some $k'$, then (C1) and (C2) guarantee that, again, ${\mathcal {L}}_c \rightarrow -\infty$.

Let us now consider the case where $\vert \mu _{k'} \vert \rightarrow +\infty$. It is readily seen that this implies $f(x\vert \mu _{k'}, \sigma _{k'}) \rightarrow 0$, whatever the values of x and the other parameters. Therefore also in this case ${\mathcal {L}}_c \rightarrow -\infty$. The case where an arbitrary number of means diverges is no different.

Finally, it remains to be shown that ${\mathcal {L}}_c \rightarrow -\infty$ even when taking limits on $\pmb {\mu }$ and $\pmb {\sigma }$ simultaneously. We have two main cases, namely: $\vert \mu _{k'} \vert \rightarrow +\infty$ and $\sigma _{k} \rightarrow +\infty$, or $\vert \mu _{k'} \vert \rightarrow +\infty$ and $\sigma _{k} \rightarrow 0$. Note that if some $\sigma _k$ diverges or vanishes, then, because of (C1), all block variances diverge/vanish at the same rate, so it is not important which index k we are referring to. If more than one mean diverges, the arguments that follow do not change. In the first case we have two sub-cases, depending on the relative rate of divergence between $\pmb {\mu }$ and $\pmb {\sigma }$.

• a) $\mu _{k'} / \sigma _k \rightarrow c \in {\mathbb {R}}$: this implies $f(x \vert \mu _{k'}, \sigma _{k'}) \rightarrow 0$ ($f(x \vert \mu _{k'}, \sigma _{k'})$ is $o(1/\sigma _k)$), therefore ${\mathcal {L}}_c \rightarrow -\infty$.

• b) $\vert \mu _{k'} \vert / \sigma _k \rightarrow +\infty$: in this case $f(x \vert \mu _{k'}, \sigma _{k'}) \rightarrow 0$ exponentially and so ${\mathcal {L}}_c \rightarrow -\infty$.

When $\vert \mu _{k'} \vert \rightarrow +\infty$ and $\sigma _{k} \rightarrow 0$, $\vert \mu _{k'} \vert / \sigma _k \rightarrow +\infty$ and so we fall in case b) above.

[Poisson case] If $\lambda _{k'} \rightarrow +\infty$ for some $k'$, then $f(x\vert \lambda _{k'}) \rightarrow 0$, for any fixed x, and so ${\mathcal {L}}_c \rightarrow -\infty$.

In both cases, if $\{ \pmb {\vartheta }_t \}$ leaves every compact set, then $\sup {\mathcal {L}}_c$ cannot be achieved, since one would have ${\mathcal {L}}_c \rightarrow -\infty$ but $\sup {\mathcal {L}}_c > -\infty$. So, if $\{ \pmb {\vartheta }_t \}$ is such that

$$\begin{aligned} \lim _{t} {\mathcal {L}}_c = \sup _{\pmb {\vartheta }} {\mathcal {L}}_c =M, \end{aligned}$$

necessarily $\{ \pmb {\vartheta }_t \} \subset K$, where K is a compact. Hence, $\{ \pmb {\vartheta }_t \}$ admits a subsequence–that we can still denote by $\{ \pmb {\vartheta }_t \}$–converging to a limit $\pmb {\vartheta }^*$ in K. In an arbitrarily small neighbourhood of $\pmb {\vartheta }^*$ the assignment functions $z_k$ and $w_l$ are constant, so ${\mathcal {L}}_c$ is continuous and the thesis follows. $\hfill\square$

3.3.3 Robustness

With respect to the robustness of our proposed method, note that the same results on the finite sample breakdown point as in Farcomeni (2009) apply in our case. In more detail, by following the arguments in Farcomeni (2009) it is straightforward to show that

$$\begin{aligned} \varepsilon _{np}^{cell} \le \frac{\lceil \alpha _1 n \rceil + \lceil \alpha _2 p \rceil + 1}{n p} \quad \text { and } \quad \varepsilon _{np}^{bi} \le \frac{\lceil \alpha _1 n \rceil + \lceil \alpha _2 p \rceil + 1}{\max \{n, p\}}, \end{aligned}$$

generally hold for the mixture parameters of the model, where $\varepsilon _{np}^{bi}$ is defined as the minimum between the row and column-wise breakdown points.

Whether the above expressions become an equality or not likely depends on the separateness of the regular and non-regular data. In well-separated cases, empirical evidence suggests that the upper bound is attained. However, it is known in clustering that the classical sample breakdown point is too strict, in the sense that its infimum over all possible data X is infinitesimal with respect to the sample size (Gallegos and Ritter 2005; Ruwet et al. 2013). The restricted breakdown point of Gallegos and Ritter (2005) could be considered instead. Finally, we remark that this point of view only looks at robustness of the mixture parameters estimators and not of the classification. In this respect, it may be interesting to consider the dissolution point and isolation robustness criteria introduced by Hennig (2008).

3.4 Time complexity analysis

In each full iteration of the algorithm, we first compute the class posterior probabilities. Starting from column class posteriors, by (9) their logarithm is equal to

$$\begin{aligned} \log {\hat{s}}_{ik} = \log {\hat{\pi }}_{k} + \sum _{jl} {\hat{w}}_{jl} \log f(x_{ij}\vert \hat{\pmb {\lambda }}_{kl}), \end{aligned}$$

up to an additive constant. Assuming that the p.d.f. f can be evaluated in constant time, computing ${\hat{s}}_{ik}$ requires O(pm) operations for each of the ng combinations of i and k, yielding a cost of O(npgm). Assigning each row i to its corresponding row class according to the MAP principle requires to find the class label $k^*(i)$ by maximising ${\hat{s}}_{ik}$ with cost O(g), and so line 6 in Algorithm 2 accounts for $n \cdot O(g) = O(ng)$ operations.

Lines 7 to 11 perform impartial trimming. The cost here is the computation of the $\lceil \alpha _1 n \rceil$-th order statistic of ${\hat{s}}^*_i = {\hat{s}}_{ik^*(i)}$, which can be found without sorting the entire array $({\hat{s}}^*_i)_i$ thanks to the Quickselect algorithm (Hoare 1961) or one of its variants. This has expected time complexity of just O(n), while in the worst case scenario $O(n^2)$ operations are required. However, note that the probability of the latter case decreases exponentially with n. This selection step needs to be performed just once, at the beginning of the for-loop on line 7, and the operations in the loop itself are constant. Therefore this whole block of pseudocode, in the average case, adds just a $O(n) + O(n) = O(n)$ to the total cost of the algorithm.

For the classification and trimming of the columns (lines 13–19 in Algorithm 2), the same considerations as above apply, exchanging the role of rows and columns. Therefore this part also accounts for O(npgm) on average, while in the worst case $O(npgm + m^2)$ operations are required.

The precise formulation of the M-step on line 21 of the algorithm depends on the chosen block distribution f. However, in all the cases presented in Govaert and Nadif (2014), the computation of ${\hat{\Lambda }}$ involves the matrix multiplication ${\hat{Z}}^\intercal X {\hat{W}}$ (see e.g. (4)), which asymptotically dominates the cost with O(npgm). The cost for estimating the mixing proportions is absorbed by O(npgm), as ${\hat{\pi }}_k = 1/{\sum _i {\hat{z}}_{ik}}$ and ${\hat{\rho }}_l = 1/{\sum _j {\hat{w}}_{jl}}$.

Taking everything together, the total expected time complexity of one iteration is O(npgm). In the worst case we may have $O(npgm + n^2 + p^2)$, but–besides the vanishing probability of this case as mentioned above–note that, as soon as n and p scale at most linearly with one of the other variables, the asymptotic cost reduces to O(npmg) again.

4 Simulation study

Since co-clustering is an unsupervised task, we first study the behaviour of the TBCEM algorithm through simulations, so that results can be compared against the ground truth given by the labels used to generate the synthetic data from the LBMs we consider. Simulations have been performed for continuous and count data. In both cases we compared our methodology with the non-trimmed BCEM algorithm, as well as with trimmed double k-means (Farcomeni 2009) in the case of continuous data. As for co-occurrence (count) data, to the best of our knowledge, there is no robust competitor we could compare TBCEM to. In addition to the TBCEM algorithm for the Normal and Poisson LBMs, we also ran simulations for two additional constrained versions, which assume equal row and column mixing proportions in the model, i.e., $\pi _1 = \ldots = \pi _g = 1/g$ and $\rho _1 = \ldots = \rho _m = 1/m$. Finally, before discussing the experimental setup and the results, we highlight once again that trimmed double k-means can be seen as a fully constrained version of the TBCEM algorithm for the Normal LBM, where also the block variances $\sigma ^2_{kl}$ are assumed to be equal (see Subsection 3.2). Therefore, we will occasionally refer to it and to the weight-constrained version of TBCEM as the “constrained versions of TBCEM”.

4.1 Simulation setup

We ran simulations for various combinations of matrix sizes, number of groups, model specifications, and amount of contamination (see e.g. Table 2). For each combination of these parameters we ran the algorithms on 100 different realisations of the specified model. Continuous data were simulated from a Gaussian LBM with fixed block means $\mu _{kl}$ and variances $\sigma ^2_{kl}$, and fixed mixing proportions $\pmb {\pi }$ and $\pmb {\rho }$. We chose the block parameters $\mu _{kl}$ and $\sigma ^2_{kl}$ so that the resulting co-clusters were separated well enough for the algorithm to converge reasonably easily, as our main focus was on trimming rather than on the ability of the considered algorithms to separate possibly highly overlapping groups. The block variances $\sigma ^2_{kl}$ were also chosen in a way that highlighted the advantage of having a flexible model that takes into account possible heteroscedasticity between the blocks, by producing simulations with a sufficiently marked difference in the scatter of the different co-clusters. Similarly, co-occurrence matrices were drawn from a Poisson LBM with fixed block parameters $\lambda _{kl}$, with the rationale behind their choice being the same as above. The chosen model parameters for each of the considered settings are presented in Table 1.

Table 1 Parameters used to simulate data from the Normal and Poisson LBMs for the different numbers of row and column groups (values approximated to the second decimal digit)

After simulating each data set, contamination was added by replacing a fraction of the data cells by corrupted entries, drawn from a specified contaminating distribution g. In the normal model we chose $g = 0.5 \, {\mathcal {N}}(\mu , \sigma ^2) + 0.5 \, {\mathcal {N}}(-\mu , \sigma ^2)$ with $(\mu , \sigma ^2) = (1.5 \, \max _{kl}\mu _{kl}, 15)$, while for the Poisson LBM $g = 0.5 \, {\mathcal {P}}(\lambda ') + 0.5 \, {\mathcal {P}}(\lambda '' )$, with $\lambda ' = \min _{kl}\lambda _{kl}$ and $\lambda '' = 1.5 \, \max _{kl}\lambda _{kl}$. With these choices, observations produced by the contaminating distributions were reasonably well spread while still being sufficiently distinguishable from the uncontaminated part of the data. Since g is a mixture, both anomalously high and low values are obtained. Finally, in the Poisson case this choice of g allows to simulate a higher level of dispersion of the noise component while keeping the mass of g not too far away from the non-contaminated data, something which would not be possible if one simply chose $g = {\mathcal {P}}$.

Each algorithm was initialised 100 times and the best solution in terms of the classification likelihood was retained for evaluation. In our implementation, the algorithm is initialised by randomly excluding $\lceil \alpha _1 n \rceil$ rows and $\lceil \alpha _2 p \rceil$ columns, and randomly assigning the remaining $n- \lceil \alpha _1 n \rceil$ rows and $p - \lceil \alpha _2 p \rceil$ columns to row and column groups. Then an initial (trimmed) estimate of the parameters is computed. It is known that the estimation of LBMs via both the BCEM and VEM algorithms suffers from the problem of convergence to solutions with empty groups and can depend heavily on the starting point. Therefore, choosing a sufficiently high number of initialisations is necessary. In our simulations 100 initialisations were enough, but this number should in general be chosen on a case-to-case basis, with less well-separated data sets typically requiring more initialisations. There exist more sophisticated initialisation strategies that address these issues in the non-trimmed case (Keribin et al. 2015), whose adaptation to our case could be considered in the future.

In the trimmed case, we systematically overestimated the actual contamination level of both rows and columns by 25% (i.e., $\alpha _i = 1.25 \, \alpha _i^{true}$, $i=1, 2$), and after each full run reassigned the rows and columns that were trimmed in excess to the closest group according to the class posterior probabilities of the estimated model.

The final co-clustering was assessed by means of three criteria, whose definitions follow for convenience sake.

• To assess the quality of classification, we adopted the Co-clustering Adjusted Rand Index (CARI), an index proposed by Robert et al. (2021) which ranges between $-1$ and 1 and extends the ARI to co-clustering. Given two co-clustering partitions (Z, W) and $(Z',W')$ of sizes (g, m) and $(g',m')$, the definition of CARI is given by the following formula:

  $$\begin{aligned} CARI\big ((Z,W),(Z',W')\big ) = \frac{\sum _{rs} A_{rs} - \sum _r B_r \sum _s C_s / \left( {\begin{array}{c}np\\ 2\end{array}}\right) }{\frac{1}{2} \Big ( \sum _r B_{r} + \sum _s C_{s} \Big ) - \Big ( \sum _r B_{r} \sum _s C_{s} \Big ) / \left( {\begin{array}{c}np\\ 2\end{array}}\right) } \end{aligned}$$

  where

  $$\begin{aligned} A_{rs} = \left( {\begin{array}{c}n_{rs}^{ZWZ'W'}\\ 2\end{array}}\right) , \quad B_{r} = \left( {\begin{array}{c}\sum _s n_{rs}^{ZWZ'W'}\\ 2\end{array}}\right) , \quad C_{s} = \left( {\begin{array}{c}\sum _r n_{rs}^{ZWZ'W'}\\ 2\end{array}}\right) \end{aligned}$$

  $r \in [gm], \, s \in [g'm']$, and with $n_{rs}^{ZWZ'W'}$ denoting the number of elements of the data matrix X that belong simultaneously to block r (associated to a pair of partition indices (k, l) specified by (Z, W)) and block s (identified by a pair $(k',l')$ specified by $(Z',W')$).

• In the continuous case, in addition to the CARI we computed the Sum of Squared Errors (SSE), given by

  $$\begin{aligned} SSE = \sum _{ijkl} z_{ik}w_{jl}(x_{ij} - {\hat{\mu }}_{kl})^2 \end{aligned}$$

• In the discrete case, as a second criterion we computed the $\Phi ^2(P^{ZW})$ index, a measure of association between the distributions induced by the row and column partitions, discussed for instance in Govaert and Nadif (2016). Given a co-clustering partition (Z, W), it is defined as

  $$\begin{aligned} \Phi ^2(P^{ZW}) = \sum _{kl} \frac{\big (p^{ZW}_{kl} - p^{Z}_{k\cdot } p^{W}_{\cdot l}\big )^2}{p^{Z}_{k\cdot } p^{W}_{\cdot l}} \end{aligned}$$

  where

  $$\begin{aligned} p^{ZW}_{kl} = \frac{\sum _{ij} z_{ik} w_{jl} x_{ij}}{N}, \quad p^{Z}_{k\cdot } = \sum _l p^{ZW}_{kl}, \quad p^{W}_{\cdot l} = \sum _k p^{ZW}_{kl} \end{aligned}$$

  and

  $$\begin{aligned} N = \sum _{ijkl} z_{ik} w_{jl} x_{ij}. \end{aligned}$$

  Note that in the untrimmed case $N=\sum _{ij}x_{ij}$ (as each row of Z and W sums to 1). In the following we will write $\Phi ^2$ for $\Phi ^2(P^{ZW})$, as it will be implicit that we are referring to the distribution $P^{ZW}$ and to which partitions.

• Both in the Normal and Poisson case, we also evaluated the classification log-likelihood, as defined by (2).

In the computation of all the criteria discussed above, contaminated rows and columns were excluded, that is, methods were assessed only on the regular data. By doing so, it is possible to compare the different methods and the assessment of the non-trimmed procedure is not unfavourably biased. Higher values of the CARI, $\Phi ^2$ index and $\log L_C$ are better, while for the SSE lower values are better. In Tables 2 and 3 the average values obtained for these criteria are shown, along with the average computation time taken by 100 initialisations of the method on a fixed matrix. The methods and the experiments are implemented in Python and were run on an Intel$^{\circledR }$ Xeon$^{\circledR }$ Gold 6230 CPU with a clock frequency of 2.10 GHz.

4.2 Results

The results of the experiments show that in our simulation setting trimming effectively prevents estimation from breaking down in the presence of contamination, with the unconstrained and weight-constrained versions of TBCEM consistently outperforming the non-robust BCEM algorithm.

In more detail, on continuous data the unconstrained and partially, weight-constrained versions of TBCEM–which we denote by $[\pi _k \, \rho _l \, \sigma _{kl}]$ and $[\pi \, \rho \, \sigma _{kl}]$ respectively, following Govaert and Nadif (2014)–exhibit similar performance. In our experiments they both yield almost perfect CARI scores, meaning that both the algorithms are successful at recovering the partitions used to simulate the data. Their results are also very similar in terms of mean SSE. In terms of computation time, TBCEM $[\pi _k \, \rho _l \, \sigma _{kl}]$ has a slight but consistent advantage over TBCEM $[\pi \, \rho \, \sigma _{kl}]$ in this setting, which could be due to the fact that the former algorithm requires less iterations to converge at the specified precision, here set at $\varepsilon =1.00 \cdot 10^{-16}$.

On the other hand, trimmed double k-means–corresponding to a fully constrained version of TBCEM, which we indicate by $[\pi \, \rho \, \sigma ]$–and the unconstrained and non-robust BCEM presented on average markedly worse CARI values. This is not surprising since the block variances used to generate the data were purposely quite different and, as shown in Sect. 2, the standard estimators of the Normal LBM can be arbitrarily corrupted by outliers (which is even more evident by looking at the SSE mean values). The performance of trimmed double k-means however does not decrease dramatically with higher fractions of contaminated data, conversely to what happens with the non-robust method. Therefore, the low classification performance of trimmed double k-means in this setting is due to the way the data were generated. In fact, we recall that double k-means implicitly assumes equal mixing proportions and block variances, assumptions that are clearly violated here. As one would expect, though, on average it yielded solutions with SSE close to, and often lower than, the competing robust methods. This is in agreement with the fact that double k-means optimises the SSE criterion. Looking at the values of $\log L_C$, however, confirms that the other two trimmed methods are preferable in this scenario. In terms of computation time, trimmed double k-means is by far the slowest among the algorithms we tested, while the base version of BCEM is usually faster than its robust counterparts. This may be due to two reasons: firstly, trimmed double k-means may need on average a higher number of iterations to converge, because the data are far from the method’s assumptions; secondly, initialisations that lead the algorithm to a spurious solution are not fully iterated and, likely, a robust, fully constrained method is less prone to converging to such solutions.

As for the Poisson-distributed data, similar observations can be made. In the simulations, the best performance is attained by the trimmed unconstrained procedure, while the non-robust method is clearly affected by contamination, although not as markedly as in the Gaussian case as far as classification is concerned. However, the $\Phi ^2$ and $\log L_C$ criteria confirm the superiority of the robust procedures also in this case. Execution times are not sensibly different between the competing algorithms in this case.

Table 2 Results on continuous data generated from the Normal LBM with dimensions, number or row and column groups, and contamination levels specified in the first three columns of this table, and with parameters as specified in Table 1

Table 3 Results on count data generated from the Poisson LBM with dimensions, number or row and column groups, and contamination levels specified in the first three columns of this table, and with parameters as specified in Table 1

5 Applications to real data

We illustrate our robust algorithm on both continuous and count data, by applying TBCEM for the Normal LBM in the former case and TBCEM for the unnormalised Poisson LBM in the latter. The continuous model is fitted to two data sets that have already appeared in the literature, with the purpose of checking the performances of the robust estimation approach on real data and comparing its results to those obtained with other procedures. The Poisson model is applied to two tables–one of which is still unexplored–, that are both related to customs monitoring activities carried out by European institutions.

5.1 Amiard fish data

This real data set (Caillez and Pages 1976) was used by Govaert and Nadif (2014) to illustrate co-clustering of continuous data via the Normal LBM and provides an example of the insights that robustness can add to co-clustering. The data matrix consists of 23 rows, corresponding to individual fish exposed to radiation. The fish are numbered from 1 to 16 and from 18 to 24 (fish number 17 died during the experiment). For each fish 16 variables were observed: radioactivity of eyes (REY), radioactivity of gills (RGI), radioactivity of cappings (RCA), radioactivity of fins (RFI), radioactivity of liver (RLI), radioactivity of gastrointestinal tract (RGT), radioactivity of kidney (RKI), radioactivity of scales (RSC), radioactivity of muscles (RMU), weight (WGT), length (L), standard length (SL), head width (WHE), width (W), snout width (WSN), eyes diameter (DEY). The first nine variables refer to levels of radioactivity in different body parts, while the others refer to sizes. All variables have been standardised.

Govaert and Nadif (2014) fitted the Normal LBM, with $g=5$ and $m=3$, via the LBVEM algorithm and retained the best co-clustering. Their solution contains a column group consisting of a single variable, RKI. This, as well as the PCA plots obtained by the authors and reproduced in Fig. 2, suggest that the analysis could benefit from the application of a robust method.

Fig. 2

Projection on the plane spanned by the first two principal components of observations (dots) and loadings (arrows), reproduced using function pcaFS (http://rosa.unipr.it/FSDA/pcaFS.html) in the FSDA toolbox for MATLAB (Riani et al. 2012, 2015)

More specifically, by taking a look at the variable loadings on the plane spanned by the first two Principal Components (PC), it seems that some variables (including RKI) behave quite differently from the rest. This is also supported by a visual analysis of the raw data (see for instance Fig. 4). In fact, it can be clearly seen that four columns (RKI, RMU, RLI and RGT) contain some anomalously high values, which apparently do not exhibit any kind of pattern and concern at least three units (13, 20, 23). Interestingly, these three units are also marked as outliers when performing a robust PCA (see Fig. 3).

Fig. 3

Score outlier map produced by the robust PCA implemented in the LIBRA toolbox for MATLAB (Verboven and Hubert 2005) (function robpca in https://wis.kuleuven.be/statdatascience/robust/LIBRA). Units are numbered from 1 to 23 (17 included), therefore labels i equal to or greater than 17 actually correspond to labels $i+1$ in the original data set. Starting from the top-left corner and proceeding clockwise, the first and second quadrants contain outlying units (orthogonal outliers and bad PCA-leverage points), the third contains ‘good’ leverage points and the last quadrant contains regular observations

Given these observations, we ran our method setting the proportion of column trimming to $\alpha _2 = 4/p$. Since the set of variables can be naturally split into two categories–namely, radioactivity levels on one hand and physical characteristics of the fish on the other–we set $(g,m)=(5,2)$. The need for a third column group disappears when applying trimming, as can be confirmed for instance by means of CTL curves (see Subsection 5.5). We tested the unconstrained and the two constrained versions, $[\pi \, \rho \, \sigma _{kl}]$ and $[\pi \, \rho \, \sigma ]$, of the Normal LBM, fitted via the TBCEM algorithm. We also compared these with the non-trimmed BCEM. Each procedure was initialised 500 times and the solution which yielded the highest final value of the complete-data likelihood was retained.

In all the cases presented above, TBCEM consistently marked the variables RKI, RMU, RLI and RGT as anomalous. This is in agreement with the results of the non-trimmed methods, which fit one column cluster to a single variable (RKI), as well as with the information deduced from the PCA plots.

Figure 4 represents the data matrix before and after sorting according to the ‘best’ fit of the Normal LBM with constrained weights, $(g,m)=(5,2)$ and $\alpha _2 = 4/16$. We can see how our robust procedure trimmed the four columns mentioned above and found meaningful row and column groups. In more detail, the remaining 12 columns were partitioned into two groups reflecting the natural grouping of the variables explained above, while rows were grouped into meaningful and clearly characterised clusters. Starting from the top of the rightmost plot in Fig. 4, we can observe a large row cluster with values close to zero; moving down, the second and fifth row clusters are both characterised by low and high values for variables corresponding to size and radioactivity levels respectively, with the two row clusters differing in that the fifth presents sensibly lower values in the ‘cold’ block; the third row cluster on the other hand is characterised by the opposite pattern; finally, the fourth row group presents markedly low values in both blocks. The co-clusters we have found are similar but not identical to those in Govaert and Nadif (2014), with respect to which they seem slightly more natural.

Fig. 4

Data matrix before and after sorting according to the fitted model. Warmer colours correspond to higher values

In Table 4 and Figs. 5 and 6 a comparison between the different methods is drawn. By and large, for this data set, we can make the following observations:

• Trimming made possible the identification and exclusion of anomalous columns, that did not contribute to the co-clustering, improving the end result;

• Model constraints–like, as in our case, assuming the block variances to be equal–combined with trimming can help in avoiding uninteresting solutions (e.g., row or column clusters consisting of just one element).

In addition to the last point, something that does not show in the figures nor in the comparative table but that we believe is interesting is that constrained models proved to be considerably more stable even on this small data set, that is, produced more consistent co-clusterings. This may not be very surprising, since they are less flexible models, but nonetheless it can be considered a desirable property in some situations and makes the case, also from a practical point of view, for the development of finer constraints on the parameters , such as those discussed in Subsection 3.3.

Table 4 Table showing the different row and column clusters obtained on the fish dataset with the considered methods and for the specified group numbers. For the robust methods also the trimmed columns are displayed

Fig. 5

Comparison of co-clusterings obtained with untrimmed and unconstrained Normal LBM, and different specifications of the trimmed Normal LBM. $m=2$

Fig. 6

Projection of the rows on the first two principal components of the trimmed data set, for different non-trimmed and trimmed model specifications. Each colour indicates a row cluster. $m=2$

5.2 G7 macroeconomic data

This data set was already studied in Vichi (2001) and revisited by Farcomeni (2009), using double k-means and its trimmed version, respectively. It consists of seven macroeconomic indicators relative to eight countries: the G7 countries, namely France (FRA), Germany (GER), Great Britain (GBR), Italy (ITA), United States (USA), Japan (JPA) and Canada (CAN), with the addition of Spain (SPA). The seven variables are: gross domestic product (GDP), inflation (INF), budget deficit-GDP ratio (DEF), public debt-GDP ratio (DEB), long-term interest rate (INT), trade balance-GDP ratio (TRB), and unemployment rate (UNE). Albeit small, the G7 data set is an interesting example since–conversely to the Amiard fish data example–it shows how different model assumptions can lead to the identification of different outliers.

Following the analysis in the two references above, we set $g=3$ and $m=2$. For the trimming levels, we follow Farcomeni (2009) and set $\alpha _1 = 1/8$ and $\alpha _2 = 0$ (i.e., one row is trimmed), so that robust co-clustering results are comparable. Variables are standardised before co-clustering is applied.

TBCEM with equal weights and equal block variances (i.e., trimmed double k-means), consistently selected Italy as an outlier, as was already obtained by Farcomeni (2009), even when the co-clusterings we obtained for different initialisations differed.

On the other hand, the non-constrained model produced, for some different initialisations, reasonable solutions in which Spain, and not Italy, was marked as an outlier. This is interesting, as Spain is in fact not part of the G7. In Fig. 7, two co-clusterings revealing this difference between the fully constrained and unconstrained models are shown. This disagreement between the two methods on which country should be considered an outlier could be due to the fact that the fully constrained model has a preference towards more homogeneous co-clusters–since in this case maximising the likelihood corresponds to minimising the SSE –, whereas the unconstrained model allows for greater within-co-cluster variability. We obtained similar results for the model with constrained mixing proportions and unconstrained block variances, which also marked Spain as an outlier in different co-clusterings.

What we have just observed concretely shows that, although trimming is performed in a data-driven fashion, the model does indeed play a role in defining which rows or columns are to be considered anomalous. This further supports the choice of a model-based approach, as it is transparent about the probabilistic assumptions on the non-anomalous data.

Fig. 7

Trimmed double k-means (left) and TBCEM for the unconstrained Normal LBM (right) in this case yield almost identical partitions, except for the rows corresponding to Spain and Italy: outliers are marked differently

For the sake of completeness, we highlight that the solutions presented in Fig. 7 are not optimal: configurations yielding better values for both models do exist, some of which coincide. However, we argue that:

• 1. In our experiments, double k-means was very consistent in marking Italy as an outlier and the ‘best’ solution we were able to obtain–the one presented in Farcomeni (2009)–was not drastically different from the one shown in Fig. 7.

• 2. On the other hand, the unrestricted LBM produced a wider variety of solutions. Moreover, in this case, due to the possible unboundedness of the likelihood function, designing a solution to be the ‘best’ solely based on the final value of the classification likelihood is not a sound approach. A visual assessment would lead to the selection of non-spurious solutions even though the likelihood of spurious ones (e.g., solutions with co-clusters consisting of a single element) may be higher.

• 3. On larger data sets an extensive exploration of the parameter space via different initialisations is unfeasible. Therefore, co-clusterings that offer useful insight to the practitioner, although not optimal, can be valuable.

5.3 Clothing prices data

This data set has been discussed by Riani et al. (2022) in the context of robust correspondence analysis. The data originate from COMEXT, a database of the European statistical office (Eurostat) containing detailed statistics on international trade in goods. The data set consists of occurrences in different price segments of clothing items coming from outside the European Union (EU), for the 28 EU member states indicated by their two-letter code (following ISO 3166-1 alpha-2). Riani et al. (2022) considered five price categories $x_1, \ldots , x_5$ (from low to high), determined through a methodology presented in Cerasa and Cerioli (2017) in a time period of several years, ending in 2017. Here we consider an extended version of the data set including the additional price categories $x_6, \ldots , x_{33}$.

Since we are analysing count data, we apply the Poisson version of our TBCEM algorithm. We choose $g=3$ and $m=3$ for the number of groups on the rows and on the columns, which represent countries and price segments respectively, and $\alpha _1=7/28$ and $\alpha _2=0$ as row and column trimming levels. The price categories can be intuitively grouped in low, medium and high, hence the choice of m. While natural in terms of interpretability, it could be argued that this choice is rather arbitrary. However, in our experiments we observed that the algorithm tends to preserve the order of the columns within the column groups, grouping together adjacent price segments, and that results are not largely affected by the choice of m. Furthermore, the shape of the distribution of the column marginals is unimodal after trimming, suggesting no particular group structure. Intuitively, this is in agreement with how columns have been defined. The choice of $g=3$ seems quite reasonable in the light of an exploratory analysis, which highlights three modes in the row marginal distribution. As for the trimming levels, our choice is justified by the fact that the focus is on anomalous rows and in the cited work seven outliers were identified. See Subsection 5.5 for further discussion on the choice of these model parameters.

Our method recovers a set of outlying countries that is quite similar to those found via the robust correspondence analysis in Riani et al. (2022). The rows that are marked as outliers correspond to Slovakia (SK), Great Britain (GB), Bulgaria (BG), Romania (RO), Latvia (LV), Austria (AT) and Finland (FI). The first five countries were also found in the cited work and some have been indeed found to be the object of international trade schemes where goods were declared at values below the market price, also illicitly. As for the other two countries, Austria and Finland, they are marked as outliers by our algorithm likely because of the different distribution of their price categories, which are markedly shifted towards high prices compared to the other countries.

In Fig. 8 we can see the partitions for the specified choices of hyperparameters as recovered by our algorithm. As already discussed, the column partition reflects the order in the price segments, with a highly populated group containing low prices, a less populated one containing intermediate prices and a sparse one containing high-end prices. As for the row partition, we find a large group of countries characterised by a high number of transactions concentrating in the low price segments, a smaller group with a similar pattern but a lower number of transactions, and a very small group, consisting of just Luxembourg (LU), Malta (MT) and Cyprus (CY), with a marginal number of transactions across all price categories.

Fig. 8

Clothing price segments counts. The table is sorted according to the partitions found by the Poisson TBCEM algorithm

5.4 Big-volume trade transactions data

This data set, which has not appeared in the literature before, consists of counts of particular events concerning unusual (typically very large) weights or values derived from customs declarations that EU authorities collect for all categories of traded goods. Such data are used for many purposes, including policy making, building EU-wide statistics, securing supply chains, anti-fraud, and facilitating the economic operators in their trading activities. These purposes make the data potentially sensitive and prevent us from being able to fully disclose the exact nature of the signalled events. For all cited purposes, understanding how extreme trade statistics distribute across countries and commodities is of great interest, for quality assurance analysis and estimating the likelihood of future large declarations. The 76 rows of the data set represent wide good categories, identified by a two-digit code (the so-called “Chapters” of the Harmonised System (HS) Nomenclature developed by the World Customs Organization), while the 25 columns correspond to countries, indicated again by their two-letter ISO code. The data set refers to the 2010–2022 period and contains 28,523 counts.

After an exploratory analysis of the data, we set $g=m=3$, $\alpha _1 = 2/76$ and $\alpha _1 = 2/25$ (see also Subsection 5.5). With these choices, we obtain the partitioning shown in Fig. 9. The three groups of countries exhibit different patterns across the corresponding groups of HS Chapters.

The largest group of countries is also the most sparse and roughly corresponds to Northern and Eastern Europe, whose national economies are on average smaller compared to the rest of the continent. Moving up in Fig. 9, we find a cluster of countries–comprising Austria (AT), Denmark (DK), Greece (GR), Poland (PL), Portugal (PT) and Northern Ireland (XI)–for which a moderate amount of events have been recorded, particularly for two out of the three clusters of goods. Finally, at the top of the figure we find a group of countries for which many events have been counted, across all three goods clusters. It is interesting to note that this group comprises three out of the four European G7 countries: France (FR), Great Britain (GB) and Italy (IT).

As for the groups of goods, they appear to be divided in high, medium and low signalled. In more detail:

• The smallest group, comprising the three HS Chapters 44, 85, 87, is highly signalled, across all groups of countries. These HS Chapters correspond, respectively, to: “Wood and articles of wood; wood charcoal”; “Electrical machinery and equipment and parts thereof; sound recorders and reproducers, television image and sound recorders and reproducers, and parts and accessories of such articles”; and “Vehicles other than railway or tramway rolling-stock, and parts and accessories thereof”. This group seems particularly interesting from the point of view of customs authorities, both for the nature of the goods it contains as well as for the fact that it has generated a high number of signals across all considered countries. A practitioner could inspect transactions of products belonging to this group conditionally on the country that issued the declaration.

• The mid-sized group (the first from the left in Fig. 9) presents a different pattern across the groups of countries, being moderately to highly active for the two smaller column groups and sparse for the larger one. It roughly corresponds to various types of raw materials and consumer goods.

• The largest group is also the sparsest and is a miscellaneous of HS Chapters, ranging from raw and construction materials to more sophisticated products.

Fig. 9

Customs big-volume transactions counts. The table is transposed and sorted according to the partitions found by the Poisson TBCEM algorithm

Finally, it is interesting to note that our algorithm marks as outliers the columns corresponding to Germany (DE) and the Netherlands (NL) and the rows for the HS Chapters 22 and 84, which correspond to “Beverages, spirits and vinegar” and “Nuclear reactors, boilers, machinery and mechanical appliances; parts thereof”. This is in agreement with expectations about a different pattern characterising Germany and the Netherlands in the distribution of the considered high volume events (these countries have among the largest ports in the EU), as well as with the fact that HS Chapter 22 and especially Chapter 84 are two wide categories of goods. In particular, Chapter 84 is extremely wide and diverse–as can be understood from the description provided above–and is particularly prone to being the object of unusual declarations.

5.5 On model selection

We now discuss how model selection can be performed for our methodology, i.e. the choices for the group numbers and trimming levels, by using adaptations of existing techniques to our setting.

In the context of trimmed model-based clustering, García-Escudero et al. (2011) proposed to select the model parameters by analysing the so-called Classification Trimmed Likelihood (CTL) curves. Denoting by ${\mathcal {L}}_C(\alpha _1, \alpha _2; g, m) = \log L_C(\hat{\pmb {\vartheta }}, {\hat{Z}}, {\hat{W}} \vert X)$ the classification log-likelihood of our trimmed model at the estimated parameters and partitions, we can consider the CTL curves given by $\alpha _1 \mapsto {\mathcal {L}}_C(\alpha _1, \alpha _2; g, m)$ and $\alpha _2 \mapsto {\mathcal {L}}_C(\alpha _1, \alpha _2; g, m)$, for fixed pairs (g, m). In principle, in our co-clustering setting we could consider CTL surfaces $(\alpha _1,\alpha _2) \mapsto {\mathcal {L}}_C(\alpha _1, \alpha _2; g, m)$ instead of curves. However, their interpretation is less straightforward. Finally, when we trim either on the rows or on the columns in our examples, for notational simplicity we drop the dependence on one of the two $\alpha$’s. Similarly, we can consider CTL curves for the partition sizes and again simplify the notation when using the curves to choose only one of the partition sizes.

In what follows, for the sake of convenience we recall the operational use of CTL curves. For a full exposition we refer to (García-Escudero et al. 2011). First, the algorithm is run until convergence for a desired set of group numbers and for a specified grid of trimming levels. Then, the CTL curves as defined above are plotted. Each curve corresponds to a fixed partition size and is plotted against the grid of trimming levels, sharing the same axes with the other curves. Finally, by comparing such curves, an appropriate number of groups (say g) and corresponding trimming level $\alpha _1$ are chosen. To do so, it is recommended to select the group size as the smallest g such that the gap between the g-th curve and the $(g+1)$-th curve, i.e. $\Delta _{g}(\alpha_1\!):=\log\! {\mathcal {L}}_C(\!\alpha_1;g+1\!)-{\mathcal {L}}_C(\alpha _1; g)$ (which can be proven to be non-negative under certain conditions), is small, except maybe for small values of $\alpha _1$. Then, the trimming level is chosen as the smallest $\alpha _1$ such that $\Delta _{g}(\alpha _1)$ is relatively small and remains so for larger values of $\alpha _1$.

Now let us see the application of this monitoring strategy to the Clothes data set. In this case the focus is on choosing the number of row groups and the row trimming level. The CTL curves obtained for $g \in \{2,3,4,5\}$ and $\alpha _1 \in \{i/n\}_{i=0}^10$ are shown in Fig. 10. Our choice $g=3$ and $\alpha _1=7/n$ seems reasonable in the light of the plot–although other combinations could be meaningful as well, such as $g=3$ and $\alpha _1=6/n$. In Fig. 11 the values of $\Delta _{g}(\alpha _1)$ are also shown. We highlight here that the conditions of Propositions 1 and 2 in García-Escudero et al. (2011) are not met, therefore $\Delta _{g}(\alpha _1)$ does not need to be positive. In any case, besides the trimming level, the choice $g=3$ seems by and large the most appropriate.

Fig. 10

CTL curves for the clothing prices data example

Fig. 11

Values of $\Delta _{g}(\alpha )$ for the clothing prices data example

As for the big-volume trade data set, CTL curves obtained with our method are shown in Fig. 12. In this case we screen a number of combinations of row and column partition sizes (g, m), with $g \in \{2, 3, 4, 5, 6\}$ and $m \in \{2, 3, 4, 5\}$, while $\alpha _2 \in \{i/p\}_{i=0}^6$ and $\alpha _1 = 2/n$. The choice $(g,m)=(3,3)$ seems quite appropriate, as well as $\alpha _2 = 2/n$.

Fig. 12

CTL curves for the big-volume trade transactions data example

Another possible strategy to guide the choice of the trimming levels is to rely on the G-statistic introduced in Farcomeni (2009) and presented in a broader context in Farcomeni and Greco (2015). This can be more practical when both row and column trimming levels have to be fixed. We use this approach on the big-volume trade data set, to confirm our choice $\alpha _1 = 2/n$. The G-statistic measures the maximal relative variation between the trimmed and non-trimmed parameter estimates, and can be formulated as

$$\begin{aligned} G(\alpha _1, \alpha _2) = \max _{k} \frac{\vert \hat{\pmb {\lambda }}_{(k)}^{(\alpha _1, \alpha _2)} - \hat{\pmb {\lambda }}_{(k)}^{0} \vert }{\vert \hat{\pmb {\lambda }}_{(k)}^{(\alpha _1, \alpha _2)}\vert \vee \vert \hat{\pmb {\lambda }}_{(k)}^{0} \vert } \end{aligned}$$

where $\hat{\pmb {\lambda }}^{(\alpha _1, \alpha _2)}$ and $\hat{\pmb {\lambda }}^{0}$ denote the vectorised and sorted centroid estimates obtained with row and column trimming levels $\alpha _1$ and $\alpha _2$, and without trimming, respectively. The notation $\vee$ stands for the maximum between two elements. Sorting the parameter estimates is important in order to prevent issues related to label switching. The selection procedure is summarised by Algorithm 3. Basically, the estimation algorithm is run several times, with increasing trimming levels, until no significant changes in the G-statistic (greater than a threshold $\delta >0$) are observed. When the statistic does improve, the trimming level $\alpha _i$ corresponding to the dimension that has produced the largest improvement is increased by a quantity $a_i>0$.

On the big-volume data set, setting $\delta =0.005$, $a_1 = 1/n$ and $a_2 = 1/p$ resulted in suggested trimming levels of $\alpha _1 = 2/n$ and $\alpha _2 = 2/p$, in agreement with our choice. Higher thresholds in this case do not produce satisfactory results, although the methodology still indicates $\alpha _2 = 2/p$, while lower values of $\delta$ suggest that the proportion of trimmed rows may be increased up to $\alpha _1=3/n$. With this choice, Ireland (IE) is added to the list of outlying countries, already consisting of Germany (DE) and the Netherlands (NL). Clusters vary slightly, but overall this solution seems less interesting than the one discussed above.

Finally, neither CTL curves nor the G-statistic give a definitive answer to the problem of model selection. In fact, the former are an exploratory tool, first developed in the context of one-way clustering, which requires manual inspection and is not (yet) fully adapted to our two-way setting. As for the latter, while the G-statistic was proposed specifically for co-clustering and requires less interpretation, it is dependent on the choice of the threshold $\delta$ and step sizes $a_1$, $a_2$, and could benefit from a reformulation that takes into account the model-based framework.

6 Discussion

In this work we have shown the importance of robustifying co-clustering procedures, which can be heavily impacted by the presence of outliers. The algorithm we have proposed, TBCEM, can be applied to different types of LBMs and produces robust estimates in a data-driven fashion, thanks to impartial trimming. The experiments confirm the usefulness and effectiveness of our method, which not only can prevent outlying rows or columns from breaking model estimation, but can also give additional insight into the data by identifying possible anomalies.

Another relevant topic for future research, especially from the point of view of real-world applications, is that of model selection. In our approach, in addition to the number of row and column groups, (g, m), the practitioner also has to choose the trimming levels $(\alpha _1, \alpha _2)$. While the former is a problem that has been already addressed in (non-trimmed) LBMs (for instance via the Integrated Classification Likelihood (ICL) criterion (Biernacki et al. 2000)) and in trimmed clustering (e.g., with ICL curves, as discussed above), the latter is not so well-studied. An approach similar to the one followed in Farcomeni (2009) as illustrated above, inspired by the forward search (Torti et al. 2021), could be attempted and could take advantage of the probabilistic setting of the LBMs used in this paper. Also, whether the number of groups or the trimming levels should be fixed first is debatable and open to further research.

An additional aspect that could be developed in the future is that of adding constraints to the algorithm, in order to obtain a well posed optimisation problem for the model likelihood even in the normal case, as argued in Sect. 3.3 Further improvements of our methodology could also include its extension to LBMs with row and column effects, which are quite relevant in the application to text mining and in general in the case of count data, when one wants to take into account normalisation with respect to row and/or column sums.

Finally, on the theoretical side, properties of the solutions of the trimmed problem (7)–such as consistency–remain to be proven. This might be a rather difficult feat, since in the non-trimmed case results have been obtained only quite recently (see for instance (Biernacki et al. 2022) for an overview).

Supplementary information

The software to reproduce the results in the paper is available in Python on request. Our new co-clustering functions will be also included in future releases of the FSDA toolbox in MATLAB, available at https://www.mathworks.com/matlabcentral/fileexchange/72999-fsda. All data sets will also be made available in FSDA or upon request (http://rosa.unipr.it/FSDA/datasets_mv.html).