Sparsifying the least-squares approach to PCA: comparison of lasso and cardinality constraint

Abstract

Sparse PCA methods are used to overcome the difficulty of interpreting the solution obtained from PCA. However, constraining PCA to obtain sparse solutions is an intractable problem, especially in a high-dimensional setting. Penalized methods are used to obtain sparse solutions due to their computational tractability. Nevertheless, recent developments permit efficiently obtaining good solutions of cardinality-constrained PCA problems allowing comparison between these approaches. Here, we conduct a comparison between a penalized PCA method with its cardinality-constrained counterpart for the least-squares formulation of PCA imposing sparseness on the component weights. We compare the penalized and cardinality-constrained methods through a simulation study that estimates the sparse structure’s recovery, mean absolute bias, mean variance, and mean squared error. Additionally, we use a high-dimensional data set to illustrate the methods in practice. Results suggest that using cardinality-constrained methods leads to better recovery of the sparse structure.

1 Introduction

Principal component analysis (PCA) is a widely used analysis technique for dimension reduction and exploratory data analysis. PCA can be formulated as a variance maximization problem or a residual sum of squares minimization problem with both formulations yielding the same solution (see e.g., Jolliffe 1986; Adachi and Trendafilov 2016). The component scores resulting from PCA are linear combinations of all variables, making their interpretation difficult, especially in the high-dimensional setting. Therefore, obtaining component scores that are based on a linear combination of a few variables only while still retaining most of the information in the original data is attractive. Such methods are categorized as sparse PCA.

Sparse PCA problems are usually formulated either as an extension of the PCA formulations by adding a cardinality constraint or as a convex relaxation of the constrained PCA formulation by adding penalties. Sparsity is attained either on the weights or loadings, and unlike in PCA, their solutions are not longer equivalent (see e.g., Guerra-Urzola et al. 2021). In the context of the variance maximization PCA formulation, d’Aspremont et al. (2007), Yang et al. (2014), Berk and Bertsimas (2019) added cardinality constraints on the weights, while d’Aspremont et al. (2008), Journée et al. (2010), formulated the problem as a convex relaxation thereof adding different penalties. Additionally, Richtárik et al. (2021) presented eight different formulations based on either cardinality constraints or sparseness inducing penalties. For the least-squares formulation of PCA, most sparse PCA methods rely on the use of different penalties (Zou et al. 2006; Shen and Huang 2008; Van Deun et al. 2009; Gu and Van Deun 2016). Adachi and Trendafilov (2016) considered the sparse PCA problem in this least-squares context by imposing a cardinality constraint on the loadings. In this paper we consider the sparse version of the least-squares formulation of PCA, where the sparsity is imposed on the weights.

Penalized methods for sparse PCA rely on alternating optimization procedures where the update of the sparse structure (weights or loadings) usually boils down to a penalized regression problem. Penalized regressions, such as LASSO (Tibshirani 1996), have been put forward in the literature to obtain sparse solutions due to their computational tractability (Tibshirani 2011) and their statistical nature of shrinking the nonzero coefficients. This shrinkage avoids inflation of the coefficients resulting in a better bias-variance trade-off of the estimators. However, penalized methods are heuristics that, although they provide feasible solutions, are not able to find the best subset of coefficients unless stringent conditions on the data hold (Tibshirani 2011, p. 277). Finding the optimal subset of coefficients is a NP-hard problem (Natarajan 1995). Nevertheless, significant progress has been recently made in solving the sparse linear regression problem via cardinality constraints for a large number of variables to optimality (Bertsimas et al. 2016; Bertsimas and Parys 2020). This work is the departing point for our study. First, it shows that due to the advances in optimization it is natural to reconsider the solvability/quality relation between cardinality based and convex penalized relaxations of sparse formulations. Second, it opens the venue to use procedures for solving the cardinality-constrained linear regression as a subroutine to solve cardinality-constrained versions of sparse PCA.

In this paper we compare the well-known sparse PCA method proposed by Zou et al. (2006) to its cardinality-constrained counterpart (problem 2). Both methods rely on sparsifying the weights in the least-squares formulation of PCA. To our knowledge, the cardinality-constrained approach for this formulation has not yet been proposed in the literature; Therefore, we introduce it in Sect. 2.2. Both methods use an alternating scheme where sparsity is achieved via a penalized or cardinality-constrained linear regression step. We compare the performance of the methods in a simulation study using different measures such as the recovery rate of the sparse structure, mean absolute bias, mean variance, and mean squared error. Additionally, we illustrate the use of the methods in practice with an empirical data set containing gene expression profiles of lymphoblastoid cells used to distinguish different forms of autism (Nishimura et al. 2007). The results from the simulation study suggest that cardinality-constrained PCA has a better recovery of the sparse structure yet similar bias-variance trade-off as the penalized counterpart.

The remainder of this paper is structured as follows: First, Sect. 2 introduces PCA, sparse PCA, and penalized PCA. In Sect. 3, we present the simulation study comparing the performance of the methods on different measures. Sect. 4 presents an example using a real high-dimensional data set. Finally, in Sect. 5, conclusions are presented.

2 Methods

We first present the notation used in the remainder of the paper. Matrices are denoted by bold uppercase, the transpose of a matrix by the superscript $^\top$ (e.g., $\mathbf{A}^{\top }$), vectors by bold lowercase, and scalars by lowercase italics, and we use capital letters for the last value of a running index (e.g., j running from 1 to J). Given a vector $\mathbf{x}\in {\mathbb {R}}^{J}$, its j-th entry is denoted by $x_j$. The $l_1$-norm is defined by $\left\| \mathbf{x}\right\| _{1} = \sum _{j=1}^{J} \left| x_j \right|$, and the Euclidean distance by $\left\| \mathbf{x}\right\| _{2} = (\sum _{j=1}^{J} x_{j}^{2})^{1/2}$. Given a matrix $\mathbf{X}\in {\mathbb {R}}^{I\times J}$, its i-th row and j-th column entry is denoted by $x_{i,j}$, and $\left\| \mathbf{X}\right\| _{F}^{2}= \sum _{i=1}^{I} \sum _{j=1}^{J}\left| x_{i,j} \right| ^{2}$ denotes the squared Frobenius norm.

In this section, we introduce the PCA formulation on which the paper focuses. Sparse PCA variants of the formulation are then obtained by either adding a cardinality constraint or a convex penalty to the PCA objective.

2.1 PCA

Given a data matrix ${\mathbf {X}}\in {\mathbb {R}}^{I \times J}$ that contains I observations on J variables, in PCA, it is assumed that the data can be decomposed as,

$$\begin{aligned} {\mathbf {X}} = \mathbf {XWP}^\top + {\mathbf {E}}, \end{aligned}$$

where ${\mathbf {W}}\in {\mathbb {R}}^{J \times K}$ is the weights matrix, ${\mathbf {P}}\in {\mathbb {R}}^{J \times K}$ is the loadings matrix, ${\mathbf {E}}\in {\mathbb {R}}^{I \times J}$ is the residual matrix, and ${\mathbf {P}}^\top {\mathbf {P}} = {\mathbf {I}}$. Ordinary PCA can be formulated as the following least squares optimization problem:

$$\begin{aligned} \begin{aligned} \mathbf {{\widehat{W}},{\widehat{P}}} = \arg \min _{\mathbf {W,P}}\quad&\left\| {\mathbf {X}} - \mathbf {XWP}^\top \right\| ^{2}_{F} \\ \text {s.t.}\quad&{\mathbf {P}}^\top {\mathbf {P}} = {\mathbf {I}}. \end{aligned} \end{aligned}$$

(1)

The solution to the PCA formulation in (1) can be obtained using the truncated Singular Value Decomposition (SVD) of the data matrix ${\mathbf {X}}=\mathbf {UDV^{\top }}$ (Jolliffe 2002), with ${\mathbf {U}}\in {\mathbb {R}}^{I\times K}$ and ${\mathbf {V}}\in {\mathbb {R}}^{J\times K}$ semi-orthogonal matrices, and $\mathbf {{\widehat{W}}={\widehat{P}} =V}$. The linear combinations $\mathbf {T=XW}$ represent the component scores. In general, the estimated weights matrix resulting from the truncated SVD contains all nonzero elements making the interpretation of the component scores difficult when J is large.

2.2 Cardinality-constrained PCA

Starting from PCA formulation (1), the sparse PCA problem can be formulated as a best subset selection problem for a subset of size $\rho$ (where $\rho$ between 0 and $J\cdot K$ is given) as follows,

$$\begin{aligned} \begin{aligned} \mathbf {{\widehat{W}},{\widehat{P}}} =\arg \min _{\mathbf {W,P}} \quad&\left\| {\mathbf {X}}-{\mathbf {X}}{\mathbf {W}}{\mathbf {P}}^\top \right\| ^{2}_{F} \\ \text {s.t.}\quad&{\mathbf {P}}^\top {\mathbf {P}} = {\mathbf {I}}, \\&\left\| {\mathbf {W}}\right\| _{0} \le \rho , \end{aligned} \end{aligned}$$

(2)

with $\Vert {\mathbf {W}}\Vert _0$ denoting the number of nonzero coefficients in ${\mathbf {W}}$. Sparse PCA methods based on the least squares criterion in (1) have been only considered by adding penalties (see Sect. 2.3 for details). A solution to the cardinality-constrained problem (2) has not been proposed yet. Here, we propose an alternating optimization procedure to obtain feasible solutions of good quality. That is, fix ${\mathbf {W}}$ and obtain $\mathbf {{\widehat{P}}}$ by the well-known reduced rank Procrustes rotation (ten Berge 1993; Zou et al. 2006),

$$\begin{aligned} \begin{aligned} \mathbf {{\widehat{P}}} =\arg \min _{{\mathbf {P}}} \quad&\left\| {\mathbf {X}}-{\mathbf {X}}{\mathbf {W}}{\mathbf {P}}^\top \right\| ^{2}_{F} \\ \text {s.t.}\quad&{\mathbf {P}}^\top {\mathbf {P}} = {\mathbf {I}}. \end{aligned} \end{aligned}$$

(3)

Also, fix ${\mathbf {P}}$ and obtain $\mathbf {{\widehat{W}}}$ via the cardinality-constrained linear regression problem,

$$\begin{aligned} \begin{aligned} \mathbf {{\widehat{W}}}=\arg \min _{{\mathbf {W}}} \quad&\left\| \text {vec}({\mathbf {X}}) - ({\mathbf {P}} \otimes {\mathbf {X}})\text {vec}({\mathbf {W}})\right\| ^{2}_{2} \\ \text {s.t.}\quad&\left\| \text {vec}({\mathbf {W}})\right\| _0 = \rho , \end{aligned} \end{aligned}$$

(4)

where $\otimes$ denotes the Kronecker product, and $\text {vec}(\cdot )$ the vectorization of a matrix which converts the matrix into a column vector. A numerical procedure that solves problem (4) was proposed by Adachi and Kiers (2017) as a special case of a majorize-minimize (Hunter and Lange 2004) or iterative majorization (Kiers 2002) procedure. The update for $\mathbf {{\widehat{W}}}$ in each iteration is given by:

$$\begin{aligned} \text {vec}({\mathbf {W}}_{new}) = T_{\rho }\left( \text {vec}({\mathbf {W}}_{old}-\alpha ^{-1} {\mathbf {X}}^{\top }{\mathbf {X}}[{\mathbf {W}}_{old} - {\mathbf {P}}])\right) , \end{aligned}$$

(5)

where $\alpha$ is the maximum eigenvalue of ${\mathbf {X}}^{\top }{\mathbf {X}}$ and, for a vector ${\mathbf {x}}\in {\mathbb {R}}^{n}$, the thresholding operator $T_{\rho }({\mathbf {x}})\in {\mathbb {R}}^{n}$ denotes the vector obtained from ${\mathbf {x}}$ keeping the values of the $\rho$ elements of ${\mathbf {x}}$ having the largest absolute value, and setting the remaining ones equal to zero. Notice that the updating step for ${\mathbf {W}}$ in Eq. (5) is equal to the update of a projected gradient scheme with fixed step size $\alpha ^{-1}$. The use of majorization ensures that the resulting sequence of loss values is non-increasing. At each iteration, to obtain an approximate solution to (4), our algorithm relies on a procedure where the main complexity is to sort a matrix of dimension $J \times K$, and thus, this procedure can be applied even for large values of J. We call the full alternating procedure cardinality-constrained PCA (CCPCA). In Appendix 6.1, the CCPCA algorithm is presented in detail.

It is important to mention that the proposed algorithm does not guarantee finding a global optimum of problem (4). Instead, with each conditional update of either the component weights or loadings, the loss function is monotonically decreasing. For alternating algorithms of the type considered here, obtaining a stationary point is guaranteed under some compactness assumptions on the feasible set of the subproblems (Tseng 2001; Huang et al. 2016). Such compact structure can be obtained by adding the constraint $\left\| {\mathbf {w}}_{k} \right\| _{2} \le 1$ for $k=1,\ldots ,K$. However, this type of regularization constraint does not appear in the least square error formulation of PCA (see problem (1)) and therefore has not been added to the cardinality-constrained version of the sparse formulation either.

Defining sparse PCA as a best subset problem, has not been the method of choice in the statistical literature given that it belongs to the class of NP-hard problems. Another reason to find sparse solutions by adding convex penalties such as the LASSO, is the belief that these have a better bias-variance tradeoff resulting in better predictive accuracy in the context of regression. Recently, given the algorithmic and computational-power progress in the last few decades, it has been shown that the cardinality-constrained regression problem can be solved for a large number of variables (in the 100,000s) (Bertsimas and Parys 2020). For instance, Bertsimas et al. (2016) found the cardinality-constrained regression approach to be superior to LASSO regression not only in terms of recovering the correct subset of variables but also in terms of predictive performance, which is contrary to expectations based on the bias-variance trade-off. However, Hastie et al. (2017) have extended the simulations of (Bertsimas et al. 2016) focusing on prediction accuracy and found that the cardinality-constrained regression approach outperformed the LASSO regression only when there was a high signal to noise ratio.

2.3 Penalized PCA

A well-known sparse PCA method based on penalizing (1) was proposed by Zou et al. (2006). The method, named SPCA, is based on the following formulation,

$$\begin{aligned} \begin{aligned} \mathbf {{\widehat{W}}}, \mathbf {{\widehat{P}}} =\arg \min _{{\mathbf {W}}, {\mathbf {P}}}\quad&\left\| {\mathbf {X}} -{\mathbf {X}} {\mathbf {W}} {\mathbf {P}}^\top \right\| ^{2}_{F} + \lambda \sum _{k=1}^{K}\left\| \mathbf{w}_{k} \right\| ^{2}_{2}+ \sum _{k=1}^{K}\lambda _{k}^{l} \left\| \mathbf{w}_k \right\| _{1} \\ \text {s.t.} \quad&{\mathbf {P}}^\top {\mathbf {P}} = {\mathbf {I}}, \end{aligned} \end{aligned}$$

with $\sum _{k=1}^{K} \left\| \mathbf{w}_k \right\| _{1}$ the LASSO penalty (tuned using $\lambda _{k}^{l} \ge 0$) and $\sum _{k=1}^{K} \left\| \mathbf{w}_{k} \right\| ^{2}_{2}$ the ridge penalty (tuned using $\lambda \ge 0$). For fixed values of $\lambda _{k}^{l}$ and $\lambda$, SPCA is an alternating minimization algorithm that updates ${\mathbf {W}}$ given ${\mathbf {P}}$ and vice-versa. Obtaining $\mathbf {{\widehat{P}}}$ given a fixed value for ${\mathbf {W}}$ is also done via the reduced rank Procrustes Rotation problem (ten Berge 1993). And obtaining $\mathbf {{\widehat{W}}}$ given a fixed value for ${\mathbf {P}}$ is achieved using the elastic net penalized regression problem (Zou and Hastie 2005) that is defined by adding the LASSO and ridge penalties to the ordinary regression problem. The LASSO penalty sets some of the coefficients to exactly zero, while the ridge penalty shrinks the coefficients and it regularizes the problem in the high-dimensional setting ($J>I$); i.e., it allows for more nonzero coefficients than the number of observations, see also Zou et al. (2006).

Using a penalized regression as one of the alternating steps presents some advantages and disadvantages. On the one hand, shrinkage of all coefficients reduces the variance of the estimated coefficients; hence the coefficients estimated under a penalized regime may be more accurate than those obtained via cardinality constraints (Hastie et al. 2017). On the other hand, although penalized regressions find sparse feasible solutions, the correct subset of nonzero variables is only recovered under stringent conditions (see Bertsimas et al. 2016 and references therein). In the next section, we assess and compare the performance of CCPCA and SPCA in a simulation study. We focus on sparse structure recovery (zero and nonzero weights) and the accuracy of the estimated weights.

3 Simulation study

To compare the statistical properties of the penalized and the cardinality-constrained sparse PCA methods described in Sect. 2 above, we conducted a simulation study where two types of measures are of interest: the recovery of the weights support matrix (correctly identifying the set of non-zero weights) and the accuracy of the estimates in terms of bias and variance. To measure the former, we use the total sparse structure recovery rate (TSS%), and for the latter, we use the mean absolute bias (MAB), mean variance (MVAR), and mean squared error (MSE).¹

3.1 Design

We set the number of observations to $I=100$, the number of variables to $J=50,100,500$, and the number of components to $K=3$. We have also set the level of sparsity to $20\%$ and $80\%$ (i.e., when $J\cdot K =300$, we have 60 and 240 weights that are equal to zero, respectively), and the noise level to $5\%$, $20\%$, and $80\%$. The design results in $3 \cdot 2 \cdot 3 = 18$ different design conditions. For each condition $R=100$ data sets were generated. The data generation procedure is detailed in “Appendix 6.2”. The resulting data sets were analyzed using the CCPCA algorithm programmed in the R software for statistical computing (R Core Team 2020), and SPCA with LARS using the elastic net R-package (Zou and Hastie 2018). Both algorithms were run with one initial value, based on the SVD decomposition of the data. We supplied the analysis with the actual number of components. The tuning parameter of the ridge penalty for SPCA was left at the default value of $10^{-6}$; this is a small value such that the focus remains on comparing the cardinality constraint to the LASSO penalty as a means to sparsify the PCA problem in (1).

The analysis is divided in two cases depending on whether the cardinality of ${\mathbf {W}}$ is known or not. When the cardinality is known, we supply the analysis with the true cardinality. When the cardinality is unknown, we rely on a data-driven method, namely the Index-of-sparseness (IS) introduced by Trendafilov (2014). The IS has been shown to outperform other methods such as cross-validation and the BIC in estimating the actual proportion of sparsity (Gu et al. 2019). The IS is defined as

$$\begin{aligned} IS = \text {PEV}_{sparse}\cdot \text {PEV}_{pca}\cdot (1-\tfrac{\rho }{J\cdot K}) \end{aligned}$$

with $\text {PEV}_{sparse}$ and $\text {PEV}_{pca}$ denoting the proportion of explained variance using a sparse method and ordinary PCA, respectively. The IS value increases with the goodness-of-fit $\text {PEV}_{sparse}$, the higher adjusted variance $\text {PEV}_{pca}$, and the sparseness. The cardinality of the weights is determined by maximizing the IS.

To assess the recovery of the weights matrix, we calculate the total sparse structure recovery rate, defined as:

$$\begin{aligned} \text {TSS}\% = \frac{ \sum _{j,k} \text {supp}({\mathbf {W}},\mathbf {{\widehat{W}}})_{j,k} }{J\cdot K} \end{aligned}$$

(6)

where

$$\begin{aligned} \text {supp}({\mathbf {W}},\mathbf {{\widehat{W}}})_{j,k} = \left\{ \begin{array}{lccc} 1, &{} w_{j,k}=0&{} \text {and}&{}{\widehat{w}}_{j,k}=0\\ 1, &{} w_{j,k}\ne 0&{} \text {and}&{}{\widehat{w}}_{j,k}\ne 0\\ 0, &{} \text {Otherwise.} &{} &{} \end{array}\right. \end{aligned}$$

Therefore, $\text {TSS}\%$ takes into account both correct identification of the zero and nonzero values. To assess the accuracy of the actual value of the estimates, we calculate the MAB, MVAR, and MSE. These measures are defined as,

$$\begin{aligned}&\text {MAB} = \frac{1}{J \cdot K\cdot R} \sum _{j} \sum _{k} \sum _{r}|\overline{{\widehat{w}}}_{j,k} - w_{j,k}^{(r)}|, \\&\text {MVAR} = \frac{1}{J\cdot K\cdot R} \sum _{j} \sum _{k} \sum _{r} (\overline{{\widehat{w}}}_{j,k} - {\widehat{w}}^{(r)}_{j,k} )^{2},\\&\text {MSE} = \frac{1}{J\cdot K\cdot R} \sum _{j} \sum _{k} \sum _{r} (w_{j,k} - {\widehat{w}}^{(r)}_{j,k})^{2}, \end{aligned}$$

where $\overline{{\widehat{w}}}_{j,k}=\frac{1}{R} \sum _{r} {\widehat{w}}_{j,k}^{(r)}$ and $r = 1 \ldots R$ a running index for the generated data sets. As CCPCA and SPCA solutions are indeterminate with respect to the sign and order of the component weight vectors ${\mathbf {w}}_k$, we matched $\widehat{{\mathbf {w}}}_k$ to the true ${\mathbf {w}}_k$ based on the highest proportion of total recovery in Eq. (6).

3.2 Results

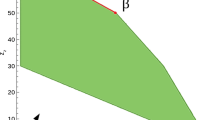
Figures 1 and 2 show the total recovery rate with cardinality either set to the cardinality used to generate the sparse weights or to the value that maximizes the IS, respectively. From Fig. 1, it can be observed that in almost all conditions, CCPCA has a higher proportion of correctly identified weights than SPCA. Only when the noise level is $80\%$ and the proportion of sparsity $20\%$, both methods present similar results on average. When the cardinality of the component weights is treated as unknown and tuned using the IS, we observe in Fig. 2 that the recovery rate mainly depends on the proportion of sparsity. When $PS = 20\%$, SPCA has a higher recovery rate, and when $PS = 80\%$, CCPCA has a higher recovery rate. This result may be explained by the fact that CCPCA can achieve more variance with less variables than SPCA (see Fig. 5). Therefore, the cardinality of CCPCA is always lower than SPCA’s cardinality and the cardinality used to generated the data sets (see Fig. 6)

Fig. 1

Proportion of correctly identified weights with same the cardinality as used to generate the data. The dashed line at 0.6 indicates the minimum recovery rate that can be obtained given 20% or 80% of sparsity

Fig. 2

Proportion of correctly identified weights with cardinality tuned using the index of sparseness

The MAB, MVAR, and MSE of the estimators from CCPCA and SPCA are reported in Tables 1 and 2 when the cardinality is set equal to the cardinality used to generate the weights and as tuned with the IS, respectively. It can be observed in Table 1 that the MAB of CCPCA is higher than the SPCA’s MAB, although by a small margin only. The MVAR of the CCPCA weights is approximately equal to the MVAR of SPCA weights when there is little noise in the data (5%). In the case of a higher noise level (20% and 80%), the MVAR of SPCA is lower than that of CCPCA; this can be attributed to the shrinkage effect of the penalties in SPCA. The MSE in case of little noise in the data and 20% of sparsity is slightly lower for CCPCA than SPCA, while the MSE is lower for SPCA in case of 20% noise and 80% sparsity. If we turn to the case where the cardinality was tuned using the IS (Table 2), in all conditions the MAB is smaller for CCPCA than for SPCA while the MVAR and MSE are higher for CCPCA than for SPCA: here, we clearly see the beneficial effect of the shrinkage penalties that introduce a higher bias though resulting in a much lower variance.

Overall, these results suggest that CCPCA recovers better the sparse structure, especially under high levels of sparsity and noise. When the cardinality of the component weights is known, the recovery rates are in general satisfactory to good. When the cardinality is not known, and the IS is used to tune the cardinality, SPCA performs reasonably well on data with low levels of sparsity while CCPCA performs reasonably well on data with high levels of sparsity. Additionally, as mentioned in the statistical literature, the penalized method (SPCA) has higher bias though lower variance while the cardinality-constrained method (CCPA) has less bias but higher variance.

Table 1 MAB, MVAR, and MSE of the estimators from CCPCA and SPCA

Table 2 MAB, MVAR, and MSE of the estimators from CCPCA and SPCA with cardinality tuned using the index-of-sparseness

4 Empirical application

In this section, we use an empirical data set to illustrate how the methods described in this study can be used in practice as a pre-processing step to reduce a large set of variables in the context of classification. We use a publicly available gene expression data set comparing 14 male control subjects to 13 male autistic subjects.² The autism subjects were further subdivided into two groups: a group of six with autism caused by a fragile X mutation (FMR1-FM) and seven with autism caused by a 15q11–q13 duplication (dup15q). The transcription rates of 43,893 probes, corresponding to 18,498 unique genes, were obtained for each subject.

Prior to analyzing the data, we centered and scaled each column to unit variance, and followed Nishimura et al. (2007) to chose the number of component $K=3$. Therefore, the total cardinality of the components weights is 131,679. To select the cardinality, we rely on the IS. Figure 3 shows the IS and PEV as a function of the cardinality of the weights using CCPCA and SPCA.³ The maximal PEV with three components, obtained with ordinary PCA, accounts for 32% of the variance. The maximum value of IS for CCPCA is reached at a cardinality of 23,499 with a PEV of 30% while the maximal IS for SPCA is reached at a cardinality of 42,283 with a PEV of 22%. This is also in accordance with our earlier observation in the simulation study, which showed that CCPCA can explain more variance with less variables than SPCA.

When plotting the second component score against the third one (Fig. 4a, b), we observe a separation of the individuals with autism from the control group and between the individuals with autism caused by the fragile X mutation and by the 15q11-q13 duplication. The former could be expected as the largest source of variation in the data is the distinction between control and autistic subjects. One may notice that in Nishimura et al. (2007) this classification of the three groups is observed as well. However, Nishimura et al. (2007) constructed component scores using a subset of 293 probes with a significant difference in expression between the three groups in an analysis of variance (ANOVA). This means that an informed approach was used to select the relevant genes while CCPCA and SPCA do not construct component scores with the aim of discrimination; still, a separation between the three groups can be observed from Fig. 4a, b.

Fig. 3

Index of sparseness (IS) and proportion of explained variance (PEV) against cardinality

Fig. 4

Scatter plot of the component scores of component 2 against component 3

5 Conclusion

We introduced a cardinality-constraint based method (CCPCA) and compared its performance with the performance of a penalty based method (SPCA). Both methods are designed to attain sparse weights in PCA. Both follow an alternating optimization procedure where sparsity is achieved via either a penalized or a cardinality-constrained linear regression problem. Penalized regressions have been propounded in the statistical literature for reasons of computational and statistical efficiency. Recently, significant progress has been made in solving cardinality -constrained regression problems finding feasible solutions in the case of many variables.

We compared the CCPCA and SPCA methods through a simulation study assessing the recovery of the sparse structure (zero and nonzero) and the accuracy of the estimates. Regarding the recovery rate, CCPCA showed better results than SPCA in almost all conditions when both methods were supplied with actual cardinality. When the cardinality needed to be estimated, CCPCA presented a better solution when the cardinality was set to a small number of variables. For the accuracy of the estimates, both presented similar performance with known cardinality, while SPCA shows more bias and less variance with unknown cardinality. Additionally, we used real, high-dimensional data to evaluate these methods in practice. CCPCA and SPCA efficiently reduced the dimension without losing much of the explained variance using only a fraction of the original variables in the data. From the simulation and the real example, CCPCA can explain more variance with fewer variables than SPCA.

CCPCA and SPCA are freely available to be used in R-software. When using them, it is essential to consider that both methods are subject to local minima. It is a common practice to implement a multi-start procedure and select the solution with the smallest objective function, but the obtained solutions will still be subject to local optima. For future work, it would be interesting to analyze the conditions for optimality for sparse PCA methods.

Appendix

1.1 Algorithm: CCPCA

We present a detailed description of the algorithm used to solve formulation (2). We have implemented an alternating procedure fixing one variable a at time. To estimate ${\mathbf {P}}$ with ${\mathbf {W}}$ fixed (see problem (3)), Procruste rotation has been used (ten Berge 1993; Zou et al. 2006). That is, the solution to (3) is $\mathbf {{\widehat{P}}} = \mathbf {UV}^\top$, where ${\mathbf {U}}$ and ${\mathbf {V}}$ are the left and right truncated singular vectors of ${\mathbf {X}}^{\top }\mathbf {XW}$, respectively. To estimate ${\mathbf {W}}$ with ${\mathbf {P}}$ fixed (see problem (4)), the cardinality-constrained regression algorithm in (Adachi and Kiers 2017) is implemented, which uses a majorization minimization approach (for a short overview see Hunter and Lange 2004).

Following Kiers (2002), we can majorize (4) as follows,

$$\begin{aligned} \left\| \text {vec}({\mathbf {X}}) - ({\mathbf {P}} \otimes {\mathbf {X}})\text {vec}({\mathbf {W}})\right\| ^{2}_{2} \le c + \alpha \Vert {\mathbf {b}} - \text {vec}({\mathbf {W}})\Vert ^{2}_{2}, \end{aligned}$$

(7)

where c is a constant with respect to ${\mathbf {W}}$, $\alpha$ is the maximum eigenvalue of ${\mathbf {X}}^{\top }{\mathbf {X}}$ and ${\mathbf {b}}$ is given by ${\mathbf {b}} = \text {vec}({\mathbf {W}})-\alpha ^{-1} \text {vec}\left( {\mathbf {X}}^{\top }{\mathbf {X}}({\mathbf {W}} - {\mathbf {P}})\right)$. The right hand side in (7) is minimized when ${\mathbf {b}}=T_{\rho }\left( \text {vec}({\mathbf {W}}) \right)$. In fact, the same updating formula of the weights appears in the proximal gradient algorithm presented in (Bertsimas et al. 2016, Equation 3.8 in Algorithm 1)

In some instances, it can be more useful to specify the cardinality constraint per column of ${\mathbf {W}}$. This leads to more control over the sparsity level in the weights pertaining to specific components. This can be done by adding a cardinality constraints per ${\mathbf {w}}_k$ as follows,

$$\begin{aligned} \begin{aligned} \mathbf {{\widehat{W}}}=\arg \min _{{\mathbf {W}}} \quad&\left\| \text {vec}({\mathbf {X}}) - ({\mathbf {P}} \otimes {\mathbf {X}})\text {vec}({\mathbf {W}})\right\| ^{2}_{2}&\\ \text {s.t.}\quad&\left\| {\mathbf {w}}_{k}\right\| _{0} = \rho _{k}&\forall k=1,2,3,\ldots ,K, \end{aligned} \end{aligned}$$

where $\rho _{k}$ denotes the number of nonzero per component weight. In this case, the updating formula in each iteration becomes,

$$\begin{aligned} {\mathbf {w}}_{k,new}:=T_{\rho _k}\left( {\mathbf {w}}_{k,old} - \alpha ^{-1}{\mathbf {X}}^{\top }{\mathbf {X}}({\mathbf {w}}_{k,old} - {\mathbf {p}}_{k})\right) . \\ \end{aligned}$$

An implementation of Algorithm (1) is freely available in R-software (R Core Team 2020) and downloadable from the corresponding author’s github page: https://github.com/RosemberGuerra/CCPCA.git. As discussed in Sect. 2, This algorithm does not guarantee finding a global optimum of problem (4). A way of improving the solution is by initializing ${\mathbf {W}}$ with the estimates $\widehat{{\mathbf {W}}}$ from PCA. This “warm” start will nudge the algorithm in the right direction, minimizing the risk that the algorithm will end up in a local minimum of large value, far from optimal. Another way to improve the solution is by using multiple starts. The procedure can be started multiple times with different values for ${\mathbf {W}}_{0}$, and the result with the smallest loss function value is retained. Multiple starts are more costly, which especially adds up when K and $\rho$ still need to be determined using model selection.

1.2 Data generation

The data for the simulation study was generated from the following decomposition,

$$\begin{aligned} {\mathbf {X}} = {\mathbf {X}}{\mathbf {W}}{\mathbf {P}}^\top , \end{aligned}$$

where ${\mathbf {W}}\in {\mathbb {R}}^{J\times K}$, ${\mathbf {W}}^\top {\mathbf {W}} = {\mathbf {I}}$ and ${\mathbf {P}} = {\mathbf {W}}$. The orthogonality condition on ${\mathbf {W}}$ links to the PCA identification constraints and it has been considered before in simulation studies (Camacho et al. 2020, 2021; Guerra-Urzola et al. 2021). The matrix ${\mathbf {W}}$ is constructed such that it contains a given level of sparsity. To achieve this, we used the following iterative procedure. First, a random matrix ${\mathbf {W}}$ is generated with zero weights in the desired places. Then, orthogonality of the columns is attempted by applying the Gramm-Schmidt orthogonalization procedure only in the intersection of the nonzero weights between two columns of ${\mathbf {W}}$. When ${\mathbf {W}}$ only has sets of columns that contain non-overlapping sparsity patterns, this immediately results into orthogonal columns, but when the columns in ${\mathbf {W}}$ have overlapping sparsity patterns the procedure will not always lead to ${\mathbf {W}}^\top {\mathbf {W}} ={\mathbf {I}}$ on the first pass. In such cases, multiple passes are needed in order to achieve orthogonality (additional coefficients might need to be set equal to zero). Some sparsity patterns are not possible, for example, an initialization where ${\mathbf {W}}$ does not have full column rank, or an initial set that degenerates to a linearly dependent set after multiple passes. In those cases, the algorithm fails to converge.

After a suitable ${\mathbf {W}}$ has been obtained, $\varvec{\Sigma }$ is constructed by taking $\varvec{\Sigma } = {\mathbf {W}}{\varvec{\Lambda }}{\mathbf {W}}^\top$. Here, ${\varvec{\Lambda }}$ is a diagonal matrix with eigenvalues of the J components underlying the full decomposition. We specify these eigenvalues such that the first K components account for a set amount of structural variance and the remaining eigenvalues for a set amount of noise variance. The data matrices ${\mathbf {X}}$ having a desired underlying sparse structure and noise level can then be obtained by sampling from the multivariate normal distribution with zero mean vector and variance-covariance $\varvec{\Sigma }$. Note that the generation scheme used here is very restrictive and may not be applicable to empirical data. Additionally, in our experiments, generating non-orthogonal weights did not change the results in any noticeable way. This code is publicly available at the author’s github page: https://github.com/RosemberGuerra/CCPCA.git.

1.3 Additional plots

See Figs. 5 and 6

Fig. 5

Proportion of explained variance (PEV) with cardinality tuned using index of sparseness

Fig. 6

Estimated proportion sparsity with cardinality tuned using index of sparseness