Quantile composite-based path modeling: algorithms, properties and applications

Abstract

Composite-based path modeling aims to study the relationships among a set of constructs, that is a representation of theoretical concepts. Such constructs are operationalized as composites (i.e. linear combinations of observed or manifest variables). The traditional partial least squares approach to composite-based path modeling focuses on the conditional means of the response distributions, being based on ordinary least squares regressions. Several are the cases where limiting to the mean could not reveal interesting effects at other locations of the outcome variables. Among these: when response variables are highly skewed, distributions have heavy tails and the analysis is concerned also about the tail part, heteroscedastic variances of the errors is present, distributions are characterized by outliers and other extreme data. In such cases, the quantile approach to path modeling is a valuable tool to complement the traditional approach, analyzing the entire distribution of outcome variables. Previous research has already shown the benefits of Quantile Composite-based Path Modeling but the methodological properties of the method have never been investigated. This paper offers a complete description of Quantile Composite-based Path Modeling, illustrating in details the method, the algorithms, the partial optimization criteria along with the machinery for validating and assessing the models. The asymptotic properties of the method are investigated through a simulation study. Moreover, an application on chronic kidney disease in diabetic patients is used to provide guidelines for the interpretation of results and to show the potentialities of the method to detect heterogeneity in the variable relationships.

1 Introduction

Several are the approaches to study the relationships among different constructs and between each construct and its corresponding observed or manifest variables (MVs). In most common models, each block of MVs measures a construct, and prior knowledge is used to define the theoretical model. Two are the main parameters in this type of model: the path coefficients and the loadings. Path coefficients represent the relationships between constructs while loadings measure the relationship between constructs and the corresponding MVs.

Covariance structure analysis (Jöreskog 1978) and Partial Least Square Path Modeling (PLS-PM) (Esposito Vinzi et al. 2010; Hair et al. 2017) are the two mainstream approaches. Even if they are commonly considered as alternative, they belong to two different families of statistical methods. Covariance structure analysis, essentially used in factor-based Structural Equation Modeling (SEM), exploits the covariance matrix of MVs to estimate the model parameters. PLS-PM instead summarizes each block of MVs in a component, or composite, namely an exact linear combination of the MVs, focusing on the explained variance of MVs (Wold 1982, 1985). Each composite is a proxy of the construct associated to the correspondent block. For the aforesaid reasons, PLS-PM is commonly referred to as a component-based, composite-based or variance-based approach. Herman Wold, who proposed the PLS-PM, referred to this approach as “Soft Modeling”. The name indicates that the method requires “soft” distributional assumptions, in contrast to the estimation method for factor-based models, which requires strong assumptions on the error distributions (thus the name “hard modeling”) (Wold 1975, 1982; Tenenhaus et al. 2005; Chin 1998).

PLS-PM exploits least square regression to estimate the model coefficients and therefore focuses on the conditional mean of the response variables. Many are the cases where the analysis of the average alone could produce an incomplete view of the complex structure of the relationships among variables. When heteroscedastic variances of least square regression residuals occurs, and/or when response variables are highly skewed, the study of the conditional distribution at locations different from the mean can complement the classical approach and provide a richer picture of the investigated phenomenon. Following this idea, Quantile Composited-based Path Modeling (QC-PM), proposed by Davino and Esposito Vinzi (2016), exploits quantile regression (Koenker and Basset 1978) to look beyond the average. It is a valuable tool to study the relationships among variables, and to model location, scale and shape of the responses. QC-PM can be used to complement PLS-PM to investigate whether the effects of explanatory constructs change over the entire distribution of the response constructs. It is worth emphasizing that PLS-PM and QC-PM are not competing methods, and therefore their comparison in terms of performance is of little interest. The two methods have different objectives: PLS-PM focuses on the conditional means of the dependent variables providing an instant summary, while QC-PM explores relationships among variables outside of conditional mean. Finding that estimated coefficients vary across the conditional quantiles does not imply that the PLS-PM results are invalid.

Previous research (Davino et al. 2016, 2017, 2018, 2020; Davino and Esposito Vinzi 2016) was oriented to show the relative advantages of QC-PM when the interest is in the effects of explanatory constructs on the entire distribution of the response constructs, and to assist in the interpretation of results and in their use combined with PLS-PM results.

The aim of this paper is to provide a complete and organic description of QC-PM, since its methodological properties have never been investigated. This goal is pursued through several innovative contributions introduced in the paper: a clear and detailed explanation of the method introducing also the case of one block and two blocks, an improvement of the method allowing to handle the measurement invariance issue, an application with artificial data that allows to highlight the potential of the method. More specifically, in order to clarify the characteristics of the method, a step-by-step description of the algorithms, the partial optimization criteria, and the formalization of the models are provided. A relevant part of the present work is devoted to studying the properties of QC-PM, which have never been investigated before.

An analytical discussion of the properties of the involved estimators is a daunting task, due to the complexity of composite-based path modeling. This is a fertile ground for the use of simulation studies, which provide information on the performance of the method in terms of bias, efficiency and robustness of the estimates (Paxton et al. 2001). In particular, we exploit a Monte Carlo simulation design generating data from a composite-based population and considering a set of different scenarios. This allows us to assess the effects of several drivers: correlation within the blocks of MVs, correlation among constructs, effect of heavy-tails and skewness of MV distributions, effect of sample size.

A discussion on the asymptotic properties of the method is offered, along with empirical evidence on the behaviour of the estimators in terms of bias and efficiency. An innovative contribution to the estimation of the outer model is also provided to fulfil the measurement invariance required to compare path coefficients estimates over quantiles.

Moreover, an application on Chronic Kidney Disease (CKD) in diabetic patients is provided to show benefit of using QC-PM as a supplement to PLS-PM. In particular, we apply QC-PM on data already used in a research that proposed a quantile approach to factor based SEM (Wang et al. 2016). Because the original data were not available, they have been artificially derived mimicking the model, the relations among variables and the estimates obtained in the original study (Wang et al. 2016). As the artificial data are generated from a scenario where relationships among variables change with quantiles, the application highlights the potentialities of the method in detecting the heterogeneity in the variable relationships and stressing its complementary role with the traditional methods for composite-based path modeling.

The paper is organized as follows: Sect. 2 describes QC-PM in detail, formalizing the estimation process starting from the simplest case of one block of MVs and moving until the general path model for multi-block data. Section 3 illustrates the assessment measures of QC-PM in terms of goodness of fit and statistical significance of the estimated coefficients. Section 4 shows the simulation design and the main results, while the applicative potentialities of QC-PM, along with guidelines for the interpretation of results, are provided through the study on the artificial data set concerning CKD in diabetic patients in Sect. 5. Finally, a summary of the proposal and an outline for future developments are given in Sect. 6.

2 QC-PM: quantile composite-based path modeling

QC-PM is strongly related to PLS-PM. Therefore the modeling and estimation procedures have much in common, the same holds for their properties. The theoretical foundations are framed in the iterative algorithm proposed by Wold (1966a, 1966b), the Nonlinear estimation by Iterative PArtial Least Squares (NIPALS) algorithm, an alternative algorithm for implementing principal component analysis. More broadly, Partial Least Squares (PLS) refers to a set of iterative alternating Ordinary Least Squares (OLS) algorithms, extending the NIPALS algorithm to implement a large number of multivariate statistical techniques (Esposito Vinzi and Russolillo 2013), depending on the involved MVs. For example, in case of one block of MVs, PLS provides principal component analysis. In case of two blocks of MVs, multivariate regularized regression can be obtained (PLS regression). In case of multi-block data, PLS algorithm produces PLS-PM (Lohmöller 1989).

The numerical solutions of all these methods are obtained through an iterative algorithm, which is the first stage of the procedure. The basic idea of the PLS iterative algorithm, which computes the weights used to define the composites, is to partition the set of model parameters to be estimated in subsets. At each step of the algorithm, one subset of parameters is considered known and held fixed, while the other subset is estimated (Lohmöller 1989). A least squares criterion is adopted to estimate the parameters in each step. The name PLS comes from the use of OLS to face with the least square criterion at each step. For example, in case of multi-block data, namely PLS-PM, the procedure comes down to a set of simple and multiple OLS regressions, and Pearson correlation computation.

The QC-PM algorithm follow exactly the same steps of the PLS-PM algorithm, but replacing simple and multiple OLS regression with their Quantile Regression (QR) counterparts (Koenker 2005). The same for classical Pearson correlation, which is replaced with quantile correlation (Li et al. 2014). As well as PLS-PM, QC-PM is based on a two-stage procedure. The first stage aims at computing the outer weights by an iterative procedure (these weights are then used for computing the composites). In the second stage, model parameters (loadings and path coefficients) are estimated through regression analysis using the composites. As for PLS-PM, partial criteria are optimized at each step.

The use of quantile based tools in all phases of the algorithm shifts the focus to the entire conditional distributions of the involved response variables, allowing to estimate partial conditional quantiles. Through the use of different conditional quantiles, the whole response distribution can be inspected. Therefore QC-PM is a valuable complement to PLS-PM, as much as quantiles are a complement to the average. For the sake of illustration, next subsections present QC-PM for the simplest model (one block of MVs), for two blocks of MVs, and for multi-block data (the general model), respectively.

The presentation of the QC-PM algorithm will follow the same steps and the same approach generally used to present the PLS-PM algorithm (Lohmöller 1989; Tenenhaus et al. 2005; Esposito Vinzi and Russolillo 2013). A basic knowledge of QR is assumed. Appendix provides a basic introduction of QR idea and goals. For a more detailed description of QR, please refer to Koenker and Basset (1978), Davino et al. (2013) and Furno and Vistocco (2018).

2.1 Quantile path modeling for one block of manifest variables

The simplest model involves one block of MVs and a construct. The relationships between them are depicted in Fig. 1. MVs are denoted with $\mathbf{X = \{x_{ip}\}}$ and represented through rectangles. It is worth to recall that $i = 1, \ldots , n$ refers to the observations, n denoting their number, and $p = 1, \ldots , P$ refers to the MVs, P denoting the number of MVs in each block. The corresponding construct is labeled with $\varvec{\xi } = \{\xi _{i}\}$ and is placed in oval or circle. This diagram is called path diagram.

Fig. 1

A path diagram for an hypothetical one-block model

The relationships among MVs and construct in the path diagram can be translated into a system of simultaneous equations. In particular, for each considered quantile $\theta \in (0,1)$, the link between each MV $\mathbf{x} _{p}$ and $\xi$ is defined through the following equation:

$$\begin{aligned} {x}_{ip} = \alpha _{p}\left( \theta \right) + \lambda _{p}\left( \theta \right) {\xi }_i + {\epsilon }_{ip}\left( \theta \right) , \end{aligned}$$

(1)

where $\alpha _{p}$ is a location parameter, $\lambda _{p}$ is the loading coefficient, capturing the effect of $\varvec{\xi }$ on $\mathbf{x} _{p}$, and $\varvec{\epsilon }_p=\{\epsilon _{ip}\}$ is the error term vector. The only assumption is that the generic $\theta$th conditional quantile of $\mathbf{x} _{p}$ can be expressed as:

$$\begin{aligned} Q_{\theta }\left( {\mathbf {x}}_{p} | \varvec{\xi } \right) = \alpha _{p}\left( \theta \right) + \lambda _{p}\left( \theta \right) \varvec{\xi } \end{aligned}$$

(2)

which implies that the $\theta$th quantile of the error term $\varvec{\epsilon }_p\left( \theta \right)$ is equal to zero and $\varvec{\epsilon }_p\left( \theta \right)$ is independent of $\varvec{\xi }$. No assumptions on the error distribution are required.

The model captures the common variation among the MVs in $\mathbf{X}$ that depends on the construct $\varvec{\xi }$. The use of QR allows to encompass the effect of $\varvec{\xi }$ on the whole conditional distribution of each ${\mathbf {x}}_{p}$, effect that might not be equal at different locations, i.e. quantiles. In fact, the construct could be a weak factor at some location of the MV distributions, exerting a stronger effect at other conditional quantiles. In other cases the effect could be almost uniform along the entire distribution. The quantile model offers the opportunity to investigate the possible different situations.

Parameters are estimated through the classical PLS algorithm for one block of variables, replacing OLS regression with QR at each step of the procedure. This corresponds to iteratively optimize a quantile partial criterion. The algorithm consists of three main steps. In the initialization step, arbitrary values are set for the outer weights $\hat{\mathbf{w }}_{p}$, namely the coefficients used to compute the composite $\varvec{\hat{\xi }}$, which expresses the construct as a linear combination of the MVs. Starting from such initialization values, a first approximation of the composite is computed as a linear combination of the MVs in $\mathbf{X}$, $\varvec{\hat{\xi }}^{(0)}\!\!= \sum _{p=1}^{P}{{\hat{w}}}^{(0)}_p\mathbf{x} _{p}$. Then, a loop starts and at each sth iteration $(s=0,1,2, \ldots )$, each MV $\mathbf{x} _{p}$ is regressed on the composite, minimizing the following quantile loss function:

$$\begin{aligned} \hat{{w}}^{(s)}_p\left( \theta \right) = \mathop {\mathrm{argmin}}\limits _{{w}_p\left( \theta \right) } \sum \limits _{i=1}^n \rho _{\theta } \left( {\varvec{x}}_{ip}-{\alpha }_p\left( \theta \right) - {{\varvec{\xi }}}^{(s-1)}_i {w}_{p}\left( \theta \right) \right) , \end{aligned}$$

(3)

where $\rho _{\theta } \left( .\right)$ is the check function, which asymmetrically weights positive and negative residuals, namely:

$$\begin{aligned} \rho _{\theta }(r)= \left\{ \begin{array}{lll} \theta {r} &{} \qquad \text{ if } &{} {r} > 0 \\ \left( \theta -1\right) {r} &{} \qquad \text{ if } &{} {r}\le 0. \end{array} \right. \end{aligned}$$

(4)

The outer weights are then iteratively computed until convergence through simple QR models, where each MV is the response variable and the composite is the regressor. In each step the estimated weights are normalized and used to update the $\varvec{\hat{\xi }}$, obtained as a linear combination of the response MVs $\mathbf{x} _{p}$.

By weighting the MVs considering their quantile covariation with the construct, for each quantile $\theta$ the proposed algorithm chooses a linear combination of MVs that is a consistent quantile composite. Once convergence is reached or the maximum number of iterations is achieved, loadings are estimated by means of simple QRs over the corresponding scores. The pseudo–code of the QC-PM iterative algorithm for the case of one block of MVs is provided in Algorithm 1.

2.2 Quantile path modeling for two blocks of manifest variables

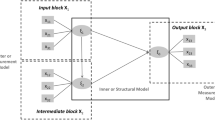
Figure 2 depicts the path diagram for an hypothetical two-block model. In such a case, let $\mathbf{X} =\{x_{ip}\}$ and $\mathbf{Y} = \{y_{ij}\}$ denote the two blocks of MVs. In particular, the former consists of the explanatory MVs and the latter of the response MVs. We denote with P the number of explanatory MVs, as in the previous subsection, and with J the number of response MVs, ${\varvec{y}}_{j}$ being the generic response MV. Moreover, $\varvec{\xi }=\{\xi _{i}\}$ is the construct representing the explanatory block, and $\varvec{\eta }=\{\eta _{i}\}$ the construct representing the dependent block. The general model consists of two sub-models: the inner model and the outer model. The inner model refers to the relationships between the constructs, the outer model between each construct and its block of MVs.

Fig. 2

A path diagram for an hypothetical two-block model

By referring to the outer model, for each quantile $\theta \in (0,1)$, the MVs $\mathbf{x} _{p}$ in the explanatory block, and the MVs $\mathbf{y} _{j}$ in the dependent block, are related to their correspondent constructs through the following system of bilinear equations:

$$\begin{aligned} {x}_{ip}&= \alpha _{xp}\left( \theta \right) + \lambda _{xp}\left( \theta \right) {\xi }_i + {\epsilon }_{ip}\left( \theta \right) , \end{aligned}$$

(5)

$$\begin{aligned} {y}_{ij}&= {\alpha _{yj}}\left( \theta \right) + \lambda _{yj}\left( \theta \right) {\eta }_i + {\omega }_{ij}\left( \theta \right) . \end{aligned}$$

(6)

where $\alpha _{xp}$ and $\alpha _{yj}$ are location parameters, $\lambda _{xp}$ is the loading coefficient capturing the effect of $\varvec{\xi }$ on $\mathbf{x} _{p}$, $\lambda _{yj}$ is the loading coefficient capturing the effect of $\varvec{\eta }$ on $\mathbf{y} _{j}$, while $\varvec{\epsilon }=\{\epsilon _{ip}\}$ and $\varvec{\omega }=\{\omega _{ij}\}$ are the error terms. The usual assumptions on the error terms already mentioned above are required.

The inner model specifies the dependence relationships between the two constructs. The dependent construct $\varvec{\eta }$ is linked to the explanatory construct $\varvec{\xi }$ by the following model:

$$\begin{aligned} {\eta }_{i}\left( \theta \right) = \beta _{0}\left( \theta \right) + \beta _1\left( \theta \right) {\xi }_{i}+{\zeta }_{i}\left( \theta \right) , \end{aligned}$$

(7)

where $\beta _1$ is the so-called path coefficient capturing the effects of $\varvec{\xi }$ on the dependent construct $\varvec{\eta }$, and $\varvec{\zeta }=\{\zeta _{i}\}$ is the inner error variable.

The procedure for the estimation of the model parameters requires a multi-step algorithm and follows the same structure of the PLS algorithm for two blocks of MVs, defined for example in Esposito Vinzi and Russolillo (2013), where partial criteria are optimized iteratively. The pseudo code of the QC-PM algorithm for the case of two blocks of MVs is detailed in Algorithm 2.

In the initialization step of the algorithm, arbitrary values are set for the outer weights $\hat{\mathbf{w }}_{xp}$ to compute a first approximation of the composite as a linear combination of the MVs in $\mathbf{X}$, $\varvec{\hat{\xi }}^{(0)}=\sum _{p=1}^{P}{{\hat{w}}}^{(0)}_{xp}{} \mathbf{x} _{p}$. Then, the iterative algorithm step proceeds over two phases. At each sth iteration $(s=0,1,2,\ldots )$, the response MVs $\mathbf{y} _{j}$ are regressed on the approximation of the composite $\varvec{\hat{\xi }}^{(s-1)}$, minimizing the following quantile loss function:

$$\begin{aligned} \hat{w}^{(s)}_{yj}\left( \theta \right) =\mathop {\mathrm{argmin}}\limits _{{w}_{yj}\left( \theta \right) } \sum _{i=1}^n \rho _{\theta } \left( {y}_{ij}-{\alpha }_p\left( \theta \right) - {\hat{\xi }}^{(s-1)}_i w_{yj}\left( \theta \right) \right) , \end{aligned}$$

(8)

where $\rho _{\theta } \left( .\right)$ is the check function defined as above.

In the second phase, the estimated $\hat{w}^{(s)}_{yj}\left( \theta \right)$, for $j = 1, \ldots , J$, are used to compute the composite $\varvec{\hat{\eta }^{(s)}}$ through a linear combination of the response MVs $\mathbf{y} _{j}$, and then the explanatory MVs $\mathbf{x} _{xp}$, are regressed on the obtained linear combination, minimizing the following quantile loss function:

$$\begin{aligned} \hat{w}^{(s)}_{xp}\left( \theta \right) =\mathop {\mathrm{argmin}}\limits _{{w}_{xp}\left( \theta \right) } \sum _{i=1}^n \rho _{\theta } \left( {x}_{ip} - {\alpha }_p\left( \theta \right) - \hat{\eta }^{(s)}_i w_{xp}\left( \theta \right) \right) . \end{aligned}$$

(9)

Finally, an updated approximation of the composite $\varvec{\hat{\xi }}^{(s)}$ is obtained as a linear combination of the explanatory MVs $\mathbf{x} _{p}$, using the weigths $\hat{w}^{(s)}_{xp}\left( \theta \right)$.

These two phases are iteratively repeated until convergence of the outer vectors, ${\varvec{w}}_{x}\left( \theta \right) =\{w_{xp}\left( \theta \right) \}$ and ${\varvec{w}}_{y}\left( \theta \right) =\{w_{yj}\left( \theta \right) \}$, is achieved. Then loadings and path coefficients are estimated through quantile regression.

QC-PM algorithm returns, for each quantile $\theta$, a linear combination of the explanatory MVs $\mathbf{x} _{xp}$ by weighting the corresponding MVs on the basis of their quantile covariation with the linear combination of the response MVs $\mathbf{y} _{j}$.

2.3 Quantile path modeling for multi-block data

Figure 3 depicts a path model for multi-block data using the case of three blocks. The general model for K blocks follows the same logic. Let us assume that P variables are collected in a table $\mathbf{X}$ of data partitioned in K blocks: $\mathbf{X} = [\mathbf{X} _1,\mathbf{X} _2 \ldots , \mathbf{X} _K]$. Let $\mathbf{X} _k = \{x_{ip_k}\}$ be a generic block of MVs, where $i = 1, \ldots , n$, with n denoting the number of observations, $p_k = 1, \ldots , P_k$, with $P_k$ being the number of MVs in the kth block. We denote by $\varvec{\xi }_k = \{\xi _{ik}\}$ and $\mathbf{x} _{p_k} = \{x_{ip_k}\}$ the LV and a generic MV of the kth block, respectively.

A construct that never appears as a dependent variable in the model is called exogenous, while the endogenous constructs play only the role of dependent variables or of both dependent and explanatory variables. In Fig. 3, for example, $\varvec{\xi }_1$ is an exogenous construct and $\varvec{\xi }_2$ and $\varvec{\xi }_3$ are endogenous constructs.

Fig. 3

A path model with three blocks of MVs

As for the case of two blocks of MVs, the general model consists of the inner model and the outer model. For each quantile $\theta \in (0,1)$, in the outer model it is assumed that each MV $\mathbf{x} _{p_k}$ is related to its own construct through the following equations:

$$\begin{aligned} {x}_{ip_k}&= \alpha _{p_k}\left( \theta \right) + \lambda _{p_k}\left( \theta \right) {\xi }_{ik}+ {\epsilon }_{ip_k}\left( \theta \right) , \end{aligned}$$

(10)

where $\alpha _{p_k}$ is the location parameter, $\varvec{\xi }_k=\{\xi _{ik}\}$ is the construct representing the kth block of MVs, $\lambda _{p_k}$ is the loading coefficient, capturing the effect of $\varvec{\xi }_k$ on $\mathbf{x} _{p_k}$ and ${\epsilon _k}=\{\epsilon _{ip_k}\}$ is the error term vector, using the usual above mentioned assumption on the errors.

The inner model captures and specifies the dependence relationships among constructs. A generic endogenous construct, $\varvec{\xi }_{k'}$, is linked to the related explanatory constructs, ${\varvec{\xi }}_{k}$, $k\in {J_{k'}}$, where $J_{k'}=\lbrace k: \varvec{\xi }_{k'} \text { is predicted by } \varvec{\xi }_{k} \rbrace$, by:

$$\begin{aligned} {\xi }_{ik'}\left( \theta \right) =\beta _{k'0}\left( \theta \right) +\sum _{k\in {J_{k'}}}\beta _{k'k}\left( \theta \right) {\xi }_{ik} +{\zeta }_{ik'}\left( \theta \right) , \end{aligned}$$

(11)

where $\beta _{k'k}$ is the path coefficient capturing the effects of $\varvec{\xi _k}$ on the dependent construct $\varvec{\xi _k'}$, and $\varvec{\zeta _k'}=\{\zeta _{ik'}\}$ is the inner error variable vector, with the usual assumption on the errors.

A description of the general QC-PM algorithm is provided in Algorithm 3.

The weight vector $\varvec{{w}}\left( \theta \right) =\{{w}_{p_k}\left( \theta \right) \}$, $(p_k=1,\ldots ,P_k; k=1,\ldots ,K)$, used to define the composites, is computed by an iterative algorithm that proceeds over two phases, so-called inner and outer approximation phases, iteratively repeated until convergence of the outer vectors ${\varvec{w} (\theta )}$ is achieved (i.e., the change of the outer weights from one iteration to the next is smaller than a predefined tolerance).

In the inner phase, composites are approximated as weighted aggregates of the adjacent composites: two composites are adjacent if there exists a link in the inner model connecting the corresponding constructs, that is, an arrow going from one construct to the other in the path diagram, independently of the direction. The inner weights are defined as the values of the quantile correlation between the composites obtained at the previous step. According to the PLS-PM terminology, this mode to compute inner weights is called factorial inner scheme. Another scheme can be also applied, called centroid scheme, where the inner weights are computed as the signs of the quantile correlation between the composites (Tenenhaus et al. 2005). These two schemes generally provides very close results, but factorial scheme is more advisable when correlation between composites is close to zero. In this case, correlation may oscillate from small negative to small positive values during the iteration cycles, and factorial scheme is more advisable because it takes into account the strength of the correlation, instead of just the sign. It is worth to note that unlike Pearson correlation, quantile correlation is not a symmetric measure (Li et al. 2014), hence it is necessary to specify the role played by the involved constructs in each equation (i.e., explanatory or dependent one) for the calculation of the inner weights.

In the outer estimation phase, composites are approximated through a normalized weighted aggregate of the corresponding MVs. Outer weights are computed through simple quantile regressions, where each MV is regressed on the corresponding inner approximation composite. Then, the weights are normalized so that var$[\mathbf{X} _k\mathbf{w} _k\left( \theta \right) ]=1$. According to the PLS-PM terminology (Tenenhaus et al. 2005), this mode to compute outer weights is called Mode A. The so-called Mode B is also feasible in QC-PM, computing the outer weights as regression coefficients in the quantile multiple regression of the inner approximation composite on its own MVs. Basically, Mode B takes account of collinearity among MVs of the some blocks, while Mode A ignores this collinearity.

In the QC-PM iterative procedure, at each sth iteration $(s=0,1,2,\ldots )$, the following partial criterion are then optimized:

$$\begin{aligned} \hat{\mathbf{w }}_{p_k}\left( \theta \right) =\mathop {\mathrm{argmin}}\limits _{{w}_{p_k}(\theta )} \sum _{i=1}^n \rho _{\theta } \left( x_{ip_k}-{\alpha }_p\left( \theta \right) - \xi _{ik}^{(s-1)} {w_{p_k}}\left( \theta \right) \right) \end{aligned}$$

(12)

where $\rho _{\theta } \left( .\right)$ is the check function defined as above.

When Mode B is applied, the following criterion is instead minimized:

$$\begin{aligned} \hat{\mathbf{w }}^{(s)}_k\left( \theta \right) =\mathop {\mathrm{argmin}}\limits _\mathbf{w _k(\theta )} \sum _{i=1}^n \rho _{\theta } \left( \xi _{ik}^{(s-1)} (\theta ) -{\alpha }_p\left( \theta \right) - \mathbf{X} _{ik}{} \mathbf{w} _k\left( \theta \right) \right) \end{aligned}$$

(13)

When convergence is achieved, loadings and path coefficients are estimated through QR.

As a matter of fact, QC-PM provides, for each quantile of interest, a set of outer weights, loadings and path coefficients, offering a more complete picture of the relationships among variables both in the outer model and in the inner model.

The algorithm provides quantile-based composites, and it is useful to deal with heterogeneity both in the structural model and in the measurement model. In such a case the interest is in evaluating how weights and composites vary across quantile. However, if the interest is in comparing estimated models over quantiles, the measurement invariance (Henseler et al. 2016) has to be fulfilled. If weights, and consequently composites, change over quantiles, a proper comparison among path coefficients estimated at different quantiles is indeed not reliable, because the same concept may not be measured across quantiles. To this end, a test on the weights defined as a variant of the Wald test described in Koenker and Basset (1982) can be exploited. The null hypothesis of the test states that the weights are identical. In case of significant differences among weights, or in case there is the requirement to keep the weights fixed, a new variant of QC-PM can be implemented simply setting the quantile to the median in the iterative procedure. The use of the median in the iterative procedure (step 2) of the algorithm is in line with the approach proposed in Wang et al. (2016) for factor-based SEM. In such an approach the quantile varies only in step 3, to obtain quantile-dependent path coefficients. The median approach can be generalized to the whole iterative process to provide measurement invariance.

3 Model assessment and validation

Once the algorithm converges and estimates for loadings and path coefficients are obtained, there are many tools for assessing both the inner and outer model. Results, namely loadings and path coefficients, can also be validated from an inferential point of view (Davino et al. 2016).

Goodness of fit measures most commonly used in PLS-PM cannot be directly adapted to QC-PM. Moving from OLS to QR requires indeed amendment. The introduction of an effective goodness of fit approach in QR is still an open issue in the scientific literature (Koenker and Machado 1999; He and Zhu 2003). This does make it odd to directly compare OLS and QR, even considering that the two methods optimize different criteria. Therefore, a direct comparison between PLS-PM and QC-PM is not possible.

Starting with the inner model, the coefficient of determination $R^2$ of the endogenous constructs (Esposito Vinzi et al. 2010) is the criterion mostly used in PLS-PM. Considering that QR loss function is not based on a least squares criterion but rather on a least absolute deviation criterion in terms of weighted residuals, the use of $R^2$ in QC-PM goes against the underlying rationale of the method. This issue is particularly relevant since most of the assessment indexes in PLS-PM are based on the multiple linear determination coefficient or squared Pearson correlation coefficient. It is against this background we employ the pseudo-$R^2$ proposed by Koenker and Machado (1999), so to have a measure that simulates the role and interpretation of the $R^2$ for QC-PM assessment. It is important, however, to bear in mind that the pseudo–$R^2$ is designed differently.

QC-PM estimates a set of parameters for each conditional quantile $\theta$ of interest and, consequently, it requires a set of assessment measures for each estimated model. In particular, for each $\theta$, the pseudo–$R^2$ compares the residual absolute sum of weighted differences using the selected model (RASW) with the total absolute sum of weighted differences using a model with the only intercept (TASW). RASW corresponds to the residual sum of squares in classical regression, TASW to the total sum of squares of the dependent variable. pseudo–$R^2$ aims to evaluate if the full model (i.e. the model with the regressors) is better in terms of residuals the “restricted” (the model with the only intercept). More precisely, the pseudo–$R^2$ is calculated as one minus the ratio between RASW and TASW. In essence, pseudo-$R^2$ can be considered as a local measure of goodness of fit for a particular quantile as it measures the contribute of the selected regressors to the explanation of the dependent variable with respect to the trivial model without regressors. With an $R^2$, pseudo–$R^2$ values range between 0 and 1: the more it is close to 1, the more the model with regressors can be considered a good model (i.e., the $\theta$th conditional quantile function is significantly altered by the effect of the covariates). If on one hand the pseudo–$R^2$ will always be smaller than the $R^2$ and a direct comparison with $R^2$ in PLS-PM is not feasible, on the other hand pseudo–$R^2$ is useful to the end of identifying locations in the distribution of outcome variable where model may show a better/worse fit (for example, if the model fits in the tail, there’s not guarantee that it fits well anywhere else) (Kováč and Želinský 2013).

For the sake of generality, we consider below the case of multi-block QC-PM. Once convergence is reached and composites are obtained, several QRs are carried out in the inner part of the model, according to the number of considered quantiles. Such QRs estimate the path coefficients linking endogenous and exogenous constructs. As stated in Sect. 2.3, a generic endogenous construct, $\varvec{\xi }_{k'}$, is linked to the related explanatory constructs, ${\varvec{\xi }}_{k}$, $k\in {J_{k'}}$, where $J_{k'}=\lbrace k: \varvec{\xi }_{k'} \text { is predicted by } \varvec{\xi }_{k} \rbrace$. For the convenience of the reader, we report again Eq. (11) that describes this relationship:

$$\begin{aligned} {\xi }_{ik'}\left( \theta \right) =\beta _{k'0}\left( \theta \right) +\sum _{k\in {J_{k'}}}\beta _{k'k}\left( \theta \right) {\xi }_{ik}\left( \theta \right) +{\zeta }_{ik'}\left( \theta \right) . \end{aligned}$$

(14)

Since $\varvec{\hat{\zeta }}_{k'}(\theta )$ represents the residuals of the model explaining the $k'$th endogenous construct, for each considered quantile $\theta$, RASW is the corresponding minimizer:

$$\begin{aligned} RASW_{k'}\left( \theta \right) =\sum _{\hat{\zeta }_{k'}(\theta )\ge 0}\theta \left| \hat{\zeta }_{k'}(\theta )\right| + \sum _{\hat{\zeta }_{k'}(\theta )< 0} (1-\theta ) \left| \hat{\zeta }_{k'}(\theta )\right| , \end{aligned}$$

(15)

where positive and negative residuals are asymmetrically weighted, respectively with weights equal to $\theta$ and $(1-\theta )$. The TASW is instead:

$$\begin{aligned} TASW_{k'}\left( \theta \right) =\sum _{\xi _{k'}\ge \theta } \theta \left| \xi _{k'}-{\theta }\right| +\sum _{\xi _{k'}< \theta } (1-\theta ) \left| \xi _{k'}-{\theta }\right| . \end{aligned}$$

(16)

Therefore, the obtained pseudo–$R^2$ can be computed as follows:

$$\begin{aligned} pseudo {-}R_{k'}^2\left( \theta \right) =1-\frac{RASW_{k'}\left( \theta \right) }{TASW_{k'}\left( \theta \right) }. \end{aligned}$$

(17)

The pseudo—$R^2$ ranges between 0 and 1, since $RASW\left( \theta \right)$ is always less than or equal $TASW\left( \theta \right)$. It indicates, for each considered quantile, whether the presence of the covariates influences the correspondent conditional quantile of the response variable. It is worth noticing that the pseudo-$R^2$ is not a symmetric measure, assuming a different value when the role of the variables is reversed. The index, computed for each inner equation, measures the amount of variability of a given endogenous construct explained by its explanatory constructs. The average of all the pseudo—$R^2$ indexes provides a synthesis of the evaluations regarding the inner model.

As regards to the outer model, the assessment is carried out considering the relations between each construct and its own MVs and the estimate of the error term vector ${\hat{\epsilon }_k}$. The pseudo—$R^2$ can be used to assess convergent validity for each outer model, applying for each block the average of the pseudo—$R^2$ indexes of the related MVs, and can be used for assessing the quality of the whole outer models computing a weighted average of all measures over all the blocks, using the number of MVs for each block as weights. In particular, a $pseudo {-}R^2_{pk}(\theta )$ is computed on the basis of Eq. (10) considering the kth block, for each MV and for each considered quantile $\theta$. This measure, called $Communality_{pk}(\theta )$, with $p=1, \ldots , P$, $k=1, \ldots , K$, indicates how much of the MV’ variance can be explained by the corresponding component. The communality of the block k results:

$$\begin{aligned} Communality_{k}(\theta )=\frac{1}{P_k}\sum _{pk=1}^{P_k} pseudo- R^2_{pk}\left( \theta \right) . \end{aligned}$$

(18)

The quality of the whole outer model is finally obtained through the average of the Communality indexes of all the blocks.

It should be noted that, as described in Sect. 2.3, if the quantile in the iterative procedure is set equal to the median to solve the measurement invariance issue, the assessment of the outer model is limited to the quantile $\theta =0.5$.

Another measure of assessment is provided by the Redundancy index, which is defined only for the endogenous block. Please note that low levels of redundancy does not necessarily mean that the structural model is poorly specified. This index only combines the evaluations of both the inner model and the outer model (Lohmöller 1989; Hair et al. 2011), thus can be used as a measure of assessment of the global model, but specific measures for the two sub-models are also needed.

Redundancy can be computed for each endogenous MV or for the whole block, as an average of the redundancies of its MVs. For each MV of the endogenous block $\mathbf{x} _{pk'}$, Redundancy is computed multiplying its Communality measure by the pseudo—$R^2$ obtained in the corresponding inner model:

$$\begin{aligned} Redundancy_{pk'}(\theta )=Communality_{pk'}(\theta ) \times pseudo- R_{k'}^2(\theta ) \end{aligned}$$

(19)

The overall Redundancy of the block $k'$ is obtained averaging the measures associated to the MVs of the endogenous block:

$$\begin{aligned} Redundancy_{k'}(\theta )=\sum _{p_{k'}=1}^{P_{k'}} \frac{Redundancy_{pk'}(\theta )}{P_{k'}}. \end{aligned}$$

(20)

Possible variants could exploit different goodness of fit measures available in the quantile framework as well as the amendment of some assessment indexes proposed in PLS-PM literature (Benitez et al. 2020; Hair et al. 2020, 2017, 2019; Amato et al. 2004).

Two main approaches can be used to evaluate the statistical significance of the coefficients related to the different quantiles. The first approach exploits the asymptotic normal distribution of QR estimators (Koenker and Basset 1978). Such estimators are indeed asymptotically normal, with variance–covariance matrix depending on the model assumptions. Independent and identically distributed errors, independent and not identically distributed errors, and dependent errors determine obvious differences in the variance–covariance matrix. The alternative resorts to bootstrap theory (Efron and Tibshirani 1993), commonly used both in PLS-PM and QR. Bootstrap permits to estimate the standard errors of the coefficients using a distribution free approach. QR literature counts several bootstrap procedures, the xy-pair method (Parzen et al. 1994) being the simplest and widespread solution. It is also known as design matrix bootstrap. Bootstrap standard errors are exploited to compute confidence intervals and to perform hypothesis tests. Resampling methods are also useful in case of small samples. For example, a jackknife approach could be used to estimate the standard errors of the coefficients. Statistical tests could be also easily introduced in QC-PM to test if coefficients at different quantiles can be considered statistically different (Gould 1997). We will not expand on the details here. Readers who are interested can consults Davino et al. (2013) and Furno and Vistocco (2018) for a thorough explanation and all bibliographic indications on inference in QR.

4 A simulation study

A Monte Carlo simulation study has been designed to investigate the performance of QC-PM considering different scenarios. As already stated above, QC-PM and PLS-PM are complementary rather than alternative approaches. Therefore, it is advisable to use both methods in real data application: in many cases, indeed, the focus on conditional mean is not sufficient and a more comprehensive look at the entire conditional distribution is necessary.

Nevertheless, since there is not a real competing method to QC-PM, namely a composite-based approach focusing on conditional quantile, we chose to investigate properties of the QC-PM estimators comparing them with PLS-PM results. It is well known that PLS-PM produces consistent estimates for composite-based model parameters and performs well in the considered scenarios.

4.1 Simulation design and data generation

We operate in the context proposed by Schlittgen et al. (2020), generating data from composite-based populations using the cbsem R package (Schlittgen 2019). Determination of the covariance matrix in the procedure proposed by Schlittgen et al. (2020) can be derived considering three scenarios, named formative–formative (ff), formative–reflective (fr) and reflective–reflective (rr). We used the scenario rr, where outer weights are not required. The procedure requires path coefficients, loadings and variances and covariances of exogenous constructs. The parameters must be chosen such that sets of weights can be found to fulfill the equation defining the covariance matrix (see the Vignette from the cbsem R package for further details) (Schlittgen 2019).

We set the relationships in the model assuming the theoretical path model represented in Fig. 3 and then we simulated data for the given values of the parameters. The postulated inner model is:

$$\begin{aligned} {\xi }_{2}= & {} \beta _{20} + \beta _{21}{\xi }_{1}+{\zeta }_{2} \\ {\xi }_{3}= & {} \beta _{30} + \beta _{31}{\xi }_{1} + \beta _{32}{\xi }_{2} + {\zeta }_{3}. \end{aligned}$$

The outer model can be instead written as:

$$\begin{aligned} {x}_{11}&= \alpha _{11} + \lambda _{11}{\xi }_1 + {\epsilon }_{11} \\ {x}_{21}&= \alpha _{21} + \lambda _{21}{\xi }_1 + {\epsilon }_{21} \\ {x}_{31}&= \alpha _{31} + \lambda _{31}{\xi }_1 + {\epsilon }_{31} \\ {x}_{12}&= \alpha _{12} + \lambda _{12}{\xi }_2 + {\epsilon }_{12} \\ {x}_{22}&= \alpha _{22} + \lambda _{22}{\xi }_2 + {\epsilon }_{22} \\ {x}_{32}&= \alpha _{32} + \lambda _{32}{\xi }_2 + {\epsilon }_{32} \\ {x}_{13}&= \alpha _{13} + \lambda _{13}{\xi }_3 + {\epsilon }_{13} \\ {x}_{23}&= \alpha _{23} + \lambda _{23}{\xi }_3 + {\epsilon }_{23} \\ {x}_{33}&= \alpha _{33} + \lambda _{33}{\xi }_3 + {\epsilon }_{33}. \end{aligned}$$

The simulation study considered different scenarios both in the outer and in the inner part of the model. Moreover, the effect of sample size and non-normality distributions were also considered. The cases of homogeneous blocks (no differences among loadings) and heterogeneous blocks (large differences among loadings) were used to assess the outer model. For the inner model, the effect of different correlation levels between constructs was investigated.

That, in short, are the design-factors we considered for the simulation study: sample size, homogeneity of blocks, size effect and variable distributions. In particular, we used the following levels for each design-factor.

• Sample sizes. We set n $\in \{50, 100, 200, 300, 400, 500, 1000\}$. The value n=50 allows us to investigate the performance of the method in case of application with small sample size. The other values used for n are instead typically encountered in research applications, the largest values being useful to study the asymptotic properties of QC-PM estimators.

• Loadings. We set $\lambda _{p_k}=0.9\,\,(p = 1, 2, 3; k = 1,2,3)$ for homogeneous blocks and loadings $\lambda _{1_k}=0.9,\lambda _{2_k}=0.6, \lambda _{3_k}=0.3\,\,(k=1,2,3)$ for heterogeneous blocks, these last values to reflect very large differences among loadings.

• Path coefficients. We set, for all inner relationships, $\beta _{k'k} \in \{0.2, 0.3, 0.4, 0.5\}$ to take into account different levels of correlations among constructs.

• Skewness and Kurtosis. We set both equal to 0 for normal distribution, while skewness $=$ 2 and kurtosis $=$ 6 were used for mimicking exponential distributions.

The total number of scenarios obtained from the combination of the above described levels of the design-factors is equal to 112 (7 sample sizes $\times$ 2 loadings $\times$ 4 path coefficients $\times$ 2 skewness and kurtosis). For each considered scenario, we generated 500 replications.

A synthesis schema of the simulation design is offered in Table 1.

Table 1 Levels of the design-factors considered in the simulation design

The R software environment (R Core Team 2020) for statistical computing were used to generate and analyze data.

Data with non-normal distribution were generated using the technique described in Vale and Maurelli (1983), who extended the method proposed by Fleishman (1978).

The performance of QC-PM was assessed considering the Relative Bias (RBias) and the Root Mean Square Error (RMSE) of the estimates on the basis of the 500 replications. RBias was computed as:

$$\begin{aligned} { RBias} = \frac{1}{S}\sum _{s=1}^S\frac{(\hat{\theta }_{s}-\theta )}{\theta } \qquad s=1,2,\ldots ,500 \end{aligned}$$

where S represents the number of replications in the simulation, $\hat{\theta _s}$ is the estimate for the generic replication, and $\theta$ is the corresponding population parameter. Instead, RMSE was computed as:

$$\begin{aligned} \sqrt{\frac{1}{S}\sum _{s=1}^S(\hat{\theta _s}-\theta )^2} \qquad s=1,2,\ldots ,500 \end{aligned}$$

Clearly, because $MSE=Var(\hat{\theta })+bias(\hat{\theta })^2$, RMSE entails information on both bias and variability of the estimates.

4.2 Simulation results

In presenting simulation results, we choose to focus on the effect of sample size on the bias and efficiency, and, consequently, on the consistency of the estimates. Since the number of considered scenarios (112) is too large, in the following we focus only on the more interesting and enlightening scenarios. In particular, we present results for all the considered levels of loadings in the three blocks of variables for PLS-PM and for QC-PM at quantile $\theta =0.5$ (measurement model was indeed restricted to the median regression model).

Additionally, since there are interesting differences between homogeneous blocks and heterogeneous blocks, we reported results for both the cases.

For the inner model, we present results for all the three path coefficient estimates obtained through PLS-PM and QC-PM at quantiles $\theta \in \{0.25, 0.5, 0.75\}$, but only for $\beta _{k'k}=0.3$, a small/moderate effect. Indeed, as known in literature (Tenenhaus 2008), results are similar as correlations between composites increases.

The following subsections details results according to the three considered factors, that is sample size, level of heterogeneity within blocks and degree of skewness/kurtosis of the distribution. The resulting scenarios are organized in three groups:

• Group 1, focusing at the effect of sample size,

• Group 2, focusing at the effect of the level of heterogeneity within blocks,

• Group 3, focusing at the effect of the degree of skewness/kurtosis of the distribution.

4.2.1 The effect of sample size

The first set of considered scenarios (from hereinafter Group 1) allows us to focus only on the effect of sample size, neutralising, as far as possible the effect of the other factors: outer blocks are considered homogeneous with high correlations among the MVs (all $\lambda$ values set equal to 0.9), data generated from normal distributions and path coefficients set equal to 0.3. These settings result in seven scenarios for Group 1.

Fig. 4

Diminutive distribution charts of the loadings of scenarios belonging to Group 1 with $n \in \{50, 100, 200, 300, 400, 500, 1000\}$, homogeneous blocks, path coefficients equal to 0.3 and Normal distributed data

Figure 4 shows the distribution of loadings for such scenarios for the outcome block (Block 3). The results for the other two blocks are not shown since they do not differ much from those of Block 3. The two columns of Fig. 4 depict the results for PLS-PM and QC-PM (recall that we set $\theta$=0.5 for the outer model). The seven scenarios of the group, corresponding to the different values of the sample size n, are represented on the horizontal axis. Finally, the rows refer to the coefficients $\lambda _{13}$, $\lambda _{23}$, $\lambda _{33}$ associated with the MVs of the block.

Table 2 Values of RBias and RMSE for loadings of the scenarios belonging to Group 1 with $n \in \left\{ 50, 100, 200, 300, 400, 500, 1000\right\}$, homogeneous blocks, path coefficients equal to 0.3 and Normal distributed data (levels of the varying factor, sample size, are in the first column)

Data are represented through diminutive distribution charts (Rudis 2019), a variant of boxplots aimed to visualize distribution characteristics: each box ranges from the 10th percentile to the 90th percentile, the triangle indicates the mean value of the distribution and the circle the median. Both PLS-PM and QC-PM show distributions that converge to the true parameter value (horizontal line at the value 0.9) as n increases. Moreover, the variability of the estimates is rather small, although for QC-PM slightly higher. Regarding bias, it is interesting to note, that for the quantile model, the 10th percentile has a smaller distance from the true parameter than the PLS-PM, whatever the value of n.

Fig. 5

Diminutive distribution charts of the path coefficients of scenarios belonging to Group 1 with $n \in \left\{ 50, 100, 200, 300, 400, 500, 1000\right\}$, homogeneous blocks, path coefficients equal to 0.3 and Normal distributed data

Table 3 Values of RBias and RMSE for the path coefficients of scenarios belonging to Group 1 with $n \in \left\{ 50, 100, 200, 300, 400, 500, 1000\right\} ]$, homogeneous blocks, path coefficients equal to 0.3 and Normal distributed data (the levels of the varying factor, the sample size, are in the first column)

Table 2 reports the values of RBias and RMSE for each loading distribution. In particular, the table shows the average values of RBias and RMSE for each block (columns) and each scenario (rows). The table is row-partitioned according to the model. The values of RBias and RMSE for the loading estimates do not change substantially between QC-PM and PLS-PM when blocks are homogeneous and variables are normally distributed, with large sample sizes (at least 300 observations). At the lowest considered sample size ($n=50$), QC-PM always shows higher bias compared to PLS-PM and such behavior is also confirmed combining bias with variability of the estimates (see RMSE columns).

The distribution of the path coefficients (Fig. 5) is also affected by sample size and shows less marked differences between the two methods (the comparison between Figs. 4 and 5 must be done with caution because the two figures have different vertical scales). As in Fig. 4, each diminutive distribution chart refers to a scenario (horizontal axis) but here the three rows refer to the path coefficient ($\beta _{21}$, $\beta _{31}$, $\beta _{32}$). Each vertical block refers to a model: PLS-PM and QC-PM for $\theta \in \left\{ 0.25, 0.5, 0.75\right\}$. It is interesting, in the case of the path coefficients, the correspondence of the mean and median values of the estimates with the true value of the parameter (horizontal line at 0.3).

Table 3 shows, for each horizontal block, the results obtained from the corresponding model in terms of RBias and RMSE values for the path coefficient estimates, in the seven scenarios. PLS-PM and QC-PM perform very similar both in terms of bias and efficiency. In general, as sample size increases, RMSE decreases for all path coefficient estimates. The RMSE is slightly higher in QC-PM at quantile $\theta =0.25$ and $\theta =0.75$.

4.2.2 The effect of the level of heterogeneity

The convergence of estimates as n increases is also confirmed in the case of heterogeneous blocks. Figure 6 shows the diminutive distribution charts of the loadings of the scenarios belonging to the second group of scenarios, Group 2, still encompassing normal distributions and with path coefficients equal to 0.3 but with MVs differently correlated to each construct (0.9, 0.6 and 0.3).

In this group of scenarios, unlike Group 1, the distribution of loadings gets closer to the true population parameter especially for $\lambda _{13}$. However, the heterogeneity of the blocks has a distortive effect on the estimates of the path coefficients (Fig. 7) both in case of PLS-PM and QC-PM. Tables 4 and 5 confirm decreasing bias and variability as n increases. In this case but both RBias and RMSE are always higher than the homogeneous case.

4.2.3 The effect of the degree of skewness/kurtosis

Fig. 6

Diminutive distribution charts of the loadings of scenarios belonging to Group 2 with $n \in \left\{ 50, 100, 200, 300, 400, 500, 1000\right\}$, heterogeneous blocks, path coefficients equal to 0.3 and Normal distributed data

Fig. 7

Diminutive distribution charts of the path coefficients of scenarios belonging to Group 2 with $n \in \left\{ 50, 100, 200, 300, 400, 500, 1000\right\}$, heterogeneous blocks, path coefficients equal to 0.3 and Normal distributed data

Table 4 Values for the RBias and RMSE for the loadings (averages for each block) of the scenarios belonging to Group 2 with $n \in \left\{ 50, 100, 200, 300, 400, 500, 1000\right\}$, heterogeneous blocks, path coefficients equal to 0.3 and Normal distributed data (the levels of the varying factor, the sample size, are in the first column)

Table 5 Path coefficients RBias and RMSE values of scenarios belonging to Group 2 with $n = [50, 100, 200, 300, 400, 500, 1000]$, heterogeneous blocks, path coefficients equal to 0.3 and Normal distributed data (the levels of the varying factor, the sample size, are in the first column)

The third group of scenarios, Group 3, worth to be mentioned aims to show the effect of an asymmetric distribution in the data generation process. Also this group includes seven scenarios (varying the sample size), with homogeneous loadings (equal to 0.9) and path coefficients equal to 0.3. Data are here generated by an Exponential distribution. Convergence is confirmed for this group as well, but there are differences between the PLS-PM and QC-PM. As regards loadings (Fig. 8), the distributions are always more variable in QC-PM than in PLS-PM. Nevertheless QC-PM always manages to capture the true parameter value within the 90% of central values. Considering the average values of RBias and RMSE in all blocks (Table 6), better performance of QC-PM in terms of efficiency and unbiasedness is confirmed especially for larger sample sizes. Looking at the distribution of path coefficient estimates (Fig. 9), we note the ability of QC-PM to capture the positive skewness of the distribution used to generate the data: the variability of the estimates is smaller for $\theta$ = 0.25 and larger in the right tail ($\theta$ = 0.75) and the parameter is overestimated at the lowest quantile and underestimated at the highest quantile. For $\theta$ = 0.5 both methods provide unbiased estimates. The RBias values in Table 7 confirm the reduction in the bias as n increases. More complex is the interpretation of the RMSE values, which combine bias and variability: the estimates at quantile 0.25, for example, are more biased but less variable than those at quantile 0.5, so the RMSE is affected by a kind of trade-off between variability and bias.

Fig. 8

Diminutive distribution charts of the loadings of scenarios belonging to Group 3 with $n \in \{50, 100, 200, 300, 400, 500, 1000\}$, homogeneous blocks, path coefficients equal to 0.3 and exponential distributed data

Fig. 9

Diminutive distribution charts of the path coefficients of Group 3 of scenarios belonging to Group 3 with $n \in \{50, 100, 200, 300, 400, 500, 1000\}$, homogeneous blocks, path coefficients equal to 0.3 and exponential distributed data

Table 6 Values of RBias and RMSE for the loading (averages for each block) of the scenarios belonging to Group 3 with $n \in \{50, 100, 200, 300, 400, 500, 1000\}$, homogeneous blocks, path coefficients equal to 0.3 and Exponential distributed data (the levels of the varying factor, the sample size, are in the first column)

Table 7 Values of RBias and RMSE for the Path coefficients of the scenarios belonging to Group 3 with $n \in \{50, 100, 200, 300, 400, 500, 1000\}$, homogeneous blocks, path coefficients equal to 0.3 and Exponential distributed data (the levels of the varying factor, the sample size, are in the first column)

5 An application on Chronic Kidney Disease in diabetic patients

QC-PM potentialities are described through an artificial dataset which simulates a study on CKD in diabetic patients. The original study was proposed by Wang et al. (2016) who used real data to examine the potential risk factors of CKD through a quantile approach to factor-based SEM. In particual, data were generated mimicking the model and estimates obtained by Wang et al. (2016), since the original data were not available. Even if we use artificial data, the involved variables and their relations are in line with the study by Wang et al., allowing a clear practical interpretation of results. Both studies are quantile based, even if Wang et al. exploited factor-based SEM while we focus on composite-based path modeling.

The main objective of this section is to show QC-PM in action, stressing its complementarity with the traditional methods for composite-based path modeling (PLS-PM), which focus only on conditional means. The advantage of using artificial data allows us to obtain a scenario where relationships among variables change with quantiles (i.e., there are different relations considering the different parts of the dependent variable distributions). Our main objective was not recovering parameters, but evaluate if QC-PM is able to detect this heterogeneity in the variable relationships.

5.1 Data description

This application aims to study the effect of some risk factors on CKD. We started from the original path model in Wang et al. (2016) and removed the non significant predictors. In particular, the study investigates Type 2 diabetic patients who might have experienced CKD. Data consist of 300 patients. Diagnosis and staging of CKD were based on urinary albumin-creatinine ratio (ACR) and estimated glomerular filtration rate (eGFR). These two variables are the MVs of the outcome block named Kidney disease. The considered risk factors were Blood pressure and Lipid. The former was measured by systolic blood pressure (SBP) and diastolic blood pressure (DBP), while the latter by total cholesterol (TC), high-density lipoprotein (HDL), and triglycerides (TG). Therefore, the inner model underpinning our design and subsequent analyses consists of two exogenous constructs, Blood pressure ($\xi _1$) and Lipid ($\xi _2$), and one endogenous construct, Kidney disease ($\xi _3$). Figure 10 depicts the corresponding path diagram.

Fig. 10

Theoretical model for Chronic Kidney Disease data, following Wang et al. (2016)

Data generation process exploits the classical covariance-based approach for SEM. As above mentioned, the results of the original study by Wang et al. (2016) represent the starting point for the generation of artificial data. Therefore, the parameters of the SEM are set to the values of the model estimated in that study. In particular, Blood pressure was positively correlated with the severity of Kidney disease, and the correlation was stronger for higher quantiles. Lipid was found to be positively correlated with Kidney disease and, also for this variable, the correlation was stronger for higher quantiles. The resulting variance–covariance matrix characterizes the multivariate distribution used to generate data. The generation process was carried out using the software EQS 6.1 (Bentler 2006), computation and analysis using R (R Core Team 2020).

Heterogeneity in the inner model was introduced in the artificial data assuming that the exogenous constructs exert a different effect on the different parts of the endogenous construct distribution. It results that the path coefficients differ across quantiles. In order to generate data with these features, we supposed that two different populations exist, and for each population the model parameters are different. In particular we divided the patients in two groups. The first group was represented by patients with low severity of kidney disease, and thus the relationship between kidney disease and each of the two exogenous constructs is weaker (Fig. 11a). The second group was represented by patients with high severity of kidney disease: in such a case, the relationship between kidney disease and each exogenous constructs is stronger (Fig. 11b). In order to focus only on heterogeneity in the inner model, as in Wang et al. (2016), the loadings between constructs and the corresponding MVs were set all equal to 1 for both the populations.

Fig. 11

Theoretical models for the simulated data: patients with low (a) and high (b) severity of kidney disease

The simulation procedure was articulated in the following three steps:

• 1. data were generated from a multivariate normal population, ${\varvec{X}}\sim {N}({\varvec{0}},\varvec{\Sigma }$), where $\varvec{\Sigma }$ is the population covariance matrix using the values in Fig. 11a for the parameters of the model. The sample size was set equal to 300. For each of the two MVs of Kidney disease block (ACR and eGFR), we removed the observations higher than the quantile 0.6 of the same MV. In other words, once the observations were sorted in non decreasing order with respect to the values on each MV, we kept the first 60% of observations, i.e. the first 180 observations. Then, the MVs of the endogenous block were transformed in order to have realistic values ranging from 1 to 6 for ACR, and from 50 to 90 for eGFR;

• 2. data were generated from a multivariate normal population, ${\varvec{X}}\sim {N}({\varvec{0}},\varvec{\Sigma }$), where $\varvec{\Sigma }$ is the population covariance matrix using the values in Fig. 11b for the parameters of the model. The sample size was set again equal to 300. For each of the two MVs of the Kidney disease block, we kept the 40% of central observations around the MV mean (100 units), namely 20% on the left-neighborhood of the mean and the other 20% on its right-neighborhood. The two resultings MVs were transformed so to have values ranging from 6 to 10 for ACR, and from 90 to 120 for eGFR;

• 3. the two data sets generated at the previous steps were stacked obtaining an unique data set with sample size 300. Note that the MVs of the exogenous blocks in the two models come from the same population, while obviously the same does not hold for the MVs of the endogenous block.

According to such data generation process, we expect that QC-PM provides estimates for the parameters of model (a) for quantiles smaller than 0.6, and estimates for the parameters of model (b) for quantiles larger than 0.6.

Table 8 Check for block unidimensionality and internal consistency

5.2 Results

This section describes a complete application of QC-PM, from the preliminary analysis to the evaluation of the goodness of fit. The aim is to illustrate the potential of the method along with the guidelines for the interpretation of the results.

An initial inspection of unidimensionality and internal consistency of blocks was performed. To check unidimensionality, we carried out a principal component analysis for each block of MVs. If a block is unidimensional, the first eigenvalue is expected to be the only one greater than 1 and much higher than the second one.

The internal consistency of each block of MVs was instead evaluated through the Cronbach’s $\alpha$. Such index assumes equal population covariances among the indicators of one block, and such assumption is likely not met in empirical research. However, this index can be used as a lower bound for reliability (Benitez et al. 2020). We also consider Dijkstra–Henseler’s $\rho$ (Dijkstra and Henseler 2015) to evaluate composite reliability. Table 8 shows that all the blocks are unidimensional and internally consistent. The method used to obtain the artificial data in Sect. 5 provides equal loadings and therefore the values of Dijkstra–Henseler’s $\rho$ (DH.rho) are all equal to 0.99.

Fig. 12

Path coefficient estimates (y-axis) across quantiles (x-axis) linking Blood pressure (a) and Lipid (b) to Kidney disease. The horizontal solid lines represent the PLS-PM estimates and the vertical dotted line drawn at quantile 0.6 refer to the threshold used in the data generation process

Table 9 Path coefficients and corresponding standard error from a classical PLS-PM (first row) and from a QC-PM applied on the inner model for a selected set of quantiles ($\theta \in \{0.25, 0.50, 0.75\}$)

Model parameters were estimated through PLS-PM and QC-PM by setting the quantile in the iterative procedure to the median and considering a dense grid of quantiles in the inner model. The two panels in Fig. 12 show the different QC-PM path coefficient estimates across quantiles and the PLS-PM path coefficient estimates: Fig. 12a depicts the path coefficient connecting Blood pressure to Kidney disease, while Fig. 12b refers to Lipid. In particular, quantiles are represented on the horizontal axis and coefficients on the vertical axis. The horizontal solid lines represent the PLS-PM estimates while the broken lines represent the QC-PM estimates over quantiles. The vertical dotted line drawn at quantile 0.6 in each figure refers to the threshold used in the data generation process (we expect that for quantiles smaller than 0.6, QC-PM produces estimates for the parameters specified in the model shown in the Fig. 11a, while for quantiles larger than 0.6, QC-PM produces estimates for the parameters specified in the model shown in the Fig. 11b). Figure 12 shows the ability of the QC-PM to detect the structure underlying the simulated data (Fig. 11). QC-PM was indeed able to distinguish the different effects in the different parts of the Kidney disease distribution: both path coefficients increase with quantiles and results are consistent with the true values specified in the population models shown in Fig. 11. Table 9 reports the path coefficient estimates (± standard errors) obtained using PLS-PM (first row) and QC-PM for the quantiles $\theta \in \{0.25, 0.50, 0.75\}$. Standard errors of estimates were obtained using bootstrap. All path coefficients were statistically significant. On the whole, except for coefficients at $\theta$=0.75, PLS-PM estimates are slightly more efficient than QC-PM ones. This is in line with theory: just like mean is more efficient than median, OLS regression estimates are usually more efficient than QR estimates. Both Blood pressure and Lipid have a positive impact on Kidney disease, which increases for patients with higher levels of CKD. This positive and increasing effect is well-known in literature: hypertension, high presence of cholesterol, lipoprotein and triglycerides are all considered leading causes of CKD (Bakris and Ritz 2009).

Table 10 Communalities for PLS-PM and QC-PM ($\theta$ = 0.50)

The assessment of the models is carried out using the measures introduced in Sect. 3. It is worth to recall again that a direct comparison of the measures of fit of the two methods is not appropriate, since the two methods optimize different criteria. Hence, the objective is neither to compare PLS-PM and QC-PM results nor to identify the best model. Instead, we aim to illustrate how to use the measures define above for the assessment of QC-PM results.

With respect to the inner model, PLS-PM produces an $R^2$ equal to 0.214, while QC-PM provides $pseudo\!-\!R^2$ values increasing from lower to higher quantiles (0.051, 0.123, 0.185), for the quantiles $\theta \in \{0.25, 0.50, 0.75\}$. This result was expected and coherent with the data structure, as relationships among constructs increase with quantiles. The assessment of the outer model is carried out in two steps. Table 10 shows, for each block, the communality values related to each MV and to the whole block (in bold) both for PLS-PM and QC-PM. For the latter, obviously, estimates refer only to the median because, as specified in Sect. 2.3, quantiles are allowed to vary only in the inner model. Overall, the communality of blocks is satisfactory. From the average communality of each block (last row in each block—values in bold), each construct explains much of the variability of its own MVs. Considering the individual communality of each MV, we did not find much differences, coherently with the way data were generated (i.e., all loadings are equal). The global communalities are satisfactory showing a good fit of the outer model.

Finally, Redundancy values are reported in Table 11, PLS-PM on the first column and QC-PM on the subsequent columns. Results reveal a low ability of predictor constructs to explain the variability of the outcome MVs for low quantiles, while redundancies achieved almost moderate levels for high quantiles and for PLS-PM (Latan and Ramli 2013; Latan and Ghozali 2015).

Table 11 Redundancy measures for PLS-PM and QC-PM applied on a selected set of quantiles ($\theta \in \{0.25, 0.50, 0.75\}$)

6 Conclusions and insights for future works

The original proposal of QC-PM was presented for the first time at the 8th International Symposium on PLS and Related Methods (PLS’14) which took place in 2014 in Paris (www.pls14.org). The method was proposed with the aim to extend classical least squares methods for conditional mean to the estimation of conditional quantile functions in the context of composite-based path modeling. QC-PM complements the well-known and consolidated PLS-PM by exploring heterogeneous effects of explanatory constructs over the entire conditional distributions of the response constructs.

The present paper has formalized QC-PM and the iterative procedure for parameter estimation, starting from the simplest case of one block of MVs and moving until the general path model for multi-block data. In addition, a methodological variation in the estimation phase of the outer model is also proposed. The applicative potentialities of QC-PM, along with guidelines for the interpretation of results, were provided through the analysis of an artificial data set on CKD in diabetic patients. The example highlights how QC-PM can complement traditional methods for composite-based path modeling in presence of heterogeneity in the relationships among variables. The properties of the method across different scenarios were investigated through a simulation study. The simulation design took into account the factors that typically affect the results of composite-based path modeling methods: sample size, strength of the relationship within the blocks (homogeneous vs heterogeneous blocks), different levels of correlations between constructs and shape of distributions in the outcome blocks. Data were generated from composite-based populations. The comparison among the different scenarios was carried out in terms of RBias and RMSE of estimates obtained from 500 replications for each scenario. Several similarities between QC-PM and PLS-PM emerged comparing the performance of the two methods in all generated scenarios. Nevertheless, some differences were identified. However, it is worth to recall that the spirit of the simulation study is to show the properties of QC-PM rather than to provide a comparison with PLS-PM. In fact, QC-PM and PLS-PM are not alternative but complementary methods.

Simulations point out similar results for QC-PM and PLS-PM, both in terms of bias and RMSE. This confirms our insight to consider QC-PM as a supplementary method to PLS-PM, with similar features but able to assess relationships between variables in different parts of the distribution. However, it is noted that variability of the QC-PM estimates is always greater even though the bias is smaller (the true population parameter is always within the 90% range of the central values for large samples). Even if the convergence of estimates is confirmed as the sample size increases in the case of heterogeneous blocks, both RBias and RMSE are always higher than the homogeneous case. The new element that emerges in the case of an asymmetric distribution is the ability of QC-PM to capture the positive skewness of the distribution used to generate the data. The variability of the path coefficient estimates is smaller for $\theta$ = 0.25 and larger in the right tail ($\theta$ = 0.75) and the parameter is overestimated at the lowest quantile and underestimated at the highest quantile.

From a methodological point of view, a promising extension of QC-PM will accommodate the case of observed or unobserved heterogeneity among observations. In the PLS-PM literature several contributions allows to treat both kind of heterogeneity (Sarstedt et al. 2016, 2011b; Lamberti et al. 2016; Sarstedt et al. 2011a; Esposito Vinzi et al. 2008). In the QR literature, Davino and Vistocco (2018) proposed an innovative approach to identify group effects through a quantile regression model. Future studies will be devoted to combine these approaches into QC-PM. Moreover, since a recent work by Davino et al. (2020) exploited the ability of QC-PM for in-sample prediction, future research will further evaluate the proposed approach from an out-of-sample prediction perspective.

A further development, albeit a minor one, will consider the implementation of another way of calculating outer weights based on a measure of quantile correlation. Several contributions in the literature extends the first proposal of quantile correlation (Li et al. 2014) introducing different alternatives to measure the linear correlation between any two random variables for a given quantile (Tang et al. 2021; Xu et al. 2020). The introduction of a descriptive measure such as quantile correlation into the process of calculating outer weights would have an interesting computational advantage over traditional modes requiring the estimation of regression models.

Appendix

Quantile Regression was proposed by Koenker and Basset (1978) as a complementary and robust approach to classical regression analysis. In their seminal paper, the authors remind that “in statistical parlance the term robustness has come to connote a certain resilience of statistical procedures to deviations from the assumptions of hypothetical models” and that the need for robust statistics alternative to least squares estimation dates back to the nineteenth century.

Just one year earlier, Mosteller and Tukey (1977) sensed the need to identify more robust regression methods by stating that “What the regression curve does is give a grand summary for the averages of the distributions corresponding to the set of X’s. We could go further and compute several different regression curves corresponding to the various percentage points of the distributions and thus get a more complete picture of the set. Ordinarily this is not done, and so regression often gives a rather incomplete picture. Just as the mean gives an incomplete picture of a single distribution, so the regression curve gives a correspondingly incomplete picture for a set of distributions”.

Quantile Regression (QR) was introduced precisely for the purpose of going beyond the study of average effects in a regression model and to provide a description of the whole conditional distribution of a response variable in terms of a set of regressors. QR can be exploited in case of location, scale and shape shifts on the dependent variable but also when a monotone transformation of the response and/or the explanatory variables is advisable.

In order to show QR in action, we introduce an example dealing with a sample of $n = 10{,}000$ observations generated from the following model:

$$\begin{aligned}&\mathbf{y} = 1 + 2\mathbf{x} + (1 + \mathbf{x} )\mathbf{e} \\&\mathbf{x} \sim N(10; 1) \\&\mathbf{e} \sim N\left( (-1+20x);e^{x/3}\right) . \end{aligned}$$

The scatterplot in Fig. 13 (left-hand side) shows the typical fan-like shape, sign that the amount of variability over the expected value of the dependent variable for a given value of the explanatory variable x is not the same at every level of x, but varies systematically with the level of x.

Estimating a least-squares regression model (solid line in Fig. 13) would not fully capture the relationship between the two variables. In such a case, it is more interesting to explore the effect of the regressor at different parts of the distribution of the dependent variable.

Fig. 13

Left-hand side: Scatterplot with simulated data, ordinary least square regression line (solid line) and quantile lines (dashed lines). Right-hand side: representation of QR slopes, dashed horizontal line corresponding to OLS slope

A QR model for a given conditional quantile and for the ith observation can be formulated as follows:

$$\begin{aligned}&y_i = \mathbf{x} _i{\beta }(\theta )+\epsilon _i(\theta ) \\&Q_\theta (\hat{{\mathbf {y}} }| {\mathbf {X}}) = {\mathbf {X}} \hat{{\beta }}(\theta ) \end{aligned}$$

where X is the regressor matrix and $\mathbf{x} _i$ a row of this matrix, y the vector containing the dependent variable, $0< \theta < 1$ is a generic quantile, $Q_\theta (. | . )$ denotes the conditional quantile function for the $\theta$th quantile and $\epsilon$ is the error term such that $Q_\theta (\epsilon (\theta )| {\mathbf {X}}) = 0$.

QR offers a complete view of a response variable providing a method for modelling the rates of changes at multiple points (conditional quantiles) of its distribution (Koenker 2005; Davino et al. 2013) without requiring assumptions on the errors. Although different functional forms can be used, we will deal here only with simple linear regression models.

For each quantile, a regression line is estimated and, as a consequence, the estimated values of the response variable conditioned to given values of the regressors, provides the conditional quantiles of the dependent variable.

Going back to the example with simulated data, five QR lines have been estimated considering the following set of $\theta$ values: 0.1, 0.25, 0.5, 0.75, 0.9. The dashed lines in Fig. 13 (left-hand side) are obtained by estimating the effect of x on the selectd conditional quantiles of y. They confirm the positive impact of the regressor but showing that this contribution increases as we move on the distribution of the y variable.

In Fig. 13 (right-hand side), the slopes of the estimated quantile lines are graphically represented. The horizontal axis displays the different quantiles while the effect of the regressor is represented on the vertical axis. The dashed line parallel to the horizontal axis corresponds to the ordinary least squares coefficient. This graphical representation allows to visually catch the different effect of the regressor on the y variable.

The parameter estimates in QR linear models have the same interpretation as those of any other linear model. The intercept measures the value of the dependent variable setting to zero all the regressors. Each slope coefficient $\hat{\beta }_i (\theta ) = \frac{\partial {Q_{\theta }(\mathbf {y | {\mathbf {X}}})}}{\partial {{\mathbf {x}}_i}}$ can be interpreted as the rate of change of the $\theta$th conditional quantile of the dependent variable per unit change in the value of the ith regressor, holding constant the other regressors.

The conditional quantile estimator is obtained as a generalisation of the unconditional quantile estimator:

$$\begin{aligned} \hat{\beta }(\theta )= \mathop {\mathrm{argmin}}\limits _{\beta } E\left[ \rho _\theta (\mathbf{y} - {\mathbf {X}} \beta )\right] \end{aligned}$$

(21)

where $\rho _\theta (.)$ is an asymmetric absolute loss function which uses an unbalanced weighting system (weight equal to (1-$\theta$) for the sum of negative deviations and weight equal to $\theta$ for the sum of positive deviations).

The most widespread algorithm for finding QR estimates is the one proposed in Koenker and d’Orey (1987) as a variant of the Barrodale and Roberts (1974) simplex algorithm. Although it is theoretically possible to extract infinite quantiles, a finite number is numerically distinct in practice. This is known as quantile process. A fairly accurate approximation of the whole quantile process can be obtained using a dense grid of equally spaced quantiles in the unit interval (0, 1) (Davino et al. 2013).