1 Introduction

In recent years the growing availability of data of various types and often collected from different sources requires changes in the classical statistical methods. Ad hoc techniques must be tailored for managing data arranged in different types of structures. In complex domains it is very common that the observed variables are grouped into homogeneous blocks measuring partial aspects of the phenomenon under investigation. Such data is usually labelled as multi-block data and the statistical tecniques used for their analysis are called multi-block methods (Smilde et al. 2000). Important examples of multi-block data comes from several application fields (marketing, sociology, econometrics, sensory analysis, spectroscopy, ecology, image analysis, etc.). The basic requirement of multi-block methods is that all blocks have one dimension (mode) in common. The way in which the blocks are connected to each other gives rise to different data structure. Different sets of variables can be measured on the same units. Examples of this structure are several: many sets of indicators to describe different aspects of a complex concept, quality of life, for instance (Davino and Romano 2014); different components (i.e, teaching, research, internationalisation) to define a university ranking (Romano and Davino 2016); different dimensions that affect the quality of teaching in high schools (motivation, emotions, strategies, teaching) (Romano and Palumbo 2013). Another possible structure consists of a set of two-way matrices of the same units and variables (three-way data). Three-way data is widely used in sensory analysis when the scores of the judges are not averaged so that the three sources of variation are products, attributes and judges (Romano et al. 2008, 2015; Bro et al. 2008). This three-way data structure can also be related to a dependent data set (Romano et al. 2011). Finally, another possible structure comes out when blocks of different dimensions are connected through a common dimension. Examples in consumer studies concern the link of product attributes, liking scores and consumers’ characteristics (Martens et al. 2005; Romano et al. 2014; Davino et al. 2015).

Different types of approaches can be used for the analysis of these multi-block data structures, the choice being based on the type of relationship between the various blocks (Höskuldsson 2008; Cariou et al. 2018). An exploratory multi-block approach (Hanafi and Kiers 2006) has to be employed in case no specific causal relationship is assumed among the different blocks. A supervised approach (Westerhuis et al. 1998), is instead used whereas a structure of relationships is assumed between the blocks. Here, the blocks of predictor variables are generally called input blocks, while the block of dependent variables is named output block. If there is a chain of relationships among the blocks, the data follows the typical structure of the structural equations models (Jöreskog and Wold 1982; Bollen 2014).

The present paper deals with multi-block data where all blocks of variables are observed on the same units and both input blocks and a single output block are available. Therefore the approach is supervised since the aim is to explore the dependence structure between the input blocks and the output one. Consumer analysis is considered as a field of application, since data is generally collected into multi-block structures (Næs et al. 2011). Here, the output block generally corresponds to the liking scores given by a sample of consumers on a predefined set of products. The input blocks can concern both other sensory variables, defined drivers of liking (or specific liking), and other additional variables on consumers (demographic, habits, attitudes). The relationships between the input blocks and the output block can be investigated through different strategies, each corresponding to a different way of arranging the data into blocks (Næs et al. 2010). The simplest strategy is to transform each block into a single vector by stacking the corresponding columns and estimating a multiple linear regression model. This strategy does not take into account heterogeneity among consumers, which is a further source of complexity of data coming from consumer studies. To this end, some approaches propose to estimate separate regression models for each consumer to be aggregated a posteriori, by a simple arithmetic average or by clustering procedures, to highlight segments of homogeneous consumers with respect to the liking model (Menichelli et al. 2013; Asioli et al. 2016).

This paper proposes a multi-step procedure to deal with heterogeneity in multi-block data. It exploits Quantile Regression (QR) (Koenker and Basset 1978; Davino et al. 2013; Furno and Vistocco 2018) to evaluate the effect of the regressors on the entire distribution of the dependent variable. The idea is to complement the classical approach based on the least squares regression (LSR) to focus beyond the conditional mean. In the case of consumer data this complementary information can be crucial given the typical asymmetric distributions of liking scores. QR has already been used in consumer studies: for estimating the conditional quantiles of liking when segments of consumers obtained according to their acceptance pattern are related to additional consumer characteristics (Davino et al. 2015); for assessing heterogeneity across product similarities (Davino et al. 2018). The proposed strategy has significant implications so that the results can be used to adopt appropriate marketing strategies. In particular, the information obtained concerns the identification of consumer groups that have similar liking models, that is, for each group it is possible to identify the effect of each driver of liking on the overall liking. In addition to the different liking models, the detailed analysis of each group in terms of liking for the individual products also allows for useful information for the product development.

This paper extends a QR multi-step procedure used to assess heterogeneity (Davino and Vistocco 2018) to multi-block data. The main idea is to explore if and how the effects of the drivers on the overall liking differ for groups of consumers at the lower and higher levels of liking. The strategy consists of three main steps. The first step aims to identify the best model for each consumer, based on the quantile that best represents each consumer. In the second step, consumers segments are identified according to similarities in the dependence structure, using cluster analysis. In the final step, a different model is estimated for each group of consumers identified in the previous step (a group can also consist of a single consumer). The proposed procedure is tested on data from consumer study. The basic aim of the proposal is to learn knowledge from a complex data structure, where information gathered in several blocks is combined and analysed in the different steps. The use of QR allows to deal with heterogeneity, a typical source of variation in many fields of applications. Note that this is one of the main strengths of QR as compared to the classical LSR. Such an aspect is exploited in using QR once selecting different models for each consumer according to his/her position (quantile) in the dependent variable distribution. In addition, the QR is used in the final step of the procedure when identifying the representative quantiles of the groups obtained from the cluster procedure. The estimation of different QR models on predefined quantiles using all the observations of the samples allows statistical comparisons between the groups both with respect to the entire model and to individual coefficients.

The paper is structured as follows. In Sect. 2 the main notation is introduced and the quantile regression based strategy is described. Data used for testing the procedure are described in Sect. 3, while the corresponding results are included in Sect. 4. Finally, some concluding remarks and directions of future avenues of research are described in Sect. 5.

Fig. 1
figure 1

Description of different multi-block data-structures

Full size image

2 Methodology

2.1 Main notation

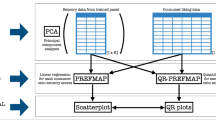
Let us consider a particular multi-block data arranged as three-way data table, where an array Z is partitioned in G blocks: \(\mathbf{Z} =\left[ \mathbf{Z} _1, \ldots , \mathbf{Z} _G\right] \). In this paper, each block \(\mathbf{Z} _g\) (\(g=1, \ldots , G\)) has dimensions \(N \times (P+1)\) because it is a column partitioned matrix composed by the vector (\(\mathbf{y} _g\)) for the response variable (a single element of the output block as defined in Sect. 1) and a data matrix (\(\mathbf{X} _g\)) for the regressors. The dimension G can represent any possible stratification variable, even time. In the empirical analysis provided in Sects. 3 and 4, the N rows represent a set of products, the P+1 variables are the liking attributes with the dependent variable (the overall liking), while G is the set of consumers. Figure 1 shows three different points of view to represent and analyse such a kind of multi-block data. For the rest of the paper we will refer to the structure represented in Fig. 1c, where the G blocks obtained from the stratification variable are stacked. However, the proposed approach will not consider a single model on all stacked blocks simultaneously. A multistep strategy is proposed in which the response variable and corresponding predictors are related to each other for each individual block.

The aim of the paper is to model and cluster the data simultaneously. That means analysing the relationship among the dependent variable and the set of regressors but highlighting possible similarities in the G levels of the stratification variable. It is a matter of fact that if two units show a very similar dependence structure, they can be considered belonging to the same group.

2.2 Quantile regression based strategy

The strategy proposed in this paper consists of three main steps. The first step consists of identifying the best model for each level g of the stratification variable, based on the quantile of the response variable that best represents each level. Subsequently, the G levels of the stratification variable are grouped according to similarities in the dependence structures. Finally, a different model is estimated for each group identified in the previous step.

The procedure has been introduced by Davino and Vistocco (2018) and applied in consumer science to handle products effects by Davino et al. (2018). In the present paper, the approach is adapted in the case of multi-block data with a large number of blocks. As discussed in Sect. 1, the aim of this paper is to consider an additional source of complexity in the data given by heterogeneity. Since this involves a great number of blocks, the strategy proposed in Davino and Vistocco (2018) is here combined with clustering techniques.

The main strength point of the procedure is represented by the exploitation of QR in the whole process of analysis. QR allows to estimate the whole distribution of the conditional quantiles of the response variable thus replacing the classical estimate of a single value (conditional mean) with estimates of several values (conditional quantiles). A typical QR model is formulated as:

$$\begin{aligned} Q_{\theta }(\hat{\mathbf{y }} \vert \mathbf{X} )=\mathbf{X} \hat{\beta }(\theta ), \end{aligned}$$
(1)

where \(Q_{\theta }(. \vert .)\) is the conditional quantile function for the \(\theta \)-th conditional quantile with \(0< \theta <1\). Each \(\hat{\beta }_{p}(\theta )\) coefficient represents the rate of change in the \(\theta \)-th conditional quantile of the dependent variable per unit change in the value of the p-th regressor \((p = 1, \ldots ,P)\), holding the others constant. Although it is theoretically possible to estimate an infinite number of quantiles, a finite number is numerically distinct, the so-called quantile process. Also for QR, several are the functional forms that can be considered. The paper will refer to linear regression models. The interested reader may refer to the reference literature for methodological details (Koenker and Basset 1978; Davino et al. 2013; Furno and Vistocco 2018).

The approach to model and cluster the G levels is structured in the three steps detailed below.

(1) Identification of the best model for each level

In the first step, a representative quantile \(\theta _g^{best}\) is identified for each level g. It will be named from now on as the best quantile. In particular, computing the empirical cumulative distribution function \(F(\cdot )\) on the overall \(\mathbf{y}\) variable, the best quantile representative of each block g will be obtained as:

$$\begin{aligned} \theta _g^{best} = \sum _{y \in \mathbf{y_g}} \frac{F(y)}{N}, \end{aligned}$$
(2)

where N denotes the number of units of the generic block g. By computing the empirical cumulative distribution function on \(\mathbf{y}\), we refer to the percentile rank of each observation, i.e. the location of each \(y_i\) (\(i = 1, \ldots , N \times G\)). For a discussion on the use of the percentile ranks and the choice of the proper location index to summarise them, see (Davino and Vistocco 2018).

(2) Identification of the group dependence structure

QR is then carried out on data arranged as in Fig. 1c (for each single block), using the representative quantiles, that is, the G quantiles \(\theta _g^{best}\) previously identified. Each model provides a set of coefficients, one for each level g and for each regressor: \(\hat{\beta }_{p}\left( \theta _g^{best}\right) \) (\(p=1, \ldots , P\)). Such coefficients can be arranged into a matrix \(\hat{\mathbf{B }}\left( \theta ^{best}\right) _{[G \times (P+1)]}\) where the additional column refers to the intercept.

The aim of the second step is to identify if there are similar dependence structures among the G levels. For this purpose, a hierarchical cluster analysis (CA) is performed on the \(\hat{\mathbf{B }}\left( \theta ^{best}\right) \) matrix and a partition of G in K groups is identified (\(k=1, \ldots , K\)). Each group will be then characterised by a different quantile deriving from an average of the \(\theta ^{best}\) associated to the units assigned to the group (\(\bar{\theta }^{best}\)).

(3) Estimation of the group dependence structure

In the final step, QR is carried out again on data arranged as in Fig. 1c using the representative quantiles, that is, the K quantiles assigned to the K groups in the previous step. Each of the K estimated models provides a set of coefficients, one for each regressor; differences among the coefficients highlight differences in the group dependence structure. It is worth of noticing that coefficients can be compared because all of them are estimated on the whole sample (\(N \times G\)). A testing procedure is implemented to evaluate the significance of the differences among the coefficients related to each cluster, exploiting the classical inferential tools available in the QR framework. Two models estimated at two different quantiles can be compared using a joint tests on all slope parameters or separate tests on each of the slope parameter. The hypothesis of interest is that the slope coefficients of two models are identical and the test statistic is a variant of the Wald test described in Koenker and Bassett (1982).

Let us consider the case of the comparison among the coefficients related to the p–th regressor and estimated at two different quantiles, \(\theta ^{best}_k\) and \(\theta ^{best}_{k^{'}}\). The null is \(H_0: \beta _p(\theta ^{best}_k)=\beta _p(\theta ^{best}_{k^{'}})\), and the test statistic is:

$$\begin{aligned} T=\frac{\left[ \hat{\beta }_p(\theta ^{best}_k)-\hat{\beta }_p(\theta ^{best}_{k^{'}})\right] ^2}{\hat{var}\left[ \hat{\beta }_p(\theta ^{best}_k)-\hat{\beta }_p(\theta ^{best}_{k^{'}})\right] }, \end{aligned}$$
(3)

where \(p=1, \ldots , P\) and \(k,k^{'}\in [1, K]\). Under the null hypothesis, the test statistic has an approximate \(\chi ^2\) distribution with one degree of freedom.

Such a test statistic can be exploited for coefficients pairwise comparisons. An extension of it is used as global test on all the slopes. The standard errors, used to evaluate the statistical significance of the coefficients, can be estimated using resampling methods (Parzen et al. 1994).

3 Data description

The empirical analysis is based on data from a consumer testing on 11 tortilla chips, in which 73 consumers expressed their overall liking for each product on a 9-point hedonic scale (from \(1 =\) dislike extremely to \(9 =\) like extremely) (Meullenet et al. 2008). Furthermore, consumers themselves have provided a judgment on some drivers (appearance, flavor, texture) using the same 9-point hedonic scale. Considering the notation introduced in Sect. 2, the structure of the tortilla dataset is made by \(N=11\) products, \(P+1=4\) liking variables and \(G=73\) consumers (levels).

Figure 2 shows the distribution of the overall liking scores on the whole sample of consumers (marginal) and for each single product. All products show a left skewed distribution, even if some of them present a higher variability and a less pronounced skewness (MIS, OAK, MED, GUY, GMG).

Fig. 2
figure 2

Distributions for the overall liking: marginal (top) and product specific (from bottom to second to last)

Full size image

A multivariate analysis of consumers’ liking is carried out using a principal component analysis (PCA) on the output block (\(products \times consumers\)) (data arranged as in Fig. 1b). Results demonstrate that consumers show preferences for different products. In Fig. 3 consumer vectors are mainly concentrated in the positive verse of the first dimension, even if there are a few consumers also lying along the second dimension. Individual differences among consumers for the likings of specific products can be further understood from Fig. 4, which represents the products arranged on all four quadrants. Specifically, the most liked products are SAN, TOB and TOR, along the main PCA dimension, followed by MIS, MIT and TOM on the second dimension.

Fig. 3
figure 3

Loading plot by principal component analysis on the overall liking

Full size image
Fig. 4
figure 4

Score plot by principal component analysis on the overall liking

Full size image

4 Results

Heterogeneity among consumers described through the PCA in Sect. 3 can be further investigated linking the overall liking of the consumers to their specific likings (appearance, flavor, texture) by following the QR based strategy described in Sect. 2.2.

In the first step, a representative quantile is identified for each consumer through the average rank percentile of the overall liking she/he has expressed on the considered set of products. The histogram in Fig. 5 shows the distribution of the rank percentiles on the sample of consumers. It is worth noting that there exist a variability on the \(\theta ^{best}\) and thus an heterogeneity in the liking.

Fig. 5
figure 5

Histogram of the rank percentiles

Full size image

QR is then carried out on data arranged as in Fig. 1c using the representative quantiles, that is, the G quantiles \(\theta _g^{best}\) assigned to the each consumer. Each model provides a set of coefficients, one for each driver, that can be arranged in a matrix consumers \(\times \) coefficients. The information gathered into such a matrix is crucial for highlighting the individual differences/similarities among consumers in the way they weight the drivers linked to the overall linking. To this end, the second step consists of identifying consumers’ segments by a CA on the different dependence structures estimated by the QR on the G quantiles \(\theta _g^{best}\).

On the tortilla dataset, the elbow rule identifies as best partition the one with \(k=3\) groups of consumers, homogenous with respect to the liking models. Table 1 describes each cluster through the following information: size, minimum, maximum and average of the \(\theta _g^{best}\) of the consumers assigned to the cluster. The last four columns of the table describe the average values of the original variables. Note that for the rest of the paper the \(\bar{\theta }^{best}\) will be considered as the quantile representative of each group. Results show that each cluster is characterised by a different position in the ranking of the overall liking. Specifically, the first cluster corresponds to the consumers’ segment with lower \(\theta ^{best}\), i.e. to consumers scoring products lower than the others. The last two clusters, which are the most interesting because of their size, behave in the opposite way. Note that the third cluster show a wider range of the \(\theta ^{best}\) as highlighted by the minimum and maximum vales in the Table 1. This emphasises a higher degree of heterogeneity in this cluster as compared to the others. Another relevant information from Table 1 comes from the analysis of the average values both on liking and drivers. On one hand, the first cluster has a very small size, with a low degree of liking that can hardly be modified. On the other hand, clusters 2 and 3 show higher overall liking values than can be further improved by acting on the specific likings, in particular on the flavor that reveals the lowest averages inside each cluster.

Table 1 Description of clusters exploiting summaries of \(\theta ^{best}\) and original variables (average)
Full size table

In the final step, QR is carried out again on data arranged as in Fig. 1c using the representative quantiles assigned to each cluster (\(\bar{\theta }^{best}\)). Coefficients in Table 2 are all significant for \(\alpha \le 0.05\) but intercept and texture coefficient in group 2, which are significant for \(\alpha \le 0.10\). Moreover the intercept in group 3 is not significant at all.

Combining the information in Tables 1 and 2 it is possible to argue that flavor is the most interesting driver to improve the overall liking of the less satisfied consumers (cluster 1 and 2). If on one hand, flavor has the highest QR coefficients, on the other hand consumers score this driver lower than the others, with averages close to the threshold of sufficiency in a scale ranging for 1 to 9.

Table 2 QR coefficients for the three representative quantiles of the three clusters
Full size table

Results in Table 3 complements the characterisation of the groups by testing their difference in terms of both the whole model (joint test) and the specific coefficients. The classical Bonferroni correction (Shaffer 1995) has been applied. The p-values included in the table show that the three models for the three clusters are significantly different. Focusing on differences among cluster 2 and 3, the p-values emphasise that even if the size of the flavor and the texture coefficients in the two clusters is quite similar, they can be considered different from an inferential perspective.

Table 3 p-values derived from pairwise comparisons on the whole model and on single coefficient
Full size table

Starting from the results of the testing procedure showing that flavor and texture are the most discriminating predictors for clusters 2 and 3, a deepen analysis of differences among products in each cluster would be useful in a product development perspective. At this aim Fig. 6 visualizes the averages of the variables (each single panel) in the three clusters (different colors and symbols), partitioned by products (labels on the left side). The most relevant information from the figure is that the differences between these two clusters are evident for the flavor and the texture, where it is possible to highlight, among the most liked products, those presenting the wider range between the averages in the two clusters. Specifically the liking of TOR, TOM and BYW that present lower averages in cluster 2 will be more affected by an improvement in the flavor. Such information in terms of the liking for products inside each cluster can be used to suggest appropriate decisions both for marketing and product development departments.

Fig. 6
figure 6

Description of the clusters according to the original variables partitioned by products

Full size image

5 Concluding remarks and further developmnents

The paper has shown how to treat an additional source of complexity given by heterogeneity in fields of applications where data follows multi-block structures. Focus has been on one specific data structure, within the supervised framework, where blocks of variables (a single output block and several input blocks) are observed on the same statistical units. A QR based strategy has been proposed as a multi-step procedure able to model and cluster units according to similar dependent structures. The proposal originates from alternative approaches that combine the estimation of separate dependent relations for each single units with a clustering on the model results. For instance in conjoint studies (Gustafsson et al. 2003), where a preference model for each consumer is estimated and then results from the estimated models are synthesised by simple averages or clustering procedures. The strategy proposed only in some aspects can be traced back to classic approaches. For example, the logic of obtaining different models for individual consumers and then synthesizing them is in common. The peculiarity of the proposal is already in the selection of the model, which is based on the selection of the quantile that best represents each consumer. This aspect makes the proposal complementary and not alternative to the classic approaches, which are limited to the study of the effects on average. Any comparison with classical methods would lead to the classical conclusions deriving from a comparison between QR and LSR: the two models provides similar results when the homoscedasticity assumption is satisfied. This means that the different blocks (consumers) present the same dependence structure linking the overall to the specific liking.

The innovative contribution of the proposed approach consists of the following aspects:

  • The use of QR in alternative to the classical LSR to model the whole distribution of the dependent variable.

  • The identification of different models for each unit obtained by defining the quantile that best represent the position of the unit in the distribution of the dependent variable.

  • The estimation of the model characterizing each cluster obtained on all the units and not only on the ones belonging to the cluster. This is a relevant aspect since the estimation of the models using all units allows comparisons among the clusters both for the whole models and for the specific coefficients.

  • The description of each cluster according to the corresponding specific quantile, which provides information on the location of the response conditional distribution mainly affected by the units of the cluster.

Further developments are in the direction of the selection of the best clustering partition (Bruzzese and Vistocco 2015; Tibshirani and Walther 2001) and on the assessment of results in terms of stability. The second aspect is even more relevant in application fields where the number of statistical units (products) is low, like in consumer analysis.