Abstract
We present a novel nonparametric Bayesian approach for performing cluster analysis in a context where observational units have data arising from multiple sources. Our approach uses a particle Gibbs sampler for inference in which cluster allocations are jointly updated using a conditional particle filter within a Gibbs sampler, improving the mixing of the MCMC chain. We develop several approaches to improving the computational performance of our algorithm. These methods can achieve greater than an order-of-magnitude improvement in performance at no cost to accuracy and can be applied more broadly to Bayesian inference for mixture models with a single dataset. We apply our algorithm to the discovery of risk cohorts amongst 243 patients presenting with kidney renal clear cell carcinoma, using samples from the Cancer Genome Atlas, for which there are gene expression, copy number variation, DNA methylation, protein expression and microRNA data. We identify 4 distinct consensus subtypes and show they are prognostic for survival rate (\(p < 0.0001\)).
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Cluster analysis can broadly be described as the task of inferring an underlying group structure in a dataset. Groups are defined such that observations within a cluster are more similar to one another than they are to observations in other clusters. Cluster analysis has proven a popular exploratory tool and found application areas in market segmentation, machine learning, data compression, and genomic analysis.
In analysing genomic data we may aim to infer risk cohorts among patients suffering particular diseases given their genetic make-up, or we may look to infer groups of genes to help gain an understanding of their function. However, these application areas pose issues not typically encountered in other contexts, owing in particular to the fact that each unit of observation (i.e. patients in the former example) may have data arising from multiple data sources, e.g. gene expression, DNA methylation, or copy number variations. These data sources each give complementary, but differing, views of the underlying processes and, thus, it is vital that analyses of such data can encompass these data sources in a single, integrative analysis.
Integrative clustering algorithms infer a cluster structure for a group of observational units for which data is available from multiple sources. While we wish to assign these observational units to clusters accounting for the different variation in each data source, it is not essential that the cluster structure is identical across datasets. What complicates this task is that the data sources need not be of a shared type, for example, we may need to integrate continuous data with discrete data, and so we cannot simply concatenate the various sources of data into a single data matrix. Many approaches to integrative cluster analysis exist: performing cluster analysis at the level of underlying latent variables (see, e.g., Shen et al. 2009; Gabasova et al. 2017; McParland et al. 2014, 2017, ); or ensemble methods which average over independent clustering solutions for multiple datasets (see, e.g., Monti et al. 2003; Lock and Dunson 2013, ). Across these and other similar methods, the terms ‘correlated clustering’, ‘consensus clustering’ or ‘multi-view clustering’ may be used in place of ‘integrative clustering’. In this paper, we propose a novel integrative clustering algorithm built within the framework of multiple dataset integration (MDI) (Kirk et al. 2012), a flexible model-based integrative clustering algorithm which facilitates the sharing of information between datasets.
The remainder of this paper is structured as follows: Sect. 2 introduces MDI; Sect. 3 introduces ParticleMDI, our development upon MDI which updates cluster allocations using a conditional particle filter; Sects. 3.1 and 3.2 present several techniques for improving the computational performance of ParticleMDI which are applicable more generally in the single dataset context; Sect. 4 outlines example applications of the method to synthetic and real datasets, demonstrating an ability to infer clinically meaningful subgroups; Sect. 5 concludes.
2 Multiple dataset integration
MDI (Kirk et al. 2012) is a framework for the integrative cluster analysis of multiple data sets of potentially different data types. It generalises the standard mixture model to the context of multiple datasets, allowing for the cluster structure in pairs of datasets to inform one another. The extent to which information is shared between datasets is inferred by the model, allowing different levels of information to be shared for different pairs of datasets depending on their structural similarity. These cross-dataset comparisons are made at the level of the inferred cluster allocations, affording MDI the flexibility to model different data types naturally. Savage et al. (2013) demonstrate how MDI can uncover clinically meaningful groups in genomic datasets.
We begin by describing the generating model of an integrative mixture model in which no information is shared across datasets in Eq. 1 (Kirk et al. 2012). We assume that K datasets are observed on the same n observational units. Dataset k has \(p_k\) features which are collected in the \((n\times p_k)\)-dimensional data matrix \(X_k\) with \((i, j)-th\) entry \(x_{i, j, k}\). The ordering of observations is consistent across datasets, such that row i of \(X_k\) and \(X_l\) correspond to the same observational unit—if we aim to infer clusters of people these quantities refer to different measurements made on the same person. Throughout this paper, we will use the notation \(x_{a:b}\) to represent the sequence \(x_{a}, x_{a+1}, \dots , x_{b-1}, x_{b}\). The model is
A latent cluster allocation variable \(c_{i, k} \in {1, 2, \dots , N}\) relates an observation \(x_{i, k}\) to one of the N components in the mixture model. Each component is characterised by a particular probabilistic model, F, with cluster-specific parameter \(\theta _{c_{i, k}, k}\) with conjugate prior \(G^0_k\). The cluster labels, \(c_{i, k}\), have associated weights \(\pi _{1:N, K}\), which Kirk et al. (2012) assign a prior of a finite approximation to the Dirichlet process (Ishwaran and Zarepour 2002) which defines a Dirichlet-multinomial allocation mixture model (Green and Richardson 2001). The algorithm does not require a specification of the number of clusters a priori, but rather a maximum number of possible clusters, N, to be fit to the data. This is often referred to as an overfitted mixture model, as the number of clusters specified by the model is likely greater than the true number. Rousseau and Mengersen (2011) demonstrate that the posterior distribution of such models tends to concentrate on a sparse representation in which any superfluous clusters are not occupied by any data points. While the value of N is shared across all datasets, the number of clusters inferred (the number of occupied components) in each need not be the same. Although in practice N may be specified as large as the number of observations, the choice will often be dictated by the computational time and resources available; Kirk et al. (2012) propose using one-half of the number of observations as a compromise.
Note that Eq. 1 models the cluster structure of each of the datasets independently. To facilitate the sharing of information across datasets, Kirk et al. (2012) introduce a \({K \atopwithdelims ()2}\)-dimensional concordance parameter, \(\varPhi \), reflecting the level of dependence in cluster structure between pairs of datasets, as shown in Fig. 1. The joint distribution of \(c_{i, 1}, c_{i, 2}, \dots , c_{i, K}\) in Eq. 1 is replaced by the following choice
Each element of \(\varPhi \) reflects the pairwise agreement in the cluster structure across datasets at the level of the cluster labels, with \(\phi _{k, l}\) indicating the strength of the relationship between the cluster structures in datasets k and l. To capture the dependence across datasets, the \(\varPhi \) values are used to upweight the likelihood of an observation belonging to the same cluster in two or more datasets. For example, if \(\phi _{1,2}\) is large, MDI will more strongly favour placing observations in datasets 1 and 2 in the same cluster. Different \(\varPhi \) values allow different levels of partial agreements between datasets without requiring strict agreement, for example if \(\phi _{k, l} = 0\), then the cluster allocations in datasets k and l would not affect one another.
A graphical model representation of MDI and ParticleMDI in a three dataset case \((K = 3)\). \(x_{i, k}\) denotes observation i in dataset k arising from cluster \(c_{i, k}\) with parameters \(\theta _{c_{i, k}, k}\), which are given a prior \(G_k^{(0)}\). Clusters in dataset k have prior allocation weights, \(\pi _k\) which themselves are given a \(Dirichlet(\alpha /N)\) prior. The \(\varPhi _{i, j}\) value allows the allocations in data sets i and j to inform one another.[Figure recreated from (Kirk et al. 2012)]
Algorithm 1 shows the approach of Kirk et al. (2012) to inference in the MDI model, a Gibbs sampling approach alternating between updating the cluster allocations and updating the hyperparameters. Cluster allocations are updated in a similar way as in the standard k-means approach: following an initial allocation of observations to clusters, observations are iteratively shifted between clusters, conditional on all other cluster allocations remaining fixed. Specifically, given a current allocation of observations to clusters, MDI iterates through each observation, calculates the marginal likelihood of moving it to each cluster, and probabilistically assigns it a cluster label based on these marginal likelihoods. Such one-at-a-time approaches to updating cluster labels can potentially inhibit the mixing of the Gibbs sampling chain, meaning subsequent samples from the algorithm can be highly correlated. Thus, the algorithm may be slow to explore the sample space and struggle to move away from local optima once discovered, as it can be difficult to propose a better assignment of observations to clusters if it is not similar to the current proposal. Such highly autocorrelated MCMC chains may be unrepresentative of the posterior distribution in the short run as they over-represent the local area of exploration in the chain. In the long-run these problems can be mitigated via the generation of more samples and subsequent thinning. However, this comes at the additional computational cost of having to generate these samples and, depending on the extent that mixing is inhibited, these additional samples may be prohibitively expensive to generate.

3 ParticleMDI
In this paper we present ParticleMDI, an algorithm built within the framework of MDI which maintains MDI’s strengths in modelling flexibility but changes the inference approach from Gibbs sampling to particle Gibbs sampling (Andrieu et al. 2010) by updating cluster labels using a conditional particle filter which allows us to update groups of cluster allocations jointly.
Particle filters or sequential Monte Carlo (SMC) are typically used for inference in state space models where we wish to learn about a latent variable, \(x_n\), given an observation, \(y_n\), at time i. The approaches aim to approximate sequentially the sequence of densities \(p(x_{1:n}|y_{1:n})\) for \(n \ge 1\) as well as the sequence of marginal likelihoods
for \(n\ge 1\). They do so by breaking the problem down into sampling from a sequence of intermediate densities \(p(x_{1:i}|y_{1:i})\) for \(i = 1, \dots , n\). At each i, the method works by first generating M ‘particles’ from a proposal distribution using the approximation for \(i-1\). The particles are random samples representing different potential realisations of the latent variable, \(x_{1:n}\). Each of the particles is reweighted according to an importance weight \({\xi ^{(m)}}\) for \(m = 1, \dots , M\) which depends on the proposed value of \(x_i\) and the observed value of \(y_i\). The notation of a superscripted index in parentheses refers to the particular particle in question. After the reweighting step, some particles will have negligible weights and so a resampling step replaces the weighted sample of particles with an unweighted set by removing particles with low weights and replacing with those with relatively high weights. Various resampling techniques exist (see Hol et al. 2006), of which we implement systematic resampling as it has been found to offer significantly improved mixing over other methods and decrease the level of path degeneracy (Chopin and Singh 2015; Griffin 2014). This allows for exploitation of the information gained by these higher weight particles by concentrating computational resources on them. It is typically not advised to resample at every step of the particle filter, and so resampling is often only performed when the effective sample size (ESS)—measured by the variance of the particle weights—falls below a certain threshold (Liu and Chen 1995). This is often chosen as half of the number of particles (Doucet and Johansen 2009). In the context of inference in mixture models, Griffin (2014); Bouchard-Côté et al. (2017) find that adaptive resampling leads to greater performance than resampling at every step.
The task of cluster analysis, however, is not typically one viewed as evolving over time and so would not appear suitable for sequential methods. Nevertheless, particle filter methods have been successfully applied to the task (see, e.g., Chopin 2002; Fearnhead 2004; Griffin 2014; Bouchard-Côté et al. 2017, ). The approach involves treating the observation index, 1 : n, as an artificial time index. As in the standard mixture model approaches, a latent variable, \(c_{i}\), is introduced reflecting the cluster label assigned to observation \(x_{i}\). The problem then can be stated as performing inference for \(p(c_{1:n}|x_{1:n})\) for \(n \ge 1\), via the intermediate densities \(p(c_{1:i}|x_{1:i})\) for \(i = 1, \dots , n\). Fearnhead (2004) demonstrates that the incremental particle weight associated with assigning observation \(x_i\) to cluster a can be calculated as
where f(.) is the posterior predictive density for observation \(x_i\) given the observations in \(x_{1:(i-1)}\) for which \(c_{1:(i - 1)}^{(m)} = a\). This approach facilitates the modelling of data of different types, provided we can analytically derive the posterior predictive distribution.
The SMC method for mixture models can be extended to the integrative MDI model by treating each particle as a realisation of the cluster allocations across all K datasets. That is, we wish to infer \(p(c_{1:n, 1:K}|X_1, \dots , X_K)\) with observations assigned to clusters conditional only on the allocations within that dataset. We update Eq. 3 for the integrative context as follows
We infer the \(\varPhi \) values and cluster labels via a particle Gibbs sampler (Andrieu et al. 2010), a particle MCMC extension of the Gibbs sampler in which a particle \(c_{1:n, 1:K}^{(1)}\) is used to update the hyperparameters and subsequently used as an input to the following pass of the particle filter. The conditional distributions for the hyperparameters are described in Kirk et al. (2012), although we derive an alternative conditional distribution for \(\varPhi \) in the supplementary material. The particle is sampled from an initial pass of the particle filter, and its survival of the resampling step is ensured throughout the following sweep of the conditional particle filter. As this particle was inferred using the entire sequence of observations, it helps guide the remaining particles towards a good region of the sample space. We outline this conditional particle filter in Algorithm 2.
The specification of the algorithm is flexible because it allows for the modelling of any statistical distribution for which we can analytically derive a posterior predictive distribution. Throughout this paper, we model continuous-valued data as arising from a Gaussian distribution, with a normal-gamma prior (see Murphy 2007) and we model discrete-valued data as draws from a categorical distribution with a Dirichlet prior (see Bernardo and Smith 2001). Other data types could also be included using conjugate pairs such as the Poisson and gamma distributions. For computational speed, we treat the features as independent, however dependent features can also be incorporated. Treating the features as independent also allows us to incorporate the feature selection approach specified in (Savage et al. 2013). In this instance, the probability of a specific feature being selected relates to the Bayes factor, the ratio of the marginal likelihood of the data in that feature under the inferred cluster model compared with a null model in which all observations belong to a shared cluster.
The particle Gibbs approach to MDI, however, is more computationally intensive. While a trade-off can be made between the computation time of an algorithm and its mixing time—the number of iterations required to approach the posterior distribution—the algorithm does not strike the right balance between the two. Throughout the remainder of this section, we explore some techniques for improving the computational efficiency of the algorithm.

3.1 Block-updating Gibbs sampler
Consider the propagation step in the particle Gibbs sampler described in Algorithm 2. For each observation, \(x_{i,1:p_k, k}\), a cluster label, a, is sampled proportional to the posterior predictive distribution \(f(x_{i,1:p_k, k}|c_{1:i, k}, x_{1:(i-1), 1:p_k, k})\). That is, observation i in dataset k is assigned a cluster label, a, on the basis of the cluster assignments of the first \(i - 1\) observations. When \(i \approxeq n\) this will give a meaningful estimate of the cluster label \(c_{i, 1}, \dots , c_{i, K}\). However, when, for example, \(i = 3\), this estimate will be much less meaningful. Thus, there is a dependence in the results on the order in which the data are incorporated in the particle filter. One approach to reducing this dependency (as done in Algorithm 2 and Griffin (2014)) is to update \(c_{1:(i-1), 1}, \dots , c_{1:(i-1), K}\) during the resampling step. While this means all cluster labels can be updated using the full set of data, this greatly increases the computational complexity of the algorithm. In a scheme where resampling is not adaptive, or a worst-case scenario in an adaptive scheme, this would result in i operations being required at each iteration, i, increasing computational complexity from \({\mathcal {O}}(n)\) to \({\mathcal {O}}(n^2)\), assuming each individual step can be carried out in constant time. This solution also compounds the computational problem of wasteful calculations assigning observations to clusters on the basis of very few previous observations.
Furthermore, there is a problem specific to the integrative context. As shown in Eq. 4 we inflate particle weights for inter-dataset agreement as indicated by observations sharing the same cluster label. Although we carry out label matching between passes of the particle filter, there can be no assurances within a pass that the cluster labels refer to the same partition of observations across datasets.
We tackle both of these problems with an augmentation of the particle Gibbs sampler, proposing to only update a portion of the cluster allocations in each pass of the particle filter. The remaining allocations are held fixed from the previous pass; we term this portion as \(\rho \), where \(0< \rho < 1\). We select at random a subset of the indices 1 : n of size \(\lfloor n\rho \rfloor \) and assign these observations to the same clusters as in the reference particle from the standard particle Gibbs sampler. Although the algorithm is based on a sequential Monte Carlo sampler, the order of the data is, in fact, not important. As such, it is inconsequential to permute the order of observations randomly and assume the first \(\lfloor n\rho \rfloor \) observations to have their cluster allocations fixed from the previous pass of the particle filter. The permutation ensures we do not condition on the same portion of observations at each pass and placing the fixed portion at the beginning obviates the potentially challenging task of defining a proposal to bridge between separate fixed sections of the particles. We term the function for permuting the observation indices \(\sigma (\cdot )\), ensuring that the same permutation is carried out for each dataset. The algorithm then proceeds as before, with future allocations updated conditional on previously observed data. That is, where the particle Gibbs sampler typically samples alternately from \(p(\theta |x_{1:n}, c_{1:n})\) and \(p_{\theta }(c_{1:n}|x_{1:n})\) (where \(\theta \) represents hyperparameters which are fixed at each run of the particle filter), ParticleMDI samples alternately from \(p(\theta |x_{1:n}, c_{1:n})\) and \(p_{\theta }(\sigma (c)_{\lceil n\rho \rceil :n}|x_{1:n}, \sigma (c)_{1:\lfloor n\rho \rfloor })\) (Fig. 2).
The standard particle Gibbs scan (a) in a three particle, single-dataset case. A single reference particle (\(m = 1\)) is conditioned upon (as indicated by the shaded circles), guaranteeing it survives the resampling step. The values indicated in the circles are \(c_{i, 1}^{(m)}\). In our augmentation (b) a subset of cluster allocations are conditioned upon such that all particles share a chunk of observations (\(\rho \), here 3/n) the same as the reference particle. So that the same observations are not held fixed at every iteration the order of observations is shuffled according to a permutation function \(\sigma (\cdot )\)
This idea of updating only a subset of sequential observations in a particle Gibbs sampler was proposed in the original particle Gibbs paper (Andrieu et al. 2010). Given that we can trivially reorder our data, this is a particularly suitable application of this augmentation of the particle Gibbs sampler; the approach was explored in the particle Gibbs split-merge (PGSM) algorithm(Bouchard-Côté et al. 2017), in which a particle Gibbs scan was restricted to just the observations sharing a cluster label with two randomly selected ‘anchor’ points. The PGSM algorithm then proceeds to ‘split’ this cluster if both anchor points belonged to the same cluster, or ‘merge’ them otherwise.
Provided \(\rho \) is suitably chosen, this augmentation can minimise the dependency on the order in which the data are observed. Thus, we propose a greedy version of Algorithm 2, wherein cluster allocations are not updated during the resampling step as described in Algorithm 3. Assuming each step can be performed in constant time, the computational complexity of this algorithm is now \({\mathcal {O}}(\lceil n\times (1 - \rho ) \rceil )\), although given only a portion of the cluster labels are updated, the comparison with Algorithm 2 is not entirely accurate.

Finding a value of \(\rho \) which is ‘suitably chosen’, however, may not be straightforward. The choice of \(\rho \) involves a trade-off between computation time and mixing time with larger values reducing computation time at the cost of updating fewer cluster allocations. However, the trade-off between computation time and mixing time is not linear, as very low values may induce a dependence on the order of incorporation of the observations. The greedy nature of the algorithm is predicated on the conditioned-on chunk of data being an adequate summary of the dataset as a whole. This is important, first of all, in the context of inflating the weight of particles which assign observations to the same cluster label. It is important to ensure that \(\rho \) is large enough so as to imbue some meaning on the cluster labels, ensuring that the cluster labels refer, insofar as is practicable, to the same partitions of the observational units. This should be the case in the reference particle, as we align cluster labels across datasets in this particle. Thus, \(\rho \) should be specified such that this meaning persists throughout the remaining observations. For example, if the conditioned portion of observations were small enough to exclude many clusters entirely, there could be no guarantee that labels assigned to these clusters, once encountered, will agree across datasets. It is important, also, that \(\rho \) be specified at a value large enough to overcome the dependence on the order in which the data are incorporated in the conditional particle filter. For example, were we to condition only on a single observation these data would not hold sufficient weight to guide the subsequent observations. Proliferation of the reference particle through resampling, however, can help alleviate both of these problems, but may not remove them entirely. We explore the impact of the choice of \(\rho \) in Sect. 4.1.
3.2 Exploiting the redundancy in the particle filter
The accuracy of particle filter methods requires the specification of a large value for M, the number of particles. In the context of mixture models, Griffin (2014) found that good performance could be achieved even with relatively few particles. In ParticleMDI, for each particle we require storage of the assigned cluster labels, as well as summary statistics to facilitate the propagation of particles. This necessitates a large amount of memory access which can hamper the computational performance of the algorithm.
Not all this storage is necessary, however, as particle filters by their nature induce redundancy in the particles. The resampling step generates duplicates of some particles, while removing others. Following resampling, the particles are propagated as an additional observation arrives. Propagation requires evaluation of the posterior predictive densities for the new observation at each cluster, as shown in Eq. 4. These calculations will be identical for each copy of a particle and can add significantly to the computational burden of the algorithm. More specifically to our problem, given that we are dealing with a discrete state space there are very few possible distinct offspring for each particle, the result being that it is likely that, even without resampling, we generate many identical particles.
These redundancies have been discussed previously by Fearnhead (2004) who proposed an augmentation to the resampling algorithm in order to minimise the number of duplicated particles. The rationale for this is that, for example, a set of particle indices \(\left[ 1, 1, 2, 2\right] \) with respective weights \(\left[ 0.1, 0.2, 0.3, 0.4\right] \) is equivalent to having just two particles with weights \(\left[ 0.3, 0.7\right] \) as all possible particle descendants can be considered. Fearnhead (2004) proposes to retain all particles with normalised weights above a threshold performing resampling on the remaining particles, minimising the number of particle duplicates.
Instead of minimising the redundancy we try to exploit it. In order to avoid performing redundant calculations, we need to be able to identify which particles are identical to others. We can identify those particles which are identical due to the resampling step from the resampled particle indices. For others, we propose assigning each particle a running ID as described in Algorithm 4, and only calculating the incremental importance weight once for each unique particle and storing in a hash table. However, this approach will not capture all duplicate particles. Consider two particles which are identical up to a permutation of the cluster labels. These particles will not share a particle ID as the IDs are constructed based on the assigned labels. This can be seen in Fig. 3, where particles 1 and 2 can be made identical by switching allocation labels. Consider also a case where two particles are mostly identical, for example out of 10 inferred clusters, the two particles have assigned the same labels to eight of them, while the remaining two clusters have differing labels. Again, these particles will not be identified as duplicates, despite the evaluation of the incremental importance weight being identical in both. To overcome this, we shift the general setup of the algorithm from particles containing distinct environments to a scenario where there is a global environment into which each of the particles index, as shown in Fig. 3. Thus, when calculating the incremental importance weight, we now need only to evaluate the posterior predictive density for the observation belonging to each of the unique clusters inferred in the data.

To examine the benefits which can be achieved using these approaches, we examined the growth in computation time as the number of particles grow. As the benefit of avoiding redundant calculations will vary according to the complexity of the particular dataset being analysed, we consider two cases: a simple Gaussian dataset containing two well-defined clusters with means \(+5\) and \(-5\), respectively, across 100 observations; and Fisher’s Iris dataset (Fisher 1936) which contains three clusters, two of which are not well-separated across 150 observations. The first dataset represents a best-case scenario, illustrating the kind of improvements in computation time which are possible from our manner of implementing ParticleMDI, while the Iris dataset might represent the more modest improvements which can be expected in practice. Figure 4 shows the empirical effect on computation time as a function of the number of particles in these datasets. All analyses were run for 1, 000 MCMC samples with \(\rho = 0.25\), and the results presented are the mean of 100 such runs. Under the traditional approach, computation time would be expected to grow linearly with the number of particles. Under ParticleMDI, however, a sublinear growth is evident in both cases, with \(M = 1{,}024\) particles taking approximately \(15\times \) as long to complete as \(M = 2\) for the synthetic data, and \(161\times \) as long for the Iris dataset. This represents approximately \(3\%\) and \(31.5\%\) respectively of the time expected under the standard implementation, representing the potential for greater than an order-of-magnitude improvement in computation time. It should be noted that the improved scaling with particles is only one aspect of the improvement in computation time, as due to the identification of redundant clusters, even when \(M=2\) there are improvements made in computation time. These improvements, it is important to recall, come at no cost in terms of the accuracy of the inferred cluster allocation, as we are only avoiding the evaluation of redundant calculations.
Two representations of the same particle filter system. a Shows a standard implementation in which each particle contains an isolated environment of clusters. The mutation step involves evaluating a posterior predictive density for a future observation belonging to each cluster in each particle. b Represents the implementation in ParticleMDI, in which each particle indexes into a global environment of clusters. In this case, the posterior predictive density need only be evaluated for each unique cluster in the global cluster environment
3.3 Extracting consensus clusters
The output of ParticleMDI is a chain of cluster labels for each observation in each dataset. As these cluster labels are exchangeable across iterations, we cannot simply calculate the posterior probability of an observation belonging to a particular cluster. Instead, we calculate the posterior similarity matrix (PSM) (Monti et al. 2003) for each of the K datasets. The PSM is an \(n \times n\) matrix whose (i, j)-th entry takes a value in \(\left[ 0, 1\right] \) indicating how frequently observations i and j are assigned to the same cluster. An overall consensus across datasets can then be derived as the element-wise average of each of these PSMs (Savage et al. 2013). The PSMs can be visualised as a heatmap as shown in Figs. 6 and 7. A final consensus cluster allocation can be inferred from the PSM by applying hierarchical clustering methods using \((1 - PSM)\) as a distance matrix (Medvedovic et al. 2004; Fritsch et al. 2009; Rasmussen et al. 2009). The dendrogram resulting from this analysis will produce an ordering of observations such that pairs of observations most frequently assigned to the same cluster can be positioned adjacently in the heatmap allowing for a heuristic identification of the underlying cluster structure.
4 Applications
In this section, we demonstrate the capability of ParticleMDI to infer cluster structure in synthetic and real datasets, and explore the impact on cluster accuracy of the block-updating in the particle Gibbs sampler described in Sect. 3.1. Further examples are included in the supplementary material.
4.1 The impact of the choice of \(\rho \)
To explore how the choice of \(\rho \) impacts the balance between mixing time and computation time, we run ParticleMDI in a single-dataset context with a fixed computational budget of 1 second. While we acknowledge that such restrictions are unlikely in practice, it is sufficient to gain an insight into the balance between these competing objectives in a synthetic data setting. We generate the synthetic datasets as follows:
-
1.
Generate cluster weights
$$\begin{aligned} \pi \sim Dirichlet(0.2, 0.2, 0.2, 0.2, 0.2) \end{aligned}$$ -
2.
Generate cluster allocations
$$\begin{aligned} c_{1:100, 1} \sim Multinomial(1, \pi ) \end{aligned}$$ -
3.
Generate dataset
$$\begin{aligned} x_{i, 1:32, 1} \sim {\left\{ \begin{array}{ll} {\mathcal {N}}(0, 1) &{} \text {for } c_{i, 2} = 1 \\ {\mathcal {N}}(2, 1) &{} \text {for } c_{i, 2} = 2 \\ {\mathcal {N}}(4, 1) &{} \text {for } c_{i, 2} = 3 \\ {\mathcal {N}}(- 4, 1) &{} \text {for } c_{i, 2} = 4 \\ {\mathcal {N}}(- 2, 1) &{} \text {for } c_{i, 2} = 5. \end{array}\right. } \\ x_{i, 17:32, 1} \sim {\mathcal {N}}(0, 1) \end{aligned}$$
We generate 100 datasets as such with \(n = 100\) observations, and for each we generate samples from ParticleMDI up to a fixed computational budget of 1s. We divide the range [0, 1] seconds into 250 equal bins, and for the last sample generated at the end of each time bin we calculate the adjusted Rand Index Rand (1971) as a measure of the accuracy of the current cluster allocation. Figure 5 shows the median ARI at each of these time points for a range of values of \(\rho \). It can be seen that very large values of \(\rho \)—0.75 and 0.95—appear to perform distinctly poorly. In these cases, ParticleMDI only updates very small portions of the data at each iteration and, so, it takes a long time to move away from the initial allocation. Conversely, choosing a value of \(\rho \) which is too low—0.01 in this case—is also associated with poor performance as convergence is slow as relatively few samples are generated. Values of \(\rho \) between 0.25 and 0.35 appear to offer a suitable balance between computation time and mixing time; we use a value of \(\rho =0.25\) throughout the remaining examples.
4.2 The impact of \(\varPhi \)
In order to demonstrate the impact of the parameter \(\varPhi \) in allowing ParticleMDI to share information across datasets, we present an illustrative example application of ParticleMDI to Fisher’s Iris dataset (Fisher 1936), a canonical example application in clsuter analysis. The dataset contains 150 observations on three different species of iris: setosa, virginica, and versicolor, each representing an equal portion of the dataset. The results of applying ParticleMDI to these data in Fig. 6a highlight that while one species—setosa—is distinctly identifiable, the other two exhibit a significant degree of overlap. In order to address this, we conduct this analysis in an integrative setting, by complementing the Iris data with an additional categorical dataset containing the true cluster labels. While we concede that it is unlikely to have a dataset with such perfect signal of the ground truth cluster structure, Fig. 6b illustrates how ParticleMDI is able to use information from one dataset to inform the cluster structure in the other. Not only is the true cluster structure evident in the overall consensus PSM, but the cluster structure inferred in the raw data now shows separation between the three species.
4.3 Subtype discovery in cancer patients
The primary motivation for MDI is the integrative analysis of multiple biological datasets. In this section, we explore an application of ParticleMDI to inferring clusters of patients presenting with a particular form of cancer, with genomic and other ‘omic’ measurements recorded on each. We use these inferred groups to retrospectively predict the risk profile of patients.
4.3.1 Data
We consider the Cancer Genome Atlas pan-cancer dataset previously analysed by Yuan et al. (2014), who discovered that clinical covariates mostly outperformed ‘omic’ features in predicting the survival probability of individuals when considered independently, while integrative approaches conferred additional prognostic power. Specifically, we focus on patients presenting with kidney renal clear cell carcinoma (KIRC), a group of 243 patients for whom each of the ‘omic’ data types were available, as well as data on survival times. We use the data as prepared by Yuan et al. (2014). We provide an additional application of ParticleMDI to a dataset on patients with ovarian serous cystadenocarcinoma in the supplementary material. While ParticleMDI is capable of simultaneously performing feature selection and cluster analysis, we complement this by an initial reduction in the number of features for computational purposes. This initial reduction is based on the variability of the individual clusters as this relates to the ‘clusterability’ (Steinley and Brusco 2008) of a feature, and has been performed in other similar analyses (Shen et al. 2009; Lawlor et al. 2016). Post-hoc analysis of the selected features and inferred cluster allocations can be potentially illuminating of the particular genes driving patient prognosis. The data available are as follows:
-
Messenger RNA (mRNA)—The data platform is Illumina HiSeq 2000 RNA Sequencing V2. Of 20, 203 mRNA features present we select the 100 most variant of these. We treated these data as continuous and modelled them as arising from a Gaussian distribution.
-
microRNA (miRNA)—The data platform is Illumina Genome Analyzer/HiSeq 2000. Of 795 miRNA features, we select the 100 most variant. We treated these data as continuous and modelled as arising from a Gaussian distribution.
-
Reverse-phase protein array (RPPA)—The data platform is MD Anderson Reverse Phase Protein Array Core platform. Of 166 features, we retain the 100 most variant. We treated these data as continuous and modelled as arising from a Gaussian distribution.
-
DNA methylation (methyl)—The data platform is Illumina Infinium Human DNA Methylation 450K. Of 16, 484 DNA methylation features, we select the 100 most variant. We discretised these at a threshold of 0.85 and removed any features with fewer than 10 ‘hits’. The remaining features were modelled as arising from a categorical distribution.
-
Somatic copy number alterations (SCNA)—SCNAs are known to be extremely common in cancer, with acquisition a known driver of cancer. The data platform is Affymetrix Genome-Wide Human SNP Array 6.0. 69 SCNA features were available, which we discretised, with values \(> 0.1\) indicating an amplification, and values \(< -0.1\) indicating a deletion. These values were modelled as categorical data.
-
Clinical data—Clinical and administrative data are available for the patients including age, gender, tumour grade, and survival times. For the purposes of this analysis, we consider the survival data, and tumour grading, as means of assessing how meaningful the inferred clusters are.
4.3.2 Results
The PSMs shown in Fig. 7 show the cluster structure inferred across the five datasets. The overall consensus PSM suggests the existence of one large cluster (bottom left) which appears to strongly reflect the cluster structure of the SCNA and methylation data. This cluster can be further subdivided using the structure inferred in the protein data. The dendrogram obtained by applying hierarchical cluster analysis to the consensus posterior similarity matrix is cut to give four clusters. The posterior mean \(\varPhi \) values are shown in Fig. 8f, showing that the strongest agreement in cluster structure is between the methylation and the SCNA data.
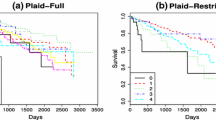
Despite the granularity evident in the inferred clusters in the mRNA data, it can be seen in Fig. 8a that cluster 3 corresponds generally to a group of patients with particularly high levels of expression in the selected genes, relative to the other clusters, and similarly cluster 2 contains patients with typically low expression. Cluster 3 is also distinct in the methylation data, Fig. 8d, showing distinctly high levels of methylation, and in Fig. 8e it can be seen that patients belonging to cluster 3 and cluster 1 exhibit greater levels of copy number alterations than clusters 2 and 4. The tumour grading scores presented in Fig. 8 suggest that individuals in clusters 1 and 3 typically have higher tumour grading scores, suggesting poorer outcomes for these individuals relative to those in other clusters. This is confirmed by the Kaplan-Meier survival curves shown in Fig. 9, showing a significant difference in the survival rates in the inferred groups (log-rank p-value = \(1.197133\times 10^{-7}\)). The Tarone-Ware test (Tarone and Ware 1977), which is sensitive to early differences in the survival curves also suggests significant difference in the survival curves (\(p<0.0001\)). We present both results as tests for significance in survival analysis are often limited by crossing occurring in the survival curves, as discussed by Li et al. (2015). Of note, cluster 3 which was identified as having unique characteristics across multiple datasets, is seen to have distinctly poorer survival prognosis than the other clusters. The median survival time for the 24 patients belonging to cluster 3 is just 866 days, in comparison with 1979 days for the patient cohort as a whole. Patients in cluster 1 (\(n = 79\)), who were characterised as having high levels of somatic copy number alterations, have a median survival time of 1625 days. Patients in cluster 2 (\(n = 47\)), who were noted for having lower levels of mRNA expression, are seen to have a much better prognosis with a median survival time of 2830 days, which is close to the end of the study period. Further analysis of the biological significance of the inferred cluster structure is presented in the supplementary material.
a–e Heatmaps for each of the KIRC datasets with the inferred cluster allocations from ParticleMDI highlighted with a dashed white line and the grey bars along the right margin. The bar on the furthest right reflects tumour grading scores, with brighter colours indicating higher (worse) grading scores. Posterior feature selection probabilities are indicated by the bars on the lower margin. f The inferred \(\varPhi \) for pairs of datasets in ParticleMDI
Running specifications 100, 000 samples were generated from ParticleMDI, thinned to one sample for every ten. The first \(50\%\) of samples were discarded as burn-in. The inferred \(\varPhi \) values were checked for convergence (see supplementary material). A total of 1, 024 particles were used, and \(\rho \) was set to 0.25.
5 Discussion
We have presented ParticleMDI, a novel method for the integrative cluster analysis of multiple datasets using particle Monte Carlo methods. While we have focused on applications with Gaussian and categorical data, our methods are easily generalisable to other data types where a posterior predictive distribution can be analytically derived, including multivariate Gaussian models with a full covariance structure. We have presented novel means of improving the computational efficiency of our algorithm, with experimental results demonstrating improvements of an order of magnitude or more with no penalty in accuracy. Our approaches are applicable more broadly in the context of particle filters applied to discrete state-spaces. We have demonstrated the efficacy of our approach to uncovering the ground truth in synthetic data. We have applied our algorithm to real biological data from the Cancer Genome Atlas, demonstrating the capability of our approach to infer clinically meaningful subgroups as shown by the significantly different survival profiles of the patients contained within. Membership of these groups is not governed by the variation in just a single dataset, highlighting the importance of using integrative methods. ParticleMDI is freely available as a package in the statistical programming language Julia (Cunningham et al. 2019)
References
Andrieu C, Doucet A, Holenstein R (2010) Particle Markov chain Monte Carlo methods. J R Stat Soc Ser B Stat Methodol 72(3):269–342
Bernardo JM, Smith AF (2001) Bayesian Theory
Bouchard-Côté A, Doucet A, Roth A (2017) Particle Gibbs split-merge sampling for Bayesian inference in mixture models. J Mach Learn Res 18(28):1–39
Chopin N (2002) A sequential particle filter method for static models. Biometrika 89(3):539–552
Chopin N, Singh SS (2015) On particle Gibbs sampling. Bernoulli 21(3):1855–1883
Cunningham N, Griffin JE, Wild DL, Lee A (2019) Bayesian Statistics: New Challenges and New Generations, vol 2018, Springer
Doucet A, Johansen AM (2009) A tutorial on particle filtering and smoothing: fifteen years later. Handb Nonlinear Filter 12(656–704):3
Fearnhead P (2004) Particle filters for mixture models with an unknown number of components. Stat Comput 14(1):11–21
Fisher RA (1936) The use of multiple measurements in taxonomic problems. Ann Eugen 7(2):179–188
Fritsch A, Ickstadt K et al (2009) Improved criteria for clustering based on the posterior similarity matrix. Bayesian Anal 4(2):367–391
Gabasova E, Reid J, Wernisch L (2017) Clusternomics: integrative context-dependent clustering for heterogeneous datasets. PLoS Comput Biol 13(10):e1005781
Green PJ, Richardson S (2001) Modelling heterogeneity with and without the Dirichlet process. Scand J Stat 28(2):355–375
Griffin J (2014) Sequential Monte Carlo methods for mixtures with normalized random measures with independent increments priors. Stat Comput 27(1):131–145
Hol JD, Schon TB, Gustafsson F (2006) On resampling algorithms for particle filters. In: nonlinear statistical signal processing workshop, 2006 IEEE, IEEE, pp 79–82
Ishwaran H, Zarepour M (2002) Exact and approximate sum representations for the Dirichlet process. Can J Stat 30(2):269–283
Kassambara A, Kosinski M (2018) survminer: Drawing Survival Curves using ’ggplot2’. R package version (4):2
Kirk P, Griffin JE, Savage RS, Ghahramani Z, Wild DL (2012) Bayesian correlated clustering to integrate multiple datasets. Bioinformatics 28(24):3290–3297
Lawlor N, Fabbri A, Guan P, George J, Karuturi RKM (2016) multiclust: an r-package for identifying biologically relevant clusters in cancer transcriptome profiles. Cancer Inf 15:CIN-S38000
Li H, Han D, Hou Y, Chen H, Chen Z (2015) Statistical inference methods for two crossing survival curves: a comparison of methods. PLoS One 10(1):e0116774
Liu JS, Chen R (1995) Blind deconvolution via sequential imputations. J Am Stat Assoc 90(430):567–576
Lock EF, Dunson DB (2013) Bayesian consensus clustering. Bioinformatics 29(20):2610–2616
McParland D, Gormley IC, McCormick TH, Clark SJ, Kabudula CW, Collinson MA (2014) Clustering South African households based on their asset status using latent variable models. Ann Appl Stat 8(2):747
McParland D, Phillips CM, Brennan L, Roche HM, Gormley IC (2017) Clustering high-dimensional mixed data to uncover sub-phenotypes: joint analysis of phenotypic and genotypic data. Stat Med 36(28):4548–4569
Medvedovic M, Yeung K, Bumgarner R (2004) Bayesian mixture model based clustering of replicated microarray data. Bioinformatics 20(8):1222–1232
Monti S, Tamayo P, Mesirov J, Golub T (2003) Consensus clustering: a resampling-based method for class discovery and visualization of gene expression microarray data. Mach Learn 52(1–2):91–118
Murphy KP (2007) Conjugate Bayesian analysis of the Gaussian distribution. Tech. rep
Rand WM (1971) Objective criteria for the evaluation of clustering methods. J Am Stat Assoc 66(336):846–850
Rasmussen C, de la Cruz B, Ghahramani Z, Wild D (2009) Modeling and visualizing uncertainty in gene expression clusters using Dirichlet process mixtures. IEEE/ACM Trans Comput Biol Bioinf 6(4):615–628
Rousseau J, Mengersen K (2011) Asymptotic behaviour of the posterior distribution in overfitted mixture models. J R Stat Soc Ser B Stat Methodol 73(5):689–710
Savage RS, Ghahramani Z, Griffin JE, Kirk P, Wild DL (2013) Identifying cancer subtypes in glioblastoma by combining genomic, transcriptomic and epigenomic data. arXiv preprint arXiv:1304.3577
Shen R, Olshen AB, Ladanyi M (2009) Integrative clustering of multiple genomic data types using a joint latent variable model with application to breast and lung cancer subtype analysis. Bioinformatics 25(22):2906–2912
Steinley D, Brusco MJ (2008) Selection of variables in cluster analysis: an empirical comparison of eight procedures. Psychometrika 73(1):125
Tarone RE, Ware J (1977) On distribution-free tests for equality of survival distributions. Biometrika 64(1):156–160
Yuan Y, Van Allen EM, Omberg L, Wagle N, Amin-Mansour A, Sokolov A, Byers LA, Xu Y, Hess KR, Diao L et al (2014) Assessing the clinical utility of cancer genomic and proteomic data across tumor types. Nat Biotechnol 32(7):644
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Cunningham, N., Griffin, J.E. & Wild, D.L. ParticleMDI: particle Monte Carlo methods for the cluster analysis of multiple datasets with applications to cancer subtype identification. Adv Data Anal Classif 14, 463–484 (2020). https://doi.org/10.1007/s11634-020-00401-y
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11634-020-00401-y