Abstract
Examining the efficacy of composite-based structural equation modeling (SEM) features prominently in research. However, studies analyzing the efficacy of corresponding estimators usually rely on factor model data. Thereby, they assess and analyze their performance on erroneous grounds (i.e., factor model data instead of composite model data). A potential reason for this malpractice lies in the lack of available composite model-based data generation procedures for prespecified model parameters in the structural model and the measurements models. Addressing this gap in research, we derive model formulations and present a composite model-based data generation approach. The findings will assist researchers in their composite-based SEM simulation studies.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Research in the social sciences often involves inference about concepts such as attitudes, perceptions, and behavioral intentions. Since such concepts cannot be measured directly, observed variables (also referred to as indicators) are used to represent them as latent variables (or constructs) in statistical models. Structural equation modeling (SEM) has become the standard tool to validate the indirect measurement of unobservable concepts and analyze complex interrelations between latent variables. Researchers can choose from two conceptually different approaches to SEM: factor- and composite-based SEM (Jöreskog and Wold 1982; Rigdon et al. 2017).
In factor-based SEM unobservable conceptual variables are approximated by common factors under the assumption that each latent variable exists as an entity independent of observed variables. This latent variable serves as the sole source of the associations among the observed variables. That is, when controlling for the impact of the latent variable, the indicator correlations are zero. One of the first and most prominent formulations of factor-based SEM has been established by Jöreskog (1978). On the contrary, composite-based SEM represents latent variables by weighted composites of observed variables, assuming each one to be an aggregation of observed variables (Sarstedt et al. 2016). Although many methods fall into the domain of composite-based SEM, partial least squares (PLS; Lohmöller 1989; Wold 1982) and generalized structured component analysis (GSCA; Hwang and Takane 2004) constitute the most advanced and frequently used approaches in the field (Hwang et al. 2020; Hwang and Takane 2014).
As factor- and composite-based SEM both try to achieve the same aim – estimating a series of structural equations that represent causal processes – researchers have routinely compared their relative efficacy on the grounds of simulated data (Rigdon et al. 2017). However, the studies usually have evaluated composite-based SEM methods on the grounds of factor model data, where the indicator covariances define the nature of the data (Sarstedt et al. 2016). These studies univocally show that composite-based SEM methods produce biased results that typically manifest themselves in measurement model parameters (i.e., indicator loadings and weights) being overestimated and structural model parameters being underestimated (Goodhue et al. 2012; Lu et al. 2011; Reinartz et al. 2009). However, these results are not considering that the estimated models were misspecified with regard to the data generation process in the simulation studies—as noted by numerous authors (Marcoulides et al. 2012; Rigdon 2012; Rigdon et al. 2017).Footnote 1
In fact, very few simulation studies have assessed composite-based SEM using data that are consistent with the assumptions of the method. We believe that the reason for the scarcity of research in this field lies in the lack of suitable date generation procedures. Specifically, while the data generation process for factor-based SEM is well documented and frequently discussed in the literature (e.g., Reinartz et al. 2002), this is not the case with composite-based SEM. Generating data for composite-based simulation studies in an SEM context is challenging because the size of the path coefficients, which define the strength of relationships between latent variables, are inextricably tied to the target variable’s coefficient of determination. A composite model-based data generating process must consider such dependencies. Even though needed for simulation studies, corresponding procedures have remained nontransparent.
Our research seeks to fill this gap by discussing the specification of covariance matrices in composite-based data generation, which can serve as input for simulation studies. Our approach allows researchers to generate data for composite models with pre-specified indicator weights and path coefficients or coefficients of determination to assess the method’s efficacy. The package cbsem (Schlittgen 2019) of the statistical software R (R Core Team 2019) contains all functions described in the further course of this article.
2 The composite-based model
Consider two sets of indicator variables, \({\varvec{x}}=(X_1,\ldots ,X_{p_1})\) and \({\varvec{y}}=(Y_1,\ldots ,Y_{p_2})\), whereby all the variables should be standardized, \(\hbox {E}(X_i)=0\) and \({\mathrm{Var}}(X_i)=1\); the same applies to \(Y_i\). The relationships between these two sets of variables are modelled using composites in the structural model.Footnote 2 The independent composites \(\xi \) use \({\varvec{x}}\) as indicators in their measurement models, whereas the dependent composites \(\eta \) employ the indicators \({\varvec{y}}\). Independent composites do not depend on any other composite in the structural model. Each of the composites \(\eta \), which result from the \({\varvec{y}}\) indicator variables, is dependent and, as such, is regressed on at least one other composite, regardless of whether it is an independent composite \(\xi \) or another dependent composite \(\eta \). The number of independent composites is \(q_1\), while the number of dependent composites is \(q_2\).
The measurement models allow to determine the composites of the structural model (i.e., their scores) by using a specific set of observed variables as indicators for each composite. Linear combinations of the \({\varvec{x}}\) and \({\varvec{y}}\) indicator variables generate the scores of each composite. The indicators of \(\xi _g\) build a subvector \({\varvec{x}}_g\) of \({\varvec{x}}\), \(g=1,\ldots ,q_1\). The corresponding weights vectors are denoted by \({\mathbf {w}}_{g}^{(1)}\). \(\eta _h\) has indicators \({\varvec{y}}_h\) with weights \({\mathbf {w}}_{h}^{(2)}\), \(h=1,\dots ,q_2\). The parameter vectors are column vectors whereas the random vectors are row vectors. This formal representation is not very common but has the advantage that the equations have the same appearance as the corresponding data matrices’ relations. The weights relations are (Semadeni et al. 2014):
with
The composites have unit variances, \({\mathrm{Var}}(\xi _g)=1\) and \({\mathrm{Var}}(\eta _h)=1\). This implies that the weights are standardized, \({\mathbf {w}}_g^{(1) ^\prime } \varvec{\Sigma }_{{{{\varvec{x}}}}_g{{{\varvec{x}}}}_g}{\mathbf {w}}_g^{(1)}=1\) where \(\varvec{\Sigma }_{{{{\varvec{x}}}}_g{{{\varvec{x}}}}_g}\) is the population indicators’ matrix of block g. The same applies to \({\mathbf {w}}_h^{(2)}\).
While the measurement models determine the composites using the weights \({\mathbf {W}}_1\) and \({\mathbf {W}}_2\), the structural model provides the relationships between the two sets of indicators by means of the resulting two sets of composites:
The matrix \({\mathbf {B}}\) can be arranged as a lower triangular with zeros on the diagonal for recursive models, which applies here; \({\varvec{\zeta }}\) is a vector of errors, whereby the errors are presumed to be uncorrelated and also uncorrelated in respect of the other random vectors. The formulation with row vectors implies that the transposes of \(\varvec{\Gamma }\) and \({\mathbf {B}}\) appear in Eq. (2). The path coefficients in \(\varvec{\Gamma }\) and \({\mathbf {B}}\) are the parameters of primary interest. They describe the composites’ interrelations. From the structural model’s recursiveness, it follows that \(({\mathbf {I}} - {\mathbf {B}}^\prime )\) is regular and a reduced form of Equation (2) exists:
3 The covariance matrix of the composites
Establishing the covariance matrix of a path model with composites requires determining the main parameters. In the structural model, these include (a) the path coefficients, (b) the independent composites’ correlations, and (c) the dependent composites’ coefficients of determination; in the measurement model, the relevant parameters are (d) the weights.
The specification of the path coefficients and the coefficients of determination are interrelated. When path coefficients are of primary concern, the coefficients of determination result from the structural model requiring uncorrelated errors. Researchers can establish the covariance matrix of the dependent composites, \(\varvec{\Sigma }{{{{\varvec{\eta }}}}{{{\varvec{\eta }}}}}\), as follows:
The computation of \(\varvec{\Sigma }_{{{{\varvec{\eta }}}}{{{\varvec{\eta }}}}}\) employs a nonlinear optimization to determine the diagonal matrix \(\varvec{\Sigma }_{{{{\varvec{\zeta }}}}{{{\varvec{\zeta }}}}}\) such that the composites have unit variances (Fig. 1).
When specifying the dependent composites’ coefficients of determination a priori, researchers must determine the path coefficients accordingly. Consider the structural regression equation for the dependent composite \(\eta _c\) given in Eq. (2):
Here \({\varvec{\beta }}_{c,1:c-1}\) is the row vector consisting of the first \(c-1\) elements of row c of \({\mathbf {B}}\). \({\varvec{\eta }}_{1:c-1}\) is the vector of the dependent composites related to rows 1 to \(c-1\) of \({\mathbf {B}}\). The coefficients of the composites that do not appear in the regression equation of \(\eta _c\) are zero. These considerations, together with the covariance matrix \(\varvec{\Sigma }_{(q_1+c-1),(q_1+d-1)}\) of \(({\varvec{\xi }},{\varvec{\eta }}_{1:c-1})\) and \(({\varvec{\xi }},{\varvec{\eta }}_{1:d-1})\), results in the following equations:
These equations provide the relations required to compute the composites’ covariance matrix.
For simulations that focus on the path coefficients in the structural model, no further information is needed. Here, the \(R^2\) depends on the pre-specified structural model relationships. In contrast, one determines \({\mathbf {B}}\) a priori to obtain a specific vector \({\varvec{r}}^2=(R^2_1,\dots ,R^2_{q_2})\) of the dependent composites’ coefficients of determination in the structural model. More specifically, the coefficient of determination for the regression of \(\eta _c\) on \(({\varvec{\xi }},{\varvec{\eta }}_{1:c-1})\), which is based on Eq. (6c), follows with the assumption \({\mathrm{Var}}(\eta _c)=1\):
One needs to work through matrix \({\mathbf {B}}\) from row \(q_1+1\) to the last one in order to modify the path coefficients in a way that they arrive at the desired coefficients of determination. The first part of the covariance matrix is given by \(\varvec{\Sigma }_{{{{\varvec{\xi }}}}{{{\varvec{\xi }}}}}\). After the modification of the path coefficients in row \(q_1+c\) of \({\mathbf {B}}\), the covariance matrix of the composites must be augmented by row and column c before the coefficients of row \(c+1\) can be modified. Initially, choose the row vector \({\varvec{\beta }}_{q_1+c}\) as preferred. Subsequently, this preliminary value is multiplied by a factor \(\tau \), which allows to fulfill Eq. (7):
4 The covariance matrix of the models’ indicators
4.1 Computation
The covariance matrix of the indicators is used to simulate the model. With a choice of \(\varvec{\Sigma }_{{{{\varvec{\xi }}}}{{{\varvec{\xi }}}}}\), the covariance matrix of the \({\varvec{x}}\)-indicators and the weights \({\mathbf {W}}_1\) must be determined so that
is fulfilled. This formulation is en par with the general comprehension of composite-based models as formative measurement (Rhemtulla et al. 2020). Several options are available to choose \(\varvec{\Sigma }_{{{{\varvec{x}}}}{{{\varvec{x}}}}}\) and the standardized weights, resulting in a given \(\varvec{\Sigma }_{{{{\varvec{\xi }}}}{{{\varvec{\xi }}}}}\). For instance, researchers can first deal with each block of indicators of the different exogenous composites separately, which only requires to ensure the standardization of the composites. This means that \(\xi _g = {\varvec{x}}_g{\mathbf {w}}_g\),\({\mathbf {w}}_g^\prime \varvec{\Sigma }_{{{{\varvec{x}}}}_g{{{\varvec{x}}}}_g}{\mathbf {w}}_g=1\) must be fulfilled. One can meet this requirement, for example, by setting \(\varvec{\Sigma }_{{{{\varvec{x}}}}_g{{{\varvec{x}}}}_g}\) as the identity matrix and choosing the weights vectors such that \({\mathbf {w}}_g^\prime {\mathbf {w}}_g=1\). In an alternative approach, researchers can choose the covariance matrix arbitrarily and subsequently scale it to fulfill Eq. (9). If the exogenous composites are uncorrelated, one uses \(\varvec{\Sigma }_{{{{\varvec{x}}}}_g{{{\varvec{x}}}}_h} = {\mathbf {0}}\) for \(g \ne h\). In contrast, if two composites are correlated, one must appropriately select the correlations between the indicators in the two related blocks of indicators. A straightforward solution uses \(\varvec{\Sigma }_{{{{\varvec{x}}}}_g{{{\varvec{x}}}}_h}\) and scales it such that \({\mathbf {w}}_g^\prime \varvec{\Sigma }_{{{{\varvec{x}}}}_g{{{\varvec{x}}}}_h}{\mathbf {w}}_h = \sigma _{\xi _g\xi _h}\). Becker et al. (2013) used this approach in their study on latent class analysis in PLS.
In the next step, \({\mathbf {B}}\) is given, or must be determined according to the given vector \({\varvec{r}}^2\) of the coefficients of determination (Sect. 3). With this information, one can obtain \(\varvec{\Sigma }_{{{{\varvec{\eta }}}}{{{\varvec{\eta }}}}}\) as described in Sect. 3. \(\varvec{\Sigma }_{{{{\varvec{y}}}}{{{\varvec{y}}}}}\) and the weights \({\mathbf {W}}_2\) are determined in the same way as the covariance matrix of the X-indicators, using
The covariances of the exogenous and the endogenous composites can be used to determine \(\varvec{\Sigma }_{{{{\varvec{x}}}}{{{\varvec{y}}}}}\). First, from Eq. (1) it follows that:
whereas Eq. (3) leads to:
The combination of these two equations provides a necessary condition that must be fulfilled:
Choosing the covariance matrix \(\varvec{\Sigma }_{{{{\varvec{x}}}}{{{\varvec{y}}}}}\) as
permits to meet the requirement of Eq. (13). To arrive at this result, it is necessary to insert this expression into the left-hand side of Eq. (13) and to consider the relations for the covariance matrices of the composites. Figure 2 offers a quasi-code for the computation of the covariance matrices of the indicators. Equation (14) ensures that Eq. (13) is fulfilled. In special constellations other solutions may exist for the given matrices \({\mathbf {W}}_1\), \({\mathbf {W}}_2\) and \(\varvec{\Sigma }_{{{{\varvec{\xi }}}}{{{\varvec{\eta }}}}}\). In any case, the resulting covariance matrices of the composites are the same. Therefore, a possible non-uniqueness does not affect the estimated results of the structural model.
4.2 Example
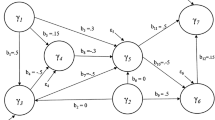
In the following, we present an example to illustrate how to establish the covariance matrix of the indicators. We consider the following structural model, which includes three independent and three dependent composites and their three partial regression models with pre-specific coefficients for the data generation propose:
The covariance matrix of the independent composites and the coefficients of determination of the regressions for the independent composites are set to:
The pre-specified path coefficients are \(\gamma _{11} = \gamma _{22} =0.6\), \(\gamma _{12} = \gamma _{23} =0.5\), \(\beta _{31} = \beta _{32} =0.4\).
The next step in determining the covariance matrix of composites is to recalculate the path coefficients. First, one needs to consider the regression model \(\eta _1 = \gamma _{11}\xi _1 +\gamma _{12}\xi _2 + \zeta _1\). Based on \({\mathrm{Var}}(\eta _1) = \gamma _{11}^2 + \gamma _{12}^2 + 2\gamma _{11}\gamma _{12}{\mathrm{Cov}}(\xi _1,\xi _2)+ {\mathrm{Var}}(\zeta _1)= 1\) it is possible to obtain \({\mathrm{Var}}(\zeta _1)=0.15\). In order to achieve \(R^2_1= 1-{\mathrm{Var}}(\zeta _1) = 0.8\) the coefficients \(\gamma _{11}, \gamma _{12}\) are multiplied by \(\tau =\sqrt{0.8/0.85}\). The second regression model \(\eta _2 = \gamma _{22}\xi _2 +\gamma _{23}\xi _3 + \zeta _2\) results in \({\mathrm{Var}}(\zeta _2)=0.21\). From this, one derives the factor \(\tau =\sqrt{0.7/0.79}\). Up to this point the modified path coefficients are: \(\gamma _{11} =0.582\),\(\gamma _{12} = 0.485\), \(\gamma _{22} = 0.565\), \(\gamma _{23} = 0.471\).
Computing the factor of the third regression computation requires researchers to establish the covariance matrix of \(({\varvec{\xi }},\eta _1,\eta _2)\). Equations (6a) to (6c) result in:
Based on these covariances, one proceeds as with the first two regressions. This gives the factor \(\tau =\sqrt{0.6/0.346}\). Subsequently the matrices \(\varvec{\Gamma }\) and \({\mathbf {B}}\) are:
Next, the computation of the complete covariance matrix of the composites, again, uses Eqs. (6a) to (6c).
Finally, the indicators’ covariance matrix is determined on the basis of previously established parameters. For this purpose, we build on the results already obtained in Step 1 of Fig. 2. For the next Step 2, let
where 1 is a 3\(\times \)3 matrix of ones, \({\mathbf {w}}_1 = (0.4,0.5,0.6)^\prime \) and \({\mathbf {0}}\) a vector of zeros.
First, \({\mathbf {W}}_1\) has to be standardized. This is done by computing \({\varvec{w}}_1/\sqrt{f}\) with \(f = {\mathbf {w}}_1^\prime {\mathbf {K}}{\mathbf {w}}_1 = 1.106\), and by substituting the new vector for the old \({\mathbf {w}}_1\). \({\mathbf {w}}_2\) and \({\mathbf {w}}_3\) are standardized analogously. Subsequently, blocks of ones in \(\varvec{\Sigma }_{{{{\varvec{x}}}}{{{\varvec{x}}}}}\) have to be changed such that the covariances in \(\varvec{\Sigma }_{{{{\varvec{\xi }}}}{{{\varvec{\xi }}}}}\) are recovered. For example, to obtain \(\sigma _{13} = 0.469\), the ones in the first three rows and the last three columns are modified to \(0.469/({\mathbf {w}}_1^\prime {\mathbf {1}} {\mathbf {w}}_3)\).
Analogously, one obtains the matrix \({\mathbf {W}}_2\) by considering \(\varvec{\Sigma }_{{{{\varvec{\eta }}}}{{{\varvec{\eta }}}}}\). Finally, \(\varvec{\Sigma }_{{{{\varvec{x}}}}{{{\varvec{y}}}}}\) is computed using Eq. (14). As a result, one receives the complete covariance for data generation. Based on this covariance matrix follows the data generation as explained in the following section.
5 Data generation
The covariance matrix can be used to generate a dataset for composite model-based simulation studies. This is particularly easy when the indicators are normally distributed. Then a (\(n,p_1+p_2\)) matrix of independent standard normal random variables is generated and multiplied from the right by the Cholesky factor of the covariance matrix. On the other hand, several suggestions exist for generating data from nonnormal distributions with pre-specified parameters. For instance, Vale and Maurelli (1983) extended the Fleishman (1978) method to generate multivariate random numbers with specified intercorrelations and univariate means, variances, skewness values, and kurtoses. To begin with, they produce a suitably sized matrix of independent, normally distributed random numbers. Then, they subsequently compute the Fleishman’s transformation coefficients and use them an intermediate correlation matrix from the desired indicators’ correlation matrix. A principal components factorization allows to obtain the intermediate correlation matrix. The resulting factor is multiplied with the matrix of independent normally distributed random numbers. Finally, the component-wise application of the Fleishman transformation follows to generate the indicator data.
This method was used for a small simulation experiment to compare the estimates of GSCA and PLS. The experiment changes the generated indicator data’s levels of skewness \(\sqrt{\beta _1}\) and excess kurtosis \(\beta _2\). These levels correspond to normal, Laplace, exponential and t\(_5\)-distributions (although the empirical values of the kurtosis are smaller than those of the target ones). We used the model of the example in Sect. 4 to generate 50 samples of size \(n=100\) for each distribution. Schlittgen’s (2018) gscals (i.e., for GSCA) and plspath (i.e., for PLS) implementations have been used to obtain the model estimation results. Figure 3 shows the differences between the estimates and the path coefficients used for the simulation.
The results show that the normal data situation does not produce different results compared to the other distributions. Overall, the differences between the two estimation methods’ results are marginal. However, the GSCA results are a bit closer to pre-specified value (higher precision) while the PLS estimates are more closely grouped around the pre-specified value (higher robustness).
6 Conclusion
The data generation of pre-specified models is an important issue in composite-based SEM, especially when conducting simulation studies. Reinartz et al. (2002) investigate the simulation of common factor-based models when the latent variables are generated first. This is a sensible approach in these models, but not in composite-based ones since they comprise linear combinations of indicators (Sarstedt et al. 2016). Their distributions, therefore, depend on the distributions of the indicators and will be nearer to the normal distribution if the weights do not deviate strongly from each other.
This article contributes to the literature on SEM by discussing properties of data generation in composite-based models. The pre-specified model parameters allow to obtain the indicators’ covariance matrices to be used as input for data generation. Furthermore, we offer an example of nonnormally distributed indicators using Vale and Maurellis’ (1983) approach.
Our findings are important for researchers who run simulation studies to compare the efficacy of existing, expanded, and newly developed algorithms for the estimation of composite-based SEM models. Also, researchers who like to analyze methodological extensions for composite-based SEM—such as the efficiency of existing and new segmentation algorithms (e.g., Schlittgen et al. 2016)—will take advantage of this research. Future research should further evaluate our approach, for example, in terms of more extreme forms of nonnormality or multimodal distributions. A promising extension would be to adjust the approach to accommodate nonlinear relationships whose use has gained momentum in applications of composite-based SEM (Sarstedt et al. 2020).
Notes
The concepts of factor and composite model data need to be differentiated from reflective and formative measurement, which refers to the theoretical specification of the constructs on the grounds of measurement theory (Sarstedt et al. 2016). Regardless of whether researchers use reflective or indicators, composite-based SEM methods always compute weighted composites of observed variables to represent conceptual variables in the statistical model (Hwang et al. 2020).
In the following, we refer to composites rather than latent variables to denote entities that are conceptual variables in a statistical model.
References
Becker J-M, Rai A, Rigdon EE (2013) Predictive validity and formative measurement in structural equation modeling: embracing practical relevance. In: Proceedings of the international conference on information systems, Milan
Fleishman AI (1978) A method for simulating non-normal distributions. Psychometrika 73:521–532
Goodhue DL, Lewis W, Thompson R (2012) Does PLS have advantages for small sample size or non-normal data? MIS Q 36:981–1001
Hwang H, Takane Y (2004) Generalized structured component analysis. Psychometrika 69:81–99
Hwang H, Takane Y (2014) Generalized structured component analysis: a component-based approach to structural equation modeling. Chapman & Hall, New York
Hwang H, Sarstedt M, Cheah J-H, Ringle CM (2020) A concept analysis of methodological research on composite-based structural equation modeling: bridging PLSPM and GSCA. Behaviormetrika 47:219–241
Jöreskog KG (1978) Structural analysis of covariance and correlation matrices. Psychometrika 43:443–477
Jöreskog KG, Wold HOA (1982) The ML and PLS techniques for modeling with latent variables: historical and comparative aspects. In: Wold HOA, Jöreskog KG (eds) Systems under indirect observation, part I. North-Holland, Amsterdam, pp 263–270
Lohmöller J-B (1989) Latent variable path modeling with partial least squares. Physica, Heidelberg
Lu IRR, Kwan E, Thomas DR, Cedzynski M (2011) Two new methods for estimating structural equation models: an illustration and a comparison with two established methods. Int J Res Mark 28:258–268
Marcoulides GA, Chin WW, Saunders C (2012) When imprecise statistical statements become problematic: a response to Goodhue, Lewis, and Thompson. MIS Q 36:717–728
R Core Team (2019) R: a language and environment for statistical computing. R foundation for statistical computing, Vienna
Reinartz WJ, Echambadi R, Chin WW (2002) Generating non-normal data for simulation of structural equation models using Mattson’s method. Multivar Behav Res 37:227–244
Reinartz WJ, Haenlein M, Henseler J (2009) An empirical comparison of the efficacy of covariance-based and variance-based SEM. Int J Res Mark 26:332–344
Rhemtulla M, van Bork R, Borsboom D (2020) Worse than measurement error: Consequences of inappropriate latent variable measurement models. Psychol Methods 25:30–45
Rigdon EE (2012) Rethinking partial least squares path modeling: in praise of simple methods. Long Range Plann 4:341–358
Rigdon EE, Sarstedt M, Ringle CM (2017) On comparing results from CB-SEM and PLS-SEM: five perspectives and five recommendations. Mark ZFP 39:4–16
Sarstedt M, Hair JF, Ringle CM, Thiele KO, Gudergan SP (2016) Estimation issues with PLS and CBSEM: where the bias lies!. J Bus Res 69:3998–4010
Sarstedt M, Ringle CM, Cheah J-H, Ting H, Moisescu OI, Radomir L (2020) Structural model robustness checks in PLS-SEM. Tour Econ (in press, online available)
Schlittgen R (2019) R package sempls: simulation, estimation and segmentation of composite based structural equation models (version 1.0.0). https://cran.r-project.org/web/packages/cbsem/index.html. Accessed 21 May 2020
Schlittgen R (2018) Estimation of generalized structured component analysis models with alternating least squares. Comput Stat 33:527–548
Schlittgen R, Ringle CM, Sarstedt M, Becker J-M (2016) Segmentation of PLS path models by iterative reweighted regressions. J Bus Res 69:4583–4592
Semadeni M, Withers MC, Trevis Certo S (2014) The perils of endogeneity and instrumental variables in strategy research: understanding through simulations. Strateg Manag J 35:1070–1079
Vale CD, Maurelli VA (1983) Simulating multivariate nonnormal distributions. Psychometrika 48:465–471
Wold HOA (1982) Soft modeling: the basic design and some extensions. In: Jöreskog KG, Wold HOA (eds) Systems under indirect observations, part II. North-Holland, Amsterdam, pp 1–54
Acknowledgements
Open Access funding provided by Projekt DEAL. Even though this research does not use the statistical software SmartPLS (http://www.smartpls.com), Ringle acknowledges a financial interest in SmartPLS.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Schlittgen, R., Sarstedt, M. & Ringle, C.M. Data generation for composite-based structural equation modeling methods. Adv Data Anal Classif 14, 747–757 (2020). https://doi.org/10.1007/s11634-020-00396-6
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11634-020-00396-6
Keywords
- Composite models
- Data generation
- Generalized structural component analysis
- GSCA
- Partial least squares
- PLS
- Structural equation modeling
- SEM