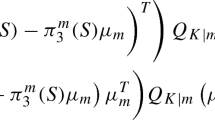Abstract
Several methods for variable selection have been proposed in model-based clustering and classification. These make use of backward or forward procedures to define the roles of the variables. Unfortunately, such stepwise procedures are slow and the resulting algorithms inefficient when analyzing large data sets with many variables. In this paper, we propose an alternative regularization approach for variable selection in model-based clustering and classification. In our approach the variables are first ranked using a lasso-like procedure in order to avoid slow stepwise algorithms. Thus, the variable selection methodology of Maugis et al. (Comput Stat Data Anal 53:3872–3882, 2000b) can be efficiently applied to high-dimensional data sets.






Similar content being viewed by others
Notes
SelvarClustIndep is implemented in C\(++\) and is available at http://www.math.univ-toulouse.fr/~maugis/.
SelvarMixR package is available at https://CRAN.R-project.org/package=SelvarMix.
clustvarselR package is available at https://CRAN.R-project.org/package=clustvarsel.
References
Banfield JD, Raftery AE (1993) Model-based Gaussian and non-Gaussian clustering. Biometrics 49(3):803–821
Biernacki C, Celeux G, Govaert G (2000) Assessing a mixture model for clustering with the integrated completed likelihood. IEEE Trans Pattern Anal Mach Intell 22(7):719–725
Bouveyron C, Brunet C (2014) Discriminative variable selection for clustering with the sparse Fisher-EM algorithm. Comput Stat 29:489–513
Celeux G, Govaert G (1995) Gaussian parsimonious clustering models. Pattern Recognit 28(5):781–793
Celeux G, Maugis C, Martin-Magniette ML, Raftery AE (2014) Comparing model selection and regularization approaches to variable selection in model-based clustering. J Fr Stat Soc 155:57–71
Dempster AP, Laird NM, Rubin DB (1977) Maximum likelihood from incomplete data via the EM algorithm (with discussion). J Roy Stat Soc B 39(1):1–38
Fraiman R, Justel A, Svarc M (2008) Selection of variables for cluster analysis and classification rules. J Am Stat Assoc 103:1294–1303
Friedman J, Hastie T, Tibshirani R (2007) Sparse inverse covariance estimation with the graphical lasso. Biostatistics 9(3):432–441
Friedman J, Hastie T, Tibshirani R (2014) glasso: graphical lasso—estimation of Gaussian graphical models. https://CRAN.R-project.org/package=glasso. Accessed 22 July 2014
Gagnot S, Tamby JP, Martin-Magniette ML, Bitton F, Taconnat L, Balzergue S, Aubourg S, Renou JP, Lecharny A, Brunaud V (2008) CATdb: a public access to arabidopsis transcriptome data from the URGV-CATMA platform. Nucleic Acids Res 36(suppl 1):D986–D990
Galimberti G, Montanari A, Viroli C (2009) Penalized factor mixture analysis for variable selection in clustered data. Comput Stat Data Anal 53:4301–4310
Kim S, Song DKH, DeSarbo WS (2012) Model-based segmentation featuring simultaneous segment-level variable selection. J Mark Res 49:725–736
Law MH, Figueiredo MAT, Jain AK (2004) Simultaneous feature selection and clustering using mixture models. IEEE Trans Pattern Anal Mach Intell 26(9):1154–1166
Lebret R, Iovleff S, Langrognet F, Biernacki C, Celeux G, Govaert G (2015) Rmixmod: the R package of the model-based unsupervised, supervised and semi-supervised classification mixmod library. J Stat Softw 67(6):241–270
Lee H, Li J (2012) Variable selection for clustering by separability based on ridgelines. J Comput Graph Stat 21:315–337
Maugis C, Celeux G, Martin-Magniette M (2009a) Variable selection for clustering with Gaussian mixture models. Biometrics 65(3):701–709
Maugis C, Celeux G, Martin-Magniette ML (2009b) Variable selection in model-based clustering: a general variable role modeling. Comput Stat Data Anal 53:3872–3882
Maugis C, Celeux G, Martin-Magniette ML (2011) Variable selection in model-based discriminant analysis. J Multivar Anal 102:1374–1387
Meinshausen N, Bühlmann P (2006) High-dimensional graphs and variable selection with the Lasso. Ann Stat 34(3):1436–1462
Murphy TB, Dean N, Raftery AE (2010) Variable selection and updating in model-based discriminant analysis for high-dimensional data with food authenticity applications. Ann Appl Stat 4:396–421
Nia VP, Davison AC (2012) High-dimensional Bayesian clustering with variable selection: the R package bclust. J Stat Softw 47(5):1–22
Pan W, Shen X (2007) Penalized model-based clustering with application to variable selection. J Mach Learn Res 8:1145–1164
Raftery AE, Dean N (2006) Variable selection for model-based clustering. J Am Stat Assoc 101(473):168–178
Schwarz G (1978) Estimating the dimension of a model. Ann Stat 6(2):461–464
Scrucca L, Raftery AE (2014) clustvarsel: a package implementing variable selection for model-based clustering in R. arXiv:1411.0606
Scrucca L, Fop M, Murphy TB, Raftery AE (2016) mclust 5: clustering, classification and density estimation using Gaussian finite mixture models. R J 8(1):289
Sun W, Wang J, Fang Y (2012) Regularized k-means clustering of high dimensional data and its asymptotic consistency. Electron J Stat 6:148–167
Tadesse MG, Sha N, Vannucci M (2005) Bayesian variable selection in clustering high-dimensional data. J Am Stat Assoc 100(470):602–617
Wang S, Zhu J (2008) Variable selection for model-based high-dimensional clustering and its application to microarray data. Biometrics 64(2):440–448
Xie B, Pan W, Shen X (2008) Penalized model-based clustering with cluster-specific diagonal covariance matrices and grouped variables. Electron J Stat 2:168–212
Zhou H, Pan W, Shen X (2009) Penalized model-based clustering with unconstrained covariance matrices. Electron J Stat 3:1473–1496
Funding
Funding was provide by Paris- Saclay-DIGITEO and ANR (Grant No. ANR-13-JS01-0001-01).
Author information
Authors and Affiliations
Corresponding author
Procedures to maximize penalized empirical contrasts
Procedures to maximize penalized empirical contrasts
1.1 The model-based clustering case
The EM algorithm for maximizing criterion (2) is as follows (Zhou et al. 2009). The penalized complete loglikelihood of the centered data set \(\bar{\mathbf {y}} = \big (\bar{\mathbf {y}}_1, \ldots , \bar{\mathbf {y}}_n \big )'\) is given by
where \(\varTheta _k=\varSigma _k^{-1}\) denotes the precision matrix of the kth mixture component. The EM algorithm of Zhou et al. (2009) maximizes at each iteration the conditional expectation of (5) given \(\bar{\mathbf {y}}\) and a current parameter vector \(\alpha ^{(s)}\): \({\mathbb {E}}\Big [L_{\text {c},(\lambda , \rho )}\big (\bar{\mathbf {y}}, \mathbf {z}, \alpha \big ) \mid \bar{\mathbf {y}}, \alpha ^{(s)}\Big ].\) The following two steps are repeated from an initial \(\alpha ^{(0)}\) until convergence. At the sth iteration of the EM algorithm:
-
E-step: The conditional probabilities \(t^{(s)}_{ik}\) that the ith observation belongs to the kth cluster are computed for \(i=1,\ldots ,n\) and \(k=1,\ldots ,K\),
$$\begin{aligned} t^{(s)}_{ik} = \mathbb {P}\big (z_{ik} = 1 \mid \bar{\mathbf {y}}, \alpha ^{(s)}\big ) = \frac{\pi _k^{(s)} \phi \Big ( \bar{\mathbf {y}}_i \mid \mu ^{(s)}_k,\varSigma ^{(s)}_k \Big )}{ \sum _{k' = 1}^K \pi _{k'}^{(s)} \phi \Big (\bar{\mathbf {y}}_i \mid \mu ^{(s)}_{k'}, \varSigma ^{(s)}_{k'} \Big )}. \end{aligned}$$ -
M-step : This step consists of maximizing the expected complete log-likelihood derived from the E-step. It leads to the following mixture parameter updates:
-
The updated proportions are \(\pi ^{(s+1)}_k = \frac{1}{n} \sum _{i = 1}^n t^{(s)}_{ik}\) for \(k=1,\ldots ,K\).
-
Compute the updated means \(\mu ^{(s+1)}_1, \ldots , \mu ^{(s+1)}_K\) using formulas (14) et (15) of Zhou et al. (2009): the jth coordinate of \(\mu ^{(s+1)}_k\) is the solution of the following equations:
$$\begin{aligned} \text {if} \quad \left| \sum _{i = 1}^n t^{(s)}_{ik} \left[ \underset{v \ne j}{\sum _{v = 1}^p} \left( \bar{\mathbf {y}}_{ij} - \mu ^{(s)}_{k v}\right) \varTheta ^{(s)}_{k,v j} + \bar{\mathbf {y}}_{ij} \varTheta ^{(s)}_{k,jj}\right] \right| \le \lambda , \quad \text {then} \quad \mu ^{(s+1)}_{kj} = 0, \end{aligned}$$otherwise:
$$\begin{aligned}&\left[ \sum _{i = 1}^n t^{(s)}_{i k}\right] \mu ^{(s+1)}_{kj} \varTheta ^{(s)}_{k,jj} + \ \lambda \ \text {sign}\left( \mu ^{(s+1)}_{kj}\right) \\&\quad = \sum _{i = 1}^n t_{ik}^{(s)} \sum _{v = 1}^p \bar{y}_{iv} \varTheta ^{(s)}_{k,v j} \\&\qquad - \left[ \sum _{i = 1}^n t^{(s)}_{i k}\right] \left[ \left( \sum _{v = 1}^p \mu ^{(s)}_{kv} \varTheta ^{(s)}_{k,vj}\right) - \mu ^{(s)}_{kj} \varTheta ^{(s)}_{k, jj}\right] . \end{aligned}$$ -
For all \(k=1,\ldots ,K\), the covariance matrix \(\varSigma _k^{(s+1)}\) is obtained via the precision matrix \(\varTheta _k^{(s+1)}\). The glasso algorithm (available in the R package glasso of Friedman et al. 2014) is used to solve the following minimization problem on the set of symmetric positive definite matrices (denoted \(\varTheta \succ 0\)):
$$\begin{aligned} \underset{\varTheta \succ 0}{\mathop {\mathrm {arg\,min}}}\left\{ -\ln \text {det}\left( \varTheta \right) + \text {trace}\left( S_k^{(s+1)} \varTheta \right) + \rho _k^{(s+1)} \Vert \varTheta \Vert _1\right\} , \end{aligned}$$where \( \rho _k^{(s+1)} = 2 \rho \left( \sum _{i = 1}^n t^{(s)}_{ik}\right) ^{-1}\) and
$$\begin{aligned} S^{(s+1)}_k = \frac{\sum _{i = 1}^n t^{(s)}_{ik}(\bar{\mathbf {y}}_i - \mu ^{(s+1)}_k) (\bar{\mathbf {y}}_i - \mu ^{(s+1)}_k)^\top }{\sum _{i = 1}^n t^{(s)}_{ik}}. \end{aligned}$$
-
1.2 The classification case
The maximization of the regularized criterion (4) at \(\mu _1, \ldots , \mu _K\) and \(\varTheta _1, \ldots , \varTheta _K\) is achieved using an algorithm similar to the one presented in Sect. A.1 when the labels \(z_i\) are known.
The jth coordinate of the mean vector \(\mu _k\) is the solution of the following equations:
otherwise:
To estimate the sparse precision matrices \(\varTheta _1, \ldots , \varTheta _K\) from the data set \(\mathbf {y}\) and the labels \(\mathbf {z}\), we use the glasso algorithm to solve the following minimization problem on the set of symmetric positive definite matrices
for each \(k = 1, \ldots , K\). The \(\ell _1\) regularization parameter in (6) is given by \(\rho _k = 2 \rho \left( \sum _{i = 1}^n \mathbb {1}_{\{z_{i} = k\}}\right) ^{-1}\) and the empirical covariance matrix \(S_k\) by
Then, coordinate descent maximization in \((\mu _1, \ldots , \mu _K)\) and \((\varTheta _1, \ldots , \varTheta _K)\) is run until convergence.
Rights and permissions
About this article
Cite this article
Celeux, G., Maugis-Rabusseau, C. & Sedki, M. Variable selection in model-based clustering and discriminant analysis with a regularization approach. Adv Data Anal Classif 13, 259–278 (2019). https://doi.org/10.1007/s11634-018-0322-5
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11634-018-0322-5