Simulating mixtures of multivariate data with fixed cluster overlap in FSDA library

Abstract

We extend the capabilities of MixSim, a framework which is useful for evaluating the performance of clustering algorithms, on the basis of measures of agreement between data partitioning and flexible generation methods for data, outliers and noise. The peculiarity of the method is that data are simulated from normal mixture distributions on the basis of pre-specified synthesis statistics on an overlap measure, defined as a sum of pairwise misclassification probabilities. We provide new tools which enable us to control additional overlapping statistics and departures from homogeneity and sphericity among groups, together with new outlier contamination schemes. The output of this extension is a more flexible framework for generation of data to better address modern robust clustering scenarios in presence of possible contamination. We also study the properties and the implications that this new way of simulating clustering data entails in terms of coverage of space, goodness of fit to theoretical distributions, and degree of convergence to nominal values. We demonstrate the new features using our MATLAB implementation that we have integrated in the Flexible Statistics for Data Analysis (FSDA) toolbox for MATLAB. With MixSim, FSDA now integrates in the same environment state of the art robust clustering algorithms and principled routines for their evaluation and calibration. A spin off of our work is a general complex routine, translated from C language to MATLAB, to compute the distribution function of a linear combinations of non central $\chi ^2$ random variables which is at the core of MixSim and has its own interest for many test statistics.

1 Introduction

The empirical analysis and assessment of statistical methods require synthetic data generated under controlled settings and well defined models. Under non-asymptotic conditions and in presence of outliers the performances of robust estimators for multiple regression or for multivariate location and scatter may strongly depend on the number of data units, the type and size of the contamination and the position of the outliers.

For example, Riani et al. (2014) have shown how the properties of the main robust regression estimators (the parameter estimates, their variance and bias, the size and power curves for outlier detection) vary as the distance between the main data and the outliers, initially remote, decreases. The framework is parametrised by a measure of overlap $\lambda$ between the two groups of data. Then, a theoretical overlapping index is defined as the probability of intersection between the cluster of outliers and a strip around the regression plane where the cluster of “good” data resides. An empirical overlap index is computed accordingly by simulation. The left panel of Fig. 1 shows examples from Riani et al. (2014) of cluster pairs generated under this parametrised overlap family and used to show how smoothly the behavior of robust regression estimators change with the overlap parameter $\lambda$.

Fig. 1

Left typical cluster pairs for different overlap parameter values $\lambda$, simulated in the regression framework proposed by Riani et al. (2014); the parallelogram defines an empirical overlapping region. Right the more complex M5 dataset of Garcia-Escudero et al. (2008), simulated by careful selection of the mixture model parameters ($\beta =8$ and $(a,b,c,d,e,f)=(1,45,30,15,-10,15)$ in Eqs. (1) and (2) respectively, with proportions chosen so that the first cluster size is half the size of clusters two and three; uniformly distributed outliers are added in the bounding box of the data)

More in general, to address realistic multivariate scenarios, much more complex cluster structures, possibly contaminated by different kind of outliers, are required. Typically, the data are generated by specifying directly the groups location, scatter and pairwise overlap, but this approach can be laborious and time consuming even in the simple bivariate case. Consider for example the M5 dataset in the right panel of Fig. 1 proposed by Garcia-Escudero et al. (2008) for assessing some trimming-based robust clustering methods. The data are obtained from three normal bivariate distributions with fixed centers but different scales and proportions. One of the components strongly overlaps with another one. A 10 % background noise is added uniformly distributed in a rectangle containing the three mixture components in an ad hoc way to fill the bivariate range of simulated data. This configuration was reached through careful choice of six parameters for the groups covariance matrices (Eq. 2), to control the differences between their eigenvalues and therefore the groups scales and shapes, and a parameter (together with its opposite) for the groups centroid (Eq. 1), to specify how strongly the clusters should overlap.

$$\begin{aligned} \mathbf {\mu _1}= & {} (0,\beta ) \ \qquad \;\;\, \mathbf {\mu _2} = (\beta ,0) \qquad \;\;\, \, \mathbf {\mu _3} = (-\beta ,-\beta ) \qquad \end{aligned}$$

(1)

$$\begin{aligned} \mathbf {\Sigma _1}= & {} \begin{pmatrix} 1 &{}\quad 0 \\ 0 &{}\quad a \\ \end{pmatrix} \qquad \mathbf {\Sigma _2} = \begin{pmatrix} b &{}\quad 0 \\ 0 &{}\quad c \\ \end{pmatrix} \qquad \mathbf {\Sigma _3} = \begin{pmatrix} d &{}\quad e \\ e &{}\quad f \\ \end{pmatrix} \end{aligned}$$

(2)

Small values of $\beta$ produce heavily overlapping clusters, whereas large values increase their separation. In $v>2$ dimensions, Garcia-Escudero et al. (2008) simply set the extra $v-2$ elements of the centroids to 0, the diagonal elements of the covariance matrices to 1 and the off-diagonal elements to 0. Popular frameworks for multivariate normal mixture models that follow this data generation approach include EMMIX (McLachlan and Peel 1999) and MIXMOD (Biernacki et al. 2006).

There are therefore two general approaches to simulate clustered data, one where the separation and overlap between clusters are essentially controlled by the model parameters, like in Garcia-Escudero et al. (2008), and another where, on the contrary, a pre-specified nominal overlap level determines the model parameters, as in Riani et al. (2014) in the context of multiple outlier detection. We have adopted and extended an overlap control scheme of the latter type called MixSim, by Maitra and Melnykov (2010). In MixSim, samples are generated from normal mixture distributions according to a pre-specified overlap defined as a sum of misclassification probabilities, introduced in Sect. 3. The approach is flexible, applies in any dimension and is applicable to many traditional and recent clustering settings, reviewed in Sect. 2. Other frameworks specifically conceived for overlap control are ClusterGeneration (Qiu and Joe 2006) and OCLUS (Steinley and Henson 2005), which have however some relevant drawbacks. ClusterGeneration is based on a separation index defined in terms of cluster quantiles in the one-dimensional projections of the data space. The index is therefore simple and applicable to clusters of any shape but, as it is well known, even in the bi-dimensional case conclusions taken on the basis of projections can be partial and even misleading. OCLUS can address only three clusters overlap at the same time, has limitations on generating groups with different correlation structures and, finally, is no longer available as software package.

This paper describes three types of contributions that we have given to the MixSim framework, computational, methodological and experimental.

First of all, we have ported the MixSim R package, including the long and complex C code at the basis of the misclassification probabilities estimation, to the MATLAB FSDA toolbox of Riani et al. (2012). Flexible Statistics for Data Analysis (FSDA) is a statistical library providing a rich variety of robust and computationally efficient methods for the analysis of complex data, possibly affected by outliers and other sources of heterogeneity. A challenge of FSDA is to grant outstanding computational performances without resorting to compiled of parallel processing deployments, which would sacrifice the clarity of our open source codes. With MixSim, FSDA now integrates in the same environment several state of the art (robust) clustering algorithms and principled routines for their evaluation and calibration. The only other integrated tool, similar in aim and purpose but at some extent different in usability terms, is CARP, also by the MixSim authors (Melnykov and Maitra 2011): being a C-package based on the integration of user-provided clustering algorithms in executable form, CARP has the shortcoming to require much more familiarity of the user with programming, compilation and computer administration tasks.

We have introduced three methodological innovations (Sect. 4). The first is about the overlap control. In the original MixSim formulation, the user can specify the desired maximum and/or average overlap values for k groups in v dimensions. However, given that very different clustering scenarios can produce the same value of maximum and/or average overlap, we have extended the control of the generated mixtures to the overlapping standard deviation. We can now generate overlapping groups by fixing up to two of the three statistics. This new feature is described in Sect. 4.1. The second methodological contribution relates to the control of the cluster shape. We have introduced a new constraint on the eigenvalues of the covariance matrices in order to control the ratio among the lengths of the ellipsoids axes associated with the groups (i.e. departures from sphericity) and the relative cluster sizes. This new MixSim feature allows us to simulate data which comply with the TCLUST model of Garcia-Escudero et al. (2008). The new constraint and its relation with the maximum eccentricity for all group covariance matrices, already in the MixSim theory, are introduced in Sects. 2 and 3; then, they are illustrated with examples from FSDA in Sect. 4.2.

Our third contribution consists in providing new tools for either contaminating existing datasets or adding contamination to a mixture simulated with pre-specified overlap features. These new contamination schemes, which range from noise generated from symmetric/asymmetric distributions to component-wise contamination, passing through point mass contamination, are detailed in Sect. 4.3.

Our experimental contributions, summarized in Sect. 5 and detailed in the supplementary material, focus on the validation of the properties of the new constraints, on goodness of fit to theoretical distributions and on degree of coverage of the parameter space. More precisely, we show by simulation that our new constraints give rise to clusters with empirical overlap consistent with the nominal values selected by the user. Then we show that datasets of different clustering complexities typically used in the literature (e.g. the M5 dataset of Garcia-Escudero et al. (2008)) can be easily generated with MixSim using the new constraints. We also investigate the extent to which the hypothesis made by Maitra and Melnykov (2010) about the distribution of pairwise overlaps holds. A final experimental exercise tries to answer an issue left open by the MixSim theory, which is about the parameter space coverage. More precisely, we investigate if different runs for the same pre-specified values of the maximum, average and (now) standard deviation of overlap lead to configuration parameters that are essentially different.

In “Appendix 1” we describe a new MATLAB function to compute the distribution function of a linear combination of non central $\chi ^2$ random variables. This routine is at the core of MixSim and was only available in the original C implementation of his author. However, given the relevance of this routine also in other contexts (see, e.g., Lindsay 1995; Cerioli 2002), we have created a stand alone function which extends the MATLAB existing routines. In “Appendix 2” we discuss the time required to run our open code MATLAB implementation in relation to the R MixSim package which largely relies on compiled C code.

2 Model-based (robust) clustering

Our interest on methods for simulating clustered data under well defined probabilistic models and controlled settings is naturally linked to the model-based approach to clustering, where data $x_1, \ldots ,x_n$ are assumed to be a random sample from k sub-populations defined by a v-variate density $\phi (\cdot ;\theta _j)$ with unknown parameter vectors $\theta _j$, for $j=1,\ldots , k$. It is customary to distinguish between two frameworks for model-based clustering, depending on the type of membership of the observations to the sub-populations (see e.g. McLachlan 1982):

• The mixture modeling approach, where there is a probability $\pi _j$ that an observation belongs to a mixture component ($\pi _j \ge 0; \; \sum _{j=1}^{k} \pi _j=1$). The data are therefore assumed to come from a distribution with density $\sum _{j=1}^k \pi _j \phi (\cdot ;\theta _j)$, which leads to the (mixture) likelihood

  $$\begin{aligned} \prod _{i=1}^n \left[ \sum _{j=1}^k \pi _j \phi (x_i;\theta _j) \right] . \end{aligned}$$

  (3)

  In this framework each observation is naturally assigned to the cluster to which it is most likely to belong a posteriori, conditionally on the estimated mixture parameters.

• The “Crisp” clustering approach, where there is a unique classification of each observation into k non-overlapping groups, labeled as

  $$\begin{aligned} R_1, \ldots ,R_k. \end{aligned}$$

  Assignment is based on the (classification) likelihood (e.g. Fraley and Raftery (2002) or McLachlan and Peel (2004)):

  $$\begin{aligned} \prod _{j=1}^k \prod _{i\in R_j} \phi (x_i;\theta _j). \end{aligned}$$

  (4)

Traditional clustering methods are based on Gaussian distributions, so that $\phi (\cdot ;\theta _j)$, $j=1,\ldots ,k$, is the multivariate normal density with parameters $\theta _j = (\mu _j ; \Sigma _j)$ given by the cluster mean $\mu _j$ and the cluster covariance matrix $\Sigma _j$: see, e.g., Eqs. (1) and (2). This modeling approach often is too simplistic for real world applications, where data may come from non-elliptical or asymmetric families and may contain several outliers, either isolated or intermediate between the groups. Neglecting these complications may lead to wrong classifications and distorted conclusions on the general structure of the data. For these reasons, some major recent developments of model-based clustering techniques have been towards robustness (Garcia-Escudero et al. 2010; Ritter 2014).

In trimmed clustering (TCLUST) (Garcia-Escudero et al. 2008), the popular robust clustering approach that we consider in this work, the “good” part of the data contributes to a likelihood equation that extends the classification likelihood (4) with unknown weights $\pi _j$ to take into account the different group sizes:

$$\begin{aligned} \prod _{j=1}^k \prod _{i\in R_j} \pi _j \phi (x_i;\mu _j,\Sigma _j). \end{aligned}$$

(5)

In addition, in order to cope with the potential presence of outliers, the cardinality of $\bigcup _{j=1}^k R_j$ is smaller than n and it is equal to $\lfloor n (1-\alpha )]\rfloor$. That is, a proportion $\alpha$ of the sample which is associated with the smallest contributions to the likelihood is not considered in the objective function and in the resulting classification. In our FSDA implementation of TCLUST, it is possible to choose between Eqs. (3), (4) and (5) together with the trimming level $\alpha$.

Without constraints on the covariance matrices the above likelihood functions can easily diverge if, even for a single cluster j, during the optimization process $\text{ det }(\hat{\Sigma _j})$ becomes very small. As a result, spurious (non-informative) clusters may occur. Traditionally, constraints are imposed on the kv, $\frac{1}{2}kv(v + 1)$ and $(k-1)$ model parameters, associated respectively to all $\mu _j$, $\Sigma _j$ and $\pi _j$, on the basis of the well known eigenvalue decomposition, proposed in the mixture modeling framework by Banfield and Raftery (1993). TCLUST, in each step of the iterative trimmed likelihood optimization procedure, imposes the constraint that the ratio between the largest and smallest eigenvalue of the estimated covariance matrices of the k groups $\hat{\Sigma }_j, \; j = 1 , \ldots , k$, does not exceed a predefined maximum eccentricity constant, say $e_{tclust}\ge 1$:

$$\begin{aligned} \frac{\text{ max }_{j}d_{1j}}{\text{ min }_{j}d_{vj}} \le e_{tclust}, \end{aligned}$$

(6)

where $d_{1j}\ge d_{2j}\ge \ldots \ge d_{vj}$ are the ordered eigenvalues of the covariance matrix of group j, $j=1, \ldots , k$. Clearly, if the ratio of Eq. (6) reduces to 1 we obtain spherical clusters (i.e. the trimmed k-MEANS solution). The application of the restriction involves a constrained minimization problem cleverly solved by Fritz et al. (2013) and now implemented also in FSDA.

Recently, Garcia-Escudero et al. (2014) have specifically addressed the problem of spurious solutions and how to avoid it in an automatic manner with appropriate restrictions. In stressing the pervasiveness of the problem, they show that spurious clusters can occur even when the likelihood optimization is applied to artificial datasets generated from the known probabilistic (mixture) model of the clustering estimator itself. This motivates the need of data simulated under the same restrictions that are assumed in the clustering estimation process and, thus, the effort we made to extend the TCLUST restriction (6) to the MixSim simulation environment.

3 Simulating clustering data with MixSim

MixSim generates data from normal mixture distributions with likelihood (3) according to pre-specified synthesis statistics on the overlap, defined as sum of the misclassification probabilities. The goal is to derive the mixture parameters from the misclassification probabilities (or overlap statistics). This section is intended to give some terms of reference for the method in order to better understand the contribution that we give. The details can be found in Maitra and Melnykov (2010) and, for its R implementation, in Melnykov et al. (2012).

The misclassification probability is a pairwise measure defined between two clusters i and j ($i \ne j =1, \ldots , k$), indexed by $\phi (x; \mu _i,\Sigma _i)$ and $\phi (x; \mu _j,\Sigma _j)$, with probabilities of occurrence $\pi _i$ and $\pi _j$. It is not symmetric and it is therefore defined for the cluster j with respect to the cluster i (i.e. conditionally on x belonging to cluster i):

$$\begin{aligned} w_{j|i} = Pr[ \pi _i \phi (x;\mu _i,\Sigma _i) < \pi _j \phi (x;\mu _j,\Sigma _j)]. \end{aligned}$$

(7)

We have that $w_{j|i} = w_{i|j}$ only for clusters with same covariance matrix $\Sigma _i=\Sigma _j$ and same occurrence probability (or mixing proportion) $\pi _i=\pi _j$. As in general $w_{j|i} \ne w_{i|j}$, the overlap between groups i and j is defined as sum of the two probabilities:

$$\begin{aligned} w_{ij} = w_{j|i} + w_{i|j} \quad i,j=1,2,\ldots , k \end{aligned}$$

(8)

In the MixSim implementation¹, the matrix of the misclassification probabilities $w_{j|i}$ is indicated with OmegaMap. Then, the average overlap, indicated with BarOmega, is the sum of the off-diagonal elements of OmegaMap divided by $k(k-1)/2$, and the maximum overlap, MaxOmega, is $\max _{i \ne j}w_{ij}$. The central result of Maitra and Melnykov (2010) is the formulation of the misclassification probability $w_{j|i}$ in terms of the cumulative distribution function of linear combinations of v independent non-central $\chi ^2$ random variables $U_l$ and normal random variables $W_l$. The starting point is matrix $\Sigma _{j|i}$ defined as $\Sigma ^{1/2}_i \Sigma ^{-1}_j \Sigma ^{1/2}_i$. The eigenvalues and eigenvectors of its spectral decomposition are denoted respectively as $\lambda _l$ and $\gamma _{l}$, with $l=1, \ldots , v$. Then, we have

$$\begin{aligned} \displaystyle \omega _{j \vert i}= & {} Pr_{N_p(\mu _i,\Sigma _i)} \left[ \sum \limits _{\begin{array}{c} l=1\\ l: \lambda _l \ne 1 \end{array}} ^v (\lambda _l-1)U_l+ 2 \sum \limits _{\begin{array}{c} l=1\\ l: \lambda _l = 1 \end{array}} ^v \delta _l W_l \right. \nonumber \\&\qquad \qquad \qquad \quad \left. \le \sum \limits _{\begin{array}{c} l=1\\ l: \lambda _l \ne 1 \end{array}} ^v \frac{\displaystyle \lambda _l \delta _l^2}{\displaystyle \lambda _l-1}- \sum \limits _{\begin{array}{c} l=1\\ l: \lambda _l = 1 \end{array}} ^v \delta _l^2+ \log \frac{\displaystyle \pi _j^2\vert \Sigma _i\vert }{\displaystyle \pi _i^2\vert \Sigma _j\vert } \right] \end{aligned}$$

(9)

with $\delta _l = \gamma ^{'}_{l}\Sigma _{i}^{-1/2}(\mu _i-\mu _j)$.

Note that, when all $\lambda _l = 1$, $\omega _{j \vert i}$ reduces to a combination of independent normal distributions $W_l=N(0,1)$. On the other hand, when all $\lambda _l\ne 1$, $\omega _{j \vert i}$ is only based on the non-central $\chi ^2$-distributions $U_l$, with one degree of freedom and with centrality parameter $\lambda _{l}^{2}\delta _{l}^{2}/(\lambda _{l}-1)^{2}$. The computation of the linear combination of non-central $\chi ^2$-distributions has no exact solution and requires the AS 155 algorithm of Davies (1980), which involves the numerical inversion of the characteristic function (Davies 1973). Computationally speaking, this is the more demanding part of MixSim. In the appendices we give the details of our MATLAB implementation of this routine.

To reach a pre-specified maximum or average level of overlap, the idea is to inflate or deflate the covariance matrices of groups i and j by multiplying them by a positive constant c. In MixSim, this is done by the function FindC, which searches the constant in intervals formed by positive or negative powers of 2. For example, if the first interval is $\left[ 0 \;\; 1024 \right]$, then if the new maximum overlap found using $\hbox {c}=512$ is smaller than the maximum required overlap, then the new interval becomes $\left[ 512 \;\; 1024 \right]$ (i.e. c has to be increased and the new candidate is $c=(512+1024)/2$), else the new interval becomes $\left[ 0 \;\; 512 \right]$ (i.e. c has to be decreased and the new candidate is $c=(0+512)/2$).

So, the mixture model used to simulate data by controlling the maximum or the average overlap between the mixture components is reproduced by MixSim in three steps:

• 1. First of all, the occurrence probabilities (mixing proportions) are generated in $\left[ 0 \;\; 1 \right]$ under user-specified constraints and the obvious condition $\sum _j^k \pi _j=1$; the cluster sizes are drawn from a multinomial distribution with such occurrence probabilities. The mean vectors of the mixture model $\mu _j$ (giving rise to the cluster centroids) are generated independently and uniformly from a v-variate hyper-cube within desired bounds. Random covariance matrices are initially drawn from a Wishart distribution. In addition, restriction (10) is applied to control cluster eccentricity. This initialization step is repeated if these mixture model parameters bring to an asymptotic average (or maximum) overlap, computed using limiting expressions given in Maitra and Melnykov (2010), larger than the desired average (or maximum) overlap.

• 2. Equation (9) is used to estimate the pairwise overlaps and the corresponding BarOmega (or MaxOmega).

• 3. If BarOmega (or MaxOmega) is close enough to the desired value we stop and return the final mixture parameters, otherwise the covariance matrices are rescaled (inflated/deflated) and step 2 is repeated; for heterogeneous clusters, it is possible to indicate which clusters participate to the inflation/deflation.

To control simultaneously the maximum or average overlap levels, MixSim first applies the above algorithm with the maximum overlap constraint. Then, it keeps fixed the two components with maximum overlap and applies the inflation/deflation process to the other components to reach the average overall overlap. Note that not every combination of BarOmega and MaxOmega can be reached: restrictions are BarOmega $\le$ MaxOmega, and MaxOmega $\le k(k-1)/2\cdot$ BarOmega.

To avoid degeneracy of the likelihood function (3), eigenvalue constraints are considered also in MixSim, but the control of an eccentricity measure, say $e_{mixsim}$, is done at individual mixture component level and only in the initial simulation step. By using the same notation as in (6), we thus have that for all $\hat{\Sigma }_j$

$$\begin{aligned} \sqrt{1-\frac{d_{vj}}{d_{1j}}} = e_{j} \le e_{mixsim}. \end{aligned}$$

(10)

Therefore, differently from (6), in MixSim only the r covariance matrices which violate condition (10) are independently shrunk so that $e^{new}_{j_{1_{}}} = e^{new}_{j_{2}} = \ldots e^{new}_{j_{r}} = e_{mixsim}$ being $j_{1}, j_{2}, \ldots j_{r}$ the indexes of the matrices violating (10).

4 MixSim advances in FSDA

We now illustrate the two main new features introduced with the MATLAB implementation of MixSim distributed with our FSDA toolbox. The first is the control of the standard deviation of the $k(k-1)/2$ pairwise overlaps (that we call StdOmega), which is useful to monitor the variability of the misclassification errors. This case was not addressed in the general framework of Maitra and Melnykov (2010) even if its usefulness was explicitly acknowledged in their paper, together with the difficulty of the related implementation. In fact, in order to circumvent the problem, in package CARP Melnykov and Maitra (2011, 2013) included a new generalized overlap measure meant to be an alternative to the specification of the average or the maximum overlap. The performance of this alternative measure has yet to be studied under various settings.

The second is the restrfactor option which is useful not only to avoid singularities in each step of the iterative inflation/deflation procedure, but also to control the degree of departure from homogeneous spherical groups.

The third consists in new contamination schemes.

4.1 Control of standard deviation of overlapping (StdOmega)

The inflation/deflation process described in the previous section, based on searching for a multiplier to be applied to the covariance matrices, is extended to the target of reaching the required standard deviation of overlap. StdOmega can be searched on its own or in combination with a prefixed level of average overlapping BarOmega.

In the first case we have written a new function called FindCStd. This new routine contains a root-finding technique and is very similar to FindC described in the previous section. On the other hand, if we want to fix both the average and the standard deviation of overlap (i.e both BarOmega and StdOmega) the procedure is much more elaborate and it is based on the following steps.

• 1. Generate initial cluster parameters.

• 2. Check if the requested StdOmega is reachable. We find the asymptotic (i.e. maximum reachable) standard deviation, defined as

  $$\begin{aligned} {\widehat{\texttt {StdOmega}}}_\infty = \sqrt{{\texttt {BarOmega}}\cdot ({{\widehat{\texttt {MaxOmega}}}}_\infty -{\texttt {BarOmega}})} \end{aligned}$$

  where ${{\widehat{\texttt {MaxOmega}}}}_\infty$ is the maximum (asymptotic) overlap defined by Maitra and Melnykov (2010) which can be obtained by using initial cluster parameters. If ${{\widehat{\texttt {StdOmega}}}}_\infty < \texttt {StdOmega}$ discard realization and redo step 1, else go to step 2 which loops over a series of candidates ${\widehat{\texttt {MaxOmega}}}$.

• 3. Given a value of ${\widehat{\texttt {MaxOmega}}}$ (as starting value we use 1.1 $\texttt {BarOmega}$) we find, using just the two groups which in step 1 produced the highest overlap, the constant c which enables to obtain ${\widehat{\texttt {MaxOmega}}}$. This is done by calling routine findC. We use this value of c to correct the covariance matrices of all groups and compute the average and maximum overlap. If the average overlap is smaller than BarOmega, we immediately compute ${\widehat{\texttt {StdOmega}}}$, skip step 3 and go directly to step 4, else we move to step 3.

• 4. Recompute parameters using the value of c found in previous step and use again routine $\texttt {findC}$ in order to find the value of c which enables us to obtain ${\texttt {BarOmega}}$. Routine $\texttt {findC}$ is called excluding from the iterative procedure the two clusters which produced ${\widehat{\texttt {MaxOmega}}}$ and using as upper bound of the interval for c the value of 1. Using this new value of $0<c<1$, we recalculate the probabilities of overlapping and compute ${\widehat{\texttt {StdOmega}}}$

• 5. if the ratio $\texttt {StdOmega}/ {{\widehat{\texttt {StdOmega}}}}>1$, we increase the value of ${\widehat{\texttt {MaxOmega}}}$ else we decrease it by a fixed percentage, using a greedy algorithm.

• 6. Steps 2–4 are repeated until convergence. In each step of the iterative procedure we check that the decrease in the candidate ${\widehat{\texttt {MaxOmega}}}$ is not smaller than BarOmega. This happens when the requested value of StdOmega is too small. Similarly, in each step of the iterative procedure we check whether ${\widehat{\texttt {MaxOmega}}}>{\texttt {MaxOmega}}_\infty$. This may happen when the requested value of StdOmega is too large. In these last two cases, a message informs the user about the need of increasing/decreasing the required StdOmega and we move to step 1 considering another set of candidate values. Similarly, every time routine findC is called, in the unlikely case of no convergence we stop the iterative procedure and move to step 1 considering another set of simulated values.

The new function, which enables us to control both the mean and the standard deviation of misclassification probabilities is called OmegaBarOmegaStd.

Fig. 2

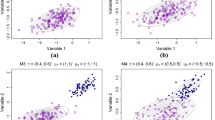
Datasets obtained for $k=4$, $v=5$, $n=200$ and BarOmega $\ =$ 0.10, when StdOmega is 0.15 (top) or 0.05 (bottom). Under the scatterplots, the corresponding matrices of misclassification probabilities (OmegaMap in the MixSim notation). The MATLAB output structure largesigma is obtained for StdOmega $\,\ =0.15$, while smallsigma is obtained for StdOmega $\,\,\ =0.05$. Note that when StdOmega is large, two groups show a strong overlap ($\omega _{3,4}\,+\,\omega _{4,3}=0.4040$) and that $\min ($ largesigma.OmegaMap+largesigma.OmegaMap $^T)\,<\,$ $\min ($ smallsigma.OmegaMap+smallsigma.OmegaMap $^T)$

Fig. 3

Convergence of the ratio between the standard deviation of the required overlap and the standard deviation of the empirical overlap, for the examples of Fig. 2. Left panel refers to the case of StdOmega = 0.15

Figures 2 and 3 show the application of the new procedure when the code

is run with $k=4$, $v=5$, $n=200$ and two overlap settings where BarOmega $\,=\,0.10$ and StdOmega is set in one case to 0.15 and in the other case to 0.05. Of course, the same initial conditions are ensured by restoring the random number generator settings. When StdOmega is large, groups 3 are 4 show a strong overlap ($\omega _{3,4}=0.1476$), while groups 1, 2, 3 are quite separate. When StdOmega is small, the overlaps are much more similar. Note also the boxplots on the main diagonal of the two plots. When StdOmega is small the range of the boxplots is very similar. The opposite happens when StdOmega is large. Figure 3 shows that the progression of the ratio for the two requested values of StdOmega is rapid and the convergence to 1, with a tolerance of $10^{-6}$, is excellent.

4.2 Control of degree of departure from sphericity (restrfactor)

In the original MixSim implementation constraint (10) is applied just once when the covariance matrices are initialized. On the other hand, we implement constraint (6) in each step of the iterative procedure which is used to obtain the required overlapping characteristics without deteriorating the computational performance of the method.

The application of the restriction factor to the matrix containing the eigenvalues of the covariance matrices of the k groups is done in FSDA using function restreigen. There are two features which make this application very fast. The first is the adoption of the algorithm of Fritz et al. (2013) for solving the minimization problem with constraints without resorting to the Dykstra algorithm. The second is that, in applying the restriction on all clusters during each iteration, matrices $\Sigma _1^{0.5}, \ldots , \Sigma _k^{0.5}$, $\Sigma _1^{-1}, \ldots , \Sigma _k^{-1}$ and scalars $|\Sigma _1|, \ldots , |\Sigma _k|$, which are the necessary ingredients to compute the probabilities of misclassification [see Eq. (9)], are computed using simple matrix multiplication, exploiting the restricted eigenvalues previously found. For example if $\lambda _{1j}^*, \ldots , \lambda _{vj}^*$ are the restricted eigenvalues for group j and $V_j$ is the corresponding matrix of the eigenvectors, then

$$\begin{aligned} \Sigma _j^{-1}= & {} V_j \text{ diag }( 1/\lambda _{1j}^*, \ldots , 1/\lambda _{vj}^*) V_j^T \\ \Sigma _j^{0.5}= & {} V_j \text{ diag }(\sqrt{\lambda _{1j}^*}, \ldots , \sqrt{\lambda _{vj}^*}) V_j^T \\ |\Sigma _j|= & {} \prod _{r=1}^v {\lambda _{rj}^*}. \end{aligned}$$

These matrices (determinants) are then used in their scaled version (e.g. $c^{-1} \Sigma _j^{-1}$) for each tentative value of the inflation/deflation constant c. Note that the introduction of this restriction cannot be addressed with the standard procedure of Maitra and Melnykov (2010), as in Eq. (9) the summations in correspondence of the eigenvalues equal to 1 were not implemented.

Below we give an example of application of this restriction.

In the first case we fix restrfactor to 1.1 in order to find clusters that are roughly homogeneous. In the second case, no constraint is imposed on the ratio of maximum and minimum eigenvalue among clusters, so elliptical shape clusters are allowed. In both cases the same random seed together with the same level of average and maximum overlap is used.

Fig. 4

Effect of the restrfactor option: when set to a value very close to 1 (top), clusters are forced to be roughly homogeneous. When the constraint is not used (bottom) the clusters are clearly heterogeneous

Figure 4 shows the scatterplot of the datasets generated with

for $n=200$ (where spmplot is the FSDA function to generate a scatterplot with additional features such as multiple histograms or multiple boxplots along the diagonal, and interactive legends which enable to show/hide the points of each group). In the bottom panel of the figure there is one group (Group 3, with darker symbol) which is clearly more concentrated than the others: this is the effect of not using a TCLUST restriction close to 1.

As pointed out by an anonymous referee, the eigenvalue constraint which is used is not scale invariant and this lack of invariance propagates to the estimated mixture parameters. This makes even more important the need of having a very flexible data mixture generating tool capable to address very different simulation schemes.

4.3 Control on outlier contamination

In the original MixSim implementation it is possible to generate outliers just from the uniform distribution. In our implementation we allow the user to simulate outliers from the following 4 distributions (possibly in a combined way): uniform, $\chi ^2$, Normal, and Student T. In the case of the last three distributions, we rescale the candidate random draws in the interval [0 1] by dividing by the max and min over 20,000 simulated data. Finally, for each variable the random draws are mapped by default in the interval which goes from the minimum to the maximum of the corresponding coordinate. Following the suggestion of a referee, to account for the possibility of very distant (extreme) outliers, it is also possible to control the minimum and maximum values of the generated outliers for each dimension. In order to generalize even more the contamination schemes we have also added the possibility of point mass and component-wise contamination (see, e.g., Farcomeni 2014). In this last case, we extract a candidate row from the matrix of simulated data and we replace just a single random component with either the minimum or the maximum of the corresponding coordinate. In all contamination schemes, we retain the candidate outlier if its Mahalanobis distance from the k existing centroids exceeds a certain confidence level which can be chosen by the user. It is also possible to control the number of tries to generate the requested number of outliers. In case of failure a warning message alerts the user that the requested number of outliers could not be reached.

Fig. 5

Four groups in two dimension generated imposing BarOmega $\,=\,$0.1 with uniform noise (left) and normal noise (right) shown with filled (red) circles

Fig. 6

Four groups in two dimension generated imposing BarOmega $=$ 0.1 with $\chi ^2_5$ noise (top left), $\chi ^2_{40}$ noise (top right panel), component-wise contamination (bottom left) and $\chi ^2_5$ combined with Student T with 20 degrees of freedom noise (bottom right). The first noise component is always shown with filled (red) circles, while the second noise component (bottom right) is displayed with ‘times’ (magenta) symbol

In Figures 5 and 6 we superimpose to 4 groups in two dimensions generated using BarOmega $\,=\,$0.10, 10,000 outliers with the constraint that their Mahalanobis distance from the existing centroids is greater than the quantile $\chi ^2_{0.999}$ on two degrees of freedom. This gives an idea of the varieties of contamination schemes which can be produced and of the different portions of the space which can be covered by the different types distributions. The two panels of Fig. 5 respectively refer to uniform and normal noise. The two top panels of Fig. 6 refer to $\chi ^2_5$ and $\chi ^2_{40}$. The bottom left panel refers to component-wise contamination. In the bottom right panel we combined the contamination based on $\chi ^2_5$ with that of Student T with 20 degrees of freedom. These picture show that, while the data generated from the normal distribution tend to occupy mainly the central portion of the space whose distance from the existing centroids is greater than a certain threshold, the data generated from an asymmetric distribution (like the $\chi ^2$) tend to be much more condensed in the lower left corner of the space. As the degrees of freedom of $\chi ^2$ and T reduce, the outliers which are generated (given that they are rescaled in the interval [0 1] using 20,000 draws) will tend to occupy a more restricted portion of the space and when the degrees of freedom are very small they will be very close to a point-wise contamination. Finally, the component-wise contamination simply adds outliers at the boundaries of the hyper cube data generation scheme.

In a similar vein, we have also enriched the possibility of adding noise variables from all the same distributions described above.

In the current version of our algorithm, noise observations are defined to be a sample of points coming from a unimodal distribution outside the existing mixture components in (3). Although more general situations might be conceived, we prefer to stick to a definition where noise and clusters have conceptually different origins. A similar framework has also proven to be effective for separating clusters, outliers and noise in the analysis of international trade data (Cerioli and Perrotta 2014). We acknowledge that some noise structures originated in this way (as in Figs. 5 and 6) might resemble additional clusters from the point of view of data analysis. However, we emphasize that the shape of the resulting groups is typically very far from that induced by the distribution of individual components in (3). It would thus be hard to detect such structures as additional isolated groups by means of model-based clustering algorithms, even in the robust case. More in general, however, to define what a “true cluster” is and, therefore, distinguish clusters from noise, are issues where there is no general consensus (Hennig 2015).

The two options which respectively control the addition of outliers and noise variables are called respectively noiseunits and noisevars. If these two quantities are supplied as scalars (say r and s) then the X data matrix will have dimension $(n+r)$ $\times$ $(v+s)$, the type of noise which is used comes from uniform distribution and the outliers are generated using the default confidence level and a prefixed number of tries. On the other hand, more flexible options such as those described above are controlled using MATLAB ‘structure arrays’ combining fields of different types. In the initial part of file simdataset.m we have added a series of examples which enable the user to easily reproduce the output shown in Figs. 5 and 6. In particular, one of them shows how to contaminate an existing dataset. For example, in order to contaminate the M5 denoised dataset with r outliers generated from $\chi ^2_{40}$ and to impose the constraint that the contaminated units have a Mahalanobis distance from existing centroids greater than the quantile $\chi ^2_{0.99}$ on two degrees of freedom one can use the following syntax

where $\texttt {Y}$ is the 1800-by 2 matrix containing the denoised M5 data, Mu is a matrix $3 \times 2$ matrix containing the means of the three groups, S, is a 2-by-2-by-3 array containing the covariance of the 3 groups and pigen is the vector containing the mixing proportions (in this case case $\texttt {pigen}\,=\,$[0.2 0.4 0.4]. Figure 7 shows both the contamination with uniform noise (left panel) and $\chi ^2_{40}$. In order to have an idea about space coverage we have added 1000 outliers.

The possibility to add very distant outliers beyond the range of the simulated clusters, suggested by a referee and mentioned at the beginning of this section, is implemented by the field interval of optional structure noiseunits. This type of extreme outliers can be useful in order to compare (robust) clustering procedures or when analyzing “breakdown point” type properties in them.

Fig. 7

Contamination of denoised M5 with uniform noise (left) and $\chi ^2_{40}$ noise (right). While the uniform noise fills all the gaps, the noise generated from asymmetric distributions is much more concentrated in a particular portion of the space

5 Simulation studies

In the on line supplementary material to this paper the reader can find the results of a series of simulation studies in order to validate the properties of the new constraints, to check goodness of fit of the pairwise overlaps to their theoretical distribution and to investigate the degree of coverage of parameter space.

6 Conclusions and next steps

In this paper we have extended the capabilities of MixSim, a framework which is useful for evaluating the performance of clustering algorithms, on the basis of measures of agreement between data partitioning and flexible generation methods for data, outliers and noise. Our contribution has pointed at several improvements, both methodological and computational. On the methodological side, we have developed a simulation algorithm in which the user can specify the desired degree of variability in the overlap among clusters, in addition to the average and/or maximum overlap currently available. Furthermore, in our extended approach the user can control the ratio among the lengths of the ellipsoids axes associated with the groups and the relative cluster sizes. We believe that these new features provide useful tools for generating complex cluster data, which may be particularly helpful for the purpose of comparing robust clustering methods. We have focused on the case of multivariate data, but similar extensions to generate clusters of data along regression lines is currently under development. This extension is especially needed for benchmark analysis of anti-fraud methods (Cerioli and Perrotta 2014).

We have ported the MixSim R package to the MATLAB FSDA toolbox of Riani et al. (2012), thus providing an easy-to-use unified framework in which data generation, state-of-the art robust clustering algorithms and principled routines for their evaluation are now integrated. Our effort to produce a rich variety of robust and computationally efficient methods for the analysis of complex data has also lead to an improved algorithm for approximating the distribution function of quadratic forms. These computational contributions are mainly described in “Appendix1” and “Appendix 2” below. Furthermore, we have provided some simulation evidence on the performance of our algorithm and on its ability to produce “sensible” clustering structures under different settings. Although more theoretical investigation is required, we believe that our empirical evidence supports the claim that, under fairly general conditions, fixing the degree of overlap among clusters is a useful way to generate experimental data on which alternative clustering techniques may be tested and compared.

Appendices

Appendix 1: Davies’ algorithm

Many test statistics and quadratic forms in central and non-central normal variables (e.g. the ratio of two quadratic forms) converge in distribution toward a finite weighted sum of non central $\chi ^2$ random variables $U_j$, with $n_j$ degrees of freedom and $\delta _j^2$ non-centrality parameters, so the computation of its cumulative distribution function

$$\begin{aligned} pr(Q<x) \quad \text{ for } \;\; Q=\sum _{j=1}^{r} a_j U_j + \sigma N(0,1) \qquad a_j \in \mathfrak {R}\end{aligned}$$

(11)

is a problem of general interest that goes beyond Eq. (9) and the scope of this paper. Duchesne and De Micheaux (2010) have compared the properties of several approximation approaches to problem (11) with “exact” methods that can bound the approximation error and make it arbitrarily small. All methods are implemented in C language and interfaced to R in the package CompQuadForm. Numerical conclusions, in favor of exact methods, confirm the appeal of Davies’ exact algorithm. Our porting of the algorithm from C to MATLAB, in the routine ncx2mixtcdf, gives to the statistical community the possibility of testing, experimenting and understanding this method in a very easy way.

The accuracy of Davies’ algorithm relies on the numerical inversion of the characteristic function (Davies 1973) and the control of its numerical integration and truncation errors. For this reason, the call to our routine

optionally returns in tracert details on the integration terms, intervals, convergence factors, iterations needed to locate integration parameters, and so on, which are useful to appreciate the quality of the cdf value returned in qfval.

Fig. 8

Cumulative distribution function (cdf) values returned by ncx2mixtcdf for various tolerances on the integration error and various integration terms. The value at the bottom left of the figure is the cdf for the best combination ($\hbox {tolerance}=10^{-8}$, integration terms = $10^{10}$). The other values are differences between this optimal value and those obtained with other tolerances

Figure 8 plots a set of qfval values returned for the same x point and for combinations of tolerance on the integration error (‘tol’ option) and integration terms (‘lim’ option) specified in the tolerance and integration_terms arrays. The right panel of the figure also specifies the parameters of the mixture of two $\chi ^2$ distributions used (the degrees of freedom df of the 2 distributions, the coefficients lb of the linear combination and the non centrality parameters nc of the 2 distributions). From the figure it is clear that the tolerances on the integration error impact on the estimates more than the number of integration terms used, here reported in reverse order. However, for the two stricter tolerances (the sequences of triangles ‘$\triangle$’ and crosses ‘$\times$’ symbols at the bottom of the plot) some estimates have not been computed: this is because the number of integration terms was too small for the required precision. In this case, one should increase the integration terms lim or relax the tolerance tol options.

Fig. 9

Time (in seconds) to run MixSim. In the figures the solid and dotted lines refer respectively to the FSDA and R implementations. The table reports the FSDA timing for some choices of v. The results for $k=10$ are the median of 25 replicates, while the results for $k=100$ are for one run monitored with timeit, a MATLAB function specifically conceived for avoiding long tic-toc replicates

Appendix 2: Time complexity of MixSim

The computational complexity of MixSim depends on the number of calls to Davies’ algorithm in Eq. (9), which is clearly quadratic in k as MixSim computes the overlap for all pairwise clusters. Unfortunately the time complexity of Davies’ algorithm, as a function of both k and v, has no simple analytic form but Melnykov and Maitra (2011) found empirically that MixSim is affected more by k than by v. We followed their time monitoring scheme, for various values of v and two group settings ($k=10$ and $k=100$), to evaluate the run time of our FSDA MixSim function. Figure 9 compares the results, in the table, with those obtained with the MixSim R package implementation (solid lines vs dotted lines in the plots). The gap between the two implementations is due to the fact that R is mainly based on C compiled executables. However, the relevant point here is a dependence of the time from v that may not be intuitive at first sight: computation is demanding for small v and becomes much easier for data with 3–100 variables. This is one of the positive effects of the course of dimensionality, as the space where to accommodate the clusters rapidly increases with v.