Discrete-frequency convergence of iterative learning control for linear time-invariant systems with higher-order relative degree

Abstract

In this paper, a discrete-frequency technique is developed for analyzing sufficiency and necessity of monotone convergence of a proportional higher-order-derivative iterative learning control scheme for a class of linear time-invariant systems with higher-order relative degree. The technique composes of two steps. The first step is to expand the iterative control signals, its driven outputs and the relevant signals as complex-form Fourier series and then to deduce the properties of the Fourier coefficients. The second step is to analyze the sufficiency and necessity of monotone convergence of the proposed proportional higher-order-derivative iterative learning control scheme by assessing the tracking errors in the forms of Paserval’s energy modes. Numerical simulations are illustrated to exhibit the validity and the effectiveness.

1 Introduction

As one of intelligent control methodologies, the concept of iterative learning control (ILC) was proposed by Arimoto in 1980s for a robot manipulator to track a desired trajectory while it attempts to execute a sequence of repetitive tasks over a fixed time interval[1]. The fundamental mechanism of the ILC is to utilize the proportional, integral and/or derivative tracking error(s) at the current iteration to compensate for its control input so as to iteratively generate the control input for the next iteration. The aim is to achieve that the constructed iterative control inputs drive the system to track the desired trajectory as precisely as possible as the iteration index goes to infinity. A number of ILC investigations have been emerged in favor of less system information requirement and distinct algorithmic structure[2–6].

In the ILC community, one of the involved concepts is the relative degree of the system, which describes the grade of the system control input to directly feed the output bridged by the system dynamics such as the system matrix, the input matrix as well as the output matrix. Regarding the ILC investigation for the system with a higher-order relative degree, Sun et al.[7] proposed a learning algorithm with initial rectifying action for a class of nonlinear systems with higher-order relative degree. Song et al.[8] proposed a first-order derivative-type (D-type) ILC based on a dummy model for nonlinear system with unknown relative degree. Meanwhile, the sampled-data ILC and the anticipatory ILC methods have been developed for single-input-single-output (SISO) nonlinear system with arbitrary relative degree[9, 10]. Recently, Ruan et al. [11] investigated the monotone convergence of the r-th-order derivative-type (D^(r)-type) ILC scheme for linear time-invariant systems with a higher relative degree r being larger than identity, in which the tracking error is measured in the form of Lebesgue-p norm[11]. The investigations convey that efficiency achieved by the derivative-type ILC law mainly hinges on the wellness of the order in terms of the derivative in the ILC algorithm which matches the system relative degree. However, the above-mentioned contributions involve only the sufficient conditions for convergence. As the necessity for convergence is illuminant and beneficial, it is inspiring to exploit any sufficient and necessary condition for monotone convergence.

From an engineering point of view, the frequency domain technique is sometimes preferable as it may exhibit the spectrum feature of a signal and may take advantage of its lower computation complexity in a multiplication form of the transfer functions converted by Laplace transform[12–14]. Usually in engineering, the spectrum function F(jω)of a signal f(t) for all t ≥ 0 is induced directly from its Laplace transform defined as F(s) = L(f(t)) = f₀^+∞ f(t)e^−stdt by setting the real part of the complex variable s = σ + jω to be zero, i.e., Re(s)= σ = 0. This implies that the spectrum function F(jω) is obtained on the premise that the Laplace integral F(s) is existent for the case when Re(s)=0. But, mathematically, for some functions, the existence of the abnormal type of Laplace integral F(s) requires the real part of the complex variable s = σ + jω to be no less than a positive constant. In addition, as a frequency domain technique, Laplace transform is fit for the system operating over the whole time duration from zero to infinity and thus the spectrum function is frequency-continuous. Note that the ILC scheme is implementable for a system with multiple operations, where each operation is performed over a finite time interval. This implies that the Laplace-transform spectrumbased ILC results reported in [12–14] need to be refined in a rigorous manner. However, Dirichlet has exploited a discrete-frequency technique by which a Dirichlet-type signal over a finite time interval is expanded as a Fourier series. This makes it possible to adopt Fourier series for enlightening the ILC significance. The aforementioned expectations motivate the paper to investigate sufficient and necessary assumptions in discrete frequency domain for monotone convergence of a proportional-higher-order-derivative-type iterative learning control (PD^(r)-type ILC) algorithm for a class of linear time-invariant system with a relative degree r > 1.

The remaining of the paper is organized as follows. Section 2 exhibits preliminaries including the concept of the system relative degree, the well-known Dirichlet theorem, some relevant properties of the Fourier coefficients and the discrete frequency-domain Parseval’s energy equality. Section 3 constructs a PD^(r)-type ILC scheme and derives the Fourier coefficients of the tracking errors. In Section 4, sufficiently and necessarily monotonous convergence of the proposed PD^(r)-type ILC algorithm is analyzed in discrete frequency domain. Numerical simulations are displayed in Section 5, and Section 6 concludes the paper.

2 Preliminaries

Consider a class of single-input-single-output linear timeinvariant systems described as

$$\left\{{\matrix{{\dot x(t) = Ax(t) + Bu(t)} \hfill \cr{y(t) = Cx(t),t \in [0,T]} \hfill \cr}} \right.$$

(1)

where [0, T] is the time interval of system operation, x(t) ∈ Rⁿ, u(t) ∈ R and y(t) ∈ R denote the n-dimensional state vector, scalar control input and output, respectively. A, B and C are matrices with appropriate dimensions.

• Definition 1[15]. Suppose that the system (1) satisfies the following conditions:

  $$\left\{{\matrix{{C{A^{i - 1}} = 0,\;i = 1,2, \cdots ,r - 1} \hfill \cr{C{A^{r - 1}}B \neq 0.} \hfill \cr}} \right.$$

  (2)

Then, the relative degree of system (1) is said to be r, where r is an integer larger than one and Aⁱ(i = 0, 1, ⋯, r−1) represents the i-th power of matrix A.

For the system dynamics (1), the following derivation is helpful in understanding the concept of the system relative degree.

If the relative degree r =1, then CB ≠ 0. Thus, it yields

$$\matrix{{y(t) = Cx(t)} \hfill \cr{\dot y(t) = C\dot x(t) = CAx(t) + CDu(t).} \hfill \cr}$$

If the relative degree r = 2, it implies that CB =0 and CAB ≠ 0. Therefore,

$$\matrix{{\dot y(t) = CAx(t)} \hfill \cr{\ddot y(t) = {{{\rm{d}}\left({\dot y(t)} \right)} \over {{\rm{d}}t}} = CA\dot x(t) = CA(Ax(t) + Bu(t)) =} \hfill \cr{\quad \;\;C{A^2}x(t) + CABu(t).} \hfill \cr}$$

Likewise, if the relative degree r = 3 which indicates CAB = 0 and CA²B ≠ 0, then ÿ(t) = CA²x(t) which gives rise to

$$\dddot y(t) = CA^2 \dot x(t) = CA^2 (Ax(t) + Bu(t)) = CA^3 x(t) + CA^2 Bu(t).$$

In general, if the relative degree of the system (1) is r > 1, we get

$$\left\{{\matrix{{{y^{(i)}}(t) = C{A^i}x(t),0 \leq i \leq r - 1} \hfill \cr{{y^{(r)}}(t) = C{A^r}x(t) + C{A^{r - 1}}Bu(t).} \hfill \cr}} \right.$$

(3)

From equation (3), it is seen that the relative degree r turns to be the lowest derivative order of the output y(t) whose lowest-order derivative y^(r) (t) is explicitly fed by the control input u(t) bridged by the system matrices.

• Dirichlet Theorem[16]. If a periodic function f(t), t ∈ (−∞, + ∞)with a period T is piecewise monotone on the interval [0, T] and is continuous except possibly for a finite number of discontinuous points of the first type, then the function f(t) can be decomposed as a Fourier series in a complex form as

  $$S(t) = \sum\limits_{n = - \infty}^{+ \infty} {{C_n}{{\rm{e}}^{{\rm{j}}n\omega t}}}$$

  (4)

  where

  $$\begin{array}{*{20}c} {\begin{array}{*{20}c} {\omega = \frac{{2\pi }} {T},} & {j^2 = - 1,} & {e^{jn\omega t} = \cos (n\omega t) + j\sin (n\omega t)} \\ \end{array} } \\ {\begin{array}{*{20}c} {C_0 = \frac{1} {T}\int_0^T {f(t)dt,} } & {C_n = \frac{1} {T}\int_0^T {f(t)e^{ - jn\omega t} dt} } \\ \end{array} } \\ {n = 0, \pm 1, \pm 2, \cdots } \\ {S(t) = \left\{ {\begin{array}{*{20}c} {f(t), if t is a point of continuity,} \\ {\frac{1} {2}\left[ {\mathop {\lim }\limits_{\Delta t \to 0^ + } f(t + \Delta t) + \mathop {\lim }\limits_{\Delta t \to 0^ - } f(t + \Delta t)} \right],} \\ {if t is a point of discontinuity,} \\ {\frac{1} {2}\left[ {\mathop {\lim }\limits_{\Delta t \to 0^ + } f(0 + \Delta t) + \mathop {\lim }\limits_{\Delta t \to 0^ - } f(t + \Delta t)} \right],} \\ {if t = 0 or T.} \\ \end{array} } \right.} \\ \end{array} $$

In the summation (4), the terms sin(ωt)and cos(ωt) produced by C₋₁e^−jωt + C₁e^jωt are called fundamental sinusoidal and cosine waves, whilst the terms sin(nωt) and cos(nωt) produced by C_−ne^−jnωt + C_+ne^jnωt for n = 2, 3, ⋯, are named as higher-frequency harmonic waves. Usually, the summation $S(t) = \sum _{n = - \infty}^{+ \infty}{C_n}{{\rm{e}}^{{\rm{j}}nwt}}$ is called as a Fourier series expansion of the function f(t) and denoted by $f(t) = \sum _{n = - \infty}^{+ \infty}{C_n}{{\rm{e}}^{{\rm{j}}nwt}}$ for convenience. The above function f(t) is called as a Dirichlet-type function.

Denote the Fourier coefficient C _n of the function f(t)as F(nω), i.e.,

$$F(n\omega) = {C_n} = {1 \over T}\int_0^T {f(t){{\rm{e}}^{- {\rm{j}}n\omega t}}{\rm{d}}t,\quad n = 0, \pm 1, \pm 2, \cdots .}$$

Then,

$$f(t) = \sum\limits_{n = - \infty}^{+ \infty} {F(n\omega){{\rm{e}}^{{\rm{j}}n\omega t}}} .$$

Thus, F(nω)and f(t) can be regarded as a Fourier pair.

For the sake of simplifying the context statement, in following content, all of the formulations in terms of discrete frequency “nω” represent that they are fit for all frequency orders, n = 0, ±1, ±2, ⋯.

• Lemma 1.

• Property 1. If ${F_1}(nw) = {1 \over T}\int_0^T {{f_1}(t){{\rm{e}}^{- {\rm{j}}nwt}}{\rm{d}}t}$ and ${F_2}(nw) = {1 \over T}\int_0^T {{f_2}(t){{\rm{e}}^{- {\rm{j}}nwt}}{\rm{d}}t}$, then $\alpha {F_1}(nw) + \beta {F_2}(nw) = {1 \over T}\int_0^T {\left({\alpha {f_1}(t) + \beta {f_2}(t)} \right){{\rm{e}}^{- {\rm{j}}nwt}}{\rm{d}}t}$ α and β are constants.

• Property 2.

  $$\matrix{{{F^{(r)}}(n\omega) = {1 \over T}\int_0^T {{f^{(r)}}} (t){{\rm{e}}^{- {\rm{j}}n\omega t}}{\rm{d}}t =} \hfill \cr{\quad \;\;{{({\rm{j}}n\omega)}^r}F(n\omega) + {1 \over T}\sum\limits_{i = 0}^{r - 1} {{{({\rm{j}}n\omega)}^{r - 1 - i}}} \left({{f^{(i)}}(T) - {f^{(i)}}(0)} \right),} \hfill \cr{\quad \;\;r = 1,2,3, \cdots .} \hfill \cr}$$

• Proof. If r = 1, then we get

  $$\matrix{{{F^{(1)}}(n\omega) = {1 \over T}\int_0^T {{{{\rm{d}}f(t)} \over {{\rm{d}}t}}} {{\rm{e}}^{- {\rm{j}}n\omega t}}{\rm{d}}t =} \hfill \cr{\quad {1 \over T}\left[ {\left. {f(t){{\rm{e}}^{- {\rm{j}}n\omega t}}} \right\vert _0^T + {\rm{j}}n\omega \int_0^T {f(t){{\rm{e}}^{- {\rm{j}}n\omega t}}} {\rm{d}}t} \right] =} \hfill \cr{\quad {1 \over T}\left[ {(f(T) - f(0)) + {\rm{j}}n\omega \int_0^T {f(t){{\rm{e}}^{- {\rm{j}}n\omega t}}} {\rm{d}}t} \right] =} \hfill \cr{\quad {1 \over T}\left({f(T) - f(0)} \right) + {\rm{j}}n\omega F(n\omega).} \hfill \cr}$$

  If r =2, then we get

  $$\matrix{{{F^{(2)}}(n\omega) = {1 \over T}\int_0^T {f^{\prime\prime}} {{\rm{e}}^{- {\rm{j}}n\omega t}}{\rm{d}}t =} \hfill \cr{\quad {\rm{j}}n\omega {F^{(1)}}(n\omega) + {1 \over T}(f^{\prime}\left({T) - f^{\prime}(0)} \right) =} \hfill \cr{\quad {{({\rm{j}}n\omega)}^2}F(n\omega) + {\rm{j}}n\omega {1 \over T}\left({f(T) - f(0)} \right) +} \hfill \cr{\quad {1 \over T}\left({f^{\prime}(T) - f^{\prime}(0)} \right).} \hfill \cr}$$

  Again, if r =3, then

  $$\matrix{{{F^{(3)}}(n\omega) = {1 \over T}\int_0^T {{f^{(3)}}(t)} {{\rm{e}}^{- {\rm{j}}n\omega t}}{\rm{d}}t =} \hfill \cr{\quad {\rm{j}}n\omega {F^{(2)}}(n\omega) + {1 \over T}\left({f^{\prime\prime}(T) - f^{\prime\prime}(0)} \right) =} \hfill \cr{\quad {{({\rm{j}}n\omega)}^3}F(n\omega) + {{(jn\omega)}^2}{1 \over T}\left({f(T) - f(0)} \right) +} \hfill \cr{\quad {\rm{j}}n\omega {1 \over T}\left({f^{\prime}(T) - f^{\prime}(0)} \right) + {1 \over T}\left({f^{\prime\prime}(T) - f^{\prime\prime}(0)} \right).} \hfill \cr}$$

  Analogously,

  $$\matrix{{{F^{(r)}}(n\omega) = {1 \over T}\int_0^T {{f^{(r)}}(t)} {{\rm{e}}^{- {\rm{j}}n\omega t}}{\rm{d}}t = {{({\rm{j}}n\omega)}^r}F(n\omega) +} \hfill \cr{\quad \quad {1 \over T}\sum\limits_{i = 0}^{r - 1} {{{({\rm{j}}n\omega)}^{r - 1 - i}}\left({{f^{(i)}}(T) - {f^{(i)}}(0)} \right).}} \hfill \cr}$$

  □

• Property 3. ∣F(−nω)∣ = ∣F(nω)∣.

• Proof.

  $$\matrix{{\vert F(- n\omega)\vert = \left\vert {{1 \over T}\int_0^T {f(t){{\rm{e}}^{- {\rm{j}}(- n\omega)t}}{\rm{d}}t}} \right\vert =} \hfill \cr{\quad \quad \left\vert {{1 \over T}\int_0^T {f(t)\overline {{{\rm{e}}^{- {\rm{j}}n\omega t}}} {\rm{d}}t}} \right\vert = \left\vert {{1 \over T}\int_0^T {f(t)} \overline {{{\rm{e}}^{- {\rm{j}}n\omega t}}} {\rm{d}}t} \right\vert =} \hfill \cr{\quad \quad \left\vert {F(n\omega)} \right\vert = \vert F(n\omega)\vert .} \hfill \cr}$$

  □

• Property 4.

  $${1 \over T}\int_0^T {{f_1}(t)} {f_2}(t){\rm{d}}t = \sum\limits_{n = - \infty}^{+ \infty} {{F_1}(n\omega)} {F_2}(- n\omega).$$

• Proof.

  $$\matrix{{{1 \over T}\int_0^T {{f_1}} (t){f_2}(t){\rm{d}}t =} \hfill \cr{\quad \quad {1 \over T}\int_0^T {{f_2}(t)} \sum\limits_{n = - \infty}^{+ \infty} {{F_1}} (n\omega){{\rm{e}}^{{\rm{j}}n\omega t}}{\rm{d}}t =} \hfill \cr{\quad \quad \sum\limits_{n = - \infty}^{+ \infty} {{F_1}(n\omega)} {1 \over T}\int_0^T {{f_2}} (t){{\rm{e}}^{{\rm{j}}n\omega t}}{\rm{d}}t =} \hfill \cr{\quad \quad \sum\limits_{n = - \infty}^{+ \infty} {{F_1}(n\omega)} {1 \over T}\int_0^T {{f_2}} (t)\overline {{{\rm{e}}^{- {\rm{j}}n\omega t}}} {\rm{d}}t =} \hfill \cr{\quad \quad \sum\limits_{n = - \infty}^{+ \infty} {{F_1}(n\omega)} \overline {{1 \over T}\int_0^T {{f_2}(t)} {{\rm{e}}^{- {\rm{j}}n\omega t}}{\rm{d}}t} =} \hfill \cr{\quad \quad \sum\limits_{n = - \infty}^{+ \infty} {{F_1}(n\omega)} {F_2}(- n\omega).} \hfill \cr}$$

  □

If f₁ (t)= f₂(t) = f (t), then the above Property 4 turns to be the well-known discrete frequency-domain Parseval’s energy equality as shown in [17] as

$${1 \over T}\int_0^T {\vert f(t){\vert ^2}{\rm{d}}t = \sum\limits_{n = - \infty}^{+ \infty} {\vert F(n\omega){\vert ^2} = {1 \over 4}} \sum\limits_{n = - \infty}^{+ \infty} {A_n^2}}$$

(5)

where $\left| {F(nw)} \right| = {1 \over 2}An$, A _n is the magnitude of the sinusoidal and cosine waves with frequency nω, n = 0, ±1, ±2, ⋯. Thus, A _n is called as the spectrum of the sinusoidal and cosine waves at the frequency nω, n = 0, ±1, ±2,⋯.

From the above Parseval^’senergyequality(5), it is observed that the average energy of a signal in continuous domain can be expressed as a quarter of the summation of the square spectrums of all frequencies nω, n = 0, ±1, ±2, ⋯, in discrete frequency domain. What follows is to adopt the discrete-frequency energy formula $\sum _{n = - \infty}^{+ \infty}{\left| {F(nw)} \right|^2}$ for evaluating the tracking performance.

3 Iterative learning control scheme

Consider a class of linear time-invariant SISO systems taking the form as

$$\left\{{\matrix{{{{\dot x}_k} = A{x_k}(t) + B{u_k}(t)} \hfill \cr{{y_k}(t) = C{x_k}(t),\quad t \in [0,T]} \hfill \cr}} \right.$$

(6)

where [0, T] is an operation time interval, the subscript k refers to the operation number. x _k (t) ∈ Rⁿ, u _k (t) ∈ R and y _k (t) ∈ R denote an n-dimensional state vector, a scalar control input and an output at the k-th iteration, while A, B and C are matrices with appropriate dimensions. Further, assume that the relative degree r of the system (6) is greater than unity (r > 1).

For system (6), the current proportional error and its r-th-order derivative are utilized to compensate for its control input so as to generate the next control input, which forms a PD^(r)-type ILC scheme as follows: u₁ (t) is given arbitrarily

$$\matrix{{{u_{k + 1}}(t) = {u_k}(t) + {\Gamma _p}{e_k}(t) + {\Gamma _r}e_k^{(r)}(t),\quad t \in [0,T],} \hfill \cr{\quad \quad k = 1,2,3 \cdots .} \hfill \cr}$$

(7)

Here, Γ _p and Γ _r are assigned as the proportional and the r-th-order derivative learning gains, respectively.

Applying Property 2 of Lemma 1 to both sides of (6), we get

$$\left\{{\matrix{{\left[ {{1 \over T}\left({{x_k}(T) - {x_k}(0)} \right)} \right] + {\rm{j}}n\omega {X_k}(n\omega) = A{X_k}(n\omega) + B{U_k}(n\omega)} \hfill \cr{{Y_k}(n\omega) = C{X_k}(n\omega),\quad n = 0, \pm 1, \pm 2, \cdots} \hfill \cr}} \right.$$

where

$$\matrix{{{X_k}(n\omega) = {1 \over T}\int_0^T {{x_k}(t){{\rm{e}}^{- {\rm{j}}n\omega t}}} {\rm{d}}t} \hfill \cr{{U_k}(n\omega) = {1 \over T}\int_0^T {{u_k}(t){{\rm{e}}^{- {\rm{j}}n\omega t}}{\rm{d}}t}} \hfill \cr{{Y_k}(n\omega) = {1 \over T}\int_0^T {{y_k}(t){{\rm{e}}^{- {\rm{j}}n\omega t}}{\rm{d}}t}} \hfill \cr{\omega = {{2\pi} \over T}.} \hfill \cr}$$

Further,

$$\matrix{{{X_k}(n\omega) = {{({\rm{j}}n\omega I - A)}^{- 1}}B{U_k}(n\omega) -} \hfill \cr{\quad \quad {{({\rm{j}}\omega I - A)}^{- 1}}\left[ {{1 \over T}\left({{x_k}(T) - {x_k}(0)} \right)} \right].} \hfill \cr}$$

Thus,

$$\matrix{{{Y_k}(n\omega) = C{{({\rm{j}}n\omega I - A)}^{- 1}}B{U_k}(n\omega) -} \hfill \cr{\quad \quad C{{({\rm{j}}n\omega I - A)}^{- 1}}\left[ {{1 \over T}\left({{x_k}(T) - {x_k}(0)} \right)} \right].} \hfill \cr}$$

Analogously, the PD^(r)-type ILC law (7) leads to

$$\matrix{{{U_{k + 1}}(n\omega) = {U_k}(n\omega) + \left({{\Gamma _p} + {\Gamma _r}{{({\rm{j}}n\omega)}^r}} \right){E_k}(n\omega) +} \hfill \cr{\quad \quad {1 \over T}{\Gamma _r}\sum\limits_{i = 0}^{r - 1} {{{({\rm{j}}n\omega)}^{r - 1 - i}}} \left({e_k^{(i)}(T) - e_k^{(i)}(0)} \right).} \hfill \cr}$$

(8)

Here, ${E_k}(nw) = {1 \over T}\int_0^T {{e_k}(t){{\rm{e}}^{- {\rm{j}}nwt}}{\rm{d}}t}$. Owing to

$${e_{k + 1}}(t) = {y_d}(t) - {y_{k + 1}}(t) = {e_k}(t) - \left({{y_{k + 1}}(t) - {y_k}(t)} \right)$$

then,

$$\matrix{{{E_{k + 1}}(n\omega) = {e_k}(n\omega) - \left({{Y_{k + 1}}(n\omega) - {Y_k}(n\omega)} \right) =} \hfill \cr{\quad {E_k}(n\omega) - C{{({\rm{j}}n\omega I - A)}^{- 1}}\left({{U_{k + 1}}(n\omega) - {U_k}(n\omega)} \right) +} \hfill \cr{\quad C{{({\rm{j}}n\omega I - A)}^{- 1}} \times {1 \over T}\left[ {\left({{x_{k + 1}}(T) - {x_k}} \right) -} \right.} \hfill \cr{\quad \left. {\left({{x_{k + 1}}(0) - {x_k}(0)} \right)} \right].} \hfill \cr}$$

(9)

Substituting (8) into (9) reduces

$$\matrix{{{E_{k + 1}}(n\omega) = {E_k}(n\omega) -} \hfill \cr{\quad C{{({\rm{j}}n\omega I - A)}^{- 1}}B\left({{\Gamma _p} + {\Gamma _r}{{({\rm{j}}n\omega)}^r}} \right){E_k}(n\omega) -} \hfill \cr{\quad C{{({\rm{j}}n\omega I - A)}^{- 1}}B{{{\Gamma _r}} \over T}\sum\limits_{i = 0}^{r - 1} {{{({\rm{j}}n\omega)}^{r - 1 - i}}\left({e_k^i(T) - e_k^i(0)} \right) +}} \hfill \cr{\quad C{{({\rm{j}}n\omega I - A)}^{- 1}}{1 \over T}\left[ {\left({{x_{k + 1}}(T) - {x_k}(T)} \right) -} \right.} \hfill \cr{\quad \left. {\left({{x_{k + 1}}(0) - {x_k}(0)} \right)} \right].} \hfill \cr}$$

(10)

Let

$$\matrix{{{G_{P{D^{(r)}}}}(n\omega) = 1 - C{{({\rm{j}}n\omega I - A)}^{- 1}}\left({{\Gamma _p} + {\Gamma _r}{{({\rm{j}}n\omega)}^r}} \right)} \hfill \cr{{\psi _k}(n\omega) = {1 \over T}\sum\limits_{i = 1}^{r - 1} {{{({\rm{j}}n\omega)}^{r - 1 - i}}\left({e_k^{(i)}(T) - e_k^{(i)}(0)} \right)}} \hfill \cr{{\Phi _k}(0) = {1 \over T}\left({{x_{k + 1}}(0) - {x_k}(0) - {{({\rm{j}}n\omega)}^{r - 1}}{\Gamma _r}B{e_k}(0)} \right)} \hfill \cr{{\Phi _k}(T) = {1 \over T}({x_{k + 1}}(T) - {x_k}(T) - {{({\rm{j}}n\omega)}^{r - 1}}{\Gamma _r}B{e_k}(T)).} \hfill \cr}$$

Arranging (10), we get

$$\matrix{{{E_{k + 1}}(n\omega) = {G_{P{D^{(r)}}}}(n\omega){E_k}(n\omega) -} \hfill \cr{\quad C{{({\rm{j}}n\omega I - A)}^{- 1}}B{\Gamma _r}{\psi _k}(n\omega) + C{{({\rm{j}}n\omega I - A)}^{- 1}} \times} \hfill \cr{\quad ({\Phi _k}({\rm{T}}) - {\Phi _k}(0)).} \hfill \cr}$$

(11)

• Remark 1. It is found from (11) that, for the PD^(r)-type ILC law (7), the spectrum of the tracking error at the next iteration is composed of three parts. The first part is the spectrum of the current tracking error which dominates the convergence. The second part includes the values at the current iteration including the initial and terminal states as well as the initial and terminal tracking error derivatives whose orders range from zero to r − 1. The third part consists of the values at the next iteration of the initial and terminal states.

4 Convergence analysis

• Theorem 1. Assume that the PD^(r)-type ILC (7) is applied to the linear time-invariant systems (6) with relative degree r > 1. Suppose $e_k^{(i)}(T) = 0,e_k^{(i)}(0) = 0$, for all i = 0, 1, 2, ⋯, r − 1, and the initial and terminal states are resectable. Then, the propositions

  $$\sum\limits_{n = - \infty}^{+ \infty} {\vert {E_{k + 1}}(n\omega){\vert ^2}} < \sum\limits_{n = - \infty}^{+ \infty} {\vert {E_k}(n\omega){\vert ^2}}$$

  (12)

  and

  $$\mathop {\lim}\limits_{k \rightarrow + \infty} \sum\limits_{n = - \infty}^{+ \infty} {\vert {E_{k + 1}}(n\omega){\vert ^2} = 0}$$

  (13)

  hold if and only if

  $$\vert {G_{{\rm{P}}{{\rm{D}}^{(r)}}}}(n\omega)\vert < 1$$

  (14)

  where

  $$\vert {G_{{\rm{P}}{{\rm{D}}^{(r)}}}}(n\omega)\vert = \vert 1 - C{({\rm{j}}n\omega I - A)^{- 1}}\left. {B\left({{\Gamma _p} + {\Gamma _r}{{({\rm{j}}n\omega)}^r}} \right)} \right\vert .$$

• Proof. Sufficiency:

Because $e_k^{(i)}(T) = 0$ and $e_k^{(i)}(0) = 0$, for i = 0, 1, 2,⋯, r − 1, and the initial and terminal states are resectable, (11) becomes

$${E_{k + 1}}(n\omega) = {G_{{\rm{P}}{{\rm{D}}^{(r)}}}}(n\omega){E_k}(n\omega).$$

(15)

Denote ${Q_k} = \sum _{n = - \infty}^ + {\left| {{E_k}(nw)} \right|^2}$. By taking the assumption $\left| {{G_{{\rm{PD}}(r)(nw)}}} \right| < 1$ into account, it is induced that 0 ≤ Q_k+1 < Q _k < ⋯ < Q₁. This means that the sequence {Q _{k +1}} is lower-bounded and monotonically decreasing. Therefore, lim_{k → + ∞} Q_k+1 exists.

What follows is to prove that lim_{k → + ∞} Q_k+1 = 0 by reduction to absurdity.

Suppose that lim_{k → + ∞} Q_k+1 = Q > 0. Then, for the given constant ${\varepsilon _1} = {Q \over 2}$, there exists such a positive integer K₀ that, for all k > K₀, the inequality ${Q_{k + 1}} > Q - {\varepsilon _1} = {Q \over 2}$ holds.

Recall that the series ${Q_{k + 1}} = \sum _{n = - \infty}^{+ \infty}{\left| {{E_{k + 1}}(nw)} \right|^2}$ is convergent. This means that, for all k > K₀, the limit exists for the partial summation sequence ${Q_{k + 1}}(m) = \sum _{n = - m}^{+ m}|{E_{k + 1}}(nw){|^2}$ with respect to the index m. In specific, lim_{m → ∞} Q_k+1 (m) = Q _{k +1}. This implies that, for the given constant ${\varepsilon _2} = {Q \over 4}$, there exists a positive integer N₀ so that, for all m > N₀, the inequality

$${Q_{k + 1}}(m) = \sum\limits_{n = - m}^{+ m} {\vert {E_{k + 1}}(n\omega){\vert ^2} > {Q_{k + 1}} - {\varepsilon _2} > Q - {\varepsilon _1} - {\varepsilon _2}}$$

is true.

In particular, it yields that

$${Q_{k + 1}}(2{N_0}) = \sum\limits_{n = - 2{N_0}}^{+ 2{N_0}} {\vert {E_{k + 1}}(n\omega){\vert ^2} > Q - {\varepsilon _1} - {\varepsilon _2}.}$$

(16)

As the total number of the terms in the Q_k+1 (2N₀) formulation is equal to 4N₀ + 1, the inequality (16) implies that there at least exists an integer n₀ so that −2N₀ < n₀ < 2N₀ and

$$\vert {E_{k + 1}}({n_0}\omega){\vert ^2} > {{Q - {\varepsilon _1} - {\varepsilon _2}} \over {4{N_0} + 1}} = {Q \over {4(4{N_0} + 1)}} > 0.$$

(17)

On the other hand, (15) reduces to

$${E_{k + 1}}({n_0}\omega) = {({G_{{\rm{P}}{{\rm{D}}^{(r)}}}}({n_0}\omega))^k}{E_1}({n_0}\omega).$$

By considering the assumption $|{G_{{\rm{PD}}(r)}}({n_0}w)| < 1$, it results in

$$\mathop {\lim}\limits_{k \rightarrow \infty} {E_{k + 1}}({n_0}\omega) = 0.$$

This is contradictory to the conclusion (17).

The contradiction leads that the propositions (12) and (13) are true.

This completes the proof of sufficiency.

Necessity:

Assume that (14) does not always hold. Then, there exists at least such a number n₀ that

$$\vert {G_{{\rm{P}}{{\rm{D}}^{(r)}}}}({n_0}\omega)\vert \geq 1.$$

The equality (15) leads to

$$\vert {E_{k + 1}}({n_0}\omega)\vert = \vert {G_{{\rm{P}}{{\rm{D}}^{(r)}}}}({n_0}\omega){\vert ^k}\vert {E_1}({n_0}\omega)\vert \geq \vert {E_1}({n_0}\omega)\vert .$$

Consequently,

$$\sum\limits_{n = - \infty}^{+ \infty} {\vert {E_{k + 1}}(n\omega){\vert ^2} \geq \vert {E_{k + 1}}({n_0}\omega){\vert ^2} \geq \vert {E_1}({n_0}\omega){\vert ^2}}$$

and

$$\mathop {\lim}\limits_{k \rightarrow \infty} \sum\limits_{n = - \infty}^{+ \infty} {\vert {E_{k + 1}}(n\omega){\vert ^2} \geq} \mathop {\lim}\limits_{k \rightarrow \infty} \vert {E_1}({n_0}\omega){\vert ^2} = \vert {E_1}({n_0}\omega){\vert ^2}.$$

It is possible to select U₁(nω) and Y _d (nω) such that ∣E₁(n₀ω)∣ > 0, which contradicts to the postulate (12).

This completes the proof of necessity. □

• Remark 2. In Theorem 1 the sufficient and necessary assumptions for the monotone convergence require that not only all of the initial states and tracking errors are resectable, but also all of the terminal states and the tracking errors are resectable. It is well-known that, up to this date, in the existing ILC investigations for guaranteeing the convergence, the requirement for the resetting of the initial states and tracking errors, has been accepted in ILC community. But the requirement for the resetting of the terminal states and tracking errors is new. Thus, the convergent assumptions in Theorem 1 seem to convey that, in discrete frequency domain, the assumptions are quite critical and different from the existing results in continuous-time domain. However, the assumptions are possibly satisfied for a stable system without steady-state error.

  Without involving the reset assumptions, it is found that, in discrete frequency domain, the recursive spectrums relationship ${E_{k + 1}}(nw) = {G_{{\rm{PD}}(r)}}(nw){E_k}(nw)$ of two adjacent iterations is directly acquired in a precise equality form rather than the time-domain relationship $\left\| {{e_{k + 1}}(\cdot)} \right\| < \tilde \rho \left\| {{e_k}(\cdot)} \right\|$ in an inequality form by an appropriate relaxation technique. The discrepancy perhaps delivers that the sufficient assumption (14) in discrete frequency domain is more efficient than that of possibly achieved in continuous time domain. We guess that it is the milder convergent condition (14) that incurs the additional requirement for the resetting of the terminal states and the tracking errors. However, the conjectures need to be clarified in a rigorous manner.

• Remark 3. From the formulation of the proportional-r-th-order derivative-type ILC scheme (7), it is seen that the scheme will be degenerated to a proportional-type ILC scheme when the r-th-order derivative learning gain Γ _r is null. Then, under the assumption of the initial and terminal resetting, it is not difficult to deduce that the sufficient and necessary condition for guaranteeing the monotone convergence becomes

  $$\vert {G_{\rm{P}}}(n\omega)\vert = \vert 1 - C{({\rm{j}}n\omega I - A)^{- 1}}B{\Gamma _p}\vert < 1.$$

5 Numerical simulations

To show the effectiveness of the learning control law (7) in discrete frequency domain, consider an SISO linear timeinvariant system described as

$$\left\{ {\begin{array}{*{20}c} {\left[ {\begin{array}{*{20}c} {\dot x_1 (t)} \\ {\dot x_2 (t)} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} 0 & 1 \\ { - \frac{1} {3}} & { - \frac{1} {4}} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {x_1 (t)} \\ {x_2 (t)} \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} 0 \\ 1 \\ \end{array} } \right]u(t)} \\ {y(t) = \left[ {\begin{array}{*{20}c} {\frac{1} {3}} & 0 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {x_1 (t)} \\ {x_2 (t)} \\ \end{array} } \right]} \\ {x(0) = \left[ {\begin{array}{*{20}c} {x_1 (0)} & {x_2 (0)} \\ \end{array} } \right]^T = \left[ {\begin{array}{*{20}c} 0 & 0 \\ \end{array} } \right]^T .} \\ \end{array} } \right.$$

(18)

It is testified that CB = 0 and $CAB = {1 \over 3} \ne 0$. This means that the relative degree of system (18) is equal to 2, i.e., r = 2. The operation time interval of system (18) is set as [0, 40]. The desired trajectory is chosen as ${y_d}(t) = 1 - {{\rm{e}}^{- 0.25{t^2}}}$ and the beginning control input is chosen as u₁(t) = 1. As x _k 0) = 0, it is obvious that e _k 0) = 0 and $e_k^{(1)}(0) = 0$. By solving (18), it is easy to testify that the system (18) is stable with no steady-state error for steptype inputs. This implies that the resetting of the terminal states and tracking errors is inherently guaranteed. For the PD⁽²⁾-type ILC scheme (7), the learning gains are selected as Γ _p = 0.8 and Γ₂ = 2.4. It is computed that

$$\vert {G_{{\rm{P}}{{\rm{D}}^{(2)}}}}(n\omega)\vert = {\left({{{5.76{n^4}{\omega ^4} - 5.16{n^2}{\omega ^2} + 0.64} \over {144{n^4}{\omega ^4} - 87{n^4}{\omega ^4} + 16}}} \right)^{{\textstyle{1 \over 2}}}} < 1$$

where $\omega = {{2\pi} \over {40}} \approx 0.157$, which means the convergent condition $|{G_{{\rm{PD}}(r)}}(nw)| < 1$ holds. Fig. 1 displays the tracking performance of the output at the 2nd and 15th implementations.

Fig. 1

Outputs at the 2nd and 15th iterations

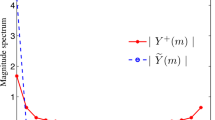
Fig. 2 depicts the spectrums of the frequency-wise tracking errors in the discrete frequency domain. It is seen that the tracking error spectrum at each fixed frequency is monotonously decreasing in the iteration direction. The monotone convergence related to the spectrums of the tracking errors made by the PD^(r)-type ILC law (7) is illustrated in Fig. 3 and the monotonicity in terms of the average power of the tracking error is manifested in Fig. 4, respectively.

Fig. 2

Spectrums at the 3rd, 5th and 7th iterations

Fig. 3

Tracking error tendency in discrete-frequency domain

Fig. 4

Tracking error tendency in continuous-time domain

Conclusions

In this paper, for a class of linear time-invariant systems with relative degree r > 1, a PD^(r)-type ILC law is developed and its sufficiency and necessity for monotone convergence is analyzed by means of evaluating the tracking error in Parseval’s energy form in discrete frequency domain. For analysis, the properties of Fourier coefficients regarding the system dynamics as well as the proposed ILC algorithm are discussed. In discrete frequency domain, the mathematical representation of signals, initial and terminal assumptions and the recursive relationship mode of the tracking errors between two adjacent operations are quite different from those of continuous time domain, and as such, the sufficiently convergent equivalence of the two domains is not obvious. This type of discrepancy needs to be further clarified in the future. In addition, the perturbation, noise as well as system parametric uncertainties are unavoidable in real applications. Therefore, robustness of the proposed ILC scheme to these perturbations, e.g., load and measurement perturbations, sensitivity due to the higher-order derivation computation, remains a challenging issue. It will be addressed in future.