1 Introduction

With the exploration of the moon, the idea of building permanent or semi-permanent stations on moon’s surface to exploit lunar resources has been put on agenda by many countries. Moon is very rich in mineral resources, if these can be taken back to the earth, which can alleviate the burden of resource depletion on the earth. But a problem we have to notice is that how to bring the huge amount of goods back to earth effectively[1, 2]. So far, the main way we use to design return orbit from moon is the patched conic scheme in which a spacecraft firstly escapes from the moon’s influence sphere along a hyperbolic orbit, then comes into earth’s influence sphere and finally reentries the earth’s atmosphere at the perigee[3]. This return method costs only 3–7 days to complete the whole task and so it is very suitable for manned missions. However, this return way has to spend too much fuel on pushing the spacecraft into the hyperbolic orbit so that it is not economical for the freight. Because generally the goods’ quality is stable, so there is no need to bring them back to the earth in such a short time. In this case, saving fuel is a better choice than saving time. In 2005, Ivashkin[4] proposed a new method to design the return trajectory by making use of the multi-body dynamics. In his approach, the spacecraft is pushed to a large elliptical orbit around the moon and escapes from the earth-moon L2 libration point. Then the orbit perigee’s altitude is reduced gradually by sun’s gravity till the spacecraft goes into earth’s atmosphere. The whole return process is just opposite to the Hiten’s mission and it will cost about 100 days while over 25% fuel is saved at the same time[5]. Nevertheless, this new method exposes another problem that the designing of the optimal return orbit indicates an impulsive transfer which is not realizable actually, so we need transform this impulse into a finite thruster strategy which can finish the same transfer mission. Generally, it is a typical two-point boundary value problem and its solution can be divided into two categories, which include the direct method and the indirect one. For the direct method, such as GPM, because of the long transfer time, it needs thousands of Gauss points to guarantee the interpolation’s accuracy so that the computation is often slow and easy to diverge. As a result, the application of GPM is restricted to a short period and simple dynamic model case[6, 7]. Liu et al.[8, 9] designed the transfer orbit to the Mars by using electric propulsion and rapid transfer orbit near the earth, but the dynamic model was a two body problem. Begum and Rao[10] designed an aero assisted orbital transfer trajectory but the time period is only over 200s at most for each phase. For the indirect method, such as the Pontryagin maximum principle, because of the strong nonlinear feature involved in this system, the domain of convergence is so narrow that it would take a long time to integrate the whole orbit. To solve the problem, the virtual satellite method is proposed, in which a “virtual satellite” is assumed to be running on the target orbit. The spacecraft would carry out an orbital maneuver to make soft rendezvous with the virtual satellite. If the terminal speed and position error between the spacecraft and the virtual satellite becomes zero, the spacecraft will enter the target orbit accurately. One advantage of the virtual satellite method (VSM) is that it only needs to integrate the phase of soft rendezvous, which can reduce the amount of calculation sharply. The other one is that the terminal index is very simple. We only guarantee the relative position and the relative velocity to be zero[11, 12]. However, the VSM has some disadvantages, too. Because the optimal direction of the thruster is achieved by the maximum principle, it is hard to guess the initial value of the costate when target orbit is extremely different from the initial orbit. For the optimization of the low energy return orbit, we have to find a way to make full use of VSM’s advantages and avoid its disadvantages. A direct yet effective way is the integration of GPM and VSM. There are 2 advantages for the integration. Firstly, with GPM, we can evade the guess of the costate in VSM. Besides, the time for rendezvous is much shorter than that for the whole return progress, it needs only dozens of Gauss points to get an accurate solution. So in this paper, VSM and GPM are combined to get the optimal thrust strategy for the spacecraft to transfer to the nominal low energy return orbit.

2 Dynamic model and nominal trajectory

2.1 Dynamic model of the spacecraft

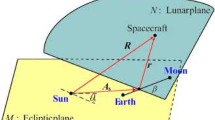
To “cut down” the energy for returning to the earth, it is necessary to use the gravitation assistance of the moon and sun because the elliptical movement of moon could help the spacecraft to escape from its influence sphere with a lower energy and sun’s gravity can lower the perigee of the spacecraft passively[13, 14]. So the dynamic model of the spacecraft should be an elliptical four-body model which is shown in Fig. 1.

Fig. 1
figure 1

The elliptical four-body model

Full size image

Firstly, the dynamic model of the spacecraft is studied in the earth-moon rotating frame (EMRF), of which the origin is at the mass center of the earth and the moon. The z-axis points to the direction of the moon’s orbital angular momentum. The y-axis completes the right-handed coordinate system. The differential equations of the spacecraft can be given as

$$\matrix{{\ddot r = - {{\dot \omega}_r} \times r - {\omega _r} \times ({\omega _r} \times r) - 2{\omega _r} \times v -} \hfill \cr{\quad {{{\mu _e}} \over {r_{ep}^3}}{r_{ep}} - {{{\mu _m}} \over {r_{mp}^3}}{r_{mp}} - \left({{{{\mu _s}} \over {r_s^3}}{r_{sp}} - {{{\mu _s}} \over {r_{so}^3}}{r_{so}}} \right)} \hfill \cr}$$
(1)

where ω r is the rotating angular velocity of EMRF, r ep , r mp and r sp are the position vectors from the earth, moon and sun to the probe, μ e , μ m and μ s are the gravitational constants of earth, moon and sun. r so is the position vector from sun to the origin of EMRF.

In the dynamic equation, the distances from the moon to the earth and to the sun are not constant. And the main bodies’ movement can be described with the real ephemeris data.

2.2 Nominal optimal return trajectory

Let’s assume that the spacecraft initially locates in a moon-equatorial circular orbit with a height of 100 km. To get a nominal low energy return trajectory, the spacecraft will go away from the initial orbit with an impulse along the tangential direction of the orbit so that it inserts into a large elliptical orbit with a semi-major axis of 28 000 km and the orbit energy of −1.6080km2/s2. Then, we just need to decide the departure time and the maneuver’s initial selenocentric longitude. Fig. 2 shows the distribution map of terminal perigee’s radius corresponding to different launch times and initial longitudes.

Fig. 2
figure 2

Terminal perigee of the spacecraft

Full size image

From Fig. 2, we can see that within a month as the initial launch time varies, we get four regions in the distribution map. In region B, the spacecraft cannot escape from moon’s influence sphere. In region C, the spacecraft escapes via earth-moon L1 point but is not able to approach the earth closely enough to enter the atmosphere. And in region D, the spacecraft just escapes via earth-moon L2 point and goes into the deep space, never comes back. Only region A indicates low energy return trajectories, in which the spacecraft escapes from L2 point and approaches the earth-sun L2 point, then the perigee declines gradually to a small value with which the spacecraft could return to the earth eventually. When the launch energy becomes lower, the region A will shrink to a point and the corresponding trajectory is the optimal one. In this paper, a nominal low energy return orbit is given via the genetic algorithm, because of its advantages on global searching and convergence abilities[15, 16], in which the launch time, initial selenographical longitude and total impulse are the design variables and the weighted sum of launch energy and terminal radius of perigee are the target function. By solving the optimization problem in January of 2020, we can get the optimal nominal return orbit that is shown in Table 1.

Table 1 Parameters of the optimal return trajectory
Full size table

With the optimized parameters, the spacecraft will be injected into the low energy return orbit. From Fig. 3, we can see that the spacecraft will get far from the earth-moon system firstly after escaping from cislunar orbit and the maximum range from the earth is about 1.5 million kilometers. Then, the spacecraft will turn to the earth and finally reentry the atmosphere. The whole return process costs about 91 days, over 10 times than traditional methods, while over 25% of energy is saved.

Fig. 3
figure 3

Optimal return trajectory

Full size image

We have to notice that the optimal returning trajectory is generated with an assumption that the spacecraft inserts into the target orbit with an impulsive maneuver which is not realizable. So it is necessary to transform it to a series of finite thrust controls. Because the whole return process costs about 100 days, the integration of whole orbit will cost a long time, so calculation becomes a core factor which seriously limits the efficiency of the optimization process. To solve the problem, GPM/VSM is used to calculate the optimal thruster strategy and its steps are developed in the next chapter.

3 Obtaining the optimal thruster strategy with GPM/VSM

3.1 Virtual satellite method

Because the thrust arc is really a small part compared to the whole return trajectory, a lot of calculations in the optimization process will be performed if the post boost trajectory is included in the integration. To avoid this problem, the virtual satellite method is introduced. In the virtual satellite method, it is assumed that there is a virtual satellite S1 running on the target orbit, as shown in Fig. 4, and the real spacecraft S starts off from the initial orbit and implements a finite thrust control to rendezvous with S1.

Fig. 4
figure 4

Optimal return trajectory

Full size image

In order to describe the relationship between the virtual satellite and the spacecraft clearly, the rendezvous coordinates frame is described first. The frame’s origin locates at S1 while the x axis points to the center of moon, the z axis points to the direction of the orbit’s angular momentum and the y axis completes a right-handed Cartesian coordinate system. In the rendezvous frame, the dynamic equation describing the spacecraft’s relative motion with respect to S1 is given below, where the disturbance from earth’s and sun’s gravity has been taken into account.

$$\matrix{{\ddot \rho = \left({- {{{\mu _m}} \over {r_{mp}^3}} - {{{\mu _e}} \over {r_{ep}^3}} - {{{\mu _s}} \over {r_{sp}^3}}} \right)\rho + \left({- {{{\mu _m}} \over {r_{mp}^3}} + {{{\mu _m}} \over {R_{mp}^3}}} \right){R_{mp}} +} \hfill \cr{\quad \left({- {{{\mu _e}} \over {r_{ep}^3}} + {{{\mu _e}} \over {R_{ep}^3}}} \right){R_{ep}} + \left({- {{{\mu _s}} \over {r_{sp}^3}} + {{{\mu _s}} \over {R_{sp}^3}}} \right){R_{sp}} +} \hfill \cr{\quad \dot \omega \times \rho + 2\omega \times \dot \rho + \omega \times (\omega \times \rho) + {{Fu} \over m}} \hfill \cr}$$
(2)

where ρ denotes the relative position of the spacecraft Rmp, Rep, and Rsp are the vectors from the moon, earth and sun to the virtual satellite, respectively, R mp = ∥Rmp∥, R ep = ∥R ep ∥, R sp = ∥R sp ∥, r mp = ∥R mp + ρ∥, r ep = ∥R ep + ρ∥ and r sp = ∥R sp + ρ∥. ω is the angular velocity of the rendezvous frame with respect to the inertial frame. F and m are the thrust force and the spacecraft’s mass, and u denotes the control direction. In the simulation, because the nominal trajectory is given previously, the motion of the virtual satellite is a function of time when the initial state is fixed. So the rendezvous trajectory of the spacecraft is only affected by the control u. We also need to choose a proper initial states for the virtual satellite and real spacecraft to start the simulation.

To perform the optimization, we should firstly construct the state function of real spacecraft as below, which involves the spacecraft’s mass m as a state.

$$\dot X = \left[ {\matrix{{\dot \rho} \cr{\dot v} \cr{\dot m} \cr}} \right] = \left[ {\matrix{v \cr{\ddot \rho} \cr{\dot m} \cr}} \right] = \left[ {\matrix{v \cr{f(\rho ,v,t) + {{Fu} \over m}} \cr{{F \over {{I_{sd}}}}} \cr}} \right]$$
(3)

where X = [ρ v m]T denotes the spacecraft’s state, I sg denotes the specific impulse.

Given the initial states of the spacecraft, our task is to design the optimal control strategy making the terminal relative position and relative velocity zero. In a traditional VSM, the control strategy is generated via the maximum principle, but it is hard to guess the initial value of the co-states and the optimization is easy to diverge when the system is of strong nonlinearity. To improve the robustness and efficiency of the optimization, the Gauss pseudospectral method is applied to get the optimal result.

3.2 Gauss pseudo-spectral method

In the Gauss pseudo-spectral method, an optimal control problem’s time span, states and control are discretized to the corresponding optimal variables at a series of Legendre-Gauss points (LG points). These discrete optimal variables should satisfy certain constrains. Therefore, the optimal control problem is transformed into a non-linear programming problem which we can deal with by appropriate approaches such as the sequential quadratic programming (SQP) method.

Firstly, the time needs to be transformed into another style so as to fulfill the discretization.

$$t = {{{t_f} - {t_0}} \over 2}\tau + {{{t_f} + {t_0}} \over 2},\quad \tau \in [ - 1,1].$$
(4)

The state can be expressed approximately based on N + 1 Lagrange interpolating polynomials L i (τ), τ = 0, ⋯, N as

$$x(\tau) \approx X(\tau) = \sum\limits_{i = 0}^N {X({\tau _i}){L_i}(\tau)}$$
(5)

where \({L_i}(\tau) = \mathop \prod \limits_{j = 0,j \neq i}^N {{\tau - {\tau _j}} \over {{\tau _i} - {\tau _j}}},{\tau _k}(k = 1, \cdots ,N)\) denote the Legendre-Gauss points and τ0 = −1. The LG points are the roots of Legendre polynomials P K , which can be expressed as \({P_K}(\tau) = {1 \over {{2^K}K!}}{{{{\rm{d}}^K}} \over {{\rm{d}}{\tau ^K}}}\left[ {{{({\tau ^2} - 1)}^K}} \right]\).

Similarly, the control is discretized at a series of LG points like

$$u(\tau) \approx U(\tau) = \sum\limits_{i = 0}^N {U({\tau _i})L_i^{\ast}(\tau)}$$
(6)

where \(L_i^{\ast}(\tau) = \mathop \prod \limits_{j = 0,j \neq i}^N {{\tau - {\tau _j}} \over {{\tau _i} - {\tau _j}}}\).

To get the dynamical constrains, we differentiate the state expression in (5) and obtain

$$\dot x(\tau) \approx \dot X(\tau) = \sum\limits_{i = 0}^N {X({\tau _i}){{\dot L}_i}(\tau).}$$
(7)

In the Gauss pseudo-spectral method, the system should satisfy the dynamic constrains in (7) at each LG point. At LG points, the differential of each Lagrange polynomial can be expressed in a differential approximation matrix D ∈ RN × N + 1, whose elements can be calculated via

$$D_{ki} = \dot L_i \left( {\tau _k } \right) = \left\{ {\begin{array}{*{20}c} {\frac{{\left( {1 + \tau _k } \right)\dot P_K \left( {\tau _k } \right) + P_K \left( {\tau _k } \right)}} {{\left( {\tau _k - \tau _i } \right)\left[ {\left( {1 + \tau _i } \right)\dot P_K \left( {\tau _i } \right) + P_K \left( {\tau _i } \right)} \right]}},} & {i \ne k} \\ {\frac{{\left( {1 + \tau _i } \right)\ddot P_K \left( {\tau _i } \right) + 2\dot P_K \left( {\tau _i } \right)}} {{2\left[ {\left( {1 + \tau _i } \right)\dot P_K \left( {\tau _i } \right) + P_K \left( {\tau _i } \right)} \right]}},} & {i = k} \\ \end{array} } \right.$$
(8)

where i = 0, 1, ⋯, N and k = 1, 2, ⋯, N.

Based on the differential approximation matrix D, the dynamical constrains can be rewritten into algebraic constraints as

$$\sum\limits_{i = 0}^N {{D_{ki}}{X_i} - {{{t_f} - {t_0}} \over 2}f({X_k},{U_k},{\tau _k};{t_0},{t_f}) = 0}$$
(9)

where X k ≡ X(τ k ), U k ≡ U(τ k ), k = 1, ⋯, N, and f is the dynamic equation of the spacecraft.

According to the Gauss integral expression, the terminal state can be calculated as

$${X_f} = {X_0} + {{{t_f} - {t_0}} \over 2}\sum\limits_{k = 1}^N {{\omega _k}f({X_k},{U_k},{\tau _k};{t_0},{t_f})}$$
(10)

where X0 = X(−1) and the Gauss weight ω k could be gotten by the expression

$${\omega _i} = \int_{- 1}^1 {{L_i}(\tau){\rm{d}}\tau = {2 \over {(1 - \tau _i^2){{\left[ {{{\dot P}_K}({\tau _i})} \right]}^2}}},\quad i = 1, \cdots ,K.}$$
(11)

Also, the cost function can be approximated as

$$J = \phi ({X_0},{t_0},{X_f},{t_f}) + {{{t_f} - {t_0}} \over 2}\sum\limits_{k = 1}^N {{\omega _k}f({X_k},{U_k},{\tau _k};{\tau _0},{t_f}).}$$
(12)

The boundary constrains are

$$\Phi ({X_0},{t_0},{X_f},{t_f}) = 0.$$
(13)

And the path constrains are

$$C({X_k},{U_k},{\tau _k};{t_0},{t_f}) \leqslant 0,\quad k = 1, \cdots ,N.$$
(14)

A non-linear programming problem is defined in which (12) is the cost function, (9), (10) and (13) are equation constrains and (14) includes all path constrains. So far, we have transformed the parameter optimization problem into a corresponding non-linear programming problem which can be solved via the SQP approach.

4 Simulation and results

4.1 Steps of optimization

The detailed steps to get the optimal thruster strategy are summarized below:

  1. 1)

    Generate the nominal trajectory of the virtual satellite.

  2. 2)

    Set the time of the virtual satellite orbit’s perilune point to be zero.

  3. 3)

    Set the time constrain to be \(t \in \left[ {- {T \over 2},{T \over 2}} \right]\), where T is the orbit period of the spacecraft.

  4. 4)

    Set the path constrain to be r > 1738 km.

  5. 5)

    Set the boundary constrain to be r0 = 1838 km, v0 = 1.633 km/s, r · v0 = 0 and \({\rho _f} = {{\dot \rho}_f} = 0\).

Substitute the above data into the GPM solver and get the results.

Then, the simulation is carried out with computer. After several iterations, we can get the optimal control strategy and the transfer trajectory of the spacecraft to its target orbit.

4.2 Simulation results

In the simulation of the low energy return mission, it is assumed that the spacecraft’s initial mass is 500 kg and its single thruster has a propulsive force of 490 N with a specific impulse of 3000 m/s.

Substituting these initial values into the GPM solver, the design variables include the start time, end time, initial state of the spacecraft, initial thrust angle and its rate of change. The number of LG points is 50, and with 8 times of iterations, we can get an accurate result. Besides, with an Intel Pentium 2.9 GHz machine and Matlab 8.0 programming environment, the computation only takes less than 1 min to get the result.

Simulation shows that the transfer starts at moment − 290 s when the virtual satellite’s true anomaly is 212.3 degrees. The spacecraft’s maneuver history is shown in Fig. 5.

Fig. 5
figure 5

Optimal control strategy

Full size image

Fig. 5 indicates that during the whole transfer process the thrust’s direction changes smoothly, which is easier to implement in actual operation than direction’s abrupt and huge change.

With the action of thrust, orbit elements and the spacecraft’s mass will change, too. As the result, the spacecraft is transferred into a large elliptical orbit from its original orbit within 600 s and its mass has declined by 93 kg, as shown in Fig.6.

Fig. 6
figure 6

Time history of orbit parameters

Full size image

Fig. 7 gives the whole transfer sketch in which the spacecraft transfers from the original orbit to its target orbit.

Fig. 7
figure 7

Transfer trajectory from initial to target orbit

Full size image

The distance from the spacecraft and the virtual satellite to the moon’s center varies along the spacecraft’s selenocentric longitude. Their relationship is shown in Fig. 8. It is obvious that the spacecraft’s moon-center longitude has changed about 34 degrees during the transfer.

Fig. 8
figure 8

Two spacecraft’s selenocentric distances’ change with corresponding longitudesx

Full size image

From Fig. 9, we can see that the relative distance between the spacecraft and virtual satellite comes to a small value with the control. At the transfer’s end point, the relative distance and relative velocity between the real craft and the virtual satellite is too small, i.e., the relative distance is less than 20 m and relative velocity less than 0.1 m/s to fail the return mission. The actual orbit is close to the nominal one, as shown in Fig. 10, and the probe will successfully return to the earth.

Fig. 9
figure 9

Time history of the relative distance

Full size image
Fig. 10
figure 10

Nominal and actual return trajectories

Full size image

5 Conclusions

An elliptical four-body dynamic model is constructed and then used to analyze the existence of low energy moon return trajectory, which is more economical than the traditional return method. Fortunately, we get an economical and nominal optimal return orbit in this case. However, it needs a huge and non-realizable impulse to transfer the spacecraft from selenocentric circular orbit to the target low energy return orbit. The VSM and GPM are combined to design the finite thrust control strategy which could be used to substitute the non-realizable impulse. In the VSM, the control model is constructed in the rendezvous coordinates system, which has two advantages: the final index is very simple and the huge amount of calculation can be cut because we only need optimize the thrust arc. Finally, the GPM is introduced to solve the optimal control problem and get the optimal result, which can avoid guessing the co-states’ initial value in the maximum principle. All steps of the optimization are listed. The simulation results show that the GPM/VSM can offer us the optimal control strategy with a high accuracy and efficiency. The final error is small enough to guarantee the successful return.