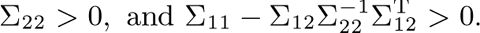1 Introduction

During the past decades, the study of fractional differential calculus[1, 2] has attracted increasing interest. Various subtle results on fractional-order systems have been presented[3–6]. It was found that many systems in interdisciplinary fields could be elegantly described with the help of fractional-order systems[1, 2]. Furthermore, fractional order controllers[5, 6] have so far been implemented to enhance the robustness and the performance of the closed loop control systems.

It is notable that the stabilization problem of fractional-order nonlinear systems[7–9] is much more difficult than that of the linear[10–12] and linear delay ones[13]. Using generalization of Gronwall-Bellman lemma, the stability problem of fractional-order nonlinear affine differential equations was investigated[7–8]. Based on fractional sliding mode control, Aghabab[9] proposed a robust stabilization and synchronization method. As a fundamental tool to analyze the stability of nonlinear systems, Ahn et al.[14] introduced Lyapunov method. But, how to construct simple direct Lyapunov functions remains an open problem[15]. Using the frequency distributed fractional integrator equivalent model, an indirect Lyapunov method to fractional nonlinear differential equations was addressed in [16]. The main advantage of these contributions is not to calculate the fractional derivatives of the Lyapunov functions.

On the other hand, as is well known, in real-world systems, some of the system states are not measurable and all the designer knows are the output and input of the plant. In this case, the estimation of system states or observers is often needed[12]. Recently, there were many researches on the observer design for nonlinear systems in both integral-order case and fractional-order ones. To obtain the stability condition for the error dynamic system, the broad design approaches, such as algebra Riccati equation[17] and LMI-based techniques[18], are often adopted. Using indirect Lyapunov method and LMI techniques, Boroujeni et al.[19] investigated the observer design for fractional-order nonlinear systems.

In fact, it has been shown that the solution of the Riccati equation or LMI depends strongly on the Lipschitz constant[20]. In other word, when the Lipschitz constant becomes large, most of the existing results fail to provide a solution. In order to enlarge the domain of attraction and the class of nonlinear systems that can be considered, the one-sided Lipschitz condition was first proposed[21]. For many problems, the one-sided Lipschitz constant is significantly smaller than the usual Lipschitz constant, which makes it much more suitable for estimating the influence of nonlinear part[22]. For the sake of simple calculation, recent efforts were focused on the LMI-based solution to address the observer design. For example, Zhao et al.[23] discussed the full-order observer design for one-sided Lipschitz nonlinear systems and showed that the one-sided Lipschitz condition makes the applicable class larger than the Lipschitz condition for observer design. Zhang et al.[24] presented a full-order observer design for such systems and showed that the proposed condition also guaranteed the existence of a reduced-order observer. For one-sided Lipschitz discrete-time systems, Zhang et al.[25, 26] investigated the full-order and reduced-order observer designing, respectively.

In this paper, inspired by the above work and taken into account the fact that the conditions given for the full-order observer design also guarantee the existence of a reduce-order observer[24–26], we mainly investigate the problem of the full-order observer design for fractional-order one-sided Lipschitz nonlinear systems. The main contribution of this paper is of twofold. First, by using an indirect Lyapunov approach, we constructed a novel monochromatic Lyapunov function corresponding to the elementary frequency and presented the LMI-based sufficient conditions for asymptotic stability of the observer error dynamic systems, which are less conservative than some existing ones. Second, the proposed techniques are also applicable to reduced order observer design and to the synthesis problems described by fractional-order nonlinear uncertain systems involving locally Lipschitz as well as one-sided Lipschitz nonlinear functions.

The rest of this paper is organized as follows. In Section 2, some preliminaries and problem formulation are presented. The full-order observer design is given in Section 3. The efficiency of the approach is shown through an illustrative example in Section 4. Finally, some conclusions are drawn in Section 5.

Throughout this paper, R n denotes an n-dimensional Euclidean space, R n×m is the set of all n × m real matrices. I means an identity matrix of appropriate order, X > 0 (X < 0) indicates that the matrix X is positive (negative) definite, X T denotes the transpose of X. 〈·, ·〉} is the inner product in R n, i.e., given x, y ∈ R n, 〈x,y〉 = x T y. || · || denotes the Euclidean norm. ||A|| \(\sqrt {{\lambda _{\max }}\left( {{A^T}A} \right)} \) is the induced 2-norm of matrix A, where λmax(S) is the maximum eigenvalue of the symmetric matrix S. In symmetric block matrices, an asterisk * represents a term induced by symmetry.

2 Preliminaries and problem formulation

In this section, some basic definitions and properties are introduced, which will be used in the following sections.

Definition 1[1]. The definition of fractional integral is described by

where Γ(·) is the well-known Gamma function which is defined by Γ(z ) = \(\int_0^\infty {{e^{ - z}}{t^{z - 1}}{\text{d}}t} \).

Definition 2[1]. The Riemann-Liouville derivative is defined by

$$_{{t_0}}^{RL}\mathcal{D}_t^af(t) = \mathcal{D}_{{t_0}}^m\mathcal{D}_t^{a - m}f(t),\quad a \in [m - 1,m)$$

where m ∈ Z +, D m is the classical m-th order derivative.

Definition 3[16]. Let h(t) be the impulse response of a linear system. The diffusive representation (or frequency weighting function) of h(t) is called μ(ω) with the following relation:

$$h(t) = \int_0^\infty {\mu (\omega ){\operatorname{e} ^{ - \omega t}}\operatorname{d} \omega .} $$

Remark 1[16]. The fractional order integral operator \(_{{t_0}}D_t^{ - a}f(t)\) can be written as

$${t_0}\mathcal{D}_t^{ - a}f(t) = h(t) * f(t)$$

where * denotes convolution operator and \(h(t) = \frac{{{t^{q - 1}}}}{{\Gamma (q)}}\), while the diffusive representation of h(t) is introduced as

$$\mu (\omega ) = \frac{{\sin (a\pi )}}{\pi }{\omega ^{ - a}}.$$

Lemma 1[16]. The fractional-order nonlinear differential equality

$${t_0}D_t^ax(t) = f(x(t))$$

due to the continuous frequency distributed model of the fractional integrator, can be expressed as

$$\left\{ {\begin{array}{*{20}{l}} {\frac{{\partial z(\omega ,t)}}{{\partial t}} = - \omega z(\omega ,t) + f(x(t))} \\ {x(t) = \int_0^\infty {\mu (\omega )z(\omega ,t)\operatorname{d} \omega } } \end{array}} \right.$$

where μ(ω) is the same as in Remark 1.

Lemma 2[27]. Given real matrices H and E of appropriate dimensions,

for all F(t) satisfying F T(t)F(t) < I, if and only if there exists an ɛ > 0 such that

Lemma 3[28](Schur complement). For a real matrix Σ = Σ T , the following assertions are equivalent:

  1. 1)
  2. 2)
  3. 3)

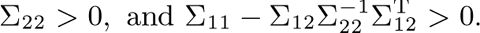
In this paper, we consider the fractional-order nonlinear system described by the following form:

$$\left\{ {\begin{array}{*{20}{l}} {{D^a}x(t) = \tilde Ax(t) + \Phi (x(t),u(t))} \\ {y(t) = Cx(t)} \end{array}} \right.$$
((1))

where D a denotes the Riemann-Liouville derivative, 0 < a < 1 is the fractional commensurate order, x(t) ∈ R n is the state of the plant, u(t) ∈ R m and y(t) ∈ R p are the control input and output, respectively. Ã and C are system matrices of appropriate dimensions, Ã = A + ∆A(t), and ∆A(t) represents the following admissible time-variant uncertainties

$$\Delta A(t) = {D_A}{F_A}(t){E_A}$$
((2))

where D A and E A are known constant matrices, and F A (t) is an unknown matrix with Lebesgue measurable elements satisfying

((3))

We first introduce the following properties that are used in the follows.

The nonlinear function Φ(x,u) : R n → R n is said to be locally Lipschitz in a region D including the origin with respect to x, uniformly in u, if there exists a constant γ > 0 satisfying:

$$\left\| {\Phi ({x_1},{u^*}) - \Phi ({x_2},{u^*})} \right\| \leqslant \gamma \left\| {{x_1} - {x_2}} \right\|.$$
((4))

The nonlinear function Φ(x,u) is said to be one-sided Lipschitz[21] if there exists a constant ρ ∈ R such that for all x 1, x 2 ∈ D,

$$\left\langle {\Phi ({x_1},{u^*}) - \Phi ({x_2},{u^*}),{x_1} - {x_2}} \right\rangle \leqslant \rho {\left\| {{x_1} - {x_2}} \right\|^2}.$$
((5))

The nonlinear function Φ(x,u) is said to be quadratically inner-bounded[21] in the region D if there exist two constants δ, φ ∈ R such that for all x 1, x 2 ∈ D

((6))

Remark 2. Unlike the well-known Lipschitz condition, constants ρ, δ and φ can be positive, negative or zero. In addition, if function Φ is Lipschitz, then it is also both onesided Lipschitz and quadratically inner-bounded, but the converse is not true[21]. The one-sided Lipschitz condition provides a less conservative condition (See the example in Section 5) than the classical Lipschitz one[22,23]. The concept of quadratic inner-boundedness is very useful to provide tractable LMI stability conditions[23–26].

The purpose in this paper is to study the design problem of the fractional-order observer for the fractional-order nonlinear system (1).

3 Full-order observer design

In this section, we investigate the design problem of full-order observer for the fractional-order nonlinear system (1). In the following, we consider the following full-order Luenberger-type non-fragile observer[19,24]:

$$\left\{ {\begin{array}{*{20}{l}} {{D^a}\hat x(t) = \tilde A\hat x(t) + \Phi (\hat x(t),u(t)) + \tilde L(y(t) - \hat y(t))} \\ {\hat y(t) = C\hat x(t)} \end{array}} \right.$$
((7))

where

$$\tilde L = L + \Delta L(t) = L + {D_L}{F_L}(t){E_L}$$
((8))

in which L is the gain matrix to be designed, D L and E L are known constant matrices, and F L (t) is an unknown matrix with Lebesgue measurable elements satisfying

((9))

Let \(e(t) = x(t) - \hat x(t)\) denote the error signal. Then the observer error dynamic system can be written as

$${D^a}e(t) = (\tilde A - \tilde LC)e(t) + \tilde \Phi $$
((10))

where \(\tilde \Phi = \Phi (x(t),u(t)) - \Phi (\hat x(t),u(t))\).

Now, the design problem can be transformed to a robust stabilization problem of the fractional-order nonlinear uncertain system (10).

Theorem 1. For the fractional-order nonlinear system (1), assume that condition (4) is true and the full-order observer holds the form of (7). Then the observer error dynamic system is asymptotically stable if there exist a symmetrical matrix P > 0, matrix Z of appropriate dimensions together with real scalars ε 1 > 0, ε 2 > 0 and ε 3 > 0 such that

((11))

where

Moreover, the observer gain can be chosen as

$$L = {P^{ - 1}}Z.$$
((12))

Proof. It follows from Lemma 1 that the observer error dynamic system (10) can be written as

$$\left\{ {\begin{array}{*{20}{l}} {\frac{{\partial Z(\omega ,t)}}{{\partial t}} = - \omega Z(\omega ,t) + {A_{cl}}e(t) + \tilde \Phi } \\ {e(t) = \int_0^\infty {\mu (\omega )Z(\omega ,t)\operatorname{d} \omega } } \end{array}} \right.$$
((13))

where \({A_{cl}} = \tilde A - \tilde LC\).

Consider two Lyapunov functions: v(ω, t) is the monochromatic Lyapunov function corresponding to the elementary frequency ω, and V(t) is the Lyapunov function summing all the monochromatic v( ω,t) with the weighting function μ(ω). Thus, we can define our monochromatic Lyapunov function as

((14))

The time derivative of V(t) taken along the solution trajectories of (13) is

((15))

Clearly, if

then V(t) < 0, which implies that the dynamic system (13) is robustly stable.

Note that, if

((16))

then using Lemma 2 and condition (4), we have

((17))

where ε 1 > 0.

Thus, the dynamic system (13) is robustly stable if

((18))

Again using Lemma 2 together with conditions (3) and (9),

((19))

is equivalent to

((20))

where ε 2 > 0 and ε 3 > 0.

Therefore, taking into account inequalities (18)–(20), defining PL = Z and using the Schur complement, we obtains inequality (11). □

Remark 3. Note that the feasible LMI problem (11) in Theorem 1 is affine with all the respective arguments. Hence, Theorem 1 provides an LMI-based method of designing a full-order non-fragile observer for fractional-order nonlinear system (1). Furthermore, the observer gain matrix L can be directly solved by utilizing the powerful Matlab LMI toolbox[28].

Remark 4. If ∆A(t) = 0 and \(\left\| {\Delta L} \right\| \leqslant r\), then we can set ∆L = D L F L E L , where D L = I, F L = (sint)I and \(\left\| {E_L^T{E_L}} \right\| \leqslant r\). Following Theorem 1, the stability condition (11) is altered to

((21))

where

In particular, if simply setting P = αI, Z = αL and Q = αA − ZC, the stability condition (21) is equivalent to (See [19])

((22))

where \(M = \frac{{Q + {Q^T}}}{2} + \frac{{{\varepsilon _1}}}{2}{\gamma ^2}I + \frac{{{\varepsilon _2}{r^2}}}{2}{C^T}C\).

Note that the stability condition (22) is the same as that of Theorem 1[19]. So, their result can be regard as a special case of Theorem 3. On the other hand, not fixing P may result in a more suitable choice of P. One can give some examples to show that condition (22) has no solution, but (21) is still feasible. An example is presented in Section 5.

The following theorem presents a design method of full-order observer for fractional-order one-sided Lipschitz and quadratically inner-bounded nonlinear system (1).

Theorem 2. For the fractional-order nonlinear system (1), if conditions (5) and (6) hold true, and the full-order fractional-order non-fragile observer has the form of (7), then the observer error dynamic system is asymptotically stable if there exist a symmetrical matrix P > 0, matrix Z of appropriate dimensions together with real scalars ε i > 0, i = 1,2,3,4, such that

((23))

where

Moreover, the observer gain matrix L is given by L = P − 1 Z.

Proof. It follows from the proof of Theorem 1 that

((24))

where \(X = {[e(t)\,\,\,\tilde \Phi ]^T},{\Lambda _1} = A_{cl}^TP + P{A_{cl}}\).

On the other hand, from condition (5), we get \(\rho {e^T}(t)e(t) - {e^T}(t)\tilde \Phi \), which implies that for any positive scalar ε 1,

((25))

Similarly, from condition (6), for any positive scalar ε 2, we have

((26))

Then, adding the terms on the left-hand sides of (25) and (26) to the right-hand side of (24), it yields

((27))

where

Therefore, V(t) < 0, which implies that the error dynamic system is robustly stable if

((28))

From the proof of Theorem 1, we know that inequality

((29))

is equivalent to

((30))

where ε 3 > 0 and ε 4 > 0.

Therefore, defining Z = PL and using the Schur complement together with (27)–(30), condition (28) is equivalent to (23). □

Remark 5. If a = 1, ∆L(t) = 0 and \(L = \frac{\sigma }{2}{P^{ - 1}}{C^T}\), then the stability condition (28) is altered to

((31))

where N = PA + A T P + (ε 1 ρ + ε 2 δ)I − σC T C, which is the same as the integral order case[24]. In other words, the derived result in this section is still true for a = 1.

4 Numerical example

Consider the following fractional-order nonlinear model of a moving object in the cartesian coordinates:

$$\left\{ {\begin{array}{*{20}{l}} {{D^a}x(t) = Ax(t) + \Phi (x(t))} \\ {y(t) = Cx(t)} \end{array}} \right.$$
((32))

where a = 0.9 and

$$\left\{ {\begin{array}{*{20}{l}} {A = \left[ {\begin{array}{*{20}{c}} 1&1 \\ { - 1}&1 \end{array}} \right]} \\ {C = \left[ {\begin{array}{*{20}{c}} 1&0 \end{array}} \right]} \\ {\Phi (x(t)) = \left[ {\begin{array}{*{20}{l}} { - {x_1}(x_1^2 + x_2^2)} \\ { - {x_2}(x_1^2 + x_2^2)} \end{array}} \right].} \end{array}} \right.$$

As usual, the full-order observer is defined by the form

$$\left\{ {\begin{array}{*{20}{l}} {{D^a}\hat x(t) = A\hat x + \Phi (\hat x) + (L + \Delta L)(y - \hat y)} \\ {y = C\hat x} \end{array}} \right.$$
((33))

where \(\left\| {\Delta L} \right\| \leqslant 2\).

We first assume that the Lipschitz constant of the nonlinear function Φ(x(t)) satisfies γ = 0.6. Using the proposed method presented in [19] and solving the LMI feasible problem (22) in Remark 3, we cannot find a feasible solution. However, we resolve the feasible problem (21) in Remark 3. We find it is feasible, the feasible solution is

If not fixing the Lipschitz constant, after solving the feasible problem (21) in Remark 3, we can obtain the admissible Lipschitz constant γ = 0.99 < 1.

Next, we consider the quadratically inner-bounded property of Φ(x(t)). As pointed out in [24, 26], the nonlinear function Φ(•) is locally Lipschitz, and on any set D = {x ∈ R 2 : ||x|| < sr}, the Lipschitz constant is 3r 2. Furthermore, let

One can verify the quadratically inner-bounded property of Φ(x(t)) in D with constants δ and φ[24, 26].

Assume that system matrix A has admissible uncertainties as in (2), where

$$\begin{array}{*{20}{l}} {{D_A} = \left[ {\begin{array}{*{20}{c}} {0.2}&0 \\ 0&{0.1} \end{array}} \right]} \\ {{E_A} = \left[ {\begin{array}{*{20}{c}} 1&0 \\ {0.1}&0 \end{array}} \right]} \\ {{F_A} = \left[ {\begin{array}{*{20}{c}} {\sin \;0.1\pi t}&0 \\ 0&{\cos \;0.1\pi t} \end{array}} \right].} \end{array}$$

Since \(\left\| {\Delta L} \right\| \leqslant 2\), we can assume that

$$\begin{array}{*{20}{l}} {\Delta L(t) = {D_L}{F_L}{E_L} = } \\ {\quad \quad \quad \;\;\left[ {\begin{array}{*{20}{c}} 1&0 \\ 0&1 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\sin \;t}&0 \\ 0&{\cos \;t} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} 2 \\ 0 \end{array}} \right]} \end{array}$$

Setting φ = −100, δ = −99, we find the LMI (23) in Theorem 3 is feasible. The stabilizing gain matrix is L = [138.7331 2.7872]T.

Note that in this case, the admissible Lipschitz constant γ = 3r 2 = 75. However, under the above assumption, the admissible Lipschitz constant γ = 0.99 by solving the feasible problem (11) in Theorem 1. Clearly, the one-sided Lipschitz condition provides a less conservative condition and makes the applicable class larger than the class Lipschitz one.

$$\omega (t) = 0.1\;\sin \;2\pi t.$$

Figs.1 and 2 show the trajectories of x 1(t), x 2(t) and their estimations, respectively. It can be seen that the proposed non-fragile observer is robust, asymptotically stable and accurately tracks the system states.

Fig.1
figure 1

The simulation for state x 1 by full-order observer

Full size image
Fig. 2
figure 2

The simulation for state x 2 by full-order observer

Full size image

5 Conclusions

In this paper, based on the continuous frequency distributed equivalent model and indirect Lyapunov approach, an LMI approach to design a full-order observer for fractional-order nonlinear system has been presented. The obtained condition for observer error dynamic systems is less conservative than some existing one in recent literatures. The validity of the method is verified by a numerical example.