Avoid common mistakes on your manuscript.
INTRODUCTION
Odds ratios (OR) commonly appear in the medical literature summarizing the comparative effects of interventions and exposures in observational studies, randomized trials, and meta-analyses. Clinicians find it difficult to understand odds and odds ratios as measures of association, although they may be comfortable with the parallel concepts of risk and risk ratios. Probably, no one (with the possible exception of certain statisticians) intuitively understands a ratio of odds.1,2 Nevertheless, odds ratios are frequently encountered in research reports as the principal measure of association.3–5
Odds and risk constitute parallel statistical metrics for measuring frequency and ratios of frequency. Their relationship might be compared to the use of different scales such as Fahrenheit and Centigrade to report absolute values of and relationships between different temperatures. Until recently, the choices between the odds and risk metrics were determined largely on the basis of their statistical properties rather than on the basis of their usefulness as means of communicating the results of research to clinicians and their patients. In a previous article, we have demonstrated approaches to helping teachers and learners to master the concepts of risk, relative risk, and risk reduction as the preferred framework for the purposes of clinical application.6 The content of that article may be regarded as pre-requisite knowledge for the purposes of the present discussion and demonstration.
This article presents an approach in helping clinician understand what odds and odds ratios mean and when can they numerically substitute risk and risk ratio for odds and odds ratios. Odds ratios may be chosen as the measure of association by authors of studies conforming to a variety of designs, only some of which mandate their use in preference to risk ratios. These include randomized trials, systematic reviews, case control studies, and studies involving the use of logistical regression. In teaching clinical learners who are not familiar with this measure of outcome, we have found it important to concentrate initially on the conceptual understanding of odds and odds ratios and to avoid combining this with discussion of study design issues. We have correspondingly not included discussion of these issues in this article.
We will present interactive approaches that educators have developed to overcome ‘stumbling blocks’ among learners. To help the reader envision these approaches, we present sequenced advice for teachers and characteristic learner responses. The “tips” in this article are adapted from approaches developed by educators with experience in teaching evidence-based medicine skills to clinicians. We present a full description of the development of the tips in this series and pertinent background information elsewhere.7
Each tip includes section on “when to use the tip,” “The script,” the “bottom line,” and a “summary card.” The first tip helps learners to understand the relationship between odds and probability (risk) and to define circumstances when odds and risks are similar. The second tip builds on the first and helps learners understand what an odds ratio is and when it is similar to the risk ratio.
TEACHING TIP 1: UNDERSTANDING THE RELATIONSHIP BETWEEN ODDS AND RISK
When to Use this Tip
This tip is suitable for all clinicians and clinical trainees who want to understand the concept of odds. This tip takes about 25 minutes to complete. By the end of this tip learners should be able to:
-
–Understand the relationship between odds and risk
-
–Convert odds to risk and vice-versa
-
–Appreciate that, when risk is less than 10%, odds numerically approximate risk
This tip is useful for learners who are critically appraising an article about therapy or harm and who have already understood the concept of probability and risk.
The Script
First, determine the type of game the audience might be interested in. In the USA and Canada, it might be baseball, in Asia, football (soccer), and in some places like India and Pakistan, it may be cricket. Gambling in general might constitute another option.
Then ask the learners: what do people mean when they say—the odds of your country team winning this match is 1:1? Some learners would say “1 out of 2 chances of winning, the same chance of losing”. Others might reply: “It means your country has 1 out of 2 or 50% chance of winning this match”. You may then choose to propose a more challenging example, such as a 3:1 odds of winning, corresponding to a 75% chance.
In medicine, we often talk of risk of an unfavorable outcome. Draw Figure 1 and make the audience come up with the odds in each case. Some teachers may choose to adapt or simplify this figure when using this tip. First, present the learners successively with values for risk in the first column and ask them to identify the corresponding odds. Usually, someone will come up with the correct answer corresponding to the third column of the figure. Ask whoever got the right answer to explain how they arrived at it and fill in the corresponding entry under the second column. Finally, complete the fourth column of the figure as a graphic illustration of how odds are generated using objects in successive columns. As a result, the learners see an example of risk expressed as a decimal (0.80), odds expressed as a ratio (4:1), and odds expressed as a decimal (4.0).
After most of learners are coming up with correct answers for the third column, introduce the fourth column, illustrated using symbols of any sort (e.g., XXXX/X) and point out that the odds is the ratio of the symbols corresponding to those with the outcome to the symbols corresponding to those without the same outcome. Depending on your assessment of the learner’s comfort with the concept, you may ask them to generate formulas going in both directions, i.e., odds = risk/(1-risk) and risk = odds/(odds + 1).
After the figure has been completed, ask the learners: Do you see any pattern here? If there are no answers, ask: when are risk and odds close to each other? Some learners may point out: the smaller the risk, the closer the odds and risks are to one another. Further, when the risk goes below 10%, odds and risk become virtually identical, which is the key to knowing when odds can be treated as a valid estimate of risk.
The Bottom Line
-Risk is a proportion or percentage of an entire population having a given characteristic or outcome. Odds is a ratio of those with and those without the characteristic or outcome within the population.
-As risk falls below 20%, odds and risk become more and more similar and virtually identical below a risk of 10%.
See Appendix 2 for the summary card for this tip.
Addenda to Tip 1
-
–The formulae to convert risk to odds and vice-versa are not really crucial to move to the next tip. This can be avoided completely if there is time-constraint.
-
–The main (and if necessary, the only) concept to emphasize in this teaching tip is that the lower the risk, the closer the approximation of odds to risk, and that when risk goes below 10%, odds is almost equal to risk.
TEACHING TIP 2: UNDERSTANDING ODDS RATIOS AND THEIR RELATIONSHIP TO RISK RATIOS
When to Use this Tip
This tip is suitable for all clinicians and clinical trainees who already understand risk and risk ratios (RR) but who do not have a clear understanding of the concept of odds ratios (OR). The objective is to foster this understanding. This tip takes 30 minutes to complete.
By the end of this tip, learners should be able to:
-
Understand what an odds ratio (OR) is.
-
Understand that OR is an alternative to RR as an effect measure in treatment studies.
-
Understand that OR = 1 when there is no treatment effect
-
Understand that, compared to RR, OR makes the effect appear larger.
This tip is useful for learners who are critically appraising an article or a meta-analysis about a therapy or a harmful association and encounter results reported as odds ratios. Characteristically, clinical learners find risk and ratios of risk intuitive but find odds and ratios of odds unfamiliar, non-intuitive, and mystifying. Their confusion revolves around 2 stumbling blocks. Firstly, they do not understand how odds ratios are calculated. Secondly, they do not understand how to interpret the clinical importance of results when they are reported as odds ratios. If learners have worked through tip 1, they are comfortable with the notion of odds as an alternative measure of frequency and its relationship to the more familiar measure, risk. This tip uses that familiarity as a point of departure to demystify the concept of ratios of odds in relationship to the more familiar ratios of risk.
The Script
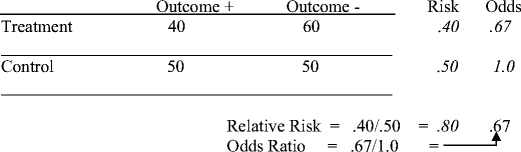
The first step is to translate what the learners have already absorbed in tip 1 into the framework of a 2 × 2 table such as in Figure 2. Tell the learners to imagine that the figure represents the results of a therapeutic trial comparing an outcome such as mortality between treatment and control groups. They are already familiar with this kind of a table by virtue of understanding risk and risk ratios.6 Complete the 2 × 2 grid with the numbers as shown, telling the group that they correspond to the number of study subjects in each cell. Ask the group: What is the risk of the outcome in the treatment group? After a moment, a participant offers “40 over 100.” Create a new column labeled ‘Risk’ to the right of the 2 × 2 grid and write 0.40 across from the ‘treatment’ row. Now ask, what is the odds of the outcome in the treatment group? After a little thought, someone suggests “40 over 60.” Create a new column, labeled ‘Odds’, to the right of the ‘Risk’ column and write 0.67 across from the ‘treatment’ row.
The learners now work through the same process for the control group, and you write 0.50 and 1 under the risk and odds columns, respectively. Now ask: What is the relative risk of the outcome? Someone proposes “40% over 50%.” You ask the group to verify the correctness of this response and then write the result in a column below the 2 × 2 grid. You now ask, what is the ratio of the odds of the outcome between the treatment and control groups? After some thought, someone catches on and suggests “0.67 over 1.” You congratulate the group for having grasped the gist of the demonstration and write 0.67 in the bottom row under the ‘odds’ column.
At this point, it is usually appropriate to acknowledge the common inconsistencies in terminology that one encounters in the literature. For example, one characteristically encounters ‘relative risk’ and ‘odds ratio’, although it would be equally appropriate to use the terms ‘risk ratio’ and ‘relative odds’, respectively.
At this stage, some learners may ask, “what does a relative odds of 0.67 mean, and why is this different from the relative risk?” The demonstration has partially demystified odds ratios for the group, but it has not made them any more intuitive.
Returning to the punch line of tip 1, point out that there are two things that a clinician needs to understand about the relationship between risk ratios and odds ratios: (1) when are odds ratios sufficiently close to risk ratios to be considered to be equivalent and (2) when they are not the same, in what direction is the difference? To address the second principle, you point to the two values in Figure 2 and ask the group “Are these two numbers close enough to be considered to be the same?” Most of the group will say no, and after further deliberation, someone will usually suggest that the odds ratio of 0.67 corresponds to an importantly larger treatment effect. Someone else may suggest that, taken as an approximation of the risk ratio, it would imply a risk reduction of 33%, in contrast to the true risk reduction of 20%. You agree with these observations and suggest that, as a general rule, when the two measures yield different numbers, the odds ratio, if taken as identical to the risk ratio, overestimates the treatment effect, sometimes substantially.
To approach the second issue of when can the two measures be taken as interchangeable, you can either give the group a ‘rule of thumb’ that this is appropriate when the event rate in the control group is not higher than 30% or you can demonstrate it quantitatively by working through an additional demonstration using a control event rate of 20%, 25%, and 30%.
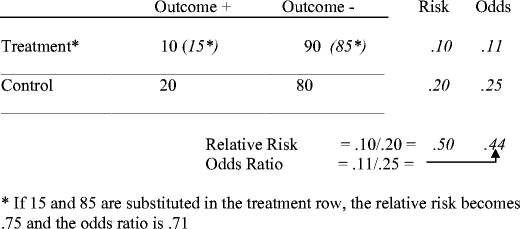
Figure 3 illustrates the relationship between RR and OR when the control event rate is 20%.
Even with risk reduction as high as 50%, the OR of 0.44 is closer to the RR of 0.50 than when the control event rate was 50%. If a smaller effect size of 25% risk reduction had been used in this second example, the two estimates become even closer. The resulting relative risk of 0.75 is now quite close to the OR of 0.71.
To understand odds ratios in terms of relative risk, you can use a non-quantitative approach. The rules are:
-
1.
The RR will always be closer to 1.0 than the OR.
-
2.
If the baseline risk (the risk of adverse events in the control group) is low (say, less than 30%), the difference between RR and OR is unlikely to be important. Therefore, the two may be used interchangeably for interpreting results.
-
3.
If the OR is near 1.0, the difference between RR and OR is unlikely to be important.
-
4.
Following directly from the above, the only time you are likely to run into trouble treating the OR as an RR is when the baseline risk is high (over 30%) and the OR is not close to 1.0 (say less than 0.67 or greater than 1.3). Under these circumstances, the RR is likely to be appreciably closer to 1.0 than the OR.
For those mathematically inclined, one can be much more precise using the formula below.
As you can see, here too you need to know the event rate in the control group to be able to do this conversion. There are also published tables that convert OR to RR.1,2
Throughout this demonstration, we have assumed that learners are comfortable with the clinical interpretation of relative risk and that understanding the relationship between odds ratios and relative risk renders the former comprehensible. Helping learners grasp the clinical significance of relative risk requires different demonstrations, which have been described elsewhere.6
The Bottom Line
-
–Stumbling block: learners are unfamiliar with how odds ratios are calculated and how to interpret their clinical importance.
-
–Odds ratios are calculated from a 2 × 2 table in a fashion completely analogous to the calculation of risk ratios.
-
–If the baseline risk is less than 30%, the difference between odds ratios and risk ratios is unlikely to be important.
-
–When odds ratios are different from the corresponding risk ratios, they are further from 1, implying a greater treatment effect.
-
–When interpreting the clinical importance of results expressed in OR, treat OR as RR.
See Appendix 2 for the summary card for this tip.
Addendum to Tip 2
-
–You may want to point out that when the risk of death (or any outcome) with the experimental treatment is the same as that with the control treatment, say 20% in each arm, then RR = 1 and also OR = 1. You may like to take the learners through Figure 2 using 20 in the Outcome + cells and 80 in the Outcome − cells for both treatment and control groups.
-
–Some learners may mention that they have encountered the use of ‘relative odds reductions’ as measures of therapeutic effectiveness. This is most commonly found in reports of stroke trials8 but also may be encountered in evidence-based summaries.9 To address this, first point out that ‘relative odds reduction’ is an alternative measure of effect to relative risk reduction. Then, remind learners of what they just learned in tip 2, i.e., that, when RR and OR are different, relative risk will always be closer to 1 than OR. From this and learners’ prerequisite knowledge of the relationship between relative risk and relative risk reduction, learners should immediately grasp that, when different, relative odds reduction will always be numerically larger than relative risk reduction. You may also point out that, for this reason, authors seeking to inflate the apparent effectiveness of a study drug may be motivated to report the results as ROR instead of as RRR.
-
–Interpretation of OR for a case control study and logistic regression follows on similar lines; however, it may be worth noting that case control studies usually address association of a disease with etiologic agents, and a causal association in such studies is usually reported with OR more than 1. The larger the OR, the stronger is the association.
Report on Field Testing
We field test the tips to verify the clarity and practicality of the descriptions. Field testing frequently generates examples of the kinds of variations in approach that occur when an experienced teacher of evidence-based medicine adapts the approaches to their own style, context, and learner level. One of the authors (S.K.), an experienced teacher of evidence-based medicine who was not involved in developing them, field tested the scripts used in this article on two occasions with 10 residents and 15 third year medical students, respectively. Learners ranged from very naive with little exposure to upper level residents with much experience in EBM principles. After initially focusing the learners on the issue of the relationship between odds and risk, S.K. proceeded to engage them with tip 1, using a pre-printed form sheet derived from Figure 1. In tip 1, S.K. handed out a blank table that only had the first column (Risk) filled in. S.K. also had pre-prepared a flip chart with the same blank table and asked the learners if they could provide corresponding odds for any row. Each time there were long periods of silence before someone said that risk of 0.5 was equal to odds of 1:1. Tip 1 required 25 minutes of teaching time, whereas tip 2 took 30 minutes.
Some learners still required other examples (such as pictures) to illustrate the concepts. For retention, the learners voiced that it would have been easier for them to understand the importance of odds if we had discussed it in the context of a particular paper or clinical problem. Of note, at every level, the learners were not comfortable with the concept of odds and at first seemed to not even know why we were reviewing this. For both groups, S.K. needed to teach fundamental concepts. When the discussion of the relationship between odds ratios and risk ratios arises from discussion of an article that has been identified as relevant to a problem arising from a patient encounter, the relevance issue is likely to be much less important, and many of us prefer to avoid this and other statistical topics with clinical learners until such an occasion arises. When this topic must be presented outside of the context of a specific clinical problem, the teacher may find it useful to have on hand one or more examples drawn from current medical literature.3,5
References
Sackett DL. Down with odds ratios!. Evidence Based Med. 1996;1:164–166.
Sinclair JC, Bracken MB. Clinically useful measures of effect in binary analyses of randomized trials. J Clin Epidemiol. 1994;47:881–889.
Everitt HA, Little PS, Smith PWF. A randomised controlled trial of management strategies for acute infective conjunctivitis in general practice. BMJ. 2006;333:321–326.
Laird NM, Mosteller F. Some statistical methods for combining experimental results. Int J Technol Assess Health Care. 1990;6:5–30.
Nathan JA, Pearce L, Field C, et al. A randomized controlled trial of follow-up of patients discharged from the hospital following acute asthma: best performed by specialist nurse or doctor? Chest. 2006;130:51–57.
Barratt A, Wyer PC, Hatala R, et al. Tips for teachers of evidence-based medicine: 1. Relative risk reduction, absolute risk reduction and number needed to treat. CMAJ. 2004;171:353–358. (Online Appendix).
Wyer PC, Keitz Sm, Hatala R, et al. Tips for learning and teaching evidence based-medicine: introduction to the series. CMAJ. 2004;171:347–348.
Ringleb PA, Schellinger PD, Schranz C, Hacke W. Thrombolytic therapy within 3 to 6 hours after onset of ischemic stroke. Stroke. 2002;33:1437–1441.
Anonymous. Aspirin in high risk patients. Bandolier. 2003;108.
Conflict of Interest
None disclosed.
Author information
Authors and Affiliations
Consortia
Corresponding author
Additional information
Members of the Evidence-Based Medicine Teaching Tips Working Group: Peter C. Wyer (project director), College of Physicians and Surgeons, Columbia University, New York, NY; Deborah Cook, Gordon Guyatt (general editor), Ted Haines, Roman Jaeschke, McMaster University, Hamilton, Ont.; Rose Hatala, University of British Columbia, Vancouver, BC; Robert Hayward (editor, online version), Bruce Fisher, University of Alberta, Edmonton, Alta.; Sheri Keitz (field test coordinator), Miami Veterans Affairs Medical Center and University of Miami, Miami, Florida; Alexandra Barratt, University of Sydney, Sydney, Australia; Antonio L. Dans, University of the Philippines College of Medicine, Manila, The Philippines; Cassie Kennedy and Victor M. Montori, Mayo Clinic College of Medicine, Rochester, Minn; Jennifer Kleinbart, Emory University School of Medicine, Atlanta, Ga.; Anna Lee, Anthony Ho and Gavin M Joynt, The Chinese University of Hong Kong; Rosanne Leipzig, Thomas McGinn, Mount Sinai Medical Center, New York, NY; Virginia Moyer, University of Texas, Houston, Tex.; Thomas B. Newman, University of California, San Francisco, San Francisco, Calif.; Kameshwar Prasad, All India Institute of Medical Sciences, New Delhi, India; W. Scott Richardson, Wright State University, Dayton, Ohio; Mark C. Wilson, University of Iowa, Iowa City, Iowa.
Contributors: Kameshwar Prasad, as principal author, contributed to tip 1, drafted the manuscript, coordinated the input from coauthors and from field-testing and revised all drafts. Roman Jaeschke provided comments throughout development and reviewed final draft. Sheri Keitz conducted field-testing of the tips and contributed material from the field-testing to the manuscript as well as revised field testing portion of final manuscript. Peter Wyer edited drafts and provided guidance in developing the final format. Gordon Guyatt contributed to tips 1 and 2, helped to write the manuscript, and revised all drafts.
Electronic supplementary material
Below is the link to the electronic supplementary material.
Fig. S1
Video object (mpg 227 MB)
Appendices
Appendix 1: Derivation of Formula to Convert Odds to Risk
For learners who like a bit of algebra, use the following to demonstrate conversion of odds to risk:
-
Odds = risk/(1-risk). Therefore, 1/odds = (1-risk)/risk = (1/risk) − 1.
-
Taking 1 to the other side, (1/odds) + 1 = 1/risk.
-
Taking inverse on both sides and transposing, risk = 1/[(1/odds) + 1] = odds/(odds + 1).
Other audiences might prefer to avoid the formulas and the algebra altogether.
Appendix 2: Summary Cards for 2 Teaching Tips on Understanding and Interpreting Odds Ratios in Studies of Therapy or Harm
This appendix has been designed so that it can be printed on a single sheet of 8 1/2 × 11-inch paper. The individual summary cards can then be cut out, if desired, for use during teaching sessions.
Teaching Tip 1 Summary Card: Understanding the Relationship Between Odds and Risk
Scenario
Select a game with which the learners are likely to identify. Ask them to explain what is meant by any given odds of one team winning a game or match over another one.
-
1.
Construct a figure on a blackboard or flip chart with risk expressed as a decimal (e.g., 0.25), odds expressed as a ratio (e.g., 1:3), odds expressed as a decimal (e.g., 0.33) and odds illustrated using markers (e.g., X/XXX) in successive columns.
-
2.
Write in values for risk under the first column, beginning with high values such as 0.8 and successively lower values down to 0.1. Ask the learners to give the odds corresponding to the risk in each case. Write down the odds corresponding to each risk as decimal values in the third column and notate how the calculation was done in the second column.
-
3.
Fill in the fourth column with the symbols you have selected to further illustrate the process.
-
4.
As you approach the lower risk values, lead the learners to the realization that the decimal values for risk and odds converge and are virtually identical at the point the risk is 0.10.
Summary Points
-
–Risk is a proportion or percentage of an entire population having a given characteristic or outcome. Odds is a ratio of those with and those without the characteristic or outcome within the population.
-
–As risk falls below 20%, odds and risk become more and more similar and virtually identical below a risk of 10%.
Teaching Tip 2 Summary Card: Understanding Odds Ratios and their Relationship to Risk Ratios
Scenario
Present a scenario involving a therapeutic trial with a dichotomous outcome such as mortality. Construct a 2 × 2 table identical to what the learners are used to seeing in connection with calculating relative risk.
-
1.
Fill in the table with 40 of 100 treated patients and 50 of 100 control patients in the outcome positive column.
-
2.
Have the learners calculate the risk of the outcome in the treatment group (0.4) and put this in a new column to the right of the table. Then, have them calculate the odds of the outcome in the treatment group (0.67) and write this in still another new column to the right of the odds column. Do likewise with the control patients. (0.5 and 1.0, respectively).
-
3.
Ask the learners to calculate the ratio of risk for the outcome between the groups (0.4/0.5 = 0.80).
-
4.
Ask the learners to calculate the ratio of odds for the outcome between the groups (0.67/1.0 = 0.67)
-
5.
Lead the learners to understand that the relative odds are further from 1 than the relative risk, implying a greater relative reduction in frequency of the outcome.
-
6.
To illustrate that the similarity of risk ratio and odds ratio is greater when the baseline risk is smaller, consider repeating the exercise using risks of 0.1 and 0.2 in the treatment and control groups, respectively.
Summary Points
-
–Stumbling block: learners are unfamiliar with how odds ratios are calculated and how to interpret their clinical importance.
-
–Odds ratios are calculated from a 2X2 table in a fashion completely analogous to the calculation of risk ratios
-
–If the baseline risk is less than 30%, the difference between odds ratios and risk ratios is unlikely to be important
-
–When odds ratios are different from the corresponding risk ratios, they are further from 1, implying a greater treatment effect.
-
–When interpreting the clinical importance of results expressed in OR, treat OR as RR.
Rights and permissions
Open Access This is an open access article distributed under the terms of the Creative Commons Attribution Noncommercial License ( https://creativecommons.org/licenses/by-nc/2.0 ), which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
About this article
Cite this article
Prasad, K., Jaeschke, R., Wyer, P. et al. Tips for Teachers of Evidence-Based Medicine: Understanding Odds Ratios and Their Relationship to Risk Ratios. J GEN INTERN MED 23, 635–640 (2008). https://doi.org/10.1007/s11606-007-0453-4
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11606-007-0453-4