Introduction

One of the main goals of earthquake seismology is the quantitative imaging of the Earth’s interior. This helps us understand the geodynamical processes and the geologic evolution of our planet. Knowledge of the velocity structure of the Earth is necessary for earthquake location, ground motion prediction, dynamic earthquake rupture modeling and inversion, among others. Teleseismic earthquake records are useful data for these goals, which have proved useful to map discontinuities at regional and global scales.

Imaging of the Earth’s structure with teleseismic data has evolved significantly since the introduction of travel time tomography (TTT; Aki et al. 1977) and receiver function analysis (RF; Langston 1977). TTT allows mapping volumetric variations of Earth’s velocity structure. Due to its infinite-frequency (ray) formulation, the ray’s sensitivity kernel is assumed to be concentrated along the path connecting the source to the receiver, limiting the resolution of the method. On the other hand, RF is useful to identify interfaces beneath seismic arrays, but it cannot determine their depths. The techniques for inverting the velocity structure from RF usually assume, at least locally, 1D Earth models (e.g., Ammon et al. 1990), limiting their application to complex environments. The availability of large volumes of data from dense seismic arrays led to the application of migration methods, developed in seismic reflection, to the imaging of crust and mantle structures. Bostock et al. (2001) showed the use of teleseismic P wave and its coda for high-resolution lithospheric imaging. Based on the combination of ray and the Born approximation, their method is a linearized waveform inversion that determines perturbations of the material properties with respect to a predefined background medium. They showed the importance of considering free-surface reflections to image short-wavelength structures. One advantage of this method is that scattering is treated in 2D and 3D. However, there is a strong dependency on the chosen background model and the inverted results. In addition, the infinite-frequency assumption of ray theory makes the forward modeling fail in cases where complex wave propagation is important.

The natural step forward for high-resolution imaging is nonlinear full waveform inversion (FWI). In its first versions (Lailly 1983; Tarantola 1984), FWI was formulated as a nonlinear optimization process that seeks to minimize the least squares waveform difference between observed and synthetic seismograms. An initial model is refined iteratively until a user’s misfit criterion is met. The main advantage of FWI is that it accounts for all possible seismic waves in the forward modeling and sensitivity kernel calculation. While migration fits the scattered waveforms with a constant background medium, FWI reconstructs both the background model and the short-wavelength structures by fitting every wiggle’s amplitude and phase in the entire waveform. Consequently, FWI has the potential to image structures at half the propagated wavelength (Virieux and Operto 2009). However, this comes at a price. For example, due to the size of the inverse problem, local gradient-based optimization techniques are preferred to global ones. Fortunately, the adjoint-state method (Plessix 2006) provides an efficient way to compute the gradients for the optimization process as it requires a maximum of three numerical simulations of the wave equation for each source at each iteration. Additionally, due to nonlinearity, the initial model must predict the travel times of observed waveforms with a difference of less than half the period to avoid cycle-skipping and convergence to local minima (Virieux and Operto 2009). Therefore, inversion strategies must be carefully designed (e.g., Bunks et al. 1995; Sirgue and Pratt 2004).

The primary limitation of FWI is the high computational cost of solving the wave equation repeatedly. In an N-dimensional medium, the computational cost of the simulation scales with frequency to the power of N + 1 (Thrastarson et al. 2020). For this reason, global numerical simulations at higher frequencies (1 s for P waves, 3–6 s for S waves) are still far from practical (Liu and Gu 2012). One attractive solution is the use of hybrid methods based on the decomposition of the computational domain into two subdomains, background and local. Different solvers are used in each subdomain with the aim of reducing computer memory and time. The incident wavefield computed in the background model is injected by appropriate boundary conditions in the local region where the response of local heterogeneities to the incident wavefield is computed. In this way, high-frequency global simulations are computationally affordable since intensive computations are restricted to the local domain. The choice of the two solvers depends on several considerations such as the geometry of the model (flat or spherical), types of waves included (e.g., P, S or surface waves), grid compatibility and efficiency. Several hybrid methods have been developed for FWI using teleseismic data. The first attempts were carried out in the frequency domain (Roecker et al. 2010; Pageot et al. 2013). Subsequent hybrid methods rely on time-domain approaches. The spectral-element method (SEM) has been coupled with the direct solution method (SEM-DSM; Monteiller et al. 2013) and the FK method (SEM-FK; Tong et al. 2014). Another hybrid method couples a time–space optimized finite difference (FD) method with FK (Ma et al. 2018). A series of contributions to FK-based hybrid methods were presented by Liang et al. (2021), Ba et al. (2022) and Wu et al. (2022), where they developed a hybrid SEM-FK for viscoelastic modeling in localized regions considering source-path-site effects. Though they focus on engineering purposes (frequencies > 10 Hz), their method might be applicable to teleseismic FWI if a lower frequency range is considered. However, it is viscoelastic FWI that poses major challenges due to the increased interparameter cross talk between seismic velocities and quality factors (Pan and Wang 2020). For this reason, teleseismic FWI real data applications have been restricted to the elastic case (Wang et al. 2016; Zhang et al. 2021; Kan et al. 2023).

No single hybrid method can be used for all problem configurations. For example, the DSM computes the incident wavefield accounting for Earth’s and wavefront curvature, making it possible to model all global teleseismic phases, but it has a high computational cost. A simpler choice is to use the FK method (Zhu and Rivera 2022) and consider the incident wavefield to be composed of single plane waves computed in a flat-layered Earth model. This assumption is valid when the region of interest is smaller than several hundred km (Rondenay 2009). In this case, computations can be done efficiently since computation time scales linearly with frequency (Monteiller et al. 2021). Regarding the heterogeneous region, SEM and FD are by far the two most frequently used methods. SEM is known to be more accurate than FD since the mesh can honor complex geologic interfaces. However, SEM has a critical drawback: The mesh must be carefully designed (Lyu et al. 2020). On the other hand, FD provides a good balance between accuracy and computational efficiency (Moczo et al. 2014). FD schemes can be computationally more efficient than SEM on a regular space–time grid (Moghaddam et al. 2018). In particular, the SGFD (Virieux 1984) is attractive as it is more accurate and stable than conventional grid FD schemes (Liu et al. 2023). In seismic imaging, we often do not have precise knowledge of the location of the geologic interfaces. Therefore, working with relatively smooth earth parameters at the wavelength scale is often sufficient in FWI (Virieux et al. 2011).

In this paper, we present new SGFD-FK hybrid method to compute the elastic response of plane body waves impinging at oblique incidence on a 2D heterogeneous domain embedded in a multilayered half space. The FK method is used to compute the incident teleseismic wavefield in a flat-layered Earth. Then, the SGFD method is used to continuate the teleseismic wave propagation in a heterogeneous region. Since the FK and SGFD are computed on the same time–space grid, the incident wavefield is computed on the fly, and thus, little memory is needed. The FK provides the five dynamic fields (two velocities and three stresses) necessary to SGFD modeling. We use convolutional perfectly matched layers (CPML; Komatitsch and Martin 2007) to absorb the reflections at the boundaries of waves scattered by the heterogeneities in the local region. The efficiency of the FK method (to solve the global region) combined with SGFD (to solve the heterogeneous region) results in an efficient and accurate method for high-frequency teleseismic modeling. We benchmark the accuracy of the proposed hybrid method against the analytical FK method itself and the SEM-FK, achieving similar accuracy. Finally, we describe the theory of FWI in the context of our method and present a 2D FWI algorithm for teleseismic model configurations. We believe our new hybrid approach can be useful in 2D teleseismic FWI due to its efficiency and accuracy. A synthetic example illustrates the potential and limitations of this FWI approach.

Forward problem: SGFD-FK hybrid method

Elastic wave propagation in an isotropic heterogeneous 2D medium is described by the velocity-stress formulation of the equations of motion:

$$\rho \frac{{\partial v_{x} }}{\partial t} = \frac{{\partial \sigma_{xx} }}{\partial x} + \frac{{\partial \sigma_{xz} }}{\partial z} + f_{x} ,$$
(1)
$$\rho \frac{{\partial v_{z} }}{\partial t} = \frac{{\partial \sigma_{xz} }}{\partial x} + \frac{{\partial \sigma_{zz} }}{\partial z} + f_{z} ,$$
(2)

and Hooke’s law

$$\frac{{\partial \sigma_{xx} }}{\partial t} = \left( { \lambda + 2\mu } \right)\frac{{\partial v_{x} }}{\partial x} + \lambda \frac{{\partial v_{z} }}{\partial z},$$
(3)
$$\frac{{\partial \sigma_{zz} }}{\partial t} = \left( {{ }\lambda + 2\mu } \right)\frac{{\partial v_{z} }}{\partial z} + { }\lambda \frac{{\partial v_{x} }}{\partial x},$$
(4)
$$\frac{{\partial \sigma_{xz} }}{\partial t} = \mu \left( {\frac{{\partial v_{x} }}{\partial z} + \frac{{\partial v_{z} }}{\partial x}} \right).$$
(5)

Here, \(t\) denotes time, \(x\) and \(z\) denote the horizontal and vertical directions, respectively. \({v}_{x}\) and \({v}_{z}\) are the particle velocity fields, \({\sigma }_{xx}\), \({\sigma }_{zz}\) and \({\sigma }_{xz}\) are stress tensor components, \({f}_{x}\) and \({f}_{z}\) are point body forces acting in their respective directions and \(\lambda\), \(\mu\) and \(\rho\) denote the Lamé elastic constants and density. This set of equations is discretized in space and time according to the fourth-order accurate in space, second-order accurate in time, scheme proposed by Levander (1988). Free-surface boundary condition is imposed using the mirroring technique, and CPML boundaries are applied along the lateral and bottom interfaces. Instabilities due to large impedance contrasts are avoided using harmonic averages for \(\mu\) and arithmetic average for \(\rho\) (Moczo et al. 2002).

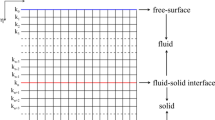
Consider the case of teleseismic sources with incident motion consisting of P or SV plane waves. We use the FK method to compute the incident wavefield in a number of homogeneous layers (Fig. 1a) using the propagator matrix formalism (Haskell 1953). Ground motion is integrated over the whole frequency range but only for a single wavenumber, which makes the computations efficient. Tong et al. (2014) described in detail the FK method we use and showed that the solution can be determined when free-surface boundary conditions are imposed. When a plane wave impinges on the boundaries of the local domain (gray rectangle in Fig. 1a), which contains heterogeneities, the FK method is no longer valid. On this boundary, the incident plane wavefield is used to excite the SGFD grid to compute ground motion inside the local heterogeneous region. The coupling of the FK method with SGFD is implemented using the total-field/scattered-field formulation (TF/SF; Taflove and Hagness 2005), also known as the grid injection method (Robertsson and Chapman 2000). This approach is based on linearity of wave equation and the decomposition of the total wavefield, \({U}_{{\text{tot}}}\), as:

$$U_{{{\text{tot}}}} = U_{{{\text{FK}}}} + U_{{{\text{scat}}}} ,$$
(6)

where the incident wavefield, \({U}_{{\text{FK}}}\), is computed with the FK method and the scattered wavefield, \({U}_{{\text{scat}}}\), is initially unknown. The SGFD algorithm uses Eq. (6) to divide the domain into two regions separated by the injection surface, Si (yellow line in Fig. 1a). SGFD operates on both incident and scattered wavefields in the shaded region in Fig. 1b, while it operates only on SF in the unshaded region. The latter serves to impose CPML boundary conditions. Region E (shaded in blue in Fig. 1a and 1b) includes nodes from both regions and allows information exchange to take place. The values of \({U}_{{\text{FK}}}\) must be known at all time steps at all nodes within E. For a fourth-order accurate in space scheme (Levander 1988), we need to store the \({U}_{{\text{FK}}}\) wavefields for a 3-node-thick layer surrounding Si. This is shown in Fig. 1b, where we have zoomed in the left side of region E. Note that the number of layers in region E is equal to n–1, where n is the order of approximation of spatial derivatives.

Fig. 1
figure 1

Schematic of the SGFD-FD hybrid method. a The TF region (gray rectangle), which contains heterogeneities (red body), is embedded in a 1D layered medium (SF region) bounded by the black dashed line. These regions are separated by the injection surface Si (yellow line). The E (blue region) serves to exchange information between TF and SF regions. Teleseismic plane waves enter the bottom of the layered medium with an incidence angle \(\theta\). b Zoom in on the red dashed rectangle of a

Full size image

Sufficiently far from region E, the equations to update SGFD for total and scattered wavefields are consistent and trivial to implement. However, for nodes within region E, the required spatial derivatives are taken across Si, which causes a problem of consistency since TF and SF nodes are involved in the same updating equation. These nodes require a modification using the values of the incident \({U}_{{\text{FK}}}\) field. To illustrate this process, consider the magenta stencil shown in Fig. 1b and the following equation:

$$\begin{aligned} {v_{{z, {\text{scat}} }}}_{{\left( {i,j} \right)}}^{k + 1/2 } = &\, {v_{{z, {\text{scat}} }}}_{{\left( {i,j} \right)}}^{k - 1/2 } \\ & + \frac{\Delta t }{{\Delta x\rho_{{\left( {i,j + 1/2} \right)}} }}\left[ {a_{0} \left( {{\sigma_{{xz, {\text{tot}} }}}_{{\left( {i,j} \right)}}^{k } - {\sigma_{{xz, {\text{FK}} }}}_{{\left( {i,j} \right)}}^{k } - {\sigma_{{xz, {\text{scat}} }}}_{{\left( {i - 1,j} \right)}}^{k } } \right)} \right. \\ & \left. + a_{1} \left( {\sigma_{{xz, {\text{tot}} }}}_{{\left( {i + 1,j} \right)}}^{k } - {\sigma_{{xz, {\text{FK}} }}}_{{\left( {i + 1,j} \right)}}^{k } - {\sigma_{{xz, {\text{scat}} }}}_{{\left( {i - 2,j} \right)}}^{k } \right) \right] \\ & + \frac{\Delta t }{{\Delta z\rho_{{\left( {i,j + 1/2} \right)}} }}\left[ {a_{0} \left( {\sigma_{{zz, {\text{scat}} }}}_{{\left( {i,j + 1} \right)}}^{k } - {\sigma_{{zz, {\text{scat}} }}}_{{\left( {i,j} \right)}}^{k } \right)} \right.\\ &\left. + a_{1} \left( {{\sigma_{{zz, {\text{scat}} }}}_{{\left( {i,j + 2} \right)}}^{k } - {\sigma_{{zz, {\text{scat}} }}}_{{\left( {i, j - 1} \right)}}^{k } } \right) \right], \\ \end{aligned}$$
(7)

where \(\Delta x\) and \(\Delta z\) are the spatial grid sizes in the \(x\) and \(z\) direction, respectively, \(\Delta t\) is the time step, \(k\), \(i\) and \(j\) are integers used to evaluate time \(t\), \(x\) and \(z\), respectively, at discrete points as \(t\hspace{0.17em}=\hspace{0.17em}k\Delta t\), \(x\hspace{0.17em}=\hspace{0.17em}i\Delta x\) and \(z\hspace{0.17em}=\hspace{0.17em}j\Delta z\), \({a}_{0}\) and \({a}_{1}\) are the finite difference weighting coefficients and their values are given by Levander (1988) as \(9/8\) and \(-1/24\). If we ignore the terms of the incident FK fields (the terms \({\sigma }_{xz, {\text{FK}}}\) in the first square brackets of Eq. (7)), it is incorrect because we add unlike shear stresses in the first bracket. This equation may be easily corrected by adding the FK terms since:

$$\sigma_{{xz,{\text{tot}}}} = \sigma_{{xz,{\text{FK}}}} + \sigma_{{xz,{\text{scat}}}} .$$
(8)

Equation (8) effectively converts the values of the total shear stress wavefield to scattered-field quantities. Similar corrections must be made for all the other elastic wavefields whose nodes are within the E region. The effect of this correction procedure is to inject ingoing waves along Si into the heterogeneous region, while canceling outgoing waves. To absorb the scattered energy, the SF region must be extended to be able to apply absorbing boundaries conditions. We use CPML boundaries since they have proved to be efficient in eliminating spurious waves even at grazing incidence (Komatitsch and Martin 2007).

Forward modeling numerical examples

We present some numerical examples to show the accuracy of our hybrid code for plane waves propagating in a 2D domain. We compare our numerical solution to the analytical FK and the one computed by the SEM-FK method. The first example is the incidence of a P plane wave on a homogeneous isotropic half space of dimensions 200 \(\times\) 200 km. The elastic properties of the medium are listed in the first row of Table 1, corresponding to a typical crust. The incident signal is given by the Gaussian pulse:

$$f\left( t \right) = \frac{{f_{0} }}{\sqrt \pi }e^{{ - \left( {f_{0} t} \right)^{2} }} ,$$
(9)

where \({f}_{0}\) is the cutoff frequency of the pulse (2 Hz). For the SGFD-FK, the spatial grid sizes are \(\Delta x\hspace{0.17em}=\hspace{0.17em}\Delta z\hspace{0.17em}=\hspace{0.17em}0.2\)km, and the time step is \(\Delta t\hspace{0.17em}=\hspace{0.17em}0.012\)s. These choices satisfy the stability and dispersion criteria, ensuring 8 points per minimum wavelength (PPW). Except for the free surface on top, the other boundaries include a 13-node-thick CPML, with the parameters used in Komatitsch and Martin (2007). For the SEM-FK simulation, the average size of the element is \(\Delta h\hspace{0.17em}=\hspace{0.17em}1\)km and the time step is the same as that of the SGFD simulation.

Table 1 Elastic properties of the crust-over-mantle model
Full size table

Figure 2a, c shows the horizontal and vertical synthetic seismograms computed with our method. They are compared to the solutions obtained by the FK method, the exact solution for this problem, and the numerical result approximated using the SEM-FK methods. The station is located at \(x\hspace{0.17em}=\hspace{0.17em}170\)km and \(z=120\)km. The three solutions are very similar. Figure 2b, d shows the relative differences among the three synthetics shown in Fig. 2a, c. Our hybrid method has smaller errors than the SEM-FK for all seismic phases. The largest errors appear in the vertical component of the Ps wave for the SEM-FK method. The traces showing the relative differences between the three methods show that some spurious waves slipped in the numerical solutions. However, their relative amplitude is smaller than 2% of the incident wave amplitude.

Fig. 2
figure 2

a Horizontal and c vertical velocity seismograms computed by the FK (blue), SGFD-FK (black) and SEM-FK (red dotted line) methods, and its corresponding errors b and d. Errors are relative to the FK solution. The direct P, converted Pp and Ps phases are labeled as 1, 2 and 3, respectively. Apart from these phases, some spurious waves may be appreciated clearly in b and d

Full size image

A second example reproduces the layer over half space computed in Tong et al. (2014). Table 1 gives the properties of the media. The layer is \(30\)km thick. The 2D grid covers a section of 100 \(\times\) 60 km. Excitation is given by an incident plane P wave with an angle of incidence of 15°. All other parameters remain the same as in the previous example. Figure 3a shows snapshots of the horizontal displacement field propagating at different time steps. We note that the CPML boundaries perform well; the TF region shows insignificant spurious reflections. We evaluate again the accuracy of our simulation comparing our result with those of the semi-analytical FK and the SEM-FK methods. The receiver is located on the free surface at \(x=70\) km. Figure 3b, c shows the synthetic seismograms computed by the three methods. The relative errors along the time computed from the differences between traces are shown in Fig. 3d, e. The amplitude of the direct P wave shows is correctly modeled by SGFD-FK and SEM-FK. However, our approach has significantly larger errors for the PsPms phase, 8%. The largest errors in our approach come from an inaccurate estimate of the phase of the waves; amplitudes are accurately modeled. Different tests showed that the phase differences are caused by the definition of the material interfaces in the staggered grid scheme. Indeed, it is not possible to place material interfaces at their exact depth; they are defined half a spatial grid away from their correct location.

Fig. 3
figure 3

a Snapshots of the horizontal displacement field generated by an incident plane P wave with an angle of incidence \(\theta \hspace{0.17em}\)= 15° that enters the domain from the left side. The black dashed lines represent crust–mantle boundary. b Horizontal and c vertical velocity seismograms computed by the FK (blue), SGFD-FK (black) and SEM-FK (red dotted) methods and its corresponding errors d and e. The errors are relative to the FK solution. These seismograms are recorded by a station located at \(x\hspace{0.17em}=\hspace{0.17em}70\) km on the free surface (inverted magenta triangle). Some teleseismic phases labeled in b and c correspond to 1 Pp, 2 Ps, 3 PpPmp, 4 PpPms 5 PsPms, 6 PpPmpPmp and 7 PsSms

Full size image

In a third example, we show the effectiveness and stability of the CPML applied in our hybrid method to absorb scattered waves. To the previous model, we have added a square scatterer, with a size 20 \(\times\) 20 km in the half space (Fig. 4a). The top surface of the scatterer is 20 km below the interface between layer and half space, and it has a + 20% perturbation in velocities and density relative to the half space. The computational model has 100 \(\times\) 100 km dimension. The excitation is a P plane wave with a 15° angle of incidence. Spatial and temporal discretization parameters remain the same as the previous example. The simulation last 200 s to test the stability of the CPML conditions for long-time simulations. Figure 4b, c shows three snapshots at 10, 25 and 50 s, comparing the results with (Fig. 4a) and without (Fig. 4c) absorbing boundaries. The results show clearly the need to include absorbing boundaries to avoid spurious waves reflected into the heterogeneous domain. Figure 4d shows the comparison between horizontal synthetics computed with and without absorbing boundaries for a point at x = 1.3 km on the free surface. Following Komatitsch and Martin (2007), Fig. 4e shows the energy decay as a function of time inside the FD grid. Maximum energy corresponds to the incident P wave and its surface reflection. By the end of the simulation, energy has decreased by roughly 4 orders of magnitude, which highlights the efficiency and stability of the CPML boundaries.

Fig. 4
figure 4

Teleseismic plane wave entering the local domain with an angle of incidence \(\theta \hspace{0.17em}=\hspace{0.17em}15^\circ\). a Elastic models considered for this example. b Snapshots of the horizontal at different time steps with CPML boundary condition. The black dashed lines denote the contours of the crust–mantle boundary and the scatterer. c Same as b but using Dirichlet boundary conditions. d Velocity seismogram comparison for simulations considering CPML (black) and no-CPML (red dotted) recorded by a station located at \(x\hspace{0.17em}=\hspace{0.17em}1.3\) km on the free surface. e Seismic energy reduction with time for the simulation showed in b

Full size image

Inverse problem: FWI

An efficient solver for the forward problem is a useful tool for the inverse problem. FWI searches for the model parameters that reproduce at best the observed data by minimizing the least squares difference between observed and synthetic seismograms. Given that this problem is highly nonlinear, local gradient-based optimization algorithms are preferred but they require an efficient tool to compute the gradients, such as the adjoint-state method. In the following we summarize the choices we have made to formulate a FWI algorithm based on our time-domain SGFD-FK simulation method.

Most algorithms use the formulation given by Tarantola (1984), where the misfit between observations and synthetics is evaluated by the least squares objective function, E, given by:

$$E\left( {\varvec{m}} \right) = \frac{1}{2}\left( {{\varvec{u}}^{{{\text{syn}}}} - {\varvec{u}}^{{{\text{obs}}}} } \right)^{T} \left( {{\varvec{u}}^{{{\text{syn}}}} - {\varvec{u}}^{{{\text{obs}}}} } \right),$$
(10)

where \({{\varvec{u}}}^{{\text{syn}}}\) and \({{\varvec{u}}}^{{\text{obs}}}\) are the time-domain synthetic and observed seismograms, respectively, T denotes the transpose operator, and m is the model parameters. The problem consists in finding \({\varvec{m}}\) that minimizes the objective function. In general, this nonlinear optimization problem is solved with iterative approaches, where the model parameters are updated along a descent direction \({{\varvec{s}}}_{k}\) as:

$${\varvec{m}}_{k + 1} = {\varvec{m}}_{k} + \alpha_{k} {\varvec{s}}_{k} ,$$
(11)

where \({\alpha }_{k}\) is the scalar step length at the k-th iteration. Depending on the chose of \({\varvec{s}}\), the optimization algorithm has many variants, such as the steepest descent, conjugate gradient or Newton’s method. All of them require the computation of the gradients of the misfit function with respect to the model parameters, \(\partial E({\varvec{m}})/\partial {\varvec{m}}\), at each iteration.

According to the adjoint-state method, the gradients can be computed through the zero-lag cross correlation between displacements wavefields. For an isotropic elastic Earth model, they are given by Köhn et al. (2012) as:

$$\begin{gathered} \frac{{\partial E\left( {m} \right)}}{{\partial \lambda }} = - \mathop \sum \limits_{{{\text{event}}}} \mathop \int \limits_{0}^{T} \left( {\frac{{\partial {\vec{u}}_{x} }}{{\partial x}} + \frac{{\partial {\vec{u}}_{z} }}{{\partial z}}} \right)\left( {\frac{{\partial {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftarrow}$}}{u} }_{x} }}{{\partial x}} + \frac{{\partial {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftarrow}$}}{u} }_{z} }}{{\partial z}}} \right){\text{d}}t \hfill \\ \frac{{\partial E\left( {m} \right)}}{{\partial \mu }} = - \mathop \sum \limits_{{{\text{event}}}} \mathop \int \limits_{0}^{T} \left( {\left( {\frac{{\partial {\vec{u}}_{x} }}{{\partial z}} + \frac{{\partial {\vec{u}}_{z} }}{{\partial x}}} \right)\left( {\frac{{\partial {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftarrow}$}}{u} }_{x} }}{{\partial z}} + \frac{{\partial {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftarrow}$}}{u} }_{z} }}{{\partial x}}} \right) + 2\left( {\frac{{\partial {\vec{u}}_{x} }}{{\partial x}}\frac{{\partial {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftarrow}$}}{u} }_{x} }}{{\partial x}} + \frac{{\partial {\vec{u}}_{z} }}{{\partial z}}\frac{{\partial {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftarrow}$}}{u} }_{z} }}{{\partial x}}} \right)} \right){\text{d}}t \hfill \\ \frac{{\partial E\left( {m} \right)}}{{\partial \rho }} = - \mathop \sum \limits_{{{\text{event}}}} \mathop \int \limits_{0}^{T} \left( {\frac{{\partial ^{2} {\vec{u}}_{x} }}{{\partial t^{2} }}\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftarrow}$}}{u} _{x} + \frac{{\partial ^{2} {\vec{u}}_{z} }}{{\partial t^{2} }}{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftarrow}$}}{u} }_{z} } \right){\text{d}}t, \hfill \\ \end{gathered}$$
(12)

where \(\overrightarrow{{\varvec{u}}}\) is the regular forward modeled wavefield and \(\overleftarrow{{\varvec{u}}}\) is the adjoint wavefield. This last one is generated by backpropagating the data residuals to the receiver positions. In this way, between 2 and 3 simulations are required for each event (i.e., earthquake). The necessary displacement fields are calculated from the modeled velocity wavefields of Eqs. (1) and (2) by numerical integration. According to Köhn et al. (2012), expressing these gradients in terms of seismic velocities and density reduces the creation of artifacts in the inverted density model. The corresponding expressions are:

$$\begin{aligned} \frac{{\partial E\left( {\varvec{m}} \right)}}{{\partial V_{p} }} = & 2\rho V_{p} \left( {\frac{{\partial E\left( {\varvec{m}} \right)}}{\partial \lambda }} \right) \\ \frac{{\partial E\left( {\varvec{m}} \right)}}{{\partial V_{s} }} = & - 4\rho V_{s} \left( {\frac{{\partial E\left( {\varvec{m}} \right)}}{\partial \lambda }} \right) + 2\rho V_{s} \left( {\frac{{\partial E\left( {\varvec{m}} \right)}}{\partial \mu }} \right) \\ \frac{{\partial E\left( {\varvec{m}} \right)}}{{\partial \rho_{{{\text{Vel}}}} }} = & \left( {V_{p}^{2} - 2V_{s}^{2} } \right)\left( {\frac{{\partial E\left( {\varvec{m}} \right)}}{\partial \lambda }} \right) + V_{s}^{2} \left( {\frac{{\partial E\left( {\varvec{m}} \right)}}{\partial \mu }} \right) + \left( {\frac{{\partial E\left( {\varvec{m}} \right)}}{\partial \rho }} \right). \\ \end{aligned}$$
(13)

Once the gradients are computed, the optimization problem may be solved iteratively. The nonlinear conjugate gradient method offers a good compromise between low-memory requirements and efficiency. It also avoids the crisscross pattern of the steepest descent method. In this method, the descent direction for the k-th iteration is given by:

$${\varvec{s}}_{k} = - \left( {\frac{{\partial E\left( {\varvec{m}} \right)}}{{\partial {\varvec{m}}}}} \right)_{k} + \beta_{k} \left( {\frac{{\partial E\left( {\varvec{m}} \right)}}{{\partial {\varvec{m}}}}} \right)_{k - 1} .$$
(14)

The algorithm has many variants depending on the chosen weighting scalar parameter \(\beta\). In our case, we choose \(\beta\) as:

$$\beta_{k} = \frac{{\left( {\frac{{\partial E\left( {\varvec{m}} \right)}}{{\partial {\varvec{m}}}}} \right)_{k} \cdot \left[ {\left( {\frac{{\partial E\left( {\varvec{m}} \right)}}{{\partial {\varvec{m}}}}} \right)_{k} - \left( {\frac{{\partial E\left( {\varvec{m}} \right)}}{{\partial {\varvec{m}}}}} \right)_{k - 1} } \right]}}{{\left( {\frac{{\partial E\left( {\varvec{m}} \right)}}{{\partial {\varvec{m}}}}} \right)_{k} \cdot \left( {\frac{{\partial E\left( {\varvec{m}} \right)}}{{\partial {\varvec{m}}}}} \right)_{k - 1} }}.$$
(15)

This choice is among the three most efficient.

The final element needed is the value of the step length \(\alpha\). From the different proposals, we chose to compute it using the parabolic fitting method (Vigh and Starr 2008). In this method, the objective function is evaluated for three different steps, \({\alpha }_{t1}\), \({\alpha }_{t2}\) and \({\alpha }_{t3}\), satisfying the conditions:

$$\left\{ {\begin{array}{*{20}l} {E\left( {{\varvec{m}}_{k} + \alpha_{t1} {\varvec{s}}_{k} } \right) < E\left( {{\varvec{m}}_{k} } \right)} \hfill \\ {E\left( {{\varvec{m}}_{k} + \alpha_{t2} {\varvec{s}}_{k} } \right) > E\left( {{\varvec{m}}_{k} + \alpha_{t1} {\varvec{s}}_{k} } \right).} \hfill \\ {0 < \alpha_{t1} < \alpha_{t2} .} \hfill \\ \end{array} } \right.$$
(16)

Next, a parabola is interpolated through the evaluated points of \(E\). The minimum value of this curve provides the desired \(\alpha\). In the best-case scenario, only two extra forward simulations are required.

We do not consider anelastic attenuation. However, in elastic wave propagation, amplitudes are attenuated by geometrical spreading causing the gradient to focus on short distances from the source. The result is the loss of information for large offsets. This effect may be compensated by using a spatial preconditioner on the gradients. The only preconditioner we use is the illumination factor (Kaelin and Guitton 2006) defined as:

$${\varvec{H}}_{p}^{ - 1} = \left\{ {\int \left| {\left( {v_{x} + v_{z} } \right)} \right|^{2} {\text{d}}t} \right\}^{ - 1} .$$
(17)

The least squares objective function depends strongly on the initial model. High frequencies create many local minima in that function. One solution was proposed by Bunks et al. (1995): a multiscale approach. The inversion starts using the low frequency content of data to constrain the long wavelength Earth structure. Once the inversion converges, iterations are stopped, and the frequency content of data is increased. The final model of the first stage is used as initial model for the next stage using higher frequencies. This procedure is repeated until the desired frequency range is covered.

Inverse numerical example

To demonstrate the feasibility of FWI based on the forward SGFD-FK method, we apply our algorithm to a synthetic model representing a simplified subduction zone. The model consists of two layers, a 30 km thick crust underlain by 170 km of mantle. The Moho interface has the shape of a sine function with an amplitude 10 km and period 200 s (Fig. 5a–c). The elastic properties of these layers are given in Table 1. Our Earth model is very simple. However, it serves to demonstrate the accuracy of our approach. Further developments could include finer layering of the crust (Ba et al. 2021), as well as the topographic effects (e.g., hills, basins and canyons; Sanchez-Sesma and Luzon 1995; Mossessian and Dravinski 1987) without any problem. However, here we are interested in imaging lithospheric structures. The subducting slab is represented by a 36 km thick rectangle with a 33.7° dip. This slab has Vp, Vs and density 5% larger than the mantle. The size of the model is 200 \(\times\) 200 km, and it is discretized using \(\Delta x=\Delta z=500\) m. The lateral and bottom boundaries are truncated by a 13-node-thick CPML. It is not possible to use as initial model a simple layer over half space. The large impedance contrast between those two media creates a strong gradient signature near the interface and the algorithm would not converge. To avoid this problem, we smoothed that interface using a spatial Gaussian filter. Thus, in the initial model the transition crust to mantle develops over 30 km. The synthetic data were computed simulating the ground motion to incident P waves from 10 teleseismic events with incident angles ranging from − 27 to 27°, with a step of 6°. The source time function is the same for each event, the Gaussian pulse shown in Eq. (10), with a dominant frequency \({f}_{0}=\) 0.5 Hz. The total duration of simulated waveforms is 120 s with a time step \(\Delta t=0.03\) s. The wavefield is recorded by 40 receivers placed on the free surface with an even spacing of 5 km, between \(x=3\) and \(x=198\) km.

Fig. 5
figure 5

a–c True Vp, Vs and density models. d–f Initial Vp, Vs, and density models. g–i Inverted Vp, Vs and density models from the first stage (0.1 Hz). j–l same as g–i but from stage fourth stage (0.4 Hz). m–o Finals Vp, Vs and density models after 200 iterations

Full size image

We use multiscaling to divide the inversion into eight frequency stages, from 0.1 to 0.8 Hz with a step of 0.1 Hz. At each stage, the synthetics were filtered with a low-pass Butterworth filter of order 5 with the corresponding cutoff frequency. The gradients were built using the time window [− 10, 60] s, where 0 is the time of the P wave arrival at each receiver and 25 iterations were computed for each frequency stage. The inverted model after the first stage (Fig. 5g–i) clearly shows the presence of the subducting slab although it is not well defined. The amplitude of the anomalies in the elastic parameters (5%) is correctly estimated. The irregular shape of the Moho is also captured already although some artifacts are present. Figure 5j–l shows the result after the final iteration for the 0.4 Hz stage. The slab and the irregular Moho are better defined while artifacts have significantly shrinked. Figure 5m–o shows the final model, after 200 iterations. The true model is correctly retrieved except at large depths, with few artifacts.

Figure 6 shows the efficiency of the multiscale approach to achieve good results in a wide frequency range. For each frequency band, 25 iterations were used to decrease the misfit in the inversion process. It is clear that the lower the frequency, the faster and larger is the decrease of the misfit. The final error at each stage increases with increasing frequency. Figure 7 shows, as an example, the vertical profiles of the elastic parameters at \(x=100\)km for the true, initial and final models. The amplitudes of the anomalies are correctly recovered. The final model shows a ringing effect at the different interfaces. This effect is related to the magnitude of the impedance contrast at the corresponding interface. For this reason, it is larger at the crust–mantle boundary.

Fig. 6
figure 6

Misfit reduction as a function of iterations for the different stages (0.1–0.8 Hz)

Full size image
Fig. 7
figure 7

Comparison of the true, initial and final inverted depth profiles for Vp, Vs and density at \(x\hspace{0.17em}=\hspace{0.17em}100\) km

Full size image

Conclusions

We have developed a new hybrid method that combines the FK method, for global simulations, with the SGFD method, for heterogeneous media. The coupling between them uses the TF/SF formulation. It has low-memory requirements since the incident FK wavefields are computed on the fly. Additionally, the two methods highly are compatible since they are computed on the same time–space grid. We implemented CPML boundary conditions on the edges of the local domain to efficiently absorb scattered waves generated by the local heterogeneities. The combination of these techniques allows modeling teleseismic body waves and their coda up to 2 Hz, with an accuracy comparable to the SEM-FK method. We have used our SGFD-FK as modeling tool to develop an elastic FWI algorithm adapted for teleseismic configurations. The inversion is solved by the conjugate gradient method, where the required gradients are computed using the adjoint-state method. The accuracy of our FWI algorithm was tested using a synthetic example of a subducted slab within a crust–mantle structure. A synthetic data set was generated from 10 teleseismic events. The results showed an excellent reconstruction of the elastic parameters of the initial model, with the correct amplitude. The obtained resolution was close to the propagated wavelength. Of course, we are aware of the limitations of this method. We only considered a simple 2D structure, did not include anelastic attenuation, and our synthetic signals are noise-free. Moreover, we assume that the signal at the sources is known. These shortcomings are the focus of our future work, including its application to real data, as well as its extension to 3D.