Surface water load and earthquake stress interactions near the Pirrís reservoir, Costa Rica

Abstract

This study analyzes the relationships between the stress changes produced by the water load variations due to the filling operations at the Pirrís Reservoir, Costa Rica, and the stress changes generated by three relevant earthquakes after the first impoundment. The earthquakes differ in their magnitude, distance from reservoir and depth. Two of them correspond to a shallow crustal faulting, and the third earthquake corresponds to a subduction thrust-fault. The first filling operations began in March 2011 and the daily time history of water levels was available until December 2017. The seismicity has been recorded by a dense local network of seismological stations operating since January 2008. Effects of both types of sources (water loads and earthquakes) were combined to obtain the total Coulomb Failure Stress in the reservoir area, analyzing which of them was dominant in each case and time. We then analyzed the effects of the pore pressure diffusion due to the water loads on the nearby seismicity including two of the studied earthquakes. Results lead to different conclusions depending on the characteristics of each earthquake. An important result is observed after the occurrence of the subduction earthquake, where the coseismic effects become dominant along the entire study area, eclipsing the effect of water loading at all depths. This shows that in a regime stressed by a regional earthquake, albeit of its moderate magnitude, and regional distance, the effect of water loads is barely perceptible. In the absence of tectonic activity, however, the impact of water loading is notable.

Introduction

There are several examples of studies on seismic swarms associated with artificial reservoirs, and various key aspects that affect spatiotemporal seismicity patterns near reservoir areas are widely recognized (e.g., Foulger et al. 2022). These include among others, the rate of change in the water level, the loading time intervals, the duration time of maximum water level, the reservoir area itself, height of the maximum water column, and variations in hydrogeological conditions or the crustal faulting regime, among others (e.g., Gupta et al. 1972a, b; Gupta 2002; Qiu and Fenton 2014).

The complex interaction of all these factors has been examined in different studies to better understand the changes in seismic activity related to the filling of large reservoirs. After examining more than 120 cases of reservoir-triggered seismicity (RTS) worldwide, Qiu and Fenton (2014) find that most of the evaluated events occurred along normal faults or strike-slip fault environments. Moreover, the US Commission on Large Dams (USCOLD) found an increase in RTS cases in reservoir areas with dam heights above 100.0 m (Gupta 2002). Most triggered seismic events associated with reservoir operations are earthquakes of small or moderate magnitude. Generally, low-magnitude earthquakes should not pose a problem for the dynamic behavior of dams, since the dam structures are usually designed to withstand seismic events of large magnitudes (Mw > 7.0, particularly in zones with high seismicity). However, in certain cases, low-magnitude RTS may present problems for buildings or structures close to the dam, particularly if these constructions are not adequately designed or are not built according to structural-design recommendations or seismic-construction regulations. Similarly, in areas with low seismic hazard but high exposure and population density, RTS seismicity may become a cause of concern since people in such areas might not be used to experiencing strong ground motions. Hence, low-magnitude earthquakes could give rise to considerable social alarm. Analyzing seismicity in the vicinity of reservoirs and determining the parameters of any dominant physical processes which might be potentially responsible for seismicity rates is thus of great importance, both for implementing mitigation strategies to guarantee the safety of the population and for other related activities. Some of the most important cases of RTS are summarized by Gupta (2002) and a complete list of reported cases of RTS to date (June 2022) by reservoir impoundment (191) can be found in the HIQuake database (Wilson et al. 2017; Foulger et al. 2022). Analysis and monitoring of microseismicity near reservoirs are an essential task when it comes to detecting any change in seismic activity and its possible relationship with reservoir operations. One example of microseismicity during reservoir impoundment is provided, among many other more recent studies, by Santoyo et al (2010, 2016), in which the seismicity recorded by a local network is shown to be correlated with groundwater changes at the Itoiz reservoir (Spain).

In this scenario, Coulomb failure stress (∆CFS) and pore pressure (PP) changes are usually calculated in order to explain variations in spatiotemporal seismicity patterns and other processes which may potentially trigger earthquakes (e.g., Bell and Nur 1978; Hill et al. 1993; Harris 1998). Different studies have furnished strong observational evidence to indicate that static stress transfer may hasten or delay earthquakes (e.g., Dieterich 1994; Parsons 2005). Here, a positive ∆CFS value brings the fault close to failure—and thus to earthquake occurrence—while many cases also indicate that negative ∆CFS values might delay the occurrence of earthquakes (e.g., Stein 1999; Freed 2005). A more recent work by Lei (2011) evaluates changes in ∆CFS and assesses their role in local seismicity and their potential impact on the Mw=7.9 Wenchuan earthquake, near the Zipingpu Reservoir (China), the greatest reservoir-triggered event to date. Among the first important analyses of ∆CFS associated with artificial reservoir impoundment and RTS have been studied by Gough and Gough (1970) and Beck (1976) who analyzed the relationship between seismicity and stress changes in Lake Kariba (Zambia) and Lake Oroville (California), respectively. Among many other cases analyzed (e.g., Bell and Nur 1978; Simpson et al. 1988; Deng et al. 2010), one of the most relevant in Spain was the occurrence of a noticeable increase in seismicity near the Itoiz Reservoir in 2004. Santoyo et al. (2010) analyzed the effects of changes in surface water loads on the subsurface state of stress and pore pressures in Itoiz and showed a resulting positive correlation between variations in water level and the occurrence of the seismic series (Mw = 4.6). For the case of the Pirrís reservoir, Ruiz-Barajas et al. (2019) analyzed the observed seismicity in three time periods: before, during, and after the impoundment, and studied its possible relation with the stress variations due to the water level evolution. A clear overall increment in seismicity was observed once impoundment was completed for magnitudes between 2.0 < Mw < 3.0 and Depths D ≤ 10 km around the reservoir area. A detailed description of the impoundment operation and seismicity can be found in Ruiz-Barajas et al. (2019).

However, in many of these earlier studies, including that of Ruiz-Barajas et al. (2019), the mutual stress interaction between the water loads and the nearby tectonic earthquakes has barely been investigated. Being this the aim and main contribution of the present work, here, we study the two-way relationship between the ∆CFS due to water loads variations and nearby selected important earthquakes close to the Pirrís Reservoir, analyzing the interaction in terms of their mutual influence in the subsurface stress patterns changes. In addition, we also compute the 3D poroelastic diffusive pore pressure changes due to the water loads variations due to the dam operation and analyze them with respect to the nearby seismicity.

Thus, in this study, we evaluate which of the different sources of stress (water loads or earthquake stress transfers) becomes dominant depending on the characteristics of the tectonic event in question. To this end, we first calculate the stress changes by ∆CFS due to variations in the reservoir water levels, and then, those produced by three different tectonic earthquakes. We analyze the possible interaction between water loads and tectonic earthquakes in two reciprocal senses, i.e., the impact of coseismic stress under the dam media and the possible effect of water loads on the occurrence of the three earthquakes. Finally, we show the overall ∆CFS generated by both types of stress change sources and the effects of the pore pressure changes on the nearby seismicity including two of the nearest studied earthquakes.

The general scheme of this study is shown in Figure 1, summarized in the following four steps: a) In a first step (Block 1), a detailed analysis was made of static stress changes associated with the surface water load in the reservoir. We evaluated the effects of the water column for different horizontal observation planes situated under the reservoir basin, at depths ranging from D_obs= 0.5 km to D_obs=19.0 km. The spatial and temporal evolution of the ∆CFS were computed taking into account different states of water loads and different values of the apparent coefficient of friction (µ’). Stress changes were resolved along the strike, dip, and rake angles based on the local predominant (or average) mechanism and taking into account the focal mechanism calculated for the earthquakes closest to the reservoir. (b) In a second step (Block 2), the coseismic stress changes attributable to the different tectonic earthquakes which occurred in the reservoir area were computed by means of the equation for internal elastic dislocation in a homogeneous elastic half-space. This aspect will be described in more detail in the next section. (c) In a third step (Block 3), based on the water loads variations, a 3D pore pressure diffusion analysis was carried out in order to study its possible effects on the occurrence of the nearby seismicity, with emphasis on two of the studied earthquakes. (d) Finally, a joint analysis was performed by considering the results obtained in the previous steps. On the one hand, we evaluated the impact of the tectonic earthquake on ∆CFS due to water level variations; and on the other, we studied the effects of water load variations on the coseismic ∆CFS (Block 4).

Fig. 1

Flowchart of the study. (1) Block 1 shows the process followed for the computation of the Coulomb Failure Stress changes (∆CFS) due to the surface water loads evolution, resolved along the different slip directions of interest (see text for details). (2) Block 2 shows the process for the computation of ∆CFS produced by the different earthquake faults, using a theoretical finite slip distribution, and resolved along the different slip directions of interest (see text for details). (3) Block 3 shows the process for the computation of the 3D pore pressure diffusion at the different earthquake locations of interest (see text for details). (4). Block 4 shows the process for the ∆CFS analysis from surface water loads and earthquakes faults (see text for details). Results from Block 1, label (A), are plotted in Fig. 3; Results from Block 1, label (B), are plotted in Fig. 7; Results from Block 3, label (C), are plotted in Figs. 8, 9 and 10, and Results from Block 4, label (D), are plotted in Figs. 4, 5 and 6

Seismotectonic setting

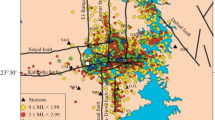
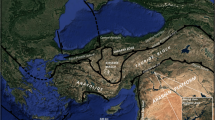
The Pirrís Reservoir is located in the Central Pacific zone of Costa Rica, along the fore-arc region within a geologically complex region with high seismic and tectonic activity (Barquero and Climent 2007; Ruiz-Barajas et al. 2019). The seismicity in this area is associated with several sources:(a) the subduction process of the oceanic Cocos Plate under the continental Caribbean Plate (Fig. 2a) and b very active fore-arc seismicity with several shallow local crustal faults (Fig. 2b). The majority of these faults usually produce strike-slip dextral ruptures, together with other types of faulting, i.e., some sinistral, oblique and few normal and reverse faults (Alvarado et al. 2017). Given this tectonic and geological setting, the reservoir comprises a relatively high potentiality to trigger seismicity (Ruiz-Barajas et al. 2019) where, after the first filling operations of the reservoir in March 2011, the nearby microseismicity increased during the first two years with a nearly annual periodic behavior, following the same progression of the water level’s evolution of the lake (Ruiz-Barajas et al. 2019). During the studied period, the mean annual water level change between the minimum and the maximum water height was close to Δh = 35.0 m, which based on the DEM of the reservoir basin implies a mean variation of the annual storage volume of ~ 2.0 × 10⁷ m³. Recently, a new seismological zonation for Central America has been proposed based on the seismotectonic framework, the geological context (e.g., Alvarado et al. 2017). At local scale, various studies (e.g., Barquero and Climent 2007) indicate the existence of seismically active faults in the area near the reservoir.

Fig. 2

Location and seismic data in the Pirrís reservoir. A. General location and tectonic setting of the studied region. B Seismicity around the Pirrís reservoir. The seismic events are distinguished by color: green, yellow and red, representing the occurrence periods before, during, and after the impoundment, respectively. Focal mechanisms of the three analyzed earthquakes, selected for computation of ∆CFS, are also shown: EQ-1 (December 27, 2011, Mw = 4.2), EQ-2 (August 17, 2016, Mw = 4.4) and EQ-3 (November 13, 2017, Mw = 6.6). See text for details

Materials and methods

Stress changes produced by reservoir water loads

The evolution of surface water load was computed based on two data sets, i.e., the temporal evolution of the reservoir water level, and the Digital Elevation Model (DEM) of the zone used to reproduce the reservoir basin. The combination of these two data sets enables a highly accurate estimate to be made of the evolution of water load and spatial load distribution over time, owing to the relatively high spatial sampling rate of elevations in the DEM used here (20.0 m x 20.0 m). A full description of the methodology employed to calculate stress changes is to be found in Ruiz-Barajas et al. (2019). Surface vertical loads are obtained by assuming F(x,y,t)= k₀h(x,y,t) where k₀ =ρgS, ρ is the water density, g is the mean terrestrial gravitational acceleration, S is the spatial sampling-rate area in the DEM, and h(x,y,t) is the water column height that depends on the spatial location (x,y) at surface relative to the reservoir basin and the time (t) during reservoir impoundment. Calculation of stresses at depth is based on the classical Boussinesq solution for vertical forces on a homogeneous elastic half-space (e.g., Jaeger and Cook 1969). Stress changes were evaluated by computing the 3D stress tensor at subsurface depth throughout the dam’s entire operating period, in order to be able to perform a complete 3D rotation of the stress tensor. The spatiotemporal elastic stress changes varying in time were obtained by means of the Coulomb failure criterion for different impounding times, and for different horizontal observation planes at different depths below the reservoir lake. Each observation plane was discretized with a ∆x=1.0 km, ∆y=1.0 km spatial grid, along N–S and E–W directions, respectively. Given the 3D stress tensor at each grid point and each computed time along the horizontal observation planes, the ∆CFS was obtained by:

$$\Delta {\text{CFS}} = \Delta \tau + \mu \Delta \sigma_{n} ({1} - B),$$

(1)

where ∆τ is the shear stress change calculated along the slip direction of a given fault plane, ∆σ_n is the normal stress change, µ indicates the dry friction coefficient, and B is Skempton’s coefficient of the rock-fluid mixture. While B is theoretically supposed to range between 0.0 and 1.0 depending on the level of the fluid saturation, different experimental values show it ranging from 0.3 through 1.0 (e.g., Cocco and Rice 2002; Zhang et al. 2009). Denoting the apparent coefficient of friction µ’= µ (1-B), the ∆CFS can thus be expressed as follows:

$$\Delta {\text{CFS}} = \Delta \tau + \mu^{\prime}\Delta \sigma_{n}.$$

(2)

Here, the water saturation values of the medium are considered through the specific values of the apparent coefficient of friction µ’, with B = −  ∆p/(∆σ_kk/3) being the ratio of induced pore pressure to the change in mean stress; under undrained conditions and negative sign indicating compression, B= 1.0 implies that changes in stress are totally transferred to the change in pore pressure (Rice and Cleary 1976). In contrast, when B= 0.0, this indicates that there is no change in the pore pressure following changes in stress. Accordingly, µ’= 0.0 implies that either µ= 0.0 or B= 1.0, which in the latter case indicates that the rock is completely saturated. In real environments, µ’~0.0 when B~1.0 (saturated rock) and µ has low values under undrained conditions. ∆CFS is generally resolved by the 3D rotation of the stress tensor and selecting from the rotated tensor its components along the direction of the fault plane and rake angle of slip of interest; here, we obtained these directions from the focal mechanism of the earthquakes of interest that occurred after the beginning of impoundment. These parameters can also be obtained from the direction of local predominant faults in the area.

Stress changes due to tectonic earthquakes

The occurrence of earthquakes (Mw > 4.0) at close distances to the reservoir provides an opportunity to evaluate and analyze the interaction between the impoundment activities and these seismic events. For the analysis purposes, on the one hand, we evaluated the possible impact that the water load changes can have on the occurrence of tectonic earthquakes, especially those at close epicentral distances (R < 20.0 km) and magnitudes Mw > 4.0. In this way, we explored the possible triggering effects on seismicity. On the other hand, we estimated the possible impact of the coseismic stress changes due to tectonic earthquakes under the reservoir area and added these stress changes to those produced by the water loads to obtain the total stress changes in the reservoir area due to both effects.

To this end, the coseismic stress changes due to three tectonic earthquakes (Mw ≥ 4.0) were calculated, using the analytical procedure proposed by Okada (1985, 1992) to evaluate the static strains and stresses produced by an internal elastic dislocation in a homogeneous elastic half-space. The 3D stress tensor was thus computed considering different global empirical relations being used to set the size and aspect ratios of rupture areas assigned to each of the earthquakes analyzed (Wells and Coppersmith 1994; Thingbaijam, et al. 2017). Since no information was available on the slip distribution of the selected earthquakes, we assumed a tapered semi-ellipsoidal distribution of slips over the fault plane in all cases (Santoyo et al. 2010). To evaluate the stress changes we applied in the same way as above, the Coulomb failure criterion ∆CFS resolved along the direction of the fault planes and rake angles of slip of each studied earthquake; here, we obtained these directions from the focal mechanism of the earthquakes of interest that occurred after the beginning of impoundment, and the stress tensors are computed by means of Eq. 1 along the different depths of horizontal observation planes, ranging from 1.0 km below the reservoir down to the hypocentral depth for each studied earthquake.

Pore pressure diffusion due to water loads

In the low frequency limit of the Biot equations, the variations of the pore pressure in a fluid saturated elastic medium can be approximately described by a Homogeneous Diffusion Equation (HDE) which can be considered as an uncoupled problem (e.g., Rice and Cleary 1976). In this case, the elastic stresses and pore pressure are independent of each other in the governing partial differential equations. For those phenomena, where it is necessary to consider the systematic influence of elastic stresses and pore pressure on each other, this case is known as a coupled problem. The intermediate problem in which pore pressure does not influence the elastic stresses whereas the stresses influence the pressure is known as the decoupled problem (e.g., Roeloffs 1988); this approximation leads to an Inhomogeneous Diffusion Equation (IDE). The solution of this problem can be expressed by the sum of two partial solutions P = P_BC + P_IC (Kalpna and Chander 2000). P_BC is the term due to the Dirichlet boundary conditions of the problem (the term due to the pore pressure diffusion), and P_IC corresponds to the initial conditions of the pore pressure in the medium. In water reservoirs and with the Dirichlet boundary condition, the pore pressure P_BC diffuses from the free surface into the poroelastic media to reach the equilibrium, allowing this approximation to analyze the pore pressure variations next to dams, due to the time varying water loads in their reservoirs.

In this work, we estimate the diffusive 3D pore pressure changes from the decoupled problem, where the term due to the pore pressure diffusion P_BC is obtained by means of the Green’s functions of the problem, and for which the subsurface stress changes due to the water loads are computed for a 3D half-space. The complete description of the solution for the P_BC term is detailed in Luzón et al. (2010). Using this method, the effects of the surface water loads on the 3D subsurface state of the diffusive pore pressure and its possible relation with seismicity are computed by using the time histories of the lake levels and the Digital Elevation Model (DEM) of the zone. For this analysis, we assumed different hydraulic diffusivities C in order to analyze the effects of each C value on the nearby seismicity, including the two closest studied earthquakes EQ-1 and EQ-2.

Earthquake data

The shallow crustal tectonic earthquakes used here were selected considering those that, during the studied period (March 2011—December 2017), had a magnitude Mw > 4.0, an epicentral distance less than 10.0 km, and its focal mechanism available. We also considered a Mw = 6.6 regional earthquake being that this one occurred within the studied period, along the tectonic interface, and off the pacific coast closer to the reservoir. The earthquakes analyzed in this work have the following characteristics (Fig. 2b): Earthquake 1 (EQ-1; Lat = 9.693°N, 84.097°W) was a shallow earthquake of relatively low moment magnitude (Mw = 4.2) close to the dam site (R = 5.0 km), with depth D_EQ-1 = 5.0 km. This earthquake took place on December 27, 2011, occurring five months after the first full impoundment of the dam was completed during August, 2011. Its focal mechanism corresponded to a normal fault with strike-slip component (Strike = 223, Dip = 28, Rake = − 43). Earthquake (EQ-2; Lat = 9.665°N, Lon = 84.095°W) was also a relatively low-magnitude (Mw = 4.4) earthquake, which occurred near to the reservoir with its hypocenter also close to the dam site (R = 2.5 km), rupturing at a comparatively greater depth than the first one (D_EQ-2 = 19.0 km). This one took place on August 17, 2016, being also a normal faulting with strike-slip component (Strike = 205, Dip = 60, Rake = − 54). Earthquake 3 (EQ-3; Lat = 9.46°N, 84.562°W) was a relatively shallow subduction seismic event occurred on November 13, 2017, with depth D_EQ-3 = 19.0 km and moderate moment magnitude (Mw = 6.6), which occurred at a regional distance from the reservoir (R = 55.0 km). This earthquake is associated with the subduction process along the middle America trench at the tectonic interface between the Cocos and the Caribbean plates. The focal mechanism from the CMT catalog shows a shallow inverse thrust faulting earthquake (Strike = 293, Dip = 24, Rake = 85).

Results

Stress changes due to the water loads and earthquakes

The evolution of ∆CFS due to water level variations was computed for different µ’ values of the medium, along an area of 20.0 km x 20.0 km of horizontal observation planes at different depths. First, we resolved the computed ∆CFS along one of the preferred directions of faulting for the area (Strike = 212, Dip = 66, Rake = − 33), previously defined by Ruiz-Barajas et al. (2019). Figure 3 summarizes the results for three different observation depths, two different times (i.e., the dates when the water column was at its maximum and its minimum), and three µ’ conditions of the medium (µ’₁= 0.1, µ’₂= 0.4 and µ’₃= 0.9). In this way, Figure 3a shows the spatial evolution of ∆CFS for the water column in the reservoir at its maximum, and taking into account two extreme saturation conditions, µ’= 0.1 and µ’= 0.9, for three different observation depths (D_obs= 0.5 km, 3.0 km and 9.0 km); similarly, Figure 3b shows the temporal evolution of ∆CFS for dates with maximum and minimum water levels, observed at the same three different depths, and setting the apparent coefficient of friction at µ’= 0.4.

Fig. 3

Map view of the spatiotemporal distribution of ∆CFS due to water loads in the Pirrís reservoir, resolved along the preferred direction of faulting for the area at three different observation plane depths: D_obs = 0.5 km, D_obs = 3.0 km and D_obs = 9.0 km (see text for details). a ∆CFS is computed assuming an apparent coefficient of friction µ’ for two extreme cases of water saturation of the medium (µ’ = 0.1 and µ’ = 0.9); b ∆CFS distribution for two extreme water levels of the lake, assuming an apparent coefficient of friction µ’ = 0.4. Color scales are for stress in MPa × 10^–1

These results show a near-field positive ∆CFS effect at shallow depths on the western side of the reservoir, coincident with the dam wall location. This effect tends to vanish when the observation depth increases. Moreover, in the case of maximum water level and saturated rock, the positive ∆CFS almost reproduces the reservoir shape at a depth of D_obs=0.5 km. At greater depths, the influence of positive stresses was observed to extend to the southern side of the reservoir.

For the case of the ∆CFS produced by tectonic earthquakes, these changes were also evaluated on different depths of horizontal observation planes, and along a shallow horizontal surface of 20.0 km x 20.0 km, 1.0 km under the region studied. Our results show that along the shallowest observation level (D_obs= 1.0 km), each earthquake induces significantly different coseismic ∆CFS patterns. EQ-1 generates a large positive ∆CFS along the entire area below the dam of ∆CFS ~ 0.1 MPa at shallow depths, while EQ-2 produces different ∆CFS negative patterns between 0.1 and 0.5 MPa at different depths below the reservoir area. In the case of EQ-3, this generates a very large positive stress change between 0.05 and 0.1 MPa across the entire zone, despite the fact that the epicentral distance is greater than 50.0 km. After computing the ∆CFS due to water loads and tectonic earthquakes separately, both effects were combined to obtain the total elastic stress changes in the reservoir area. The resulting stress patterns at shallow depths may reach variations of ∆CFS= ±0.1MPa, being these thresholds consistent with published results for similar earthquakes and distances (e.g., Santoyo et al. 2010). The stress change interaction was thus calculated in two ways: (1) by considering the instantaneous ∆CFS due to the water loads and each independent earthquake and (2) by considering the cumulative effects of the water loads and respective earthquakes at the time of occurrence of each event, i.e.,

$$\Delta {\text{CFS}}_{t} = \Delta {\text{CFS}}_{{{\text{hwater}}}} + \Delta {\text{CFS}}_{e1} + \Delta {\text{CFS}}_{e2} + \Delta {\text{CFS}}_{e3},$$

(3)

where ∆CFS_t is the total stress change, ∆CFS_hwater is the stress change due to the water level of the lake at the time of ocurrence of each event, and ∆CFS_e1, ∆CFS_e2 and ∆CFS_e3 are the stress changes caused by the tectonic earthquakes EQ-1, EQ-2 and EQ-3, respectively. The final results of this combination of water-induced and tectonic ∆CFS are shown in Figures 4, 5 and 6, respectively. The ∆CFS due to water loads correspond to the times of occurrence of each tectonic event considered, assuming a µ’= 0.4 (Mikumo et al. 2002; Santoyo et al. 2005). In Figure 4, the first column of color plots shows the map view of the stress change distribution produced by the surface water loads observed at Dobs=1.0 km and Dobs=6.0 km depths, while the second column of plots shows the stress changes produced by earthquake EQ-1 at the same Dobs=1.0 km and Dobs=6.0 km depths; the third column shows the sum of both stresses at each spatial position (x,y) along the observation planes for each depth. The D_obs= 6.0 km depth shows in this case the stress changes in the vicinity of the hypocentral location. In the case of Figures 5 and 6, the same operation applies for earthquakes EQ-2 and EQ-3, and in a final fourth column of color plots, they show the combination of the stress changes due to the water loads and the cumulative changes by the corresponding previous seismic events. For EQ-2 and EQ-3, the hypocentral depth is shown for the observation plane at Dobs=19.0 km.

Fig. 4

Map view of the spatiotemporal evolution of ∆CFS due to water loads and the crustal earthquake EQ-1, resolved along the slip direction of this same earthquake, evaluated along two different horizontal observation plane depths (D_obs = 1.0 km and D_obs = 6.0 km). The first column of color plots shows the map view of the stress change distribution produced by the surface water loads, while the second column of plots shows the stress changes produced by earthquake EQ-1 at the same depths; the third column shows the sum of both stresses at each spatial position (x,y) along the observation planes for each depth. EQ-1 relative hypocenter location is shown by a green star. Color scale is for stress in MPa × 10^–1

Fig. 5

Map view of the spatiotemporal evolution of ∆CFS due to water loads and the crustal earthquake EQ-2, resolved along the slip direction of this earthquake, along two different horizontal observation plane depths (D_obs = 1.0 km and D_obs = 19.0 km). The first column of color plots shows the map view of the stress change distribution produced by the surface water loads, while the second column of plots shows the stress changes produced by earthquake EQ-2 at the same depths; the third column shows the sum of both stresses at each spatial position (x,y) along the observation planes for each depth. The fourth column of color plots shows the cumulative sum of ∆CFS due to water loads, EQ-1 and EQ-2. EQ-2 relative hypocenter location is shown by a green star. Color scale is for stress in MPa × 10⁻¹

Fig. 6

Map view of the spatiotemporal evolution of ∆CFS due to water loads and the subduction earthquake EQ-3, resolved along the slip direction of earthquake EQ-3, along two different horizontal observation plane depths (D_obs = 1.0 km and D_obs = 19.0 km). The first column of color plots shows the map view of the stress change distribution produced by the surface water loads, while the second column of plots shows the stress changes produced by earthquake EQ-3 at the same depths; the third column shows the sum of both stresses at each spatial position (x,y) along the observation planes for each depth. The fourth column of color plots shows the cumulative sum of ∆CFS due to water loads, EQ-1, EQ-2 and EQ-3. Color scale is for stress in MPa × 10⁻¹

In the case of EQ-1 (Mw=4.2), R= 5.0 km, D_EQ-1=5.0 km, the coseismic stress shows a dominant effect, both at shallow depths and in particular at the hypocentral depth of the event (D_EQ-1= 5.0 km, D_obs= 6.0 km), where changes due to water load are barely seen in the combined state (Figure 4a). Given the magnitude (Mw=4.2) of this earthquake, the corresponding equivalent dimensions of the fault plane obtained together with the relatively shallow hypocentral depth, and the observation plane depth was set to 6.0 km instead of 5.0 km to avoid possible singularities. In this case, the stress distribution shows a distribution similar to that of the solely coseismic stress (Figure 4b).

Regarding EQ-2 (Mw=4.4), R = 2.5 km, D_EQ-2=19.0 km (Figure 5), for shallow observation depths (D_obs= 1.0 km), the ∆CFS distribution shows different negative patterns particularly right under the reservoir lake. However, the instantaneous stress changes produced by this earthquake along the hypocentral depth (D_obs= 19.0 km) exhibit a positive pattern several times larger than those produced by water loads. In this case, at a greater depth, any interrelation is hardly observed between the two types of effect. When the cumulative coseismic stresses are calculated by taking the sum of ∆CFS_hwater + ∆CFS_e1+ ∆CFS_e2, the total ∆CFS spatial pattern significantly changes at a depth of D_obs=1.0 km, where the stress changes produced by EQ-1 can be clearly observed.

Finally, the result of combining the ∆CFS by including the stresses produced by EQ-3 (Figure 6) shows a considerable influence of this earthquake regardless of the depth of observation. In this case, the coseismic ∆CFS due to the moderate regional Mw=6.6 earthquake is completely dominant, displaying a positive stress change in the reservoir region, even though this earthquake occurred R=55.0 km away from the reservoir lake. While this effect can also be seen in the combined ∆CFS due to all three events at shallower depths, at a depth of D_obs=19.0 km, the effect of EQ-2 is observable in the area closest to the reservoir.

To better understand the possible effects of water level variations in the reservoir lake on the ∆CFS at the hypocenter of each of the studied earthquakes, we performed a temporal evolution analysis of the stress changes for all possible µ’ values (0.0 < µ’< 1.0) and resolving the ∆CFS along the rupture vector direction of each event. The analysis was performed for the complete time interval of the water level time series, considering a five-year period since the beginning of impoundment to December 31, 2016. Computation of stress changes for all possible values of µ’ makes it possible to analyze the water saturation conditions within the earthquake source volume, through the assumption of the possible values of the Skempton coefficient. For the purposes of this analysis, we computed the stress change ∆CFS_i (µ’, t) at each hypocentral location produced by the reservoir water load at each point in time, for all possible values of µ’ by means of the relation:

$$\Delta {\text{CFS}}_{i} \left( {\mu^{\prime},t} \right) = \mathop \sum \limits_{j = 1}^{N} \Delta \tau_{i} \left( {j,t} \right) + \mu^{\prime}\Delta \sigma_{i} \left( {j,t} \right),$$

(4)

where ∆CFS_i (µ’, t) is the Coulomb Stress Change at hypocenter i at time t, with apparent friction coefficient µ’; ∆τ_i(j,t) is the shear stress change at the hypocenter i due to water column j at time t, and ∆σ_i(j,t) is the normal stress change at the hypocenter i , from water column j at time t. N is the total number of contributing water column elements at the maximum water level of the lake. The variation range of µ’and t is 0.0< µ’< 1.0 and t₀<t<t_f ; t₀ is the initial date of impoundment, and t_f is the final date of the water level time series. It is important to note that during the evolution of the lake’s water levels over time, and some of the water column elements will make no contribution to ∆CFS for different times t, because depending on the DEM the surface of the water body decreases as the water level drops. Figure 7 shows the effects of evolution of dam water levels on the stress transferred to the epicentral location of each earthquake studied, as a function of the water saturation of the medium. Figure 7a, b and c show these effects at the epicentral locations of EQ-1, EQ-2 and EQ-3, respectively. From this analysis, all the three plots in Figure 7 show that not only the total amount, but also the sign of the stress transferred to each epicentral location, strongly depend on the water level.

Fig. 7

Temporal evolution of the stress changes based on the evolution of the reservoir water loads, for the interval of µ’ values 0.0 < µ’ < 1.0, which is equivalent to the water saturation level in the subsurface media. ∆CFS is computed at each hypocentral location and resolved along the rupture vector direction of each of the studied events. The analysis is performed for the complete time interval of the studied water level time series since the beginning of impoundment to December 31, 2016. a Results for EQ-1; b results for EQ-2; c results for EQ-3. Color scale is for stress in MPa

Pore pressure diffusion

As stated, the diffusive pore pressures were computed by means of the Green’s Functions for the P_BC term of the decoupled problem described in Luzón et al. (2010), based on the time histories of the lake water levels and on the Digital Elevation Model (DEM) of the zone, which together generates a 3D surface water loads spatiotemporal evolution. The pore pressures are calculated along the complete time interval of the water level time series since the beginning of impoundment. To do this, we assume five different hydraulic diffusivities for the media: C = 1.0, C = 1.5, C = 2.0, C = 3.0 and C = 5.0 m²/s, a Skempton’s coefficient of B = 1.0 and a Poisson coefficient equal to ν = 0.25. In Fig. 8, we show the time evolution of the water level and the solution corresponding to the diffusive P_BC component of pore pressures for each of the considered “C” values at the hypocenter location of earthquake EQ-1. The different observed delayed responses of the pore pressure are the result of the effects of the C values on the diffusion of the pore pressure, initiating at surface below the reservoir down to the hypocentral zone. In this same Fig. 8, we also show by open green bars the monthly seismicity close to the reservoir and with vertical lines the occurrence time of earthquakes EQ-1 and EQ-2. Ruiz-Barajas et al. (2019) have shown that before the initial impoundment, the background seismicity was relatively sparse; because of this, the seismicity is shown here after the initial operation of the dam. Note that in the P_BC solution, as the value of C increases, the delayed response of the pore pressure diffusion is enhanced. Given this, at the time of occurrence of EQ-1 shown in Fig. 8 by a magenta dashed line, which corresponds to day 310 after the initial impoundment, the P_BC values vary between 6.5 × 10^–4 MPa and 9.5 × 10^–4 MPa at the hypocenter, depending on the assumed value of “C”; this earthquake occurred just after the sharp increase in the pore pressure.

Fig. 8

Pore pressure time evolution in days since the beginning of impoundment computed at the hypocentral location of earthquake EQ-1, D_EQ-1 = 5.0 km depth. Time evolution of pore pressure diffusion is shown for five different C hydraulic diffusivity values C = 1.0, 1.5, 2.0, 3.0, and 5.0 m²/s, plotted with dark brown, pink, red, orange and yellow lines, respectively. The Skempton’s coeffictient was assumed B = 1.0. The monthly nearby number of earthquakes occurred within a 20.0 × 20.0 km² area around the reservoir is shown by green open bars, and the water level time evolution is shown with a light blue line. The date of occurrence of earthquake EQ-1 (Dec 27, 2011) in shown by a magenta vertical dashed line

In the same way, Figure 9 shows the time evolution of the water level and the solution corresponding to the diffusive part of pore pressures for four of the considered “C” values at the hypocenter of earthquake EQ-2, C=1.0, C=1.5, C=2.0, and C=3.0 m2/s, which time of occurrence (August 17, 2016) is also shown by a vertical magenta dashed line. The observed delayed responses for each of the computed C values show that, at the time of occurrence of earthquake EQ-2, pore pressures vary between 8.0x10⁻⁵ MPa and 1.1x10⁻⁴ MPa. These results show that the trend of the monthly seismicity, shown by open green bars, corresponds well with the behavior of the delayed pore pressures after a five-year water loads yearly cycles at these depths, appearing also delayed with respect to the time evolution of instantaneous water loads. Here, the occurrence of this earthquake corresponds to the maximum values of the pore pressure for C=2 and C=3 values.

Fig. 9

Pore pressure time evolution in days since the beginning of impoundment computed at the hypocentral location of earthquake EQ-2, D_EQ-2 = 19.0 km depth. Time evolution of pore pressure diffusion is shown for four different C hydraulic diffusivity values C = 1.0, 1.5, 2.0 and 3.0 m2/s, plotted with dark brown, pink, red, and orange lines, respectively. The Skempton’s coeffictient was assumed B = 1.0. The monthly nearby number of earthquakes occurred within a 20.0 × 20.0 km² area around the reservoir is shown by green open bars and the water level time evolution is shown with a light blue line. The date of occurrence of earthquake EQ-2 (Aug 17, 2016) in shown by a magenta vertical dashed line

Figure 10 shows a map view from the pore pressure values at different depths at the time of occurrence of earthquake EQ-1, below the reservoir area. Here, the spatial evolution of the pore pressures after 310 days after the beginning of impoundment shows that at shallow depths, the pore pressures reproduce well the shape of the surface water loads due to the configuration of the bathymetry at the time of occurrence of the earthquake; however, at the hypocentral depth, the pore pressures appear more homogeneous due to the diffusion effect, leading a relatively smooth distribution of pressures at this depth.

Fig. 10

Map view of the pore pressure (PP) at the Pirrís reservoir for 27 December, 2011 (date of earthquake EQ-1) 310 days since the beginning of impoundment, for six different depths and C = 3.0 m2/s. PP values are shown for six different depths; a D_obs = 100 m; b D_obs = 200 m; c D_obs = 500 m; d D_obs = 1000 m; e D_obs = 2000 m; f D_obs = 5000 m. Color scale in MPa. Note that different PP intervals are defined for each observation depth. The yellow star at the upper side of each Fig. 10a, b, c, d,e shows the projection of the epicentral location of earthquake EQ-1 along the observation plane. In Fig. 10f, the yellow star shows the hypocentral location of EQ-1 at D_EQ-1 = 5.0 km depth

Discussion and conclusions

In this work, we analyze the stress changes and interaction produced by the water loads evolution and three different tectonic earthquakes occurring, during and after the first filling operations in the Pirris reservoir. Two of the tectonic earthquakes analyzed, EQ-1 (Mw = 4.2) and EQ-2 (Mw = 4.4), corresponding to a crustal normal faulting in the fore-arc region, occurred at local distances from the reservoir, within R = 5.0 km of epicentral distance. Both earthquakes have relatively shallow hypocentral depths of D_EQ-1 = 5.0 km and D_EQ-2 = 19.0 km, respectively, and occurred during the filling operations. A third earthquake occurred after the filling operations R = 55.0 km from the reservoir, associated with the subduction process between the Cocos plate under the Caribbean plate, with a moment magnitude Mw = 6.6 and D_EQ-3 = 19.0 km of hypocentral depth. To analyze whether the coseismic stress patterns produced by moderate local and regional earthquakes could generate important changes on the patterns produced by the water loads, our analysis focused on distinguishing the possible stress interaction between the stresses produced by the water loads and the coseismic stresses from earthquakes considering their magnitudes, distances and depths. In the same sense, the cumulative stress changes due to these events have also been evaluated taking into account the total sum of ∆CFS. As already expressed, ∆CFS is resolved along the different directions of the fault planes and rake angles of the slips of interest. Due to the inherent uncertainties on the fault orientation parameters, usually, small variations on the resolving rotation angles from earthquake sources would produce perceptible changes in the spatial stress patterns, especially at close distances. However, in the case of surface water loads, it can be observed from Figs. 3, 4 and 5 that small variations in the resolving rotation angles, in general produce relatively smaller changes on the stress patterns than those from the variations in µ’, or water loads, even at close distances.

In the case of the results in Fig. 7, we show that for a given value of water saturation in the media, the stress values increase as water level increases; likewise, for a given value of water level in the dam, stresses transferred increase as water saturation in the media increases. Hence, for a given stress contour of EQ-1, the zero contour line (∆CFS = 0.0 which initiates at the beginning of impoundment for µ’ = 0.6), as water levels increase, the zero contour steps down toward lower values of µ’, reaching a minimum for µ’ = 0.25 when the water level of the dam reaches its highest value. This in turn means that, as the water level increases, lower water saturation (µ’) is required to obtain positive values in the stresses at the hypocentral locations. This same situation occurs in EQ-2 and EQ-3 where, for a given saturation the stresses transferred increase as water levels increase, being the ∆CFS for these cases always positive, regardless of the amount of water saturation (Figs. 7b and c).

Based on these considerations, any possible triggering due to dam operation in the case of EQ-1 would strongly depend on both aspects, i.e., the water level of the dam and the saturation values of the media. Hence, for µ’>0.5, the more saturated the media, the more likely the triggering effect will be. The same happens in the case of EQ-2, in which ∆CFS values are always positive, so that any value for µ’ would produce this effect, always bearing in mind that in this case, the highest ∆CFS will occur when the dam is completely full. In the case of EQ-3, however, the long distance from the dam means that the absolute values obtained by the water loads are almost negligible, indicating that the possible effect for earthquake triggering due to the dam operation would also be also negligible.

Pore pressure results show that, in case of the possible triggered-reservoir seismicity at the dam, this is not only due to a rapid response produced by the coseismic stresses, but to the combination of these together with the pore pressure diffusion from the reservoir to the hypocenter. This seems to be the case for earthquake EQ-1, where the pore pressure and ΔCFS reach its maximum at the same occurrence time (Figure 8) of this event. In fact, this is also the same for the monthly seismicity level which also become at its maximum during the same month (December 2011). An interesting point results for the 2015 impoundment yearly period, where the monthly seismicity increases while the water level decreases. This question is solved when computing the pore pressures at greater depths where the time delaying effect due to the pore pressure diffusion P_BC strongly increases, obtaining its maximum at the same time occurrence of earthquake EQ-2 (Figure 9).

The Coulomb stress changes produced by the three earthquakes under consideration show large positive lobes at shallow depths, with amplitudes ΔCFS ≥ 0.01 MPa in all cases. In particular, the ΔCFS generated by the Mw = 6.6 earthquake shows positive values in some specific areas, with at least 2 orders of magnitude larger than the stress change produced by maximum water loads at D_obs = 6.0 km depth. When combining the stress changes due to water loads with those induced by local earthquakes, it can be observed that at shallow depths, the stress distribution is effectively modified by both type of sources. In some areas, this modification leads to an effective change in the sign of stresses along the main fault orientation. In the case of the Mw = 6.6 subduction event, the earthquake was the predominant cause of stress change, even at shallow depths, and the combination leads to charged zones with ΔCFS of at least + 0.1 MPa.

It can be concluded that the effects of water load depend not only on the absolute surface loads, focal mechanism and distance to the earthquake, but also strongly on the water saturation and pore pressure of the underground media. In summary, the two smaller earthquakes occurring close to the reservoir show that when the earthquake ruptures at shallow depths (as in EQ-1), the sum of ∆CFS close to the surface results in a combined pattern of the coseismic and water load changes. In contrast, when the crustal tectonic earthquake occurs at a greater depth, the stress changes close to the surface are dominated by the water loads (as in EQ-2). However, in the case of the subduction earthquake with a larger magnitude (EQ-3), the coseismic effect becomes highly dominant throughout the study area, and the ∆CFS produced by the water load is overshadowed at all depths. This finding indicates that, shortly after the occurrence of a moderate subduction earthquake along the tectonic interface close to the dam, the reservoir impoundment operations would barely alter the subsurface stress field.