Abstract
Probabilistic properties of dates of winter, summer and annual maximum flows were studied using circular statistics in three catchments differing in topographic conditions; a lowland, highland and mountainous catchment. The circular measures of location and dispersion were used in the long-term samples of dates of maxima. The mixture of von Mises distributions was assumed as the theoretical distribution function of the date of winter, summer and annual maximum flow. The number of components was selected on the basis of the corrected Akaike Information Criterion and the parameters were estimated by means of the Maximum Likelihood method. The goodness of fit was assessed using both the correlation between quantiles and a version of the Kuiper’s and Watson’s test. Results show that the number of components varied between catchments and it was different for seasonal and annual maxima. Differences between catchments in circular characteristics were explained using climatic factors such as precipitation and temperature. Further studies may include circular grouping catchments based on similarity between distribution functions and the linkage between dates of maximum precipitation and maximum flow.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
The timing of the flood event and the degree of seasonality are important characteristics of flood processes. The seasonality of annual maximum flows (AM) is one of flood process indicators (Merz and Blöschl 2003). Studies on flood seasonality can be helpful in recognizing changes in flood driving processes (Hall 2014). Both the climate forcing mechanisms (for example, temperature changes and atmospheric patterns) and local soil and geophysical properties are reflected in the dates of floods. A useful basis for assessing the seasonality of environmental variables is circular statistics (Fisher 1993; Mardia and Jupp 2000). The method provides a practical approach for studying the timing of the flood event (Burn 1997; Bayliss and Jones 1993). Seasonal indices based on circular statistics represent an important indicator of flood processes that can be used as a pooling characteristic in the regional flood frequency analysis (Kriegerová and Kohnová 2005). New methods for identifying flood seasons based on circular measures have been introduced (Chen et al. 2013) based on the division of the flood season using the circular standard deviation of flood occurrences and of flood occurrences combined with flood magnitudes. The first advantage of the use of circular instead of linear statistics on the dates of annual maximum flows (DAM) is that they can reflect the closeness of the dates that occur at the end and at the beginning of the hydrological year. The next advantage is that the dates of floods are almost error-free.
Circular statistics had been applied in measures of similarity in catchment hydrologic response (Burn 1997; Cunderlik and Burn 2002; Cunderlik et al. 2004; Castellarin 2001). The methods were used in studies on floods in Great Britain (Bayliss and Jones 1993), on seasonality of rainfall- and snowmelt-induced floods in mid-sized catchments in Slovakia (Kriegerová and Kohnová 2005), on seasonality of precipitation and runoff characteristics in Slovakia and Austria (Parajka et al. 2009), on seasonal variation in flood date in Peak Over Threshold model (Ouarda et al. 1993), in flood seasonality regionalization (Ouarda et al. 2006), on predicted impact of climate change on low flows in catchments in Germany (Demirel 2013) and in studies on projected changes in flood seasonality under climate change in six catchments in Norway (Vormoor et al. 2015). A comprehensive statistical analysis of the dates of extreme precipitation at stations in the USA was conducted by Dhakal et al. (2015) who studied nonstationarity in seasonality. The circular statistics were also used by Blöschl et al. (2017) who revealed patterns of change in flood timing in many parts of Europe.
The main objective of the paper is to identify the probabilistic properties of the date of winter, summer and annual maximum river flow using the circular statistics and the circular theoretical distribution function. Three catchments with different hydrological regime were selected to the study. To the best of the authors’ knowledge, the methods such as identifying the theoretical distribution function as the mixture of von Mises distribution functions have not yet been applied to the date of annual and seasonal maximum flow in hydrological literature. All symbols and abbreviations used in this paper are placed in Table 1.
Data and study areas
The date of occurrence of summer maximum river flow, winter maximum river flow and annual maximum river flow was studied in the Zagożdżonka river (gauging station: Płachty Stare), in the Czarna Przemsza river (gauging station: Piwoń) and in the Poprad river (gauging station: Muszyna). The data for the Czarna Przemsza river and for the Poprad river were obtained from the Institute of Meteorology and Water Management National Research Institute, Poland (Polish acronym: IMGW-PIB). The data for the Zagożdżonka river were collected by the Department of Hydraulic Engineering, Warsaw University of Life Sciences SGGW.
All rivers contribute to water resources of the Vistula river basin, the longest river in Poland.
The Zagożdżonka river is a left tributary of the Vistula river. The watershed is located in central Poland, ca. 100 km south from Warsaw. Its topography is typically lowland. Local depressions which do not contribute to direct runoff constitute a significant part of the area. In respect of the mean value of the long-term precipitation, the wettest month is July with rainfall depth equal to 13% of the annual value. In respect of discharge, the wettest month is March with the mean value of over 70% larger than the mean annual discharge. The reader interested more in hydrological conditions of the watershed is referred to papers (Banasik and Hejduk 2012, 2013; Banasik et al. 2013; Hejduk and Hejduk 2014; Kaznowska and Banasik 2011).
The Czarna Przemsza river has its source in the Kraków-Czȩstochowa Upland in southern Poland. This is a typical highland catchment. Most of the catchment is an agricultural area lying in the Piedmont Plateau with permeable soils.
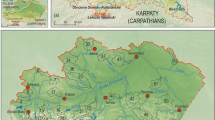
The Poprad river has its source in the High Tatra Mountains which is the highest part of the Carpathian Mountains. The river flows through part of Slovakia, forms the border between Slovakia and Poland and enters the Dunajec river in Poland. The Poprad river drains water from the Tatra Mountains where precipitation levels are very high. The river contributes considerably to the water resources of the Upper Vistula river basin, the region in Poland which is highly susceptible to flooding and where mountain rivers pose a very high flood hazard (Punzet 1978; Cyberski et al. 2006; Kundzewicz et al. 2016). Two main climatic conditions characterize the Poprad river basin to the Muszyna station: prolonged snow cover, low air temperature, small temperature inversion and a very high annual precipitation reaching 2000 mm in the western, high mountainous part (upper course of the Poprad river) and a highland character with a substantial temperature inversion and a lower level of annual precipitation, reaching 900 mm in the eastern part (lower course) (Šatalová and Kenderessy 2017; Trizna 2004). The three catchments were shown in Fig. 1.
Catchment characteristics and data were presented in Table 2.
The three catchments have mixed snowmelt/rainfall regimes. Therefore, the annual maximum flows are either summer or winter flows. Winter floods dominate in the Zagożdżonka catchment and in the Czarna Przemsza catchment while summer floods dominate in the Poprad catchment.
Methods
Circular statistics
In every catchment, the dates of the seasonal (winter, summer) and annual maxima flows were selected for the samples. Then, every date from the calendar dates of the annual flows was converted to \(D_i, i=1, ..., n\), the number of day of the maximum river flow in the hydrological year. To be more specific, \(D_i=1\) for 1st November and \(D_i=365\) for 31st October and when it is not a leap year. Similarly, every date from the dates of winter flows was converted to \(D_i\), namely \(D_i=1\) for 1st November and \(D_i=181\) for 30th April. For dates of summer flows, in turn, \(D_i=1\) for 1st May and \(D_i=184\) for 31st October. Subsequently, every number of day \(D_i\) was converted to angular value (angular date) using the formula:
In leap years, the denominators for annual and winter days above were increased by one. Finally, three samples of angular dates \(\Theta _i\) were obtained for every river, namely DWM (winter maxima dates), DSM (summer maxima dates), and DAM (annual maxima dates). The angular dates \(\Theta _i\) are in radians. The value \(\Theta _i\) is a measure of the counterclockwise-directed angle between the vectors [1, 0] and \([x_i, y_i]\), assigned to a point (0, 0) with endpoints on the unit circle where \((x_i, y_i)=(\cos \Theta _i, \sin \Theta _i)\). Therefore, the dates \(\Theta _i\) can be depicted as points located on the unit circle (DAM), on the upper unit semicircle (DWM), and on the lower unit semicircle (DSM).
The mean flood date \(\bar{\Theta }\in [0, 2\pi )\), a measure of location, is uniquely determined by the pair \((\bar{x}, \bar{y})=(\frac{1}{n}\sum _{i=1}^n \cos \Theta _i,\frac{1}{n}\sum _{i=1}^n \sin \Theta _i)\) as
If \(\bar{x}=0\) and \(\bar{y}=0\) then \(\bar{\Theta }\) is not defined.
The measures of variability enable the dispersion between the mean flood date and the angular dates of flood occurrences to be assessed [see e.g. Chen et al. (2013); Cunderlik and Burn (2002); Mardia and Jupp (2000)]. The mean resultant length, \(\bar{r}=\sqrt{\bar{x}^2+\bar{y}^2}\), is the most commonly used measure of dispersion. It should also be noted that \(0<\bar{r}\le 1\) and that \(\bar{r}\) near to 1 (to 0) implies little (large) variation and a high concentration (wide dispersion) of data. The sample circular variance \(CIV=1-\bar{r}\) and the standard deviation \(\sigma =\sqrt{-2\ln \bar{r}}\) are also used as measures of dispersion.
Attention should be paid to the method of conversion of the number of day into angular date using formulas (1) for winter and summer dates. Thanks to the formula, we have DWM\(\in (0, \pi ]\) and DSM\(\in (\pi , 2\pi ]\) which makes the DWM to be located on the upper semicircle and the DSM on the lower semicircle. But, because the denominators in formulas (1) are different (the denominators are the winter and summer lengths for non-leap year), the angular difference between two consecutive days is lower in the DSM than in the DWM. Therefore, for example, the angular winter date of the 10th Nov is 0.208 (approx) and the angular summer date of the 10th May is not \(\pi +0.208\) but \(\pi +0.204\). The incompatibility between the DWM and the DSM is very low and results in a difference much lower than one day.
Circular distribution function
The von Mises distribution on the unit circle is often used because of its highly developed inference methods. Many tests of von Mises distributions are presented in Mardia and Jupp (2000), for example, tests of the mean direction and of the concentration parameter in one population and tests to ascertain the equality of mean directions or equality of concentration parameters in several populations (Dobson 1978; Stephens 1969; Upton 1973; Yamamoto and Yanagimoto 1995). Many of these methods are based on large-sample approximate statistics. The role of this distribution is similar to that of the normal distribution for linear data. The von Mises distribution function \(M(\mu , \kappa )\) has circular probability density function (PDF)
where \(\mu \in [0, 2\pi )\) is a mean direction parameter and \(\kappa \ge 0\) is a concentration parameter which reflects the dispersion of the \(\Theta\) values around the mean direction \(\mu\). The parameter \(\kappa\) is small for variables with large variance and vice versa. The function \(I_0\) is the modified Bessel function of the first kind of order 0 where the modified Bessel function of the first kind of order m (\(m=0, 1, 2, ...\)) is (Fichtenholz 2007)
The version of the von Mises distribution on high-dimensional sphere is the von Mises–Fisher distribution which is used in directional statistics.
The shape of the empirical pdf of seasonal or annual maximum is unimodal or multimodal. Multimodality suggests the existence of several sub-populations in the dates; therefore, the mixture of von Mises distributions was used with the PDF equal to
where \(p=(p_1, ..., p_S), \mu =(\mu _1, ..., \mu _S), \kappa =(\kappa _1, ..., \kappa _S)\). The parameters \(p_s\) are positive weights that sum to one and that reflect the contribution of every sub-population to the population of dates. The parameter \(\mu _s\) is the mode of the sth component distribution. It is the mean value of the sth population. The parameter \(\kappa _s\) reflects the concentration around the mode, i.e. the larger is the value of \(\kappa _s\), the greater is the clustering around the sth mode. Finite mixtures of von Mises–Fisher distributions were introduced in Banerjee et al. (2005) to directional data.
The Maximum Likelihood Estimates (MLE) of the parameters \(\mu , \kappa\) of a single von Mises distribution are \(\hat{\mu }=\bar{\Theta }, \hat{\kappa }=A_1^{-1}(\bar{r})\) where \(A_1(z)=\frac{I_1(z)}{I_0(z)}\) is the ratio of the modified Bessel functions of the first kind of order 1 and 0. However, the problem of finding the maximum of the log-likelihood function both for single von Mises distribution and for mixture of them cannot be solved analytically because it leads to equation with inverse of the ratio of two Bessel functions of different order. Thus, numerical procedures must be applied. The issue was tackled by many researchers for the von Mises–Fisher distribution, for example by Amos (1974), Dempster et al. (1977), Banerjee et al. (2005), Tanabe et al. (2007), Sra (2012), Hornik and Grün (2014), among others. In this paper, the method of Hornik and Grün was applied (Hornik and Grün 2014) where bounds for the inverse of the ratio of Bessel functions were derived which yielded the improvement of the previous approximate methods.
The Expectation–Maximization (EM) algorithm (Dempster et al. 1977; McLachlan and Peel 2000) was used in the estimation of parameters of the mixture of von Miseses using MLE. The EM algorithm was introduced as early as in 1950 by Ceppellini et al. (1955) in gene frequency estimation. In the first step (E-step) of the algorithm, each observation is associated with an unobserved value equal to one or zero depending on the location of the observation. Then the expected value of the log-likelihood function for the complete-data is estimated. In the second step (M-step), the expected values are maximized. The two steps are repeated until convergence of parameter estimates. Various variants of the EM algorithms are known in the literature, for example the soft-clustering (used in this paper) or hard-clustering. The high efficacy of these algorithms for fairly skewed empirical distribution function was shown in Banerjee et al. (2005).
The final choice of the number of components S was based on the Akaike Information Criterion. The corrected version, namely the AICc, was used (Hurvich and Tsai 1989). The rationale for this choice is that AICc is recommended when the number of parameters is a substantial fraction of the sample size because it tends to select a more parsimonious model than the AIC. It should also be noted that the mixture model (5) has as many as eight parameters for three components and eleven parameters for four components, while the sample sizes of maxima dates have between fifty and seventy elements. This high number of parameters certifies the use of the AICc. The formula \(AICc=AIC+\frac{2(w+1)(w+2)}{n-w-2}\) was used where \(AIC=-2\log L(\Theta _1,..., \Theta _n, \hat{p}, \hat{\mu }, \hat{\kappa })+2w\) and where L is the likelihood function and \(\it {w}\) is the number of parameters. The model with the minimum value of the AICc was selected for further study.
To assess the goodness of fit, the congruence between empirical and theoretical quantiles of the same order was evaluated by means of \(r_c\), the circular correlation coefficient (Jammalamadaka and Sarma 1988; Jammalamadaka and SenGupta 2001). Suppose a sample of n pairs of angles is \((\Theta _{11},..., \Theta _{1n}), (\Theta _{21},..., \Theta _{2n})\), then
where \(\bar{\Theta }_1, \bar{\Theta }_2\) are the mean dates of the first and second sample, respectively. To test whether the circular correlation coefficient between populations of dates is significantly different from zero, the test statistic
was derived where \(\lambda _{kj}=\frac{1}{n}\sum _{i=1}^n\sin ^k(\Theta _{1i}-\bar{\Theta }_1) \sin ^j (\Theta _{2i}-\bar{\Theta }_2)\). If the null hypothesis is true, then the theoretical distribution of \(z_r\) is N(0, 1).
Next, the Kuiper’s and the Watson’s tests for uniformity were used (Mardia and Jupp 2000). Although these methods are designed for testing uniformity of circular data, they can also be used for testing goodness of fit to any other continuous distribution function on a circle by taking \(2\pi F(\Theta _i)\) as the data sample where F is the theoretical (hypothetical) cumulative distribution function (CDF). The Kuiper’s test statistic is (Kuiper 1960; Mardia and Jupp 2000)
where \(U_i=\frac{\Theta _{(i)}}{2\pi }\) with dates ordered to \(\Theta _{(1)}\le ... \le \Theta _{(n)},\, i=1, ..., n\). The statistic \(V_n\) is a measure of deviation between empirical and theoretical CDFs. It is rotation-invariant.
The Watson’s test statistic (Watson 1961; Mardia and Jupp 2000) is
The Watson’s \(U^2\) test is an analog to the Cramér–von Mises test for linear data. Approximations of critical values given in Stephens (1970), Mardia and Jupp (2000) were used both for the Kuiper’s and the Watson’s tests.
The estimation with the mixture of von Mises distributions was carried out for the DWM, DSM and DAM variables.
The non-parametric bootstrap procedure was implemented to estimate the confidence intervals of the parameters. The bootstrap samples of length n were drawn with replacement \(N=10^3\) times by sampling from the original sample. For every bootstrap sample, the parameters of the von Mises distribution function (or of a mixture) were estimated. Thus, N estimates of every parameter were obtained, \(\hat{p}, \hat{\mu }, \hat{\kappa }\). The lower and upper confidence limits of the parameter were the quantiles of order \(\frac{\alpha }{2}\) and \(1-\frac{\alpha }{2}\) of the sample of N estimates.
All calculations were carried out in R (R Core Team 2017, Lund et al. 2017, Hornik and Grün 2017, Tsagris et al. 2017). The significance level equal to \(\alpha =5\%\) and the confidence level equal to \(1-\alpha =95\%\) were used in this paper.
Results and discussion
Circular statistics
In the series of AM, winter floods dominate over summer floods with proportion from 88 to 12% and 59 to 41% in the Zagożdżonka catchment and in the Czarna Przemsza catchment, respectively. In the Poprad catchment this relation is reversed, from 38% to 62%.
The circular statistics (see Sect. 3.1) are presented in Table 3.
In the Zagożdżonka river, the circular mean flood dates are on 4th March (DWM), 11th July (DSM), and 8th March (DAM). In the Czarna Przemsza and the Poprad rivers, the mean dates are, respectively, 28th February and 16th March (DWM), 1st July and 5th July (DSM), and 11th April and 29th May (DAM).
Water is retained in snow cover during winter time. The two main factors influencing the DWM are snow depth and temperature. Sometimes, the winter floods are amplified by rainfall. Usually, the warm periods during which the snow may melt are at the end of winter in the Zagożdżonka catchment, mainly in March (Hejduk and Hejduk 2014). Similar conditions are found in the Czarna Przemsza catchment where the negative temperatures only rarely occur in April. Therefore, the mean date of the DWM in these two rivers is comparable. The Poprad catchment differs from the two catchments in the mean of DWM because of different winter climate conditions (Sect. 2). In the western, high mountainous part, the snow is accumulated even in May and June due to negative temperatures, with the mean value of the DWM lagging by several weeks in comparison with the Zagożdżonka and Czarna Przemsza catchments. This is due to extreme floods caused mainly by snowmelt in March as also rain or snow floods which appear in later spring months prevailing in April. The mean values of the DSM are, in turn, comparable in all three catchments and located between the end of June and the first ten days of July.
The concentration of DWM is comparable in all three catchments because the values of \(\bar{r}, CIV\) and \(\sigma\) are similar. The largest variation of the DSM is observed in the Zagożdżonka river while the lowest dispersion is in the Poprad river. What can be observed about the DAM, the Czarna Przemsza river shows the largest variation in the date of maximum flow.
In Fig. 2, the rose diagrams of the DWM in the three catchments were shown. The mean flood date \(\bar{\Theta }\) is depicted in every figure. The length of the left arm of the angle is \(\bar{r}\), the mean resultant length value. The arm is long if the dates are highly concentrated around \(\bar{\Theta }\) and it is short if the dates are more dispersed. The shapes in both Zagożdżonka and Czarna Przemsza rivers are similar with somewhat higher frequency in March in the Czarna Przemsza river. The shape of the Poprad diagram is much different because of two dominating frequencies in March and in April while other months are much less frequent.
Rose diagram of the DWM in the a Zagożdżonka, b Czarna Przemsza, c Poprad rivers. Every bar represents one month with the height reflecting the number of winter maxima that occurred in this month during the study period. The angle \(\bar{\Theta }\) is the sample mean DWM and the length of the left arm of the angle is \(\bar{r}\), the mean resultant length value of the DWM (the longer the arm the higher the concentration).
In Fig. 3, the rose diagrams of the DSM in the three catchments were shown. The lowest dispersion in the Poprad river is reflected in a high \(\bar{r}\) value. It is induced by the highest July frequency. The extreme summer floods, caused prevailingly by convective rains are dominant in the Slovakian part of High Tatra Mountains for all catchments. The shape of the summer Zagożdżonka diagram shows some similarity to uniform distribution which explains its large dispersion reflected in a low \(\bar{r}\) value and in a high \(\sigma\) value in Table 3.
Rose diagram of the DSM in the a Zagożdżonka, b Czarna Przemsza, c Poprad rivers. Every bar represents one month with the height reflecting the number of summer maxima that occurred in this month during the study period. The angle \(\bar{\Theta }\) is the sample mean DSM and the length of the left arm of the angle is \(\bar{r}\), the mean resultant length value of the DSM (the longer the arm the higher the concentration)
In Fig. 4, the rose diagrams of the DAM in the three catchments were depicted. The rose diagram is mostly stretched over the winter season with the highest frequency in March in the Zagożdżonka catchment while the summer season is much less occupied. In the Czarna Przemsza catchment, both the winter and summer parts are comparable, although the March frequency also dominates. The rose diagram shape in the Poprad catchment is unlike the two others because summer season apparently dominates with the highest frequencies in June and July. However, the March frequency is also quite high in the winter season. In the Poprad river, the annual highest flows only rarely occur in months from August to November because of relatively low precipitation from December to February because all rain accumulates in snow cover.
Rose diagram of the DAM in the a Zagożdżonka, b Czarna Przemsza, c Poprad rivers. Every bar represents one month with the height reflecting the number of annual maxima that occurred in this month during the study period. The angle \(\bar{\Theta }\) is the sample mean DAM and the length of the left arm of the angle is \(\bar{r}\), the mean resultant length value of the DAM (the longer the arm the higher the concentration)
It can be observed that due to dominating July frequency in the Poprad river and March frequency in the Zagożdżonka river, the mean date in the DAM is by as many as 82 days later in the former than in the latter (see Table 3).
Circular distribution function
The parameters of the distribution were estimated using the MLE method. The numerical algorithm was based on the method presented in Hornik and Grün (2013, 2014). Using results of the the AICc criterion, shown in Table 4, the number of mixture components equal to \(S=2\) was identified in all three catchments in the DWM and to \(S=3\) and \(S=2\) in the Czarna Przemsza river and in the Poprad river in the DSM, respectively. The estimation failed in the Zagożdżonka river in the DSM. In this catchment, \(S=4\) was identified using the AICc criterion; however, huge values of the estimates of the concentration parameters, equal to several hundreds, were obtained. This topped the rugged circular PDF curve with several distortions. This can be explained by the shape of the circular diagram of the DSM in the Zagożdżonka river in Fig. 3a , which is more similar to a uniform than to a peaked distribution. In the DAM, the number of components equal to \(S=1\) was identified in the Zagożdżonka river, to \(S=3\) in the Czarna Przemsza river and to \(S=2\) in the Poprad river. Therefore, every parameter among \(p, \mu , \kappa\) in the formula (5) has two coordinates in the DWM in all three catchments, three and two parameters in the DSM in the Czarna Przemsza and Poprad rivers and one, three and two parameters in the DAM in the Zagożdżonka, Czarna Przemsza and Poprad rivers, respectively.
The estimates are listed in Table 5. In the DAM, the \(\hat{\mu }\) value in the Zagożdżonka river, \(\hat{\mu }_1\) in the Poprad river and \(\hat{\mu }_1\) and \(\hat{\mu }_2\) in the Czarna Przemsza river are located in the winter season. It is worth observing that in the DAM in the Czarna Przemsza river, the estimate of the total weight of components with the circular mean date from the winter season, i. e. \(\hat{p}_1+\hat{p}_2\) approximately equals the contribution of the WM to the AM series, namely 0.51 as against 0.59. Therefore, the long-term contribution of seasonal maxima to annual maxima is reflected in \(\hat{p}\) in the Czarna Przemsza river. In the Poprad river, the difference is greater and amounts to 0.25 as against 0.38 (see Sect. 4.1).
In the Zagożdżonka river, the second component prevails in the DWM (\(\hat{p}_2=0.51, \hat{\mu }_2=2.60, \hat{\kappa }_2=14.03\)) which confirms the dominating role of the March maxima flows because the angular value 2.60 is located in March, after conversion. This can be also observed in the March mode equal to 2.20 in the DAM. A large contribution of the second component (\(\hat{p}_2=0.32\)) and a large concentration \(\hat{\kappa }_2=30.34\) around the \(\hat{\mu }_2=2.39\) is observed in the DAM in the Czarna Przemsza river. Similarly, the second component in the DWM has very similar mode (\(\hat{\mu }_2=2.40\)) and contributes to a large degree to the DWM in the Czarna Przemsza river (\(\hat{p}_2=0.57, \hat{\kappa }_2=11.00\)). This can be explained by the dominating role of the March maxima flows. The role of the third component in the DAM is also considerable and shows the second dominant date in June (\(\hat{p}_3=0.49, \hat{\mu }_3=4.06, \hat{\kappa }_3=1.70\)). In the Poprad river, the dominating June and July frequency is reflected in a large contribution of the second component to the DAM (\(\hat{p}_2=0.75, \hat{\kappa }_2=1.6\)) with the mode at \(\hat{\mu }_2=4.10\).
To verify the hypothesis that the distribution function of the DWM, DSM and the DAM is of von Mises or a mixture of von Miseses, the Kuiper’s and the Watson’s tests were used [(Eqs. (8), (9)] to \(2\pi F(\Theta _i)\) sample values where F is the hypothetical CDF. Both tests did not reject the null hypothesis on uniformity in all three catchments. Results of the goodness-of-fit analysis are shown in Table 6. Both the Kuiper’s V and the Watson’s \(U^2\) test statistics are lower than the critical values of these tests equal to 1.747 and 0.187, respectively, (Stephens 1970, Mardia and Jupp 2000). This meant that the null hypothesis on the theoretical distribution function was not rejected. The circular correlation coefficient \(r_c\) between empirical and theoretical date of maximum river flow and the test statistic \(z_r\) are also shown in Table 3. Values of \(r_c\) are very near to 1, and values of \(z_r\) are much higher than the critical value equal to 1.645, which confirms the high congruence between dates.
In Figs. 5 and 6, the circular estimates of the PDF of the DWM and DSM are shown. The shape of every estimate follows that of the rose diagram. It is worth observing that the body of the PDF plot is extremely concentrated on the quarter \((\frac{\pi }{2}, \pi )\) (days between the 92nd and 181st day in the winter season, i.e. from 30th Jan to 30 Apr) in the DWM in the Poprad river and on the quarter \((\pi , \frac{3\pi }{2})\) (182nd–273th in hydrological year, from 1st May to 31st Jul) in the DSM in the Czarna Przemsza and Poprad rivers.
The circular PDF estimate of the DWM in the a Zagożdżonka, b Czarna Przemsza, c Poprad rivers. Every thick blue point depicts the mean direction parameter estimate \(\hat{\mu }_s\) of the sth subpopulation. The area under the sth subpopulation is equal to \(p_s\) while the height of the sth part of the curve reflects the concentration around the \(\hat{\mu }_s\) value
The circular PDF estimate of the DSM in the a Czarna Przemsza, b Poprad rivers. Every thick blue point depicts the mean direction parameter estimate \(\hat{\mu }_s\) of the sth subpopulation. The area under the sth subpopulation is equal to \(p_s\) while the height of the sth part of the curve reflects the concentration around the \(\hat{\mu }_s\) value
In Fig. 7, the circular PDF estimates of the DAM are shown. The main body of the PDF is concentrated on the quarter \((\frac{\pi }{2}, \pi )\) (92nd–181rd day in hydrol. year, from 30th Jan to 30 Apr) in the Zagożdżonka river, on the interval \((\frac{\pi }{3}, \frac{5\pi }{3}, )\) (61st–304th day, from 31st Dec to 31st Aug) in the Czarna Przemsza river and on the semicircle \((\frac{\pi }{2}, \frac{3\pi }{2})\) (92nd–273th day, from 31st Jan to 31st Jul) in the Poprad river. The plot is smooth in the Zagożdżonka and more diverse in the Czarna Przemsza and Poprad rivers. All densities only differ somewhat from zero on dates with a very low frequency, i.e. from September to November in the Zagożdżonka river, and from October to January in the Czarna Przemsza river, and from November to February in the Poprad river. This means that it is nearly unlikely that the annual maximum flow date is from these periods. It is worth observing that in the Zagożdżonka river, where the high \(\bar{r}\) value was obtained in the DAM (\(\bar{r}=0.59\)) due to a high concentration of dates, the single von Mises distribution was sufficient to reflect the distribution of the date of maximum flow. In the Poprad river, where the sample concentration was moderate (\(\bar{r}=0.50\)), the two components in the mixture of von Miseses had to be used. In the Czarna Przemsza river, in turn, as many as three components were identified because of the lowest concentration (\(\bar{r}=0.43\)) of the dates of maxima flows. Comparing results from Tables 3 and 5, the perfect agreement between the mean date \(\bar{\Theta }\) and the \(\hat{\mu }\) value can be observed in the DAM in the Zagożdżonka river (because the MLE estimate of \(\mu\) is \(\bar{\Theta }\)). In the Poprad river, the modes \(\mu _1=2.42\) and \(\mu _2=4.10\) of the two components belong to the winter and summer season, respectively, and are similar to the mean angular dates of winter and summer maxima equal to 2.33 and 4.25.
The circular PDF estimate of the DAM in the a Zagożdżonka, b Czarna Przemsza, c Poprad rivers. Every thick blue point depicts the mean direction parameter \(\hat{\mu }_s\) of the sth subpopulation. The area under the sth subpopulation is equal to \(p_s\) while the height of the sth part of the curve reflects the concentration around the \(\hat{\mu }_s\) value
In Table 7 the confidence intervals of the parameters were shown. The confidence intervals were obtained with ease if \(S=1\) (DAM, the Zagożdżonka river). However, they were derived with computational difficulty for mixtures because the EM algorithm diverged for certain bootstrap samples and the procedure had to be repeated until convergence. In the Czarna Przemsza river (DSM), however, the procedure of estimation of confidence intervals using nonparametric bootstrap was not applicable because huge concentration parameter estimates were obtained in the bootstrap samples. The possible causes behind the divergence of the algorithm are a very high or very low concentration of data in the bootstrap sample and that the width of the collapsing mixture components may become zero for many data repetitions (Archambeau et al. 2003). This may also cause a large width of confidence intervals and a lack of symmetry around several parameter estimates that can be observed in Table 7. Further studies on this issue are needed in the future.
As mentioned in Sect. 1, the issue with the estimation with the von Mises distribution (or with the mixtures of them) relies on numerical difficulty. Therefore, apart from the Hornik&Grün algorithm (Hornik and Grün 2014), other methods were also applied to check whether results can depend on the method of approximation of the ratio of Bessel functions. The methods presented in Banerjee et al. (2005), Tanabe et al. (2007), Hornik and Grün (2013) were used. In total, three additional methods were applied for each of nine series of data. It was observed that if the number of iterations was sufficiently high, i.e. at least equal to \(10^6\), the AICc pointed at the same S values apart from two cases, namely in the Czarna Przemsza river (\(S=3\) in the DAM) and in the Zagożdżonka river (\(S=2\) in the DWM) in the method based on Newton algorithm Hornik and Grün (2014)). A difference by approx. 0.5 in values of the \(\mu _s\) parameters was only observed in the Czarna Przemsza river (DAM) in the methods based on Newton and Newton–Fourier algorithm (Hornik and Grün 2013). This leads to conclusion that results were congruent. It should be noted that the number of components in the mixture (Eq. (5)) relied on the AICc value and that another criterion can lead to another number of components.
Results show that in the lowland Zagożdżonka catchment, with a low contribution of summer maxima to the total number of annual maxima, the AICc indicated only one component of the von Mises distribution as the estimate of the PDF of the DAM. In the highland Czarna Przemsza catchment and in the mountainous Poprad catchment, the number of components was larger than one for both seasonal and annual maxima dates, which reflected the large complexity of hydrological processes influencing the dates, namely sudden melting at the end of winter or heavy downpours from thunderstorm cells with high rainfall intensity in summer, which can lead to flash floods that cause the large diversity between maxima dates.
The example of the DAM in the Poprad river shows that the mixture can cover the sample asymmetry because both densities with modes at 2.42 (rad) (first component) and 4.10 (rad) (second component) together contribute to a large part of the area under the PDF on the interval between these two values. Additionally, the contribution is different because \(\hat{p}_1=0.25\) and \(\hat{p}_2=0.75\). Therefore, the contribution is lower for the former and higher for the latter component because of the dominating role of the July dates, which makes the PDF estimates asymmetrical, with the larger part of the body on the lower semicircle. Similarly, the asymmetry was reflected in other PDFs, for example in the DWM in all three catchments and in the DSM in the Poprad river. In the Czarna Przemsza river, in turn, the mixture has three components in the DAM with mean directions at 1.46, 2.39 and 4.06 (rad). Because the March maxima dominate in the series, the PDF is asymmetrical and the main part of the body is concentrated on the upper semicircle. It can be observed in the DAM that most mean direction values \(\mu _s\) are located in the interval \((\frac{\pi }{2}, \frac{3\pi }{2})\) (days 91–273, from 30th Jan to 31st Jul) which makes the PDF curve estimate very thin in months from August to February (Poprad), from June to November (Zagożdżonka) and from September to December (Czarna Przemsza). This reflects a very low contribution of these frequencies to the total DAM frequencies.
A similar analysis was performed for assessment of changes in the dates of extreme precipitation at ten stations in the USA (Dhakal et al. 2015). From statistical point of view, the main difference between Dhakal et al. (2015) and this study relies on testing of uniformity by means of various statistical tests in Dhakal et al. (2015) and testing of mixture of von Mises distributions in this paper.
Conclusions
The von Mises distribution can cover a large variety of both the sample mean circular values and the dispersion values which are reflected in mean direction and concentration parameters, respectively. The conclusion can be drawn that it is an useful estimate of symmetrical or nearly symmetrical, unimodal empirical distribution function of the date of annual maximum flow.
If several sub-populations are identified in the sample of dates of maximum flows, the mixture of von Mises distributions can be used to properly reflect the sample multimodality. The AIC or the AICc criterion can be used for selecting the number of components. Further studies may include the issue of the use of another criterion. However, the mixture was not useful when the empirical distribution was similar to uniform. In this case, this method is not recommended.
Attention should be drawn to the difficulty of parameter estimation of the mixture of von Mises distributions. Further studies can include testing various variants of the EM algorithm and various methods of estimating the concentration parameter.
The methods presented here can also be applied to dates of the maximum precipitation totals. Then, further studies may include linkage between the circular characteristics of precipitation and river flow. The next issue involves grouping catchments according to similarity measures based on the circular approach.
References
Amos DE (1974) Computation of modified Bessel functions and their ratios. Math Comput 28(125):239–251. https://doi.org/10.1090/S0025-5718-1974-0333287-7
Archambeau C, Lee JA, Verleysen M (2003) On Convergence Problems of the EM Algorithm for Finite Gaussian Mixtures. In: ESANN’2003 proceedings—European Symposium on Artificial Neural Networks Bruges (Belgium), 23-25 April 2003, ISBN 2-930307-03-X, pp. 99–106
Banasik K, Hejduk L (2012) Long-term Changes in Runoff from a Small Agricultural Catchment. Soil & Water Resources 2: 64–72. http://www.agriculturejournals.cz/publicFiles/64803.pdf . Accessed on 9 Oct 2017
Banasik K, Hejduk L, Hejduk A, Kaznowska E, Banasik J, Byczkowski A (2013) Wieloletnia zmienność odpływu z małej zlewni rzecznej w regionie Puszczy Kozienickiej. Sylwan 157(8):578–586
Banasik K, Hejduk L (2013) Flow duration curves for two small catchments with various records in Lowland part of Poland. Annu Set Environ Protect 15:287–300
Banerjee A, Dhillon IS, Ghosh J, Sra S (2005) Clustering on the unit hypersphere using von Mises-Fisher distributions. J Mach Learn Res 6(12):1345–1382
Bayliss AC, Jones RC (1993) Peaks-over-threshold flood database: summary statistics and seasonality. Wallingford, UK
Blöschl G, Hall J, Parajka J, Perdigão RAP, Merz B, Arheimer B, Aronica GT, Bilibashi A, Bonacci O, Borga M, Čanjevac I, Castellarin A, Chirico GB, Claps P, Fiala K, Frolova N, Gorbachova L, Gül A, Hannaford J, Harrigan S, Kireeva M, Kiss A, Kjeldsen TR, Kohnová S, Koskela JJ, Ledvinka O, Macdonald N, Mavrova-Guirguinova M, Mediero L, Merz R, Molnar P, Montanari A, Murphy C, Osuch M, Ovcharuk V, Radevski I, Rogger M, Salinas JL, Sauquet E, Šraj M, Szolgay J, Viglione A, Volpi E, Wilson D, Zaimi K, Živković N (2017) Changing climate shifts timing of European floods. Science 357(6351):588–590
Burn DH (1997) Catchment similarity for regional flood frequency analysis using seasonality measures. J Hydrol 202:212–223
Castellarin A, Burn DH, Brath A (2001) Assessing the effectiveness of hydrological similarity measures for flood frequency analysis. J Hydrol 241:270–285
Cebulska M, Szczepanek R, Twardosz R (2013) Rozkład przestrzenny opadów atmosferycznych w dorzeczu górnej Wisy. Opady średnie roczne (19521981) [The spatial distribution of precipitation in the upper basin of the Vistula River. Mean annual precipitation (19521981)]. Kraków. WIŚ PK IGiGP UJ. ISBN 978-83-88424-91-5 pp. 84
Ceppellini R, Siniscalco M, Smith CA (1955) The estimation of gene frequencies in a random-mating population. Ann Hum Genet 20(2):97–115
Chen L, Singh VP, Guo S, Fang B, Liu P (2013) A new method for identification of flood seasons using directional statistics. Hydrol Sci J 58(1):28–40
Cunderlik MJ, Burn DH (2002) Analysis of the linkage between rain and flood regime and its application to regional flood frequency estimation. J Hydrol 262:115–131
Cunderlik MJ, Ouarda TBMJ, Bobeé B (2004) Determination of flood seasonality from hydrological records. Hydrol Sci J 49(3):511–526. https://doi.org/10.1623/hysj.49.3.511.54351
Cyberski J, Grześ M, Gutry-Korycka M, Nachlik E, Kundzewicz ZW (2006) History of floods on the River Vistula. Hydrol Sci J 51(5):799–817. https://doi.org/10.1623/hysj.51.5.799
Demirel MC (2013) Impacts of climate change on the seasonality of low flows in 134 catchments in the River Rhine basin using an ensemble of bias-corrected regional climate simulations. Hydrol Sci J 17:4241–4257
Dempster AP, Laird NM, Rubin DB (1977) Maximum likelihood from incomplete data via the EM algorithm. J R Stat Soc Ser B (Methodol) 39(1):1–38
Dhakal N, Jain S, Gray A, Dandy M, Stancioff E (2015) Nonstationarity in seasonality of extreme precipitation: a nonparametric circular statistical approach and its application. Water Resour Res 51(6):4499–4515. https://doi.org/10.1002/2014WR016399
Dobson AJ (1978) Simple approximations for the von Mises concentration statistic. J R Stat Soc Ser C (Appl Stat) 27(3):345–347
Fichtenholz GM (2007) Rachunek różniczkowy i całkowy, vol 2. Wydawnictwo Naukowe PWN, Warszawa, 696 pp
Fisher NI (1993) Statistical analysis of circular data. Cambridge University Press, Cambridge
Hall J, Arheimer B, Borga M, Brázdil R, Claps P, Kiss A, Kjeldsen TR, Bloschl G (2014) Understanding flood regime changes in Europe: a state of the art assessment. Hydrol Earth Syst Sci 18:2735–2772. https://doi.org/10.5194/hess-18-2735-2014(2014)
Hejduk A, Hejduk L (2014) Thermal and snow conditions of winters and winter floods on example of Zagożdżonka River. Ann Warsaw Univ Life Sci SGGW Land Reclam 46(1):3–15
Hornik KB, Grün B (2013) Amos-type bounds for modified Bessel function ratios. J Math Anal Appl 408(1):91–101
Hornik K, Grün B (2014) On maximum likelihood estimation of the concentration parameter of von Mises-Fisher distributions. Computat Stat 29(5):945–957
Hurvich CM, Tsai CL (1989) Regression and time series model selection in small samples. Biometrika 76:297–307
Hornik K, Grün B (2017) movMF: an R package for fitting mixtures of von Mises-Fisher distributions. J Stat Softw 58(10):1–31. https://doi.org/10.18637/jss.v058.i10
Jammalamadaka S, Sarma Y (1988) A correlation coefficient for angular variables. Statistical theory and data analysis 2. North Holland: New York
Jammalamadaka SR, SenGupta A (2001) Topics in circular statistics, section 8.2. World Scientific Press, Singapore
Kaznowska E, Banasik K (2011) Streamflow droughts and probability of their occurrence in a small agricultural catchment. Ann Warsaw Univ Life Sci SGGW Land Reclam 43(1):57–69
Kriegerová I, Kohnová S (2005) Seasonality analysis of flood occurrence in mid-sized catchments in Slovakia. J Hydrol Hydromech 53(3):154–163
Kundzewicz ZW, Stoffel M, Niedźwiedź T, Wyżga B (2016) Flood Risk in the Upper Vistula Basin. Earth and Planetary Sciences. Springer International Publishing, GeoPlanet
Kuiper NH (1960) Tests concerning random points on a circle. Math Stat 38–47
Lund U, Agostinelli C, Arai H, Gagliardi A, Portugues EG, Giunchi D, Irisson JO, Pocernich M, Rotolo F (2017) R package ’circular’: circular statistics (version 0.4-93). url = https://r-forge.r-project.org/projects/circular/circular.pdf
Mardia KV, Jupp PE (2000) Directional statistics. Wiley, Wiley Series in Probability and Statistics, Chichester
McLachlan GJ, Peel D (2000) Finite mixture models. Wiley, New York
Merz R, Blöschl G (2003) A process typology of regional floods. Water Resour Res 39(12):1340. https://doi.org/10.1029/2002WR001952
Ouarda TBMJ, Ashkar F, El-Jabi N (1993) Peaks over threshold model for seasonal flood variations. In: Kuo CY (ed) Proceedings of the engineering hydrology symposium, 2530 July 1993, San Francisco, CA. New York: American Society of Civil Engineers, pp 341-346
Ouarda TBMJ, Cunderlik JM, St-Hilaire A, Barbet M, Bruneau P, Bobée B (2006) Data-based comparison of seasonality based regional flood frequency methods. J Hydrol 330:329–339
Parajka J, Kohnová S, Merz R, Szolgay J, Hlavcová K, Blöschl G, (2009) Comparative analysis of the seasonality of hydrological characteristics in Slovakia and Austria. Hydrol Sci J 54(3):456–473
Punzet J (1978) Water resources of the upper Vistula river basin. Maximum water discharge, their spatial variability and occurrence probability. IMGW-PIB, Warszawa (in Polish)
R Core Team (2017) R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing, Vienna, Austria, url = http://www.R-project.org/
Šatalová B, Kenderessy P (2017) Assessment of water retention function as tool to improve integrated watershed management (case study of Poprad river basin, Slovakia). Sci Total Environ 599–600:1082–1089
Sra S (2012) A short note on parameter approximation for von Mises-Fisher distributions: and a fast implementation of \(I_S(x)\). Comput Stat 27(1):177–190
Stephens MA (1969) Tests for the von Mises distribution. Biometrika 56(1):149–160
Stephens MA (1970) Use of the Kolmogorov-Smirnov, Cramér-von Mises and related statistics without extensive tables. J R Stat Soc Ser B (Methodol) 32(1):115–122
Tanabe A, Fukumizu K, Oba S, Takenouchi T, Ishii S (2007) Parameter estimation for von MisesFisher distributions. Computat Stat 22(1):145–157
Trizna M (2004) Klimageografia a hydrogeografia Slovenska (climate geography and hydrogeography of Slovakia). Geografika, Bratislava
Tsagris M, Athineou G, Sajib A, Amson E (2017) Directional: Directional Statistics. R package version 3.0. url = https://cran.r-project.org/web/packages/Directional/Directional.pdf
Upton GJG (1973) Single-sample tests for the von Mises distribution. Biometrika 61:87–99
Vormoor K, Lawrence D, Heistermann M, Bronstert A (2015) Climate change impacts on the seasonality and generation processes of floods projections and uncertainties for catchments with mixed snowmelt/rainfall regimes. Hydrol Earth SystSci 19:913–931. https://doi.org/10.5194/hess-19-913-2015
Watson GS (1961) Goodness of fit tests on a circle. Biometrica 48:109–114
Yamamoto E, Yanagimoto T (1995) A modified likelihood ratio test for the mean direction in the von Mises distribution. Commun Stat Theory Methods 24:1706–2659
Acknowledgements
The research was supported by the Ministry of Science and Higher Education of the Republic of Poland. This support is gratefully acknowledged. The investigation described in the contribution was also partially financed by the Slovak Grand Agency under Vega project No. 1/0710/15 and by the Slovak Research and Development Agency contract APVV 15-0497.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
On behalf of all authors, the corresponding authors state that there is no conflict of interest.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Rutkowska, A., Kohnová, S. & Banasik, K. Probabilistic properties of the date of maximum river flow, an approach based on circular statistics in lowland, highland and mountainous catchment. Acta Geophys. 66, 755–768 (2018). https://doi.org/10.1007/s11600-018-0139-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11600-018-0139-9