Abstract
River flow projections for two future time horizons and RCP 8.5 scenario, generated by two projects (CHASE-PL and CHIHE) in the Polish-Norwegian Research Programme, were compared. The projects employed different hydrological models over different spatial domains. The semi-distributed, process-based, SWAT model was used in the CHASE-PL project for the entire Vistula and Odra basins area, whilst the lumped, conceptual, HBV model was used in the CHIHE project for eight Polish catchments, for which the comparison study was made. Climate projections in both studies originated from the common EURO-CORDEX dataset, but they were different, e.g. due to different bias correction approaches. Increases in mean annual and seasonal flows were projected in both studies, yet the magnitudes of changes were largely different, in particular for the lowland catchments in the far future. The HBV-based increases were significantly higher in the latter case than the SWAT-based increases in all seasons except winter. Uncertainty in projections is high and creates a problem for practitioners.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Under the framework of the Polish-Norwegian Research Programme, two cross-cutting research projects have been carried out: (1) Climate Change Impacts for Selected Sectors in Poland (CHASE-PL) and (2) Climate Change Impact on Hydrological Extremes (CHIHE). Although the objectives of these projects were entirely different, there were several important issues of importance and interest to both projects. The goal of the CHASE-PL project was to contribute to improvement of understanding of climate change in Poland and its impacts on selected sectors in the country, whilst the objective of the CHIHE project was to investigate the effect of climate change on extreme flows (floods and droughts) in selected twinned catchments in Poland and Norway (Romanowicz et al. 2016). Hence, the objective of CHASE-PL was considerably broader, with major contribution from three fields: climatology, hydrology and environmental science. The CHIHE perspective was more focused, with hydrology as the primary discipline involved. In result of different project objectives also the spatial coverage of both projects was different. The CHIHE project focused on ten Polish and eight Norwegian small and middle-sized, nearly natural, catchments, whereas within the CHASE-PL, depending on the context, spatial coverage followed one of the following three possibilities: (1) the entire Polish territory, (2) the area of the Vistula and Odra basins (VOB) covering most of the Polish territory and parts of neighbouring countries, or (3) the union of both areas, (1) and (2). The main common feature of the CHASE-PL and the CHIHE was that both projects, independently of each other and for the first time in Poland, developed the ensembles of bias-corrected projections of climate change, based on state-of-the-art EURO-CORDEX data (Jacob et al. 2014). These ensembles of model-based climatic projections were used in both projects to drive hydrological models in order to investigate the effect of climate change on: (1) various hydrological indicators for the VOB area covering 312,873 km2 (CHASE-PL), and (2) flood and drought indicators for selected ten Polish catchments ranging in area between 296 and 1554 km2 (CHIHE). Two Polish-Norwegian projects employed two contrasting hydrological models over different spatial domains. The semi-distributed, process-based, SWAT model (Arnold et al. 1998) was used in the CHASE-PL project for the VOB area, whilst the lumped, conceptual, HBV model (Bergström 1995) was used in the CHIHE project for selected Polish catchments. Existing thematic and spatial overlap between CHASE-PL and CHIHE created a unique opportunity to compare climate and hydrological projections for eight Polish catchments from CHIHE (out of the total of ten) that belong to the VOB. These two overlaps constitute the context of the present paper.
A well-established procedure of investigating hydrological impacts of climate change at the catchment scale consists of forcing hydrological models with climate data derived from the general circulation models (GCMs) or the regional climate models (RCMs) (Krysanova et al. 2016; Teutschbein and Seibert 2010; Osuch et al. 2016a). The modelling chain typically contains multiple choices that affect the final results and result in dissimilarities between projections (Kundzewicz et al. 2017). Among the most prominent choices, there are: the choice of emission scenarios, climate models, downscaling and bias correction methods, hydrological models, indicators used and time periods (reference and future), etc. Over past several years, a number of hydrological model inter-comparison studies were carried out at various spatial scales, e.g. for small or medium-sized catchments (Dams et al. 2015; Karlsson et al. 2016), as well as for large river basins (Gosling et al. 2011; Hattermann et al. 2017) and the entire globe (Schewe et al. 2014). A number of studies focused on cross-scale comparisons (Gosling et al. 2011; Piniewski et al. 2013; Gosling et al. 2016; Hattermann et al. 2017). For example, Piniewski et al. (2013) reported a high consistency of mean annual runoff change projections obtained from SWAT and a global-scale WaterGAP model (Alcamo et al. 2003) in the Narew basin in NE Poland. On the other hand, there was only a moderate agreement between projections of high and low runoff, and SWAT generally projected changes of larger magnitude than WaterGAP. The nature of comparison carried out in the present paper is also cross-scale, due to a large difference in catchment sizes, reaching two–three orders of magnitude. In contrast to Piniewski et al. (2013), here the SWAT acts as a large-scale model.
The objective of this study is to compare annual and seasonal river flow projections obtained from two different hydrological models: SWAT and HBV. The latter were set up for eight Polish catchments representing different climatic and physiographic conditions, derived within the two projects, CHASE-PL and CHIHE. The main point of discussion is how changes of input variables (air temperature and precipitation) are transformed into changes of model output (mean annual and seasonal flows). A secondary objective is: how reliable are changes in hydrological projections when different (although comparable) climate projections are used as input variables?
Materials and methods
Study area
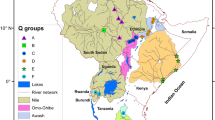
The study area consists of eight Polish catchments (Fig. 1) having different physiographic and climatic conditions. Four catchments, Nysa Kłodzka (hereafter: Nysa), Wisła, Dunajec, and Biała Tarnowska (hereafter: Biała), are located in southern, mountainous, part of Poland. Mean elevation of Dunajec catchment (920 m a.s.l.) is distinctly higher than the elevation of the other three catchments (377–581 m a.s.l.; Table 1). Four catchments are situated on the Polish Plain: Oleśnica, Myśla, Flinta and Narewka, ranging in mean elevation between 73 and 179 m a.s.l. Selected catchments drain the areas ranging in size between 275 (Flinta) to 1084 km2 (Nysa). All of them are characterised by semi-natural conditions, with little pressure on water resources coming from river regulation or land cover change. Agriculture is the dominating land cover type in the majority (five) of catchments (Myśla, Flinta, Oleśnica, Biała and Dunajec). In two catchments, Wisła and Narewka, forests prevail and in the Nysa catchment forest and agricultural areas are similar in size. Artificial surfaces do not exceed 8% in all catchments. Climatic conditions largely follow geographical and topographical conditions (cf. “Hydrological models” for comparison of temperature and precipitation). Climatic and physiographic differences are reflected in river flow statistics, as shown in Table 1 for mean and extreme specific discharges.
Romanowicz et al. (2016) classified the flood regime of selected rivers as either snowmelt regime, characteristic for the four lowland catchments (Oleśnica, Mysla, Flinta and Narewka), rainfall (Dunajec) or mixed (Nysa, Wisła, Biała). Selected catchments belong to five out of seven natural flow regime classes occurring in Poland. Piniewski (2017) classified Polish flow regimes into four plain (lowland) classes P1–P4, one upland class U1 and two mountain classes M1–M2. Of these, only classes P1 (predominantly coastal rivers) and U1 (rare class of loess- or limestone-bedrock rivers) are not represented in our sample. As shown in Fig. 1, mean annual runoff coefficients, i.e. fractions of annual total runoff volume that is a part of the total annual sum of precipitation, vary significantly among catchments: from extreme dry (the Flinta catchment, 0.14) to extreme wet (the Dunajec catchment, 0.59). For further information on catchment selection and properties, refer to Osuch et al. (2016b) and Romanowicz et al. (2016).
Hydrological models
The HBV model is a lumped conceptual model, originally developed in the 1970s by Sten Bergström in the Swedish Meteorological and Hydrological Institute to predict the inflow to hydropower plants (Bergström 1976, 1995), but nowadays it is widely applied across the world for runoff simulation. The HBV model (Lindström et al. 1997) was used in Matlab® platform. Conceptually, the hydrological processes are simplified to mathematical functions. In the lumped version of HBV it is assumed that the catchment is one single unit and that parameters do not change spatially across the catchment. The HBV model consists of four main modules: (1) snowmelt and snow accumulation reservoir; (2) soil moisture reservoir; (3) fast runoff reservoir and (4) slow runoff reservoir. The HBV model uses daily sum of precipitation, daily mean air temperature and estimated potential evapotranspiration (PET) as input to generate runoff. In this study, the temperature-based Hamon method was used to estimate PET (Hamon 1961).
The Soil and Water Assessment Tool (SWAT) model is a semi-distributed, process-based, continuous-time hydrological model that simulates the transport of water, sediment and nutrients on a catchment scale with a daily time step (Arnold et al. 1998). It is a river basin scale model developed to quantify the impact of land management practices in large, complex watersheds. In this study, SWAT2012 rev. 635 model version was used. In SWAT, river basins are partitioned into sub-basins, which are further divided into hydrological response units (HRUs), the objects based on a combination of soil, land cover and slope overlay within each sub-basin. All water balance components are calculated separately for each HRU, spatially aggregated at the sub-basin level and routed through the river network to the basin outlet. In the present study, the temperature-based Hargreaves method was used for calculation of potential evapotranspiration (PET). The modified USDA Soil Conservation Service (SCS) curve number method was selected for calculating surface runoff. The redistribution component of SWAT uses a linear storage routing technique to predict flow in each soil layer in the root zone. Channel routing was modelled using the Muskingum method.
Table 2 summarises the similarities and differences in various modelling concepts between the two models, SWAT and HBV. Both models use the degree-day method for snow melt calculation and recession constant method for baseflow calculation. Otherwise, particular concepts are different in both models. Whilst HBV, due to its lumped conceptual nature, has only 14 parameters, SWAT has hundreds or thousands of them, and only a few are calibrated.
The main difference between the applications of SWAT and HBV in the present study is the fact that the HBV model setups were created for each catchment individually, whilst for SWAT, the model setup was created for two large river basins of the Vistula and the Odra. Four of selected catchments (Myśla, Flinta, Oleśnica and Nysa) belong to the Odra basin, whereas the other four (Wisła, Dunajec, Biała, Narewka) to the Vistula basin. For the purpose of this study, model inputs and outputs related to selected catchments are extracted from the SWAT model databases. The reader is referred to other studies for the full description of model setup, calibration and validation: Romanowicz et al. (2016) and Osuch et al. (2016b) for HBV and Piniewski et al. (2017c) for SWAT. Below, a short summary is presented for reader convenience.
Different observational climate data were used to drive hydrological models in the reference period. For HBV, catchment average of daily mean air temperatures and daily precipitation totals were calculated using Thiessen polygon method from point observations at meteorological stations. The number of stations ranged between 1 and 5, depending on the catchment (Osuch et al. 2016b). For SWAT, CHASE-PL Forcing Data-Gridded Daily Precipitation and Temperature 5 km (CPLFD-GDPT5; Berezowski et al. 2016) dataset was used. This product contains daily precipitation and minimum and maximum temperature for the whole area of Poland interpolated from over 700 meteorological stations (including all those used in the HBV application) onto a 5 km grid using a combination of different kriging techniques. Another difference is that precipitation data in CPLFD-GDPT5 were corrected for gauge under-catch using Richter method (Richter 1995). This method, as described in more detail in Berezowski et al. (2016), applies different correction factors depending on precipitation type (rain, snow or mixed) and wind speed (higher in the mountains and along the coast). As reported in the report of the WMO Solid Precipitation Measurement Inter-comparison project (Goodison 1998), Richter correction factors (i.e. per cent increase in the raw precipitation) varied between 9% in summer to 25% in winter for a case study on the Havel–Oder Canal in Germany.
Table 3 shows the comparison of observed climate forcing mean annual values between HBV and SWAT. For six catchments, there are negligible differences (not higher than 0.2 °C) in air temperature values. For Nysa and Biała catchments, mean annual temperature estimated as HBV input is 0.9° and 0.6° higher, respectively, than temperature estimated as SWAT input. However, patterns in spatial variability in mean temperature are similar for both cases: the Dunajec catchment is the coolest one, with mean temperature of less than 5.5 °C, and there are several catchments (Wisła, Oleśnica, Myśla and Flinta) with mean temperature above 8 °C. Larger differences can be observed for precipitation input. There is a systematic, although variable, difference between HBV and SWAT, with SWAT estimates consistently higher than their HBV counterparts. The highest relative difference can be noted for three mountainous catchments: Nysa (28%), followed by Wisła (21%) and Biała (20%). One of the possible reasons for observed differences are different interpolation methods: the Thiessen polygon method can lead to under-estimation in mountainous areas, particularly if stations are located in the valley bottoms, which is often the case. Other potential reasons are the differences in source stations used for interpolation and gauge under-catch correction methods, although a detailed investigation is outside the scope of this study. On the other hand, Benninga et al. (2016) estimated the influence of elevation on precipitation in the Biała catchment as only 3.7%.
Both models, HBV and SWAT, were calibrated and validated using different approaches, optimisation routines, objective functions and time periods—fit for the purpose of each application. The study of Osuch et al. (2016b) demonstrated that HBV performs well in selected catchments, with Nash–Sutcliffe Efficiency above 0.5 for each catchment in calibration and validation periods. There was a tendency of slightly lower performance for validation period in the lowland catchments. In the case of SWAT, NSE values were lower than those obtained for the HBV in seven out of eight catchments (Supplementary Material Table S1). It should be noted that, due to a larger scale of the model, no individual catchment calibration was made. Instead, a dataset of 80 relatively unmodified catchments was selected and aggregated into eight clusters based on flow regime similarity. Each cluster was calibrated independently, with an objective of achieving satisfactory fit for clusters as a whole, rather than for each individual catchment. This objective was fulfilled, with the cluster-median daily Kling-Gupta Efficiency (KGE, Gupta et al. 2009) above 0.5 in calibration and validation periods. The KGE values were also higher than 0.5 for each of 30 gauges selected for spatial evaluation, which showed that the designed regionalisation scheme worked well. In summary, it was concluded that HBV and SWAT can be applied for climate change impact assessment in selected catchments in Poland.
Climate projections
Climate projections used in this study originate from the EURO-CORDEX dataset (Jacob et al. 2014). The CHASE-PL project used nine GCM-RCM combinations from EURO-CORDEX, whereas the CHIHE project used seven, of which all were included in the CHASE-PL ensemble. For this reason, the subset of seven climate model simulations, common for both projects, was used in this paper (Table 4). Future horizons in both studies are 2021–2050 (near future, hereafter denoted as NF) and 2071–2100 (far future, denoted as FF), whereas the reference period is 1971–2000. All projections are available under two representative concentration pathways, RCPs 4.5 and 8.5, yet only projections for RCP 8.5 are examined in this paper. They were bias-corrected using empirical quantile mapping method (Piani et al. 2010) independently within CHASE-PL and CHIHE.
In the CHIHE project, the corrections were carried out for daily data, for each individual climate model, catchment and month of the year, so that discrepancies in seasonal patterns, particularly of rainfall, could be corrected. There were differences in the way precipitation, and air temperature was corrected. The precipitation values were changed together with the number of wet days whilst air temperature residuals were corrected after removing the difference in the air temperature between the reference and the future periods to maintain the climate change signal in the air temperature (Hempel et al. 2013).
The derived bias-corrected ensemble in the CHASE-PL project covers the union of Poland and the Vistula and Odra basins and is available for research use in a data repository (Mezghani et al. 2016). The robustness and uncertainty aspects related to temperature and precipitation projections over the Vistula and Odra basins were discussed in Piniewski et al. (2017a).
For both CHASE-PL and CHIHE projections, projected changes were expressed as the differences between future and reference values for temperature (°C), and as relative changes for precipitation (%). For the sake of comparison of projected changes in temperature and precipitation between two sources (resulting from CHASE-PL project and CHIHE project, or SWAT input and HBV input), for each catchment, climate model and future period the differenceΔ were calculated:
where \(X_{\text{SWAT}}\) and \(X_{\text{HBV}}\) are projections of changes in temperature or precipitation used as input in SWAT and HBV model, respectively.
Results
In each box plot of the subsequent figures, boxes are defined by the 25th and 75th percentiles, the horizontal line within the box represents the median, whereas the whiskers represent the non-outlier range. Outliers are marked as circles (they are present only in some figures). Independent two-sample t test was applied for testing whether the differences between (temperature, precipitation and flow) change projections are statistically different between two sources.
Temperature changes
The comparison of annual and seasonal change of projected temperature between the reference and near future (NF) and far future (FF) periods used in the HBV and SWAT models in eight studied catchments, shown as box plots across climate models, demonstrates that there is very little difference between the two sources (Fig. S1, Supplementary Material). The warming is ubiquitous and fairly uniform spatially. There is little difference between seasonal temperature increases in the near future, and a considerable difference in the far future, with the highest level of warming occurring in the winter season (mean across all catchments, climate models and sources was 4.2 °C), and the lowest in summer season (3.1 °C). In general, climate model spread is higher than the differences between catchments. Model spread varies across seasons and future horizons. For example, for winter season, it is higher for the near future than for the far future, whilst for spring and summer season, the opposite takes place. The lowest spread occurs in summer in the near future (below 0.5 °C for all catchments), and the highest for spring in the far future (above 2 °C for five catchments).
In order to compare temperature change signals from both sources in a more explicit manner, differences in temperature change projections between CHASE and CHIHE (cf. Eq. 1) were calculated (Fig. 2). The results for the far future are shown, as in the near future the differences were generally lower. There is a good agreement between projections from both projects for mean annual and summer and autumn season temperatures, in which case the differences in terms of the absolute values are lower than 0.5 °C for every catchment and model. However, larger discrepancies can be observed for the Wisła catchment in spring and summer, and the Nysa catchment in spring. In the worst case, CM1, CM2 and CM4 show the increases in temperature in the Wisła catchment larger by 0.8–1.0 °C in CHASE (SWAT) than in CHIHE (HBV). In contrast, projections used in HBV show a larger increase in spring temperature by 0.6–0.8 °C than projections used in SWAT for CM5 and CM7 in the Wisła and Nysa catchments.
Differences (i.e. Δ values calculated using Eq. 1) in mean annual and seasonal temperature change projections (°C) for the far future between CHASE-PL (SWAT) and CHIHE (HBV) for eight studied catchments and seven climate models
Precipitation changes
Precipitation forcing data used in HBV and SWAT were not as consistent between each other as air temperature data (Fig. 3). In 95 out of 112 individual cases (eight catchments, seven climate models, two time horizons), projected changes in annual sums of precipitation used as HBV input were higher than the corresponding changes in the SWAT input. Mean projected change across these 112 cases is 12.7% in HBV and 9.3% in SWAT. In three catchments (marked with asterisks in Fig. 3), Narewka (near future), Wisła and Myśla (far future) the differences were statistically significant at the level = 0.05. Overall, projections from both sources agree that wetter conditions are expected for both horizons and all catchments. In the far future, a higher magnitude of increase in precipitation is projected for catchments situated on the Polish Plain than for mountainous catchments.
Comparison of projected mean annual and seasonal precipitation changes (per cent) via multi-model ensemble in the near and far future used as input in HBV and SWAT models for eight selected catchments. Asterisks denote cases with statistically significant differences (\(p = 0.05\)) between results from CHASE-PL and CHIHE projects
Projections of seasonal precipitation change also differ between the inputs used by the HBV and SWAT (Fig. 3). For all four seasons, the arithmetic mean of changes across 112 individual cases is higher for HBV input than SWAT input by 3–5%. Although statistically significant difference occurs only once (spring precipitation in the Narewka catchment in the far future), there are more cases with visually different results (e.g. winter precipitation in the Wisła catchment or summer precipitation in the Myśla catchment in the far future). Spatial differences in projected changes are much higher for precipitation than for temperature. However, patterns differ among seasons and time horizons. Climate model spread also varies: for example, in the near future in winter the mean spread across catchments is nearly the double of the corresponding value for summer (which is approximately 15%), for both sources of precipitation input. A further insight into the differences in precipitation change projections between the two sources is possible through analysing the differences between the projected changes used as SWAT input and projected changes used as HBV input for various catchments and models (Fig. 4). As in Fig. 2, only the results for the far future are shown, because the magnitude of difference for the near future is much lower. They strongly vary with temporal aggregation, catchments and climate models, but the last factor has the most pronounced effect. The main message is that, with very few exceptions, projections of changes used as SWAT input are lower than corresponding projections used as HBV input. At annual level, in the majority of cases the difference (Δ) is about 5%. In the lowland catchments (Oleśnica, Flinta, Myśla and Narewka) the projections of precipitation used in the HBV model are larger by more than 5% than the corresponding projections used in the SWAT model for some climate models and even reach 15% for Myśla for the CM2. Much higher differences can be noted at seasonal level, particularly for CM2 in spring and summer and for the Myśla catchment for spring, summer and autumn.
Differences (i.e. Δ values calculated using Eq. 1) in mean annual and seasonal precipitation change projections (per cent) for the far future between CHASE-PL (SWAT) and CHIHE (HBV) for eight studied catchments and seven climate models
For each climate model, there exists at least one season-catchment combination for which the difference is higher than 15%. Due to the fact that in all catchments summer precipitation has the highest share in annual precipitation, the differences in summer contribute most to the differences observed at the annual level. In three cases, the difference between projections from both sources is large and consistent between climate models:
-
1.
In three mountainous catchments, Dunajec, Wisła and Nysa, the difference in winter precipitation change is higher than 10% for six (Dunajec) and four (Wisła and Nysa) climate models.
-
2.
In the Narewka catchment, five climate models, and in Myśla, one climate model, suggest that the change in spring precipitation used as SWAT input is lower by at least 15% than the corresponding change used as HBV input.
-
3.
In summer, for all the lowland catchments except Narewka, the difference in precipitation is higher than 10% for a number of climate models.
In autumn the spread of differences larger than 10% is more equally distributed among the catchments, with only three models showing 15% difference for Myśla and Narewka.
Flow bias in the reference period
Prior to analysing projected changes in river flow in selected catchments, it is worth to analyse the bias of simulation of mean annual and seasonal flows by HBV and SWAT driven by the ensemble of climate models in the reference period (Fig. 5). Ensemble median bias in mean annual flow is within the range of −/+25% for both hydrological models and all catchments except Myśla. In the latter, ensemble median bias is over 40%, and for SWAT there are three climate models for which it is above 70%. The biases in seasonal flows vary among seasons and catchments. Both HBV and SWAT tend to underestimate mean winter flow in mountainous catchments, HBV underestimates mean spring flow in mountainous catchments, whilst SWAT overestimates it in all catchments except Wisła. The mean summer flow is overestimated in all mountainous catchments by HBV and underestimated by SWAT (except for the Biała catchment). Finally, HBV simulations of the mean autumn flow have low bias in mountainous catchments, whereas in SWAT it is underestimated in all catchments except Biała.
A more complex picture is visible for the lowland catchments (Fig. 5). For the Oleśnica catchment, HBV flow projections have lower bias than SWAT simulations for spring and summer seasons, but the opposite takes place in autumn and winter seasons. Fairly similar pattern exists for the Flinta catchment, with one exception: here, both SWAT and HBV overestimate mean summer flow. The Myśla catchment is the most challenging case for both models—SWAT considerably overestimates mean flow for all seasons, whereas HBV has totally different results for winter and spring (low bias) and summer and autumn (very high ensemble median bias of 184 and 110%, respectively). For the Narewka catchment, the HBV bias is low in all season but summer, whilst the SWAT model underestimates autumn and winter flow. In general, the SWAT spread of bias is much larger for all lowland catchments than the HBV spread for the same catchments.
River flow changes
In the second stage of analysis, the projected changes in mean annual and seasonal flows simulated by the HBV and SWAT models for two future periods were calculated. Both hydrological models agree on the dominating upward direction of change in all catchments and time periods, although four mountainous catchments: Biała, Dunajec, Nysa and Wisła, have variable directions of change in the near future (Fig. 6). In general, there is a high agreement among hydrological models on the magnitude of change in the near future (no statistically significant differences, at \(p = 0.05\)), whereas in the far future there is a high disagreement (all differences statistically different, at \(p = 0.05\)). Both, the magnitude of projected change, and the climate model variability grow with time for most catchments. In most cases, for the lowland catchments, mean annual projections obtained with the help of SWAT model for the far future provide increases lower by the factor of two to three than the corresponding increases obtained with the help of the HBV model. The disagreement between the hydrological models is lower for four highland catchments, for which the magnitude of change is also lower.
Figure 6 shows projected changes in mean seasonal discharge according to the HBV and SWAT models. As with the mean annual discharge, there is a relatively good agreement between hydrological models in the near future and a much weaker agreement in the far future. In winter season, increases are dominating throughout all combinations of catchments, models and periods. Despite the fact that SWAT gives lower increases in the mean annual discharge in the far future, it projects higher increases in the far future mean winter discharge in mountainous catchments than HBV. For seven out of 16 cases, SWAT flow projections are statistically higher than HBV projections in winter (\(p = 0.05\)).
For spring season in the near future, climate model variability dominates and both HBV-based and SWAT-based projections show changes in different directions (Fig. 6). The Flinta catchment is the only one for which there is a statistically significant difference between HBV and SWAT. In contrast, in the far future, mean spring discharge is projected to increase according to the HBV model in each catchment, whereas according to SWAT it is projected to increase only in lowland catchments (and by a lower percentage). In each case in the far future, the difference is statistically significant at the level \(p = 0.05\). In mountainous catchments SWAT projects changes in variable directions, although decreases are dominating.
Projected flow changes in summer and autumn season between the hydrological models in the near future are very similar but they considerably diverge in the far future (Fig. 6). Indeed, in none of the 16 cases is the difference in flow projections in the near future statistically significant (\(p = 0.05\)). Increases in summer flow projected by SWAT in the far future in all catchments are statistically significantly lower than corresponding increases projected by HBV. For some climate models in the lowland catchments, increases projected by the HBV model are three-fold, and in one case (summer flow in the Oleśnica catchment) they are almost six-fold. For the Dunajec catchment, summer flow simulated by SWAT is projected to decrease according to most of climate models, whereas changes in the opposite direction are simulated by the HBV model. On the other hand, there is a fairly good agreement among the two hydrological models on projected changes of flow in the autumn season in the mountainous catchments and the Narewka catchment.
Figure 6 shows changes in flow indices expressed as percentage. It should be noted that the comparison of changes between catchments would give different outcomes if they were expressed as differences between future horizons and the reference period (e.g. in mm). The reason for this is a large variability in runoff coefficients and precipitation among catchments (cf. Fig. 1; Table 2). For example, a 10% increase in mean annual flow in the Dunajec catchment corresponds to an increase in runoff by more than 70 mm per year. Such a magnitude of increase in runoff in the Flinta catchment would correspond to an increase in mean annual flow by more than 80%.
Flow-climate sensitivity
Some insight into the way that hydrological models transform the climate change signal can be obtained from a simple analysis of mean annual flow change (ΔQ) as function of mean annual precipitation change (ΔP) (Fig. 7) for particular combinations of climate models, hydrological models, catchments and projection horizons. There are large differences between the nature of this response for different catchments and models.
Scatterplot of mean annual flow change versus mean annual precipitation change for eight selected catchments: a HBV in the near future, b HBV in the far future, c SWAT in the near future, d SWAT in the far future. Individual points within each plot refer to a single climate model-catchment combination
For the HBV model results, catchments have different sensitivity for the near future and far future. The catchment sensitivities increase for far future but also become much more scattered, in particular for the lowland catchments. Mountainous catchments show nearly the same response to changes in precipitation in near- and far future. However, in the lowland catchments the changes of flow in the response to changes in precipitation are doubled in far future.
The SWAT model results show similar variability of sensitivity as the HBV model for the near future and much smaller scatter of the sensitivity values for the lowland catchments in the far future. The mountainous catchments show the sensitivity for the far future stabilising around 20–30%, which is lower than for the same precipitation change in the HBV model. This is consistent with the fact that changes in mean annual flow projected by SWAT were found to be lower than those for HBV in the far future (Fig. 6). In the SWAT model, the nature of flow response does not strongly depend on the projection horizon.
Despite some differences between SWAT and HBV revealed by this analysis, there are also some similarities, even in the far future. For example, the four lowland catchments are positioned in the same zones of the scatter plots for HBV (Fig. 7b) and SWAT (Fig. 7d). More precisely, two models consistently show that the Narewka catchment has a weaker response in mean annual flow change to a relatively high precipitation change than the Flinta catchment, even though the latter is exposed to a lower magnitude of precipitation change than the Narewka. Two other lowland catchments, i.e. the Oleśnica and the Myśla, are situated in the middle zone of Fig. 7b, d, between points representing the Flinta and the Narewka catchments.
Flow change vs. runoff coefficients
In order to examine the spatial variability of projected changes in mean annual flow, they are plotted in Fig. 8, for each climate model against the runoff coefficients of each catchment (cf. Fig. 1 for the map of runoff coefficients). Results for the far future are only shown, as the magnitude of changes and differences are higher in this case than in the near future (cf. Figs. 6, 7). Although the number of catchments is rather small, some clear relationships are present. Both HBV- and SWAT-based projections show that in catchments with lower runoff coefficients, a higher magnitude of changes can be expected. Although regression lines were not plotted, for both hydrological models and each climate model (except for the SWAT-CM2 combination) the relationship has a convex parabolic shape, with a vertex situated for runoff coefficient values between 0.5 and 0.7. In the case of CM2, the results are consistent with Fig. 3: this is the climate model for which precipitation projections used as SWAT input are considerably lower in the lowland catchments than projections used as HBV input. This difference is now reflected in Fig. 8: mean annual CM2-driven flow change projected by SWAT in three catchments with the lowest runoff coefficients (Flinta, Myśla and Oleśnica) is equal to approximately 10%, whereas the corresponding change projected by HBV yields 80%. Certainly, this analysis neglects the effect of precipitation and temperature changes that vary across catchments and climate models.
Figure 8c shows the differences in mean annual flow change projections between SWAT and HBV as a function of runoff coefficient. This relationship also has a parabolic form, although this time concave. Four clusters of catchments characterised by decreasing values of runoff coefficients are also characterised by large discrepancy between SWAT-based and HBV-based projections. More specifically: (1) the Dunajec and Wisła catchments have mean runoff coefficient equal to 0.58, and mean difference in mean annual flow equal to 13%; (2) for the Biała and Nysa catchment, the same parameters are 0.41 and 20%; (3) for the Narewka catchment it is 0.27 and 36%; (4) for the last cluster composed of the Flinta, Myśla and Oleśnica catchments it is 0.17 and 71%.
Discussion
The main objective of this study was to compare mean annual and seasonal projections of river flows in eight Polish catchments obtained from two hydrological models of different complexity, SWAT and HBV for two future periods, the near future (2021–2050) and the far future (2071–2100). One important message arising from this study, consistent with previous impact studies based on the bias-corrected EURO-CORDEX ensemble for Poland (Piniewski et al. 2017b; Osuch et al. 2016b) and other countries in Central (Germany) and Northern (Estonia) Europe (Hattermann et al. 2016 and Tamm et al. 2016, respectively), is that there is going to be more water in this part of Europe, both in terms of precipitation and runoff. Another source of data for comparison are European-level assessments of climate change impacts on water resources, e.g. Alfieri et al. (2015), Papadimitriou et al. (2016) and Roudier et al. (2016). However, due to a significant scale mismatch, it is impossible to compare the outputs from their models to those presented in this study. As reported by Piniewski et al. (2017b), all available pan-European studies corroborate the findings on the projected runoff increase in Poland.
A more scrutinised look on the results presented in this study allows to note that HBV-based and SWAT-based projections of future annual and seasonal flow changes differ considerably between each other. One could perhaps expect that such simple flow indicators as those used in this study should undergo comparable changes when generated by two different models driven by similar climate change forcing. Yet, this is not the case for the far future, and particularly not for the lowland catchments. As pointed out by Meresa et al. (2016), these catchments are characterised by a lower correlation between precipitation and one of the flow indices, the Standardised Runoff Index. One of the previous model inter-comparisons carried out in Polish catchments reported more comparable changes in flow patterns between SWAT and WaterGAP, than those presented here for SWAT and HBV (Piniewski et al. 2013). It should be noted though, that the latter study investigated only the near future period, whereas in the present paper major discrepancies arise in the far future. The results of the analysis of projections of low-flow indices presented by Osuch (2017), for the nearly the same catchments (except Myśla) and the same RCP 8.5 scenario using the HBV model, show that the lowland catchments are becoming substantially wetter in the far future period in comparison with the reference period. This supports the HBV results for the lowland catchments on the increased sensitivity of flow changes with the increase in precipitation changes shown in Fig. 7. However, further studies are needed to support this hypothesis.
The results also showed that the runoff coefficient, highly correlated with topography (cf. Fig. 1; Table 2) explains the spatial variability in projected flow changes from both models, as well as the difference between them, quite well. The lower the runoff coefficient, (1) the higher the change in mean annual flow for both models; (2) the higher the difference in mean annual flow changes between two models. The first conclusion corroborates results of other studies reporting a similar direction of flow change as a function of runoff coefficient (Jones et al. 2006; Arnell 1992). The parabolic-shape relationship obtained here (Fig. 8a, b) is very similar to the one reported by Arnell (1992) for a set of 15 UK catchments of similar size as in the present study. As regards the second statement, the reason for large differences in annual and seasonal flow projections between HBV and SWAT, frequently exceeding 100% for the Myśla, Flinta and Oleśnica catchments (characterised by the lowest runoff coefficients) remains unknown at this stage and requires further investigation. It is clear that such water-limited catchments are more challenging for hydrological modelling, which was shown in Fig. 5 (particularly high value of flow bias for the Myśla catchment in summer), and also reported by other authors in a larger scale (Rakovec et al. 2016). Since the reasons for which large discrepancies are the largest (summer and autumn) include the typical low-flow periods, it should be also noted that both SWAT and HBV models were not calibrated with a focus on low-flow simulation, so it is understandable that the uncertainty in these seasons is larger.
Few studies available in the literature compared HBV and SWAT with regard to future flow projections. Those that did (Vetter et al. 2015), used slightly different models: SWIM instead of SWAT, and a semi-distributed instead of lumped version of HBV. They were also applied on larger scales (the Rhine, Niger and Yellow river basins). In their study, hydrological models were an incomparably less important source of uncertainty compared to RCPs and GCMs for the Rhine basin (the most similar conditions to Poland). Future flow projections obtained from SWIM and HBV for the Rhine basin were much more similar to each other than the projections analysed in the present study. Otherwise, there are model inter-comparison studies that did not use the same set of hydrological models, but at least these models were applied on a similar scale as in the present study: the Odense catchment in Denmark (Karlsson et al. 2016) and Kleine Nete catchment in Belgium (Dams et al. 2015). Both these studies underlined the hydrological model structure uncertainty in projections of future flows. However, Karlsson et al. (2016) reported fairly similar projections of changes in mean annual and mean monthly flows from SWAT and a lumped, conceptual model NAM, comparable to HBV.
One of the main limitations of this study is the small catchment sample (\(N = 8\)). In order to draw more credible conclusions, especially with regard to the spatial variability of projected changes and the influence of catchment properties on results, it would be recommended to use a much higher number of catchments. Since in this study the results for eight catchments were extracted from the available projections of the SWAT model for the Vistula and Odra basins (Piniewski et al. 2017b), an optimal solution would be to carry out the climate change impact assessment using HBV or other models in a larger number of sub-catchments (for example, selected based on flow regime similarity) within this spatial domain. Gupta et al. (2014) coined a phrase “large-sample hydrology” motivated by the need to “balance depth with breadth”, and referring to various types of hydrological investigations that use large catchment samples. In their review, they used 30 catchments as the minimum value for inclusion in their analysis, and future climate change impact model inter-comparison studies focused on small- and medium-sized catchments should preferably follow this rule. Another possible pathway of making the results of impact assessments more generalisable is through reducing the dimensionality of the problem by clustering large samples of catchments with respect to their types of responses to climate change forcing (Addor et al. 2014).
Conclusion
The paper presents comparison of river flow projections for eight catchments in Poland, resulting from two projects in the Polish-Norwegian Research Programme. The comparison presented was based on the closest possible case studies, including the same catchments, the same future time periods and the same ensemble of climate models (although independently bias-corrected). The main differences consisted of different representation of physical processes transforming the climate projections into flows as well as the spatial scale of operation of the hydrological models. The spatial domains of both projects were the entire VOB area in the CHASE-PL project (where the semi-distributed, process-based, SWAT model was used) and selected Polish catchments in the CHIHE project (where the lumped, conceptual, HBV model was used). Hydrological simulations driven by the bias-corrected EURO-CORDEX forcing revealed a large variability in flow bias depending on the catchment, season and hydrological model. Overall, the bias was only slightly lower in HBV than in SWAT, but both models failed to accurately reproduce the seasonal flow cycle in all catchments, apart from Dunajec. The comparison of projections of future temperature and precipitation changes between both studies showed that there were substantial differences, particularly for the latter variable. In a result of different bias correction methods used, the SWAT model had from 2 to 15% lower precipitation projected for the far future period. Differences in projections of precipitation—the input signal to hydrological systems—were amplified in both projects, by two different hydrological models, in different ways. An overall tendency of increases in mean annual and seasonal flows was found by both models, yet the magnitudes of projected changes were largely different, particularly in the far future, and in lowland catchments. Analysis of sensitivity of mean annual flow response to mean annual precipitation change revealed largely different behaviours of HBV and SWAT for the far future in the lowland catchments. Spatial variability in projected changes in mean annual flow could be well explained by the runoff coefficients.
In summary, this study shows that future flow projections have a large spread that has its origin in different representation of hydrological processes in models, differences in temperature and, particularly, precipitation projections and their bias correction. Considerable differences in results of both projects create a serious interpretation issue for practitioners dealing with climate change adaptation and water management.
References
Addor N, Rössler O, Köplin N, Huss M, Weingartner R, Seibert J (2014) Robust changes and sources of uncertainty in the projected hydrological regimes of Swiss catchments. Water Resour Res 50:7541–7562. doi:10.1002/2014WR015549
Alcamo J, Döll P, Henrichs T, Kaspar F, Lehner B, Rösch T, Siebert S (2003) Development and testing of the WaterGAP 2 global model of water use and availability. Hydrol Sci J 48(3):317–337. doi:10.1623/hysj.48.3.317.45290
Alfieri L, Burek P, Feyen L, Forzieri G (2015) Global warming increases the frequency of river floods in Europe. Hydrol Earth Syst Sci 19:2247–2260. doi:10.5194/hess-19-2247-2015
Arnell NW (1992) Factors controlling the effects of climate change on river flow regimes in a humid temperate environment. J Hydrol 132(1):321–342. doi:10.1016/0022-1694(92)90184-W
Arnold JG, Srinivasan R, Muttiah RS, Williams JR (1998) Large area hydrologic modeling and assessment Part I: model development. JAWRA J Am Water Resour Assoc 34(1):73–89. doi:10.1111/j.1752-1688.1998.tb05961.x
Benninga HJF, Booij MJ, Romanowicz RJ, Rientjes THM (2016) Performance of ensemble streamflow forecasts under varied hydrometeorological conditions. Earth Syst Sci Discuss, Hydrol. doi:10.5194/hess-2016-584
Berezowski T, Szcześniak M, Kardel I, Michałowski R, Okruszko T, Mezghani A, Piniewski M (2016) CPLFD-GDPT5: high-resolution gridded daily precipitation and temperature data set for two largest Polish river basins. Earth Syst Sci Data 8(1):127–139. doi:10.5194/essd-8-127-2016
Bergström, S., (1976), Development and application of a conceptual runoff model for Scandinavian catchments. SMHI report hydrology and oceanography, No RH07, Norrköping, Sweden
Bergström S (1995) The HBV model. In: Singh VP (ed) Computer models of watershed hydrology. Water Resources Publications, Highland Ranch, pp 443–476. ISBN 0-918334-91-8
Dams J, Nossent J, Senbeta TB, Willems P, Batelaan O (2015) Multi-model approach to assess the impact of climate change on runoff. J Hydrol 529:1601–1616. doi:10.1016/j.jhydrol.2015.08.023
Goodison BE, Louie PYT, Yang D (1998) WMO solid precipitation measurement intercomparison final report. Report no. 67, WMO/TD—No. 872. Source, available from: http://www.wmo.int/pages/prog/www/reports/WMOtd872.pdf. Accessed 31 Jan 2017
Gosling SN, Taylor RG, Arnell NW, Todd MC (2011) A comparative analysis of projected impacts of climate change on river runoff from global and catchment-scale hydrological models. Hydrol Earth Syst Sci 15(1):279–294. doi:10.5194/hess-15-279-2011
Gosling SN, Zaherpour J, Mount NJ, Hattermann FF, Dankers R, Arheimer B, Breuer L, Ding J, Haddeland I, Kumar R, Kundu D, Liu J, van Griensven A, Veldkamp T, Vetter T, Wang X, Zhang X (2016) A comparison of changes in river runoff from multiple global and catchment-scale hydrological models under global warming scenarios of 1 °C, 2 °C and 3 °C. Clim Change. doi:10.1007/s10584-016-1773-3
Gupta HV, Kling H, Yilmaz KK, Martinez GF (2009) Decomposition of the mean squared error and NSE performance criteria: implications for improving hydrological modelling. J Hydrol 377(1–2):80–91. doi:10.1016/j.jhydrol.2009.08.003
Gupta HV, Perrin C, Blöschl G, Montanari A, Kumar R, Clark M, Andréassian V (2014) Large-sample hydrology: a need to balance depth with breadth. Hydrol Earth Syst Sci 18(2):463–477. doi:10.5194/hess-18-463-2014
Hamon WR (1961) Estimation of potential evapotranspiration. J Hydraul Div Am Soc Civil Eng 87(3):107–120
Hattermann FF, Huang S, Burghoff O, Hoffmann P, Kundzewicz ZW (2016) An update of the article “Modelling flood damages under climate change conditions—a case study for Germany”. Nat Hazards Earth Syst Sci 16:1617–1622. doi:10.5194/nhess-16-1617-2016
Hattermann FF, Krysanova V, Gosling SN, Dankers R, Daggupati P, Donnelly C, Flörke M, Huang S, Motovilov Y, Buda S, Yang T, Müller C, Leng G, Tang Q, Portmann FT, Hagemann S, Gerten D, Wada Y, Masaki Y, Alemayehu T, Satoh Y, Samaniego L (2017) Cross-scale intercomparison of climate change impacts simulated by regional and global hydrological models in eleven large river basins. Clim Chang. 141(3):561–576. doi:10.1007/s10584-016-1829-4
Hempel S, Frieler K, Warszawski L, Schewe J, Piontek F (2013) A trend-preserving bias correction—the ISI-MIP approach. Earth Syst Dyn 4(2):219–236. doi:10.5194/esd-4-219-2013
Jacob D et al (2014) EURO-CORDEX: new high-resolution climate change projections for European impact research. Reg Environ Change 14(2):563–578. doi:10.1007/s10113-013-0499-2
Jones RN, Chiew FHS, Boughton WC, Zhang L (2006) Estimating the sensitivity of mean annual runoff to climate change using selected hydrological models. Adv Water Resour 29(10):1419–1429. doi:10.1016/j.advwatres.2005.11.001
Karlsson IB, Sonnenborg TO, Refsgaard JC, Trolle D, Børgesen CD, Olesen JE, Jeppesen E, Jensen KH (2016) Combined effects of climate models, hydrological model structures and land use scenarios on hydrological impacts of climate change. J Hydrol 535:301–317. doi:10.1016/j.jhydrol.2016.01.069
Krysanova V, Kundzewicz ZW, Piniewski M (2016) Assessment of climate change impact on water resources. In: Singh VP (ed) Handbook of applied hydrology. McGraw-Hill Education, New York
Kundzewicz ZW, Krysanova V, Dankers R, Hirabayashi Y, Kanae S, Hattermann FF, Huang PCD, Milly M, Stoffel PPJ, Driessen P, Matczak P, Quevauviller P, Schellnhuber HJ (2017) Differences in flood hazard projections in Europe—their causes and consequences for decision making. Hydrol Sci J 62(1):1–14. doi:10.1080/02626667.2016.1241398
Lindström G, Johansson B, Persson M, Gardelin M, Bergström S (1997) Development and test of the distributed HBV-96 hydrological model. J Hydro 201(1):272–288. doi:10.1016/S0022-1694(97)00041-3
Meresa H, Osuch M, Romanowicz R (2016) Hydro-meteorological drought projections into the 21-st century for selected Polish catchments. Water 8(5):206. doi:10.3390/w8050206
Mezghani A, Dobler A, Haugen JH (2016) CHASE-PL climate projections: 5-km gridded daily precipitation & temperature dataset (CPLCP-GDPT5). Norwegian Meteorological Institute, Dataset. doi:10.4121/uuid:e940ec1a-71a0-449e-bbe3-29217f2ba31d
Osuch M, Romanowicz RJ, Lawrence D, Wong WK (2016a) Trends in projections of standardized precipitation indices in a future climate in Poland. Hydrol Earth Syst Sci 20(5):1947–1969. doi:10.5194/hess-20-1947-2016
Osuch M, Lawrence D, Meresa HK, Napiórkowski JJ, Romanowicz RJ (2016b) Projected changes in flood indices in selected catchments in Poland in the 21st century. Stoch Env Res Risk Assess. doi:10.1007/s00477-016-1296-5
Osuch M, Romanowicz RJ, Wong WK (2017) Analysis of low flow indices under varying climatic conditions in Poland. Hydrol Res (in review)
Papadimitriou LV, Koutroulis AG, Grillakis MG, Tsanis IK (2016) High-end climate change impact on European runoff and low flows–exploring the effects of forcing biases. Hydrol Earth Syst Sci 20:1785–1808. doi:10.5194/hess-20-1785-2016
Piani C, Haerter JO, Coppola E (2010) Statistical bias correction for daily precipitation in regional climate models over Europe. Theor Appl Climatol 99(1):187–192. doi:10.1007/s00704-009-0134-9
Piniewski M (2017) Classification of natural flow regimes in Poland. River Res Appl. doi:10.1002/rra.3153
Piniewski M, Voss F, Bärlund I, Okruszko T, Kundzewicz ZW (2013) Effect of modelling scale on the assessment of climate change impact on river runoff. Hydrol Sci J 58(4):737–754. doi:10.1080/02626667.2013.778411
Piniewski M, Mezghani A, Szcześniak M, Kundzewicz ZW (2017a) Regional projections of temperature and precipitation changes. Robustness and uncertainty aspects. Met Zeit 26(2):223–234. doi:10.1127/metz/2017/0813
Piniewski M, Szcześniak M, Huang S, Kundzewicz ZW (2017b) Projections of runoff in the Vistula and the Odra river basins with the help of the SWAT model. Hydrol Res 48(3):nh2017280. doi:10.2166/nh.2017.280
Piniewski M, Szcześniak M, Kardel I, Berezowski T, Okruszko T, Srinivasan R, Schuler DV, Kundzewicz ZW (2017c) Hydrological modelling of the Vistula and Odra river basins using SWAT. Hydrol Sci J 62(8):1266–1289. doi:10.1080/02626667.2017.1321842
Rakovec O, Kumar R, Mai J, Cuntz M, Thober S, Zink M, Attinger S, Schäfer D, Schrön M, Samaniego L (2016) Multiscale and multivariate evaluation of water fluxes and states over European river basins. J Hydrometeorol 17(1):287–307. doi:10.1175/JHM-D-15-0054.1
Richter D (1995) Ergebnisse methodischer Untersuchungen zur Korrektur des systematischen Messfehlers des Hellmannniederschlagsmessers, Berichte des Deutschen Wetterdienstes 194. Offenbach, German
Romanowicz R, Bogdanowicz JE, Debele SE, Doroszkiewicz J, Hisdal H, Lawrence D, Meresa HK, Napiórkowski JJ, Osuch M, Strupczewski WG, Wilson D, Wong WK (2016) Climate change impact on hydrological extremes: preliminary results from the Polish-Norwegian project. Acta Geophys 64(2):477–509. doi:10.1515/acgeo-2016-0009
Roudier P, Andersson JCM, Donnelly C, Feyen L, Greuell W, Ludwig F (2016) Projections of future floods and hydrological droughts in Europe under a +2°C global warming. Clim Change 135(2):341–355. doi:10.1007/s10584-015-1570-4
Schewe J et al (2014) Multimodel assessment of water scarcity under climate change. Proc Natl Acad Sci 111(9):3245–3250. doi:10.1073/pnas.1222460110
Tamm O, Luhamaa A, Tamm T (2016) Modeling future changes in the North-Estonian hydropower production by using. Hydrol Res 47(4):835–846. doi:10.2166/nh.2015.018
Teutschbein C, Seibert J (2010) Regional climate models for hydrological impact studies at the catchment scale: a review of recent modeling strategies. Geogr Compass 4(7):834–860. doi:10.1111/j.1749-8198.2010.00357.x
Vetter T, Huang S, Aich V, Yang T, Wang X, Krysanova V, Hattermann F (2015) Multi-model climate impact assessment and intercomparison for three large-scale river basins on three continents. Earth Syst Dyn 6(1):17–43. doi:10.5194/esd-6-17-2015
Acknowledgements
Support of the projects CHASE-PL (Climate Change Impact Assessment for Selected Sectors in Poland) and CHIHE (Climate Change Impact on Hydrological Extremes) of the Polish-Norwegian Research Programme operated by the National Centre for Research and Development (NCBiR) under the Norwegian Financial Mechanism 2009–2014 in the frame of Project Contracts No. Pol-Nor/200799/90/2014 and Pol-Nor/196243/80/2013 is gratefully acknowledged. The first author thanks the Alexander von Humboldt foundation and the Ministry of Science and Higher Education for financial support. The Institute of Meteorology and Water Management—National Research Institute (IMGW-PIB) is kindly acknowledged for providing the hydrometeorological data used in this work. All authors are thankful to two anonymous referees who provided a number of insightful comments that helped to improve the manuscript.
Author information
Authors and Affiliations
Corresponding author
Electronic supplementary material
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Piniewski, M., Meresa, H.K., Romanowicz, R. et al. What can we learn from the projections of changes of flow patterns? Results from Polish case studies. Acta Geophys. 65, 809–827 (2017). https://doi.org/10.1007/s11600-017-0061-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11600-017-0061-6