1 Introduction

Many optimization programs are motivated by situations which culminate, among other things, from uncertainty—from unknown or imprecise data, inaccurate measurements, or potentially inadequate models. In the operations research literature, there are three classical paradigms to model uncertainty: probabilistic, possibilistic, and deterministic. We consider the deterministic approach by defining domains containing the possible uncertainties. This approach has given foundation to parametric optimization [17] and robust optimization [5].

In addition to the constants and variables in all mathematical programs, a parametric program also contains parameters which model uncertainty because their values are not being solved for, but are not known. In contrast with the nonparametric program, which is solved to obtain a specific solution vector and corresponding optimal value, the parametric program is solved to obtain a solution vector-valued function and the corresponding optimal value function, both of which map the parameters to their corresponding solution spaces. The form of these solutions fundamentally changes the problem.

Studies on parametric programming go back at least to 1964 when the authors of [23] provide properties of solution functions based on the structure of the program. Since then, researchers have worked on the theory, summarized in [17, 18]. A basic penalty function algorithm is given in [17], with more algorithmic methods [13,14,15, 28] coming about with the turn of the millenium. These authors work with parameters only in the right-hand side of the constraints, but in 2006, the authors of [4] present a more versatile approximation approach, which we term the Approximate Simplex Method (ASM). The ASM allows parameters to be located, under certain conditions, in both the objective and the constraint functions. In 2011, [32] develops a more intricate interpolation method involving barycentric coordinates to solve model predictive control (MPC) problems with the same objective functions as in [4] and with linear constraints having parameters only in the right-hand side. In 2013, [12] incorporates parametric objective functions into a mixed integer program with parameters only in the right-hand side, emulating [14].

More recently, work has been done to support parameters in other locations: [27, 29] solve multiparametric programs at most bilinear in the parameter and variable, quadratic in the variable, and quadratic in the parameter for both the objective and constraint functions; [1] posits the first method for solving parametric convex quadratic programs with parameters in general locations; finally, [6, 9] apply Gröbner bases to solve the first order KKT conditions of multiparametric programs with parameters anywhere in nonlinear objective and constraint functions. Also worth noting is the use of finite element methods for solving partial differential equations to solve optimization programs by solving the KKT systems, such as in [2, 29].

In addition to uncertainty of coefficients, real-life programs frequently involve multiple objective functions; the solving of multiple objective programs relies heavily on parametric single objective programs. Due to the versatility of the algorithm which [4] provides, it appears in [22] as part of the process to solve multi-objective programs via scalarization. In that application it is found that, while the scalarizing single-objective programs do not meet the conditions put forth in [4], the ASM still succeeds on the programs examined.

To explain this unexpected success, we consult the literature, but, as detailed above, there are not any studies on the solving of parametric programs involving objectives and constraints biconvex in the variables and parameters beyond the works [27, 29]. The ability to solve programs of this nature opens up multiple scalarization methods in multiobjective programs and the application of gradient dual ascent to single-objective programs. As a result, in this work, we extend the ASM to apply to a broader set of objectives and constraints than originally posited by [4]; we supplement the presented theory with a brief numerical exploration of a set of randomly generated examples.

We begin by discussing the biconvex parametric program being solved in Sect. 1.1 along with the definitions in use, and we summarize the algorithm from [4] in Sect. 1.2. We provide the theory to extend the ASM from [4] to a broader set of objectives and constraints in Sect. 2; specifically, we examine the feasibility of the solution function in Sect. 2.1, and the new termination conditions in Sect. 2.2. Finally, in Sect. 3, we construct the algorithm and compare both termination methods when applied to a set of randomly generated examples.

1.1 Definitions and problem statement

In this paper, \(\varTheta\) represents the space from which the parameters are drawn. In the case of some theorems, convexity of \(\varTheta\) may be sufficient, but for the algorithms presented, polygonality of \(\varTheta\) is necessary.

Let \(m,n,\kappa \in {\mathbb {N}}\), \(\kappa \ge 2\), \(\varTheta \subseteq {\mathbb {R}}^{\kappa -1}\) be a bounded (convex) polyhedron, \(\pmb \theta \in \varTheta\) represent the parameters, and \(\pmb {x}\in {\mathbb {R}}^n\) represent the decision variables. Note that m is the number of nonlinear constraints, n is the number of variables, and \(\kappa\) is the number of vertices in polyhedron \(\varTheta\). Then \(\kappa -1\) is the number of parameters.

Letting \(f:{\mathbb {R}}^n\times \varTheta \rightarrow {\mathbb {R}}\) and \(g_i:{\mathbb {R}}^n\times \varTheta \rightarrow {\mathbb {R}}\), \(i\in \{1,\dots ,m\}\), be biconvex in \({\varvec{x}}\) and \(\pmb \theta\) and twice differentiable in \(({\varvec{x}},\pmb \theta )\), we consider the optimal value function \(f^*:\varTheta \rightarrow {\mathbb {R}}\) defined by the following biconvex program

$$\begin{aligned} f^*(\pmb \theta ):=\min _{{\varvec{x}}\in {\mathbb {R}}^n_{\geqq }}&\; f({\varvec{x}},\pmb \theta ) \nonumber \\ \text {s.t.}&\; g_i({\varvec{x}},\pmb \theta )\le 0,\; i\in \{1,\dots , m\}\\&\; A{\varvec{x}}+B\pmb \theta +\pmb {d}=\pmb 0.\nonumber \end{aligned}$$
(1)

If we let

$$\begin{aligned}{\mathcal {X}}(\pmb \theta ):=\{{\varvec{x}}\in {\mathbb {R}}^n_{\geqq }: g_i({\varvec{x}},\pmb \theta )\le 0, \; i=1,\dots ,m, \; A{\varvec{x}}+B\pmb \theta +\pmb {d} =\pmb 0\}\end{aligned}$$

and \({\mathcal {X}}(\varTheta ):=\cup _{\pmb \theta \in \varTheta } {\mathcal {X}}(\pmb \theta )\), then we have the following definition. Note that \({\varvec{x}}\) in (1) and \({\varvec{x}}^i\), \(i\in \{1,\dots ,\kappa \}\), in Definition 1 are vectors in \({\mathbb {R}}^n\), but \({\varvec{x}}^*\) and \({\bar{{\varvec{x}}}}\) below are vector-valued functions of \(\pmb \theta\).

Definition 1

  1. 1.

    The optimal solution function to (1), \({\varvec{x}}^*:\varTheta \rightarrow {\mathbb {R}}^n\), is defined by

    $$\begin{aligned}{\varvec{x}}^*:\pmb \theta \mapsto \text {argmin}_{{\varvec{x}}\in {\mathcal {X}}(\pmb \theta )} f({\varvec{x}},\pmb \theta )\end{aligned}$$

    and the optimal value function, \(f^*(\pmb \theta ):\varTheta \rightarrow {\mathbb {R}}\), is defined by

    $$\begin{aligned}f^*:\pmb \theta \mapsto f({\varvec{x}}^*(\pmb \theta ),\pmb \theta ).\end{aligned}$$
  2. 2.

    Define \({\bar{{\varvec{x}}}}:\varTheta \rightarrow {\mathbb {R}}^n\) and \({\bar{f}}:\varTheta \rightarrow {\mathbb {R}}\) to be the linear interpolants of \({\varvec{x}}^*\) and \(f^*\) respectively.

  3. 3.

    If \(\pmb \vartheta ^i\) is a vertex of \(\varTheta\), \(i\in \{1,\dots ,\kappa \}\), then, for all i, the vertex solution \({\varvec{x}}^i:={\varvec{x}}^*(\pmb \vartheta ^i)\) is an optimal solution of program (1) at \(\pmb \vartheta ^i\); that is, \(f^*(\pmb \vartheta ^i)=f({\varvec{x}}^i,\pmb \vartheta ^i)\).

Two generalizations of the convexity of a function are defined below.

Definition 2

Let \(\lambda _1,\lambda _2\in [0,1]\); consider convex spaces \(\varTheta \subseteq {\mathbb {R}}^{\kappa -1}\) and \({\mathcal {X}}(\varTheta )\subseteq {\mathbb {R}}^n\), with \({\varvec{x}}^1,{\varvec{x}}^2\in {\mathcal {X}}(\varTheta )\), \(\pmb \theta ^1,\pmb \theta ^2\in \varTheta\). A function \(f:{\mathcal {X}}(\varTheta )\times \varTheta \rightarrow {\mathbb {R}}\) is

  1. 1.

    jointly convex if f is convex with respect to the vector \(({\varvec{x}},\pmb \theta )\in {\mathcal {X}}(\varTheta )\times \varTheta\); that is,

    $$\begin{aligned}f(\lambda _1{\varvec{x}}^1+(1-\lambda _1){\varvec{x}}^2,\lambda _1\pmb \theta ^1+(1-\lambda _1)\pmb \theta ^2)\le \lambda _1f({\varvec{x}}^1,\pmb \theta ^1)+(1-\lambda _1)f({\varvec{x}}^2,\pmb \theta ^2),\end{aligned}$$
  2. 2.

    biconvex if f is convex with respect to \({\varvec{x}}\) when holding \(\pmb \theta\) constant and if f is convex with respect to \(\pmb \theta\) when holding \({\varvec{x}}\) constant; that is,

    $$\begin{aligned}f(\lambda _1{\varvec{x}}^1&+(1-\lambda _1){\varvec{x}}^2, \lambda _2\pmb \theta ^1+(1-\lambda _2)\pmb \theta ^2)\le \lambda _1\lambda _2f({\varvec{x}}^1,\pmb \theta ^1) \\ & +(1-\lambda _1)\lambda _2f({\varvec{x}}^2,\pmb \theta ^1)+\lambda _1(1-\lambda _2)f({\varvec{x}}^1,\pmb \theta ^2)+(1-\lambda _1)(1-\lambda _2)f({\varvec{x}}^2,\pmb \theta ^2). \end{aligned}$$

    We refer to the right-hand side of the above inequality as the biconvex-overestimator of f.

Note that biconvexity reduces to joint convexity if the function f is independent of \(\pmb \theta\). As a result, in this paper, when we say a function is biconvex, we assume that it is not jointly convex.

Finally, we make use of a version of weak differentiability of a function which is required in Sect. 2.2.3.

Definition 3

A function \(f: \varTheta \rightarrow {\mathbb {R}}^{n}\) is said to be piecewise differentiable on \(\varTheta\) if there exists \(N_f\in {\mathbb {N}}\) and a partition \(\{\varTheta _i^{f}\}_{i=1}^{N_{f}}\) for f such that

  1. 1.

    The function f is differentiable on each subset \(\varTheta _i^{f},\; i \in \{1, \ldots , N_{f} \}\) and

  2. 2.

    for all \(\bar{\varvec{t}} \in \varTheta _i^{f} \cap \varTheta _j^{f}\) and for all \(i, j \in \{1, \ldots , N_{f} \}, i \ne j, \;\; \nabla f(\bar{\varvec{t}}) = \lim _{\varvec{t} \in \text {int}({\varTheta _i^{f}}), \varvec{t} \rightarrow \bar{\varvec{t}}} \nabla f(\varvec{t})\) or \(\nabla f(\bar{\varvec{t}}) = \lim _{\varvec{t} \in \text {int}({\varTheta _j^{f}}), \varvec{t} \rightarrow \bar{\varvec{t}}} \nabla f(\varvec{t}),\) where \(\nabla f\) denotes the gradient of f with respect to \(\varvec{t}\), and \(\text {int}({\varTheta })\) denotes the interior of \(\varTheta\).

We also include the following theorem from [16], which provides the continuity and piecewise differentiability of \({\varvec{x}}^*\) and \(f^*\). The theorem is applied at \(\pmb \theta =\pmb 0\), but we apply it to \(\pmb \theta =\hat{\pmb \theta }\;{ \in \text {int}({\varTheta })}\).

Theorem 1

[16] Let \(\hat{\pmb \theta }\in \text {int}({\varTheta })\). Suppose the following about program (1).

  1. 1.

    The functions f and \(g_i\), \(i\in \{1,\dots ,m\}\), are twice continuously differentiable in \(({\varvec{x}},\pmb \theta )\) in a neighbourhood of \(({\varvec{x}}^*(\hat{\pmb \theta }),\hat{\pmb \theta })\).

  2. 2.

    The second-order sufficiency conditions for a local minimum of (1) hold at \({\varvec{x}}^*(\hat{\pmb \theta })\), with associated Lagrange multipliers \(\varvec{u}^*(\hat{\pmb \theta })\), where \(\varvec{u}^*:\varTheta \rightarrow {\mathbb {R}}^m\).

  3. 3.

    The gradients of \(g_i\), \(i\in \{1,\dots ,m\}\), are linearly independent at \(({\varvec{x}}^*(\hat{\pmb \theta }),\hat{\pmb \theta })\).

  4. 4.

    The strict complementary slackness condition holds.

Then, for \({\pmb \theta }\) in a neighbourhood of \(\hat{\pmb \theta }\), there exist unique, once continuously differentiable vector functions \({\varvec{x}}^\dagger :\varTheta \rightarrow {\mathbb {R}}^n\), \(\varvec{u}^\dagger :\varTheta \rightarrow {\mathbb {R}}^m\) satisfying the second order sufficiency conditions for a local minimum of (1) such that \({\varvec{x}}^\dagger (\hat{\pmb \theta })={\varvec{x}}^*(\hat{\pmb \theta })\) and \(\varvec{u}^\dagger (\hat{\pmb \theta })=\varvec{u}^*(\hat{\pmb \theta })\), where \(\varvec{u}^*(\hat{\pmb \theta })\) is the dual solution corresponding to \({\varvec{x}}^*(\hat{\pmb \theta })\).

Let \({\varvec{g}}:{\mathbb {R}}^n\times \varTheta \rightarrow {\mathbb {R}}^m\) denote the vector of constraint functions \(g_i\), \(i\in \{1,\dots ,m\}\). Note that, since f and \({\varvec{g}}\) are biconvex in \({\varvec{x}}\) and \({\pmb \theta }\), \({\varvec{x}}^*({\pmb \theta })\) is not just a local minimum, but a global minimum. Treating \(\varTheta\) as the disjoint union of neighbourhoods, as in Definition 3, we assume that \({\varvec{x}}^*\) is defined piecewise as the union of \({\varvec{x}}^\dagger\) over each neighbourhood; hence \({\varvec{x}}^*\) is piecewise differentiable. Thus we may conclude that \(f^*\) is differentiable except at finitely many points, faces, and facets of polytope \(\varTheta\), those where the solution changes between partitioning subsets \(\varTheta _i\subset \varTheta\).

Observe, once more, that \({\varvec{x}}^*\), \({\bar{{\varvec{x}}}}\), and \({\varvec{x}}^\dagger\) are vector-valued functions, while \({\varvec{x}}\) and \({\varvec{x}}^i\) are vectors. Indeed, for all \({\pmb \theta }\in \varTheta\), \({\varvec{x}}^*({\pmb \theta })={\varvec{x}}\) for some \({\varvec{x}}\in {\mathbb {R}}^n\).

1.2 The approximate simplex method [4]

The authors of [4] apply the following multivariate linear interpolation to solve program (1) where f and \({\varvec{g}}\) are jointly convex. Partition polytope \(\varTheta\) into simplices, and consider each simplex in turn. After \({\varvec{x}}^*\) and \(f^*\) are linearly interpolated over a given simplex, the error quantifying the difference between \({\bar{f}}\) and \(f^*\) is computed and a point is selected with which to further partition the simplex to refine the error. Without loss of generality, consider simplex \(\varTheta \subset {\mathbb {R}}^{\kappa -1}\) and let \({\pmb \theta }\in \varTheta\). Considering \(\pmb \vartheta ^i\) to be the vertices of \(\varTheta\), \(i\in \{1,\dots ,\kappa \}\), and \({\varvec{x}}^i\in {\mathbb {R}}^n\) the corresponding solution of program (1) at \(\pmb \vartheta ^i\), we let

$$\begin{aligned}M:=\begin{bmatrix} 1 &{} 1 &{} \dots &{} 1 \\ \pmb \vartheta ^1 &{} \pmb \vartheta ^2 &{} \dots &{} \pmb \vartheta ^{\kappa }\end{bmatrix}\in {\mathbb {R}}^{\kappa \times \kappa }, \quad X:=\begin{bmatrix} {\varvec{x}}^1&{\varvec{x}}^2&\dots&{\varvec{x}}^{\kappa } \end{bmatrix}\in {\mathbb {R}}^{n\times \kappa },\end{aligned}$$
$$\begin{aligned}F:=\begin{bmatrix} f({\varvec{x}}^1,\pmb \vartheta ^1)&f({\varvec{x}}^2,\pmb \vartheta ^2)&\dots&f({\varvec{x}}^\kappa ,\pmb \vartheta ^\kappa ) \end{bmatrix}^T.\end{aligned}$$

Since \(\varTheta\) is a simplex (and thus full-dimensional), M is invertible, and therefore linear interpolations for \({\varvec{x}}^*({\pmb \theta })\) and \(f^*({\pmb \theta })\) exist and are given as follows:

$$\begin{aligned} {\bar{{\varvec{x}}}}({\pmb \theta }):=XM^{-1}\begin{bmatrix} 1 \\ {\pmb \theta } \end{bmatrix}, \quad {\bar{f}}({\pmb \theta }):= FM^{-1}\begin{bmatrix} 1 \\ {\pmb \theta } \end{bmatrix}. \end{aligned}$$
(2)

We extend the ASM proposed in [4] to support f and \({\varvec{g}}\) being biconvex in \({\varvec{x}}\) and \({\pmb \theta }\).

2 Extension to biconvexity

In extending the results of [4], care must be taken in regards to the feasibility of \({\bar{{\varvec{x}}}}\) and the calculation of the error term over each simplex, both of which take advantage of the joint convexity of f and \({\varvec{g}}\). The feasibility of \({\bar{{\varvec{x}}}}\) is ensured in Sect. 2.1, based on the properties of the constraints, \({\varvec{g}}\), while bounds on the error term are computed in 2.2, based on the properties of the objective, f.

2.1 Feasibility of the solution function

While joint convexity of \({\varvec{g}}\) guarantees feasibility of \({\bar{{\varvec{x}}}}({\pmb \theta })\) for all \({\pmb \theta }\in \varTheta\), feasibility must be reconsidered when \({\varvec{g}}\) is biconvex. We present a constraint qualification, which establishes theoretical feasibility of \({\bar{{\varvec{x}}}}({\pmb \theta })\), and a practical convergence result which is incorporated into the modified ASM in Sect. 3.1.

Constraint Qualification 1 Let \({\varvec{g}}\)be biconvex, and let \({\pmb \theta }\in \varTheta\)and \(\pmb \vartheta ^k\)denote the vertices of polyhedron \(\varTheta\), \(k\in \{1,\dots , \kappa \}\) , where \(\kappa\)is the number of vertices of \(\varTheta\).The approximate solution \({\bar{{\varvec{x}}}}({\pmb \theta })\)is feasible to (1) at \({\pmb \theta }\) if, for all \(i\in \{1,\dots ,m\}\),

$$\begin{aligned}\sum _{k\ne \ell =1}^\kappa \lambda _k\lambda _\ell g_i({\varvec{x}}^k,\pmb \vartheta ^\ell )\le -\sum _{k=1}^\kappa {\lambda _k}^2g_i({\varvec{x}}^k,\pmb \vartheta ^k).\end{aligned}$$

Proof

Consider constraint \(g_i\), with \(i\in \{1,\dots ,m\}\). Let

$$\begin{aligned}\sum _{k\ne \ell =1}^\kappa \lambda _k\lambda _\ell g_i({\varvec{x}}^k,\pmb \vartheta ^\ell )\le -\sum _{k=1}^\kappa {\lambda _k}^2g_i({\varvec{x}}^k,\pmb \vartheta ^k).\end{aligned}$$

Since \(\pmb \theta \in \varTheta\), there exist \(\lambda _k\in [0,1]\), \(k\in \{1,\dots ,\kappa \}\), such that \(\sum _{k=1}^\kappa \lambda _k=1\), with \(\pmb \theta =\sum _{k=1}^\kappa \lambda _k\pmb \vartheta ^k\). The approximate solution \({\bar{{\varvec{x}}}}(\pmb \theta )\) is feasible when \(g_i({\bar{{\varvec{x}}}}(\pmb \theta ),\pmb \theta )\le 0\). By construction of \({\bar{{\varvec{x}}}}\),

$$\begin{aligned} g_i({\bar{{\varvec{x}}}}(\pmb \theta ),\pmb \theta )&=g_i\left( \sum _{k=1}^\kappa \lambda _k{\varvec{x}}^k,\sum _{k=1}^\kappa \lambda _k\pmb \vartheta ^k\right) \\&\le \sum _{k,\ell =1}^\kappa \lambda _k\lambda _\ell g_i({\varvec{x}}^k,\pmb \vartheta ^\ell )\\&=\sum _{k\ne \ell =1}^\kappa \lambda _k\lambda _\ell g_i({\varvec{x}}^k,\pmb \vartheta ^\ell )+\sum _{k=1}^\kappa {\lambda _k}^2g_i({\varvec{x}}^k,\pmb \vartheta ^k), \end{aligned}$$

where the inequality follows because \(g_i\) is biconvex. Therefore, \({\bar{{\varvec{x}}}}(\pmb \theta )\) is feasible if the premise holds. \(\square\)

Intuitively, Constraint Qualification (CQ) 1 means that the approximation of \({\varvec{x}}^*\) will be feasible as long as the other infeasible solutions are not too infeasible at any given vertex. CQ 1 is utilized to construct a biconvex overestimator bound in Theorem 3. In practice, regardless of whether CQ 1 holds, \({\bar{{\varvec{x}}}}\) converges to \({\varvec{x}}^*\) as \(\varTheta\) is partitioned into subsimplices, as proven below in Proposition 1.

Proposition 1

Let \(\underline{\pmb \theta }\in \varTheta\), let \(\{\varTheta _i\}_i\) denote a sequence of simplices such that \(\underline{\pmb \theta }\in \varTheta _i\) for all i, \(\varTheta _i\subseteq \varTheta\) for all i, and \(\varTheta _i\subset \varTheta _{i-1}\) for all \(i>1\), let \({\bar{{\varvec{x}}}}^i\) be the linear interpolant of \({\varvec{x}}^*\) over \(\varTheta _i\), \({\bar{{\varvec{x}}}}^i:\varTheta _i\rightarrow {\mathbb {R}}^n\). If the vertices of \(\varTheta _i\) converge to \(\underline{\pmb \theta }\) as \(i\rightarrow \infty\), then \({\bar{{\varvec{x}}}}^i(\underline{\pmb \theta })\) converges to \({\varvec{x}}^*(\underline{\pmb \theta })\).

Proof

Let \(\pmb \vartheta ^{ij}\) denote the jth vertex of simplex \(\varTheta _i\); as \(i\rightarrow \infty\), \(\pmb \vartheta ^{ij}\) converges to \(\underline{\pmb \theta }\) for all \(j\in \{1,\dots ,\kappa \}\). By Theorem 1, \({\varvec{x}}^*:\varTheta \rightarrow {\mathbb {R}}^n\) is continuous on \(\varTheta _i\), so, as \(i\rightarrow \infty\), \({\varvec{x}}^*(\pmb \vartheta ^{ij})\rightarrow {\varvec{x}}^*(\underline{{\pmb \theta }})\). By construction of \({\bar{{\varvec{x}}}}^i:{\mathbb {R}}^\kappa \rightarrow {\mathbb {R}}^n\), \({\bar{{\varvec{x}}}}^i(\pmb \vartheta ^{ij})={\varvec{x}}^*(\pmb \vartheta ^{ij})\) for all \(\pmb \vartheta ^{ij}\) and, for each i, \({\bar{{\varvec{x}}}}^i(\underline{\pmb \theta })\) is a convex combination of \({\varvec{x}}^*(\pmb \vartheta ^{ij})\) for all \(j\in \{1,\dots ,\kappa \}\). Hence \({\bar{{\varvec{x}}}}^i(\underline{\pmb \theta })\rightarrow {\varvec{x}}^*(\underline{\pmb \theta })\) as \(i\rightarrow \infty\). \(\square\)

As a result of Proposition 1, the interpolant \({\bar{{\varvec{x}}}}\) will approach feasibility as we partition \(\varTheta\) into smaller simplices.

2.2 Error bound computation

Consider the furthest distance between the true solution function, \(f^*\), and the linear interpolant, \({\bar{f}}\), over \(\varTheta\), that is, consider

$$\begin{aligned} ||f^*-{\bar{f}}||_\infty =\max _{\pmb \theta \in \varTheta }\{|{\bar{f}}(\pmb \theta )-f^*(\pmb \theta )|\}. \end{aligned}$$
(3)

The authors of [4] use the joint convexity of f and \({\varvec{g}}\) to simplify (3) to allow for an error calculation of the next point \(\pmb \theta ^{err}\) at which to split \(\varTheta\) into smaller simplices; they then apply the interpolation process to the resulting simplices and continue the process until the desired tolerance is reached. We need to compute \(\pmb \theta ^{err}\) differently when f and \({\varvec{g}}\) are biconvex. Except for [31], error bounds in relevant interpolation theory involve lower bounds for the error term as demonstrated in [8]. As such we propose two methods of obtaining an upper bound to yield a desired tolerance level—first a method based on the longest edge of the current simplex, followed by a method based on the biconvex overestimator from Definition 2. We compare the two methods in Sect. 3.2.

Let \(R\in {\mathbb {R}}\) and \(\pmb \theta _c\in {\mathbb {R}}^{\kappa -1}\) be the radius and center of the hypersphere circumscribing \(\varTheta\) and define \(H(f^*): \varTheta \rightarrow {\mathbb {R}}^{\kappa -1}\times {\mathbb {R}}^{\kappa -1}\) as the Hessian of \(f^*\), made of piecewise second derivatives, with \(|H(f^*)|\) being the spectral radius of the same.

2.2.1 Longest edge method

Begin by considering linear interpolation errors. When \(\kappa =1\), the error bound on a simplex (interval) \(\varTheta =[a,b]\) can be computed to be

$$\begin{aligned}\dfrac{h^2}{8}\max _{a\le \xi \le b}\Big |\dfrac{d^2f^*}{d\theta ^2}(\xi )\Big |,\end{aligned}$$

where \(h:=\max _{1\le i\le r}(t_i-t_{i-1})\) is the length of the longest subinterval \([t_{i-1},t_i]\subset [a,b]\); see [3], for example. This bound is extended to \(\kappa >2\) for twice differentiable functions in [33] and simplified in [31].

Theorem 2

Let \(f^*:{\mathbb {R}}^{\kappa -1}\rightarrow {\mathbb {R}}\) be twice differentiable and let \(\varTheta \subseteq {\mathbb {R}}^{\kappa -1}\) be a polyhedron with vertices \(\pmb \vartheta _i\), \(i\in \{1,\dots ,\kappa \}\). Suppose that \({\bar{f}}\) is a linear interpolant of \(f^*\) using points \(\pmb \vartheta _i\), \(i\in \{1,\dots ,\kappa \}\). Then, for each \(\pmb \theta \in \varTheta\), there exists the sharp inequality

$$\begin{aligned} |f^*(\pmb \theta )-{\bar{f}}(\pmb \theta )|&\le \dfrac{1}{2}(R^2-||\pmb \theta -\pmb \theta _c||_2^2)\Big |\Big | |H(f^*)| \Big |\Big |_{\infty }. \end{aligned}$$
(4)

Further, there exists the uniform bound

$$\begin{aligned} ||f^*-{\bar{f}}||_\infty&\le \dfrac{1}{2}(R^2-\min _{\pmb \theta \in \varTheta }\{||\pmb \theta -\pmb \theta _c||_2^2\})\Big |\Big | |H(f^*)| \Big |\Big |_{\infty }. \end{aligned}$$
(5)

These bounds correlate to the lengths of the simplex \(\varTheta\): Theorem 4.1 (v) in [31, p. 84] establishes that (5) simplifies to

$$\begin{aligned} ||f^* -{\bar{f}}||_\infty&\le \dfrac{\ell ^2}{8}\Big |\Big | |H(f^*)| \Big |\Big |_{\infty }, \end{aligned}$$
(6)

where \(\ell\) is the length of the longest edge.

Notice that (4) and (5) in [33] and (6) in [31] require twice continuous differentiability of the function being interpolated; however, \(f^*\) is only piecewise differentiable over \(\varTheta\). To account for this, we additionally assume that \(f^*\) is piecewise twice differentiable, and that \(\varTheta\) in program (1) is partitioned into simplices over which \(f^*\) is twice differentiable.

To use (6) to partition \(\varTheta\), assume that \(\Big |\Big | |H(f^*)| \Big |\Big |_{\infty }\) is bounded by a finite number, M. Therefore interpolating \(f^*\) accurately and decreasing the right-hand side of (3) requires decrease of \(\ell\). We then partition \(\varTheta\) in such a way that \(\ell ^2\) is minimized. To achieve an error tolerance of \(\epsilon ^{tol}\), we require that \(\ell _i\le \sqrt{\frac{8\epsilon ^{tol}}{M}}\), where \(\ell _i\) is the length of the longest edge of subsimplex \(\varTheta _i\subseteq \varTheta\). We explore two ways to do this.

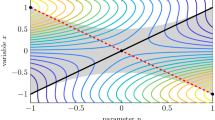
Suppose that we split \(\varTheta\) at the center every iteration, as in Fig. 1a. Note that \(\ell _i\) is constant if we consider \(\varTheta _i\) to always be the leftmost triangle, and \(\varTheta _i\) becomes ‘squatter’ as we continue splitting. However, this split method can be effective if the derivative of \(f^*\) is small along the longest edge of \(\varTheta _i\), as demonstrated for \({\mathbb {R}}^2\) in [30].

To guarantee convergence of the right-hand side of (6), we choose, instead, to split \(\varTheta\) by putting a hyperplane through the midpoint of the longest edge and all points not incident with said edge. This way, \(\ell\) always decreases, as demonstrated in Fig. 1b. Indeed, for some \(t\in {\mathbb {N}}\), halving the longest side of the simplex is guaranteed to quarter the error of the interpolation every t iterations. We refer to this method of partitioning \(\varTheta\) as the Longest Edge Method (LEM). Note that, in Fig. 1, we choose to only split the left side of the triangles to demonstrate the method clearly.

Fig. 1
figure 1

A comparison of two simple methods for partitioning a simplex into smaller simplices; a does not guarantee error reduction in (6), while b does

Full size image

2.2.2 Biconvex overestimator method

Note that (6) fails to utilize the structure of program (1). To exploit the properties of program (1), through Theorem 3, we prove that \(||f^*-{\bar{f}}||_\infty\) is bounded above when f is biconvex in \(({\varvec{x}},\pmb \theta )\), while, when f is jointly convex in \(({\varvec{x}},\pmb \theta )\), the error bound in [4] applies. We begin with the biconvex case.

Theorem 3

Over simplex \(\varTheta\), the error in (3) is bounded above as follows:

$$\begin{aligned}||f^*-{\bar{f}}||_\infty \le \epsilon , \end{aligned}$$

where

$$\begin{aligned} \epsilon&:=\max \left\{ \max _{\pmb \theta \in \varTheta }\{{\bar{f}}(\pmb \theta )-f^*(\pmb \theta )\},\;w^{err}\right\} , \end{aligned}$$
(7)

and

$$\begin{aligned} w^{err}&:=\max _{\lambda \in [0,1]^\kappa ,\pmb \theta \in \varTheta }\left\{ \sum _{i,j=1}^\kappa \lambda _i\lambda _jf({\varvec{x}}^i,\pmb \theta ^j)-{{\bar{f}}}(\pmb \theta )\Big | \pmb \theta =\sum _{i=1}^\kappa \lambda _i\pmb \theta _i\right\} . \end{aligned}$$
(8)

Proof

The absolute value in (3) yields the following:

$$\begin{aligned} \max _{\pmb \theta \in \varTheta }\{|{\bar{f}}(\pmb \theta )-f^*(\pmb \theta )|\}&=\max \left\{ \max _{\pmb \theta \in \varTheta }\{{\bar{f}}(\pmb \theta )-f^*(\pmb \theta )\},\;\max _{\pmb \theta \in \varTheta }\{f^*(\pmb \theta )-{\bar{f}}(\pmb \theta )\}\right\} . \end{aligned}$$

Consider each piece of the maximization separately.

Applying the definition of \(f^*\) yields

$$\begin{aligned} \max _{\pmb \theta \in \varTheta }\{{\bar{f}}(\pmb \theta )-f^*(\pmb \theta )\}&=\max _{\pmb \theta \in \varTheta }\{{\bar{f}}(\pmb \theta )-\min _{{\varvec{x}}\in {\mathcal {X}}(\varTheta )}\{f({\varvec{x}},\pmb \theta )\}\}\nonumber \\ \quad&=\max _{\pmb \theta \in \varTheta }\{{\bar{f}}(\pmb \theta )+\max _{{\varvec{x}}\in {\mathcal {X}}(\varTheta )}\{-f({\varvec{x}},\pmb \theta )\}\}\nonumber \\ \quad&=\max _{{\varvec{x}}\in {\mathcal {X}}(\varTheta ),\;\pmb \theta \in \varTheta }\{{\bar{f}}(\pmb \theta )-f({\varvec{x}},\pmb \theta )\}, \end{aligned}$$
(9)

which is the first part of (7). Note that (9) is a biconvex program and therefore can be solved using the methods in [19] or [25]. Now consider \(\max _{\pmb \theta \in \varTheta }\{f^*(\pmb \theta )-{\bar{f}}(\pmb \theta )\}\): the following reformulation,

$$\begin{aligned} \max _{\pmb \theta \in \varTheta }\{f^*(\pmb \theta )-{\bar{f}}(\pmb \theta )\}&=\max _{\pmb \theta \in \varTheta }\{\min _{{\varvec{x}}\in {\mathcal {X}}(\varTheta )}\{f({\varvec{x}},\pmb \theta )-{\bar{f}}(\pmb \theta )\}\} \\&=\max _{\pmb \theta \in \varTheta }\{-\max _{{\varvec{x}}\in {\mathcal {X}}(\varTheta )}\{f({\varvec{x}},\pmb \theta )\}-{\bar{f}}(\pmb \theta )\}, \end{aligned}$$

does not result in a solvable program, so we construct an overestimator of \(f^*(\pmb \theta )\) using the biconvexity of f.

We follow [23] where it is proven that, if f and \({\varvec{g}}\) are jointly convex in \(({\varvec{x}},\pmb \theta )\), then \(f^*:\varTheta \rightarrow {\mathbb {R}}\) in (1) is convex (and continuous) in \(\pmb \theta\). Continuity of \(f^*\) is guaranteed by [7], but the process from [23] fails to provide convexity of \(f^*\) in \(\pmb \theta\) when f and \({\varvec{g}}\) are biconvex. However, this process yields an upper bound of (3). Consider, first, arbitrary \(\pmb \theta ^1, \pmb \theta ^2\in \varTheta\) and feasible \({\varvec{x}}^1,{\varvec{x}}^2\in {\mathcal {X}}(\varTheta )\) such that \(f^*(\pmb \theta ^1)=f({\varvec{x}}^1,\pmb \theta ^1)\) and \(f^*(\pmb \theta ^2)=f({\varvec{x}}^2,\pmb \theta ^2)\). Define \(\lambda \in [0,1]\) such that

$$\begin{aligned}\tilde{\pmb \theta }=\lambda \pmb \theta ^1+(1-\lambda )\pmb \theta ^2, \text { and } {\tilde{{\varvec{x}}}}=\lambda {\varvec{x}}^1+(1-\lambda ){\varvec{x}}^2.\end{aligned}$$

If CQ 1 holds, then \({\tilde{{\varvec{x}}}}\) is feasible, which implies

$$\begin{aligned} f^*(\tilde{\pmb \theta })&=\min _{{\varvec{x}}\in {\mathcal {X}}(\tilde{\pmb \theta })}f({\varvec{x}},\tilde{\pmb \theta })\le f({{\tilde{{\varvec{x}}}}},\tilde{\pmb \theta }) \end{aligned}$$

Apply Definition 2 to obtain

$$\begin{aligned} f({\tilde{{\varvec{x}}}},\tilde{\pmb \theta })&\le \lambda ^2f({\varvec{x}}^1,\pmb \theta ^1)+\lambda (1-\lambda )[f({\varvec{x}}^1,\pmb \theta ^2)+f({\varvec{x}}^2,\pmb \theta ^1)]+(1-\lambda )^2f({\varvec{x}}^2,\pmb \theta ^2). \end{aligned}$$

Extending from using two points \(\pmb \theta ^1\) and \(\pmb \theta ^2\) to using every vertex of \(\varTheta\), consider \(\pmb \vartheta ^i\), \(i\in \{1,\dots ,\kappa \}\), as the ith vertex of simplex \(\varTheta\). Since \({\varvec{x}}^i\) is an optimal solution to program (1) at \(\pmb \vartheta ^i\), then, for all \(\pmb \theta \in \varTheta\) such that \(\pmb \theta =\sum _{i=1}^\kappa \lambda _i\pmb \vartheta ^i\), \(\lambda _i\ge 0\), \(\sum _{i=1}^\kappa \lambda _i=1\), we have

$$\begin{aligned} f^*(\pmb \theta )\le \sum _{i,j=1}^\kappa \lambda _i\lambda _jf({\varvec{x}}^i,\pmb \vartheta ^j), \end{aligned}$$
(10)

where the right-hand side is the biconvex overestimator from Definition 2. Therefore, we can bound the error program by another program as below:

$$\begin{aligned} \max _{\pmb \theta \in \varTheta }\{f^*(\pmb \theta )-{\bar{f}}(\pmb \theta )\}&\le \max _{\lambda ,\pmb \theta }\left\{ \sum _{i,j=1}^\kappa \lambda _i\lambda _jf({\varvec{x}}^i,\pmb \vartheta ^j)-{{\bar{f}}}(\pmb \theta )\Big | \pmb \theta =\sum _{i=1}^\kappa \lambda _i\pmb \vartheta ^i\right\} =:w^{err}, \end{aligned}$$

which completes the proof. \(\square\)

To compute \(\epsilon\) in (7), note that \({\bar{f}}(\pmb \theta )\) is affine in \(\pmb \theta\), and \(f({\varvec{x}},\pmb \theta )\) is biconvex in \({\varvec{x}}\) and \(\pmb \theta\). Therefore, program (9) is a biconcave maximization so can be solved by the methods presented in [19], if global optimality is desired, or in [25], if partial optimality is sufficient (for details, see [20]). Similarly, \(w^{err}\) in (8) can be computed in the following manner.

Since \({\bar{f}}\) is a linear interpolant as defined in (2), we can write \({\bar{f}}(\pmb \theta ):=a^T\pmb \theta +b\), so substituting \(\pmb \theta =\sum _{i=1}^\kappa \lambda _i\pmb \vartheta ^i\) into \({\bar{f}}(\pmb \theta )\) yields

$$\begin{aligned}{\bar{f}}(\pmb \theta )=a^T\pmb \theta +b=a^T\sum _{i=1}^\kappa \lambda _i\pmb \vartheta ^i+b=\sum \lambda _ia^T\pmb \vartheta ^i+b.\end{aligned}$$

Then, in (8), we really maximize

$$\begin{aligned} w(\lambda ):=\sum _{i,j=1}^\kappa \lambda _i\lambda _jf({\varvec{x}}^i,\pmb \vartheta ^j)-\sum \lambda _ia^T\pmb \vartheta ^i-b. \end{aligned}$$
(11)

That is, we solve

$$\begin{aligned} w^{err}=\max _{\lambda \in [0,1]^\kappa }\;&w(\lambda )\nonumber \\ \text {s.t. }&\sum _{i=1}^\kappa \lambda _i=1. \end{aligned}$$
(12)

This is a bilinear program, so can, like (9), be solved using the methods in [19] or [25]. We take

$$\begin{aligned}\pmb \theta ^{err}:=\sum _{i=1}^\kappa \lambda ^{err}_i\pmb \vartheta ^i,\end{aligned}$$

where \(\lambda ^{err}\) optimizes (8).

As an aside, note that the solution of program (12) occurs at a point where, for all \(i\in \{1,\dots ,\kappa \}\),

$$\begin{aligned} 0&=\dfrac{d\;w}{d\lambda _i}=\sum _{j=1}^m\lambda _j[f({\varvec{x}}^i,\pmb \vartheta ^j)+f({\varvec{x}}^j,\pmb \vartheta ^i)]-a^T\pmb \vartheta ^i,\\ 1&=\sum _{j=1}^m\lambda _j. \end{aligned}$$

This system of linear equations can be rewritten to involve a symmetric matrix, K:

$$\begin{aligned}K\begin{bmatrix}\lambda _1\\ \vdots \\ \lambda _\kappa \end{bmatrix}=\begin{bmatrix} a^T\pmb \vartheta ^1 \\ \vdots \\ a^T\pmb \vartheta ^\kappa \end{bmatrix},\end{aligned}$$

where the ijth element of matrix K is defined as

$$\begin{aligned}K_{ij}:= f({\varvec{x}}^i,\pmb \vartheta ^j)+f({\varvec{x}}^j,\pmb \vartheta ^i).\end{aligned}$$

It has been shown that matrices of the form of K are almost surely nonsingular [10]; that is, sampling from a random distribution of matrices of the form K will yield, with probability approaching 1, a nonsingular matrix.

An example of how the overestimator, \(f^*\), and interpolant, \({{\bar{f}}}\), relate appears in Fig. 2.

Fig. 2
figure 2

The overestimator is on top, \({\bar{f}}\) is the line on bottom, and the dots denote a discretization of \(f^*\) in between

Full size image

To properly implement the use of (7) to compute error bounds on \({\bar{f}}\) in the Biconvex Overestimator Method (BOM), we show that \(w^{err}\) in (12) converges to 0. Given this convergence, we use \(\pmb \theta ^{err}\) as a new vertex to partition \(\varTheta\) into smaller simplices.

Proposition 2

Let \(\underline{\pmb \theta }\in \varTheta\). If the vertices of \(\varTheta\) converge to \(\underline{\pmb \theta }\), then the biconvex overestimator in (10) of \(f^*(\pmb \theta )\) converges pointwise to \(f^*(\pmb \theta )\).

Proof

Let \(\{\varTheta _i\}_i\) denote a sequence of simplices such that \(\underline{\pmb \theta }\in \varTheta _i\) for all i, \(\varTheta _i\subseteq \varTheta\) for all i, and \(\varTheta _i\subset \varTheta _{i-1}\) for all \(i>1\). Let \(\pmb \vartheta ^{ij}\) denote the jth vertex of simplex \(\varTheta _i\). Note that as \(i\rightarrow \infty\), \(\pmb \vartheta ^{ij}\) converges to \(\underline{\pmb \theta }\) for all \(j\in \{1,\dots ,\kappa \}\). Similarly, let \({\varvec{x}}^{ij}\) denote an optimal solution to (1) at \(\pmb \vartheta ^{ij}\). Recall from [16] that \({\varvec{x}}^*:\varTheta \rightarrow {\mathbb {R}}^n\) is continuous, so, as \(i\rightarrow \infty\), \({\varvec{x}}^{ij}={\varvec{x}}^*(\pmb \vartheta ^{ij})\rightarrow {\varvec{x}}^*(\underline{\pmb \theta })=:{{\underline{{\varvec{x}}}}}\), where \({{\underline{{\varvec{x}}}}}\) is an optimal solution to (1) at \(\underline{\pmb \theta }\). Consequently, because f is biconvex, and biconvex functions are continuous, we have the following, where \(\lambda _k\in [0,1]\), \(\sum _{k=1}^\kappa \lambda _k=1\):

$$\begin{aligned}f^*(\underline{\pmb \theta })\le \sum _{h,k=1}^\kappa \lambda _h\lambda _k f({\varvec{x}}^{ih},\pmb \vartheta ^{ik}) \rightarrow \sum _{h,k=1}^\kappa \lambda _h\lambda _k f({\underline{{\varvec{x}}}},\underline{\pmb \theta })= f({\underline{{\varvec{x}}}},\underline{\pmb \theta }) \sum _{h,k=1}^\kappa \lambda _h\lambda _k=f({\underline{{\varvec{x}}}},\underline{\pmb \theta })=f^*(\underline{\pmb \theta }).\end{aligned}$$

\(\square\)

Now consider the case where \(f:{\mathbb {R}}^n\times \varTheta \rightarrow {\mathbb {R}}\) is independent of \(\pmb \theta\), that is, f is jointly convex in \(({\varvec{x}},\pmb \theta )\). Then, for all \({\varvec{x}}\in {\mathbb {R}}^n\), \(f({\varvec{x}},\pmb \theta ^1)=f({\varvec{x}},\pmb \theta ^2)\) for all \(\pmb \theta ^1, \pmb \theta ^2\in \varTheta\), that is, there exists some function \(h:{\mathbb {R}}^n\rightarrow \varTheta\) such that \(f({\varvec{x}},\pmb \theta )=h({\varvec{x}})\). Then, considering \(\lambda\) defined in (8), the following occurs:

$$\begin{aligned} \sum _{i,j}\lambda _i\lambda _j f({\varvec{x}}^i,\pmb \vartheta ^j)&= \sum _{i,j}\lambda _i\lambda _j h({\varvec{x}}^i)\\&= \sum _i\lambda _i h({\varvec{x}}^i) \sum _j\lambda _j \\&= \sum _i\lambda _i h({\varvec{x}}^i). \end{aligned}$$

Consequently, (11) becomes

$$\begin{aligned}w(\lambda )=\sum _i\lambda _i h({\varvec{x}}^i)-\sum \lambda _ia^T\pmb \vartheta ^i-b,\end{aligned}$$

so program (12) is a linear program when f is jointly convex in \(({\varvec{x}},\pmb \theta )\). Therefore the solution thereof will be a vertex of the standard simplex, that is, \(\lambda _i=1\) for some \(i\in \{1,\dots ,\kappa \}\) and \(\lambda _j=0\) for all \(j\ne i\).

Following Theorem 3 in this case will then result in choosing \(\pmb \theta ^{err}\) to be a vertex, which does not allow for a full-dimensional partitioning of \(\varTheta\). However, f is jointly convex in \(({\varvec{x}},\pmb \theta )\); consequently, as in [4], \({\bar{f}}(\pmb \theta )\ge f^*(\pmb \theta )\), so (9) is guaranteed to bound (3).

2.2.3 Improved convergence of overestimator method

The partitioning of \(\varTheta\) based on \(\epsilon\) in (7) is grounded in adaptive mesh theory, which can be found in [24, 26], and elaborated on in [8]. This theory applies to the estimation of solutions to partial differential equations (PDEs) and, more generally, problems of variation; for more details, see [8], specifically Chapter 9.

Integral to solving PDEs is the Lax-Milgram Theorem, posited here, which guarantees the existence of a unique solution to a variational problem.

Theorem 4

(Lax-Milgram Theorem [8]) Given a Hilbert space V with corresponding inner-product, a continuous, coercive bilinear form \(a:V\times V\rightarrow {\mathbb {R}}\), and a continuous linear functional \(F\in V'\), dual to V, there exists a unique \(u\in V\) such that \(a(u,v)=F(v)\) for all \(v\in V\).

We observe two items of note. First, the dual of a Hilbert space just contains bounded continuous linear functionals defined over said Hilbert Space. Second, in computing error bounds, [8] uses the \(L^2\)-norm; however, we use the \(L^\infty\)-norm; as such, we present the equivalence of the norms.

Proposition 3

Let \(f:{\mathbb {R}}^n\rightarrow {\mathbb {R}}\) be bounded and be such that \(f^2\) is integrable. Then the \(L^2\)-norm and \(L^\infty\)-norm are equivalent. That is, there exist constants \(c,C\in {\mathbb {R}}\) such that

$$\begin{aligned}c||f||_2 \le ||f||_\infty \le C||f||_2.\end{aligned}$$

Proof

Note that \(||f||_2,||f||_\infty <\infty\). The result follows by proper scaling with c and C. \(\square\)

An in-depth look at the equivalence of error bounds across the \(L^2\) and \(L^\infty\) norms can be found in Chapter 8 of [8].

In demonstrating the effectiveness of adaptive meshes, the PDEs in [24, 26] both have upper bounds, but have stronger boundary conditions than [8], which only has a lower bound to the actual error, as [8] provides theory for more general problems of variation fulfilling the more general Theorem 4. The fact that (7) is an actual upper bound is essential. Using this upper bound, we only partition simplex \(\varTheta\) into new subsimplices if \(\epsilon\) from (7) is greater than some previously chosen error tolerance. The resulting partition of \(\varTheta\) is the very definition of an adaptive mesh.

To use the Lax-Milgram Theorem, and, in turn, the results on adaptive meshes, we need \(f^*:{\mathbb {R}}^\kappa \rightarrow {\mathbb {R}}\) to be piece-wise differentiable, as stated in [8, p. 28-29].

Proposition 4

The optimal value function \(f^*\) of program (1) is piecewise differentiable.

Proof

Consider \(\pmb \theta \in \text {int}({\varTheta })\). Since \({\varvec{x}}^*\) is piecewise differentiable by Theorem 1, and f is assumed to be (twice) differentiable, the following holds by application of the generalized chain rule:

$$\begin{aligned}\nabla _{\pmb \theta } f({\varvec{x}}^*(\pmb \theta ),\pmb \theta )=J_{\pmb \theta }({\varvec{x}}^*,\pmb \theta )^T\nabla _{({\varvec{x}}^*,\pmb \theta )}f,\end{aligned}$$

where \(J_{\pmb \theta }({\varvec{x}}^*,\pmb \theta )\) is the Jacobian of \({\varvec{x}}^*\) and \(\pmb \theta\) with respect to \(\pmb \theta\), and \(\nabla _{({\varvec{x}}^*,\pmb \theta )}f\) is the vector of partial derivatives of f when treating \({\varvec{x}}^*\) and \(\pmb \theta\) as variables, not functions. By definition, \(f^*(\pmb \theta )=f({\varvec{x}}^*(\pmb \theta ),\pmb \theta )\) for every \(\pmb \theta \in \varTheta\), so \(f^*\) is piecewise differentiable. \(\square\)

Since \(f^*\) is piecewise differentiable, we can apply the Lax-Milgram Theorem 4 to solving program (1) in the following manner. Let V be the set of all piecewise differentiable functions fulfilling the boundary conditions for \(f^*\), that is, that \(\nabla v(\bar{\pmb \theta })=\nabla f^*(\bar{\pmb \theta })\) for all \(\bar{\pmb \theta }\in \partial \varTheta\) where \(\partial \varTheta\) is the boundary of \(\varTheta\). That V is a Hilbert space with respect to the standard inner product can be seen through the continuity of derivatives. Then, by letting \(a(f^*,v):=\int _{\varTheta }\alpha (\pmb \theta )\nabla f^*(\pmb \theta ) \cdot \nabla v(\pmb \theta )\;d\pmb \theta\), while \(F(v):=\int _{\varTheta } \tau (\pmb \theta )v(\pmb \theta )\; d\pmb \theta\), the Lax-Milgram Theorem yields that \(f^*\) is the solution to an unspecified but existent variational problem of the form

$$\begin{aligned} \int _{\varTheta }\alpha (\pmb \theta )\nabla f^*(\pmb \theta ) \cdot \nabla v(\pmb \theta )\;d\pmb \theta =\int _{\varTheta } \tau (\pmb \theta )v(\pmb \theta )&\; d\pmb \theta \text { for all } v\in V, \end{aligned}$$
(13)

where \(\alpha :\varTheta \rightarrow {\mathbb {R}}\) is bounded over \(\varTheta\), and \(\tau \in L^2(\varTheta )\). Recall that \(\nabla f^*\) is the gradient of \(f^*\), while \(\cdot\) denotes the standard dot product.

2.2.4 Method comparison

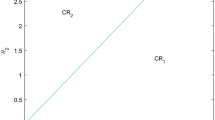
Using the BOM to select the new vertex \(\pmb \theta ^{err}\) is resource intensive as it requires the solving of two biconvex optimization programs; as a result, we justify its use over the LEM derived from [31]. Notice that, in order to guarantee convergence of \({\bar{f}}\), the LEM first requires M, an upper bound on the norm of the unknown Hessian of \(f^*\). It next has to break \(\varTheta\) into simplices all with edges shorter than \(\sqrt{\frac{8\epsilon ^{tol}}{M}}\), where \(\epsilon ^{tol}\) is the acceptable tolerance. Taking \(\epsilon ^{tol}=0.01\), Fig. 3 provides lengths of \(\ell\) based on different bounds M.

Fig. 3
figure 3

Computation of \(\ell\) on the y-axis based on values of M on the x-axis for \(\epsilon ^{tol}=0.01\)

Full size image

To the contrary, the BOM does not require the assumption that \(f^*\) be piecewise twice differentiable, nor does it require bounding of the Hessian of \(f^*\). Also, since computing \(f^*\) is equivalent to solving a variational problem, adaptive mesh theory can be applied, guaranteeing an improved convergence rate over the LEM. Finally, the BOM adds extra simplices only where the error bound, \(\epsilon\), is outside the tolerance, that is, where \(\epsilon >\epsilon ^{tol}\); as borne out by the examples, this saves substantially on memory space, which is crucial as the dimension of \(\varTheta\) grows.

3 Algorithm and examples

Having established two possible termination conditions, we now provide an algorithm for estimating \(f^*\), which we refer to as the multiparametric Biconvex Approximate Simplex Method (BASM). Aside from different error computations, the BASM is analogous to the ASM found in [4]. Given polytope \(\varTheta\) as the parameter space, we partition it into a set of simplices. For each simplex, \(\varTheta _t\), we solve program (1) at each of the simplices and construct interpolants \({\bar{f}}_t\) and \({\bar{{\varvec{x}}}}^t\). We then apply the chosen refinement method (LEM or BOM) and repeat until the desired error tolerance has been reached.

Worth noting is the fact that, although we terminate the algorithm based on properties of \({\bar{f}}\), the proof of Theorem 3 demonstrates that \(f({\bar{{\varvec{x}}}}(\pmb \theta ),\pmb \theta )\) will also be rendered accurate by the splitting of \(\varTheta\) at \(\pmb \theta ^{err}\). Also worth recalling is that Proposition 1 demonstrates that \({\bar{{\varvec{x}}}}\) approaches feasibility as we split \(\varTheta\) into subsequent simplices. Therefore Algorithm 1 solves program (1) to yield approximations to both solution functions and value functions.

3.1 Algorithm

To solve program (1) when f and \({\varvec{g}}\) are biconvex, begin in Step 0 of Algorithm 1 by selecting an acceptable error bound \(\epsilon ^{tol}>0\) and partitioning polytope \(\varTheta\) into a disjoint set of simplices \(\varTheta _t\), \(t\in \{1,\dots , s\}\), where s is the number of simplices. Let each \(\varTheta _t\) have vertices \(\{\pmb \vartheta ^{t1}, \dots , \pmb \vartheta ^{t\kappa }\}\). At each \(t\in {\mathbb {N}}\), that is, in Step t, compute the solution vectors \({\varvec{x}}^k(\pmb \vartheta ^k)\) and objective values \(f({\varvec{x}}^k(\pmb \vartheta ^{tk}),\pmb \vartheta ^{tk})\) for each \(k\in \{1,\dots ,\kappa \}\).

If using the LEM, partition \(\varTheta _t\) into two new simplices, which share \(\pmb \theta ^{err}\), the midpoint of the longest edge of \(\varTheta _t\), as their new vertices. These new subsimplices replace \(\varTheta _t\) in the set of simplices under consideration; repeat until the right-hand side in (6) is below \(\epsilon ^{tol}\) for every \(t\in \{1,\dots ,s\}\). Recall that the LEM has to assume the existence of some number \(M>0\) bounding the Hessian of \(f^*\).

If using the BOM, compute \(\pmb \theta ^{err}\) as the maximizer of \(\epsilon\) in (7) over \(\varTheta _t\), and partition \(\varTheta _t\) into \(\kappa\) new simplices having \(\pmb \theta ^{err}\) as a new vertex. As in the LEM, the new simplices replace \(\varTheta _t\) in the set of simplices. To envision this, consider \(\varTheta _1\) with vertices \(\{\pmb \vartheta ^1, \pmb \vartheta ^2, \dots , \pmb \vartheta ^\kappa \}\), then there would be new simplices with vertices \(\{\pmb \theta ^{err}, \pmb \vartheta ^2, \dots , \pmb \vartheta ^\kappa \}\), \(\{\pmb \vartheta ^1, \pmb \theta ^{err}, \dots , \pmb \vartheta ^\kappa \}\), \(\dots\), \(\{\pmb \vartheta ^1, \pmb \vartheta ^2, \dots , \pmb \theta ^{err}\}\).

Note that, in order to compute \(\pmb \theta ^{err}\), we must solve biconvex programs (9) and (12). As mentioned before, this can be done using work found in [19, 25], but, for the sake of convenience, we choose to do so using the fmincon function in MATLAB.

We apply Algorithm 1 to numeric examples using the LEM first, followed by the BOM, and compare the results.

figure a

3.2 Examples

All instances are run on a Dell Inspiron 3153 with a 128 GB SSD (6 GB free), 8 GB RAM, running an Intel Core i3-6100U 2.30 GHz processor with two cores and four logical processors running Windows 10 Enterprise. Two MATLAB functions are utilized: randn randomly generates the coefficient matrices and vectors using a standard normal distribution, and fmincon performs the minimizations at the corresponding steps of Algorithm 1 using the SQP method with the default number of iterations. Multi-Parametric Toolbox (MPT) [21] is utilized to construct the simplices. Prior to continuing, a word must be said on our chosen subroutine: fmincon is a black-box algorithm provided by MATLAB to optimize functions, convex or nonconvex, subject to linear and nonlinear constraints, and therefore may return infeasible solutions, with the purpose being to allow the operator to adjust the inputs and try again; as a result, more complicated instances cause fmincon to get stuck at infeasible points or spend too much time processing.

To construct the examples, we follow a method similar to that provided in [22], which was extended from [11]. However, since the generation of a biconvex function is simpler than the generation of a jointly convex function, we only need to add the parameters to the matrices prior to making them positive semi-definite. We choose problem sizes comparable to those chosen in [22]. We let \(\varTheta =[0.1,1.1]^{\kappa -1}\), where \(\kappa \in \{2,3,4\}\). Recall that \(\kappa\) is the number of vertices in a simplex, so \(\kappa -1\) is the number of parameters. We choose not to use interval [0, 1] to avoid disappearance of terms at \(\pmb \theta =\pmb 0\); furthermore, we consider the number of variables \(n=5\) for \(\kappa \in \{2,3\}\), and take \(n=3\) for \(\kappa =4\), due to the aforementioned shortcomings of fmincon; finally, we consider Hessian bound \(M=30\) for the LEM.

Table 1 contains the the time, in seconds, total number of subsimplices, and approximation error, averaged over the number of simplices per instance, as well as the mean, median, and standard deviations thereof, for a set of ten parametric quadratically constrained quadratic programs each with one quadratic constraint and one linear constraint. The parameters in these instances are placed in unrestricted random locations, no more complicated than bilinear or quadratic in \(\pmb \theta\); that is, \(\theta _1\theta _2\) or \({\theta _1}^2\) may be present, but not \({\theta _1}^2\theta _2\). Note that the LEM’s error calculation is independent of the program being optimized and therefore has no standard deviation in the number of simplices and error. For all instances, we use an error tolerance of \(\epsilon ^{tol}=0.01\), but for three parameters, we limit the number of simplex splits for the LEM and the BOM (twelve for the LEM and ten for the BOM) to keep the number of simplices to a number manageable for the computer, which results in the higher errors in Table 1, row \(\kappa -1=3\). Notice that, even by giving the LEM the extra two splits, the mean error is four times larger than that of the BOM.

Table 1 Comparison of LEM and BOM errors, CPU times, and number of simplices with one quadratic constraint, one linear constraint, and \(\kappa -1\) parameters, at ten instances each; averages are included after each set of ten instances
Full size table

We observe that the LEM maintains consistent results over the instances, and performs faster for one parameter. However, as expected based on the theory presented in Sect. 2.2.3, the BOM outperforms the LEM for two and three parameters; the optimization completes in half the time on average for two and three parameters, storing half as many simplices for two parameters, and a quarter as many for three parameters, achieving a better average error bound in the process. Since the LEM partitions the simplex independently of computations, the standard deviation is significantly lower than that of the BOM: the LEM computes the same number of nonlinear optimizations for every instance, with the only deviation stemming from the random instance and the processor time. When comparing to the BOM, the LEM’s computation methods occasionally consume more CPU time for comparable or less accuracy for one parameter, such as instance 3 for \(\kappa -1=1\), as well as for all subsequent instances aside from instance 7 for \(\kappa -1=2\). In contrast, the BOM runs one extra nonlinear optimization per simplex, and results in a different number of simplices for each instance; depending on the problem being solved, and the subroutine in use, this can greatly influence the time involved, as seen comparing instance 7 to instances 1, 2, 8, and 10 for \(\kappa -1=2\).

4 Conclusion

We extend the approximate simplex method found in [4] to apply to biconvex objectives and constraints rather than just jointly convex objectives and constraints. We apply said algorithm to a set of random examples using Matlab’s fmincon as a subroutine, since it has such widespread uses in the engineering community. The termination conditions are twofold: interpolation error bounds from [31, 33] allow us a choice of new datapoint without error calculations, which we refer to as the LEM; alternatively, we utilize a biconvex overestimator to compute an error estimator, the BOM, and apply properties of adaptive mesh refinement from [8] to justify its use. The LEM has the advantage of having a predetermined number of vertices at which to solve program (1), while the BOM enjoys the advantages inherent to adaptive finite element methods as presented in [26, 24], and [8].

Further questions include the comparison of the BOM and LEM with new baseline methods or a hybridization of the two, or the application of different subroutines, as found in the cvx and NLopt toolboxes; worth investigating, also, is the question of how many changes to a parameter must occur to render parametric programming faster than recomputing the optimal solution each time it is necessary. Currently no computational comparisons exist in the literature, and such comparisons would be useful for the construction of new algorithms. From a more general perspective, the extension of the approximate simplex method from programs containing jointly convex functions to those containing biconvex functions enables consideration of a wider variety of programs, including pooling problems, which tend to be bilinear (and thus biconvex) in nature, as well as various single-objective scalarizations for multi-objective programs.