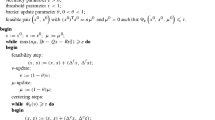A New full-newton step infeasible interior-point method for $P_*(\kappa )$-linear Complementarity problem

Abstract

In this paper, we suggest a new infeasible interior-point method (IIPM) for $P_{*}(\kappa )$-linear complementarity problem ($P_{*}(\kappa )$-LCP) based on a new class of kernel functions with full-Newton steps. Each iteration of the algorithm consists of a feasible step and a few centering steps. The feasible step is defined by the newly proposed kernel functions, while the centering step is determined by using Newton’s method. New class of kernel functions includes a logarithmic kernel function in Roos (SIAM J Optim 16:1110–1136, 2006) and a trigonometric kernel function in Moslemi and Kheirfam (Optim Lett 13:127–157, 2019), Kheirfam and Haghighi (Commun Comb Optim 3:51–70, 2018), Fathi-Hafshejani et al. (J Appl Math Comput 48:111–128, 2015) as special cases. And we show that the proposed algorithm has the best known complexity for $P_*(\kappa )$-LCP for such a method and present some numerical results.

1 Introduction

In this paper, we consider the following $P_*(\kappa )$-LCP: Find vectors $x,s \in {\textbf{R}}^{n}$ such that

$$\begin{aligned} -Mx+s=q,~~xs=0,~~(x,s) \ge 0, \end{aligned}$$

(1)

where $M\in {\textbf{R}}^{n\times n},$ a $P_*(\kappa )$-matrix, $\kappa \ge 0,$ $~ n\ge 2$, $q\in {\textbf{R}}^{n}$, and xs denotes the componentwise product.

The notion of $P_{*}(\kappa )$-matrix was introduced by Kojima et al. [1]. For $\kappa \ge 0,$ a matrix $M\in {\textbf{R}}^{n\times n}$ is called a $P_*(\kappa )$-matrix if

$$\begin{aligned} (1+4\kappa )\sum _{i\in I_{+}(x)}x_{i}(Mx)_{i}+\sum _{i\in I_{-}(x)}x_{i}(Mx)_{i} \ge 0~,~\mathrm{for \, all} \, x \in {\textbf{R}}^{n}, \end{aligned}$$

(2)

where

$$\begin{aligned} I_{+}(x)=\{ 1\le i\le n: x_{i}(Mx)_{i}>0 \} ~~\textrm{and} ~~ I_{-}(x)=\{ 1\le i\le n: x_{i}(Mx)_{i}<0 \}. \end{aligned}$$

For M,  a $P_*(\kappa )$-matrix, there is the smallest ${\hat{\kappa }}\ge 0$ for which (2) holds. The value is called the handicap of the $P_*(\kappa )$-matrix M [2]. Note that if $\kappa = 0$, then (1) is a monotone LCP. For $x,s\in {\textbf{R}}^{n}$ satisfying $-Mx+s=q$ and $(x,s) \ge 0$, we say that (x, s) is a feasible solution for (1). A feasible solution (x, s) is called a solution for (1) if $xs=0$.

After the appearance of the Karmakar’s landmark paper [3] in 1984 for linear optimization (LO), the interior-point methods (IPMs) have become an active research field and have made many changes to the numerical analysis and theoretical approaches for LO. They have polynomial complexity with its promising performance in practice. Since then, they have been widely extended to solve linear complementarity problem (LCP), semidefinite optimization (SDO), second order cone optimization (SOCO), symmetric optimization (SO), etc.

IPMs are classified into two categories: feasible IPMs (FIPMs) and infeasible IPMs (IIPMs). A feasible IPM (FIPM) assumes that the starting point satisfies the first equality constraint of (1) and lies inside the region defined by the inequality constraint and maintain feasibility during the solution process. Until recently, many researchers have been studied on the FIPMs for LO [4, 5], LCP [6], $P_*(\kappa )$-LCP [7,8,9], $P_*(\kappa )$-nonlinear complementarity problem [10], SDO [11,12,13], SOCO [14], and SO [15], etc.

However, in practice, obtaining such a feasible starting point is difficult for most problems. IIPMs start with an arbitrary positive point and feasibility is reached as optimality approached. Many IIPMs have been proposed for LO [16,17,18], monotone LCP [19], $P_*(\kappa )$-horizontal LCP [20], SDO [21], SOCO [22], and SO [23], etc.

LCP has many applications in mathematical programming and equilibrium problems, e.g., linear quadratic programming, finding Nash-equilibrium in bimatrix games, economics with institutional restrictions upon prices, contact problems with friction, optimal stopping in Markov chains, circuit simulation, free boundary problems, and calculating the interval hull of linear systems of interval equations [24, 25].

Kojima et al. [1] first showed the existence of the central path for any $P_*(\kappa )$-LCP and generalized the primal-dual interior-point method (IPM) for LO to $P_*(\kappa )$-LCP which has polynomial iteration complexity ${\mathcal {O}}\big ((1+\kappa )\sqrt{n}L)$, where L is the input size of the problem. Darvay et al. [7] introduce a new feasible corrector-predictor interior-point algorithm for $P_*(\kappa )$-LCP by using the method of algebraically equivalent transform of the nonlinear equation of the system and obtain the polynomial complexity ${\mathcal{O}}\left( {\left( {1 + 2\kappa } \right)\sqrt n \log \frac{{9n\mu ^{o} }}{{8\epsilon }}} \right)$. This complexity is still the best one for $P_*(\kappa )$-LCP for FIPMs.

Roos et al. [26] proposed the new IIPMs for LO utilizing so called the perturbed subproblem. These methods for LO are generalized to Mansouri et al. [27, 28], Kheirfam [29], and Rigó et al. [30]. In this paper, we generalize the full-Newton step IIPMs for LO [26] to $P_*(\kappa )$-LCP with new search directions and proximity measures. The new method uses only full-Newton steps. The advantage is that no line search is required. Moreover we propose new class of kernel functions and analyze IIPMs. Kernel functions define new search directions and are used to measure the distance to the central path. The new class of kernel functions includes a classical logarithmic kernel function [26], trigonometric kernel functions [31,32,33], and some of self-regular kernel functions [34] as special cases. This implies that our method proposes the new search directions and generalize previous results for $P_*(\kappa )$-LCP. In addition, the complexity bounds of the algorithm have the best known iteration bounds ${\mathcal{O}} \left( {n\left( {1 + 2\kappa } \right)^{2} \log \frac{{\max \left\{ {(x^{0} )^{T} s^{0} ,~\left\| {r^{0} } \right\|} \right\}}}{\epsilon }} \right)$, which is improved compared to ${\mathcal{O}}\left( {n\left( {1 + 2\kappa } \right)^{3} \log \frac{{\max \left\{ {(x^{0} )^{T} s^{0} ,~\left\| {r^{0} } \right\|} \right\}}}{\epsilon }} \right)$ iteration complexity suggested in [32], where $(x^0,s^0)$, an initial starting vector, $r^0:=s^0-q-Mx^0$ and $\epsilon >0$. And we show numerical results for some examples. As mentioned earlier, iteration complexity of the FIPMs for $P_*(\kappa )$-LCP looks better than IIPMs for $P_*(\kappa )$-LCP. However, FIPMs require an additional problem of finding initial starting vector. Since IIPMs do not need this step, in many cases, it is advantageous to consider IIPMs.

This paper is organized as follows. In Sect. 2, we introduce generic IPMs and IIPMs for $P_*(\kappa )$-LCP and some basic lemmas for later use. In Sect. 3, we define new class of kernel functions with some examples and the main algorithm. In Sect. 4, for the complexity analysis we derive some important properties of the new kernel functions and define the feasibility step and derive the complexity bound. In Sect. 5, we show the numerical results for some examples and give some concluding remarks in Sect. 6.

We use the following notations throughout the paper: For $x\in {\textbf{R}}^{n}$, $\Vert x \Vert _1:= \sum _{i=1}^{n} |x_{i} |$, $\Vert x \Vert _2:= \bigl (\sum _{i=1}^{n} |x_i |^2 \bigr )^{\frac{1}{2}}$, and $\Vert x \Vert _\infty :=\max _{1\le i \le n} |x_i |$. X and S are the diagonal matrices from vector x and s, i.e., $X:=$diag(x) and $S:=$diag(s). $\frac{x}{s}$ denotes the componentwise division of vectors x and s and $x^Ts$ is the scalar product of the vectors x and s. e is the n-dimensional vector of ones and I is the n-dimensional identity matrix. For $a\in {\textbf{R}}$, $\Big \lceil a \Big \rceil :=\min \{n\in {\textbf{Z}}~\vert ~n\ge a\}$, where ${\textbf{Z}}$ is the set of integers.

2 Preliminaries

In this section, we introduce generic IPMs and IIPMs for $P_*(\kappa )$-LCP and some basic lemmas.

Proposition 1

[1] Let $M\in {\textbf{R}}^{n\times n}$ be a $P_*(\kappa )$-matrix and $x,s>0$. Then

$$\begin{aligned} M' = \begin{pmatrix} -M &{} I \\ S &{} X \\ \end{pmatrix} \end{aligned}$$

is a nonsingular matrix for any positive diagonal matrices $X,S\in {\textbf{R}}^{n\times n}.$

Corollary 1

If $M\in {\textbf{R}}^{n\times n}$ is a $P_*(\kappa )$-matrix and $x,s>0$. Then for all $a\in {\textbf{R}}^{n}$ the system

$$\begin{aligned} M\Delta x - \Delta s=0~,~~S\Delta x + X\Delta s =a \end{aligned}$$

has a unique solution $(\Delta x,\Delta s)$.

Without loss of generality, we assume that $P_*(\kappa )$-LCP satisfies the interior-point condition (IPC), i.e. there exists a pair $(x^{0},s^{0})>0$ such that $s^{0} = Mx^{0}+q$. In the case of IIPMs, we call the pair $(x,s)\ge 0$ an $\epsilon$-approximate solution of $P_*(\kappa )$-LCP (1) if

$$\begin{aligned} \max \big \{ \Vert s-Mx-q \Vert ,x^{T} s \big \} \le \epsilon . \end{aligned}$$

For an $\epsilon$-approximate solution for (1), we perturb the complementarity condition, i.e., the second equation in (1), as follows:

$$\begin{aligned} Mx - s = -q,~~xs=\mu e,~~x,s > 0. \end{aligned}$$

(3)

Since M is a $P_*(\kappa )$-matrix and the IPC holds, by Lemma 4.3 in [1], the system (3) has a unique solution for each $\mu >0$. We denote by $(x(\mu ), s(\mu ))$ the solution of (3) for given $\mu >0$. We also call it the $\mu$-center for given $\mu > 0$. The solution set $\left\{ {\left( {x\left( \mu \right),s\left( \mu \right)} \right)~|~\mu > 0} \right\}$ is the central path for the system (1). Note that the sequence $(x(\mu ), s(\mu ))$ approaches to the solution (x, s) of the system (1) as $\mu \rightarrow 0$ [1]. We apply Newton’s method to the system (3). Then we have the system:

$$\begin{aligned} M\Delta x - \Delta s = 0, ~~x\Delta s + s \Delta x = \mu e - xs. \end{aligned}$$

(4)

Since M is a $P_*(\kappa )$-matrix, the system (4) uniquely defines $(\Delta x, \Delta s)$ for any $x>0$ and $s>0$. We define the following notations:

$$\begin{aligned} v:=\sqrt{\frac{xs}{\mu }},~~d_{x}:=\frac{v\Delta x}{x},~~d_{s}:=\frac{v\Delta s}{s}. \end{aligned}$$

(5)

Then we rewrite the system (4) as follows:

$$\begin{aligned} {\overline{M}}d_{x} - d_{s} = 0,~~d_{x}+d_{s}=v^{-1}-v, \end{aligned}$$

(6)

where ${\overline{M}}:=DMD$ and $D:=$ diag$\left( {\sqrt {\frac{x}{s}} } \right)$. Since M is a $P_*(\kappa )$-matrix, ${\overline{M}}$ is also a $P_*(\kappa )$-matrix.

The search directions $d_{x}$ and $d_{s}$ are obtained by solving (6). From (5) we obtain $\Delta x$ and $\Delta s$. The iteration is obtained by taking a full-Newton step according to

$$\begin{aligned} x^{+}:=x+\Delta x,~s^{+}:=s+\Delta s. \end{aligned}$$

(7)

For the analysis of the algorithm, we define a norm-based proximity measure as follows:

$$\begin{aligned} \delta (v):=\delta (x,s;\mu ):=\frac{1}{2}\Vert v^{-1}-v\Vert . \end{aligned}$$

(8)

We recall some results which are needed for the analysis of the algorithm.

Lemma 1

(Lemma II.60 in [35]) Let v and $\delta :=\delta (x,s;\mu )$ be defined in (5) and (8), respectively and $\rho (\delta ):=\delta +\sqrt{1+\delta ^2}$. Then

$$\begin{aligned} \frac{1}{\rho (\delta )}\le v_i\le \rho (\delta ),~i=1,2,\ldots ,n. \end{aligned}$$

Lemma 2

(Theorem 3.1 in [36]) Let $\delta :=\delta (x,s;\mu )<\frac{1}{\sqrt{1+4\kappa }}$. Then the full-Newton step is strictly feasible.

Lemma 3

(Theorem 3.2 in [36]) Let $\delta :=\delta (x,s;\mu )<\frac{1}{\sqrt{1+4\kappa }}$. Then

$$\begin{aligned} \delta (x^{+},s^{+};\mu ) \le \frac{\sqrt{1+(1+4\kappa )^2}\delta ^2}{2\sqrt{1-(1+4\kappa )\delta ^2}}, \end{aligned}$$

where ($x^{+},s^{+}$) are defined in (7).

Corollary 2

If $\delta :=\delta (x,s;\mu )\le \frac{1}{2(1+2\kappa )}$ and $\kappa \ge 0$, then

$$\begin{aligned} \delta (x^+, s^+;\mu )\le \sqrt{2}(1+2\kappa )\delta ^2, \end{aligned}$$

which shows the local quadratic convergence of the full-Newton step.

Proof

Since $\kappa \ge 0$, $\delta =\delta (x,s;\mu )\le \frac{1}{2(1+2\kappa )}<\frac{1}{\sqrt{2(1+2\kappa )}}<\frac{1}{\sqrt{1+4\kappa }}$. From Lemma 3, we have

$$\begin{aligned} \delta (x^{+},s^{+};\mu )\le & {} \frac{\sqrt{1+(1+4\kappa )^2}\delta ^2}{2\sqrt{1-(1+4\kappa )\delta ^2}} \le \frac{(1+2\kappa )\delta ^2}{\sqrt{1-2(1+2\kappa )\delta ^2}}\nonumber \\\le & {} \frac{(1+2\kappa )\delta ^2}{\sqrt{1-\frac{1}{2(1+2\kappa )}}}\le \sqrt{2}(1+2\kappa )\delta ^2. \end{aligned}$$

Thus, the proof is complete. $\square$

Corollary 2 implies that the centering step is quadratically convergent.

In the remainder of this section, we introduce IIPMs for $P_*(\kappa )$-LCP. For the generic IIPMs, the initial starting vector $(x^0, s^0)$ is defined as follows:

$$\begin{aligned} (x^0, s^0) = (\rho _{p}e,\rho _{d}e) ~\text {and} ~\mu ^0 = \rho _{d}\rho _{p}, \end{aligned}$$

(9)

where $\rho _{p}$ and $\rho _{d}$ are positive numbers such that

$$\begin{aligned} \Vert x^{*}\Vert _{\infty } \le \rho _{p},~\big \{ \Vert s^{*}\Vert _{\infty },\rho _{p}\Vert Me\Vert _{\infty },\Vert q\Vert _{\infty } \big \}\le \rho _{d} \end{aligned}$$

(10)

and $(x^{*},s^{*})$ is the solution of (1). We define by $r^{0}:=s^{0}-q-Mx^{0}$ the residual vector at an initial starting vector. Generally the initial iteration is infeasible, i.e., $r^0 \ne 0$. Thus we generate a sequence of perturbed problems that are feasible for the initial value. Accordingly, we define the following sequence of system, for any $\nu$ with $0<\nu \le 1$,

$$\begin{aligned} s-q-Mx=\nu r^0,~~(x,s) \ge 0. \qquad \qquad \qquad \qquad \qquad (P_{\nu }) \end{aligned}$$

Then the initial starting vector is strictly feasible for ($P_{\nu }$) when $\nu =1$. This means that if $\nu = 1$, then ($P_{\nu }$) satisfies the IPC.

Lemma 4

(Lemma 3.1 in [37]) Let the problem (1) be feasible and let $0<\nu \le 1$. Then, the perturbed problem ($P_{\nu }$) satisfies the IPC.

Assume that problem (1) is feasible and let $0<\nu \le 1$. By Lemma 4, ($P_{\nu }$) satisfies the IPC and its central path exists. By Lemma 4.3 in [1], for every $\mu >0$,

$$\begin{aligned} s-q-Mx=\nu r^0,~~xs=\mu e,~~(x,s) > 0 \end{aligned}$$

(11)

has a unique solution $\left( {x\left( {\mu ,\nu } \right),s\left( {\mu ,\nu } \right)} \right)$.

The IIPMs for $P_*(\kappa )$-LCP solve the perturbed problem ($P_{\nu }$) through one feasible step and a few centering steps. The followings are detailed iteration scheme: Let $\mu ^0$ be defined in (9) and $\tau >0$. Suppose that for some $\mu \in (0,\mu ^{0}]$, (x, s) is strictly feasible for the perturbed problem ($P_{\nu }$). This is certainly true at the initial iteration when $\mu =\mu ^0$. Then we repeatedly perform a feasible step and a few centering steps, sequentially. In the feasible step, we generate a feasible point $(x^{f},s^{f})$ for $(P_{\nu ^{+}})$ with $\nu ^{+}:=(1-\theta )\nu$ and $\mu ^{+}:=(1-\theta )\mu$, respectively, and belongs to the quadratic convergence region with respect to $\mu ^{+}$-centers of $(P_{\nu ^{+}})$. After the feasibility step, we perform a few centering steps in order to get an iteration $(x^{+},s^{+})$ which satisfies $(x^{+})^{T}s^{+}=n\mu ^+$ and $\delta (x^{+},s^{+};\mu ^{+})\le \tau$. Note that by (9) with $\nu ^0=1$, we have

$$\begin{aligned} \mu = \nu \rho _{d}\rho _{p}. \end{aligned}$$

(12)

Now we consider the feasibility step more precisely. Suppose that (x, s) is strictly feasible for ($P_{\nu }$). In the feasibility step, we need search directions $\Delta ^{f}x$ and $\Delta ^{f}s$ such that

$$\begin{aligned} (x^{f},s^{f}):=(x+\Delta ^{f}x, s+\Delta ^{f}s) \end{aligned}$$

(13)

is feasible for ($P_{\nu }$). That is,

$$\begin{aligned} M\Delta ^{f}x - \Delta ^{f} s = \theta \nu r^{0},~~x\Delta ^{f} s + s\Delta ^{f} x = \mu e -xs. \end{aligned}$$

(14)

Since M is a $P_*(\kappa )$-matrix, by Corollary 1, the system (14) has a unique solution $(\Delta ^{f} x, \Delta ^{f} s)$. Then we define the scaled search directions

$$\begin{aligned} d^{f}_{x}:=\frac{v\Delta ^{f}x}{x},~~ d^{f}_{s}:=\frac{v\Delta ^{f}s}{s}, \end{aligned}$$

(15)

where v is defined as in (5) and $\Delta ^{f}x$ and $\Delta ^{f}s$ are defined in (13). The system (14) can be expressed as follows:

$$\begin{aligned} {\overline{M}}d^{f}_{x} - d^{f}_{s} = \theta \nu v s^{-1} r^{0},~~d^{f}_{x}+d^{f}_{s}=v^{-1}-v. \end{aligned}$$

(16)

Note that the right-hand side of the second equation in (16) coincides with the negative gradient of the logarithmic barrier function $\Psi _{l}(v)$, i.e.,

$$\begin{aligned} d_{x}^{f} + d_{s}^{f} = -\nabla \Psi _{l}(v), \end{aligned}$$

(17)

where $\Psi _{l}(v):=\sum _{i=1}^{n}\psi _{l}(v_{i})$ and $\psi _{l}(t):= \frac{t^{2} - 1}{2}-\text {log}~t$, for $t>0$.

From (16), we have $d^{f}_{x}$ and $d^{f}_{s}$. Then $\Delta ^{f}x$ and $\Delta ^{f}s$ are computed via (15) and then the new iteration is obtained by (13). Thus we have a new iteration $(x^{f},s^{f})$ satisfying the first equation of ($P_{\nu }$) with $\nu = \nu ^+$.

3 New class of kernel functions

The aim of this paper is to propose new IIPMs based on a new class of kernel functions which is defined in Definition 1 below and to yield the best known complexity result for (1).

We call $\psi :(0,\infty )\rightarrow [0,\infty )$ a kernel function if $\psi$ is twice differentiable and satisfies the following conditions:

$$\begin{aligned} \psi '(1)=\psi (1)=0,~\psi ''(t)>0,~\forall t>0,~\lim _{t\rightarrow 0^{+}}\psi (t)=\lim _{t\rightarrow \infty }\psi (t)=\infty . \end{aligned}$$

Definition 1

We call a kernel function $\psi :(0,\infty )\rightarrow [0,\infty )$, defined by $\psi (t):=\frac{t^2-1}{2}-\varphi (t)$, (1/t)-bound function if the function $\psi$ is a kernel function and $\varphi$ satisfies the following conditions:

$$\begin{aligned}{} & {} 1\le \varphi ^\prime (t) \le \frac{1}{t^2} ~~,~\textrm{for}~0 < t \le 1, \end{aligned}$$

(18)

$$\begin{aligned}{} & {} \frac{1}{t^2} \le \varphi ^\prime (t) \le t~,~\textrm{for}~ t>1, \end{aligned}$$

(19)

$$\begin{aligned}{} & {} \inf _{t>0}~t\varphi ^\prime (t)>\frac{3}{10}. \end{aligned}$$

(20)

Note that a logarithmic kernel function satisfies (18), (19), (20). Moreover, any function $\varphi$ satisfying (18) and (19) is bounded above by a 1/t for $0<t\le 1$ and bounded below by a 1/t for $t>1$, respectively. From this, we call the function in Definition 1 (1/t)-bound kernel function.

In this paper, we replace the logarithmic barrier kernel function $\Psi _{l}$ in (17) by (1/t)-bound kernel function $\Psi$ as follows:

$$\begin{aligned} {\overline{M}}d^{f}_{x} - d^{f}_{s} = \theta \nu v s^{-1} r^{0},~~d^{f}_{x}+d^{f}_{s}=-\nabla \Psi (v), \end{aligned}$$

(21)

where $\Psi (v):=\sum _{i=1}^{n}\psi (v_{i})$ and $\psi (t)$ is any (1/t)-bound kernel function, i.e.,

$$\begin{aligned} d^{f}_{x}+d^{f}_{s}=\varphi '(v) - v. \end{aligned}$$

(22)

In the following, we suggest some (1/t)-bound kernel functions and derive their important properties.

Table 1 presents some examples of (1/t)-bound kernel functions, e.g., $\psi _j,~j\in \{1,2,\ldots ,7\}$, and their references. In Table 2, we give the first two derivatives of the kernel functions. In Table 3, we give the first derivative of the barrier terms and the condition (20).

In Table 1, by choosing $p=1$ for the function (15c) in [32], we have $\psi _4(t)$. For $\psi _j, 1\le j \le 7$, we obtain the following observations: First, the class of kernel functions in this paper is different from the class of eligible kernel functions defined in [38] and includes a logarithmic kernel function as a special case. Indeed, $\psi _j,~j\in \{1, 4, 5, 6, 7\}$, are eligible but $\psi _j,~j\in \{2, 3\},$ are not eligible. Secondly, IPMs based on $\psi _j, 1\le j \le 7$, yield the best known complexity result for given problems and for such methods. Finally, we have tested FIPMs based on $\psi _j, 1\le j \le 7$, for $P_{*}(1/4)$-LCP in Example 4.12 in [9].

Note that the solution of the problem is $x^* =(1,0)^T$ and $s^* =(0,1)^T$. By letting $q = (0, 3)^T$, $x^o =(1,1)^T$, $s^o =(1,1)^T$, $\epsilon =10^{-4}$, $\mu ^o =1$, $\tau =1$, and $\theta =0.6$, we obtain a similar number of iterations to have $\epsilon$-approximate solutions as follows: 11 iterations for $\psi _6$, 12 iterations for $\psi _2$ and $\psi _3$, and 13 iterations for $\psi _1$, $\psi _4$, $\psi _5$, and $\psi _7$.

Table 1 Barrier terms of (1/t)-bound kernel function

Table 2 The first two derivatives of the kernel functions

Table 3 The first derivative of barrier terms and the condition (20)

For complexity analysis, we present some lemmas for the (1/t)-bound kernel functions. We use the following lemma to prove Lemma 9.

Lemma 5

For $\varphi (t):=\varphi _j(t),~j\in \{ 1,2,\ldots ,7 \}$, we have

$$\begin{aligned} \left| 1-t\varphi '(t) \right| \le \left| t-\frac{1}{t} \right| ,~~\text {for}~t>0. \end{aligned}$$

Proof

For $0< t\le 1$, by (18), we have

$$\begin{aligned} -\frac{1}{t} \le -t\varphi '(t) \le -t. \end{aligned}$$

Since $t\le 1 \le \frac{1}{t}$,

$$\begin{aligned} t-\frac{1}{t}\le 1-\frac{1}{t} \le 1-t\varphi '(t)\le 1-t\le \frac{1}{t}-t. \end{aligned}$$

For $t>1$, by (19), we have

$$\begin{aligned} -t^2\le -t\varphi '(t) \le -\frac{1}{t}. \end{aligned}$$

Since $\frac{1}{t}-t \le t\big ( \frac{1}{t}-t \big )$,

$$\begin{aligned} \frac{1}{t}-t \le 1-t^2\le 1-t\varphi '(t) \le 1-\frac{1}{t}\le t-\frac{1}{t}. \end{aligned}$$

Thus, the proof is complete. $\square$

We use the following lemma to prove Lemma 13.

Lemma 6

For $\varphi (t):=\varphi _j(t),~j\in \{ 1,2,\ldots ,7 \}$, we have

$$\begin{aligned} \left| t-\varphi '(t) \right| \le \big (1+\frac{1}{t^2}\big ) \left| t-\frac{1}{t} \right| ,~~\text {for}~t>0. \end{aligned}$$

Proof

For $0< t\le 1$, by (18), we have

$$\begin{aligned} t-\frac{1}{t^2} \le t-\varphi '(t) \le t-1. \end{aligned}$$

From

$$\left( {t - \frac{1}{{t^{2} }}} \right) - \left( {1 + \frac{1}{{t^{2} }}} \right)\left( {t - \frac{1}{t}} \right) = \frac{{(1 - t)}}{{t^{3} }} \ge 0,$$

we have

$$\left( {1 + \frac{1}{{t^{2} }}} \right)\left( {t - \frac{1}{t}} \right) \le t - \frac{1}{{t^{2} }} \le t - \varphi ^{\prime}(t) \le t - 1{\text{ < }}0,~~{\text{for}}~0 \le t \le 1.$$

(23)

For $t>1$, in the same way as for (23) and by (19), we have

$$0 \le t - \varphi ^{\prime } (t) \le t - \frac{1}{{t^{2} }} \le \left( {1 + \frac{1}{{t^{2} }}} \right)\left( {t - \frac{1}{t}} \right).$$

Thus, the proof is complete. $\square$

4 The complexity analysis

Let (x, s) be such that $\delta (x,s;\mu )\le \tau$. Recall that at the start of the initial iteration this is certainly true, since $\delta (x^{0},s^{0};\mu ^{0})=0$. By following the feasible step, we have a new iteration $(x^{f},s^{f}) =(x+\Delta ^f x,s+\Delta ^f s)$ that satisfies $(P_{\nu ^+})$. A crucial point in the analysis is to show that $\delta (x^{f},s^{f};\mu ^{+})\le \frac{1}{2(1+2\kappa )}$ and $(x^{f},s^{f}) > 0$. From [38], we have

$$\begin{aligned} x^{f} s^{f} = & \left( {x + \Delta ^{f} x} \right)\left( {s + \Delta ^{f} s} \right) = \frac{{xs}}{{v^{2} }}\left( {v + d_{x}^{f} } \right)\left( {v + d_{s}^{f} } \right) \\ & = \mu \left( {v\left( {v + \left( {d_{x}^{f} + d_{s}^{f} } \right)} \right) + d_{x}^{f} d_{s}^{f} } \right) = \mu \left( {v\varphi ^{\prime}(v) + d_{x}^{f} d_{s}^{f} } \right), \\ \end{aligned}$$

(24)

where the second and third equalities are from (5) and the last equality is from (22).

The following lemma provides a sufficient condition for the strictly feasible step.

Lemma 7

After a feasible step, the new iteration $\left( {x^{f} ,s^{f} } \right) = \left( {x + \Delta ^{f} x,s + \Delta ^{f} s} \right)$ satisfying $(P_{\nu ^+})$, is strictly feasible if and only if

$$\begin{aligned} v\varphi '(v)+ d^{f}_{x}d^{f}_{s} > 0. \end{aligned}$$

Proof

For a step length $\alpha$ with $0\le \alpha \le 1$, we define

$$\begin{aligned} x(\alpha ):= x+\alpha \Delta ^{f}x,~~s(\alpha ):= s+\alpha \Delta ^{f}s. \end{aligned}$$

Then we have $x(0)=x$, $s(0)=s$, $x(1) = x^{f}$, $s(1)= s^{f}$ and $x(0)s(0)=xs>0$. On the other hand, from (22) and $v\varphi '(v)+ d^{f}_{x}d^{f}_{s} > 0$, we have

$$\begin{aligned} x(\alpha )s(\alpha ) & = \left( {x + \alpha \frac{{xd_{x}^{f} }}{v}} \right)\left( {s + \alpha \frac{{sd_{s}^{f} }}{v}} \right) = \mu \left( {v + \alpha d_{x}^{f} } \right)\left( {v + \alpha d_{s}^{f} } \right) \\ & = \mu \left( {v^{2} + \alpha \nu (d_{x}^{f} + d_{s}^{f} ) + \alpha ^{2} d_{x}^{f} d_{s}^{f} } \right) = \mu \left( {v^{2} + \alpha v\left( {\varphi ^{\prime } (v) - v} \right) + \alpha ^{2} d_{x}^{f} d_{s}^{f} } \right) \\ & > \mu \left( {\left( {1 - \alpha } \right)v^{2} + \alpha v\varphi ^{\prime } (v) - \alpha ^{2} \left( {v\varphi ^{\prime } (v)} \right)} \right) \\ & = \mu \left( {\left( {1 - \alpha } \right)v^{2} + \alpha \left( {1 - \alpha } \right)v\varphi ^{\prime } (v)} \right) = \mu v\left( {1 - \alpha } \right)\left( {v + \alpha \varphi ^{\prime } (v)} \right) \ge 0. \\ \end{aligned}$$

Hence, none of the entries of $x(\alpha )$ and $s(\alpha )$ vanishes, for $0<\alpha \le 1$. Since x(0) and s(0) are positive and $x(\alpha )$ and $s(\alpha )$ depend linearly on $\alpha$, this implies that $x(\alpha )>0$ and $s(\alpha )>0$ for $0<\alpha \le 1$. Hence, x(1) and s(1) are positive. Thus, the proof is complete. $\square$

In the sequel, we denote

$$\begin{aligned} \omega :=\frac{1}{2}\sqrt{\Vert d^{f}_{x}\Vert ^2 + \Vert d^{f}_{s}\Vert ^2}~. \end{aligned}$$

(25)

From (25),

$$\left\| {d_{x}^{f} d_{s}^{f} } \right\| \le \left\| {d_{x}^{f} } \right\|\left\| {d_{s}^{f} } \right\| \le \frac{1}{2}\left( {\left\| {d_{x}^{f} } \right\|^{2} + \left\| {d_{s}^{f} } \right\|^{2} } \right) = 2\omega ^{2} ,$$

(26)

$$\left| {d_{{xi}}^{f} d_{{si}}^{f} } \right| \le \frac{1}{2}\left( {\left| {d_{{xi}}^{f} } \right|^{2} + \left| {d_{{si}}^{f} } \right|^{2} } \right) \le 2\omega ^{2} ,~i = 1,2, \ldots ,n.$$

(27)

In what follows, we denote $\delta (x^{f},s^{f};\mu ^{+})$ by $\delta (v^{f})$, where $v^{f}:=\sqrt{\frac{x^{f}s^{f}}{\mu ^{+}}}$.

Lemma 8

Let $\omega$ be defined in (25). If $(x^{f},s^{f})$ is strictly feasible, then

$$\begin{aligned} v^{f}_{min} \ge \sqrt{\frac{3-20\omega ^2}{10(1-\theta )}}~, \end{aligned}$$

where $v^{f}_{min}:=\smash {\displaystyle \min _{1\le i \le n}} \{ v^{f}_{i} \}$ and $0<\theta <1$.

Proof

Using (5) and (24) and dividing both sides by $\mu ^{+} = (1-\theta )\mu$, we have

$$\begin{aligned} (v^{f})^2 = \frac{x^{f}s^{f}}{\mu ^{+}} = \frac{v\varphi '(v)+d^{f}_{x}d^{f}_{s}}{1-\theta }. \end{aligned}$$

(28)

By using (28), (27), and (20), we have

$$\begin{aligned} \left( {v_{{min}}^{f} } \right)^{2} & = \frac{1}{{1 - \theta }}\min _{i} \left( {v_{i} \varphi ^{\prime } (v_{i} ) + d_{{xi}}^{f} d_{{si}}^{f} } \right) \\ & \ge \frac{1}{{1 - \theta }}\left( {\min _{i} \left( {v_{i} \varphi ^{\prime } (v_{i} )} \right) + \min _{i} \left( {d_{{xi}}^{f} d_{{si}}^{f} } \right)} \right) \\ & \ge \frac{1}{{1 - \theta }}\left( {\frac{3}{{10}} - 2\omega ^{2} } \right). \\ \end{aligned}$$

Thus, the proof is complete. $\square$

Lemma 9

Let $\delta (v)$ and $\omega$ be defined in (8) and (25), respectively. Then the following inequality holds.

$$\begin{aligned} \Vert e-(v^{f})^2\Vert \le \frac{1}{1-\theta }\big ( \theta \sqrt{n} + 2\delta (v) + 2\omega ^2 \big ) \end{aligned}$$

where $0<\theta <1$ and $n \ge 2$.

Proof

Using (28), the triangular inequality, (26), Lemma 5, and (8), we have

$$\begin{aligned} \left\| {e - (v^{f} )^{2} } \right\| & = \left\| {e - \frac{{v\varphi ^{\prime}(v) + d_{x}^{f} d_{s}^{f} }}{{1 - \theta }}} \right\| \\ & = \frac{1}{{1 - \theta }}\left\| {\left( {1 - \theta } \right)e - v\varphi ^{\prime}(v) - d_{x}^{f} d_{s}^{f} } \right\| \\ & \le \frac{1}{{1 - \theta }}\left( {\theta \sqrt n + \left\| {e - v\varphi ^{\prime}(v)} \right\| + 2\omega ^{2} } \right) \\ & \le \frac{1}{{1 - \theta }}\left( {\theta \sqrt n + \left\| {v^{{ - 1}} - v} \right\| + 2\omega ^{2} } \right) \\ & \le \frac{1}{{1 - \theta }}\left( {\theta \sqrt n + 2\delta (v) + 2\omega ^{2} } \right). \\ \end{aligned}$$

Thus, the proof is complete. $\square$

Lemma 10

Let $\delta (v)$ and $\omega$ be defined in (8) and (25), respectively. If  $v\varphi '(v) + d^{f}_{x}d^{f}_{s} > 0$, then

$$\begin{aligned} \delta (v^{f})\le \frac{\sqrt{10}(\theta \sqrt{n} + 2\delta (v) + 2\omega ^2 ) }{2\sqrt{ (1-\theta )(3-20\omega ^2) } } ~, \end{aligned}$$

where $0<\theta <1$ and $n \ge 2$.

Proof

Using (8), we have

$$\begin{aligned} 2\delta (v^{f})= & {} \Vert (v^{f})^{-1}-v^{f} \Vert = \Vert (v^{f})^{-1}(e-(v^{f})^{2})\Vert \\\le & {} \Vert (v^{f})^{-1}\Vert _{\infty }\Vert e-(v^{f})^2 \Vert = \frac{1}{v^{f}_{min}}\Vert e-(v^{f})^2 \Vert \\\le & {} \frac{\sqrt{10}(\theta \sqrt{n} + 2\delta (v) + 2\omega ^2 ) }{\sqrt{ (1-\theta )(3-20\omega ^2) } }, \end{aligned}$$

where the last inequality is from Lemma 8 and Lemma 9. Thus, the proof is complete. $\square$

In what follows, we want to choose $0<\theta <1$, as large as possible such that $(x^{f}, s^{f})$ lies in the quadratic convergence neighborhood with respect to the $\mu ^{+}$-center of $(P_{\nu ^{+}})$, i.e., $\delta (v^{f})\le \frac{1}{2(1+2\kappa )}$. By Lemma 10, we have

$$\begin{aligned} \frac{\sqrt{10}(\theta \sqrt{n} + 2\delta (v) + 2\omega ^2 ) }{\sqrt{ (1-\theta )(3-20\omega ^2) } }\le \frac{1}{1+2\kappa }. \end{aligned}$$

(29)

Define

$$\begin{aligned} \tau = \frac{1}{16(1+2\kappa )} \end{aligned}$$

(30)

and choose any $\omega$ and $\theta$ satisfying

$$\begin{aligned} 0\le \omega \le \frac{1}{4\sqrt{1+2\kappa }}~~\text {and}~~0\le \theta \le \frac{1}{5n(1+2\kappa )}. \end{aligned}$$

(31)

Then the left-hand side of (29) is monotonically increasing with respect to $\theta$ and $\omega$. Since $\delta \le \tau$, using (30) and (31), we have the upper bound of the left-hand side of (29):

$$\begin{gathered} \frac{{\sqrt {10} \left( {\theta \sqrt n + 2\delta (v) + 2\omega ^{2} } \right)}}{{\sqrt {\left( {1 - \theta } \right)\left( {3 - 20\omega ^{2} } \right)} }} \le \frac{{\sqrt {10} \left( {\frac{1}{{4(1 + 2\kappa )}} + \frac{1}{{5(1 + 2\kappa )\sqrt n }}} \right)}}{{\sqrt {\left( {3 - \frac{5}{{4(1 + 2\kappa )}}} \right)\left( {1 - \frac{1}{{5(1 + 2\kappa )n}}} \right)} }} \hfill \\ = \frac{{4 + 5\sqrt n }}{{\sqrt {\left( {14 + 48\kappa } \right)\left( { - 1 + 5n + 10\kappa n} \right)} }}~. \hfill \\ \end{gathered}$$

Let $g(n,\kappa ):=\frac{4+5\sqrt{n}}{\sqrt{(14+48\kappa )(-1+5n+10\kappa n)}}$ . Then $g(n,\kappa )$ decreases with respect to n, so that

$$g\left( {2,\kappa } \right) \le \frac{{\left( {5 + 2\sqrt 2 } \right)}}{{\sqrt {\left( {14 + 48\kappa } \right)\left( {9 + 18\kappa } \right)} }} = \frac{{4 + 5\sqrt 2 }}{{3\sqrt {14} \left( {1 + 2\kappa } \right)}} \le \frac{1}{{1 + 2\kappa }}.$$

Hence we have (29) whenever (30) and (31) hold.

In the following we find a bound for the $\omega$ defined in (25).

Lemma 11

(Corollary 2.2 in [39]) Let x, s, a, and b be n-dimensional vectors with $x>0$ and $s>0$, and let ${\widehat{M}}\in {\textbf{R}}^{n\times n}$ be a $P_*(\kappa )$-matrix. Then the solution $({\hat{u}},{\hat{v}})$ of the linear system

$$\begin{aligned} {\widehat{M}}{\hat{u}}-{\hat{v}}=b,~~S{\hat{u}}+X{\hat{v}}=a, \end{aligned}$$

(32)

satisfies the following inequality:

$$\begin{aligned}{} & {} \Vert D{\hat{u}}\Vert ^2+\Vert D^{-1}{\hat{v}}\Vert ^2\nonumber \\{} & {} \quad \le \Vert {\tilde{a}}\Vert ^2+2\Vert {\tilde{b}}\Vert ^2+2\kappa \Vert {\tilde{c}}\Vert ^2+2\Vert {\tilde{b}}\Vert \sqrt{\Vert {\tilde{a}}\Vert ^2 +\Vert {\tilde{b}}\Vert ^2+2\kappa \Vert {\tilde{c}}\Vert ^2}, \end{aligned}$$

(33)

where $D=X^{-\frac{1}{2}}S^{\frac{1}{2}}$, ${\tilde{a}}=(XS)^{-\frac{1}{2}}a$, ${\tilde{b}}=D^{-1}b$, ${\tilde{c}}={\tilde{a}}+{\tilde{b}}$.

Consider the system (32) with $({\hat{u}},{\hat{v}})=(\Delta ^{f}x,\Delta ^{f}s)$, $b=\theta \nu r^{0}$, $a=-\mu v\nabla \Psi (v)$, and ${\widehat{M}}={\overline{M}}$ defined in (21). Then from (33) we obtain

$$\begin{aligned}{} & {} \Vert D\Delta ^{f}x\Vert ^2+\Vert D^{-1}\Delta ^{f}s\Vert ^2\nonumber \\{} & {} \quad \le \mu \Vert \nabla \Psi (v) \Vert ^2 +2\theta ^2\nu ^2\Vert D^{-1}r^{0}\Vert ^2+2\kappa \Vert \theta \nu D^{-1}r^{0}-\sqrt{\mu }\nabla \Psi (v) \Vert ^2+2\theta \nu \Vert D^{-1}r^{0} \Vert \nonumber \\{} & {} \quad \sqrt{\mu \Vert \nabla \Psi (v) \Vert ^2 + \theta ^2\nu ^2\Vert D^{-1}r^{0} \Vert ^2 + 2\kappa \Vert \theta \nu D^{-1}r^{0}-\sqrt{\mu }\nabla \Psi (v) \Vert ^2 }~. \end{aligned}$$

(34)

Using the inequality (31) in [32], we have

$$\begin{aligned} \Vert D^{-1}r^0\Vert \le \frac{3\rho _{d}}{\sqrt{\mu }v_{min}}\Vert x\Vert _{1}. \end{aligned}$$

(35)

In the following, we let $\delta :=\delta (v)$, where $\delta (v)$ is defined in (8), $\rho (\delta ):=\delta +\sqrt{1+\delta ^2}$, and $v_{min}:=\smash {\displaystyle \min _{1\le i \le n}} \{ v_{i} \}$.

Lemma 12

(Lemma 4.5 in [40]) Let (x, s) be feasible for ($P_{\nu }$) and let $(x^0,s^0)$ and $(x^{*},s^{*})$ be as defined in (9) and (10), respectively. Then,

$$\begin{aligned} \Vert x\Vert _{1}\le (1+4\kappa )\big (2+\rho (\delta )^2\big )n\rho _{p}~~\text {and}~~ \Vert s\Vert _{1}\le (1+4\kappa )\big (2+\rho (\delta )^2\big )n\rho _{d}. \end{aligned}$$

Lemma 13

Let $\nabla \Psi (v)$ be defined in (21). Then we have

$$\left\| {\nabla \Psi (v)} \right\| \le 2\delta \left( {1 + \rho \left( \delta \right)^{2} } \right).$$

Proof

Using Lemma 6, (8), and Lemma 1, we have

$$\begin{aligned} \left\| {\nabla \Psi (v)} \right\| & = \left\| {v - \varphi ^{\prime}(v)} \right\| \le \left\| {\left( {e + \left( {v^{{ - 1}} } \right)^{2} } \right)\left( {v^{{ - 1}} - v} \right)} \right\| \\ & \le e\left\| { + \left( {v^{{ - 1}} } \right)^{2} } \right\|_{\infty } \left\| {v^{{ - 1}} - v} \right\| = 2\left( {1 + \frac{1}{{v_{{min}}^{2} }}} \right)\delta \\ & \le 2\delta \left( {1 + \rho (\delta )^{2} } \right). \\ \end{aligned}$$

Thus, the proof is complete. $\square$

Using (35) and Lemma 13, we have

$$\begin{aligned} \left\| {\theta \nu D^{{ - 1}} r^{0} - \sqrt \mu \nabla \Psi (v)} \right\| & \le \theta \nu \left\| {D^{{ - 1}} r^{0} } \right\| + \sqrt \mu \left\| {\nabla \Psi (v)} \right\| \\ & \le \frac{{3\theta \nu \rho _{d} \left\| x \right\|_{1} }}{{\sqrt \mu v_{{min}} }} + 2\sqrt \mu \delta \left( {1 + \rho \left( \delta \right)^{2} } \right)~. \\ \end{aligned}$$

(36)

Therefore, using bounds in (35), (36), and $D^{-1}\Delta ^{f}s = \sqrt{\mu }d^{f}_{s}$ and $D\Delta ^{f}x=\sqrt{\mu }d^{f}_{x}$, we obtain the upper bound for (34) as follows:

$$\begin{aligned} & \left\| {d_{x}^{f} } \right\|^{2} + \left\| {d_{s}^{f} } \right\|^{2} \le 4\delta ^{2} \left( {1 + \rho (\delta )^{2} } \right)^{2} + \frac{{18\theta ^{2} \nu ^{2} \rho _{d}^{2} }}{{\mu ^{2} v_{{min}}^{2} }}\left\| x \right\|_{1}^{2} \\ & + 2\kappa \left( {\frac{{3\theta \nu \rho _{d} }}{{\mu v_{{min}} }}\left\| x \right\|_{1} + 2\delta \left( {1 + \rho (\delta )^{2} } \right)} \right)^{2} + \frac{{6\theta \nu \rho _{d} }}{{\mu v_{{min}} }}\left\| x \right\|_{1} \\ & \sqrt {4\delta ^{2} \left( {1 + \rho (\delta )^{2} } \right)^{2} + \frac{{9\theta ^{2} \nu ^{2} \rho _{d}^{2} }}{{\mu ^{2} v_{{min}}^{2} }}\left\| x \right\|_{1}^{2} + 2\kappa \left( {\frac{{3\theta \nu \rho _{d} }}{{\mu v_{{min}} }}\left\| x \right\|_{1} + 2\delta \left( {1 + \rho (\delta )^{2} } \right)} \right)^{2} } . \\ \end{aligned}$$

(37)

It is easy to observe that the right-hand side of the inequality (37) are monotonically increasing with respect to $\delta$ and $\frac{1}{v_{min}} \le \rho (\delta )$ by Lemma 1. By substituting the bound for $\delta$, $\Vert x\Vert _{1}$ defined in Lemma 12, and $\frac{1}{v_{min}}$ into (37), we have

$$\begin{aligned} \left\| {d_{x}^{f} } \right\|^{2} + \left\| {d_{s}^{f} } \right\|^{2} & \le 4\tau ^{2} \left( {1 + \rho (\tau )^{2} } \right)^{2} + 18\left( {1 + 4\kappa } \right)^{2} \theta ^{2} n^{2} \rho (\tau )^{2} \left( {2 + \rho (\tau )^{2} } \right)^{2} \\ & + 2\kappa \left( {3\left( {1 + 4\kappa } \right)n\theta \rho \left( \tau \right)\left( {2 + \rho (\tau )^{2} } \right) + 2\tau \left( {1 + \rho (\tau )^{2} } \right)} \right)^{2} \\ & + 6\left( {1 + 4\kappa } \right)n\theta \rho \left( \tau \right)\left( {2 + \rho (\tau )^{2} } \right)\left( \begin{gathered} 4\tau ^{2} \left( {1 + \rho (\tau )^{2} } \right)^{2} + 9\left( {1 + 4\kappa } \right)^{2} \theta ^{2} n^{2} \rho \left( \tau \right)^{2} \left( {2 + \rho (\tau )^{2} } \right)^{2} \hfill \\ + 2\kappa \left( {3\left( {1 + 4\kappa } \right)n\theta \rho \left( \tau \right)\left( {2 + \rho (\tau )^{2} + 2\tau \left( {1 + \rho (\tau )^{2} } \right)} \right)^{2} } \right) \hfill \\ \end{gathered} \right)^{{\frac{1}{2}}} . \\ \end{aligned}$$

(38)

From (25) and (38), (31) holds if the right-hand side of (38) is less than or equal to $\frac{1}{4(1+2\kappa )}$. Define

$$a(\tau ): = {\text{ }}3\left( {1{\text{ }} + {\text{ }}4\kappa } \right)n\theta \rho \left( \tau \right)\left( {2 + {\text{ }}\rho (\tau )^{2} } \right),{\text{ }}b\left( \tau \right): = {\text{ }}2\tau \left( {1{\text{ }} + {\text{ }}\rho (\tau )^{2} } \right),$$

where

$$\begin{aligned} \tau := \frac{1}{16(1+2\kappa )}~, ~~ \theta :=\frac{1}{106n(1+2\kappa )^2}~~\text {and}~~\rho (\tau ):=\tau +\sqrt{1+\tau ^2}~. \end{aligned}$$

(39)

If we substitute $a(\tau )$ and $b(\tau )$ in the right-hand side of (38), we have

$$\begin{gathered} b(\tau )^{2} + 2a(\tau )^{2} + 2\kappa \left( {a(\tau ) + b(\tau )} \right)^{2} \hfill \\ + 2a(\tau )\sqrt {a(\tau )^{2} + b(\tau )^{2} + 2\kappa \left( {a(\tau ) + b(\tau )} \right)^{2} } \hfill \\ \end{gathered}$$

(40)

By simple calculation, we derive an upper bound of (40) as follows:

$$\begin{aligned}{} & {} b(\tau )^2+2a(\tau )^2+2\kappa \big (a(\tau )+b(\tau )\big )^2 +2a(\tau )\sqrt{a(\tau )^2+b(\tau )^2+2\kappa \big (a(\tau )+b(\tau )\big )^2}\nonumber \\{} & {} \quad =\Big ( a(\tau )+ \sqrt{a(\tau )^2+b(\tau )^2+2\kappa \big (a(\tau )+b(\tau )\big )^2 } ~\Big )^2 \nonumber \\{} & {} \quad \le \Big ( \big (1+\sqrt{1+2\kappa }~\big )~a(\tau )+\sqrt{1+2\kappa }~b(\tau )) \Big )^2 \nonumber \\{} & {} \quad \le \Bigg (3\Big (1 + \frac{1}{\sqrt{16\tau }}\Big ) \Big (\frac{1}{8\tau } - 1\Big )\Big (\frac{(16 \tau )^2(1+2 \tau )(2 + (1+2 \tau )^2)}{106}\Big )\nonumber \\{} & {} \qquad + \frac{8\tau ^3+4\tau ^2+4\tau }{\sqrt{16\tau }}\Bigg )^2 \nonumber \\{} & {} \quad =\frac{\tau }{2809} \Big (-89 - 144 \sqrt{\tau } + 115 \tau + 672 \tau ^{\frac{3}{2}} + 710 \tau ^2 + 3264 \tau ^{\frac{5}{2}} + 1056 \tau ^3 \nonumber \\{} & {} \qquad + 4224 \tau ^{\frac{7}{2}} + 768 \tau ^4 + 3072 \tau ^{\frac{9}{2}}\Big )^2, \end{aligned}$$

(41)

where in the second inequality, from (39), we use $\rho (\tau )=\tau +\sqrt{1+\tau ^2}\le 1+2\tau$ and $1+2\kappa =\frac{1}{16\tau }$. For $\kappa \ge 0$, $\tau = \frac{1}{16(1+2\kappa )}\in (0,\frac{1}{16}]$. By basic calculation, the last term (41) is less than or equal to $4\tau$. Hence $4\omega ^2\le 4\tau =\frac{1}{4(1+2\kappa )}$ which implies that $\omega \le \frac{1}{4\sqrt{1+2\kappa }}$ satisfying (31).

So far we compute the upper bound of $\omega$ for which (31) holds. This implies that (29) holds. Thus feasible step holds. Moreover, by (29) and Lemma 10, we have $\delta (v^{f})\le \frac{1}{1+2\kappa }$ which is the condition of Corollary 2.

Then we consider the centering steps to get $(x^+,s^+)$ that satisfy $(x^+)^{T}s^+=n\mu ^+$ and $\delta (x^+,s^+;\mu ^+)$ $\le \tau .$ By Corollary 2, the required number of centering steps can easily be obtained. Indeed, we assume that $\delta (x^f, s^f;\mu ^+) \le \frac{1}{2(1+2\kappa )}$. Starting at $(x^{f}, s^{f})$, by Corollary 2, after m centering steps, we have the iteration $(x^{(m)}, s^{(m)})$ that is still feasible for $(P_{\nu ^{+}})$ and we get

$$\begin{aligned} \delta (x^{(m)}, s^{(m)};\mu ^{+})\le & {} \sqrt{2} \big ( \sqrt{1+2\kappa }~\delta (x^{(m-1)}, s^{(m-1)};\mu ^{+}) \big )^2\\\le & {} \sqrt{2}(1+2\kappa )\Big (~ \sqrt{2} \big ( \sqrt{1+2\kappa }~\delta (x^{(m-2)}, s^{(m-2)};\mu ^{+}) \big )^2 \Big )^2\\\le & {} \Big ( \sqrt{2}(1+2\kappa ) \Big )^{2^{k}-1}\delta (x^{f}, s^{f};\mu ^{+})^{2^{k}}\\= & {} \frac{1}{\sqrt{2}(1+2\kappa )}\Big ( \sqrt{2}(1+2\kappa )\delta (x^{f}, s^{f};\mu ^{+}) \Big )^{2^{k}}\\\le & {} \frac{1}{\sqrt{2}(1+2\kappa )}\big ( \frac{1}{\sqrt{2}} \big )^{2^{k}}. \end{aligned}$$

Hence we have $\delta (x^{+},s^{+};\mu ^{+})\le \tau$ after at most

$$\left\lceil {1 + {\text{log}}_{2} \left( {{\text{log}}_{2} \frac{1}{{\sqrt 2 \tau (1 + 2\kappa )}}} \right)} \right\rceil = 1 + \left\lceil {{\text{log}}_{2} \left( {{\text{log}}_{2} \frac{1}{{\sqrt 2 \tau (1 + 2\kappa )}}} \right)} \right\rceil$$

(42)

centering steps.

Note that if an iteration (x, s) satisfies $\delta (x,s;\mu )\le \tau$, then after the feasible step, $\delta (x^{f},s^{f};\mu ^{+})\le \frac{1}{2(1+2\kappa )}$. According to (42), at most

$$1 + \left\lceil {\log _{2} \left( {\log _{2} \frac{1}{{\sqrt 2 \tau \left( {1 + 2\kappa } \right)}}} \right)} \right\rceil = 3$$

(43)

centering steps are needed to get $(x^{+},s^{+})$ such that $\delta (x^{+},s^{+};\mu ^{+})\le \tau$. In each main iteration both the duality gap and the norm of the residual vector are reduced by the factor $1-\theta$. Hence, the total number of outer iterations is bounded above by

$$\begin{aligned} \frac{1}{\theta }\log \frac{\max \{ (x^{0})^{T}s^{0},~\Vert r^{0}\Vert \}}{\epsilon }. \end{aligned}$$

Thus, from $\theta =\frac{1}{106n(1+2\kappa )^2}$ and (43), the total number of inner iterations is bounded above by

$$\begin{aligned} 318n(1+2\kappa )^2\log \frac{\max \{ (x^{0})^{T}s^{0},~\Vert r^{0}\Vert \}}{\epsilon }. \end{aligned}$$

In the following we state our main result without proof.

Theorem 1

Let ${\hat{\kappa }}$ be the handicap of $P_*(\kappa )$-matrix M. Assume that $\tau =\frac{1}{16(1+2\kappa )}$, $\theta = \frac{1}{106n(1+2\kappa )^2}$ and problem (1) has a solution $(x^{*},s^{*})$ such that $\Vert x^{*} \Vert _{\infty }\le \rho _{p}$ and $\Vert s^{*} \Vert _{\infty }\le \rho _{d}$, then after at most

$$\begin{aligned} 318n(1+2\kappa )^2\log \frac{\max \{ (x^{0})^{T}s^{0},~\Vert r^{0}\Vert \}}{\epsilon } \end{aligned}$$

iterations, the algorithm finds an $\epsilon$-approximate solution of (1).

5 Numerical tests

In this section, we present some preliminary numerical results of the Algorithm 1 for some $P_*(\kappa )$-LCPs.

In the following example, we compare the Algorithm 1 in this paper with the one in [32] with the kernel function $\psi _3$ in Table 1.

Example 1

We consider the $P_*(\kappa )$-LCP, where the matrices are given in [41]:

$$\begin{aligned} M_1= \begin{bmatrix} 0.1~&{} 0~ &{} 1 \\ 0~ &{} 0~ &{} 0 \\ 0~ &{} 0~ &{} 0.1 \end{bmatrix} \quad \text {and} \quad M_2= \begin{bmatrix} 0.9~&{} 0~ &{} 0 \\ 3~ &{} 1~ &{} 0 \\ 0~ &{} 3~ &{} 0.9 \end{bmatrix}. \end{aligned}$$

In [41], the handicap of matrices $M_1$ and $M_2$ is $\hat{\kappa _1} = \hat{\kappa _2} = 6$. Let the initial vectors as $x=\rho _{p}e,~s=\rho _{d}e$, and $\mu =\rho _{p}\rho _{d}$. For the convergence of the algorithm, we take the parameters as $\tau = \frac{1}{16(1+2\kappa )}$, $\theta _1=\frac{1}{106(1+\kappa )^2}$(for the Algorithm 1), $\theta _2=\frac{1}{33n(1+2\kappa )^3}$ ( [32]), and $\epsilon = 10^{-2}$.

Note that the solutions of both problems are $x^*=(1,0,3)$ and $s^* = (0,5,0)$. For IIPMs based on $\psi _j$, $1\le j\le 7$, no centering process occurs and the methods have the same number of iterations to have $\epsilon$-approximate solutions for both $\theta$ and M.

Table 4 shows that Algorithm 1 converges faster than the one in [32] for these examples. Note that the main difference between Algorithm 1 and the algorithm in [32] is the barrier update parameter $\theta$. For $\kappa = 6$, 10, and 20, we compare the execution time for two methods under the same conditions except the parameter $\theta$.

Table 4 Computation time comparison

6 Conclusions

In this paper, we propose a new full-Newton step IIPMs for $P_*(\kappa )$-LCP based on new class of (1/t)-bound kernel functions which includes the existing kernel functions in [26, 31,32,33,34] as special cases. We prove that the convergence is guaranteed for any (1/t)-bound kernel functions. Also we show that the Algorithm 1 has the best known complexity for such a method and we show that our algorithm have good performance in the numerical tests for some examples. It is worth noting that there is no centering step in the numerical tests.

For the future research, we study the gap between the complexity theory and practice during the centering process. Furthermore, we extend our method to more general problem such as $P_*(\kappa )$-symmetric cone LCP, etc.