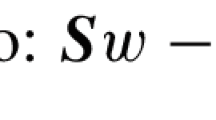Stochastic programming with primal–dual dynamics: a mean-field game approach

Abstract

This study addresses primal–dual dynamics for a stochastic programming problem for capacity network design. It is proven that consensus can be achieved on the here and now variables which represent the capacity of the network. The main contribution is a heuristic approach which involves the formulation of the problem as a mean-field game. Every agent in the mean-field game has control over its own primal–dual dynamics and seeks consensus with neighboring agents according to a communication topology. We obtain theoretical results concerning the existence of a mean-field equilibrium. Moreover, we prove that the consensus dynamics converge such that the agents agree on the capacity of the network. Lastly, we emphasize the ways in which penalties on control and state influence the dynamics of agents in the mean-field game.

1 Introduction

Motivated by a stochastic program for the network capacity design and flow optimization, we cast for the first time primal–dual dynamics in the framework of mean-field games. We consider a scenario where demand materializes at some geographic spots and goods are transported from warehouses to fulfill such demand. We first model the problem as a two stage stochastic program for supply chain network design in the same spirit as in Ch. 1.5 [28]. Demand materializes at some nodes and goods flow over the edges. The flow in each edge is subject to capacity constraints and the flows in and out of each node must satisfy flow conservation constraints. The resulting optimization model is a constrained stochastic nonlinear (quadratic) two-stage program.

Continuous-time primal–dual gradient dynamics, also known as saddle-point dynamics, were first introduced in [2, 20]. Primal–dual dynamics is used in a number of application domains such as energy resource allocation [17], cyber-physical systems [26], wireless communications networks [11], smart grids [34], just to name a few. Recent works have been dedicated to exponential stability analysis of primal–dual dynamics [12, 24, 27, 30]. Furthermore, analysis on robustness has been performed in [15, 19, 25]. Also, the global/local nature of the convexity-concavity properties of the primal–dual dynamics was examined. Explicit attention has been paid to asymptotic stability properties of the primal–dual dynamics in [13, 14, 16, 29]. Primal–dual dynamics and stochastic gradient descent has been recently studied in [8]. The extension to large scale problems is possible through parallelization and using elastic averaging stochastic gradient descent algorithms [9].

There is less work dedicated to the combination of primal–dual dynamics with mean-field games. However, there have been studies concerning Lagrangian relaxation methods to solve mean-field games, such as in [1], where a planning problem is discussed. Additionally, in [32] and [33] Lagrangian relaxation is used in mean-field game power control. More recently a primal–dual approach has been used to solve constrained mean-field games [10]. Mean-field games in the form of coupled partial differential equations originated in the works of Lasry and Lions [21,22,23]. Explicit closed-form expressions for mean-field equilibria were first proposed for linear-quadratic mean-field games [3] and have been extended to more general cases in [18]. This paper mainly follows the linear-quadratic mean-field game formulation as in [4,5,6].

The main contribution is a heuristic approach which involves the reformulation of the original problem into a large number of stochastic primal–dual dynamics which are coupled in the same spirit as in mean-field games. To be more specific, we consider the instance of a large number of agents, each assigned with a primal–dual dynamics subject to a specific realization of the demand. The players of the mean-field game have to obtain consensus over the here and now decision variables: the capacity of each edge of the supply chain network. We also consider wait and see decision variables for flow and the Lagrange multipliers coming from the primal–dual dynamics. Note the analogy with a two-player zero-sum game whereby the first player, the minimizer, sets the here and now variables required to accommodate for any potential scenario concerning flow and demand realization. Subsequently, the second player, the maximizer, sets the wait and see variables to maximize demand satisfaction given the decision of player 1 and the realized demand. The condition for convergence to a consensus value is that the communication network of agents needs to be connected, i.e., for any pair of nodes there exists a path connecting them. We first transform the primal–dual dynamics into a mean-field game, after which theoretical results are provided concerning a mean-field equilibrium solution in the same spirit as in [4,5,6]. Lastly, we provide numerical simulations to prove once again that consensus is obtained. Since the proposed methodology is heuristic in nature, the convergence values are in general sub-optimal.

The proposed model and methodology is original as it involves turning the micro-network model into a set of primal–dual dynamics and after that into a mean-field game in which each agent faces a different realization of the uncertain demand. We see this as a value and believe that the link between primal–dual dynamics and mean-field games expands the significance, meaning, and potential of mean-field games approaches beyond the ones already in the literature. Note also that the obtained mean-field game depends strongly on the micro-network optimization parameters. Actually, the incidence matrix, the penalty coefficients and the uncertain demand enter into the mean-field dynamics of the optimization flow and capacity variables as well as of the Lagrange multipliers.

This paper is organized as follows. In Sect. 2, we formulate the stochastic programming for network design. In Sect. 3, we present the primal–dual dynamics. In Sect. 4, we present the corresponding mean-field game. In Sect. 5, we state theoretical results on mean-field equilibrium and convergence. In Sect. 6, we provide a simulation example to corroborate our results. Lastly, in Sect. 7, we provide concluding remarks and discuss future works.

2 Stochastic programming for network design

Let us consider a physical flow network (referred to as micro-network) denoted as G(V, E). Let the set of nodes be $V \in \{V_1, V_2,\ldots , V_n\}$, where each node corresponds to an agent in the network. The parameter n denotes the number of nodes present in the network. Let the set of edges be $E \in \{E_1, E_2,\ldots ,E_m\}$. The parameter m denotes the number of edges in the network. The demand is described by a vector $w \in {\mathbb {R}}^{n\times 1}$ and is an uncertain random parameter. The capacity of the edges are the here and now variables and are denoted by $c \in {\mathbb {R}}^{m\times 1}$. The transported goods in each edge are the wait and see variables and are denoted by $u \in {\mathbb {R}}^{m\times 1}$. A graphical representation of the micro-network can be found in Fig. 1.

Fig. 1

A graphical representation of the directed network corresponding to the first problem instance

Let $f_1(c)=\frac{1}{2}c^T{\tilde{Q}}_1c+{\tilde{f}}_1^Tc$ be the cost associated to the capacity of the edges in the micro-network, and $f_2(u)=\frac{1}{2}u^T{\tilde{Q}}_2u+{\tilde{f}}_2^Tu$ be the cost charged for using the edges to transport goods such that the demand is satisfied. In the above costs we have a quadratic and a linear term. The matrices ${\tilde{Q}}_1,{\tilde{Q}}_2\in {\mathbb {R}}^{m\times m}$ are the cost coefficients for the quadratic term, and ${\tilde{f}}_1,{\tilde{f}}_2\in {\mathbb {R}}^m$ are the linear cost coefficients. We model the supply chain network design problem as a two-stage stochastic program as follows:

$$\begin{aligned} \begin{aligned} \min \quad f_1(c)+{\mathbb {E}}_w{\hat{Q}}(c,w)\\ \begin{aligned} s.t.\quad u,c&> 0. \end{aligned} \end{aligned} \end{aligned}$$

(1)

Note that the objective function that we wish to minimize describes the total cost of transporting goods. The optimization variables in this problem are the capacity of the edges $c\in {\mathbb {R}}^{m\times 1}$, and the flow in the edges $u\in {\mathbb {R}}^{m\times 1}$. The capacities c are the first-stage decision variables, and they are obtained before the realization of the demand. The optimal capacities are independent of the demand, however they have to accommodate any realization of it. On the other hand, the flows u are the second-stage decision variables, they depend on the values of the first-stage variables and they are obtained after observing the realized demand. In addition, ${{\tilde{B}}}\in {\mathbb {R}}^{n\times m}$ is the incidence matrix of the micro-network, ${\mathbb {E}}_w(.)$ denotes expectation with respect to w and ${\hat{Q}}(u,w)$ denotes the sub-optimal value of the second-stage problem, namely

$$\begin{aligned} {\hat{Q}}(c,w):=\min _u\{f_2(u)|{{\tilde{B}}}u =w,u\le c\}. \end{aligned}$$

Observe that as ${\hat{Q}}(c,w)$ depends on the capacities of the edges c and on the random variable w, the optimal value of the second-stage problem is also a random variable. Hence, we can obtain its expected value with respect to the demand, namely ${\mathbb {E}}_w{\hat{Q}}(c,w)$, which is included in the objective function of the two-stage stochastic program (1).

3 Primal–dual dynamics

In this section we introduce the stochastic primal–dual dynamic related to the two-stage stochastic program (1).

Let $\omega$ be a constant demand vector randomly extracted from the same distribution of w. To obtain the primal–dual dynamics associated with this particular realization of the two-stage program (1) we first derive the Lagrangian function as follows:

$$\begin{aligned} \begin{aligned} \mathcal {L}(u,c,\lambda ,\mu )&= f_1(c)+\lambda ^T({{\tilde{B}}}u-\omega )+\mu ^T(u-c) + f_2(u) \\&= f_1(c)+\left[ {{\tilde{B}}}^T\lambda +\mu \right] ^Tu-\mu ^Tc-\lambda ^T \omega + f_2(u) \\&= f_1(c) + \left[ \begin{bmatrix}I\\ -I \end{bmatrix} \mu + \begin{bmatrix} {{\tilde{B}}}^T \\ 0 \end{bmatrix}\lambda \right] ^T \begin{bmatrix}u\\ c \end{bmatrix}-\omega ^T\lambda + f_2(u), \end{aligned} \end{aligned}$$

where $\mu \in {\mathbb {R}}^{m\times 1}$ and $\lambda \in {\mathbb {R}}^{n\times 1}$ are the Lagrange multipliers.

The Lagrange dual problem can then be formulated as follows:

$$\begin{aligned} \begin{aligned} \inf _{u,c}\Biggl \{ f_1(c) + \left[ \begin{bmatrix}I\\ -I \end{bmatrix} \mu + \begin{bmatrix} {{\tilde{B}}}^T \\ 0 \end{bmatrix}\lambda \right] ^T \begin{bmatrix}u\\ c \end{bmatrix} -\omega ^T\lambda +f_2(u) \Biggr \} \end{aligned}. \end{aligned}$$

By imposing that the gradient of the Lagrangian with respect to u and c vanishes, we obtain the following Karush–Kuhn–Tucker (KKT) conditions:

$$\begin{aligned} \begin{bmatrix} \nabla _uf_2(u) \\ \nabla _cf_1(c) \end{bmatrix}+ \begin{bmatrix} I\\ {}-I \end{bmatrix} \mu +\begin{bmatrix} {{\tilde{B}}}^T\\ 0\end{bmatrix}\lambda = 0. \end{aligned}$$

(2)

The corresponding primal–dual dynamics are obtained from the gradient descent and gradient ascent dynamics over u and c respectively as shown next:

$$\begin{aligned} {\left\{ \begin{array}{ll} \begin{aligned} \dot{u}&{}=\Bigl [-\nabla _u\mathcal {L}\Bigr ]_+ =\Bigl [-{\widetilde{Q}}_2u-{\widetilde{f}}_2-\mu - {{\tilde{B}}}^T\lambda \Bigr ]_+, \\ \dot{c}&{}= \Bigl [-\nabla _c\mathcal {L}\Bigr ]_+ =\Bigl [-{\widetilde{Q}}_1c-{\widetilde{f}}_1+\mu \Bigr ]_+, \\ \dot{\lambda }&{}= +\nabla _\lambda \mathcal {L}={{\tilde{B}}}u-\omega , \\ \dot{\mu }&{}= \Bigl [+\nabla _\mu \mathcal {L}\Bigr ]_+ = \Bigl [ u-c\Bigr ]_+. \end{aligned} \end{array}\right. } \end{aligned}$$

(3)

In compact form, the above set of differential equation can be written as

$$\begin{aligned} \begin{aligned} \begin{bmatrix} \dot{u}\\ \dot{c}\\ \dot{\lambda }\\ \dot{\mu }\end{bmatrix}&=\begin{bmatrix} -{\widetilde{Q}}_2&{}0&{}-{{\tilde{B}}}^T&{}-I\\ 0&{}-{\widetilde{Q}}_1&{}0&{}I\\ B&{}0&{}0&{}0\\ I&{}-I&{}0&{}0 \end{bmatrix}\begin{bmatrix}u\\ c\\ \lambda \\ \mu \end{bmatrix}+\begin{bmatrix}-{\widetilde{f}}_2\\ {}-{\widetilde{f}}_1\\ {}-\omega \\ 0 \end{bmatrix} \\&\in {\mathbb {R}}^m_+ \times {\mathbb {R}}^m_+ \times {\mathbb {R}}^n \times {\mathbb {R}}^m_+. \end{aligned} \end{aligned}$$

(4)

In the two-stage program (1) the capacity vector c needs to be the same for any realization of the demand w, namely for any value of $\omega$ in the support of w. This implies that the primal–dual dynamics (4) obtained for different realization $\omega$ need to reach consensus on c. We show that this is possible by developing an ad-hoc mean-field game model in the following section.

4 Construction of the mean-field game

Let us now introduce a two-layer network as in Fig. 2. Layer 1 involves the communication topology among different populations (henceforth referred to as macro-network) denoted as ${{\hat{G}}}({{\hat{V}}},{{\hat{E}}}),$ whereas layer 2 comprises the physical flow network (micro-network) as introduced in Sect. 2, denoted as G(V, E). Each node in the macro-network ${\hat{G}}({\hat{V}},{\hat{E}})$ represents a different population. All populations in ${\hat{G}}$ have the same topology of their micro-network G. Hence, they are characterized by the same incidence matrix ${\tilde{B}}$ and the same cost functions $f_1$ and $f_2$. However, each agent in the population has a different realization of the demand. The aim is to obtain a feasible solution to the two-stage stochastic program (1) by reaching consensus on the capacities of the edges between any agent in the population and across all populations.

Fig. 2

Two-layer network: macro-network ${{\hat{G}}}({{\hat{V}}},{{\hat{E}}})$ in layer 1 and micro-network G(V, E) in layer 2

We use the macro-network to model a distributed optimization setting. In this section we present a heuristic approach that turns the two-stage stochastic program (1) into a mean-field game, where each player corresponds to an agent in each population, and it is assigned to a primal–dual dynamics according to its demand realization. This new approach represents a distributed optimization problem, which enables the agents to reach consensus on the edges’ capacities, and it provides a feasible solution to problem (1) by taking into account the communication between populations.

Consider $|{\hat{V}}|=p$ populations such that each agent in our game belongs to a population $k\in \left\{ 1,\ldots ,p\right\}$ and is characterized by a primal–dual dynamics (4) obtained for a particular realization $\omega$ of the demand. The generic agent in population k is characterized by its state x(t) which involves the decision variables (flows and capacities) and the Lagrange multipliers of problem (1), namely $x(t):=[u^T \, c^T \, \lambda ^T \, \mu ^T]^T \in {\mathbb {R}}^{3m+n}$. At each time t and for a given time horizon window [0, T], x(t) evolves according to the primal–dual dynamics in (4) under the control variable v as follows:

$$\begin{aligned} \begin{aligned} \underbrace{\begin{bmatrix} \dot{u}\\ \dot{c}\\ \dot{\lambda }\\ \dot{\mu }\end{bmatrix}}_{\dot{x}}&=\underbrace{\begin{bmatrix} -{\widetilde{Q}}_2&{}0&{}-{{\tilde{B}}}^T&{}-I\\ 0&{}-{\widetilde{Q}}_1&{}0&{}I\\ {{\tilde{B}}}&{}0&{}0&{}0\\ I&{}-I&{}0&{}0 \end{bmatrix}}_A\underbrace{\begin{bmatrix}u\\ c\\ \lambda \\ \mu \end{bmatrix}}_x+\underbrace{\begin{bmatrix}-{\widetilde{f}}_2\\ {}-{\widetilde{f}}_1\\ {}-\omega \\ 0 \end{bmatrix}}_C + \underbrace{\begin{bmatrix} 0 &{} \dots &{} \dots &{} 0 \\ \vdots &{} {\mathbf {1}} &{} \dots &{} \vdots \\ \vdots &{} \vdots &{} \ddots &{}\vdots \\ 0 &{} \dots &{} \dots &{} 0 \end{bmatrix}}_Bv\\&\in {\mathbb {R}}^m_+ \times {\mathbb {R}}^m_+ \times {\mathbb {R}}^n \times {\mathbb {R}}^m_+. \end{aligned} \end{aligned}$$

(5)

Here, $\omega$ is a constant sample randomly extracted from the same distribution of the demand in (1) and v is an additional control input that we use to force consensus on the edge capacities c. Note that (5) can be written in compact form as $\dot{x}=Ax+Bv+C=:f(x,v)$. Now let us consider a probability density function that describes the density of the agents in a population in state x at time t, $m_k(x,t)$, with the property $\int _{{\mathbb {R}}^{3m+n}} m_k(x,t)dx=1$. Then the mean states can be computed following ${\overline{m}}_k(t)=\int _{{\mathbb {R}}^{3m+n}} xm_k(x,t)dx$.

So far, we have considered the populations separately. To describe the interaction between populations we take into account the topology of the macro-network ${\hat{G}}$. Let us associate population k with agent k. Then we can introduce an interaction topology between agents, say ${{\hat{G}}}=\{{{\hat{V}}},{{\hat{E}}}\}$, and we can define the neighbors of an agent k in ${{\hat{G}}}$ as:

$$\begin{aligned} N(k) = \left\{ j \in {{\hat{V}}} \mid (k,j) \in {{\hat{E}}} \right\} . \end{aligned}$$

In order to reach consensus, each population is interested in knowing the local average state of its neighbours, which is given by:

$$\begin{aligned} \rho _k=\frac{\sum _{j\in N(k)}{\overline{m}}_j}{|N(k)|}. \end{aligned}$$

(6)

Here, |N(k)| denotes the cardinality of neighbor set k. Let us now consider a running cost function $g(x,\rho _k,v)$ and a terminal cost function $\psi (\rho _k,x)$, which are defined as follows:

$$\begin{aligned} \begin{aligned} g(x,\rho _k,v)&=\frac{1}{2}(\rho _k-x)^TQ(\rho _k-x)+\frac{1}{2}v^TRv,\\ \psi (\rho _k,x)&=\frac{1}{2}S(\rho _k-x)^2. \end{aligned} \end{aligned}$$

The first term in the expression for g assigns a penalty to the state deviating from the mean $\rho _k$. The second term assigns a penalty on control. The matrices Q, S and R are diagonal matrices of compatible dimensions.

Every agent in population k wishes to solve the following problem:

$$\begin{aligned} \min _{v(\cdot )}{\mathbb {E}}\int _0^T[g(x,\rho _k,v)]dt + \psi (\rho _k(T),x(T)) \end{aligned}$$

(7)

subject to

$$\begin{aligned} \dot{x}=Ax+Bv+C \in {\mathbb {R}}^m_+ \times {\mathbb {R}}^m_+ \times {\mathbb {R}}^n \times {\mathbb {R}}^m_+. \end{aligned}$$

The optimal control problem as in (7) has the structure of an optimal tracking problem. The objective function in (7) captures the minimization of the total expected cost. The aim is to reach consensus by minimizing the deviations of the state x from the local average of each population $\rho _k$. This is denoted by the quadratic error term $(\rho _k-x)^TQ(\rho _k-x)$ in the running cost function g, and by $S(\rho _k-x)^2$ in the terminal cost function $\psi$. The term $\frac{1}{2}v^TRv$ in the cost g penalises the energy of the control. The affine dynamics $\dot{x}=Ax+B\nu +C$ in the constraints comes from the primal–dual dynamics explained in the previous section.

For every population k, denote the value of the optimization problem starting at time t and state x by $\sigma _k(x,t)$. Let us also denote by $m_k(x,0)=m_{k0}(x)\in {\mathbb {R}}$ the initial density of the agents of population k in state x. This results in the following mean-field game in $\sigma _k(x,t)$ and $m_k(x,t)$:

$$\begin{aligned} {\left\{ \begin{array}{ll} \partial _t\sigma _k(x,t)+\left\{ f(x,v^*)^T\partial _x\sigma _k(x,t)+g(x,\rho _k,v^*)\right\} = 0, \\ \sigma _k(x,T) = \psi (\rho _k(T),x), \\ \partial _tm_k(x,t)+div(m_k(x,t)f(\cdot ))=0. \end{array}\right. } \end{aligned}$$

(8)

Any solution of (8) is referred to as the mean-field equilibrium, which provides the sub-optimal values for the wait and see variables. Note that the second and fourth equation from (8) are the boundary conditions, while the third equation is the advection equation.

The optimal time-varying state-feedback control can be computed for every single agent in population k and is given by:

$$\begin{aligned} \begin{aligned} v^*(x,t)&\in \arg \min _v \bigl \{ (Ax+Bv+C)^T\partial _x\sigma _k(x,t) +g(x,\rho _k(t),v) \bigr \}. \end{aligned} \end{aligned}$$

(9)

In this expression, note that the Hamiltonian appears as the argument of the minimizer.

5 Mean-field equilibrium and convergence

In this section, we obtain an expression for the mean-field control and provide results for the mean-field equilibrium dynamics.

Lemma 1

The mean-field game takes the form:

$$\begin{aligned} {\left\{ \begin{array}{ll} \partial _t\sigma _k(x,t)-\frac{1}{2}(\partial _x\sigma _k(x,t))^T \left[ BR^{-1}B^T \right] \partial _x\sigma _k(x,t) +\frac{1}{2}(\rho _k-x)^TQ(\rho _k-x)=0, \\ \sigma _k(x,T)=\psi (\rho _k(T),x), \\ \partial _tm_k(x,t) +\partial _x\left[ m_k(x,t)(Ax-BR^{-1}B^T\partial _x\sigma _k(x,t) +C) \right] =0. \end{array}\right. } \end{aligned}$$

(10)

Additionally, the optimal control is:

$$\begin{aligned} v^*=-R^{-1}B^T\partial _x\sigma _k(x,t). \end{aligned}$$

(11)

In this set of equations, the first equation corresponds to the Hamilton–Jacobi–Isaacs equation, and the third equation corresponds to the Fokker-Planck-Kolmogorov equation. The proof of Lemma 1 can be found in Appendix A.

We assume that the time evolution of the common state is known and, subsequently, investigate the solution of the Hamilton–Jacobi equation. Consider the following problem with known $\rho _k$:

$$\begin{aligned} \min _{v(\cdot )}{\mathbb {E}}\int _0^T \left[ g(X(t),\rho _k(t),v(t)) \right] dt \end{aligned}$$

(12)

where

$$\begin{aligned} \dot{x}=Ax+Bv+C \in {\mathbb {R}}^m_+ \times {\mathbb {R}}^m_+ \times {\mathbb {R}}^n \times {\mathbb {R}}^m_+. \end{aligned}$$

The next theoretical result presents the mean-field equilibrium control. In preparation to that, let us consider a probability density function that describes the density of the agents of a population in state c for the capacity of the edges at time t, $m_k(c,t)$, with the property $\int _{{\mathbb {R}}^{m}} m_k(c,t)dc=1$. Then the mean states can be computed following ${\overline{m}}_k^c(t)=\int _{{\mathbb {R}}^{m}} c m_k(c,t)dc$.

We define an agent’s objective in population k based on the aggregate kth state as:

$$\begin{aligned} \rho _k^c=\frac{\sum _{j\in N(k)}{\overline{m}}_j^c}{|N(k)|}. \end{aligned}$$

(13)

In the following, given a generic matrix $A \in {\mathbb {R}}^{(3m+n) \times (3m+n)}$ we denote by $A_c \in {\mathbb {R}}^{m}$ the matrix obtained extracting the rows and columns associated with the only variables $c \in {\mathbb {R}}^{m \times m}$. In addition, we consider the following value function:

$$\begin{aligned} \sigma _k(x,t)=\frac{1}{2}x^T\Phi (t)x+H(t)^Tx+\chi (t) \end{aligned}$$

(14)

and denote

$$\begin{aligned} {\widetilde{Z}}:=\left[ A^T-2\Phi BR^{-1}B^T \right] ^{-1}. \end{aligned}$$

Theorem 1

A mean-field equilibrium for the dynamics of (10) is obtained from the following set of equations:

$$\begin{aligned} {\left\{ \begin{array}{ll} \sigma _k(x,t)=\frac{1}{2}x^T\Phi (t)x+H(t)^Tx+\chi (t), \\ \begin{aligned} \dot{{\overline{m}}}_k(t)&{}=\left[ A-BR^{-1}B^T\Phi (t)\right] {\overline{m}}_k(t)\\ &{}-BR^{-1}B^TH(t)+C, \end{aligned} \end{array}\right. } \end{aligned}$$

(15)

where

$$\begin{aligned} {\left\{ \begin{array}{ll} \begin{aligned} \dot{\Phi }(t)&{}+A^T\Phi (t)+\Phi ^T\left[ -BR^{-1}B^T\right] \Phi (t)+Q=0 \\ &{}\in [0,T[,\quad \Phi (T)=S, \end{aligned}\\ \begin{aligned} \dot{H}(t)&{}-2\Phi (t) BR^{-1}B^T H(t)+A^TH(t)\\ &{}+\Phi (t)^TC-Q\rho _k(t)=0 \in [0,T[,\\ &{}\quad H(T) = -S\rho _k(T), \end{aligned} \\ \begin{aligned}\dot{\chi }&{}+H(t)^T\left[ BR^{-1}B^T\right] H(t)+H(t)^TC\\ &{}+\frac{1}{2}\rho _k(t)^TQ\rho _k(t)\in [0,T[,\quad \chi (T)=\frac{1}{2}\rho _k^T(T)S\rho _k(T). \end{aligned} \end{array}\right. } \end{aligned}$$

(16)

Additionally, if the inverse matrix ${\widetilde{Z}}$ exists, the mean-field equilibrium control is:

$$\begin{aligned} v^*=-R^{-1}B^T(\Phi (t)^Tx+H(t)). \end{aligned}$$

(17)

If the inverse matrix ${\widetilde{Z}}$ does not exist, let us denote by $\hat{H}(t)$ the approximation of matrix H(t) obtained by applying the least squares method. Then the mean-field equilibrium control is:

$$\begin{aligned} v^*=-R^{-1}B^T(\Phi (t)^Tx+\hat{H}(t)). \end{aligned}$$

(18)

Furthermore, for infinite time horizon $T \rightarrow \infty$, and for all aggregate states ${\overline{m}}^c = \left( {\overline{m}}_1^c,{\overline{m}}_2^c,\ldots ,{\overline{m}}_p^c \right)$, we have the following consensus-type dynamics:

$$\begin{aligned} \dot{{\overline{m}}}^c = - {{\tilde{\mathbf {Q}}}_1} {\overline{m}}^c(t) -L {\overline{m}}^c(t) +\delta , \end{aligned}$$

(19)

where ${{\tilde{\mathbf {Q}}}_1}:=diag({{\tilde{Q}}}_1)$ (diagonal matrix with block entry ${{\tilde{Q}}}_1$), $\delta =R_c^{-1} \Big ( {\widetilde{Z}}_c \Phi _c^T \mu + (-{\widetilde{Z}}_cQ_c - \Phi _c^T) \rho _c^k \Big ) +(\mu -{{\tilde{f}}}_1)$ if the inverse matrix ${\widetilde{Z}}$ exists, or $\delta =R_c^{-1} \Big (\hat{H} - \Phi _c^T\rho _c^k \Big )+(\mu -{{\tilde{f}}}_1)$ if the inverse does not exist, and L is defined as the graph-Laplacian matrix where the kjth entry is the block matrix:

$$\begin{aligned} L_{kj} = {\left\{ \begin{array}{ll} R_c^{-1} \Phi _c^T &{} \quad j=k, \\ \frac{1}{|N(k)|}R_c^{-1} \Phi _c^T &{} \quad j \ne k, j \in N(k), \\ 0 &{} \quad otherwise. \end{array}\right. } \end{aligned}$$

(20)

This result is relevant since we can solve (15) in closed form and we show that consensus is ultimately achieved among agents. The proof of Theorem 1 can be found in Appendix B.

Remark 1

Note that based on the way in which we have defined the mean-field game it is not possible to guarantee convergence to the optimal solution. We can only guarantee convergence of the agents to a feasible solution. It is important to highlight that the mean-field game introduced in this manuscript has similarities with the distributed subgradient algorithm used to solve distributed optimization problems [26]. From (19) we can observe that the term ${{\tilde{\mathbf {Q}}}_1} {\overline{m}}^c(t)$, which corresponds to the costs of the edges capacities, is related to the gradient dynamics of variable c. On the other hand, the term $L {\overline{m}}^c(t)$ enforces consensus, as it aims to minimize the deviation of $\bar{m}_k^c$ from $\rho _k^c$. It is worth mentioning that in the distributed subgradient method a step-size $\gamma (t)$ is applied, and convergence to a feasible solution is only guaranteed for a diminishing step size. Nevertheless, based on (19), one can assume that the step-size for the approach introduced in this paper is always $\gamma =1$. There exist other algorithms that can be applied to solve distributed optimization problems. One of these algorithms is the gradient tracking method [26]. This method tracks the gradient of the cost function and not only the value of the optimization variables. By applying the gradient tracking algorithm it has been proven that it is possible to reach consensus to the optimal value. However, the study of the gradient tracking algorithm is outside of the scope of this research.

6 Simulation example

In this section we present a numerical example of a capacity network design for a supply chain network. We show that the agents in the macro-network reach consensus on the edges’ capacities of their respective micro-networks. We analyse the ways in which penalties on control and state influence the dynamics of the agents in the mean-field game. Furthermore, we run various simulations under different scenarios to investigate the sub-optimality of the algorithm built on the mean-field game.

Consider a scale-free network where $p=1000$ agents. The agents only consider the local average computed over its neighbors according to (6). Furthermore, we generate stochastic demand according to the normal distribution at every time instance for the nodes of the micro-networks displayed in Fig. 1. This makes the constant term vector C change over time since $\omega$ is now renewed at every time instance. Prior to the simulation, we parametrize the system as follows:

$$\begin{aligned} \omega = \begin{bmatrix}0&0&23&7&0&0\end{bmatrix}^T,\quad {\widetilde{Q}}_1 = I^{9\times 9}, \quad {\widetilde{Q}}_2 = I^{9\times 9}\\ {\widetilde{f}}_1 = \begin{bmatrix}1&1&1&1&1&1&1&1&1\end{bmatrix}^T,\quad {\widetilde{f}}_2 = \begin{bmatrix}1&1&1&1&1&1&1&2&1 \end{bmatrix}^T \\ C = \begin{bmatrix}-{\widetilde{f}}_2 \\ -{\widetilde{f}}_1 \\ -\omega \\ {\mathbb {O}}^{9\times 1} \end{bmatrix},\quad B=\begin{bmatrix} {\mathbb {O}}^{9\times 1} \\ {\mathbf {1}}^{9\times 1} \\ {\mathbb {O}}^{15\times 1} \end{bmatrix}, \quad {\tilde{B}} = \begin{bmatrix} 1 &{} 0 &{} -1 &{} -1 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 1 &{} 0 &{} 0 &{} -1 &{} -1 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 1 &{} 1 &{} 0 &{} 0 \\ 0 &{} 0 &{} 1 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 1 \\ 0 &{} 0 &{} 0 &{} 1 &{} 1 &{} 0 &{} 0 &{} -1 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} -1 &{} 1 &{} -1 \end{bmatrix}, \\ A = \begin{bmatrix}-{\widetilde{Q}}_2 &{} {\mathbb {O}}^{9\times 9} &{} -B_I^T &{} -I^{9\times 9} \\ {\mathbb {O}}^{9\times 9} &{} -{\widetilde{Q}}_1 &{} {\mathbb {O}}^{9\times 6} &{} I^{9\times 9} \\ B_I &{} {\mathbb {O}}^{6\times 9} &{} {\mathbb {O}}^{6\times 6} &{} {\mathbb {O}}^{6\times 9} \\ I^{9\times 9} &{} -I^{9\times 9} &{} {\mathbb {O}}^{9\times 6} &{} {\mathbb {O}}^{9\times 9} \end{bmatrix}, \quad R = 1,\quad Q = \begin{bmatrix} {\mathbb {O}}^{9\times 9} &{} \dots &{} \dots &{} {\mathbb {O}}^{9\times 9} \\ \vdots &{} {\mathbf {1}}^{9\times 9} &{} \dots &{} \vdots \\ \vdots &{} \vdots &{} \ddots &{}\vdots \\ {\mathbb {O}}^{9\times 9} &{} \dots &{} \dots &{} {\mathbb {O}}^{9\times 9} \end{bmatrix} \in {\mathbb {R}}^{33\times 33}. \end{aligned}$$

Note that in our example, the penalty of using flow $u_8$ is twice the penalty on the other flows since we wish to keep the flows balancing $w_4$ and $w_3$ as much distinct as possible. In general, any route can be incentivised by adjusting penalties and this emphasizes the versatility of our approach. Furthermore, in Table 1 the following additional simulation parameters are defined: time step $\delta t$, mean and standard deviation of initial states of the primal–dual dynamics ${\widetilde{\sigma }}_0$ and ${\widetilde{\mu }}_0$; mean and standard deviation of demand at node 3, denoted ${\widetilde{\mu }}_{3}$ and ${\widetilde{\sigma }}_{3}$; and mean and standard deviation of demand at node 4, denoted ${\widetilde{\mu }}_{4}$ and ${\widetilde{\sigma }}_{4}$. The multi-population considered allows the simulation algorithm to be initialized with different initial conditions and also allows to accommodate different realizations of the wait and see variables.

Table 1 Simulation parameters and their respective values

We use the parameters mentioned above as input for the following simulation algorithm by which we compute the states of each agent over time.

Figures 3a–c depict the evolution of the edges’ capacities over time for all agents. Figure 3a shows a simulation where the penalty on control equals the penalty on state deviation, i.e., $Q=R=1$. Figure 3b presents a simulation of the mean-field game where the penalty on state deviation is increased, namely $Q=10$, $R=1$. On the contrary, the results of a mean-field game simulation where $Q=1$, $R=10$ can be found in Fig. 3c.

Fig. 3

Simulation of the mean-field game for different values of the penalty on control R and the penalty on state deviations Q

By setting the penalty on state deviation sufficiently high as it was done in the simulation of Fig. 3b, the states converge to closer values compared to the case where Q and R are equal. This is in accordance to intuition as in the case of Fig. 3b states deviation from $\rho_k$ incur in a higher penalty. Conversely, by setting the penalty on control sufficiently high, convergence is obtained quicker in comparison to the simulation where Q and R are equal. In this situation, the system is penalized more to make adjustments and this explains the thinner lines in the converged region. Another observation is that, in this case, the best strategy to pursue the minimization problem is to choose a different solution compared to the simulations of Fig. 3a, b.

From the examples presented above, let us consider the best strategy for the minimization, which is when the penalty on the states deviations is $Q=1$ and the penalty on the control is $R=10$. To analyse the sub-optimality of the algorithm for the mean-field game, we compare the flows and capacities obtained from the consensus in the mean-field game with the values obtained by solving the primal–dual dynamics as it is explained in Sect. 3, and with the real optimal values obtained by solving (1). We compare the capacities and flows obtained from the different methods by evaluating the values of the objective function in (1). Furthermore, for the mean-field game we obtain a lower bound of the objective function by relaxing the constraint on consensus on the capacities of the edges.

In Fig. 4a we display the evolution over time of the objective function for the different methods applied to solve the two-stage stochastic program (1). Note that when the agents reach consensus on the capacities, the value of the objective function obtained from the mean-field game becomes an upper bound of the real optimal value. On the other hand, we can observe that the value of the objective function when we relax the constraint on consensus becomes a lower bound of the value of the objective function of the mean-field game when we take into account the consensus constraint.

Let us denote by $F_{MFG}$, $F_{NC}$, $F_{PD}$, $F_{O}$ the value of the objective function obtained from the mean field game, the value of the objective function obtained by relaxing the constraints on consensus, the value of the objective function obtained from the primal–dual dynamics and the value of the objective function obtained from the real optimum, respectively. To analyse the differences between the different approaches, we compute the percentage errors between the values of the objective function obtained from the mean-field game and the values of the objective function using the other methods as follows:

$$\begin{aligned}&\% \text{ Error } \text{ MFG } \text{ consensus } \text{ vs } \text{ Non } \text{ Consensus }=\frac{F_{MFG}-F_{NC}}{F_{NC}},\\&\% \text{ Error } \text{ MFG } \text{ consensus } \text{ vs } \text{ Primal--dual }=\frac{F_{MFG}-F_{PD}}{F_{PD}},\\&\% \text{ Error } \text{ MFG } \text{ consensus } \text{ vs } \text{ Optimal } \text{ value }=\frac{F_{MFG}-F_{O}}{F_{O}}. \end{aligned}$$

In Fig. 4b we plot the percentage errors between the values of the objective function obtained from the mean-field game and the values of the objective function using the other methods. In the long term, the percentage error when we compare the results of the mean-field game with the results from the primal–dual dynamics is $8.47\%$. On the other hand, compared to the optimal value obtained by solving (1), the percentage error in the long term is $1.96\%$.

Fig. 4

Values of the objective function and % error

We develop the same procedure explained above for fifteen different scenarios. In these scenarios we consider different distributions of the demand, different topology for the micro-network and for the macro-network, different vectors ${\tilde{f}}_1$ and ${\tilde{f}}_2$, and different values for the penalty on the states deviations and penalty on the control. We run fifty simulations of each scenario and we obtain the average of the percentage error over all simulations.

In the first three scenarios we change the mean and standard deviation of the demand at nodes 3 and 4, and we keep the rest of the simulation parameters as in the first example. For the first scenario the mean and standard deviation are ${\widetilde{\mu }}_{3}=10$, ${\widetilde{\mu }}_{4}=20$, ${\widetilde{\sigma }}_{3}=3$ and ${\widetilde{\sigma }}_{4}=1$. For the second scenario the parameters are ${\widetilde{\mu }}_{3}=30$, ${\widetilde{\mu }}_{4}=30$, ${\widetilde{\sigma }}_{3}=1$ and ${\widetilde{\sigma }}_{4}=3$. For the third scenario the mean and standard deviation are ${\widetilde{\mu }}_{3}=5$, ${\widetilde{\mu }}_{4}=5$, ${\widetilde{\sigma }}_{3}=3$ and ${\widetilde{\sigma }}_{4}=3$. The percentage error for each scenario is depicted in Fig. 5. Observe that for lower mean and higher variance, the average percentage error increases.

Fig. 5

Average percentage error of the objective function over fifty simulations for three scenarios by changing the mean and standard deviation of the demand

For the next three scenarios we change the topology of the micro-network, and we keep the rest of the simulation parameters as in the first example. In the first scenario the network consists of $n=6$ nodes and $m=11$ edges. For the second scenario the micro-network consists of $n=6$ nodes and $m=7$ edges. For the third scenario we increase the number of nodes to $n=10$ and the number of edges to $m=16$. The percentage error for each scenario is depicted in Fig. 6. Note that when we reduce the connections between the nodes, the average percentage error increases.

Fig. 6

Average percentage error of the objective function over fifty simulations for three scenarios by changing the topology of the micro-network

Now we consider three different scenarios by changing the topology of the macro-network, and we keep the rest of the simulation parameters as in the first example. We design the topology of the macro-network by using a power law distribution, in which few nodes have high connectivity and most nodes have very low connectivity. In the first scenario the average degree of the nodes is four. In the second scenario the average degree is two. In the third scenario the average degree is six. The complex networks that we consider for these scenarios are depicted in Fig. 7a–c. As one can observe in Fig. 7d–f there is not a significant difference in the average percentage error between these three scenarios.

Fig. 7

Average percentage error of the objective function over fifty simulations for three scenarios by changing the topology of the macro-network

The next three scenarios are generated by changing the cost coefficients ${\tilde{f}}_1$ and ${\tilde{f}}_2$ and by keeping the rest of the simulation parameters as in the first example. In the first scenario the cost coefficients are ${\widetilde{f}}_1 = \begin{bmatrix}1&1&1&1&1&1&1&1&1\end{bmatrix}^T$ and ${\widetilde{f}}_2 = \begin{bmatrix}1&1&2&1&1&2&1&2&1 \end{bmatrix}^T$. In the second scenario we have ${\widetilde{f}}_1 = \begin{bmatrix}1&1&1&1&1&1&1&2&1\end{bmatrix}^T$ and ${\widetilde{f}}_2 = \begin{bmatrix}1&1&2&1&1&2&1&2&1 \end{bmatrix}^T$. In the third scenario these coefficients are ${\widetilde{f}}_1 = \begin{bmatrix}1&1&1&2&2&1&2&3&1\end{bmatrix}^T$ and ${\widetilde{f}}_2 = \begin{bmatrix}1&1&1&2&2&1&2&3&1 \end{bmatrix}^T$. We can observe in Fig. 8 that when we increase the cost coefficients for the capacities and flows, the average percentage error with respect to the primal–dual dynamics and with respect to the real optimal value are very similar.

Fig. 8

Average percentage error of the objective function over fifty simulations for three scenarios by changing the cost coefficients ${\tilde{f}}_1$ and ${\tilde{f}}_2$

The last three scenarios consist in changing the penalty on state deviation Q and the penalty on control R, and keep the rest of the simulation parameters as in the first example. In the first scenario the penalty on state deviation and the penalty on control are the same, namely $R=Q=1$. In the second scenario the penalty on state deviation is $Q=10$ and the penalty on control is $R=1$. In the third scenario we take the penalty on state deviation $Q=1$ and the penalty on control $R=10$. In accordance with the first examples analysed at the beginning of this section, we observe that when the penalty on control is sufficiently high the convergence is obtained quicker, and the percentage error is smaller than in the other two scenarios (Fig. 9).

Fig. 9

Average percentage error of the objective function over fifty simulations for three scenarios by changing the penalty on state deviation and the penalty on control

The average percentage errors, in the long-term, for the different scenarios when we compare the results of the mean-field game with the results from the primal–dual dynamics and with the optimal value obtained by solving (1) are summarized in Table 2.

Table 2 Average percentage error over different scenarios

In the long term, the total average of the percentage error over all scenarios and simulations when we compare the results of the mean-field game with the results from the primal–dual dynamics is $11.46\%$. On the other hand, compared to the optimal value obtained by solving (1), the average percentage error in the long term is $7.43\%$.

7 Concluding remarks and future work

In this paper, we have provided a heuristic method to solve a two-stage stochastic program. We have illustrated the method on a supply-chain network design problem. The underlying idea of the method is to replace the original stochastic program with a mean-field game with a large number of agents. Each agent controls a primal–dual dynamics with the double aim of moving along the gradient descent/ascent while at the same time reaching consensus on the here and now variables, which are represented by the edge capacities. We show that the resulting mean dynamics mimics elastic averaging stochastic gradient algorithms. The heuristics has been implemented on a numerical example for different values of the parameters such as the penalties on state deviation and control.

Future work involves the generalization of the method to nonlinear convex problems, the analysis of the sub-optimality performance at least for specific scenarios, the extension to mean-field dynamics with implemented (online) forecasting algorithms based on regression learning models [7, 9].

Appendices

A Proof of Lemma 1

To obtain the optimal control in (11), from (9) let us write the minimized Hamiltonian as:

$$\begin{aligned} \begin{array}{lll} \mathcal {H}(x,\partial _x\sigma _k,m_k)= \inf _v \Big \{ \frac{1}{2} v^TR v +\frac{1}{2}(\rho _k-x)^TQ(\rho _k-x) +(Ax+Bv+C)^T \partial _x\sigma _k \Big \}. \end{array} \end{aligned}$$

(21)

By differentiating with respect to v and equalizing the gradient to zero we obtain:

$$\begin{aligned} Rv+B^T\partial _x\sigma _k(x,t)=0. \end{aligned}$$

Solving for v yields the expression for $v^*$ from (11). Let us rewrite (8) in terms of the minimized Hamiltonian as:

$$\begin{aligned} {\left\{ \begin{array}{ll} \partial _t\sigma _k(x,t)+H(x,\partial _x\sigma _k(x,t),{\overline{m}}_k) = 0 \in {\mathbb {R}}, \\ \sigma _k(x,T)=\frac{1}{2}(\rho _k-x)^TS(\rho _k-x)\in {\mathbb {R}}, \\ \partial _tm_k+\partial _x(m_t\partial _pH(x,\partial _x\sigma _k(x,t),m_k) = 0 \in {\mathbb {R}}. \end{array}\right. } \end{aligned}$$

(22)

Now by substituting the optimal value $v^*$ in (11), in the Hamiltonian, we obtain:

$$\begin{aligned} \begin{aligned} \mathcal {H}&(x,\sigma _k(x,t),m_k) = \frac{1}{2}\left[ x^TQx+v^{*^T}Rv^* \right] +(\partial _x\sigma _k(x,t))^T(Ax+Bv^*+C) \\ =&-\frac{1}{2}(\partial _x\sigma _k(x,t))^T\left[ BR^{-1}B^T \right] \partial _x\sigma _k(x,t) (\partial _x\sigma _k(x,t))^T (Ax+C)+\frac{1}{2}(\rho _k-x)^TQ(\rho _k-x). \end{aligned} \end{aligned}$$

(23)

Using this expression for the Hamiltonian in (22), we obtain the Hamilton-Jacobi-Bellman equation in (10). The third equation from (10) can be obtained by substituting the optimal control (11) in (22). This concludes the proof. $\quad \square$

B Proof of Theorem 1

We start the proof by isolating the Hamilton–Jacobi–Bellman part with fixed $\rho _k$ from (10) and we obtain:

$$\begin{aligned} \begin{array}{lll} \partial _t\sigma _k(x,t)-\frac{1}{2}(\partial _x\sigma _k(x,t))^T \left[ BR^{-1}B^T \right] \partial _x\sigma _k(x,t) +(\partial _x\sigma _k(x,t))^T(Ax+C)\\ +\frac{1}{2}(\rho _k-x)^TQ(\rho _k-x)=0 \in {\mathbb {R}}\times [0,T[,\quad \\ \sigma _k(x,T)=\psi (\rho _k(T),x)\in {\mathbb {R}}. \end{array} \end{aligned}$$

(24)

Now consider the following value function:

$$\begin{aligned} \sigma _k(x,t)=\frac{1}{2}x^T\Phi (t)x+H(t)^Tx+\chi (t). \end{aligned}$$

(25)

Then (24) can be rewritten as follows:

$$\begin{aligned} \begin{array}{lll} \frac{1}{2}x^T\dot{\Phi }(t)x+\dot{H}(t)^Tx+\dot{\chi }(t) -\frac{1}{2}\left[ \Phi (t)^Tx+H(t) \right] ^T\left[ BR^{-1}B^T \right] \left[ \Phi (t)^Tx+H(t) \right] \\ +\left[ \Phi (t)^Tx+H(t) \right] ^T(Ax+C) +\frac{1}{2}(\rho _k-x)^TQ(\rho _k-x)=0\in {\mathbb {R}}\times [0,T[. \end{array} \end{aligned}$$

(26)

Since the equation above is an identity in x it reduces to the following set of three equations:

$$\begin{aligned} {\left\{ \begin{array}{ll} \begin{aligned} \dot{\Phi }(t)&{}+A^T\Phi (t)+\Phi ^T\left[ -BR^{-1}B^T\right] \Phi (t)+Q=0 \in [0,T[,\quad \Phi (T)=S, \end{aligned}\\ \begin{aligned} \dot{H}(t)&{}-2\Phi (t) BR^{-1}B^T H(t)+A^TH(t) +\Phi (t)^TC-Q\rho _k(t)=0 \in [0,T[, \, H(T) = -S\rho _k(T), \end{aligned}\\ \begin{aligned} \dot{\chi }&{}+H(t)^T\left[ BR^{-1}B^T\right] H(t)+H(t)^TC +\frac{1}{2}\rho _k(t)^TQ\rho _k(t)=0\in [0,T[,\quad \chi (T)=\frac{1}{2}\rho _k^2(T)S. \end{aligned} \end{array}\right. } \end{aligned}$$

(27)

Furthermore, the optimal control is given by:

$$\begin{aligned} v^*=-R^{-1}B^T(\Phi (t)^Tx+H(t)). \end{aligned}$$

(28)

The existence of a solution for (27) is assured by the standard convexity-concavity assumptions, which justifies the choice for the quadratic value function [31].

Lastly, we average the expression for optimal control and by substitution in $\tfrac{d}{dt}{\overline{m}}_k(t)=A{\overline{m}}_k+B{\overline{v}}^*+C$, we obtain the expression

$$\begin{aligned} \dot{{\overline{m}}}_k(t)=\left[ A-BR^{-1}B^T\Phi (t)\right] {\overline{m}}_k(t)-BR^{-1}B^TH(t)+C, \end{aligned}$$

(29)

which is the second equation from (15). Now considering the stationary case with $T \rightarrow \infty$, we obtain the following set of equations:

$$\begin{aligned} \begin{aligned} A^T\Phi +\Phi ^T\left[ -BR^{-1}B^T\right] \Phi +Q&=0, \\ -2 \Phi BR^{-1}B^T H+A^TH+\Phi ^TC-Q\rho _k&=0, \\ H^T\left[ BR^{-1}B^T\right] H+H^TC+\frac{1}{2}\rho _k^TQ\rho _k&=0. \end{aligned} \end{aligned}$$

Solving for H, when the inverse of $\left[ A^T-2\Phi BR^{-1}B^T \right]$ exists, yields the following expression:

$$\begin{aligned} H = \left[ A^T-2\Phi BR^{-1}B^T \right] ^{-1} \left[ Q\rho _k -\Phi ^TC\right] . \end{aligned}$$

(30)

We now substitute (30) in (28) and we obtain:

$$\begin{aligned} \begin{aligned} v^*=-R^{-1}B^T\bigg ( \Phi ^Tx +\left[ A^T-2\Phi BR^{-1}B^T \right] ^{-1} \left[ Q\rho _k -\Phi ^TC\right] \bigg )\\ = -R^{-1}B^T\left( \Phi ^Tx+ {\widetilde{Z}} Q\rho _k-{\widetilde{Z}} \Phi ^TC \right) , \end{aligned} \end{aligned}$$

(31)

where we denote ${\widetilde{Z}}:=\left[ A^T-2\Phi BR^{-1}B^T \right] ^{-1}$.

Averaging over population k we obtain for the mean control the following expression

$$\begin{aligned} {\bar{v}}^*= -R^{-1}B^T\left( \Phi ^T{\overline{m}}_k+{\widetilde{Z}}Q \rho _k- {\widetilde{Z}} \Phi ^TC \right) . \end{aligned}$$

This implies that the interaction of neighbors consists of local averaging and local adjustment as in the following mean state dynamics:

$$\begin{aligned} \begin{array}{lll} \dot{{\overline{m}}}_k(t) = A {\overline{m}}_k(t) -B R^{-1}B^T\left( \Phi ^T{\overline{m}}_k- {\widetilde{Z}} \Phi ^TC+{\widetilde{Z}}Q \rho _k \right) +C\\ =A {\overline{m}}_k(t) +B R^{-1}B^T \Big ( \Phi ^T (\rho _k - {\overline{m}}_k) + {\widetilde{Z}} \Phi ^TC + (-{\widetilde{Z}}Q - \Phi ^T) \rho _k \Big ) +C \\ =A {\overline{m}}_k(t) +B R^{-1}B^T \Phi ^T (\rho _k - {\overline{m}}_k) + B R^{-1}B^T \Big ( {\widetilde{Z}} \Phi ^TC + (-{\widetilde{Z}}Q - \Phi ^T) \rho _k \Big ) +C. \end{array} \end{aligned}$$

(32)

Isolating the dynamics for the here and now c vector components we obtain

$$\begin{aligned} \begin{array}{lll} \dot{{\overline{m}}}_k^c(t) =-{{\tilde{Q}}}_1 {\overline{m}}_k^c(t) +R_c^{-1} \Phi _c^T (\rho _c^k - {\overline{m}}_k^c) +R_c^{-1} \Big ( {\widetilde{Z}}_c \Phi _c^T \mu + (-{\widetilde{Z}}_cQ_c - \Phi _c^T) \rho _c^k \Big ) +(\mu -{{\tilde{f}}}_1). \end{array} \end{aligned}$$

(33)

If the inverse matrix ${\widetilde{Z}}$ does not exist, we can approximate the solution of H by finding the least squares solution. Let us define by $\mathcal {Z}:=-2 \Phi BR^{-1}B^T H+A^TH+\Phi ^TC-Q\rho _k=(-2 \Phi BR^{-1}B^T+A^T)H-(Q\rho _k-\Phi ^TC)\in {\mathbb {R}}^{3m+n}$. Hence, finding the least squares solution consists of minimizing the sum of the squares of the difference $(-2 \Phi BR^{-1}B^T+A^T)H-(Q\rho _k-\Phi ^TC)$. This can be formally represented as follows:

$$\begin{aligned} \min _H\sum _{i=1}^{3m+n}\mathcal {Z}_i^2= \min _H\sum _{i=1}^{3m+n}\left( [(-2 \Phi BR^{-1}B^T+A^T)H]_i-(Q\rho _k-\Phi ^TC)_i)\right) ^2. \end{aligned}$$

(34)

The solution of the least squares method returns an approximation of H, denoted by $\hat{H}$. The mean-field equilibrium control is then given by:

$$\begin{aligned} v^*=-R^{-1}B^T(\Phi (t)^T\overline{m}_k+\hat{H}(t)). \end{aligned}$$

(35)

Hence, the mean state dynamics is as follows:

$$\begin{aligned} \begin{array}{lll} \dot{{\overline{m}}}_k(t) = A {\overline{m}}_k(t) -B R^{-1}B^T\left( \Phi ^T{\overline{m}}_k+\hat{H}\right) +C\\ =A {\overline{m}}_k(t) +B R^{-1}B^T \Big ( \Phi ^T (\rho _k - {\overline{m}}_k) + \hat{H} - \Phi ^T \rho _k\Big )+C \\ =A {\overline{m}}_k(t) +B R^{-1}B^T \Phi ^T (\rho _k - {\overline{m}}_k) + B R^{-1}B^T \Big (\hat{H} -\Phi ^T\rho _k \Big )+C. \end{array} \end{aligned}$$

(36)

By isolating the dynamics for the here and now c vector components, we obtain:

$$\begin{aligned} \begin{array}{lll} \dot{{\overline{m}}}_k^c(t) =-{{\tilde{Q}}}_1 {\overline{m}}_k^c(t) +R_c^{-1} \Phi _c^T (\rho _c^k - {\overline{m}}_k^c) +R_c^{-1} \Big (\hat{H} - \Phi _c^T\rho _c^k \Big )+(\mu -{{\tilde{f}}}_1). \end{array} \end{aligned}$$

(37)

For all aggregate states ${\overline{m}}^c = \left( {\overline{m}}_1^c,{\overline{m}}_2^c,\ldots ,{\overline{m}}_p^c \right)$, we have the following consensus-type dynamics:

$$\begin{aligned} \dot{{\overline{m}}}^c = - {{\tilde{\mathbf {Q}}}_1} {\overline{m}}^c(t) -L {\overline{m}}^c(t) +\delta . \end{aligned}$$

(38)

Here, ${{\tilde{\mathbf {Q}}}_1}:=diag({{\tilde{Q}}}_1)$ (diagonal matrix with block entry ${{\tilde{Q}}}_1$), $\delta :=R_c^{-1} \Big ( {\widetilde{Z}}_c \Phi _c^T \mu + (-{\widetilde{Z}}_cQ_c - \Phi _c^T) \rho _c^k \Big ) +(\mu -{{\tilde{f}}}_1)$ if the inverse matrix ${\widetilde{Z}}$ exists, or $\delta =R_c^{-1} \Big (\hat{H} - \Phi _c^T\rho _c^k \Big )+(\mu -{{\tilde{f}}}_1)$ if the inverse does not exist, and L is defined as the graph-Laplacian matrix where the kjth entry is the block matrix:

$$\begin{aligned} L_{kj} = {\left\{ \begin{array}{ll} R_c^{-1} \Phi _c^T &{} \quad j=k, \\ \frac{1}{|N(k)|}R_c^{-1} \Phi _c^T &{} \quad j \ne k, j \in N(k), \\ 0 &{} \quad otherwise. \end{array}\right. } \end{aligned}$$

(39)

This concludes the proof of Theorem 1. $\quad \square$