1 Introduction

We apply the sample average approximation (SAA) to a class of strongly convex stochastic programs posed in Hilbert spaces, and study the tail behavior of the distance between SAA solutions and their true counterparts. Our work sheds light on the number of samples needed to reliably estimate solutions to infinite-dimensional, linear-quadratic optimal control problems governed by affine-linear partial differential equations (PDEs) with random inputs, a class of optimization problems that has received much attention recently [30, 40, 42]. Our analysis requires that the integrand be strongly convex with the same convexity parameter for each random element’s sample. This assumption is fulfilled for convex optimal controls problems with a strongly convex control regularizer, such as those considered in [30, 40, 42]. Throughout the paper, a function \({\mathsf {f}} : H\rightarrow {\mathbb {R}}\cup \{\infty \}\) is \(\alpha\)-strongly convex with parameter \(\alpha > 0\) if \({\mathsf {f}}(\cdot )-(\alpha /2)\Vert \cdot \Vert _{H}^2\) is convex, where \(H\) is a real Hilbert space with norm \(\Vert \cdot \Vert _{H}\). Moreover, a function on a real Hilbert space is strongly convex if it is \(\alpha\)-strongly convex with some parameter \(\alpha > 0\).

We consider the potentially infinite-dimensional stochastic program

$$\begin{aligned} \min _{u \in U}\, \{\, f(u) = {\mathbb {E}}[ {J(u, \xi )} ] + \varPsi (u) \, \}, \end{aligned}$$
(1)

where \(U\) is a real, separable Hilbert space, \(\varPsi : U\rightarrow {\mathbb {R}}\cup \{\infty \}\) is proper, lower-semicontinuous and convex, and \(J: U\times \varXi \rightarrow {\mathbb {R}}\) is the integrand. Moreover, \(\xi\) is a random element mapping from a probability space to a complete, separable metric space \(\varXi\) equipped with its Borel \(\sigma\)-field. We also use \(\xi \in \varXi\) to represent a deterministic element.

Let \(\xi ^1\), \(\xi ^2\), ... be independent identically distributed \(\varXi\)-valued random elements defined on a complete probability space \((\varOmega , {\mathcal {F}}, P)\) such that each \(\xi ^i\) has the same distribution as that of \(\xi\). The SAA problem corresponding to (1) is

$$\begin{aligned} \min _{u \in U}\, \Big \{\, f_N(u) = \frac{1}{N}\sum _{i=1}^N J(u, \xi ^i) + \varPsi (u) \, \Big \}, \end{aligned}$$
(2)

We define \(F: U\rightarrow {\mathbb {R}}\cup \{\infty \}\) and the sample average function \(F_N : U\rightarrow {\mathbb {R}}\) by

$$\begin{aligned} F(u) = {\mathbb {E}}[ {J(u, \xi )} ] \quad \text {and}\quad F_N(u) = \frac{1}{N}\sum _{i=1}^N J(u, \xi ^i). \end{aligned}$$
(3)

Since we assume that the random elements \(\xi ^1, \xi ^2, \ldots\) are defined on the common probability space \((\varOmega , {\mathcal {F}}, P)\), we can view the functions \(f_N\) and \(F_N\) as defined on \(U\times \varOmega\) and the solution \(u_N^*\) to (2) as a mapping from \(\varOmega\) to \(U\). The second argument of \(f_N\) and of \(F_N\) is often dropped.

Let \(u^*\) be a solution to (1) and \(u_N^*\) be a solution to (2). We assume that \(J(\cdot , \xi )\) is \(\alpha\)-strongly convex with parameter \(\alpha > 0\) for each \(\xi \in \varXi\). Furthermore, we assume that \(F(\cdot )\) and \(J(\cdot , \xi )\) for all \(\xi \in \varXi\) are Gâteaux differentiable. Under these assumptions, we establish the error estimate

$$\begin{aligned} \alpha \Vert u^*-u_N^*\Vert _{U} \le \Vert {\nabla F_N(u^*)- \nabla F(u^*)}\Vert _{U}, \end{aligned}$$
(4)

valid with probability one. If \(\Vert \nabla _uJ(u^*, \xi )\Vert _{U}\) is integrable, then \(\nabla F_N(u^*)\) is just the empirical mean of \(\nabla F(u^*)\) since \(F(\cdot )\) and \(J(\cdot , \xi )\) for all \(\xi \in \varXi\) are convex and Gâteaux differentiable at \(u^*\); see Lemma 3. Hence we can analyze the mean square error \({\mathbb {E}}[ {\Vert u^*-u_N^*\Vert _{U}^2} ]\) and the exponential tail behavior of \(\Vert u^*-u_N^*\Vert _{U}\) using standard conditions from the literature on stochastic programming. To obtain a bound on \({\mathbb {E}}[ {\Vert u^*-u_N^*\Vert _{U}^2} ]\), we assume that there exists \(\sigma > 0\) with

$$\begin{aligned} {\mathbb {E}}[ {\Vert \nabla _u J(u^*, \xi )- \nabla F(u^*)\Vert _{U}^2} ] \le \sigma ^2, \end{aligned}$$
(5)

yielding with (4) the bound

$$\begin{aligned} {\mathbb {E}}[ {\Vert u^*-u_N^*\Vert _{U}^2} ] \le \sigma ^2/(\alpha ^2 N). \end{aligned}$$
(6)

To derive exponential tail bounds on \(\Vert u^*-u_N^*\Vert _{U}\), we further assume the existence of \(\tau > 0\) with

$$\begin{aligned} {\mathbb {E}}[ {\exp ( \tau ^{-2}\Vert \nabla _u J(u^*, \xi )- \nabla F(u^*)\Vert _{U}^2 ) } ] \le \mathrm {e}. \end{aligned}$$
(7)

This condition and its variants are used, for example, in [15, 25, 44]. Using Jensen’s inequality, we find that (7) implies (5) with \(\sigma ^2 = \tau ^2\) [44, p. 1584]. Combining (4) and (7) with the exponential moment inequality proven in [48, Theorem 3], we establish the exponential tail bound, our main contribution,

$$\begin{aligned} {\mathrm {Prob}}(\Vert u^*-u_N^*\Vert _{U} \ge \varepsilon ) \le 2\exp (-\tau ^{-2}N \varepsilon ^2 \alpha ^2/3) \quad \text {for all}\quad \varepsilon > 0. \end{aligned}$$
(8)

This bound solely depends on the characteristics of \(J\) but not on properties of the feasible set, \(\{\, u \in U:\, \varPsi (u) < \infty \, \}\), other than its convexity. For each \(\delta \in (0,1)\), the exponential tail bound yields, with a probability of at least \(1-\delta\),

$$\begin{aligned} \Vert u^*-u_N^*\Vert _{U} < \frac{\tau }{\alpha }\sqrt{\frac{3\ln (2/\delta )}{N}}. \end{aligned}$$
(9)

In particular, if \(\varepsilon > 0\) and \(N \ge \tfrac{3\tau ^2}{\alpha ^2\varepsilon ^2}\ln (2/\delta )\), then \(\Vert u^*-u_N^*\Vert _{U} < \varepsilon\) with a probability of at least \(1-\delta\), that is, \(u^*\) can be estimated reliably via \(u_N^*\).

Requiring \(J(\cdot , \xi )\) to be \(\alpha\)-strongly convex for each \(\xi \in \varXi\) is a restrictive assumption. However, it is fulfilled for the following class of stochastic programs:

$$\begin{aligned} \min _{u \in U} \, \{\, (1/2){\mathbb {E}}[ {\Vert K(\xi )u+h(\xi )\Vert _{H}^2} ] + (\alpha /2)\Vert u\Vert _{U}^2 + \varPsi (u) \, \}, \end{aligned}$$
(10)

where \(\alpha > 0\), \(H\) and \(U\) are real Hilbert spaces, and \(K(\xi ) : U\rightarrow H\) is a bounded, linear operator and \(h(\xi ) \in H\) for each \(\xi \in \varXi\). The control problems governed by affine-linear PDEs with random inputs considered, for example, in [21, 22, 30, 41, 42] can be formulated as instances of (10). In many of these works, the operator \(K(\xi )\) is compact for each \(\xi \in \varXi\), the expectation function \(F_1 : U\rightarrow {\mathbb {R}}\) defined by \(F_1(u) = (1/2){\mathbb {E}}[ {\Vert K(\xi )u+h(\xi )\Vert _{H}^2} ]\) is twice continuously differentiable, and \(U\) is infinite-dimensional. In this case, the function \(F_1\) generally lacks strong convexity. This may suggest that the \(\alpha\)-strong convexity of the objective function of (10) is solely implied by the function \((\alpha /2)\Vert \cdot \Vert _{U}^2 + \varPsi (\cdot )\). The lack of the expectation function’s strong convexity is essentially known [6, p. 3]. For example, if the set \(\varXi\) has finite cardinality, then the Hessian \(\nabla ^2 F_1(0)\) is the finite sum of compact operators and hence \(F_1\) lacks strong convexity; see Sect. 6.

A common notion used to analyze the SAA solutions is that of an \(\varepsilon\)-optimal solution [54, 56, 57].Footnote 1 We instead study the tail behavior of \(\Vert u^*-u_N^*\Vert _{U}\) since in the literature on PDE-constrained optimization the focus is on studying the proximity of approximate solutions to the “true” ones. For example, when analyzing finite element approximations of PDE-constrained problems, bounds on the error \(\Vert w^*-w_h^*\Vert _{U}\) as functions of the discretization parameters h are often established [28, 60], where \(w^*\) is the solution to a control problem and \(w_h^*\) is the solution to its finite element approximation. The estimate (4) is similar to that established in [28, p. 49] for the variational discretization—a finite element approximation—of a deterministic, linear-quadratic control problem. Since both the variational discretization and the SAA approach yield perturbed optimization problems, it is unsurprising that similar techniques can be used for some parts of the perturbation analysis.

The SAA approach has thoroughly been analyzed, for example, in [4, 7, 50, 54, 56, 57]. Some consistency results for the SAA solutions and finite-sample size estimates require the compactness and total boundedness of the feasible set, respectively. However, in the literature on PDE-constrained optimization, the feasible sets are commonly noncompact; see, e.g., [29, Sect. 1.7.2.3]. Assuming that the function \(F\) defined in (3) is \(\alpha\)-strongly convex with \(\alpha > 0\), Kouri and Shapiro [35, eq. (42)] establish

$$\begin{aligned} \alpha \Vert u^*-u_N^*\Vert _{U} \le \Vert {\nabla F_N(u_N^*)- \nabla F(u_N^*)}\Vert _{U}. \end{aligned}$$
(11)

The setting in [35] corresponds to \(\varPsi\) being the indicator function of a closed, convex, nonempty subset of \(U\). In contrast to the estimate (4), the right-hand side in (11) depends on the random control \(u_N^*\). This dependence implies that the right-hand side in (11) is more difficult to analyze than that in (4). However, the convexity assumption on \(F\) made in [35] is weaker than ours which requires the function \(J(\cdot , \xi )\) be \(\alpha\)-strongly convex for all \(\xi \in \varXi\). The right-hand side (11) may be analyzed using the approaches developed in [53, Sects. 2 and 4].

For finite-dimensional optimization problems, the number of samples, required to obtain \(\varepsilon\)-optimal solutions via the SAA approach, can explicitly depend on the problem’s dimension [1, 55, Example 1], [25, Proposition 2]. Guigues, Juditsky, and Nemirovski [25] demonstrate that confidence bounds on the optimal value of stochastic, convex, finite-dimensional programs, constructed via SAA optimal values, do not explicitly depend on the problem’s dimension. This property is shared by our exponential tail bound.

After the initial version of the manuscript was submitted, we became aware of the papers [52, 61] where assumptions similar to those used to derive (6) and (8) are utilized to analyze the reliability of SAA solutions. For unconstrained minimization in \({\mathbb {R}}^n\) with \(\varPsi = 0\), tail bounds for \(\Vert u^*-u_N^*\Vert _{2}\) are established in [61] under the assumption that \(J(\cdot , \xi )\) is \(\alpha\)-strong convex for all \(\xi \in \varXi\) and some \(\alpha > 0\). Here, \(\Vert \cdot \Vert _{2}\) is the Euclidean norm on \({\mathbb {R}}^n\). Assuming further that \(\Vert \nabla _uJ(u^*,\xi )\Vert _{2}\) is essentially bounded by \(L > 0\), the author establishes

$$\begin{aligned} {\mathrm {Prob}}(\Vert u^*-u_N^*\Vert _{2} \ge \varepsilon ) \le 2 \exp \Big (-\tfrac{N\alpha ^2\varepsilon ^2}{2L^2} \big (1+\tfrac{\alpha \varepsilon }{3L}\big )^{-1} \Big ) \end{aligned}$$
(12)

if \(\varepsilon \in (0,L/\alpha ]\), and the right-hand side in (12) is zero otherwise [61, Corollary 2]. While (12) is similar to (8) with \(\tau = L\), its derivation exploits the essential boundedness of \(\Vert \nabla _uJ(u^*,\xi )\Vert _{2}\) which is generally more restrictive than (7). The author establishes further tail bounds for \(\Vert u^*-u_N^*\Vert _{2}\) under different sets of assumptions on \(J(\cdot , \xi )\), and provides exponential tail bounds for \(f(u_N^*) - f(u^*)\) assuming that \(J(\cdot ,\xi )\) is Lipschitz continuous with a Lipschitz constant independent of \(\xi\) (see [61, Theorem 5]). For the possibly infinite-dimensional program (1), similar assumptions are used in [52, Theorem 2] to establish a non-exponential tail bound for \(f(u_N^*) - f(u^*)\). While tail bounds for \(f(u_N^*) - f(u^*)\) are derived in [52, 61], the assumptions used to derive (6) and (8) do not imply bounds on \(f(u_N^*) - f(u^*)\).

Hoffhues et al. [30] provide qualitative and quantitative stability results for the optimal value and for the optimal solutions of stochastic, linear-quadratic optimization problems posed in Hilbert spaces, similar to those in (10), with respect to Fortet–Mourier and Wasserstein metrics. These stability results are valid for approximating probability measures other than the empirical one, which is used to define the SAA problem (2). However, the convergence rate 1/N for \({\mathbb {E}}[ {\Vert u^*-u_N^*\Vert _{U}^2} ]\), and exponential tail bounds on \(\Vert u^*-u_N^*\Vert _{U}\) are not established in [30]. For a class of constrained, linear elliptic control problems, Römisch and Surowiec [49] demonstrate the consistency of the solutions and the optimal value, the convergence rate \(1/\sqrt{N}\) for \({\mathbb {E}}[ {\Vert u^*-u_N^*\Vert _{U}} ]\) and for \({\mathbb {E}}[ {|f_N(u_N^*)-f(u^*)|} ]\), and the convergence in distribution of \(\sqrt{N}(f_N(u_N^*)-f(u^*))\) to a real-valued random variable. These results are established using empirical process theory and are built on smoothness of the random elliptic operator and right-hand side with respect to the parameters. While our assumptions yield the mean square error bound (6) and the exponential tail bound (8), further conditions may be required to establish bounds on \({\mathbb {E}}[ {|f_N(u_N^*)-f(u^*)|} ]\). A bound on \({\mathbb {E}}[ {\Vert u^*-u_N^*\Vert _{U}^2} ]\) related to (6) is established in [41, Theorem 4.1] for class of linear elliptic control problems.

Besides considering risk-neutral, convex control problems with PDEs which can be expressed as those in Sect. 6, the authors of [40, 42] study the minimization of \(u \mapsto {\mathrm {Prob}}(J(u,\xi ) \ge \rho )\), where \(\rho \in {\mathbb {R}}\) and evaluating \(J(u,\xi )\) requires solving a PDE. Furthermore, the authors of Marín et al. [40] and Martínez-Frutos and Esparza [42] prove the existence of solutions and use stochastic collocation to discretize the expected values. In [42, Sect. 5.3], the authors adaptively combine a Monte Carlo sampling approach with a stochastic Galerkin finite element method to reduce the computational costs, but error bounds are not established. Stochastic collocation is also used, for example, in [21, 34]. Further approaches to discretize the expected value in (10) are, for example, quasi-Monte Carlo sampling [26] and low-rank tensor approximations [20]. A solution method for (1) is (robust) stochastic approximation. It has thoroughly been analyzed in [38, 44] for finite-dimensional and in [22, 24, 45] for infinite-dimensional optimization problems. For reliable \(\varepsilon\)-optimal solutions, the sample size estimates established in [44, Proposition 2.2] do not explicitly depend on the problem’s dimension.

After providing some notation and preliminaries in Sect. 2, we establish exponential tail bounds for Hilbert space-valued random sums in Sect. 3. Combined with optimality conditions and the integrand’s \(\alpha\)-strong convexity, we establish exponential tail and mean square error bounds for SAA solutions in Sect. 4. Sect. 5 demonstrates the optimality of the tail bounds. We apply our findings to linear-quadratic control under uncertainty in Sect. 6, and identify a problem class that violates the integrability condition (7). Numerical results are presented in Sect. 7. In Sect. 8, we illustrate that the “dynamics” of finite- and infinite-dimensional stochastic programs can be quite different.

2 Notation and preliminaries

Throughout the manuscript, we assume the existence of solutions to (1) and to (2). We refer the reader to Kouri and Surowiec [36, Proposition 3.12] and Hoffhues et al. [30, Theorem 1] for theorems on the existence of solutions to infinite-dimensional stochastic programs.

The set \(\mathrm {dom}~{\varPsi } = \{\, u \in U:\, \varPsi (u) < \infty \,\}\) is the domain of \(\varPsi\). The indicator function \(I_{U_0} : U\rightarrow {\mathbb {R}}\cup \{\infty \}\) of a nonempty set \(U_0 \subset U\) is defined by \(I_{U_0}(u) = 0\) if \(u \in U_0\) and \(I_{U_0}(u) = \infty\) otherwise. Let \(({\hat{\varOmega }}, {\hat{{\mathcal {F}}}}, {\hat{P}})\) be a probability space. A Banach space \(W\) is equipped with its Borel \(\sigma\)-field \({\mathcal {B}}(W)\). We denote by \(( \cdot , \cdot )_{H}\) the inner product of a real Hilbert space \(H\) equipped with the norm \(\Vert \cdot \Vert _{H}\) given by \(\Vert v\Vert _{H} = \sqrt{( v, v )_{H}}\) for all \(v \in H\). For a real, separable Hilbert space \(H\), \(\eta : {\hat{\varOmega }} \rightarrow H\) is a mean-zero Gaussian random vector if \(( v, \eta )_{H}\) is a mean-zero Gaussian random variable for each \(v \in H\) [64, pp. 58–59]. For a metric space \(V\), a mapping \({\mathsf {f}}: V\times {\hat{\varOmega }} \rightarrow W\) is a Carathéodory mapping if \({\mathsf {f}}(\cdot , \omega )\) is continuous for every \(\omega \in {\hat{\varOmega }}\) and \({\mathsf {f}}(x, \cdot )\) is \({\hat{{\mathcal {F}}}}\)-\({\mathcal {B}}(W)\)-measurable for all \(x \in V\).

For two Banach spaces \(V\) and \(W\), \({\mathscr {L}}(V, W)\) is the space of bounded, linear operators from \(V\) to \(W\), and \(V^* = {\mathscr {L}}(V, {\mathbb {R}})\). We denote by \(\langle \cdot , \cdot \rangle _{{V}^*\!, V}\) the dual pairing of \(V^*\) and \(V\). A function \(\upsilon : {\hat{\varOmega }} \rightarrow W\) is strongly measurable if there exists a sequence of simple functions \(\upsilon _k : {\hat{\varOmega }} \rightarrow W\) such that \(\upsilon _k(\omega ) \rightarrow \upsilon (\omega )\) as \(k\rightarrow \infty\) for all \(\omega \in {\hat{\varOmega }}\) [31, Def. 1.1.4]. An operator-valued function \(\varUpsilon : {\hat{\varOmega }} \rightarrow {\mathscr {L}}(V, W)\) is strongly measurable if the function \(\omega \mapsto \varUpsilon (\omega )x\) is strongly measurable for each \(x \in V\) [31, Def. 1.1.27]. Moreover, an operator-valued function \(\varUpsilon : {\hat{\varOmega }} \rightarrow {\mathscr {L}}(V, W)\) is uniformly measurable if there exists a sequence of simple operator-valued functions \(\varUpsilon _k : {\hat{\varOmega }} \rightarrow {\mathscr {L}}(V, W)\) with \(\varUpsilon _k(\omega ) \rightarrow \varUpsilon (\omega )\) as \(k \rightarrow \infty\) for all \(\omega \in {\hat{\varOmega }}\). An operator \(K \in {\mathscr {L}}(V, W)\) is compact if the closure of \(K(V_0)\) is compact for each bounded set \(V_0 \subset V\). For two real Hilbert spaces \(H_1\) and \(H_2\), \(K^* \in {\mathscr {L}}(H_2, H_1)\) is the (Hilbert space-)adjoint operator of \(K \in {\mathscr {L}}(H_1, H_2)\) and is defined by \(( Kv_1, v_2 )_{H_2} = ( v_1, K^*v_2 )_{H_1}\) for all \(v_1 \in H_1\) and \(v_2 \in H_2\) [37, Def. 3.9.1]. For a bounded domain \(D\subset {\mathbb {R}}^d\), \(L^2(D)\) is the Lebesgue space of square-integrable functions and \(L^1(D)\) is that of integrable functions. The Hilbert space \(H_0^1(D)\) consists of all \(v \in L^2(D)\) with weak derivatives in \(L^2(D)^d\) and with zero boundary traces. We define \(H^{-1}(D) = H_0^1(D)^*\).

3 Exponential tail bounds for Hilbert space-valued random sums

We establish two exponential tail bounds for Hilbert space-valued random sums which are direct consequences of known results [47, 48]. Below, \((\varTheta , \varSigma , \mu )\) denotes a probability space. Proofs are presented at the end of the section.

Theorem 1

Let \(H\) be a real, separable Hilbert space. Suppose that \(Z_i : \varTheta \rightarrow H\) for \(i = 1, 2, \ldots\) are independent, mean-zero random variables such that \({\mathbb {E}}[ {\exp (\tau ^{-2}\Vert Z_i\Vert _{H}^2)} ]\le \mathrm {e}\) for some \(\tau > 0\). Then, for each \(N \in {\mathbb {N}}\), \(\varepsilon \ge 0\),

$$\begin{aligned} {\mathrm {Prob}}( \Vert Z_1 + \cdots + Z_N\Vert _{H} \ge N\varepsilon ) \le 2\exp (-\tau ^{-2}\varepsilon ^2N/3). \end{aligned}$$
(13)

If in addition \(\Vert Z_i\Vert _{H} \le \tau\) with probability one for \(i = 1, 2, \ldots\), then the upper bound in (13) improves to \(2\exp (-\tau ^{-2}\varepsilon ^2N/2)\) [47, Theorem 3.5].

As an alternative to the condition \({\mathbb {E}}[ {\exp (\tau ^{-2}\Vert Z\Vert _{H}^2)} ]\le \mathrm {e}\) used in Theorem 1 for \(\tau > 0\) and a random vector \(Z: \varTheta \rightarrow H\), we can express sub-Gaussianity with \({\mathbb {E}}[ {\cosh (\lambda \Vert Z\Vert _{H})} ]\le \exp (\lambda ^2\sigma ^2/2)\) for all \(\lambda \in {\mathbb {R}}\) and some \(\sigma > 0\). While these two conditions are equivalent up to problem-independent constants (see the proof of [11, Lemma 1.6 on p. 9] and Lemma 1), the constant \(\sigma\) can be smaller than \(\tau\). For example, if \(Z: \varTheta \rightarrow H\) is a \(H\)-valued, mean-zero Gaussian random vector, then the latter condition holds with \(\sigma ^2 = {\mathbb {E}}[ {\Vert Z\Vert _{H}^2} ]\) [48, Rem. 4]. However, if \(H= {\mathbb {R}}\) then \(\tau ^2 = 2\sigma ^2/(1-\exp (-2)) \approx 2.31\sigma ^2\) [11, p. 9].

Proposition 1

Let \(H\) be a real, separable Hilbert space, and let \(Z_i : \varTheta \rightarrow H\) be independent, mean-zero random vectors such that \({\mathbb {E}}[ {\cosh (\lambda \Vert Z_i\Vert _{H})} ]\le \exp (\lambda ^2\sigma ^2/2)\) for all \(\lambda \in {\mathbb {R}}\) and some \(\sigma > 0\) (\(i = 1, 2, \ldots\)). Then, for each \(N \in {\mathbb {N}}\), \(\varepsilon \ge 0\),

$$\begin{aligned} {\mathrm {Prob}}( \Vert Z_1 + \cdots + Z_N\Vert _{H} \ge N\varepsilon ) \le 2\exp (-\sigma ^{-2}\varepsilon ^2N/3). \end{aligned}$$

We apply the following two facts to prove Theorem 1 and Proposition 1.

Theorem 2

(See [48, Theorem 3]) Let \(H\) be a real, separable Hilbert space. Suppose that \(Z_i : \varTheta \rightarrow H\) \((i=1, \ldots , N \in {\mathbb {N}})\) are independent, mean-zero random vectors. Then, for all \(\lambda \ge 0\),

$$\begin{aligned} {\mathbb {E}}[ {\cosh (\lambda \Vert Z_1 + \cdots + Z_N\Vert _{H})} ] \le \prod _{i=1}^N {\mathbb {E}}[ {\exp (\lambda \Vert Z_i\Vert _{H})- \lambda \Vert Z_i\Vert _{H}} ]. \end{aligned}$$

Lemma 1

If \(\sigma > 0\) and \(X: \varTheta \rightarrow {\mathbb {R}}\) is measurable with \({\mathbb {E}}[ {\exp (\sigma ^{-2}|X|^2)} ] \le \mathrm {e}\),

$$\begin{aligned} {\mathbb {E}}[ {\exp (\lambda |X|) - \lambda |X|} ] \le \exp (3\lambda ^2 \sigma ^2/4) \quad \text {for all}\quad \lambda \in {\mathbb {R}}_+. \end{aligned}$$
(14)

Proof

The proof is based on the proof of [56, Proposition 7.72].

Fix \(\lambda \in [0, 4/(3 \sigma )]\). For all \(s \in {\mathbb {R}}\), \(\exp (s) \le s + \exp (9s^2/16)\) [56, p. 449]. Using Jensen’s inequality and \({\mathbb {E}}[ {\exp (|X|^2/\sigma ^2)} ] \le \mathrm {e}\), we obtain

$$\begin{aligned} \begin{aligned} {\mathbb {E}}[ {\mathrm {e}^{\lambda |X|} - \lambda |X|} ] \le {\mathbb {E}}[ {\mathrm {e}^{9\lambda ^2 |X|^2/16}} ] \le {\mathbb {E}}[ {\mathrm {e}^{|X|^2/\sigma ^2}} ]^{9\lambda ^2\sigma ^2/16} \le \mathrm {e}^{9 \lambda ^2 \sigma ^2/16}. \end{aligned} \end{aligned}$$
(15)

Now, fix \(\lambda \ge 4/(3\sigma )\). For all \(s \in {\mathbb {R}}\), Young’s inequality yields \(\lambda s \le 3 \lambda ^2 \sigma ^2/8 + 2s^2/(3\sigma ^2)\). Combined with Jensen’s inequality, \({\mathbb {E}}[ {\exp (|X|^2/\sigma ^2)} ] \le \mathrm {e}\), and \(2/3 \le 3\sigma ^2\lambda ^2/8\), we get

$$\begin{aligned} \begin{aligned} {\mathbb {E}}[ {\mathrm {e}^{\lambda |X|} - \lambda |X|} ]&\le {\mathbb {E}}[ {\mathrm {e}^{\lambda |X|}} ] \le \mathrm {e}^{3\lambda ^2 \sigma ^2/8} {\mathbb {E}}[ {\mathrm {e}^{2|X|^2/(3\sigma ^2)}} ] \le \mathrm {e}^{3\lambda ^2 \sigma ^2/8 + 2/3} \le \mathrm {e}^{3\lambda ^2 \sigma ^2/4}. \end{aligned} \end{aligned}$$

Together with (15), we obtain (14). \(\square\)

Proof

(Proof of Theorem 1) We use a Chernoff-type approach to establish (13). Fix \(\lambda > 0\), \(\varepsilon \ge 0\), and \(N \in {\mathbb {N}}\). We define \(S_N = Z_1 + \cdots + Z_N\). Using \({\mathbb {E}}[ {\exp (\tau ^{-2}\Vert Z_i\Vert _{H}^2)} ]\le \mathrm {e}\) and applying Lemma 1 to \(X= \Vert Z_i\Vert _{H}\), we find that

$$\begin{aligned} \prod _{i = 1}^N {\mathbb {E}}[ {\exp (\lambda \Vert Z_i\Vert _{H}) -\lambda \Vert Z_i\Vert _{H}} ] \le \prod _{i = 1}^N \exp (3\lambda ^2 \tau ^2/4) = \exp (3\lambda ^2 \tau ^2 N/4). \end{aligned}$$

Combined with Markov’s inequality, Theorem 2, and \(\exp \le 2 \cosh\), we obtain

$$\begin{aligned} {\mathrm {Prob}}(\Vert S_N\Vert _{H} \ge N\varepsilon )&\le \mathrm {e}^{-\lambda N\varepsilon } {\mathbb {E}}[ {\mathrm {e}^{\lambda \Vert S_N\Vert _{H}}} ] \le 2\mathrm {e}^{-\lambda N\varepsilon } {\mathbb {E}}[ {\cosh (\lambda \Vert S_N\Vert _{H})} ] \\&\le 2\mathrm {e}^{-\lambda N \varepsilon + 3\lambda ^2 \tau ^2 N/4}. \end{aligned}$$

Minimizing the right-hand side over \(\lambda > 0\) yields (13). \(\square\)

Proof

(Proof of Proposition 1) We have \(\exp (s)-s \le \cosh ( s \sqrt{3/2})\) for all \(s \in {\mathbb {R}}\). Hence, the assumptions ensure \({\mathbb {E}}[ {\exp (\lambda \Vert Z_i\Vert _{H}) -\lambda \Vert Z_i\Vert _{H}} ] \le \exp (3\lambda ^2\sigma ^2/4)\) for all \(\lambda \in {\mathbb {R}}\). The remainder of the proof is as that of Theorem 1. \(\square\)

4 Exponential tail bounds for SAA solutions

We state conditions that allow us to derive exponential bounds on the tail probabilities of the distance between SAA solutions and their true counterparts. In Sect. 6, we demonstrate that our conditions are fulfilled for many linear-quadratic control problems considered in the literature.

4.1 Assumptions and measurability of SAA solutions

Throughout the manuscript, \(u^*\) is assumed to be a solution to (1).

Assumption 1

  1. (a)

    The space \(U\) is a real, separable Hilbert space.

  2. (b)

    The function \(\varPsi : U\rightarrow {\mathbb {R}}\cup \{\infty \}\) is convex, proper, and lower-semicontinuous.

  3. (c)

    The integrand \(J: U\times \varXi \rightarrow {\mathbb {R}}\) is a Carathéodory function, and for some \(\alpha >0\), \(J(\cdot , \xi )\) is \(\alpha\)-strongly convex for each \(\xi \in \varXi\).

  4. (d)

    The function \(J(\cdot , \xi )\) is Gâteaux differentiable on a convex neighborhood of \(\mathrm {dom}~{\varPsi }\) for all \(\xi \in \varXi\), and \(\nabla _u J(u^*, \cdot ) : \varXi \rightarrow U\) is measurable.

  5. (e)

    The map \(F: U\rightarrow {\mathbb {R}}\cup \{\infty \}\) defined in (3) is Gâteaux differentiable at \(u^*\).

Lemma 2

Let Assumptions 1(a)–(c) hold. If \(u_N^* : \varOmega \rightarrow U\) is a solution to (2), then \(u_N^*\) is the unique solution to (2) and is measurable.

Proof

For each \(\omega \in \varOmega\), the SAA problem’s objective function \(f_N(\cdot , \omega )\) is strongly convex and hence \(u_N^*\) is the unique solution to (2). The function \(\inf _{u \in U}\, f_N(u,\cdot ) : \varOmega \rightarrow {\mathbb {R}}\) is measurable [12, Corollary VII-2] (see also [12, Lemma III.39]). Hence the multifunction \(\arg \inf _{u \in U}\, f_N(u, \cdot )\) is single-valued and has a measurable selection [5, Theorem 8.2.9]. Therefore \(u_N^* : \varOmega \rightarrow U\) is measurable. \(\square\)

We impose conditions on the integrability of \(\nabla _u J(u^*, \xi )-\nabla F(u^*)\).

Assumption 2

  1. (a)

    For some \(\sigma > 0\), \({\mathbb {E}}[ {\Vert \nabla _u J(u^*, \xi )- \nabla F(u^*)\Vert _{U}^2} ] \le \sigma ^2\).

  2. (b)

    For some \(\tau > 0\), \({\mathbb {E}}[ {\exp ( \tau ^{-2}\Vert \nabla _u J(u^*, \xi )- \nabla F(u^*)\Vert _{U}^2 ) } ] \le \mathrm {e}\).

Assumption 2(b) implies Assumption 2(a) with \(\sigma ^2 = \tau ^2\) [44, p. 1584]. Assumption 2(b) and its variants are standard conditions in the literature on stochastic programming [15, p. 679], [25, pp. 1035–1036], [44, Eq. (2.50)]. For example, if \(\nabla _u J(u^*, \xi )-\nabla F(u^*)\) is essentially bounded, then Assumption 2(b) is fulfilled. More generally, if \(\nabla _u J(u^*, \xi )-\nabla F(u^*)\) is \(\gamma\)-sub-Gaussian, then Assumption 2(b) holds true [17, Theorem 3.4].

4.2 Exponential tail and mean square error bounds

We establish exponential tail and mean square error bounds on \(\Vert u^*-u_N^*\Vert _{U}\).

Theorem 3

Let \(u^*\) be a solution to (1) and let \(u_N^*\) be a solution to (2). If Assumptions 1and 2(a) hold, then

$$\begin{aligned} {\mathbb {E}}[ {\Vert u^*-u_N^*\Vert _{U}^2} ] \le \sigma ^2/(\alpha ^2 N). \end{aligned}$$
(16)

If in addition Assumption 2(b) holds, then for all \(\varepsilon > 0\),

$$\begin{aligned} {\mathrm {Prob}}(\Vert u^*-u_N^*\Vert _{U} \ge \varepsilon ) \le 2\exp (-\tau ^{-2}N \varepsilon ^2 \alpha ^2/3). \end{aligned}$$
(17)

We prepare our proof of Theorem 3.

Lemma 3

If Assumptions 1and 2(a) hold, then \({\mathbb {E}}[ {\nabla _uJ(u^*, \xi )} ] = \nabla F(u^*)\).

Proof

Using Assumptions 1(a) and (c)–(e), we have \({\mathbb {E}}[ {( \nabla _u J(u^*, \xi ), v )_{U}} ] = ( \nabla F(u^*), v )_{U}\) for all \(v \in U\); cf. [25, p. 1050]. Owing to Assumptions 1(e) and 2(a), the mapping \(\nabla _u J(u^*, \xi )\) is integrable. Hence \({\mathbb {E}}[ {( \nabla _u J(u^*, \xi ), v )_{U}} ] = ( {\mathbb {E}}[ {\nabla _u J(u^*, \xi )} ], v )_{U}\) for all \(v \in U\) (cf. [9, p. 78]). \(\square\)

Lemma 4

If Assumption 1holds, then the function \(F_N\) defined in (3) is Gâteaux differentiable on a neighborhood of \(\mathrm {dom}~{\varPsi }\) and with probability one,

$$\begin{aligned} (\nabla F_N(u_2) - \nabla F_N(u_1),u_2 - u_1)_{U} \ge \alpha \Vert u_2-u_1\Vert _{U}^2 \,\,\, \text {for all}\,\,\, u_1, u_2 \in \mathrm {dom}~{\varPsi }. \end{aligned}$$
(18)

Proof

Since, for each \(\xi \in \varXi\), \(J(\cdot , \xi )\) is \(\alpha\)-strongly convex and Gâteaux differentiable on a convex neighborhood \(V\) of \(\mathrm {dom}~{\varPsi }\), the sum rule and the definition of \(F_N\) imply its Gâteaux differentiability on \(V\) and (18) [45, p. 48]. \(\square\)

Lemma 5

Let Assumption 1hold and let \(\omega \in \varOmega\) be fixed. Suppose that \(u^*\) is a solution to (1) and that \(u_N^* = u_N^*(\omega )\) is a solution to (2). Then

$$\begin{aligned} (\nabla F_N(u_N^*)- \nabla F(u^*),u^* - u_N^*)_{U} \ge 0. \end{aligned}$$
(19)

Proof

Following the proof of [32, Theorem 4.42], we obtain for all \(u \in \mathrm {dom}~{\varPsi }\),

$$\begin{aligned}&(\nabla F(u^*),u- u^*)_{U} + \varPsi (u) - \varPsi (u^*) \ge 0,\nonumber \\&(\nabla F_N(u_N^*),u- u_N^*)_{U} + \varPsi (u) - \varPsi (u_N^*) \ge 0. \end{aligned}$$
(20)

We have \(\varPsi (u^*)\), \(\varPsi (u_N^*) \in {\mathbb {R}}\). Choosing \(u = u_N^*\) in the first and \(u = u^*\) in the second estimate in (20), and adding the resulting inequalities yields (19). \(\square\)

Lemma 6

Under the hypotheses of Lemma 5, we have

$$\begin{aligned} \alpha \Vert u^*-u_N^*\Vert _{U} \le \Vert {\nabla F_N(u^*)- \nabla F(u^*)}\Vert _{U}. \end{aligned}$$
(21)

Proof

Choosing \(u_2 = u^*\) and \(u_1 = u_N^*\) in (18), we find that

$$\begin{aligned} (\nabla F_N(u^*) - \nabla F_N(u_N^*),u^* - u_N^*)_{U} \ge \alpha \Vert u^*-u_N^*\Vert _{U}^2. \end{aligned}$$

Combined with (19), and the Cauchy–Schwarz inequality, we get

$$\begin{aligned} \alpha \Vert u^*-u_N^*\Vert _{U}^2&\le (\nabla F_N(u^*) - \nabla F_N(u_N^*),u^* - u_N^*)_{U} \\&\quad + (\nabla F_N(u_N^*)- \nabla F(u^*),u^* - u_N^*)_{U} \\&\le \Vert {\nabla F_N(u^*)- \nabla F(u^*)}\Vert _{U} \Vert {u^* - u_N^*}\Vert _{U}. \end{aligned}$$

\(\square\)

Proof

(Proof of Theorem 3) Lemma 2 ensures the measurability of \(u_N^* : \varOmega \rightarrow U\). We define \(q : \varXi \rightarrow U\) by \(q(\xi ) = \nabla _u J(u^*, \xi )-\nabla F(u^*)\). Assumption 1(c) and (e) ensure that q is well-defined and measurable. Hence, the random vectors \(Z_i = q(\xi ^i)\) (\(i = 1, 2, \ldots\)) are independent identically distributed, and Lemma 3 ensures that they have zero mean. Using the definitions of \(F\) and of \(F_N\) provided in (3), the Gâteaux differentiability of \(F\) at \(u^*\) [see Assumption 1(e)], and Lemma 4, we obtain

$$\begin{aligned} \nabla F_N(u^*)-\nabla F(u^*) = \frac{1}{N} \sum _{i=1}^N \big (\nabla _u J(u^*, \xi ^i)-\nabla F(u^*)\big ) = \frac{1}{N} \sum _{i=1}^N Z_i. \end{aligned}$$

Now, we prove (16). Combining the above statements with the separability of the Hilbert space \(U\), we get \({\mathbb {E}}[ {\Vert \sum _{i=1}^N Z_i\Vert _{U}^2} ] = \sum _{i=1}^N {\mathbb {E}}[ {\Vert Z_i\Vert _{U}^2} ]\) [64, p. 79]. For \(i=1, 2, \ldots\), Assumption 2(a) yields \({\mathbb {E}}[ {\Vert Z_i\Vert _{U}^2} ] \le \sigma ^2\). Together with the estimate (21), we find that

$$\begin{aligned} \alpha ^2 {\mathbb {E}}[ { \Vert u^*-u_N^*\Vert _{U}^2} ] \le {\mathbb {E}}[ {\Vert {\nabla F_N(u^*)- \nabla F(u^*)}\Vert _{U}^2} ] \le \sigma ^2/N, \end{aligned}$$

yielding the mean square error bound (16).

Next, we establish (17). Fix \(\varepsilon > 0\). If \(\Vert u^*-u_N^*\Vert _{U} \ge \varepsilon\), then the estimate (21) ensures that \(\Vert \sum _{i=1}^N Z_i\Vert _{U} \ge N\alpha \varepsilon\). For \(i = 1, 2, \ldots\), Assumption 2(b) implies that \({\mathbb {E}}[ {\exp ( \tau ^{-2}\Vert Z_i\Vert _{U}^2 ) } ] \le \mathrm {e}\). Applying Theorem 1, we get

$$\begin{aligned}{\hbox {Prob}}\left( \left\| {u^*}-{u_{N}^*}\right\| _{U} \ge \varepsilon \right) & \le {\hbox {Prob}}\bigg (\Big \Vert {{\sum _{i=1}^N} {Z_{i}}\Big \Vert _{U}}{\ge } {N\alpha \varepsilon }\bigg )\\& \le 2\mathrm {e}^{-\tau ^{-2}\varepsilon ^2\alpha ^2 N/3}. \end{aligned}$$

Hence the exponential tail bound (17) holds true. \(\square\)

5 Optimality of SAA solutions’ exponential tail bounds

We show that the dependence of the tail bound (17) on the problem data is essentially optimal for the problem class modeled by Assumptions 1 and 2(b).

Our example is inspired by that analyzed in [55, Example 1]. We consider

$$\begin{aligned} \min _{u\in L^2(0,1)}\, {\mathbb {E}}[ {(\alpha /2)\Vert u\Vert _{L^2(0,1)}^2 - ( h(\xi ), u )_{L^2(0,1)}} ], \end{aligned}$$
(22)

where \(\alpha > 0\), \(\varphi _1\), \(\varphi _2 \in L^2(0,1)\) are orthonormal, \(h: {\mathbb {R}}^2 \rightarrow L^2(0,1)\) is given by \(h(\xi ) = \xi _1 \varphi _1 + \xi _2 \varphi _2\), and \(\xi _1\), \(\xi _2\) are independent, standard Gaussians. The solution \(u^*\) to (22) is \(u^* = 0\) since \({\mathbb {E}}[ {h(\xi )} ] = 0\), and the SAA solution \(u_N^*\) corresponding to (22) is \(u_N^* = (1/\alpha ){\bar{\xi }}_{1,N}\varphi _1 + (1/\alpha ){\bar{\xi }}_{2,N}\varphi _2\), where \({\bar{\xi }}_{j,N} = (1/N)\sum _{i=1}^N \xi _j^i\) for \(j =1, 2\). The orthonormality of \(\varphi _1\), \(\varphi _2\) yields \(\Vert u_N^*\Vert _{L^2(0,1)}^2 = (1/\alpha )^2 ({\bar{\xi }}_{1,N})^2 + (1/\alpha )^2({\bar{\xi }}_{2,N})^2\). Since \((1/\alpha ){\bar{\xi }}_{1,N}\) and \((1/\alpha ){\bar{\xi }}_{2,N}\) are independent, mean-zero Gaussian with variance \(N^{-1}\alpha ^{-2}\), the random variable \(N\alpha ^2\Vert u^*-u_N^*\Vert _{L^2(0,1)}\) has a chi-square distribution \(\chi _2^2\) with two degrees of freedom. Hence, for all \(\varepsilon \ge 0\),

$$\begin{aligned} {\mathrm {Prob}}(\Vert u^*-u_N^*\Vert _{L^2(0,1)} \ge \varepsilon ) = {\mathrm {Prob}}(\chi _2^2 \ge N\alpha ^2\varepsilon ^2) = \mathrm {e}^{-N\alpha ^2\varepsilon ^2/2}. \end{aligned}$$
(23)

Since \(J(u, \xi ) = (\alpha /2) \Vert u\Vert _{L^2(0,1)}^2 +( h(\xi ), u )_{L^2(0,1)}\) and \(F(u) = (\alpha /2)\Vert u\Vert _{L^2(0,1)}^2\), we find that \(\Vert \nabla _u J(u^*, \xi )-\nabla F(u^*)\Vert _{L^2(0,1)}^2 = \Vert h(\xi )\Vert _{L^2(0,1)}^2\). Combined with \(\Vert h(\xi )\Vert _{L^2(0,1)}^2 \sim \chi _2^2\), we obtain \({\mathbb {E}}[ {\exp (\tau ^{-2}\Vert h(\xi )\Vert _{L^2(0,1)}^2)} ] = \mathrm {e}\) for \(\tau ^2=2\mathrm {e}/(\mathrm {e}-1)\). Our computations and the tail bound (23) reveal that the exponential order of the tail bound in (17) is optimal up to the constant \(3\tau ^2/2 \approx 4.7\).

6 Application to linear-quadratic optimal control

We consider the linear-quadratic optimal control problem

$$\begin{aligned} \min _{u \in U} \, \{\, (1/2){\mathbb {E}}[ {\Vert QS(u, \xi )-y_d\Vert _{H}^2} ] + (\alpha /2)\Vert u\Vert _{U}^2 + \varPsi (u) \, \}, \end{aligned}$$
(24)

where \(\alpha > 0\), \(Q \in {\mathscr {L}}(Y, H)\), \(y_d \in H\) and \(H\) is a real, separable Hilbert space. In this section, \(U\) and \(\varPsi : U\rightarrow {\mathbb {R}}\cup \{\infty \}\) fulfill Assumptions 1(a) and (b), respectively. The parameterized solution operator \(S : U\times \varXi \rightarrow Y\) is defined as follows. For each \((u, \xi ) \in U\times \varXi\), \(S(u, \xi )\) is the solution to:

$$\begin{aligned} \text {find} \quad y \in Y: \quad A(\xi )y + B(\xi ) u = g(\xi ). \end{aligned}$$
(25)

The spaces \(Y\) and \(Z\) are real, separable Banach spaces, \(A : \varXi \rightarrow {\mathscr {L}}(Y, Z)\) and \(B : \varXi \rightarrow {\mathscr {L}}(U, Z)\), \(A(\xi )\) has a bounded inverse for each \(\xi \in \varXi\), and \(g : \varXi \rightarrow Z\).

We can model parameterized affine-linear elliptic and parabolic PDEs with (25), such as the heat equation with random inputs considered in [42, Sect. 3.1.2], and the elliptic PDEs with random inputs considered [19, 41, 59]. When \(D\subset {\mathbb {R}}^d\) is a bounded domain and \(U= L^2(D)\), a popular choice has been \(\varPsi (\cdot ) = \gamma \Vert \cdot \Vert _{L^1(D)} + I_{U_{\text {ad}}}(\cdot )\) for \(\gamma \ge 0\), where \(U_{\text {ad}}\subset U\) is a nonempty, convex, closed set [23, 58]. Further nonsmooth regularizers are considered in [32, Sect. 4.7].

Defining \(K(\xi ) = -QA(\xi )^{-1}B(\xi )\) and \(h(\xi ) = QA^{-1}(\xi )g(\xi )-y_d\), the control problem (24) can be written as

$$\begin{aligned} \min _{u \in U} \, \{\, (1/2){\mathbb {E}}[ {\Vert K(\xi )u+h(\xi )\Vert _{H}^2} ] + (\alpha /2)\Vert u\Vert _{U}^2 + \varPsi (u) \, \}. \end{aligned}$$
(26)

We discuss differentiability and the lack of strong convexity of the expectation function \(F_1 : U\rightarrow {\mathbb {R}}\cup \{\infty \}\) defined by

$$\begin{aligned} F_1(u) = (1/2){\mathbb {E}}[ {\Vert K(\xi )u + h(\xi )\Vert _{H}^2} ]. \end{aligned}$$
(27)

Assumption 3

The map \(K : \varXi \rightarrow {\mathscr {L}}(U, H)\) is strongly measurable and \(h : \varXi \rightarrow H\) is strongly measurable. For each \(u \in U\), \({\mathbb {E}}[ {\Vert K(\xi )^*K(\xi )u\Vert _{U}} ] < \infty\), and \({\mathbb {E}}[ {\Vert h(\xi )\Vert _{H}^2} ]\), \({\mathbb {E}}[ {\Vert K(\xi )^*h(\xi )\Vert _{U}} ] < \infty\).

We define the integrand \(J_1 : U\times \varXi \rightarrow {\mathbb {R}}\) by

$$\begin{aligned} J_1(u, \xi ) = (1/2)\Vert K(\xi )u+h(\xi )\Vert _{H}^2. \end{aligned}$$
(28)

Under the measurability conditions stated in Assumption 3, we can show that \(J_1\) is a Carathéodory function.

Assumption 3 implies that the function \(F_1\) defined in (27) is smooth.

Lemma 7

If Assumption 3holds, then \(F_1\) defined in (27) is infinitely many times continuously differentiable, and for all u, \(v \in U\),

$$\begin{aligned} \nabla F_1(u) = {\mathbb {E}}[ {K(\xi )^*(K(\xi )u+h(\xi ))} ] \quad \text {and}\quad \nabla ^2 F_1(u)[v] = {\mathbb {E}}[ {K(\xi )^*K(\xi )v} ]. \end{aligned}$$

Proof

The strong measurability of K implies that of \(\xi \mapsto K(\xi )^*\) [31, Theorem 1.1.6] and hence that of \(\xi \mapsto K(\xi )^* K(\xi )\) [31, Corollary 1.1.29]. Fix u, \(v\in U\) and \(\xi \in \varXi\). Since \(\Vert K(\xi )u\Vert _{H}^2 \le \Vert u\Vert _{U}\Vert K(\xi )^*K(\xi )u\Vert _{U}\) [37, p. 199], Assumption 3 ensures that \(F_1\) is finite-valued.

Using (28), we find that \(\nabla _u J_1(u, \xi ) = K(\xi )^*(K(\xi )u+h(\xi ))\) and \(\nabla _{uu} J_1(u, \xi )[v] = K(\xi )^*K(\xi )v\). Combined with Assumption 3 and [23, Lemma C.3], we obtain that \(F_1\) is Gâteaux differentiable with \(\nabla F_1(u) = {\mathbb {E}}[ {\nabla _u J_1(u, \xi )} ]\). Since \({\mathbb {E}}[ {\Vert K(\xi )^*K(\xi )w\Vert _{U}} ] < \infty\) for all \(w\in U\), \(w\mapsto {\mathbb {E}}[ {K(\xi )^*K(\xi )w} ]\) is linear and bounded [27, Theorem 3.8.2]. Combined with the fact that \(J_1(\cdot , \xi )\) is quadratic for all \(\xi \in \varXi\), we conclude that \(F_1\) is twice Gâteaux differentiable with \(\nabla ^2 F_1(u)[v] = {\mathbb {E}}[ {K(\xi )^*K(\xi )v} ]\) and hence infinitely many times continuously differentiable. \(\square\)

The function \(F_1\) defined in (27) lacks strong convexity under natural conditions; see Lemma 8. In this case, we may deduce that the strong convexity of the objective function of (24) solely comes from the function \((\alpha /2)\Vert \cdot \Vert _{U}^2 + \varPsi (\cdot )\), and that the largest strong convexity parameter of \(F(\cdot ) = F_1(\cdot )+ (\alpha /2)\Vert \cdot \Vert _{U}^2\) is \(\alpha > 0\).

Assumption 4

The mapping \(K : \varXi \rightarrow {\mathscr {L}}(U, H)\) is uniformly measurable, \({\mathbb {E}}[ {\Vert K(\xi )\Vert _{{\mathscr {L}}(U, H)}^2} ] < \infty\), and \(K(\xi )\) is compact for all \(\xi \in \varXi\). Moreover, the Hilbert space \(U\) is infinite-dimensional.

Lemma 8

If Assumptions 3and 4hold, then the expectation function \(F_1\) defined in (27) is not strongly convex.

Proof

We define \(T : \varXi \rightarrow {\mathscr {L}}(U, U)\) by \(T(\xi ) = K(\xi )^*K(\xi )\). The uniform measurability of K implies that of \(\xi \mapsto K(\xi )^*\) (cf. [9, Theorem 2.16] and [37, p. 200]) and hence that of T (cf. [31, pp. 12–13]). Since \(K(\xi )\) is compact, \(T(\xi )\) is compact [37, p. 427]. Moreover, we have \({\mathbb {E}}[ {\Vert T(\xi )\Vert _{{\mathscr {L}}(U, U)}} ] = {\mathbb {E}}[ {\Vert K(\xi )\Vert _{{\mathscr {L}}(U, H)}^2} ]\) [37, Theorem 3.9-4].

We show that \({\mathbb {E}}[ {T(\xi )} ]\) is a compact operator. Let \((v_k) \subset U\) be weakly converging to some \({\bar{v}} \in U\). Hence there exists \(C \in (0,\infty )\) with \(\Vert v_k\Vert _{U}\le C\) for all \(k \in {\mathbb {N}}\) [37, Theorem 4.8-3] which implies \(\Vert T(\xi )v_k\Vert _{U} \le C\Vert T(\xi )\Vert _{{\mathscr {L}}(U, U)}\) for each \(\xi \in \varXi\) and \(k \in {\mathbb {N}}\). Since \(T(\xi )\) is compact for all \(\xi \in \varXi\), we have for each \(\xi \in \varXi\), \(T(\xi ) v_k \rightarrow T(\xi ){\bar{v}}\) as \(k \rightarrow \infty\) [14, Proposition 3.3.3]. Combined with \({\mathbb {E}}[ {\Vert T(\xi )\Vert _{{\mathscr {L}}(U, U)}} ] < \infty\), the dominated convergence theorem [31, Proposition 1.2.5] yields \({\mathbb {E}}[ {T(\xi )v_k} ] \rightarrow {\mathbb {E}}[ {T(\xi ){\bar{v}}} ]\) as \(k \rightarrow \infty\). We also have \({\mathbb {E}}[ {T(\xi )w} ] = {\mathbb {E}}[ {T(\xi )} ]w\) for all \(w \in U\) [27, p. 85]. Thus \({\mathbb {E}}[ {T(\xi )} ]v_k \rightarrow {\mathbb {E}}[ {T(\xi )} ]{\bar{v}}\) as \(k \rightarrow \infty\). Since \(U\) is reflexive and \((v_k)\) is arbitrary, \({\mathbb {E}}[ {T(\xi )} ]\) is compact [14, Proposition 3.3.3].

Now, we show that \(F_1\) is not strongly convex. Since \(U\) is infinite-dimensional, the self-adjoint, compact operator \({\mathbb {E}}[ {T(\xi )} ]\) lacks a bounded inverse [37, p. 428], [27, Theorem 3.8.1]. Hence it is noncoercive [10, Lemma 4.123]. Combined with \(\nabla ^2F_1(0) = {\mathbb {E}}[ {T(\xi )} ]\) (see Lemma 7 and [27, p. 85]), we conclude that \(F_1\) is not strongly convex. \(\square\)

The compactness of the Hessian of \(F_1\) may also be studied using the theory on spectral decomposition of compact, self-adjoint operators [63, p. 159], or the results on the compactness of covariance operators [63, p. 174].

6.1 Examples

Many instances of the linear-quadratic control problem (24) frequently encountered in the literature are defined by the following data: \(\alpha > 0\), \(H= U\), \(Y\) is a real Hilbert space, \(Q \in {\mathscr {L}}(Y, H)\) is the embedding operator of the compact embedding \(Y\hookrightarrow H\), \(B \in {\mathscr {L}}(U, Y^*)\) and \(g : \varXi \rightarrow Y^*\) is essentially bounded. Moreover \(A : \varXi \rightarrow {\mathscr {L}}(Y, Y^*)\) is uniformly measurable and there exist constants \(0< \kappa _{\min }^* \le \kappa _{\max }^* < \infty\) with \(\Vert A(\xi )\Vert _{{\mathscr {L}}(Y, Y^*)} \le \kappa _{\max }^*\) and \(\langle A(\xi )y, y \rangle _{{Y}^*\!, Y} \ge \kappa _{\min }^*\Vert y\Vert _{Y}^2\) for all \((y,\xi ) \in Y\times \varXi\). The conditions imply that \(A(\xi )\) has a bounded inverse for each \(\xi \in \varXi\) [37, p. 101] and imply the existence of a solution to (24) when combined with Fatou’s lemma; cf. [30, Theorem 1]. Moreover  Assumptions  1–4 hold true.

We show that Assumption 2(b) is violated for the class of optimal control problems where the operator A is elliptic and defined by a log-normal random diffusion coefficient [2, 13]. Let Q and B be the embedding operators of the embeddings \(H_0^1(0, 1) \hookrightarrow L^2(0,1)\) and \(L^2(0,1) \hookrightarrow H^{-1}(0,1)\), respectively. We choose \(\varPsi = 0\), \(U= L^2(0,1)\), \(y_d(\cdot ) = \sin (\pi \cdot )/\pi ^2\), and \(A(\xi ) = \mathrm {e}^{-\xi }{\bar{A}}\), where the weak Laplacian operator \({\bar{A}}\) is defined by \(\langle {\bar{A}}y, v \rangle _{H^{-1}(0,1), H_0^1(0,1)} = (y',v')_{L^2(0,1)}\), and \(\xi\) is a standard Gaussian random variable. We have \({\mathbb {E}}[ {\mathrm {e}^{2\xi }} ] = \mathrm {e}^2\) and \({\mathbb {E}}[ {\mathrm {e}^{\xi }} ] = \mathrm {e}^{1/2}\). Since \((\pi ^2, y_d)\) is an eigenpair of \({\bar{A}}\), we find that \(u^* = -\pi ^2\mathrm {e}^{1/2}y_d/(\mathrm {e}^2+\pi ^4\alpha )\) satisfies the sufficient optimality condition of (24), the normal equation \(\alpha u^* + {\mathbb {E}}[ {\mathrm {e}^{2\xi }} ]{\bar{K}}^* {\bar{K}} u^* ={\mathbb {E}}[ {\mathrm {e}^{\xi }} ] {\bar{K}}^*y_d\), where \({\bar{K}} = -Q {\bar{A}}^{-1}B\). Hence \(u^*\) is the solution to (24) for the above data. Using the definition of \(J_1\) provided in (28), we obtain

$$\begin{aligned} \nabla _uJ_1(u^*, \xi ) = \frac{\mathrm {e}^\xi y_d}{\pi ^2} -\frac{\mathrm {e}^{1/2+2\xi }y_d}{\pi ^{2}(\mathrm {e}^2+\pi ^4\alpha )}. \end{aligned}$$

For each \(\xi \ge \ln (2(\mathrm {e}^2+\pi ^4\alpha ))-1/2\), \(\Vert \nabla _uJ_1(u^*, \xi )\Vert _{L^2(0,1)} \ge (\mathrm {e}^{\xi }/\pi ^2) \Vert y_d\Vert _{L^2(0,1)}\). Combined with \(\nabla _u J(u^*,\xi ) - \nabla F(u^*) = \nabla _u J_1(u^*,\xi ) - \nabla F_1(u^*)\), \(y_d \in L^2(0,1)\), and \({\mathbb {E}}[ {\exp (s\xi ^2/2)} ] = \infty\) for all \(s \ge 1\) [11, p. 9], we conclude that Assumption 2(b) is violated.

7 Numerical illustration

We empirically verify the results derived in Theorem 3 for finite element discretizations of two linear-quadratic, elliptic optimal control problems, which are instances of (24).

For both examples, we consider \(D= (0,1)^2\), and the mapping Q in (24) is the embedding operator of the compact embedding \(H_0^1(D) \hookrightarrow L^2(D)\). Moreover, we define \(y_d \in L^2(D)\) by \(y_d(x_1, x_2) = (1/6)\exp (2x_1)\sin (2\pi x_1)\sin (2\pi x_2)\) as in [8, p. 511]. For each \((u,\xi ) \in L^2(D) \times \varXi\), \(y(\xi ) = S(u,\xi ) \in H_0^1(D)\) solves the weak form of the linear elliptic PDE

$$\begin{aligned} -\nabla \cdot (\kappa (x,\xi )\nabla y(x,\xi )) = u(x) + r(x,\xi ), \quad x \in D, \quad y(x,\xi ) = 0, \quad x \in \partial D, \end{aligned}$$

where \(\partial D\) is the boundary of the domain \(D\). The set \(\varXi\), the parameter \(\alpha > 0\), the diffusion coefficient \(\kappa : D\times \varXi \rightarrow (0,\infty )\) and the random right-hand side \(r : D\times \varXi \rightarrow {\mathbb {R}}\) are defined in Examples 1 and 2. Defining \(\langle Bu, v \rangle _{H^{-1}(D), H_0^1(D)} = -( u, v )_{L^2(D)}\), and

$$\begin{aligned} \langle A(\xi )y, v \rangle _{H^{-1}(D), H_0^1(D)}&= \int _D\kappa (x,\xi )\nabla y(x) \cdot \nabla v(x) \mathrm {d}x, \\ \langle g(\xi ), v \rangle _{H^{-1}(D), H_0^1(D)}&= \int _Dr(x,\xi )v(x) \mathrm {d}x, \end{aligned}$$

the weak form of the linear PDE can be written in the form provided in (25).

We approximate the control problem (24) using a finite element discretization. The control space \(U= L^2(D)\) is discretized using piecewise constant functions and the state space \(Y= H^1_0(D)\) is discretized using piecewise linear continuous functions defined on a triangular mesh on \([0,1]^2\) with \(n \in {\mathbb {N}}\) being the number of cells in each direction, yielding finite element approximations of (24) and corresponding SAA problems. To simplify notation, we omit the index n when referring to the solutions to these optimization problems. The dimension of the discretized control space is \(2n^2\).

Fig. 1
figure 1

Reference solutions

Full size image

Example 1

We define \(\alpha = 10^{-3}\), \(\varXi = [0.5, 3.5] \times [-1,1]\), the random right-hand side \(r(x,\xi ) = \xi _2 \exp (2x_1)\sin (2\pi x_2)\), and \(\kappa (\xi ) = \xi _1\). The random variables \(\xi _1\) and \(\xi _2\) are independent, and \(\xi _1\) has a truncated normal distribution supported on [0.5, 3.5] with mean 2 and standard deviation 0.25 (cf. [22, p. 2092]), and \(\xi _2\) is uniformly distributed over \([-1,1]\). We choose \(\varPsi (\cdot ) = \gamma \Vert \cdot \Vert _{L^1(D)} + I_{U_{\text {ad}}}(\cdot )\) with \(\gamma = 5.5 \cdot 10^{-4}\) and \(U_{\text {ad}}= \{\, u \in L^2(D) :\, -1 \le u \le 1 \, \}\), which is nonempty, closed, and convex [29, p. 56]. Furthermore, let \(n = 256\).

Since \(\kappa (\xi ) = \xi _1\) is a real-valued random variable, we can evaluate \(\nabla F_1(u)\) and its empirical mean using only two PDE solutions which can be shown by dividing (25) by \(\kappa (\xi )\). It allows us to compute the solutions to the finite element approximation of (24) and to their SAA problems with moderate computational effort even though \(n = 256\) is relatively large.

We solved the finite element discretization of (24) and the SAA problems using a semismooth Newton method [46, 58, 62] applied to a normal map (cf. [46, Eq. (3.3)]), which provides a reformulation of the first-order optimality conditions as a nonsmooth equation [46, Sect. 3.1]. The finite element discretization was performed using FEniCs [3, 39]. Sparse linear systems were solved using a direct method.

Example 2

We define \(\alpha = 10^{-4}\), \(\varXi = [3,5] \times [0.5,2.5]\) and the piecewise constant field \(\kappa\) by \(\kappa (x,\xi ) = \xi _1\) if \(x \in (0,1) \times (1/2,1)\) and \(\kappa (x,\xi ) = \xi _2\) if \(x \in (0,1) \times (1/2,1)\) (cf. [24, Example 3]). The random variables \(\xi _1\) and \(\xi _2\) are independent and uniformly distributed over [3, 5] and [0.5, 2.5], respectively. Moreover \(r = 0\), \(\varPsi = 0\), and \(n=64\).

To obtain a deterministic reference solution to the finite element approximation of (24), we approximate the probability distribution of \(\xi\) by a discrete uniform distribution. It is supported on the grid points of a uniform mesh of \(\varXi\) using 50 grid points in each direction, yielding a discrete distribution with 2500 scenarios. Samples for the SAA problems are generated from this discrete distribution.

We used dolfin-adjoint [16, 18, 43] with FEniCs [3, 39] to evaluate the SAA objective functions and their derivatives, and solved the problems using moola’s NewtonCG method [18, 51].

Fig. 2
figure 2

For each example, 50 independent realizations of \(\Vert u^*-u_N^*\Vert _{U}\), and the empirical mean error and empirical Luxemburg norm. The convergence rates were computed using least squares

Full size image

Figure 1 depicts the reference solutions for Examples 1 and 2. To generate the surface plots depicted in Fig. 1, the piecewise constant reference solutions were interpolated to the space of piecewise linear continuous functions.

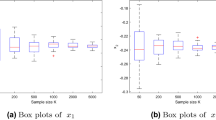
To illustrate the convergence rate \(1/\sqrt{N}\) for \({\mathbb {E}}[ {\Vert u^*-u_N^*\Vert _{U}} ]\), we generated 50 independent samples of \(\Vert u^*-u_N^*\Vert _{U}\) and computed the sample average. In order to empirically verify the exponential tail bound (17), we use the fact that it is equivalent to a certain bound on the Luxemburg norm of \(u^*-u_N^*\). We define the Luxemburg norm \(\Vert \cdot \Vert _{L_{\phi }(\varOmega ; U)}\) of a random vector \(Z: \varOmega \rightarrow U\) by

$$\begin{aligned} \Vert Z\Vert _{L_{\phi }(\varOmega ; U)} = \inf _{\nu > 0} \, \{ \, \nu : \, {\mathbb {E}}[ {\phi (\Vert Z\Vert _{U}/\nu )} ] \le 1 \, \}, \end{aligned}$$
(29)

where \(\phi : {\mathbb {R}}\rightarrow {\mathbb {R}}\) is given by \(\phi (x) = \exp (x^2)-1\), and \(L_{\phi }(\varOmega ; U) = L_{\phi (\Vert \cdot \Vert _{U})}(\varOmega ; U)\) is the Orlicz space consisting of each random vector \(Z: \varOmega \rightarrow U\) such that there exists \(\nu > 0\) with \({\mathbb {E}}[ {\phi (\Vert Z\Vert _{U}/\nu )} ] < \infty\); cf. [33, Sect. 6.2]. The exponential tail bound (17) implies

$$\begin{aligned} \Vert u^*-u_N^*\Vert _{L_{\phi }(\varOmega ; U)} \le \frac{3\sqrt{3}\tau }{\alpha \sqrt{N}}, \end{aligned}$$
(30)

and (30) ensures \({\mathrm {Prob}}(\Vert u^*-u_N^*\Vert _{U} \ge \varepsilon ) \le 2 \mathrm {e}^{-\tau ^{-2} N \varepsilon ^2 \alpha ^2/27}\) for all \(\varepsilon > 0\). These two statements follow from [11, Theorem 3.4 on p. 56] when applied to the real-valued random variable \(\Vert u^*-u_N^*\Vert _{U}\). To empirically verify the convergence rate \(1/\sqrt{N}\) for \(\Vert u^*-u_N^*\Vert _{L_{\phi }(\varOmega ; U)}\), we approximated the expectation in (29) using the same samples used to estimate \({\mathbb {E}}[ {\Vert u^*-u_N^*\Vert _{U}} ]\).

Figure 2 depicts 50 realizations of the errors \(\Vert u^*-u_N^*\Vert _{U}\), the empirical approximations of \({\mathbb {E}}[ {\Vert u^*-u_N^*\Vert _{U}} ]\) and of the Luxemburg norm \(\Vert u^*-u_N^*\Vert _{L_{\phi }(\varOmega ; U)}\) as well as the corresponding convergence rates. The rates were computed using least squares. The empirical convergences rates depicted in Fig. 2 are close to the theoretical rate \(1/\sqrt{N}\) for \({\mathbb {E}}[ {\Vert u^*-u_N^*\Vert _{U}} ]\) and \(\Vert u^*-u_N^*\Vert _{L_{\phi }(\varOmega ; U)}\); see (16) and (30).

8 Discussion

We have considered convex stochastic programs posed in Hilbert spaces where the integrand is strongly convex with the same parameter for each random element’s realization. We have established exponential tail bounds for the distance between SAA solutions and the true ones. For this problem class, tail bounds are optimal up to problem-independent, moderate constants. We have applied our findings to stochastic linear-quadratic control problems, a subclass of the above problem class.

We conclude the paper by illustrating that the “dynamics” of finite- and infinite-dimensional stochastic programs can be quite different. We consider

$$\begin{aligned} \min _{\Vert x\Vert _{2} \le 1}\, {\mathbb {E}}[ {\Vert x\Vert _{2}^2-2x^T\zeta } ], \end{aligned}$$
(31)

where \(\zeta\) is an \({\mathbb {R}}^n\)-valued, mean-zero Gaussian random vector with covariance matrix \(\sigma ^2I\) and \(\sigma ^2 > 0\). This corresponds to the choice \(m = 1\) in [55, Example 1]. For \(\delta \in (0, 0.3)\) and \(\varepsilon \in (0, 1)\), at least \(N > n\sigma ^2/\varepsilon = {\mathbb {E}}[ {\Vert \zeta \Vert _{2}^2} ]/\varepsilon\) samples are required for the corresponding SAA problem’s optimal solution to be an \(\varepsilon\)-optimal solution to (31) with a probability of at least \(1-\delta\) [55, Example 1].

The infinite-dimensional analogue of (31) is given by

$$\begin{aligned} \min _{\Vert u\Vert _{\ell ^2({\mathbb {N}})} \le 1}\, {\mathbb {E}}[ {\Vert u\Vert _{\ell ^2({\mathbb {N}})}^2-2(u,\xi )_{\ell ^2({\mathbb {N}})}} ], \end{aligned}$$
(32)

where \(\xi\) is an \(\ell ^2({\mathbb {N}})\)-valued, mean-zero Gaussian random vector, and \(\ell ^2({\mathbb {N}})\) is the standard sequence space. For each \(\varepsilon \in (0, 1)\), the SAA solution \(u_N^*\) corresponding to (32) is an \(\varepsilon\)-optimal solution to (32) if and only if we have \(\Vert (1/N)\sum _{i=1}^N \xi ^i\Vert _{\ell ^2({\mathbb {N}})}^2 \le \varepsilon\). Combined with Remark 4 in [48], we find that \(N \ge (3/\varepsilon )\ln (2/\delta ){\mathbb {E}}[ {\Vert \xi \Vert _{\ell ^2({\mathbb {N}})}^2} ]\) samples are sufficient in order for \(u_N^*\) to be an \(\varepsilon\)-optimal solution to (32), with a probability of at least \(1-\delta \in (0,1)\).

Let us compare the stochastic program (31) with (32). Whereas \({\mathbb {E}}[ {\Vert \zeta \Vert _{2}^2} ] = n \sigma ^2 \rightarrow \infty\) as \(n \rightarrow \infty\) and \({\mathbb {E}}[ {|\zeta _k|^2} ]=\sigma ^2\) (\(1\le k\le n\)), we have \({\mathbb {E}}[ {\Vert \xi \Vert _{\ell ^2({\mathbb {N}})}^2} ]< \infty\) due to the Landau–Shepp–Fernique theorem and \({\mathbb {E}}[ {|\xi _k|^2} ] \rightarrow 0\) as \(k \rightarrow \infty\) [64, p. 59]. We find that the “overall level-of-randomness” for the finite-dimensional problem (31) depends on its dimension n, while that for the infinite-dimensional analogue (32) is fixed.