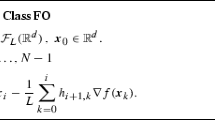1 Introduction

We consider the non-convex unconstrained optimization problem

$$\begin{aligned} \inf _{x\in \mathbb {R}^n} f(x), \end{aligned}$$
(1)

where \(f: \mathbb {R}^n\rightarrow \mathbb {R}\) is bounded from below, and let a real number \(f^\star \) denote a lower bound of problem (1). In addition, we assume throughout the paper that f has an L-Lipschitz gradient, that is

$$\begin{aligned} \Vert \nabla f(x)-\nabla f(y)\Vert \le L \Vert x-y\Vert \quad \forall x, y\in \mathbb {R}^n, \end{aligned}$$
(2)

for some (known) Lipschitz constant \(L >0\). Following the notation used by Nesterov [10], we let \(C^{1,1}_L(\mathbb {R}^n)\) denote functions with L-Lipschitz gradient.

Problem (1) arises naturally in many applications including machine learning, signal and image processing, to name but a few [1, 9]. One of the historic solution methods for problem (1) is the gradient method, proposed by Cauchy in 1847 [4].

The gradient method with fixed step lengths may be described as follows.

figure a

Nesterov [10, page 28] gives the following convergence rate (to a stationary point) for Algorithm 1 when \(t_k\in (0, \tfrac{2}{L})\), \(k\in \{1, \ldots , N\}\):

$$\begin{aligned} \min _{1\le k\le N+1} \left\| \nabla f(x^k)\right\| \le \left( \frac{f(x^1)-f^\star }{\left( \sum _{k=1}^N t_k(1-\tfrac{1}{2}Lt_k)\right) +\tfrac{1}{2L}}\right) ^{\tfrac{1}{2}}. \end{aligned}$$

In the special case \(t_k=\tfrac{1}{L}\), \(k\in \{1, \ldots , N\}\), the last bound becomes

$$\begin{aligned} \min _{1\le k\le N+1} \left\| \nabla f(x^k)\right\| \le \left( \frac{2L(f(x^1)-f^\star )}{N+1}\right) ^{\tfrac{1}{2}}. \end{aligned}$$

Recently, semidefinite programming performance estimation have been employed as a tool for the worst-case analysis of first-order methods [5, 6, 8, 12, 14]. In this method, the worst-case convergence is cast as a quadratic program with quadratic constraints and the problem is then solved by semi-definite programming methods. By employing the performance estimation method, Taylor [11, page 190], without giving a proof, states the following convergence rate:

$$\begin{aligned} \min _{1\le k\le N+1}\left\| \nabla f(x^k)\right\| \le \left( \frac{4L(f(x^1)-f^\star )}{3N}\right) ^{\tfrac{1}{2}}, \end{aligned}$$
(3)

for \(t_k=\tfrac{1}{L}\), \(k\in \{1, \ldots , N\}\). Drori [7, Corollary 1 in Appendix] considers the case that all step lengths are smaller than \(\tfrac{1}{L}\), and proves the following convergence rate

$$\begin{aligned} \min _{1\le k\le N+1} \left\| \nabla f(x^k)\right\| \le \left( \frac{4(f(x^1)-f^\star )}{\sum _{k=1}^N t_k(4-Lt_k)}\right) ^{\tfrac{1}{2}}. \end{aligned}$$
(4)

It can be observed that when the step lengths are the same for each iteration and tend to \(\tfrac{1}{L}\), the bound (4) reduces to Taylor’s convergence rate.

In this paper, we investigate the convergence rate of Algorithm 1 further. By using the performance estimation method, we provide a converge rate, which is tighter than all aforementioned bounds. For example, as a part of our main result in Theorem 2, we improve on (4) by showing, for any choice of \(t_k \in (0,\sqrt{3}/L)\) (\(k\in \{1, \ldots , N\}\)), that

$$\begin{aligned} \min _{1\le k\le N+1}\left\| \nabla f(x^k)\right\| \le \left( \frac{4(f(x^1)-f(x^{\star }))}{\sum _{k=1}^N \min (-L^2t_k^3+4t_k,-Lt_k^2+4t_k)+\tfrac{2}{L}}\right) ^{\tfrac{1}{2}}. \end{aligned}$$
(5)

As a consequence, we also prove and improve on (3) by showing, in the special case where all \(t_k = 1/L\) (\(k\in \{1, \ldots , N\}\)), that

$$\begin{aligned} \min _{1\le k\le N+1} \left\| \nabla f(x^k)\right\| \le \left( \tfrac{4L(f(x^1)-f^\star )}{3N+2}\right) ^{\tfrac{1}{2}}. \end{aligned}$$

In addition, we construct an L-smooth function that attains the given bound in Theorem 2 for certain step lengths. We also propose an optimal step length that minimizes the right-hand-side of the bound (5), namely \(t_k=\tfrac{\sqrt{4/3}}{L}\) for all \(k \in \{1,\ldots ,N\}\).

1.1 Outline

The paper is organized as follows. We describe the performance estimation technique in Sect. 2. In Sect. 3, we study the convergence rate by using performance estimation. Finally, we conclude the paper with a conjecture.

1.2 Notation

The n-dimensional Euclidean space is denoted by \(\mathbb {R}^n\). We use \(\langle \cdot , \cdot \rangle \) and \(\Vert \cdot \Vert \) to denote the Euclidean inner product and norm, respectively. For a matrix A, \(A_{ij}\) denotes its (i, j)-th entry, and \(A^T\) represents the transpose of A. The notation \(A\succeq 0\) means the matrix A is symmetric positive semi-definite.

2 Performance estimation

Computation of the worst-case convergence rate for a given iterative method and a given class of functions is an infinite-dimensional optimization problem. In their seminal paper [8], Drori and Teboulle take advantage of this idea, called performance estimation, and introduce some relaxation method to deal with this infinite-dimensional optimization problem. Performance estimation has been used extensively for the analysis of first-order methods [5, 6, 8, 12, 14].

Similar to problem (P) in [8], the worst-case convergence rate of Algorithm 1 may be formulated as the following abstract optimization problem,

$$\begin{aligned}&\max \left( \min _{1\le k\le N+1} \left\| \nabla f(x^k)\right\| \right) \nonumber \\&\quad \mathrm{s.t.}f(x^1)-f^\star \le \Delta \nonumber \\&\quad x^{N+1}, x^N, \ldots ., x^2 \ \text {are generated by Algorithm 1 w.r.t.}\ f, x^1 \nonumber \\&\quad f(x)\ge f^\star \ \forall x\in \mathbb {R}^n \nonumber \\&\quad f\in C^{1,1}_L(\mathbb {R}^n) \nonumber \\&\quad x^1\in \mathbb {R}^n, \end{aligned}$$
(6)

where \(\Delta \ge 0\) denote the difference between the given lower bound, \(f^\star \), and the value of f at the starting point. In problem (6), f and \(x^1\) are decision variables. This is an infinite-dimensional optimization problem with infinite number of constraints, and consequently intractable in general. In what follows, we provide a semidefinite programming relaxation for the problem.

Definition 1

[12, Definition 3.8.] Let \(L\ge 0\). A differentiable function \(f : \mathbb {R}^n\rightarrow \mathbb {R}\) is called L-smooth, if it satisfies the following condition,

$$\begin{aligned} \left| f(y)-f(x)-\left\langle \nabla f(x), y-x\right\rangle \right| \le \tfrac{L}{2}\left\| y-x\right\| ^2 \quad \forall x, y\in \mathbb {R}^n. \end{aligned}$$
(7)

The following proposition states a well-known characterization of L-smooth functions that follows, e.g., from [10, Lemma 1.2.3], [10, Theorem 2.1.5] and [12, Lemma 3.9].

Proposition 1

Let \(L\ge 0\). \(f : \mathbb {R}^n\rightarrow \mathbb {R}\) is L-smooth, if and only if it has an L-Lipschitz gradient.

The following well-known result is a fundamental property of gradient descent for L-smooth functions, if the step length 1/L is used.

Proposition 2

[10, page 26] If \(f : \mathbb {R}^n\rightarrow \mathbb {R}\) is L-smooth, and \(x \in \mathbb {R}^n\), then

$$\begin{aligned} f\left( x - \frac{1}{L}\nabla f(x) \right) \le f(x) - \frac{1}{2L}\Vert \nabla f(x)\Vert ^2. \end{aligned}$$

The following theorem plays a key role in our analysis. Indeed, it provides necessary and sufficient conditions for the interpolation of L-smooth functions. Using this theorem, we will formulate problem (6) as a finite dimensional optimization problem.

Theorem 1

([12, Lemma 3.9.], [7, Theorem 7 in Appendix]) Let \(\{(x^i; g^i; f^i)\}_{i\in I}\subseteq \mathbb {R}^n\times \mathbb {R}^n \times \mathbb {R}\) with a given index set I and \(L > 0\). There exists an L-smooth function f with

$$\begin{aligned} f(x^i) = f^i, \nabla f(x^i) = g^i \ \ i\in I, \end{aligned}$$
(8)

if and only if

$$\begin{aligned} \tfrac{1}{2L}\left\| g^i-g^j\right\| ^2-\tfrac{L}{4}\left\| x^i-x^j-\tfrac{1}{L}(g^i-g^j)\right\| ^2\le f^i-f^j-\left\langle g^j, x^i-x^j\right\rangle \ \ i, j\in I. \end{aligned}$$
(9)

In addition, if the triple \(\{(x^i; g^i; f^i)\}_{i\in I}\) satisfies (9), then there exists L-smooth function f for which (8) holds and \(\min _{x\in \mathbb {R}^n} f(x)=\min _{i\in I} f_i-\tfrac{1}{2L}\Vert g^i\Vert ^2\). Moreover, letting \(i^* \in \arg \min _{i\in I} f_i-\tfrac{1}{2L}\Vert g^i\Vert ^2\), a global minimizer of this function is given by \(x^\star = x_{i^*} - \frac{1}{L}g^{i^*}\).

Another proof of the first part of Theorem 1 may be found in [15, Theorem 2, Page 148]. By virtue of Theorem 1, problem (6) may be reformulated as follows,

$$\begin{aligned}&\max \left( \min _{1\le k\le N+1} \left\| g^k\right\| \right) \nonumber \\&\mathrm{s.t.}\tfrac{1}{2L}\left\| g^i-g^j\right\| ^2-\tfrac{L}{4}\left\| x^i-x^j-\tfrac{1}{L}(g^i-g^j)\right\| ^2\le f^i-f^j\nonumber \\&-\left\langle g^j, x^i-x^j\right\rangle \ \ i, j\in \left\{ 1, \ldots , N+1\right\} \nonumber \\&x^{k+1}=x^k-t_k g^k \ \ k\in \left\{ 1, \ldots , N\right\} \nonumber \\&f^k\ge f^\star \ \ k\in \left\{ 1, \ldots , N+1\right\} \nonumber \\&f^1-f^\star \le \Delta . \end{aligned}$$
(10)

In the above formulation, \(x^k,\ g^k,\ f^k\), \(k\in \left\{ 1, \ldots , N+1\right\} \), are decision variables. Note that in the above formulation, the constraints \(f(x)\ge f^\star \) for each \(x\in \mathbb {R}^n\) are replaced by \(f^k\ge f^\star , \ \ k\in \left\{ 1, \ldots , N+1\right\} \). These constraints do not necessarily impose a given L-Lipschitz function f with

$$\begin{aligned} f(x^i) = f^i, \nabla f(x^i) = g^i \ \ i\in \left\{ 1, \ldots , N+1\right\} , \end{aligned}$$

which has the lower bound \(f^\star \). Therefore, the optimal value of (6) and (10) may not be equal in general. However, if an optimal solution of problem (10) satisfies \(f^\star =\min _{1\le k\le N+1} f^k-\tfrac{1}{2L}\Vert g^k\Vert ^2\), the formulation will be exact; see the second part of Theorem 1. By Proposition 2, we have \(f(x)-\tfrac{1}{2L}\Vert \nabla f(x)\Vert ^2\ge f^\star \) for \(x\in \mathbb {R}^n\). Hence, we replace the constraint \(f^k\ge f^\star \) by \(f^k-\tfrac{1}{2L}\Vert g^k\Vert ^2\ge f^\star \) and consider the following problem:

$$\begin{aligned}&\max \left( \min _{1\le k\le N+1} \left\| g^k\right\| \right) \nonumber \\&\mathrm{s.t.}\tfrac{1}{2L}\left\| g^i-g^j\right\| ^2-\tfrac{L}{4}\left\| x^i-x^j-\tfrac{1}{L}(g^i-g^j)\right\| ^2\le f^i-f^j-\nonumber \\&\left\langle g^j, x^i-x^j\right\rangle \ \ i, j\in \left\{ 1, \ldots , N,N+1\right\} \nonumber \\&x^{k+1}=x^k-t_k g^k \ \ k\in \left\{ 1, \ldots , N+1\right\} \nonumber \\&f^k-\tfrac{1}{2L}\Vert g^k\Vert ^2- f^\star \ge 0 \ \ k\in \left\{ 1, \ldots , N+1\right\} \nonumber \\&f^1-f^\star \le \Delta . \end{aligned}$$
(11)

From the constraint \(x^{k+1}=x^k-t_k g^k\), we get \(x^i=x^1+\sum _{k=1}^{i-1} g^k\), \(i\in \left\{ 2, \ldots , N\right\} \). By using this relation to eliminate the \(x^i\) (\(i\in \left\{ 2, \ldots , N+2\right\} \)), problem (11) may be written as follows:

$$\begin{aligned}&\max \ell \nonumber \\&\mathrm{s.t.}f^i-f^j-\tfrac{1}{2L}\left\| g^i-g^j\right\| ^2+ \tfrac{L}{4}\left\| -\sum _{k=j}^{i-1} t_kg^k+\tfrac{1}{L}(g^i-g^j)\right\| ^2+ \left\langle g^j, \sum _{k=j}^{i-1} t_kg^k\right\rangle \ge 0 \ \ i> j \nonumber \\&f^i-f^j-\tfrac{1}{2L}\left\| g^i-g^j\right\| ^2 +\tfrac{L}{4}\left\| \sum _{k=i}^{j-1} t_kg^k-\tfrac{1}{L}(g^i-g^j)\right\| ^2- \left\langle g^j, \sum _{k=i}^{j-1} t_kg^k\right\rangle \ge 0 \ \ i< j \nonumber \\&\ f^k-\tfrac{1}{2L}\Vert g^k\Vert ^2- f^\star \ge 0 \ \ k\in \left\{ 1, \ldots , N+1\right\} \nonumber \\&f^\star -f^1+\Delta \ge 0\nonumber \\&\left\| g^k\right\| ^2-\ell \ge 0 \ \ \ k\in \left\{ 1, \ldots , N+1\right\} , \end{aligned}$$
(12)

where \(\ell \) is an auxiliary variable to convert problem (11) into a quadratic program. Problem (12) is a non-convex quadratic program with quadratic constraints. In the following proposition, we show that the optimal values of problems (6) and (11) (or equivalently problem (12)) are the same for step lengths in the interval \((0, \tfrac{2}{L})\).

Proposition 3

If \(t_k\in (0, \tfrac{2}{L})\), \(k\in \{1, \dots , N\}\), then problems (6) and (11) (or equivalently problem (12)) share the same optimal value.

Proof

Clearly, problem (11) is a relaxation of problem (6). Therefore, we only need to show that, for any feasible solution of (11), say \(\{(\bar{x}^i; \bar{g}^i; \bar{f}^i)\}_{1}^{N+1}\), there exists an L-smooth function f with

$$\begin{aligned} f(\bar{x}^i)=\bar{f}^i, \ \nabla f(\bar{x}^i)=\bar{g}^i, \ \ \ 1\le i\le N+1, \end{aligned}$$

and \(\min _{x\in \mathbb {R}^n} f(x)\ge f^\star \). The existence such of a function follows from Theorem 1, as all assumptions of Theorem 1 are satisfied. \(\square \)

To obtain a tractable form of problem (12), we relax it to a semidefinite program, in the spirit of [14]. To this end, we define the \((N+1)\times (N+1)\) positive semi-definite matrix G as,

$$\begin{aligned} G=&\begin{pmatrix} \left( g^1\right) ^T\\ \vdots \\ \left( g^{N+1}\right) ^T \end{pmatrix} \begin{pmatrix} g^1&\ldots&g^{N+1} \end{pmatrix}= \begin{pmatrix} \left\| g^1\right\| ^2 &{}~ \ldots &{}~ \left\langle g^1, g^{N+1}\right\rangle \\ \vdots &{}~ \ddots &{}~\vdots \\ \left\langle g^1, g^{N+1}\right\rangle &{}~ \ldots &{}~ \left\| g^{N+1}\right\| ^2 \end{pmatrix}. \end{aligned}$$

We may now formulate the following semidefinite program,

$$\begin{aligned}&\max \ell \nonumber \\&\mathrm{s.t.}f^i-f^j+\mathrm{tr}(A^{ij}G)\ge 0 \ \ \ \ i\ne j\in \{1, \ldots , N+1\} \nonumber \\&f^k- \tfrac{1}{2L}G_{kk}-f^\star \ge 0 \ \ \ \ k\in \{1, \ldots , N+1\}\nonumber \\&f^\star -f^1+\Delta \ge 0\nonumber \\&G_{kk}-\ell \ge 0 \ \ \ \ k\in \{1, \ldots , N+1\}\nonumber \\&G\succeq 0, \end{aligned}$$
(13)

where the \((N+1)\times (N+1)\) matrices \(A^{ij}\), \(i\ne j\in \{1, \ldots , N+1\}\), are formed according to the constraints (12), and \(G, \ell , f^i\), \(i\in \{1, \ldots , N+1\}\), are decision variables. Problem (13) is a relaxation of (12), but if \(n\ge N+1\) the relaxation is exact, that is the optimal values of (12) and (13) are the same. Indeed, if \(n\ge N+1\), and G is a feasible matrix in (13), then G is the Gram matrix of \(N+1\) vectors in \(\mathbb {R}^n\), and these vectors may be identified with \(g^1, \ldots , g^{N+1}\); a similar argument is used in [14, Theorem 5].

3 Worst-case convergence rate

In this section, we investigate the convergence rate of gradient method with fixed step lengths. The next theorem gives the worst-case convergence rate of Algorithm 1 to a stationary point of an L-smooth function. The technique of the proof, as is usual for SDP performance estimation, is to use weak duality. In particular, we will in fact construct a feasible solution to the dual SDP problem of (13), and thus derive an upper bound for problem (12).

In practice, this dual feasible solution is constructed in a computer-assisted manner, by solving the primal and dual SDP problems for different fixed values of the parameters, and subsequently guessing the values of the dual multipliers. (There is also dedicated software for this purpose, namely ‘PESTO’ by Taylor, Glineur, and Hendrickx [13].) In the proof of Theorem 2, we simply verify that these ‘guesses’ are correct.

Theorem 2

Let \(t_k\in (0, \tfrac{\sqrt{3}}{L})\) for \(k\in \{1, \ldots , N\}\). Consider N iterations of Algorithm 1 with step lengths \(t_k\) (\(k\in \{1, \ldots , N\}\)), applied to some L-smooth function f with minimum value \(f^\star \), with the starting point \(x^1\) satisfying \(f(x^1) - f^\star \le \Delta \), for some given \(\Delta >0\).

Then, if \(x^1,\ldots ,x^{N+1}\) denote the iterates of Algorithm 1, one has

$$\begin{aligned} \min _{1\le k\le N+1}\left\| \nabla f(x^k)\right\| \le \left( \frac{4\Delta }{\sum _{k=1}^N \min (-L^2t_k^3+4t_k,-Lt_k^2+4t_k)+\tfrac{2}{L}}\right) ^{\tfrac{1}{2}}. \end{aligned}$$
(14)

In particular, if \(t_k=\tfrac{\sqrt{4/3}}{L}\) for \(k\in \left\{ 1, \ldots , N\right\} \), we get

$$\begin{aligned} \min _{1\le k\le N+1} \left\| \nabla f(x^k)\right\| \le \left( \tfrac{6\sqrt{3}L(f(x^1)-f^\star )}{8N+3\sqrt{3}}\right) ^{\tfrac{1}{2}}. \end{aligned}$$
(15)

Similarly, if \(t_k=\tfrac{1}{L}\) for \(k\in \left\{ 1, \ldots , N\right\} \), one has

$$\begin{aligned} \min _{1\le k\le N+1} \left\| \nabla f(x^k)\right\| \le \left( \tfrac{4L(f(x^1)-f^\star )}{3N+2}\right) ^{\tfrac{1}{2}}. \end{aligned}$$
(16)

Proof

Let U denote the square of the right-side of inequality (14) and let \(B=\tfrac{U}{\Delta }\). To establish this bound, we show that U is an upper bound for problem (12). Consider the feasible point \(\left( \{g^k; f^k\}_1^{N+1}; \ell \right) \) for problem (12). Suppose that

$$\begin{aligned} \alpha _k = \tfrac{B}{2}\max \left\{ 2, t_kL+1\right\} \ \ \ k\in \left\{ 1, \ldots , N\right\} . \end{aligned}$$

In addition, we define \(\sigma _1\) and \(\sigma _k\), respectively, as follows:

$$\begin{aligned}&\sigma _1 = \tfrac{B}{4}\min \left\{ -Lt_1^2+3t_1, -L^2t_1^3+3t_1\right\} , \\&\sigma _k = \tfrac{B}{4}\min \left\{ -Lt_k^2+3t_k+t_{k-1},-L^2t_k^3+3t_k+t_{k-1}\right\} \ \ k\in \{2, \ldots , N\}, \end{aligned}$$

and \(\sigma _{N+1}=1-\sum _{k=1}^N \sigma _k=\tfrac{B}{4L}(2+Lt_N)\). As \(t_k\in (0, \tfrac{\sqrt{3}}{L})\) for \(k\in \{1, \ldots , N\}\), the \(\sigma _k\)’s will be non-negative. It is seen that

$$\begin{aligned} \sigma _k+(2\alpha _k-B)\tfrac{Lt_k^2}{4}-\tfrac{Bt_k}{2}=\tfrac{B}{4}(t_k+t_{k-1}) \ \ \ k\in \{2, \ldots , N\}. \end{aligned}$$

By using the last equality, one may verify directly through elementary algebra that

$$\begin{aligned}&\ell -U+\sum _{k=1}^{N+1} \sigma _k\left( \left\| g^k\right\| ^2-\ell \right) +B\left( f^\star -f^1+\Delta \right) +B\left( f^{N+1}-\tfrac{1}{2L}\Vert g^{N+1}\Vert ^2 -f^\star \right) \\&\quad +\sum _{k=1}^{N} \alpha _k\Big ( f^{k}-f^{k+1}-\tfrac{1}{2L}\left\| g^{k}-g^{k+1}\right\| ^2+\tfrac{L}{4}\left\| t_kg^{k}-\tfrac{1}{L}\left( g^{k}-g^{k+1}\right) \right\| ^2\\&\quad -\left\langle g^{k+1},t_kg^k\right\rangle \Big )+\sum _{k=1}^{N} \left( \alpha _k-B\right) \Big ( f^{k+1}-f^{k}-\tfrac{1}{2L}\left\| g^{k+1}-g^{k}\right\| ^2\\&\quad +\tfrac{L}{4}\left\| -t_kg^{k}-\tfrac{1}{L}\left( g^{k+1}-g^{k}\right) \right\| ^2-\left\langle g^{k},-t_kg^k\right\rangle \Big )= \tfrac{-(2\alpha _1-B)}{4L}\left\| g^1-g^{2}\right\| ^2\\&\quad +\tfrac{Bt_1}{4}\left\| g^1\right\| ^2-\tfrac{Bt_1}{2}\left\langle g^1, g^{2}\right\rangle +\tfrac{Bt_{N}}{4}\left\| g^{N+1}\right\| ^2\\&\quad +\sum _{k=2}^N\left( \tfrac{-(2\alpha _k-B)}{4L}\left\| g^k-g^{k+1}\right\| ^2+\tfrac{B(t_k+t_{k-1})}{4}\left\| g^k\right\| ^2-\tfrac{Bt_k}{2}\left\langle g^k, g^{k+1}\right\rangle \right) =\\&\quad -\sum _{k=1}^{N} Q_k, \end{aligned}$$

where

$$\begin{aligned} Q_k = {\left\{ \begin{array}{ll} \tfrac{B}{4}\left( \tfrac{1}{L}-t_k\right) \left\| g^k-g^{k+1}\right\| ^2 &{} t_k< \tfrac{1}{L}\\ 0 &{} t_k\ge \tfrac{1}{L}. \end{array}\right. } \end{aligned}$$

Since \(\sum _{k=1}^{N} Q_k\) is a non-negative quadratic function and the given dual multipliers are non-negative, we have \(\ell \le U\) for any feasible solution of (12). \(\square \)

The special step length \(t_k=\tfrac{\sqrt{4/3}}{L}\) for \(k\in \left\{ 1, \ldots , N\right\} \) used to obtain (15) will be motivated later in Theorem 3. Note that (16) gives a formal proof (with a small improvement) of the bound claimed by Taylor [11, page 190]; see (3).

An important question concerning the bound (14) is its difference with the optimal value of (6). It is known that the lower bound for Algorithm 1 is of the order \(\Omega \left( \tfrac{1}{\sqrt{N}}\right) \) [2, 3]. In what follows, we establish that the bound (14) is exact in some cases.

Proposition 4

The value

$$\begin{aligned} \left( \tfrac{4\Delta }{\sum _{k=1}^N \min \left( -L^2t_k^3+4t_k,-Lt_k^2+4t_k\right) +\tfrac{2}{L}}\right) ^{\tfrac{1}{2}} \end{aligned}$$

is the optimal value of (6) when all step lengths satisfy \(t_k\in (0, \tfrac{1}{L}]\), \(k\in \{1, \ldots , N\}\).

Proof

It suffices for a given N to demonstrate an L-smooth function f and a point \(x^1\) such that

$$\begin{aligned} \min _{1\le k\le N+1} \left\| \nabla f(x^k)\right\| = \left( \tfrac{4\Delta }{\sum _{k=1}^N \min \left( -L^2t_k^3+4t_k,-Lt_k^2+4t_k\right) +\tfrac{2}{L}}\right) ^{\tfrac{1}{2}}. \end{aligned}$$
(17)

Suppose now that \(t_k\in (0, \tfrac{1}{L}]\), \(k\in \{1, \ldots , N\}\), and U denotes the right-hand-side of equality (17). We set \(t_{N+1}=\tfrac{1}{L}\). Let

$$\begin{aligned}&l_i=U\left( \sum _{k=i}^{N+1} t_k \right) , \ \ f^i=\Delta -\tfrac{U^2}{4}\left( \sum _{k=1}^{i-1} -Lt_k^2+4t_k\right) \ \ \&i\in \left\{ 1, \ldots , N+1\right\} , \end{aligned}$$

and \(l_{N+2}=0\). By elementary calculus, one can check that the function \(f:\mathbb {R}\rightarrow \mathbb {R}\) given by

$$\begin{aligned} f(x) = {\left\{ \begin{array}{ll} \tfrac{L}{2}(x-l_1)^2+U(x-l_1)+f^1 &{} \ \ x\in \left[ \tfrac{1}{2}(l_1+l_2), \infty \right) \\ \tfrac{-L}{2}(x-l_{i+1})^2+U(x-l_{i+1})+f^{i+1} &{} \ \ x\in \left[ l_{i+1}, \tfrac{1}{2}(l_i+l_{i+1})\right] \\ \tfrac{L}{2}(x-l_{i+1})^2+U(x-l_{i+1})+f^{i+1} &{} \ \ x\in \left[ \tfrac{1}{2}(l_{i+1}+l_{i+2}), l_{i+1}\right] \\ \tfrac{L}{2}x^2 &{} \ \ x\in \left( -\infty , \tfrac{1}{2}l_{N+1}\right] \end{array}\right. } \end{aligned}$$
(18)

for \(i\in \left\{ 1, \ldots , N\right\} \), is L-smooth with the optimal value \(f^\star = 0\) and the optimal solution \(x^\star =0\). In addition, we have equality (17) for \(x^1=l_1\). Indeed,

$$\begin{aligned}&x^i=l_i \ \ \&i\in \left\{ 1, \ldots , N+1\right\} \\&\nabla f(x^i)=U \ \ \&i\in \left\{ 1, \ldots , N+1\right\} \\&f(x^i)=f^i \ \ \&i\in \left\{ 1, \ldots , N+1\right\} . \end{aligned}$$

\(\square \)

Figure 1 represents the plot of function f as constructed in the proof of Proposition 4 for different parameters and the fixed step length \(t_k=\tfrac{1}{L}\) for all k.

Note that, though we have only shown the exactness of the bound (14) for step lengths in the interval \((0, \tfrac{1}{L}]\), we also conjecture that the bound (14) is in fact exact for all step lengths in the interval \((0, \tfrac{\sqrt{3}}{L})\).

By minimizing the right-hand-side of (14), the next theorem gives the ‘optimal’  step lengths with respect to the bound.

Fig. 1
figure 1

Plot of the function f in (18) for different parameters and \(t_k=\tfrac{1}{L}\) (Dotted lines denote the endpoints of intervals)

Full size image

Theorem 3

Let f be an L-smooth function. Then the optimal step size for gradient method with respect to bound (14) is given by

$$\begin{aligned} t_k=\tfrac{\sqrt{\tfrac{4}{3}}}{L}\ \ \forall k\in \left\{ 1,\dots ,N\right\} , \end{aligned}$$

provided that \(t_k \in (0, \tfrac{\sqrt{3}}{L})\) for all \(k \in \{1,\ldots ,N\}\).

Proof

We minimize the right-hand-side of (14), that is

$$\begin{aligned} \min _{t_k\in (0,\tfrac{\sqrt{3}}{L})} \ \left( \tfrac{4\Delta }{\sum _{k=1}^N \min \left( -L^2t_k^3+4t_k,-Lt_k^2+4t_k\right) +\tfrac{2}{L}}\right) ^{\tfrac{1}{2}}, \end{aligned}$$

which is equivalent to maximizing

$$\begin{aligned} \max _{t\in \left( 0,\tfrac{\sqrt{3}}{L}\right) ^N} \ H(t):= \sum _{k=1}^N \min \left( -L^2t_k^3+4t_k,-Lt_k^2+4t_k\right) . \end{aligned}$$

Since H is a strictly concave function on \(\left( 0,\tfrac{\sqrt{3}}{L}\right) ^N\) and at \(\bar{t}\) given by

$$\begin{aligned} \bar{t}_k=\tfrac{\sqrt{\tfrac{4}{3}}}{L}\ \ \forall k\in \left\{ 1,\dots ,N\right\} , \end{aligned}$$

we have \(\nabla H\left( \bar{t}\right) =0\), which shows that \(\bar{t}\) is the unique maximum solution of H over \(\left( 0,\tfrac{\sqrt{3}}{L}\right) ^N\). \(\square \)

The step length \(\tfrac{1}{L}\) commonly is regarded as the optimal step length in the literature; see [10, Chapter 1]. Due to the example introduced in (18), we see that the worst-case convergence rate for the step length \(\tfrac{1}{L}\) cannot be better than \(\left( \tfrac{4L(f(x^1)-f^\star )}{3N+2}\right) ^{\tfrac{1}{2}}\). By our analysis, it follows that, for the step length \(\tfrac{2\sqrt{3}}{3L}\), we get the convergence rate (15), which is better than \(\left( \tfrac{4L(f(x^1)-f^\star )}{3N+2}\right) ^{\tfrac{1}{2}}\), since the constant in the bound improves from ca. \(\tfrac{4}{3}\approx 1.333\) to \(\tfrac{6\sqrt{3}}{8} \approx 1.299\).

4 Concluding remarks

In this paper, we studied the convergence rate of gradient method for L-smooth functions and we provided a new convergence rate when the step lengths belong to the interval \((0, \tfrac{\sqrt{3}}{L})\). Moreover, we have shown that this convergence rate is tight for step lengths in the interval \((0,\tfrac{1}{L}]\). As mentioned in the introduction, Algorithm 1 is convergent for the step lengths in the larger interval \((0, \tfrac{2}{L})\). Following extensive numerical experiments, where we solved the semidefinite program (13) for different parameter values, we conjecture that when \(t_k\in \left( 0, \tfrac{2}{L}\right) \) for \(k\in \left\{ 1, \ldots , N\right\} \), we have

$$\begin{aligned} \min _{1\le k\le N+1}\left\| \nabla f(x^k)\right\| \le \left( \frac{4\Delta }{\sum _{k=1}^N \min \left( -L^2t_k^3+4t_k,-Lt_k^2+4t_k\right) }\right) ^{\tfrac{1}{2}}, \end{aligned}$$

under the same conditions as for Theorem 2. The right-hand-side is again minimized by the constant step length \(t_k=\tfrac{\sqrt{4/3}}{L}\) for all \(k \in \{1,\ldots ,N\}\).