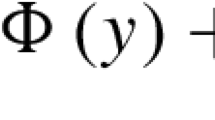On the rate of convergence of alternating minimization for non-smooth non-strongly convex optimization in Banach spaces

Abstract

In this paper, the convergence of the fundamental alternating minimization is established for non-smooth non-strongly convex optimization problems in Banach spaces, and novel rates of convergence are provided. As objective function a composition of a smooth, and a block-separable, non-smooth part is considered, covering a large range of applications. For the former, three different relaxations of strong convexity are considered: (i) quasi-strong convexity; (ii) quadratic functional growth; and (iii) plain convexity. With new and improved rates benefiting from both separate steps of the scheme, linear convergence is proved for (i) and (ii), whereas sublinear convergence is showed for (iii).

1 Introduction

The (cyclic) block coordinate descent (BCD), in the literature also referred to as non-linear block Gauss-Seidel or successive subspace correction method, is a fundamental optimization algorithm [4, 12]. Given a block structured minimization problem, it consists of the successive minimization with respect to the single blocks. Since numerous applications naturally inherit a block structure, the BCD and its variations have been of great interest for decades—especially whenever it is more convenient or feasible to solve the corresponding subproblems instead of the globally coupled problem. For an overview, we refer to the review paper [15].

The convergence of the BCD has been extensively studied in the literature—typically in Euclidean spaces. For instance, if already partial minimization is well-defined, any generated accumulation point is a stationary point [4]. Furthermore, convergence has been established under various convexity assumptions as, e.g., strong convexity [1], and quasi-convexity with respect to each block [7, 8]. Even more strongly, linear convergence has been proved in the context of (multiplicative Schwarz) domain decomposition methods for smooth and strongly convex problems, here, in Banach spaces [14], and the context of feasible descent methods under stricter convexity assumptions (e.g., strong convexity w.r.t. single blocks) [9]; for the latter, lately the overarching class of smooth convex functions with quadratic functional growth has been identified to lead to linear convergence [11]. Commonly, smoothness assumptions of global kind are made, as e.g., global Lipschitz continuity of the Jacobian.

The BCD for two blocks is entitled alternating minimization. It is worth noting that two-block structured problems, appearing in various applications, constitute an important class. In view of this work, we mention an emerging interest for iterative decoupling strategies of two-way coupled partial differential equations, cf., e.g., [5] and references within.

The presence of just two blocks allows for an improved convergence analysis of the BCD in contrast to the general case. For unconstrained smooth convex problems in finite dimensional Euclidean spaces equipped with the $l_2$ norm, linear convergence has been established under additional strong convexity [3], and moreover sublinear convergence has been showed for problems with non-smooth, block-separable contributions [2]. Both results have in common that the theoretical multiplicative constant merely depends on the minimum of the Lipschitz constants of the partial derivatives, instead of a global one. The proofs essentially utilize knowledge on first-order gradient descent methods as the (proximal) BCD. To our best knowledge, those theoretical convergence results are the finest in the literature.

The motivation for this work has been to generalize and improve the previous convergence results for the alternating minimization. For this purpose, we consider a model problem in (infinite dimensional) Banach spaces incorporating block-separable non-smooth contributions (Sect. 2). The model problem covers a large class of problems, allowing, e.g., for block-separable convex constraints or non-smooth regularization; for more examples, we refer to Beck [2]. Finally, by exploiting tailored norms in the analysis this setting can enable (A) tighter convergence results in (B) a fairly general setup. Furthermore, driven by that fact that strong convexity may be a lot to ask for, for the first time, linear convergence of the alternating minimization is investigated under two relaxations of strong convexity: quasi-strong convexity (Sect. 3), and mere quadratic functional growth without an explicitly required feasible descent property (Sect. 4). For a more complete picture, we additionally study the case of plain convex optimization but in Banach spaces (Sect. 5). An illustrative numerical PDE-based example inspired from multiphysics solved by the alternating minimization is provided in Sect. 6. The results are summarized and discussed in the concluding Sect. 7.

2 Alternating minimization for two-block structured model problem

We consider the two-block structured model problem

$$\begin{aligned} \mathrm {min} \left\{ H(x_1,x_2) \equiv f(x_1,x_2) + g_1(x_1) + g_2(x_2) \, \big | \, (x_1,x_2)\in {\mathcal {B}}_1 \times {\mathcal {B}}_2 \right\} , \end{aligned}$$

(1)

where ${\mathcal {B}}_1,{\mathcal {B}}_2,f,g_1,g_2$ satisfy the following properties:

• (P1) $({\mathcal {B}}_i,\Vert \cdot \Vert _i)$ is a Banach space with its dual $\left( {\mathcal {B}}_i^\star ,\Vert \cdot \Vert _{i,\star }\right)$ and the duality pairing $\left\langle \cdot ,\cdot \right\rangle _i$, $i=1,2$. The index will be omitted for duality pairings.

• (P2) The function $g_i: {\mathcal {B}}_i \rightarrow {\mathbb {R}} \cup \{ \infty \}$ is proper convex, (Fréchet) subdifferentiable with subdifferential $\partial g_i$ on $\mathrm {dom}\,g_i$, $i=1,2$. Let ${\mathcal {D}}:=\mathrm {dom}\,g_1 \times \mathrm {dom}\,g_2$.

• (P3) The function $f:{\mathcal {B}}_1 \times {\mathcal {B}}_2 \rightarrow {\mathbb {R}}$ is convex and (Fréchet) differentiable over ${\mathcal {D}}$. Let $\nabla f$ denote the (Fréchet) derivative of f.

• (P4) The optimal set of problem (1), denoted by $X \subset {\mathcal {B}}_1 \times {\mathcal {B}}_2$, is non-empty, and the corresponding optimal value is denoted by $H^\star$.

• (P5) For any $({\tilde{x}}_1,{\tilde{x}}_2)\in {\mathcal {D}}$, the following problems have minimizers

  $$\begin{aligned} \underset{x_1\in {\mathcal {B}}_1}{\mathrm {min}}\, H(x_1,{\tilde{x}}_2),\qquad \text {and} \qquad \underset{x_2\in {\mathcal {B}}_2}{\mathrm {min}}\, H({\tilde{x}}_1,x_2). \end{aligned}$$

Exploiting the particular two-block structure, we consider the iterative solution of (1) via the classical alternating minimization, cf. Algorithm 1.

As in [2], the partial optimality condition (2) on the initial guess has been chosen for the sake of simpler notation in the subsequent analysis; we will analyze the convergence behavior of Algorithm 1 under the following additional assumptions on the product structure and smoothness:

• (A1) ${\mathcal {B}}_1 \times {\mathcal {B}}_2$ is equipped with a separate norm $\Vert \cdot \Vert$ and $\beta _1,\beta _2\ge 0$, satisfying

  $$\begin{aligned} \Vert (x_1,x_2)\Vert ^2&\ge \beta _i\Vert x_i \Vert _i^2 \quad \text {for all }(x_1,x_2)\in {\mathcal {B}}_1 \times {\mathcal {B}}_2,\ i=1,2. \end{aligned}$$

  (5)

  Furthermore, ${\mathcal {B}}_1 \times {\mathcal {B}}_2$ is equipped with a canonical duality pairing $\left\langle \cdot , \cdot \right\rangle$.

• (A2) The partial (Fréchet) derivative of f with respect to the i-th component, denoted by $\nabla _i f \in {\mathcal {B}}_i^\star$, is Lipschitz continuous with Lipschitz constant $L_i\in (0,\infty ]$, $i=1,2$, with $\mathrm {min}\{L_1,L_2\} < \infty$; exemplarily, for $i=1$ (analogously for $i=2$) it holds that $\left\| \nabla _1 f(x_1 + h_1,x_2) - \nabla _1 f(x_1,x_2) \right\| _{1,\star } \le L_1 \Vert h_1 \Vert _1$ for all $(x_1,x_2)\in {\mathcal {D}}$, $h_1 \in {\mathcal {B}}_1$, such that $x_1+h_1 \in \mathrm {dom}\, g_1$, equivalently by a block version of the so-called descent lemma [2, 4]

  $$\begin{aligned} f(x_1+h_1,x_2) \le f(x_1,x_2) + \left\langle \nabla _1 f(x_1,x_2),h_1 \right\rangle + \frac{L_1}{2} \left\| h_1 \right\| _1^2. \end{aligned}$$

  (6)

Remark 1

(Semi-normed spaces) The following analysis does in fact not require $\Vert \cdot \Vert$ or $\Vert \cdot \Vert _i$, $i=1,2$, to be positive definite. Consequently, it is sufficient to formulate (5) and (6) as well as convexity properties (specified in each section), with respect to semi-norms. Without introducing additional notation, we also subsequently allow $\Vert \cdot \Vert$ and $\Vert \cdot \Vert _i$, $i=1,2$, to be merely semi-norms.

3 Linear convergence in the quasi-strongly convex case

In this section, linear convergence is established for the alternating minimization applied to model problem (1) under additional quasi-strong convexity for f:

• (A3a) The function $f:{\mathcal {B}}_1\times {\mathcal {B}}_2 \rightarrow {\mathbb {R}}$ is quasi-strongly convex w.r.t. X, with modulus $\sigma >0$, i.e., for all $x\in {\mathcal {D}}$ and ${\bar{x}}:=\mathrm {arg\,min}\left\{ \Vert x-y\Vert \,\big | \, y\in X \right\}$, the projection of x onto X, it holds

  $$\begin{aligned} f({\bar{x}}) \ge f(x) + \left\langle \nabla f(x), {\bar{x}} - x \right\rangle + \frac{\sigma }{2} \Vert x - {\bar{x}}\Vert ^2. \end{aligned}$$

Any strongly convex function is quasi-strongly convex. Moreover, by convexity of $g_1$ and $g_2$, H inherits quasi-strong convexity from f [with (A3a) stated for subdifferentiable functions].

Theorem 1

(Q-linear convergence under quasi-strong convexity) Assume that $\mathrm {(P1)}$–$\mathrm {(P5)}$ and $\mathrm {(A1),(A2),(A3a)}$ hold. Let $\{x^k\}_{k\ge 0}$ be the sequence generated by the alternating minimization, cf. Algorithm 1. For all $k\ge 0$ it holds

$$\begin{aligned} H^{k+1} - H^\star \le \left( 1 - \frac{\sigma \beta _1}{L_1} \right) \left( 1 - \frac{\sigma \beta _2}{L_2} \right) \left( H^{k} - H^\star \right) . \end{aligned}$$

Proof

We consider the first half-step of the alternating minimization and show

$$\begin{aligned} H^{k+1/2} - H^\star \le \left( 1 - \frac{\sigma \beta _1}{L_1} \right) \left( H^{k} - H^\star \right) \qquad \text {for all }k\in {\mathbb {N}}_0. \end{aligned}$$

(7)

By definition, it holds $\tfrac{\beta _1}{L_1} \ge 0$, whereas equality holds if $\beta _1=0$ or $L_1=\infty$. W.l.o.g. we assume that $\tfrac{\beta _1}{L_1}>0$ (since $H^{k+1/2} \le H^k$ by construction, the statement (7) follows immediately for $\tfrac{\beta _1}{L_1}=0$). We first utilize: (i) (A3a) and the definition of $\beta _1$, cf. (5); (ii) a simple rescaling; and (iii) the fact that $\tfrac{\sigma \beta _1}{L_1}\in (0,1]$ [by (5), (6), (A3a)] and Lipschitz continuity of $\nabla _1 f$, cf. (6). For this, let ${\bar{x}}^k=({\bar{x}}_1^k,{\bar{x}}_2^k):= \mathrm {arg\,min}\left\{ \Vert x-x^k\Vert \,\big | \, x\in X \right\} \in {\mathcal {D}}$, with $H^\star = H({\bar{x}}^k)$. Ultimately, it holds

$$\begin{aligned} f(x^k) - f({\bar{x}}^k)&\underset{\text {(i)}}{\le } \left\langle \nabla f(x^k), x^k - {\bar{x}}^k \right\rangle - \frac{\sigma \beta _1}{2} \left\| x^k_1 - {\bar{x}}^k_1 \right\| _1^2 \nonumber \\&\underset{\text {(ii)}}{=} \frac{L_1}{\sigma \beta _1} \left[ \left\langle \nabla _1 f(x^k), \frac{\sigma \beta _1}{L_1} \left( x^k_1 - {\bar{x}}^k_1\right) \right\rangle - \frac{L_1}{2} \left\| \frac{\sigma \beta _1}{L_1} \left( x^k_1 - {\bar{x}}^k_1\right) \right\| _1^2 \right] \nonumber \\&\qquad + \left\langle \nabla _2 f(x^k), x^k_2 - {\bar{x}}^k_2 \right\rangle \nonumber \\&\underset{\text {(iii)}}{\le } \frac{L_1}{\sigma \beta _1} \left[ f(x^k) - f\left( x_1^k+\frac{\sigma \beta _1}{L_1} \left( {\bar{x}}^k_1 - x_1^k \right) , x_2^k\right) \right] \nonumber \\&\qquad + \left\langle \nabla _2 f(x^k), x^k_2 - {\bar{x}}^k_2 \right\rangle . \end{aligned}$$

(8)

Furthermore, by convexity of $g_1$, it holds with $\tfrac{\sigma \beta _1}{L_1}\in (0,1]$ that

$$\begin{aligned} g_1\left( \frac{\sigma \beta _1}{L_1} {\bar{x}}^k_1 + \left( 1 - \frac{\sigma \beta _1}{L_1} \right) x_1^k\right) \le \frac{\sigma \beta _1}{L_1} g_1({\bar{x}}^k_1) + \left( 1 - \frac{\sigma \beta _1}{L_1}\right) g_1(x_1^k), \end{aligned}$$

or equivalently after reordering terms

$$\begin{aligned} g_1(x_1^k) - g_1({\bar{x}}^k_1) \le \frac{L_1}{\sigma \beta _1} \left[ g_1(x^k_1) - g_1\left( x_1^k + \frac{\sigma \beta _1}{L_1} \left( {\bar{x}}^k_1 - x_1^k\right) \right) \right] . \end{aligned}$$

(9)

Furthermore, the optimality condition corresponding to the second step of Algorithm 1 reads: $x_2^{k}\in \mathrm {dom}\, g_2$ and $0 \in \nabla _2 f(x^k) + \partial g_2(x_2^{k})$ for all $k\ge 0$, which by definition of a subdifferential together with ${\bar{x}}_2^k\in \mathrm {dom}\, g_2$ implies

$$\begin{aligned} g_2(x_2^k) - g_2({\bar{x}}^k_2) \le - \left\langle \nabla _2 f(x^k), x_2^k - {\bar{x}}^k_2 \right\rangle . \end{aligned}$$

(10)

Combining (i) Eqs. (8)–(10), and (ii) the optimality of $x_1^{k+1}$, cf. (3), yields

$$\begin{aligned} H^k - H^\star&\underset{\text {(i)}}{\le } \frac{L_1}{\sigma \beta _1} \left[ H^k - H\left( x_1^k+\frac{\sigma \beta _1}{L_1} \left( {\bar{x}}^k_1 - x_1^k \right) , x_2^k\right) \right] \underset{\text {(ii)}}{\le } \frac{L_1}{\sigma \beta _1} \left( H^k - H^{k+1/2} \right) . \end{aligned}$$

Reordering terms finally yields Eq. (7). By symmetry (incl. discussion of $\frac{\beta _2}{L_2}\ge 0$), it holds

$$\begin{aligned} H^{k+1} - H^\star \le \left( 1 - \frac{\sigma \beta _2}{L_2} \right) \left( H^{k+1/2} - H^\star \right) . \end{aligned}$$

(11)

Ultimately, combining Eqs. (7) and (11), proves the assertion. $\square$

3.1 Numerical test for quasi-strongly convex minimization in a Euclidean space

To assess the sharpness of Theorem 1 under the use of suitable problem-dependent norms, we consider a two-block structured, unconstrained, quadratic, convex optimization problem in a Euclidean space (here ${\mathbb {R}}^{n+m}$, $n,m\in {\mathbb {N}}$)

$$\begin{aligned} \mathrm {min}\left\{ H({\mathbf {x}}_1,{\mathbf {x}}_2) \equiv \left. \frac{1}{2} \left\| \underbrace{ \begin{bmatrix} {\mathbf {A}}_1&{\mathbf {A}}_2 \end{bmatrix} }_{=:{\mathbf {A}}} \begin{bmatrix} {\mathbf {x}}_1 \\ {\mathbf {x}}_2 \end{bmatrix} - {\mathbf {b}} \right\| _{l_2}^2 \right| \ \begin{array}{rl}{\mathbf {x}}_1 &{}\in {\mathbb {R}}^n,\\ {\mathbf {x}}_2 &{}\in {\mathbb {R}}^m\end{array} \right\} \end{aligned}$$

(12)

with ${\mathbf {A}}_1,{\mathbf {A}}_2,{\mathbf {A}},{\mathbf {b}}$ properly dimensioned. We assume that ${\mathbf {A}}$ is non-zero. Then by Theorem 8 in [11], the problem (12) is quasi-strongly convex w.r.t. the Euclidean $l_2$ norm, with $\sigma = \sigma _\mathrm {min}({\mathbf {A}})^2$, where $\sigma _\mathrm {min}(\cdot )$ denotes the minimal singular value. Furthermore, it satisfies the smoothness and convexity assumptions of Theorem 1 with $\beta _1=\beta _2=1$, $L_1=\sigma _\mathrm {max}\left( {\mathbf {A}}_1\right) ^2$, $L_2=\sigma _\mathrm {max}\left( {\mathbf {A}}_2 \right) ^2$, where $\sigma _\mathrm {max}(\cdot )$ denotes the maximal singular value. Ultimately, by Theorem 1, q-linear convergence is guaranteed for all $k\ge 0$

$$\begin{aligned} H^{k+1} - H^\star \le \underbrace{\prod _{i=1}^2 \left( 1 - \frac{\sigma _\mathrm {min}({\mathbf {A}})^2}{\sigma _\mathrm {max}({\mathbf {A}}_i)^2} \right) }_{=:\lambda } \left( H^{k} - H^\star \right) . \end{aligned}$$

(13)

However, the generality of Theorem 1 also allows for utilizing problem-dependent norms, allowing for improving the straight forward result (13). Having Remark 1 in mind, set $\Vert \cdot \Vert _i:=\Vert \cdot \Vert _{{\mathbf {A}}_i^\top {\mathbf {A}}_i}$, $i=1,2$, where $\Vert {\mathbf {x}} \Vert _{{\mathbf {S}}}^2:= {\mathbf {x}}^\top {\mathbf {S}} {\mathbf {x}}$ for any symmetric, suitably dimensioned matrix ${\mathbf {S}}$. Consequently, it is $L_1=L_2=1$. In addition, let $\eta >0$, ${\mathbf {I}}$ be the identity matrix (in any dimension), and define the norm on the product space by $\Vert \cdot \Vert :=\Vert \cdot \Vert _{{\mathbf {A}}_\eta ^2}$, with ${\mathbf {A}}_\eta := \left( \eta {\mathbf {I}} + {\mathbf {A}}^\top {\mathbf {A}}\right) ^{1/2}$. Similarly, set ${\mathbf {A}}_{i\eta }:=\left( \eta {\mathbf {I}} + {\mathbf {A}}_i^\top {\mathbf {A}}_i\right) ^{1/2}$, and the Schur complement ${\mathbf {S}}_{{\mathbf {A}}_{i\eta }^2} := {\mathbf {A}}_{i\eta }^2 - {\mathbf {A}}_i^\top {\mathbf {A}}_j {\mathbf {A}}_{j\eta }^{-2} {\mathbf {A}}_j^\top {\mathbf {A}}_i$, where $j\in \{1,2\}$, $j\ne i$, $i=1,2$. In order to determine $\sigma$ and $\beta _i$, it follows from standard linear algebra that

$$\begin{aligned} \left\| {\mathbf {A}}\begin{bmatrix} {\mathbf {x}}_1 \\ {\mathbf {x}}_2 \end{bmatrix} \right\| _{l_2}^2&\ge \sigma _\mathrm {min}\left( {\mathbf {A}} {\mathbf {A}}_\eta ^{-1} \right) ^2 \, \left\| \begin{bmatrix} {\mathbf {x}}_1 \\ {\mathbf {x}}_2 \end{bmatrix} \right\| _{{\mathbf {A}}_\eta ^2}^2 = \sigma _\mathrm {min}\left( {\mathbf {A}} {\mathbf {A}}_\eta ^{-1} \right) ^2 \, \left\| ({\mathbf {x}}_1, {\mathbf {x}}_2) \right\| ^2,\quad \text {and}\\ \left\| \left( {\mathbf {x}}_1, {\mathbf {x}}_2 \right) \right\| _{{\mathbf {A}}_{\eta }^2}^2&\ge \left\| {\mathbf {x}}_i \right\| _{{\mathbf {S}}_{{\mathbf {A}}_{i\eta }^2}}^2 \ge \sigma _\mathrm {min} \left( {\mathbf {S}}_{{\mathbf {A}}_{i\eta }^2}^{1/2} {\mathbf {A}}_{i\eta }^{-1}\right) ^2 \left\| {\mathbf {x}}_1 \right\| _{{\mathbf {A}}_{i\eta }^2}^2 \ge \sigma _\mathrm {min} \left( {\mathbf {S}}_{{\mathbf {A}}_{i\eta }^2}^{1/2} {\mathbf {A}}_{i\eta }^{-1}\right) ^2 \left\| {\mathbf {x}}_1 \right\| _i^2. \end{aligned}$$

Finally, $\sigma$ and $\beta _i$ are obtained by maximizing the singular values w.r.t. $\eta$, equivalent with the limit $\eta \rightarrow 0$. Thus, Theorem 1 predicts that for all $k\ge 0$ it holds

$$\begin{aligned} H^{k+1} - H^\star \le \underbrace{\prod _{i=1}^2\left( 1 - \underset{\eta \rightarrow 0}{\mathrm {lim}} \, \sigma _\mathrm {min}\left( {\mathbf {A}} {\mathbf {A}}_\eta ^{-1} \right) ^2 \sigma _\mathrm {min} \left( {\mathbf {S}}_{{\mathbf {A}}_{i\eta }^2}^{1/2} {\mathbf {A}}_{i\eta }^{-1}\right) ^2 \right) }_{=:\lambda _\mathrm {opt}} \left( H^{k} - H^\star \right) . \end{aligned}$$

(14)

Using a small example, we demonstrate the sharpness of (14) opposing to (13). Let

$$\begin{aligned} {\mathbf {A}}_1:= \begin{bmatrix} 0 &{} 0 \\ 1 &{} -2 \\ 1 &{} 1 \end{bmatrix},\quad {\mathbf {A}}_2:=\begin{bmatrix} 1 &{} -1 \\ 0 &{} 0 \\ -1 &{} 1 \end{bmatrix},\quad {\mathbf {b}}:= \begin{bmatrix} 1 \\ 1 \\ 1\end{bmatrix}. \end{aligned}$$

For this choice, the two bounds in (13) and (14) are given by $\lambda \approx 0.717$ and $\lambda _\mathrm {opt}\approx 0.245$, respectively. In Fig. 1, the theoretical and actual performances of the alternating minimization applied to (12) are visualized for the initial guess ${\mathbf {x}}_1^0:={\varvec{0}}$. We observe a good agreement between the practical convergence rate and the theoretical bound $\lambda _\mathrm {opt}$, stemming from the analysis using problem-dependent norms.

Fig. 1

Practical and theoretical convergence for the alternating minimization solving (12)

4 Linear convergence in the quadratic functional growth case

In this section, linear convergence is established for the alternating minimization applied to model problem (1) under additional quadratic growth for H:

• (A3b) The objective function $H:{\mathcal {B}}_1\times {\mathcal {B}}_2 \rightarrow {\mathbb {R}}$ has quadratic functional growth w.r.t. X with modulus $\kappa >0$; i.e., for all $x\in {\mathcal {D}}$ and ${\bar{x}}$ (as in $\mathrm {(A3a)}$), it holds

  $$\begin{aligned} H(x) - H({\bar{x}}) \ge \frac{\kappa }{2} \left\| x - {\bar{x}} \right\| ^2. \end{aligned}$$

Quasi-strong convexity implies quadratic functional growth [11], but not vice versa; functions satisfying (A3b) do not require to be convex [16]. We refer to [11] to examples.

Following a similar strategy as in the proof of Theorem 1, we show q-linear convergence. We stress that opposing to the analysis of general feasible descent methods for problems with quadratic functional growth, cf., e.g., [11], a feasible descent property—ensured e.g. for block coordinatewise strongly convex functions—is not explicitly required for a mere two-block structure.

Theorem 2

(Q-linear convergence under quadratic functional growth) Assume $\mathrm {(P1)}$–$\mathrm {(P5)}$ and $\mathrm {(A1)},\mathrm {(A2)},\mathrm {(A3b)}$ hold. Let $\{x^k\}_{k\ge 0}$ be the sequence generated by the alternating minimization, cf. Algorithm 1. For all $k\ge 0$ it holds

$$\begin{aligned} H^{k+1} - H^\star \le \left( 1 - \frac{\kappa \beta _1}{8 L_1} \right) \left( 1 - \frac{\kappa \beta _2}{8 L_2} \right) \left( H^{k} - H^\star \right) . \end{aligned}$$

Proof

We consider the first half-step of the alternating minimization and show

$$\begin{aligned} H^{k+1/2} - H^\star \le \left( 1 - \frac{\kappa \beta _1}{8 L_1} \right) \left( H^{k} - H^\star \right) . \end{aligned}$$

(15)

W.l.o.g. we assume that $\tfrac{\beta _1}{L_1}>0$. Let ${\bar{x}}^k:= \mathrm {arg\,min}\left\{ \Vert x-x^k\Vert \,\big | \, x\in X \right\} \in {\mathcal {D}}$, with $H^\star = H({\bar{x}}^k)$. Utilizing the convexity and smoothness of f, we then obtain

$$\begin{aligned} f(x^k) - f({\bar{x}}^k)&\le \left\langle \nabla _1 f(x^k), x_1^k - {\bar{x}}_1^k \right\rangle + \left\langle \nabla _2 f(x^k), x_2^k - {\bar{x}}_2^k \right\rangle . \end{aligned}$$

(16)

By (i) introducing $\gamma \in (0,1]$ to be specified later, (ii) using the Lipschitz continuity of $\nabla _1 f$, cf. (A2), and the convexity of f, and (iii) the definition of $\beta _1$, cf. Eq. (5), we moreover obtain

$$\begin{aligned}&\left\langle \nabla _1 f(x^k), x_1^k - {\bar{x}}_1^k \right\rangle \nonumber \\&\quad \underset{\text {(i)}}{=} \left\langle \nabla _1 f(x_1^k, x_2^k) - \nabla _1 f\left( x_1^k + \gamma \left( {\bar{x}}_1^k - x_1^k\right) ,x_2^k\right) , x_1^k - {\bar{x}}_1^k \right\rangle \nonumber \\&\qquad +\, \frac{1}{\gamma }\left\langle \nabla _1 f\left( x_1^k + \gamma \left( {\bar{x}}_1^k - x_1^k\right) ,x_2^k\right) , \gamma \left( x_1^k - {\bar{x}}_1^k\right) \right\rangle \nonumber \\&\quad \underset{\text {(ii)}}{\le } L_1 \gamma \Vert x_1^k - {\bar{x}}_1^k \Vert _1^2 + \frac{1}{\gamma } \left[ f\left( x_1^k,x_2^k\right) - f\left( x_1^k + \gamma \left( {\bar{x}}_1^k - x_1^k\right) , x_2^k \right) \right] \nonumber \\&\quad \underset{\text {(iii)}}{\le } \frac{L_1}{\beta _1} \gamma \Vert x^k - {\bar{x}}^k \Vert ^2 + \frac{1}{\gamma } \left[ f\left( x_1^k,x_2^k\right) - f\left( x_1^k + \gamma \left( {\bar{x}}_1^k - x_1^k\right) , x_2^k \right) \right] . \end{aligned}$$

(17)

Based on same grounds as utilized for deriving (9) and (10), it holds

$$\begin{aligned} g_1(x_1^k) - g_1({\bar{x}}^k_1)&\le \frac{1}{\gamma } \left[ g_1(x_1^k) - g_1\left( x_1^k + \gamma \left( {\bar{x}}_1^k - x_1^k\right) \right) \right] , \end{aligned}$$

(18)

$$\begin{aligned} g_2(x_2^k) - g_2({\bar{x}}_2^k)&\le - \left\langle \nabla _2 f(x^k), x_2^k - {\bar{x}}_2^k \right\rangle . \end{aligned}$$

(19)

By definition of H and (16)–(19), we obtain

$$\begin{aligned} H^k - H^\star \le \frac{L_1}{\beta _1} \gamma \Vert x^k - {\bar{x}}^k \Vert ^2 + \frac{1}{\gamma } \left[ H(x^k) - H\left( x_1^k + \gamma \left( {\bar{x}}_1^k - x_1^k \right) , x_2^k \right) \right] . \end{aligned}$$

(20)

Thus, by utilizing (A3b), the optimality property of $x_1^{k+1}$ based on the first step of the alternating minimization, cf. (3), and choosing $\gamma =\frac{\kappa \beta _1}{4L_1}$, it follows

$$\begin{aligned} H^k - H^\star \le \frac{1}{2} \left( H^k - H^\star \right) + \frac{4L_1}{\kappa \beta _1} \left( H^k - H^{k+1/2} \right) , \end{aligned}$$

which yields (15), after reordering. By symmetry, it analogously follows that

$$\begin{aligned} H^{k+1} - H^\star \le \left( 1 - \frac{\kappa \beta _2}{8 L_2} \right) \left( H^{k+1/2} - H^\star \right) . \end{aligned}$$

(21)

Finally, combining Eqs. (15) and (21) proves the assertion. $\square$

5 Sublinear convergence in the plain convex case

In this section, sublinear convergence is established for the alternating minimization applied to model problem (1) under the mild assumption of a compact level set of H w.r.t. the initial value, inspired by Beck [2]:

• (A3c) The functions $g_i:{\mathcal {B}}_i \rightarrow {\mathbb {R}} \cup \{ \infty \}$, $i=1,2$, are closed convex (and thereby H). Furthermore, the level set of H with respect to $H(x^0)$, ${\mathcal {L}}:= \left\{ x \in {\mathcal {D}} \, \big | \, H(x) \le H(x^0) \right\}$, be compact; let $R:= \mathrm {diam}({\mathcal {L}},X)$.

The following result predicts a two-stage behavior: first, the error decreases q-linearly until sufficiently small; after that, sublinear convergence is initiated. The shift depends on the smoothness properties of the problem.

Theorem 3

(Sublinear convergence for the non-smooth convex case) Assume that $\mathrm {(P1)}$–$\mathrm {(P5)}$ and $\mathrm {(A1),(A2),(A3c)}$ are satisfied. Let $\{x^k\}_{k\ge 0}$ be the sequence generated by the alternating minimization, cf. Algorithm 1. Define

$$\begin{aligned} m^\star :=\left[ -1 + \left\lceil \mathrm {log}_2 \left( \frac{H^0 - H^\star }{\mathrm {min}\left\{ \frac{L_1}{\beta _1},\frac{L_2}{\beta _2}\right\} R^2} \right) \right\rceil \right] _+,\quad p^\star := \frac{2\left( \frac{\beta _1}{L_1} + \frac{\beta _2}{L_2} \right) ^{-1}}{\mathrm {min}\left\{ \frac{L_1}{\beta _1},\frac{L_2}{\beta _2}\right\} }\in [1,2], \end{aligned}$$

where $\lceil \cdot \rceil$ and $[\cdot ]_+$ respectively denote the ceiling function and the restriction to the positive part. It holds for all $k\ge 0$

$$\begin{aligned} H^k - H^\star \le \mathrm {max}\left\{ \left( \frac{1}{2} \right) ^k \left( H^0 - H^\star \right) , \ \frac{4 R^2 \left( \frac{\beta _1}{L_1} + \frac{\beta _2}{L_2} \right) ^{-1}}{[k - m^\star ]_+ + p^\star } \right\} . \end{aligned}$$

In particular, for $k\ge m^\star$ at the earliest, sublinear convergence kicks in.

The proof utilizes two auxiliary results: general descent properties for each subiteration of the alternating minimization, and a criterion for concluding sublinear convergence. Those are summarized in the following two lemmas.

Lemma 1

Under the assumptions of Theorem 3, it holds for all $k\ge 0$ that

$$\begin{aligned} H^k - H^{k+1/2}&\ge \mathrm {min}\,\left\{ \tfrac{1}{2}, \tfrac{\beta _1}{4L_1 R^2} (H^k - H^\star ) \right\} (H^k - H^\star ), \end{aligned}$$

(22)

$$\begin{aligned} H^{k+1/2} - H^{k+1}&\ge \mathrm {min}\,\left\{ \tfrac{1}{2}, \tfrac{\beta _2}{4L_2 R^2} (H^{k+1/2} - H^\star ) \right\} (H^{k+1/2} - H^\star ). \end{aligned}$$

(23)

Proof

We show Eq. (22), assuming w.l.o.g. $\tfrac{\beta _1}{L_1}>0$. As in the proof of Theorem 2, Eq. (20) can be derived under given assumptions; i.e., for $\gamma \in (0,1]$ it holds

$$\begin{aligned} H^k - H^\star&\le \frac{L_1}{\beta _1} \gamma \Vert x^k - {\bar{x}}^k \Vert ^2 + \frac{1}{\gamma } \left[ H(x^k) - H\left( x_1^k + \gamma \left( {\bar{x}}_1^k - x_1^k \right) , x_2^k \right) \right] . \end{aligned}$$

By definition of R, cf. (A3c), and the monotonicity of $\{H(x^k)\}_{k=0,\frac{1}{2},1,...}$, it holds $\Vert x^k - {\bar{x}}^k \Vert \le R$. Thus, with the definition of $x^{k+1/2}$, cf. Eq. (3), it follows

$$\begin{aligned} H^k - H^\star \le \frac{L_1R^2}{\beta _1} \gamma + \frac{1}{\gamma } \left( H^k - H^{k+1/2} \right) . \end{aligned}$$

We distinguish two cases: If $H^k - H^\star > \frac{2 L_1 R^2}{\beta _1}$, we choose $\gamma =1$; otherwise, we choose $\gamma =\frac{\beta _1}{2L_1 R^2}(H^k - H^\star )$. This finally proves the first part of the assertion (22). The second part (23) analogously follows by symmetry. $\square$

The following auxiliary convergence criterion, inspired by a similar result in [3], will allow for effectively making use of the energy descent of both steps of the alternating minimization.

Lemma 2

Let $\{A_k\}_{k=0,\frac{1}{2},1,...} \subset {\mathbb {R}}_{\ge 0}$ and $\gamma _1,\gamma _2,p\ge 0$ satisfy

$$\begin{aligned}&A_{k} - A_{k+1/2} \ge \gamma _1 A_{k}^2 \quad \mathrm{for \,all }\,k\ge 0, \end{aligned}$$

(24a)

$$\begin{aligned}&A_{k+1/2} - A_{k+1} \ge \gamma _2 A_{k+1/2}^2 \quad \mathrm{for\, all }\,k\ge 0,\end{aligned}$$

(24b)

$$\begin{aligned}&A_0 \le \left( p (\gamma _1 + \gamma _2) \right) ^{-1}. \end{aligned}$$

(24c)

Then it holds for all $k\ge 0$ that $A_{k} \le \left[ (k+p) (\gamma _1 + \gamma _2)\right] ^{-1}$.

Proof

By (24a) and (24b), $\{A_k\}_{k=0,\frac{1}{2},1,\frac{3}{2},...}$ is non-increasing, and it holds

$$\begin{aligned}&\frac{1}{A_{k+1}} - \frac{1}{A_{k}} = \frac{A_{k} - A_{k+1/2}}{A_{k}A_{k+1/2}} + \frac{A_{k+1/2} - A_{k+1}}{A_{k+1/2}A_{k+1}} \ge \gamma _1 + \gamma _2, \end{aligned}$$

for $k\ge 0$. Thus, by utilizing a telescope sum and applying Eq. (24c), we obtain

$$\begin{aligned} \frac{1}{A_{k+1}}&= \left( \frac{1}{A_{k+1}} - \frac{1}{A_{k}} \right) + \left( \frac{1}{A_{k}} - \frac{1}{A_{k-1}} \right) + \cdots + \frac{1}{A_0} \ge (k+1+p) (\gamma _1 + \gamma _2). \end{aligned}$$

This proves the assertion for $k\ge 1$; for $k=0$ it follows directly from (24c). $\square$

Finally, we are able to prove Theorem 3.

Proof of Theorem 3

As long as $H^k - H^\star > 2 \,\mathrm {min}\left\{ \tfrac{L_1}{\beta _1}, \tfrac{L_2}{\beta _2} \right\} R^2$ for some $k\in {\mathbb {N}}_0$, by Lemma 1 and the monotonicity of $\{H^k\}_{k=0,1,...}$, it holds that

$$\begin{aligned} H^{k} - H^\star \le \left( \frac{1}{2}\right) ^k \left( H^0 - H^\star \right) . \end{aligned}$$

(25)

Thereby, there exists a minimal $m\ge 0$ such that $H^k - H^\star \le 2 \,\mathrm {min}\left\{ \tfrac{L_1}{\beta _1}, \tfrac{L_2}{\beta _2} \right\} R^2$ for all $k\ge m$. Assuming $m\ge 1$, Eq. (25) holds for all $k\le m-1$, and it holds

$$\begin{aligned} 2 \,\mathrm {min}\left\{ \tfrac{L_1}{\beta _1}, \tfrac{L_2}{\beta _2} \right\} R^2 < H^{m-1} - H^\star \le \frac{1}{2^{m-1}} \left( H^0 - H^\star \right) . \end{aligned}$$

Thus, it holds that $m < \mathrm {log}_2 \left( \frac{H^0 - H^\star }{\,\mathrm {min}\left\{ \tfrac{L_1}{\beta _1}, \tfrac{L_2}{\beta _2} \right\} R^2} \right)$, and consequently (including the case $m=0$), $m\le m^\star$, with $m^\star$ as defined above.

Since $\{H^k\}_{k=0,\frac{1}{2},1,...}$ is non-increasing, it also holds for $k\ge m$ that $H^{k+1/2} - H^\star \le 2 \,\mathrm {min}\left\{ \tfrac{L_1}{\beta _1}, \tfrac{L_2}{\beta _2} \right\} R^2$. Hence, by Lemma 1 it follows for all $k\ge m$ that

$$\begin{aligned} H^k - H^{k+1/2}&\ge \frac{\beta _1}{4 L_1 R^2} \left( H^k - H^\star \right) ^2, \end{aligned}$$

(26a)

$$\begin{aligned} H^{k+1/2} - H^{k+1}&\ge \frac{\beta _2}{4 L_2 R^2} \left( H^{k+1/2} - H^\star \right) ^2. \end{aligned}$$

(26b)

Using the notation of Lemma 2, we define the sequence $\{A_n\}_{n=0,\frac{1}{2},1,...}$ with $A_n := H^{n+m} - H^\star$, satisfying the assumptions of Lemma 2 with $\gamma _1 = \frac{\beta _1}{4 L_1 R^2}$, $\gamma _2= \frac{\beta _2}{4 L_2 R^2},\ p= p^\star$. Finally, the application of Lemma 2 yields

$$\begin{aligned} H^k - H^\star \le \frac{4 R^2 \left( \frac{\beta _1}{L_1} + \frac{\beta _2}{L_2} \right) ^{-1}}{k - m + p^\star } \le \frac{4 R^2 \left( \frac{\beta _1}{L_1} + \frac{\beta _2}{L_2} \right) ^{-1}}{[k - m^\star ]_+ + p^\star }\quad \text {for all }k\ge m. \end{aligned}$$

(27)

Combining Eqs. (25) and (27) proves the assertion. $\square$

Remark 2

(Exponential decay during the first iterations) In the case it holds $\,\mathrm {max}\left\{ \tfrac{L_1}{\beta _1}, \tfrac{L_2}{\beta _2} \right\} <\infty$, and the initial error satisfies $H^{0}-H^\star > 2 \,\mathrm {max}\left\{ \tfrac{L_1}{\beta _1}, \tfrac{L_2}{\beta _2} \right\} R^2$, the result of Theorem 3 can be in fact improved. By an analogous line of argumentation as in the above proof, one can conclude that $H^k - H^\star$ first contracts with a rate of $\frac{1}{4}$ for the first $k_1$ iterations, until $H^{k_1}-H^\star \le 2 \,\mathrm {max}\left\{ \tfrac{L_1}{\beta _1}, \tfrac{L_2}{\beta _2} \right\} R^2$ for some $k_1\in {\mathbb {N}}_0$. Afterwards, the convergence behavior can be qualitatively predicted as in Theorem 3. Ultimately, $m^\star$ is of the order

$$\begin{aligned} m^\star \approx \left\lceil \mathrm {log}_4 \left( \frac{H^0 - H^\star }{2 \,\mathrm {max}\left\{ \tfrac{L_1}{\beta _1}, \tfrac{L_2}{\beta _2} \right\} R^2}\right) \right\rceil + \left\lceil \mathrm {log}_2 \left( \frac{\mathrm {max}\left\{ \tfrac{L_1}{\beta _1}, \tfrac{L_2}{\beta _2} \right\} }{\mathrm {min}\left\{ \tfrac{L_1}{\beta _1}, \tfrac{L_2}{\beta _2} \right\} } \right) \right\rceil . \end{aligned}$$

6 Numerical example inspired by multiphysics

Sequential solution strategies are widely used in the context of multiphysics applications. Provided a multiphysics problem enjoys a minimization structure, a sequential solution is closely related (or even equivalent) to applying alternating minimization to the underlying minimization problem.

In the following, we numerically demonstrate the efficacy of alternating minimization to a problem, inspired by poroelasticity applications, i.e., flow in deformable porous media. The following model problem corresponds to an elasticity-like vectorial p-Laplace equation coupled with a Darcy-type equation for non-Newtonian fluids, with a Biot–Darcy-type coupling, see [5, 10] for more details. For instance, we consider the representative coupled problem

$$\begin{aligned} \mathrm {min} \left\{ \int _{\varOmega }\left[ \frac{1}{2} \left| {\varvec{\nabla }} \cdot \left( \alpha {\varvec{u}} + \beta {\varvec{q}} \right) \right| ^2 + \frac{\mu }{p} \left| {\varvec{\nabla }} {\varvec{u}} \right| ^p + \frac{\kappa }{q} \left| {\varvec{q}} \right| ^q - {\varvec{f}}\cdot {\varvec{u}}\right] dx \ \bigg | \ ({\varvec{u}}, {\varvec{q}})\in {\mathcal {U}} \times {\mathcal {Q}} \right\} , \end{aligned}$$

(28)

where ${\varOmega }= (0,1) \times (0,1) \subset {\mathbb {R}}^2$ denotes the domain, $\alpha ,\beta \in {\mathbb {R}}$, $\mu ,\kappa \in {\mathbb {R}}_{>0}$, ${\varvec{f}}\in {\mathbb {R}}^2$ are model parameters, $p,q\in (1,\infty )$, and the solution spaces are defined by

$$\begin{aligned} \mathcal {U}&:= \left\{ {\varvec{v}} \in L^p({\varOmega };{\mathbb {R}}^2) \ \big | \ {\varvec{\nabla }}{\varvec{v}} \in L^p({\varOmega };{\mathbb {R}}^{2\times 2}),\ {\varvec{\nabla }} \cdot {\varvec{v}} \in L^2({\varOmega };{\mathbb {R}}),\ {\varvec{v}}|_{\partial {\varOmega }} = {\varvec{0}}\right\} ,\\ \mathcal {Q}&:= \left\{ {\varvec{v}} \in L^q({\varOmega }; {\mathbb {R}}^2)\ \big | \ {\varvec{\nabla }} \cdot {\varvec{v}} \in L^2({\varOmega };{\mathbb {R}}),\ {\varvec{v}}|_{\partial {\varOmega }} \cdot {\varvec{n}}_{\partial {\varOmega }} = 0 \right\} \end{aligned}$$

where $L^p$ (resp. $L^q$) denotes the standard Lebesgue space and ${\varvec{n}}_{\partial {\varOmega }}$ is the outer normal vector on the boundary $\partial {\varOmega }$ of ${\varOmega }$. We note the solution spaces ${\mathcal {U}}$ and ${\mathcal {Q}}$ are closely related to the standard Sobolev spaces $W^{1,p}_0({\varOmega })$ and $H_0(\mathrm {div};{\varOmega })$, respectively. We fix $\alpha = 1$, $\beta =10$, $\mu = 1$, $\kappa =0.1$, ${\varvec{f}}=(1,1)$, $p=q=1.5$. The corresponding solution is displayed in Fig. 2a.

For the numerical solution, the problem (28) is discretized using the Galerkin method and linear finite elements for ${\varvec{u}}$ and ${\varvec{q}}$ on a Cartesian grid with uniform mesh size $2^{-N}$ with $N\in \{4,5,6\}$. The corresponding discrete minimization problem is then solved using Alg. 1 with an initial guess $({\varvec{u}}^0,{\varvec{q}}^0)=({\varvec{0}},{\varvec{0}})$. For the implementation, the DUNE project [13] and in particular the dune-functions module [6] have been utilized.

Let $H^\star$ denote the energy corresponding to the (converged discrete) solution of (28), and $H^k$ the energy of the approximation $({\varvec{u}}^k,{\varvec{q}}^k)$ of the k-th step of Algorithm 1. The decay $H^k - H^\star$ is displayed in Fig. 2b for the three mesh sizes. We observe linear, essentially mesh-independent convergence. In addition, we mention a decreasing trend for the energy values $H^\star$ for consecutively refined grid, as expected due to the consecutively more accurate discretization. In particular, it is $H^\star \approx -7.077e-3$ for $N=4$, $H^\star \approx -7.137e-3$ for $N=5$, $H^\star \approx -7.153e-03$ for $N=6$.

Fig. 2

a Discrete solution, displacement-like $u_x$ (x-component of ${\varvec{u}}$, whereas y-component is identical) and flux-like ${\varvec{q}}$ (visualized by arrows). b Error decay for different mesh sizes $2^{-N}$

We note the choices for p and q lead to a non-quadratic problem, whose coupling however is governed by a quadratic, merely semi-definite contribution. Hence, the considered problem is closely related with the small algebraic problem in Sect. 3.1, and after all leads to consistent observations. The in principle mesh-independent convergence demonstrates that convergence is most adequately described in problem-dependent, i.e., not standard Euclidean norms, which would in contrast suggest mesh-dependent convergence.

7 Discussion and concluding remarks

In this paper, we have established convergence of the alternating minimization applied to a two-block structured model problem within the class of non-smooth non-strongly convex optimization in general Banach spaces – a fairly broad setting. We have considered three cases of relaxed strong convexity: (i) quasi-strong convexity, (ii) quadratic functional growth, and (iii) plain convexity and a compact initial level set. Convergence rates have been provided, of linear type for the first two cases, and of sublinear type for the third case. To the best of the author’s knowledge, all results are novel.

Our results are direct extensions of previous results in the literature [2, 3, 11], agreeing with or partially refining them if put in the same context, and being valid also in more general scenarios. The key for arriving at our results has been the exploitation of describing smoothness properties (of the two single blocks) and convexity properties (of the full objective function) wrt. different (semi-)norms; these enter the novel rates predicting in particular that both steps of the alternating minimization separately lead to an error decrease. For the subclass of quasi-strongly convex problems, we demonstrate the sharpness of our convergence result, based on a simple numerical example. In addition, an illustrative numerical example inspired by multiphysics demonstrates the efficacy of alternating minimization for PDE-based problems. Finally, we highlight that for the first time, it is proved that quadratic functional growth is sufficient for linear convergence – without any feasible descent property as commonly required in the analysis of the general block coordinate descent [9, 11].

Ultimately, it is noteworthy that the provided results allow for a systematic development and analysis of iterative block-partitioned solvers based on the alternating minimization for problems in applied variational calculus – in particular two-way coupled PDEs arising from a convex minimization problem, see, e.g., [5].