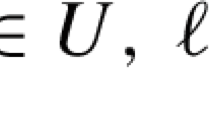On refinement strategies for solving ${\textsc {MINLP}\mathrm{s}}$  by piecewise linear relaxations: a generalized red refinement

Abstract

We investigate the generalized red refinement for n-dimensional simplices that dates back to Freudenthal (Ann Math 43(3):580–582, 1942) in a mixed-integer nonlinear program (${\textsc {MINLP}}$) context. We show that the red refinement meets sufficient convergence conditions for a known ${\textsc {MINLP}}$ solution framework that is essentially based on solving piecewise linear relaxations. In addition, we prove that applying this refinement procedure results in piecewise linear relaxations that can be modeled by the well-known incremental method established by Markowitz and Manne (Econometrica 25(1):84–110, 1957). Finally, numerical results from the field of alternating current optimal power flow demonstrate the applicability of the red refinement in such ${\textsc {MIP}}$-based ${\textsc {MINLP}}$ solution frameworks.

Introduction

Solving general ${\textsc {MINLP}\mathrm{s}}$  is to this day a very challenging task. The backbone of most approaches in this context is still branch-and-bound. In the last two decades, however, various methods have been proposed that tackle non-convex ${\textsc {MINLP}\mathrm{s}}$  by piecewise convex relaxations without direct branching of the continuous variables, see for example [7, 8, 12, 14, 16]. Although these approaches are sometimes rather different, they all need to address the following two problems: the construction of reasonable relaxations of the nonlinear functions and the incorporation of these relaxations into a mixed-integer linear program (${\textsc {MIP}}$) or convex nonlinear program (${\textsc {NLP}}$).

One way to obtain such relaxations is to compute an optimal linearization of a nonlinear function with respect to the number of breakpoints and an a priori given accuracy as in [17, 18]. Complementary, optimal polynomial relaxations of one-dimensional functions are constructed in [16]. For up to three-dimensional functions, explicit approximation techniques for general nonlinear functions are proposed in [15]. The main drawback of all these methods, however, is that the number of simplices in the approximation grows exponentially with the dimension of the function. We refer to the approach from [19] that avoids this problem in that the piecewise linear approximation is not required to interpolate the original function at the vertices of the triangulation.

There are many different ways to model piecewise linear functions as an ${\textsc {MIP}}$. A detailed overview of the various models is presented by [20]. Among the most important ones is the incremental method of Markowitz and Manne, see [13], which is originally developed for one-dimensional functions. A generalization to higher dimensions is described in [6, 11, 21]. Supplementary to this, an extension to relaxations is given in [7].

In this paper, we consider the ${\textsc {MINLP}}$ solution method proposed in [3, 6] and further developed in [2] that tackles an ${\textsc {MINLP}}$ by solving a series of ${\textsc {MIP}}$ relaxations that are based on piecewise linear functions and completely contain the graph of the function. The functions are defined on simplices, which in turn are defined by several vertices. The authors develop an iterative algorithm to find a global optimal solution of the ${\textsc {MINLP}}$ by solving these ${\textsc {MIP}}$ relaxations, which are adaptively refined. They present rather general convergence conditions for ${\textsc {MINLP}}$ solution algorithms that rely on the adaptive refinement of piecewise linear relaxations. They show that the classical longest-edge bisection fulfills these conditions and therefore is suitable for such a solution framework. In addition, they prove that triangulations that are constructed by successively applying the longest-edge bisection lead to piecewise linear relaxations that can always be modeled by the already mentioned generalization of the incremental method.

We extend this result by another refinement strategy for n-dimensional simplices: the generalized red refinement introduced by Freudenthal in [5]. This procedure is to some extent an n-dimensional generalization of the well-known red-green refinement, which is used for two-dimensional simplices. We show that the red refinement meets the convergence conditions from [3]. Moreover, we prove that the generalized incremental method is suitable to model piecewise linear relaxations that are obtained by iteratively applying the red refinement. Finally, numerical results from the field of alternating current optimal power flow demonstrate the applicability of the red refinement in an ${\textsc {MINLP}}$ solution framework as presented in [3]. More precisely, we show that this refinement strategy yields tighter dual bounds for the ${\textsc {MINLP}}$ problems.

This article is structured as follows. We introduce all necessary definitions and theorems of previous works in Sect. 2. Section 3 shows that the red refinement fulfills the convergence conditions from [3]. In Sect. 3, we prove that adaptively red refined piecewise linear relaxations can be modeled by the generalized incremental method. Section 4 presents some numerical results that illustrate the practicability of the red refinement procedure. We conclude this work in Sect. 5.

Preliminaries

The aim of this article is to prove that the generalized red refinement procedure is suitable for an ${\textsc {MINLP}}$ solution framework such as in [3].

We consider an ${\textsc {MINLP}}$ problem as an optimization problem of the following type:

$$\begin{aligned} \text {min}_{x} \quad {c^\top x} \\ \text {s.t.} \quad&A x \le b,\\&f_i(x) \le 0 \qquad \text {for all } {i \in \{1, \ldots , k\}},\\&l \le x \le u,\\&x \in \mathbb {R}^{q} \times \mathbb {Z}^p, \end{aligned}$$

(P)

where k, q, $p \in \mathbb {N}$. First, $A x \le b$ represents the linear constraints, while the nonlinear constraints are described by continuous nonlinear real-valued functions $f_i :\mathbb {R}^{q+p} \rightarrow \mathbb {R}$ for $i = 1, \ldots , k$. The variables x are bounded from below and above by $l, u \in \mathbb {R}^{q+p}$. Moreover, we denote by $\mathcal {F}$ the set of all nonlinear functions $f_i(x)$. Let $D_f \subset \mathbb {R}^{q+p}$ be the domain of a nonlinear function $f \in \mathcal {F}$. Since each variable in (P) has lower and upper bounds, the domain $D_f$ is a compact set. We consider it to be a d-dimensional box with its edges parallel to the coordinate axes, while $d \le q+p$. Equality constraints, i.e., constraints of type $f_i(x) = 0$, are implicitly contained in (P) by simply adding the constraints $f_i(x) \le 0$ and $- f_i(x) \le 0$. Please note that we are not restricted to a linear objective function $c^\top x$, because we can include any nonlinear objective function $f :{\mathbb {R}}^{q+p} \rightarrow {\mathbb {R}}$ by substituting f(x) with a variable $y \in {\mathbb {R}}$ and adding $f(x) \le y$ as a constraint to the ${\textsc {MINLP}}$ problem. Due to ${{\,\mathrm{max\,}\,}}c^\top x = - {{\,\mathrm{min\,}\,}}-c^\top x$, any maximization problem can be transformed to a minimization problem. Thus, (P) represents a general formal description of ${\textsc {MINLP}}$ problems.

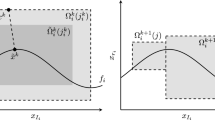
The main idea of the ${\textsc {MINLP}}$ solution approach from [3] is to use piecewise linear functions to construct ${\textsc {MIP}}$ relaxations of the underlying ${\textsc {MINLP}}$. An iterative algorithm is developed to find a global optimal solution by solving these relaxations, which are adaptively refined. With the domain $D_f$ of $f \in \mathcal {F}$, the refinement is performed on a simplicial triangulation $\mathcal {T}$ of $D_f$. A more formal description of this method is given in Algorithm 2.1.

In [3], the classical longest-edge bisection is used for the refinement procedure in Line 19 of Algorithm 2.1. In this paper, we consider the generalized red refinement instead. Please note that the theoretical results are part of the author’s Ph.D. thesis [2].

In order to be equipped with all the necessary ingredients for the following proofs, we first introduce the most relevant definitions and theorems from [3]. First, with a $\delta$-precise refinement procedure, Algorithm 2.1 is both correct and convergent:

Definition 2.1

The refinement procedure in Algorithm 2.1 is called $\delta$-precise, if for an arbitrary sequence $(S^i) \in \mathcal {T}_i$ of simplices $S^i$ that are refined by the refinement procedure with initial triangulation $\mathcal {T}_0$ of $D_f$ and given $\delta > 0$, there exists an index $N \in \mathbb {N}$, such that

$$\begin{aligned} {{\,\mathrm{diam}\,}}(S^N) < \delta \end{aligned}$$

(1)

holds, where ${{\,\mathrm{diam}\,}}(S^N) :=\sup _{x', x'' \in S^N} \{\Vert x' - x''\Vert \}$.

Proposition 2.2

(Theorem 3.6, [3]) If the refinement procedure in Algorithm 2.1 is $\delta$-precise for every $\delta > 0$, then Algorithm 2.1 is correct and terminates after a finite number of steps.

It is therefore sufficient to prove that the generalized red refinement is $\delta$-precise in order to show that its combination with Algorithm 2.1 yields a correct and convergent algorithm.

Moreover, we must prove that piecewise linear relaxations that are obtained by iteratively applying the red refinement can be described by an ${\textsc {MIP}}$ model. In Algorithm 2.1, the piecewise linear relaxations are modeled by the generalized incremental method, see [6]. There are two main ideas of the generalized incremental model. At first, any point $x^S$ inside a simplex S with its vertex set $\mathcal {V}(S) = \{\bar{x}_0^S, \ldots , \bar{x}_d^S \}$ can be expressed either as a convex combination of its vertices or equivalently as

$$\begin{aligned} x^S = \bar{x}_0^S + \sum _{j=1}^d \bigl (\bar{x}_j^S - \bar{x}_0^S\bigr )\delta _j^S \end{aligned}$$

(2)

with $\sum _{j=1}^d \delta _j^S \le 1$ and $\delta _j^S \ge 0$ for $j = 1, \ldots , d$.

The other main idea is that all simplices of a triangulation are ordered in such a way that the last vertex of any simplex is equal to the first vertex of the next one. In this way, we can construct a Hamiltonian path and model the piecewise linear approximation along this path. It is known that modeling piecewise linear functions by the generalized incremental method is possible if an ordering of the simplices with the following properties is available:

• (O1) The simplices in $\mathcal {T}= \{S_1, \ldots , S_n\}$ are ordered such that $\mathcal {V}(S_i) \cap \mathcal {V}(S_{i+1}) \not = \emptyset$ for $i = 1, \ldots , n-1$, and

• (O2) for each simplex $S_i$ its vertices $\bar{x}_0^{S_i}, \ldots , \bar{x}_d^{S_i}$ can be labeled such that $\bar{x}_d^{S_i} = \bar{x}_0^{S_{i+1}}$ for $i = 1, \ldots , n-1$.

Hence, we only have to show that a red refined triangulation has properties (O1) and (O2) to utilize the generalized incremental method.

Convergence result

In this article, we consider Algorithm 3.1 that is proposed in [1, 5] as the refinement procedure in Algorithm 2.1. It is a generalization of the red refinement strategy, which originally was only developed for triangles. It is known that the generalized red refinement procedure always delivers a triangulation of a simplex (that has to be refined) by $2^d$ sub-simplices. Moreover, the triangulation is consistent, i.e., the intersection of any two sub-simplices is either empty or a common lower-dimensional simplex with respect to the vertex sets. Consequently, a consistent triangulation does not allow for hanging nodes, i.e., nodes that are contained in the vertex set of a simplex S, but not in all vertex sets of the simplices that are adjacent to S. We again point out that the theoretical results in this and the subsequent section are part of the author’s Ph.D. thesis [2]. We first illustrate the refinement by Algorithm 3.1 using an example in dimension two.

Example 3.2

We consider a simplex $S_l$ of some triangulation of a two-dimensional nonlinear function with vertex set $\mathcal {V}(S_l) = \{\bar{x}_0, \bar{x}_1, \bar{x}_2\}$ that has to be refined. Let the scalar $\delta$ be sufficiently large such that a refinement is performed by Algorithm 3.1. Note that for $k \le 1$ the condition $\tau ^{-1}(1)< \cdots < \tau ^{-1}(k)$ is considered to be fulfilled. The same applies for the condition $\tau ^{-1}(k+1)< \cdots < \tau ^{-1}(d)$ in case of $k \ge d-1$.

First, the symmetry group ${{\,\mathrm{Sym}\,}}_2$ has two permutations: the identity $\tau _1 = {{\,\mathrm{id}\,}}$ and the permutation $\tau _2 :\{1, 2\} \rightarrow \{2, 1\}$. The identity fulfills the condition in Line 9 for all $0 \le k \le 2$.

Since $\tau _2$ does not satisfy Line 9 for $k=0$, we obtain the first corner sub-simplex $S_l^0$ for $\tau _1$. The vertices of $S_l^0$ are

$$\begin{aligned} v_0 = \bar{x}_0, \quad v_1 = v_0 + \frac{1}{2} (\bar{x}_1 - \bar{x}_0), \quad v_2 = v_1 + \frac{1}{2} (\bar{x}_2 - \bar{x}_1); \end{aligned}$$

(3)

see Fig. 1 for an illustration.

For $k=1$ both permutations $\tau _1$ and $\tau _2$ comply with Line 9. Equivalent to $k=0$, with $\tau _1$ we obtain the simplex $S_l^1$ as in (3), while now $v_0 = \bar{x}_0 + \frac{1}{2} (\bar{x}_1 - \bar{x}_0)$. We thus obtain the corner sub-simplex $S_l^1$ simply by translating the corner sub-simplex $S_l^0$ by the vector $\frac{1}{2} (\bar{x}_1 - \bar{x}_0)$. For $\tau _2$, we compute the vertices of the simplex $S_l^2$ as

$$\begin{aligned} v_0 = \frac{1}{2} (\bar{x}_1 - \bar{x}_0), \quad v_1 = v_0 + \frac{1}{2} (\bar{x}_2 - \bar{x}_1), \quad v_2 = v_1 + \frac{1}{2} (\bar{x}_1 - \bar{x}_0). \end{aligned}$$

(4)

Finally, for $k=1$ again only the identity $\tau _1$ fulfills the condition in Line 9. We obtain the simplex $S_l^3$ as in (3) with $v_0 = \bar{x}_0 + \frac{1}{2} (\bar{x}_2 - \bar{x}_0)$. The corner sub-simplex $S_l^3$ again corresponds to a translation of $S_l^0$ by the vector $\frac{1}{2} (\bar{x}_2 - \bar{x}_0)$.

Fig. 1

A red refinement of a two-dimensional simplex with corresponding ordering and labeling of the four sub-simplices. The labeled vertices of the original simplex that is refined are marked in bold blue

We now prove the $\delta$-preciseness of the refinement procedure and show how to model a refined triangulation by the generalized incremental method afterward. Let $\widetilde{\mathcal {T}}_k$ be the refined triangulation of an initial triangulation $\mathcal {T}_0$ of $D_f$ obtained by applying Algorithm 3.1 such that in every iteration $i \le k$ all simplices of $\widetilde{\mathcal {T}}_{i-1}$ are refined.

Lemma 3.3

Let $S \in {\mathbb {R}}^d$ be a simplex of $\mathcal {T}_{0}$ and e the longest edge of S. Then, the longest edge of any simplex of $\widetilde{\mathcal {T}}_{l}$ contained in (the set) S is bounded by $\frac{1}{2^l} \Vert e \Vert$ with $l \in {\mathbb {N}}$.

Proof

The lemma follows directly from Line 11 of Algorithm 3.1, since

$$\begin{aligned} \left|{\frac{1}{2} (\bar{x}_{\tau (l)} - \bar{x}_{\tau (l)-1})}\right|\le \frac{1}{2} \Vert e \Vert \end{aligned}$$

are the lengths of the edges of the sub-simplices that are constructed during the first refinement step. Applying this recursively finishes the proof. $\square$

Lemma 3.4

Let $\delta > 0$, then there is an $\tilde{N} \in \mathbb {N}$, such that $\widetilde{\mathcal {T}}_{\tilde{N}}$ is a refinement of every triangulation obtained by applying Algorithm 3.1 to $\mathcal {T}_0$ with $\delta$ as input parameter.

Proof

Let $e_0$ be the longest edge of all simplices of $\mathcal {T}_0$. With Lemma 3.3 and $\tilde{N} :=\max \big \{0, \big \lceil \ln \big (\frac{\Vert e_0 \Vert }{\delta } \big ) / \ln (2) \big \rceil \big \}$, the proof works equivalently to the one of Theorem 3.4 from [3]: After at most $\tilde{N}$ refinement steps the longest edge of any simplex of $\widetilde{\mathcal {T}}_{\tilde{N}}$ is bounded by $\delta$. Since Algorithm 3.1 only refines simplices with a longest edge larger than $\delta$ and no simplex in $\widetilde{\mathcal {T}}_{\tilde{N}}$ has an edge longer than $\delta$, it follows by the pigeonhole principle that $\widetilde{\mathcal {T}}_{\tilde{N}}$ is the finest refinement of $\mathcal {T}_{0}$ that is achievable. $\square$

Theorem 3.5

Algorithm 3.1 as refinement procedure in Algorithm 2.1 is $\delta$-precise for every $\delta > 0$. With $\tilde{N}$ as in Lemma 3.4, the number of refinement steps N as in Definition 2.1 is bounded from above by

$$\begin{aligned} N :=m (2^{\tilde{N} d} - 1) + 1, \end{aligned}$$

where m is the number of simplices contained in $\mathcal {T}_0$.

Proof

We count every single simplex that has to be refined to achieve $\widetilde{\mathcal {T}}_{\tilde{N}}$ from Lemma 3.4 and obtain

$$\begin{aligned} m (1 + 2^d + 2^{2 d} + \cdots + 2^{\tilde{N} d - 1}) = m(2^{\tilde{N} d} - 1) \end{aligned}$$

refinements in total. The rest of the proof follows by the pigeonhole principle as in the proof of Theorem 3.5 from [3]: Every sequence $(S^i) \in \mathcal {T}_i$ of simplices has an element $S^k$ with index $k \le m(2^{\tilde{N} d}-1)+1$, such that $S^k \in \widetilde{\mathcal {T}}_{\tilde{N}}$, since $\widetilde{\mathcal {T}}_{\tilde{N}}$ is a refinement of every triangulation obtained by Algorithm 3.1 with parameter $\delta$. Therefore, simplex $S^k$ has the $\delta$-preciseness property (1), as no simplex in $\widetilde{\mathcal {T}}_{\tilde{N}}$ has an edge longer than $\delta$. $\square$

The next corollary follows directly from Proposition 2.2 and Theorem 3.5.

Corollary 3.6

Algorithm 2.1 together with Algorithm 3.1 as refinement procedure is correct and terminates after a finite number of steps.

Incremental method for red refined piecewise linear relaxations

We now show that a piecewise linear approximation that results from applying Algorithm 3.1 can also be modeled with the generalized incremental method. We first prove two lemmata that are used afterward to prove the main result of this section.

Lemma 4.1

Let $\mathcal {S} = \{S^0, \ldots , S^{2^d-1}\}$ be a refinement of a simplex S by Algorithm 3.1 with $\mathcal {V}(S) = \{\bar{x}_0, \ldots , \bar{x}_d \}$. Then, each simplex of the subset of the corner sub-simplices $\mathcal {S}' = \{S^{i_0}, \ldots , S^{i_{d}}\}$ of $\mathcal {S}$ contains a vertex of the simplex S, i.e., $\bar{x}_j \in \mathcal {V}(S^{i_j})$ for all $j = 0, \ldots , d$. Moreover, for each pair of simplices $S^{i_j}, S^{i_k} \in \mathcal {S}'$ the midpoint $m_{jk}$ of the edge with endpoints $\bar{x}_j$ and $\bar{x}_k$ is contained in both vertex sets of the simplices.

Proof

First, the identity ${{\,\mathrm{id}\,}}\in {{\,\mathrm{Sym}\,}}_d$ always fulfills the conditions from Line 9 of Algorithm 3.1. Let $S^{i_j}$ be the simplex that is constructed using the starting vertex $v_0 = \frac{1}{2} (\bar{x}_0 + \bar{x}_j)$ and $\tau = {{\,\mathrm{id}\,}}$, where $j = 0, \ldots , d$. Due to the telescoping sum in Line 11, it follows that

$$\begin{aligned} v_j = \underbrace{\underbrace{\underbrace{\frac{1}{2} (\bar{x}_0 + \bar{x}_j)}_{v_0} + \frac{1}{2} (\bar{x}_1 - \bar{x}_0)}_{v_1} + \frac{1}{2} (\bar{x}_2 - \bar{x}_1)}_{\vdots } + \cdots + \frac{1}{2} (\bar{x}_j - \bar{x}_{j-1}) = x_j \end{aligned}$$

(5)

is contained in the vertex set of $S^{i_j}$.

Furthermore, due to the telescoping sum in (5), we can rewrite Line 11 as

$$\begin{aligned} v_l \leftarrow \frac{1}{2} (\bar{x}_0 + \bar{x}_j) + \frac{1}{2} (\bar{x}_{l} - \bar{x}_{0}) = \frac{1}{2} (\bar{x}_{j} + \bar{x}_{l}) \end{aligned}$$

for $\tau = {{\,\mathrm{id}\,}}$. Since $m_{jk} = \frac{1}{2} (\bar{x}_{j} + \bar{x}_{k})$, we conclude that the vertices $v_k$ and $v_j$ that occur during the construction of $S^{i_j}$ and $S^{i_k}$, respectively, are equal to $m_{jk}$. $\square$

Lemma 4.2

Let $\mathcal {S}'' = \{S^0, \ldots , S^{2^d-1-(d+1)}\}$ be a refinement of a simplex S by Algorithm 3.1 without the $d+1$ corner sub-simplices of $\mathcal {S}'$ as in Lemma 4.1. Then, the union of all simplices of $\mathcal {S}''$ is a (convex) polytope and the triangulation of $\mathcal {S}''$ has an ordering with the properties (O1) and (O2).

Proof

Alternatively to the vertex description, we can describe the simplex S by its half-space representation

$$\begin{aligned} S = \left\{ x \in {\mathbb {R}}^d \, :\, a_j^\top x \le b_j \, \text { with } a_j \in {\mathbb {R}}^d \, \text { and } b_j \in {\mathbb {R}}\, \text { for } j = 0, \ldots , d \right\} . \end{aligned}$$

(6)

We now describe the set $\mathcal {S}''$ by adding the inequalities that separate all corner sub-simplices from the set S as in (6). For a vertex of S exactly d inequalities in (6) are tight. Due to Lemma 4.1, the vertex set of the corner sub-simplex $S^{i_j} \in \mathcal {S}'$ consists of the vertex $\bar{x}_j$ and all midpoints $m_{jk}$ with $k = 0, \ldots , d$. Let $a_j^\top x \le b_j$ be the inequality that is not tight for $\bar{x}_j$. Naturally, it is tight for all other vertices of S and it follows that

$$\begin{aligned} a_j^\top m_{jk} = \frac{1}{2} \, a_j^\top (\bar{x}_k + \bar{x}_j) = \frac{1}{2} (b_j + a_j^\top \bar{x}_j). \end{aligned}$$

(7)

Moreover, since the red refinement also delivers a triangulation of S, where all interiors of the sub-simplices are disjunct, we can describe $S^{i_j}$ by substituting $a_j^\top x \le b_j$ with $a_j^\top x \le \frac{1}{2} (b_j + a_j^\top \bar{x}_j)$ in (6). Therefore, by separating all corner sub-simplices, we obtain the half-space description

$$\begin{aligned} \mathcal {S}'' =&\Bigg \{ x \in {\mathbb {R}}^d \, :\, a_j^\top x \le b_j, \ a_j^\top x \ge \frac{1}{2} (b_j + a_j^\top \bar{x}_j)\\&\text { with } a_j \in {\mathbb {R}}^d \, \text { and } b_j \in {\mathbb {R}}\, \text { for } j = 0, \ldots , d \Bigg \}. \end{aligned}$$

It follows that the union of all simplices of $\mathcal {S}''$ is a convex polytope.

The consistency of the triangulation of S translates to the triangulation of $\mathcal {S}''$, because only the corner sub-simplices are omitted. It is shown by [6] that a triangulation with the property that for each nonempty subset $\tilde{\mathcal {S}} \subsetneq \mathcal {T}$ of a triangulation $\mathcal {T}$ there exist simplices $S_1 \in \tilde{\mathcal {S}}$ and $S_2 \in \mathcal {T}{\setminus } \tilde{\mathcal {S}}$ such that $S_1, S_2$ have d common vertices, always yields a triangulation with the properties (O1) and (O2). Therefore, we only have to prove that the triangulation of $\mathcal {S}''$ has this property. To this end, we consider a nonempty subset $\tilde{\mathcal {S}}$ of $\mathcal {S}''$. Each facet of a d-dimensional simplex consists of d vertices of the simplex. Let $\tilde{\mathcal {S}}_\text {F}$ be the set of all facets of the simplices of $\tilde{\mathcal {S}}$, where the simplices are described by the convex hull of its vertices. Then, each facet in $\tilde{\mathcal {S}}_\text {F}$ is either a facet of $\mathcal {S}''$ (in the sense of convex hulls) or a common facet of two simplices of $\tilde{\mathcal {S}}$. This is due to the consistency of the triangulation. Since $\tilde{\mathcal {S}} \subsetneq \mathcal {S}''$, however, there must be a facet in $\tilde{\mathcal {S}}_\text {F}$ that is a common facet of two simplices $S_1, S_2$ such that $S_1 \in \tilde{\mathcal {S}}$ and $S_2 \in \mathcal {S}'' {\setminus } \tilde{\mathcal {S}}$. $\square$

Endowed with Lemmas 4.1 and 4.2, we are now ready to prove the main result of this section.

Theorem 4.3

Let $\mathcal {T}$ be a triangulation with the properties (O1) and (O2). Then, any triangulation $\mathcal {T}'$ obtained by applying Algorithm 3.1 to $\mathcal {T}$ maintains the properties (O1) and (O2).

Proof

For the following proof, we first show that there is an ordering of the sets $\mathcal {S}'$ and $\mathcal {S}''$ from Lemmas 4.1 and 4.2 with the properties (O1) and (O2). The second part of the proof merges these two orderings to obtain an overall ordering with the properties (O1) and (O2).

Let $\mathcal {T}= \{S_1, \ldots , S_n\}$ and $S_l$ be the simplex that has to be refined, while $\bar{x}_0^{S_l}, \ldots , \bar{x}_d^{S_l}$ are its labeled vertices. We first consider $d \ge 4$ and $d = 2, 3$ afterward. The $2^d$ simplices $S_l^0, \ldots , S_l^{2^d-1}$, into which $S_l$ is divided by the red refinement, have due to Lemma 4.1 the property that the corner sub-simplices contain the vertices of $S_l$. Without loss of generality, let $\bar{x}_j^{S_l} \in \mathcal {V}(S_l^j)$.

We first show that the set $\mathcal {S}'$ of the corner sub-simplices has an ordering with the required properties. The corner sub-simplices $S_l^j \in \mathcal {S}'$ yield a complete graph $G=(V,E)$ with the simplices as the node set V and the midpoints $m_{jk}$ as the edge set E connecting the simplices $S_l^j$ and $S_l^k$. Due to $m_{jk} = m_{kj}$, we assume in the following for the notation $m_{jk}$ that $j < k$ holds. For each Hamiltonian path in G, we can use the path itself as an ordering of the simplices that correspond to the nodes of G. An edge connecting two consecutive nodes of the path corresponds to a common midpoint of two consecutive simplices. Therefore, the ordering naturally has property (O1), which indicates that two consecutive simplices have at least one common vertex. The ordering has the property O2 as well, which states that the last vertex of any simplex is equal to the first vertex of the next one: With two consecutive simplices $S_l^j$ and $S_l^k$ that correspond to two consecutive nodes of the Hamiltonian path, we only have to set $\bar{x}_d^{S_l^j} = m_{jk}$ and $\bar{x}_0^{S_l^k} = m_{jk}$.

Moreover, it follows from Lemma 4.2 that there is an ordering

$$\begin{aligned} \left( S_l^{i_0}, \ldots , S_l^{i_{2^d-1-(d+1)}}\right) \end{aligned}$$

(8)

of the simplex set $\mathcal {S}''$ with the properties (O1) and (O2). Since the vertices of the simplices of $\mathcal {S}''$ are the midpoints $m_{jk}$, there must be two midpoints $m_{jk}$ and $m_{st}$ with

$$\begin{aligned} m_{jk} = \bar{x}_0^{S_l^{i_0}} \qquad \text {and}\qquad m_{st} = \bar{x}_d^{S_l^{i_{2^d-1-(d+1)}}}. \end{aligned}$$

We now link the orderings of $\mathcal {S}'$ and $\mathcal {S}''$ to obtain an overall ordering with the properties (O1) and O2. Let R be a Hamiltonian path in the sub-graph of G that consists of the vertices $V {\setminus } \{0, j, k, s, t, d\}$. Such a path is always attainable, because any sub-graph of a complete graph is also complete. With $j \not = k$ one of the following three cases applies to the node j: $j = s$, $j = t$, or $j \not =s \wedge j \not = t$. With $s \not = t$, we have the following three cases for the node s: $s = j$, $s = k$, or $s \not =j \wedge s \not = k$. Consequently, due to $j \not = k$ and $s \not = t$ only the following five cases are possible for the nodes j, k, s, and t:

$$\begin{aligned} j = s \,\wedge \, k \not = t, \quad j = s \,\wedge \, k = t, \quad j \not = s \,\wedge \, k = t, \quad k = s, \quad j \not = s \,\wedge \, k \not = t. \end{aligned}$$

(9)

The case $k = s$ is equivalent to the case $j = t$, since the inverse of the ordering (8) also has the properties (O1) and (O2).

Keeping the cases in (9) in mind, we define the path

Please note that if $t = d$ in (10a), we can again invert the ordering (8) such that $t \not = d$ and $k = d$. The same can be applied in case of $k = d$ in (10c) and (10d). Moreover, any permutation of the labeling $\bar{x}_i$ of the simplex $S_l^{i_0}$, where $i = 0, \ldots , d-1$ and of the simplex $S_l^{i_{2^d-1-(d+1)}}$, where $i = 1, \ldots , d$, is permissible. Thus, we can assume that $m_{st} \not = m_{0d}$ and that $m_{jk} \not = m_{0u}$ if $m_{st} = m_{ud}$. This guarantees us that the path H is always a Hamiltonian path.

The path H corresponds to an ordering, where the vertices in H are the corner sub-simplices $S_l^j \in \mathcal {S}'$. As showed above, this ordering has the properties (O1) and (O2). We now insert the ordering (8) of the simplex set $\mathcal {S}''$ into the one of H after the simplex that corresponds to the vertex j. The union of $\mathcal {S}'$ and $\mathcal {S}''$ corresponds to the set of all $2^d$ sub-simplices into which $S_l$ is divided by the red refinement. Therefore, the resulting ordering covers all $2^d$ sub-simplices. The merging of the two orderings of $\mathcal {S}'$ and $\mathcal {S}''$ via the midpoints $m_{jk}$ and $m_{st}$ finally leads to an overall ordering $(S_l^{r_0}, \ldots , S_l^{r_{2^d-1}})$ that has the properties (O1) and (O2).

In case of $d = 2$, we use the ordering $(S_l^0, S_l^1, S_l^2, S_l^3)$, where $S_l^0$, $S_l^1$, and $S_l^3$ are the three corner sub-simplices and $S_l^2$ the remaining center sub-simplex, see again Fig. 1 for an illustration.

For $d = 3$, we assume without loss of generality that the vertex $\bar{x}_3$ of the simplex that has to be refined is contained in $S_l^7$. We use the ordering $(S_l^0, S_l^1, S_l^2, S_l^{3}, S_l^{4}, S_l^{5}, S_l^{6}, S_l^7)$, where $S_l^0$, $S_l^1$, $S_l^2$, and $S_l^7$ are the four corner sub-simplices contained in $\mathcal {S}'$ and $S_l^{3}$–$S_l^{6}$ the four center sub-simplices of $\mathcal {S}''$. Finally, the orderings of $\mathcal {S}'$ and $\mathcal {S}''$ are linked via $m_{jk} = m_{02}$ and $m_{st} = m_{27}$.

With these orderings for the refined simplex $S_l$ and all dimensions $d \ge 2$, we complete the proof as follows. We order the simplices of $\mathcal {T}'$ as

$$\begin{aligned} (S_1, \ldots , S_{l-1}, S_l^{r_0}, \ldots , S_l^{r_{2^d-1}}, S_{l+1}, \ldots , S_n). \end{aligned}$$

(11)

Since the corner sub-simplices of $S_l$ yield a complete graph, we can order them such that

$$\begin{aligned} \bar{x}_d^{S_{l-1}} = \bar{x}_0^{S_l^{r_0}} \qquad \text {and}\qquad \bar{x}_d^{S_l^{r_{2^d-1}}} = \bar{x}_0^{S_{l+1}} \end{aligned}$$

holds. Therefore, the simplices $S_{l-1}$, $S_l^{r_0}$ and $S_l^{r_{2^d-1}}$, $S_{l+1}$ are linked as required in O2. Altogether, due to the inheritance from $\mathcal {T}$, we conclude that the ordering (11) of the simplices of $\mathcal {T}'$ has the properties (O1) and (O2). $\square$

Numerical results

In this section, we numerically analyze to what extent the red refinement procedure can be used beneficially in an ${\textsc {MINLP}}$ solution approach that is based on Algorithm 2.1. The key element of Algorithm 2.1 is to solve ${\textsc {MIP}}$ relaxations that provide dual bounds for the ${\textsc {MINLP}}$ problem due to the relaxation property. With increasingly finer ${\textsc {MIP}}$ relaxations, the resulting dual bounds also become tighter. Concurrently, the approximation error decreases, which yields an ${\textsc {MIP}}$ solutions that is feasible for the ${\textsc {MINLP}}$ problem from a practical point of view, e.g., if the error is smaller than $10^{-6}$.

Naturally, any objective value of a global optimal solution of an ${\textsc {MIP}}$ relaxation provides a dual bound for the ${\textsc {MINLP}}$ problem. At the same time, the dual bound of any ${\textsc {MIP}}$ relaxation is also a dual bound for the ${\textsc {MINLP}}$. Typically, in a solution framework that is based on Algorithm 2.1 this is exploited by solving a very fine ${\textsc {MIP}}$ relaxation. It is not necessary to solve this ${\textsc {MIP}}$ to global optimality, since each dual bound of the ${\textsc {MIP}}$ that is obtained during the solution process already provides a dual bound for the ${\textsc {MINLP}}$. Therefore, we can employ a very fine initial ${\textsc {MIP}}$ relaxation in Algorithm 2.1 also to find tight dual bounds.

One way to construct an initial relaxation is to specify a fixed number of simplices for each domain $D_f$ with $f \in \mathcal {F}$ and apply the refinement strategy successively to each simplex until the desired number of simplices is attained. This corresponds to an triangulation scheme such as $\widetilde{\mathcal {T}}_k$ in Lemma 3.3.

In the following, we pursue such a triangulation strategy and compare the red refinement with the longest-edge bisection (${\textsc {LEB}}$) from [3]. To this end, we consider all 20 alternating current (${\textsc {AC}}$) optimal power flow (${\textsc {OPF}}$) instances from the NESTA benchmark set (v0.7.0) with up to 300 buses, see [4]. These instances are subdivided into three operating conditions: standard, active power increase (${\textsc {api}}$), and small angle difference (${\textsc {sad}}$). We use the Extended Conic Quadratic Formulation of [9] to model an ${\textsc {AC}}$ ${\textsc {OPF}}$ instance. Thus, we obtain a total amount of 59 ${\textsc {MINLP}}$ problems, since for the case “nesta_case_6_ww” no active power increase instance is given.

We skip the details of the ${\textsc {MINLP}}$ models in order not to go beyond the scope of this article. The nonlinearities of the ${\textsc {MINLP}}$ problems consist of quadratic monomials, bivariate products, and one-dimensional trigonometric functions. The triangulations that are constructed by the red refinement and the longest-edge bisection differ for the domains of the bivariate products only, as they are identical for one-dimensional domains.

All computations are carried out using a Python implementation of Algorithm 2.1 on a cluster using 4 cores of a machine with two Xeon E3-1240 v6 “Kaby Lake” chips (4 cores, HT disabled) running at 3.7 GHZ with 32 GB of RAM. The run time limit is set to 4 h for each instance with a global relative optimality gap of 0.01%. We utilize Gurobi 9.1.1 as ${\textsc {MIP}}$ solver, see [10].

Relaxations with 8 simplices

At first, we use 8 simplices, i.e., segments in case of one-dimensional and triangles in case of two-dimensional functions, to construct an initial ${\textsc {MIP}}$ relaxation. Table 1 depicts the results for all 59 NESTA instances. Here, $d_{{{\textsc {LEB}}}}$ and $d_{{{\textsc {RR}}}}$ are the best dual bounds of the ${\textsc {MIP}}$ relaxations constructed by the ${\textsc {LEB}}$  and the red refinement (${\textsc {RR}}$). Correspondingly, $T_{{{\textsc {LEB}}}}$ and $T_{{{\textsc {RR}}}}$ are the run times until the ${\textsc {MIP}}$ relaxations are solved to global optimality, while ${\textsc {TL}}$ indicates that the time limit of 4 h has been exceeded.

A common measure for comparing two different ${\textsc {MINLP}}$ solution approaches is the shifted geometric mean. The shifted geometric mean of n numbers $t_1, \ldots , t_n$ with shift s is defined as $\Big (\prod \nolimits _{i=1}^{n}(t_i + s)\Big )^{1/n} - s$. It has the advantage that it is neither affected by very large outliers (in contrast to the arithmetic mean) nor by very small outliers (in contrast to the geometric mean). We use a typical shift $s = 10$ for both the run times and the dual bounds. Please note that if an instance runs into the time limit, we use a run time of 4 h for the calculation of the shifted geometric mean.

The geometric mean in Table 1 is 36.73 for $d_{{{\textsc {LEB}}}}$ and 36.88 for $d_{{{\textsc {RR}}}}$. Regarding the run times, we have ${256.12}\,\text {s}$ for $T_{{{\textsc {LEB}}}}$ and ${251.95}\,\text {s}$ for $T_{{{\textsc {RR}}}}$. Therefore, both refinement strategies are of equal quality, while the red refinement is slightly favorable, since it has tighter dual bounds, faster run times and is able to solve an additional instance to global optimality, namely the ${\textsc {sad}}$ instance “nesta_case_29_edin”.

Table 1 Results summary for the ${\textsc {AC}}$ ${\textsc {OPF}}$ ${\textsc {MIP}}$ relaxations with 8 simplices for each nonlinearity

Relaxations with 32 simplices

Table 2 shows the results for all 59 NESTA instances if we use 32 simplices to construct the initial ${\textsc {MIP}}$ relaxation. As the size of the relaxations increases, less instances are solved to global optimality. The geometric mean in Table 2 is 39.49 for $d_{{{\textsc {LEB}}}}$ and 39.50 for $d_{{{\textsc {RR}}}}$. Regarding the run times, we have ${1587.48}\,\text {s}$ for $T_{{{\textsc {LEB}}}}$ and ${1529.38}\,\text {s}$ for $T_{{{\textsc {RR}}}}$. Therefore, both refinement strategies are of equal quality, while the red refinement is again slightly favorable, since it has faster run times.

Table 2 Results summary for the ${\textsc {AC}}$ ${\textsc {OPF}}$ ${\textsc {MIP}}$ relaxations with 32 simplices for each nonlinearity

Table 3 Results summary for the ${\textsc {AC}}$ ${\textsc {OPF}}$ ${\textsc {MIP}}$ relaxations with 128 triangles for each two-dimensional function and 2 segments for each one-dimensional function

Relaxations with 128 simplices for bivariate products

As pointed out before, a very fine initial ${\textsc {MIP}}$ relaxation can also be utilized to obtain tight dual bounds. With a high number of simplices for the triangulations the ${\textsc {MIP}}$ size drastically increases. For one-dimensional domains the ${\textsc {LEB}}$  and ${\textsc {RR}}$  are identical. Since we are primarily interested in the difference between ${\textsc {LEB}}$  and ${\textsc {RR}}$, we now use 128 simplices to construct the initial ${\textsc {MIP}}$ relaxation, but only for all two-dimensional domains that correspond to the bivariate products of the problem. In case of one-dimensional functions, we only use 2 segments.

Table 3 contains the results for all 59 NESTA instances. The geometric mean in Table 3 is 23.36 for $d_{{{\textsc {LEB}}}}$ and 23.40 for $d_{{{\textsc {RR}}}}$. Regarding the run times, we have ${451.67}\,\text {s}$ for $T_{{{\textsc {LEB}}}}$ and ${330.84}\,\text {s}$ for $T_{{{\textsc {RR}}}}$. Hence, in the case of very fine initial relaxations the ${\textsc {RR}}$  can be very advantageous. Although the dual bounds are of the same quality, the run time is significantly better. This suggests that with the ${\textsc {RR}}$, we are able to find tight dual bounds at shorter run times.

The numerical results in this section demonstrate that red refinement can be applied advantageously for initial relaxations in Algorithm 2.1. In particular, when the red refinement is used to construct very fine ${\textsc {MIP}}$ relaxations to obtain tight dual bounds it is more favorable than the longest-edge bisection for ${\textsc {MINLP}}$ problems that arise in the field of ${\textsc {AC}}$ ${\textsc {OPF}}$.

Conclusion

In this paper, we showed that the generalized red refinement for n-dimensional simplices can be utilized for solving ${\textsc {MINLP}}$ problems by piecewise linear relaxations. We proved that the red refinement meets sufficient convergence conditions for such an ${\textsc {MINLP}}$ solution framework as proposed in [3]. Furthermore, we showed that applying this refinement procedure results in piecewise linear relaxations that can be modeled by the well-known incremental method established by Markowitz and Manne [13].

Numerical results from the field of alternating current optimal power flow illustrated that the application of the red refinement procedure as an alternative to the longest-edge bisection can be advantageous in practice. Especially, if the ${\textsc {MIP}}$ relaxation is primarily used to obtain tight dual bounds, the red refinement seems to be favorable.

The most important subject of future research is to what extent the combination of the two refinement strategies provides further potential for improvement. One possibility is to implement a hybrid approach that starts with an initial relaxation constructed by the red refinement and subsequently refines it by applying the longest-edge bisection.