A dynamic programming algorithm for solving the k-Color Shortest Path Problem

Abstract

Several variants of the classical Constrained Shortest Path Problem have been presented in the literature so far. One of the most recent is the k-Color Shortest Path Problem ($k$-CSPP), that arises in the field of transmission networks design. The problem is formulated on a weighted edge-colored graph and the use of the colors as edge labels allows to take into account the matter of path reliability while optimizing its cost. In this work, we propose a dynamic programming algorithm and compare its performances with two solution approaches: a Branch and Bound technique proposed by the authors in their previous paper and the solution of the mathematical model obtained with CPLEX solver. The results gathered in the numerical validation evidenced how the dynamic programming algorithm vastly outperformed previous approaches.

1 Introduction

In the past few decades, communication networks have swiftly become a key infrastructure in any modern society. Indeed, nowadays they play an essential role in the organization of almost every human activity. As a consequence, a growing stream of research is focused on guaranteeing network reliability and robust service. At this purpose, in the field of planning and optimization of transmission networks, recent contributions dealt with the use of path protection schemes to ensure network operation in case of single link failures [14]. In particular, in path protection two link-disjoint paths sharing the same origin and destination are stored, namely primary and back-up, such that, whenever the connection in the primary path fails, the back-up can be used to prevent traffic loss.

To broaden the applicability of the traffic optimization approach, Yuan et al. [15] considered the simultaneous outage of several links in the network. Specifically, their optimization framework took into account a network in which a single happening could cause a synchronous breakdown of multiple physical links.

This scenario is related, for example, to the nature of wavelength division multiplexing networks, in which it is customary to bundle multiple fiber links in the same conduit, so that the consequences of damages to it would affect all the links there bundled. To properly model this network topology, the authors considered an edge-colored graph—in which links that could be damaged by a single event are modeled with arcs of the same color (see Fig. 1)—and solved the failure minimization problem as a minimum-color path problem.

Fig. 1

Multiple fibers bundled in the same conduit modelled as arcs sharing the same color

In fact, with the hypothesis of mutually independent and equi-probable failure events—with probability $p\in [0,1]$—minimizing the number k of different colors traversed in the path would consequently maximize its reliability, namely $(1-p)^k$.

In particular, the above mentioned example collocates the problem of interest—the guaranty of reliability and robustness—in the framework of edge-colored networks. Actually, there is a growing interest of the scientific literature for these networks due to their ability to represent different interrelations between their nodes [2, 3].

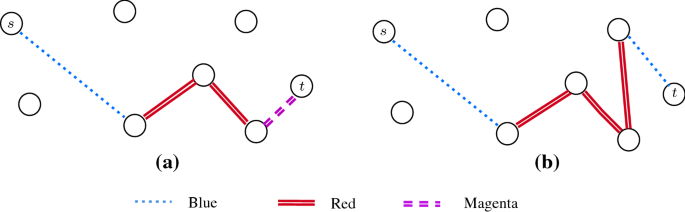
More specifically, this paper addresses a recent problem, originally proposed in [7], named k-Color Shortest Path Problem ($k$-CSPP), in which a weighted edge-colored network is considered. The objective is to find a shortest path between a source node s and a target node t, with a constraint on the maximum number k of different colors that the path can traverse. With reference to the path reliability scenario, we can observe how this problem takes into account the risk adversity while optimizing the length of the path. Considering as an example the scenario depicted in Fig. 2—with $k = 2$—the path from s to t composed by four edges and three colors in Fig. 2a is deemed infeasible, while the right-hand side path (Fig. 2b) made up by two different colors and five edges is preferable even if potentially longer.

The $k$-CSPP has already been tackled by means of a Branch and Bound algorithm; on the other hand the dynamic programming framework has been widely used to deal with Resource Constrained Shortest Path Problems [4, 5]. With this in mind, the main contribution of the present work is the design of a dynamic programming algorithm based on a path-labeling approach and an $A^*$-like exploration strategy.

The paper is organized as follows. Section 2 briefly outlines the problem. A detailed description of the devised solution approach is given in Sect. 3. Section 4 summarizes the benchmark of instances used to test the algorithms and the experiments set up. Moreover, in this section, the computational result and a comparative analysis of the performances of our algorithm with respect to the CPLEX solver and the Branch and Bound approach introduced in [7] are presented. Section 5 is devoted to conclusions and future works.

Fig. 2

Example of two different edge-colored paths. The first characterized by 4 edges and 3 different colors, and the second by 5 edges and 2 colors

2 Problem description

To formally describe the problem, an undirected weighted and colored graph $G = (V,E,w,C)$ is introduced, where $w:E\longrightarrow \mathbb {R}_0^+$ is a function that assigns a non-negative distance $w_{ij}$ to each edge $[i,j]\in E$ and $C:E\longrightarrow \mathbb {N}$ is a labeling function that assigns a color to each $[i,j]\in E$. In the following, we will refer to G as an edge-colored graph. Additionally, let $C(\hat{E})$ be the set of different colors appearing in any subset $\hat{E} \subseteq E$, and $c(\hat{E}) = \left| C(\hat{E})\right|$; thus c(E) is the total number of colors used to label the edges of G. Moreover, letting $E_h$, $\forall h\in \{1, \dots C(E)\}$, be the set of all the edges labeled with the color h, the set of edges E can be partitioned as $\bigcup _{h = 1}^{C(E)} E_h$.

Given a source node s and a target node t, $s,t\in V$, $s\not = t$, the k-Color Shortest Path Problem ($k$-CSPP) aims at finding a minimum distance path $P^*$ from s to t, consisting of edges of at most k different colors. A solution for this problem can be modelled through the introduction of a Boolean decision variable $x_{ij}$ for each edge $[i,j]\in E$ such that

$$ x_{ij} = {\left\{ \begin{array}{ll} 1, &{} \text {if } \left[ i,j\right] \text { belongs to } P^*; \\ 0, &{} \text {otherwise.} \end{array}\right. } $$

Then, as done in [7], the $k$-CSPP is formally described as the following integer linear program:

$$\begin{aligned}&z = \min \sum _{\left[ i,j\right] \in E} w_{ij} x_{ij} \end{aligned}$$

(1a)

$$\begin{aligned}&\text{ subject } \text{ to: }&\nonumber \\&\sum _{\{j\,:[i,j] \in E\}} x_{ji} - \sum _{\{j\,:[i,j] \in E\}} x_{ij} = b_i,&\forall i \in V \end{aligned}$$

(1b)

$$\begin{aligned}&x_{ij}\le y_h,&\forall [i,j]\in E_h ,h = 1,\dots , C(E) \end{aligned}$$

(1c)

$$\begin{aligned}&\sum _{h=1}^{C(E)} y_h \le k \end{aligned}$$

(1d)

$$\begin{aligned}&x_{ij} \in \{0,1\},&\left[ i,j\right] \in E \end{aligned}$$

(1e)

$$\begin{aligned}&y_h \in \{0,1\},&\forall h = 1,\dots , C(E) \end{aligned}$$

(1f)

with $b_i = -1$ for $i = s$, $b_i = 1$ for $i = t$, and $b_i = 0$ otherwise.

The objective function (1a) minimizes the total distance of the path. Constraints (1b) are classical flow-balancing restrictions; those (1c) connect edge traversal and color selection, while constraints (1d) limit the maximum number of different colors that can be used in the solution. Finally, the Boolean nature of the decision variables is expressed by (1e) and  (1f).

In [2], it is proved that finding a simple path $\bar{P}$ from s to t in an edge-colored graph, such that $c(\bar{P})\le k$ with a given k, is an $\mathbf {NP}$-complete problem. As a consequence of this computational complexity result, we have the following claim:

Lemma 1

There does not exist a polynomial-time algorithm $\mathcal {A}$ to find a feasible solution for an arbitrary instance $\mathcal {I}$ of the $k$-CSPP, unless $\mathbf {P}=\mathbf {NP}$.

Since approximation algorithms find feasible solutions with provable guarantees on solution quality, a polynomial-time approximation algorithm would find—if existing—a feasible solution in polynomial time. Consequently, Corollary 1 follows from Lemma 1.

Corollary 1

There does not exist a polynomial-time approximation algorithm for the $k$-CSPP, unless $\mathbf {P}=\mathbf {NP}$.

3 Solution approach

To optimally solve the $k$-CSPP, we propose a dynamic programming algorithm (

), whose design has been encouraged by the successful results that this family of solution framework gathered in the field of constrained shortest path problems [4, 12, 13].

To present our solution algorithm

, let $P_{si}$ be a path in G connecting the source s with a generic node i, and let $L_i=(d_i, C_i, P_{si})$ be a label associated to $P_{si}$, where $d_i$ and $C_i$ are the total distance of the path and the set of different colors traversed by $P_{si}$, respectively. Moreover, let D(i) define the set of all the labels $L_i$ associated with the different paths connecting s to i.

Following the general scheme of a label correcting technique,

explores the solution space to extend the paths under construction by analyzing the set of their labels. Given a path $P_{si}$, the result of path extension operation is a path $P_{sh}$ obtained concatenating $P_{si}$ and $[i,h]\in E{\setminus } P_{si}$, and denoted as $\left<P_{si}, [i,h]\right>$. The source node s is given an initial label $L_s = (0, \emptyset , \left<s\right>)$. Then, starting from a generic label $L_i = (d_i, C_i, P_{si})$, for each node $j\in V$ such that $[i,j] \in E,$ new labels $L_j$ are generated. In particular, the distance of the path $P_{sj}=\left<P_{si}, [i,j]\right>$ is defined as $d_j = d_i+w_{ij}$, and the set of colors traversed is $C_j = C_i \cup \{C([i,j])\}$.

Once the labels are generated, their evaluation is mainly based upon two fundamental concepts: feasibility and dominance.

Definition 1

(Feasibility) A generated label $L_j$ is feasible if $\left| C_j\right| \le k$.

Definition 2

(Dominance) Given two labels $L_i$ and $\hat{L}_i$ associated with the same node $i \in V$, $L_i$ dominates $\hat{L}_i$ if the following conditions hold:

$$\begin{aligned} d_i \le \hat{d}_i;\\ C_i \subseteq \hat{C}_i, \end{aligned}$$

and at least one of such conditions is strict.

Thus, the generated labels are discarded if they are either associated with infeasible paths or dominated by other labels.

Theorem 1

Let $L_i$ and $\hat{L}_i$ be the labels associated to the paths $P_{si}$ and $\hat{P}_{si}$, respectively. If $L_i$ dominates $\hat{L}_i$, then, for any feasible extension $\left<\hat{P}_{si}, [i,h]\right>$, there exists at least a feasible path $\mathcal {P}$ from s to h such that:

• 1. $\mathcal {P}$ is not longer than $\left<\hat{P}_{si}, [i,h]\right>$;

• 2. $C(\mathcal {P})\subseteq C\bigl (\left<\hat{P}_{si}, [i,h]\right>\bigr )$.

Proof

Let $\hat{\mathcal {P}}=\left<\hat{P}_{si}, [i,h]\right>$ be a feasible extension of the path $\hat{P}_{si}$ and let $\mathcal {P'}=\left<P_{si}, [i,h]\right>$ be the extension obtained by substituting path $\hat{P}_{si}$ with path $P_{si}$. For path $\mathcal {P'}$ two cases can occur: either it is a feasible extension too or it is an infeasible extension due to the presence of a cycle.

In the former case (Fig. 3), given the dominance of $L_i$ over $\hat{L}_i$, the extension $\mathcal {P'}$ verifies conditions 1 and 2. In fact, according to Definition 2, path feasibility is preserved—$C(\mathcal {P'}){ =C_i \cup \{C([i,h])\} \subseteq \hat{C}_i \cup \{C([i,h])\}}= C(\hat{\mathcal {P}})$—while the distance of $P_{si}$ being not greater than that of $\hat{P}_{si}$—i.e. $d_i \le \hat{d}_i$—ensures that distance-wise $\mathcal {P'}$ is not less favorable with respect to $\mathcal {\hat{P}}$. Hence, $\mathcal {P}= \mathcal {P'}$.

In the latter case, a cycle in the extension $\mathcal {P'}$ occurs when the node h is visited by the dominant path $P_{si}$, as depicted in Fig. 4.

Thus, given that $P_{sh}\subset P_{si}$ and $\hat{P}_{si} \subset \hat{\mathcal {P}}$, the dominance of $L_i$ over $\hat{L}_i$ ensures that $C(P_{sh})\subseteq C(P_{si}) \subseteq C(\hat{P}_{si})\subseteq C(\hat{\mathcal {P}})$ while the distance of $P_{sh}$ being not greater than the distance of $\hat{\mathcal {P}}$. As a consequence, the subpath $P_{sh}$ is a path from s to h which verifies conditions 1 and 2, i.e. $\mathcal {P} = P_{sh}$.

In conclusion, extending a dominated path yields to the construction of a dominated path. $\square$

Fig. 3

Feasible concatenation of a “dominant” path (curved) with the extension (dashed) of a “dominated” path (normal)

Fig. 4

Concatenation of a “dominant” path (curved) with the extension (dashed) of a “dominated” path (normal) containing a cycle

With the aim of pruning the space of solutions from those unfavourable, the dynamic programming algorithm collects in sets D(i), $\forall \ i \in V$, only feasible and non-dominated labels. It is duly noted how this approach preserves optimality, since there exists at least one optimal solution associated to a feasible and non-dominated label. In fact, if $P^*$ is an optimal path associated to a dominated label, then there exists another feasible s-t path $P^{**}$ such that $C(P^{**})\subseteq C(P^*)$, and $P^{**}$ is not longer than $P^*$. Since $P^*$ is optimal, $P^{**}$ and $P^*$ have the same length—in terms of distance—, and thus $P^{**}$ is an optimal solution.

The

algorithm is summarized in Algorithm 1. Let $\Lambda$ be the cost of the current incumbent. Lines from 2 to 4 initialize the first label, the list of labels L, the lists D(j), $\forall \ j \in V$ and the cost $\Lambda$. While L is not empty, the algorithm extracts a non-dominated feasible label $L_i$ from L (Line 6). Then, if the total distance related to $L_i$ is less than $\Lambda$, the incumbent is updated whenever $i=t$. Otherwise, the labels of each node $j \in V$ such that $[i,j] \in E$ are generated and added to the list L by means of the procedure

(Line 14). In particular, given a certain label $L_j$, this label-adding procedure includes $L_j$ in L and D(j) if it is feasible and non-dominated.

Finally,

returns the best found solution corresponding to the optimal one.

In a dynamic programming technique, the choice of a well-performing label extraction policy (Algorithm 1, line 6) can be a determining factor in favoring the fast convergence to good quality solutions, that combined with the pruning of dominated labels can increase the performances of the algorithm.

The following list briefly introduces some of the best-known strategies that can guide the label-extraction operations.

Dijkstra-like rule (DR)::

the extracted label is the one with the smallest distance;

First-In First-Out (FIFO)::

the extracted label is the one that has been in the queue for the longest time;

Last-In First-Out (LIFO)::

the last inserted label is the first extracted;

Small-Label-First (SLF):

[1]: the extraction is performed from the top of the list. Indeed, whenever a new label $L_j$ has to be added to L, its total distance $d_j$ is compared with the one $d_p$ of the currently top label $L_p$ of L. If $d_j < d_p$, label $L_j$ is entered at the top of L; otherwise $L_j$ is entered at the bottom of L ;

A*::

the extracted label is the one that presents the smallest value of the sum between the distance $d_i$ and the distance of the simple shortest path from the current node i to the target node t.

Remark 1

Interestingly enough, we observe that the function used in the A* strategy, to evaluate the length of the path from the current node i to the target node t, gives a lower bound on the cost of the optimal path from i to t. In fact, that minimum cost path is computed without taking into account constraints (1d).

As reported in [11], A* finds an optimal solution whenever the length of the path from the current node to the target one is estimated with a lower bound. As a consequence, the first feasible solution found by the A* strategy is indeed optimal, thus allowing to prune all the remaining labels. $\square$

Remark 2

As a last observation, we note how the computational effort related to the execution of a DP algorithm is related to the number of explored labels. Without assuming the use of a specific extraction policy, in the worst possible case the number of explored labels is equal to the number of feasible k-colored paths from s to any node $i\in V$.

Assuming the use of $A^*$ as extraction policy, let N(k) be the total number of combination without repetitions of l elements of C, with $l=1,\dots ,k$, i.e.

$$\begin{aligned} N(k) = \sum _{l=1}^k \left( {\begin{array}{c}\left| C\right| \\ l\end{array}}\right) . \end{aligned}$$

(2)

The number of labels extracted for each node $v\in V{\setminus } \{s,t\}$ is bounded by N(k), since for each feasible combination of colors, the $A^*$ strategy extracts only the most favorable path that dominates others characterized by the same set of colors. As a consequence of this, the number of iterations of the

algorithm is bounded by $(\left| V\right| -2) \cdot N(k)$. Each one of the operations executed in a single iteration can be carried out in O(1), except for the AddLabel operation 14, whose complexity is linear in the size of D(j). The size of D(j) can be estimated by N(k), since for each feasible combination of colors, only the dominating path is kept in memory. Therefore, an upper bound for the complexity of

with the $A^*$ strategy is $O((\left| V\right| -2) \cdot N(k)^2)$.

$\square$

4 Computational experiments

In this Section, we discuss about the computational experiments we have designed to appraise the performances of

when compared to two other different solution approaches, namely a Branch and Bound (B&B) algorithm described in [7], and the direct solution of the mathematical model obtained by means of the ILOG CPLEX 12.9 solver.

All the algorithms here compared were coded in C++ using the flags -std=c++17 -O3 and compiled with g++ 8.2. The experiments were run on a INTEL i5-6400@2.70 GHz processor with 8GB of RAM. A time limit of 10 min has been used for each solution method.

4.1 Test instances

The experimentation has been conducted on two data-sets, whose characteristics are summarized in Tables 1 and 2.

Explicitly, the first set of testing instances considered, namely $\mathcal {A}$, consists of the networks described in [7]. These instances were randomly generated through an adaption of the generator presented in [9], and can be divided in two classes: fully random and grid graphs.¹

The number m of edges in the fully random graphs has been selected to belong to $\{10 \cdot n,15 \cdot n,20 \cdot n\}$, where $n=\left| V\right|$. Moreover, the total number of colors for each instance is $p \cdot m$ with $p \in \{0.15, 0.20\}$. Finally, in order to avoid instance-triviality, the value for k has been determined solving a shortest path problem on G. In particular, if $\pi ^*$ is a shortest path connecting s and t in G, and $C^*$ is the number of different colors traversed by $\pi ^*$, then k is selected as $C^*-2$.

Each combination of graph size, denoted as $\{R1, \dots , R9, G1, \dots , G6\}$, and number of colors characterizes a collection of similar instances. Each collection contains ten different instances of the same type. The characteristics of the data-set are summarized in Table 1.

Table 1 Instance parameters for data-set $\mathcal {A}$

Moreover, in order to better analyze how the performances of the algorithms are affected by a variation in the number of colors, we generated a second set of instances, namely $\mathcal {B}$. This data-set replicates the graph sizes of set $\mathcal {A}$, but p ranges in $\{0.01, 0.02\}$ meaning that the total number of colors in the networks has been reduced. The characteristics are summarized in Table 2.

Table 2 Instance parameters of data-set $\mathcal {B}$

4.2 Analysis of the extraction policies for DP

The analysis here presented aims to appraise how the computational performance of the proposed solution approach is affected by the different label selection policies.

At this purpose, we randomly selected 2 out of 10 instances of each type from data-set $\mathcal {A}$ and left DP—with one of the extraction policies, in turn—run with a time limit of 10 min. Tables 3 and 4 report, for each instance type and each extraction policy, the average running time and the number O of optimal solutions found within the time limit.

Table 3 Comparison of extraction policies on fully random graphs

Table 4 Comparison of extraction policies on grid graphs

The results point out that the most performing strategy is A*, both in terms of number of optimal solutions found and running times. This behaviour depends on the criterion used for the selection of the label $L_i$ to be extracted: the value of the path from node i to the target t is an estimation (i.e. a lower bound) of the final cost that can be obtained starting from the path associated with $L_i$.

As a consequence, the convergence to a feasible—indeed optimal—solution is more rapid with respect to the other strategies and a significant number of opened labels can be pruned when the optimum is found (see Remark 1).

4.3 Analysis of the branching strategy

We compared a best-first (BF) and a depth-first (DF) strategy of exploration of the branching tree. On the one hand, BF extracts the branching node that presents a relaxed solution with the highest cost. On the other hand, DF extracts a node from the deepest level. The results are collected in Tables 5 and 6 and report

• the average time for the resolution of instances of the reference type;

• the number O of optimal solutions found within the time limit;

• the number F of feasible (non optimal) solutions found within the time limit.

Table 5 Comparison of branching strategy on fully random graphs

Table 6 Comparison of branching strategy on fully grid graphs

Though none of the two strategies outperforms the other one, we observe that BF presents slightly lower computational times and is able to find an extra optimal solution (compared to DF) for the grid graphs.

4.4 Algorithms comparison

Finally, the last experimentation compares

with A* extraction strategy, B&B with best-first branching strategy, and the model solved by CPLEX. The results are collected in Tables 7 and 8.

Analyzing the performances achieved by the algorithms on random instances (Table 7), it is possible to observe how the average computational times spent by

are sensibly smaller, being at least an order of magnitude lower with respect to those achieved by B&B and CPLEX. Additionally, the number of optimal solutions encountered by means of

($\nicefrac {176}{180} = 97.78\%$) almost doubles the number of optimal solutions of the second best algorithm, i.e., 93 optima found by B&B.

Table 7 Computational results on fully random graphs of the data-set $\mathcal {A}$

Instead, the solution of $k$-CSPP on grid graphs (Table 8) requires on average higher computational times and comparing the number of optimally solved instances with those reported in Table 7, it is possible to note a sensible decrease. This behavior, observed in all the solution techniques here considered, can be attributed to the specific topology characterizing grids. In fact, such graphs are much sparser than the random networks of R1-R9, and the search for a shortest path coupled with a color restriction represents a harder task. Nonetheless, both the number of optimal solutions and the average computational times exhibited by

outperform its two competitors.

Additionally, given the Remark 1, both on random and grid graphs,

either converges to the optimal solution in the time-limit or is not able to find a feasible solution. On the contrary, B&B is able to encounter feasible solutions in almost the totality of the tackled instances ($\nicefrac {277}{300} = 92.33\%$).

Table 8 Computational results on grid graphs of the data-set $\mathcal {A}$

It is properly noted how the average times alone are not sufficient to grasp the performances achieved by the algorithms. This is clear, for example, when considering the distribution of computational times spent by the algorithms on G1 instances with $p=0.20$, reported in the bar-chart of Fig. 5. Among the three methods, it is evident how

reaches the optimal solution in less than 1 s on 9 graphs, while on a single instance it is not able to encounter a feasible solution within the given time limit (600 s). The resulting average time of 60 s can not be clearly compared with the one achieved by CPLEX, equal to 42 s, resulting from generally higher times with smaller variance.

Fig. 5

Distribution of computational times on G1 instances with $p=0.20$

Once again, the study of the distribution of computational times on the whole data-set (Fig. 6) shows that

is often extremely fast in the construction of an optimal solution, and in few cases struggles in the pursuit of a feasible solution. On the contrary, for B&B and CPLEX, the number of instances requiring the whole allotted time limit, or in general times greater than few seconds, is sensibly higher.

Fig. 6

Distribution of computational times on the whole data-set

In order to study the performances while varying the number of colors, we executed the three algorithms on the instances of data-set $\mathcal {B}$, and the results are reported in Tables 9 and 10.

Table 9 Computational results on random graphs of the data-set $\mathcal {B}$

Table 10 Computational results on grid graphs of the data-set $\mathcal {B}$

Table 11 Comparison for data-sets $\mathcal {A}$ and $\mathcal {B}$

Table 11 reports a summarized comparison between the results on data-sets $\mathcal {A}$ and $\mathcal {B}$. The results highlight that

efficiency is strongly affected by the number of colors.

presents a ratio of computational time on $\mathcal {B}$ over computational time on $\mathcal {A}$ equal to 0.07 and 0.11 for random and grid graphs, respectively. This behavior was expected, since the lower the number of colors the lower the number of feasible non-dominated labels (see Remark 2).

On the contrary, it is not possible to identify a clear trend in the performances of B&B and CPLEX at varying the number of colors. On the one hand, on grid graphs, the computational times tend to decrease when lowering the number of colors. On the contrary, the trend appears to be inverse on fully random graphs.

5 Conclusions and future works

The problem addressed in this paper is collocated in the frame of Constrained Shortest Path Problems (CSPP). Specifically, we investigated a recent variant of CSPP, named k-Colored Shortest Path ($k$-CSPP) and proposed in [7].

The solution framework we devised consists of a dynamic programming (

) algorithm based on a path-labeling approach and an $A^*$-like exploration strategy. With the aim of validating this approach, we compared the performances of

with those achieved by two alternative methods: the direct solution of the mathematical model obtained with CPLEX solver, and the Branch and Bound technique described in [7]. These three techniques have been tested on two data-sets that comprises two different graph topologies: random and grid graphs. The experimental results show that

outperforms its two competitors both in terms of computational times and number of optimal solutions found within the given time limit.

Due to the computational intractability of the problem, future research streams will be mainly focused on the design of efficient heuristic approaches with the aim to solve large size instances in short computational time. Moreover, in order to properly model the complexity of real-world networks, different failure probabilities $p_c$, for each color $c \in C(E)$, could be considered; then the resulting bi-objective problem could be solved through a sim-heuristic approach [8, 10].