1 Introduction

Simple games are cooperative games that are commonly used to describe real-world voting systems. Considering a fixed, finite set M of voting members, a simple game is given by a collection \( \mathcal {W}\) of subsets of M satisfying the monotonicity property: \( C \in \mathcal {W}\) and \( C \subseteq C' \subseteq M \) implies \( C' \in \mathcal {W}\). The sets in \( \mathcal {W}\) are called winning coalitions, and each subset of M that is not in \( \mathcal {W}\) is called a losing coalition. It is convenient to require the empty coalition to be losing and the grand coalition of all voting members to be winning when dealing with real-world examples. A fundamental class of simple games are weighted games whose winning coalitions can be written as

$$\begin{aligned} \mathcal {W}= \left\{ C \subseteq M : \sum \limits _{m \in C} a_m \ge \beta \right\} \end{aligned}$$

for some \( a \in \mathbb {R}_{\ge 0}^M \) and \( \beta \in \mathbb {R}\). Note that there exist winning and losing coalitions if and only if \(0 < \beta \le \sum _{m \in M} a_m\). It is a basic fact that every simple game is the intersection of finitely many weighted games, and hence we may define the dimension of a simple game \( \mathcal {W}\) to be the smallest number of weighted games whose intersection is \( \mathcal {W}\).

In a similar way, the codimension of a simple game was defined by replacing intersection with union in the above definition [7]. As a third measure for the complexity of the description of simple games, the boolean dimension was introduced, which allows arbitrary combinations of intersections and unions [5]. The three notions are similarly interesting from a mathematical point of view. Nevertheless, the notion of dimension stands out above the others for its analogy to the \(\mathcal {H}\)-representation of polyhedra.

Determining the dimension of (simple games associated to) real-world voting systems has been of particular interest in social choice theory, see, e.g., the books by Taylor and Zwicker [14] and Taylor and Pacelli [12]. Even though it is in general NP-hard to determine the exact dimension of a given simple game [3], the dimensions of many real voting rules are known. For instance, many real world examples actually have dimension one, which is easy to verify. Examples of dimension two are given by the US federal legislative system [13] and the amendment of the Canadian constitution [10]. A voting rule of dimension three has been adopted by the Council of the European Union under the treaty of Nice [6] and by the Legislative Council of Hong Kong [2].

A new record was set with the change of the EU (European Union) council’s voting system by the Treaty of Lisbon in 2014. Based on the population data of 2014, Kurz and Napel [11] showed that its dimension is at least 7 and at most 13,368, and they posed the exact determination as a challenge to the community. In response, Chen et al. [1] were able to reduce the upper bound to 24.

We provide the first improved lower bound and show that the dimension is at least 8. Although we will not rely on this interpretation in what follows, the idea behind our lower bound is based on the observation that the dimension of a simple game \( \mathcal {W}\) can be seen as the chromatic number of a particular hypergraph H: the nodes of H are the losing coalitions, and a set of losing coalitions \( \mathcal {N}\) forms a hyperedge iff \( \mathcal {N}\cap \mathcal {W}' \ne \emptyset \) for every weighted game \( \mathcal {W}' \supseteq \mathcal {W}\). The proof of Kurz and Napel [11] establishes that H contains a clique of cardinality 7, which directly implies that the chromatic number of H is at least 7. This idea has been used previously in the context of lower bounds on sizes of integer programming formulations [4, 8, 9]. While we have not found any simple subgraph of larger chromatic number, we will show that H contains a hypergraph on 15 nodes whose chromatic number is 8.

Outline In Sect. 2 we introduce the concept of non-separable subsets of the losing coalitions of a simple game \( \mathcal {W}\). A family \( \mathcal {F}\) of such subsets can be thought of as a subgraph of the above hypergraph. Moreover, we consider the notion of a k-cover for such a set \( \mathcal {F}\), which can be seen as a node-coloring of the respective subgraph with k colors. Accordingly, we will see that if the dimension of \( \mathcal {W}\) is at most k, then there exists a k-cover for each \( \mathcal {F}\). In Sect. 3 we consider the simple game associated to the EU council and give a construction of a set \( \mathcal {F}\), for which no 7-cover exists. A proof of the latter fact will be given in Sect. 4. In the final Sect. 5, we comment on the structure of the subgraph, that is used to obtain the improved lower bound and on possible further improvements.

2 Strategy

In what follows, we consider simple games on a common fixed ground set M.

Definition 1

Let \( \mathcal {W}\) be a simple game and \( \mathcal {N}\) be any set of losing coalitions of \( \mathcal {W}\). We say that \( \mathcal {N}\) is non-separable with respect to \( \mathcal {W}\) if every weighted game \( \mathcal {W}' \supseteq \mathcal {W}\) satisfies \( \mathcal {W}' \cap \mathcal {N}\ne \emptyset \).

From the definition it is immediate that a simple game is weighted if and only if no set of losing coalitions is non-separable. So, the existence of a single non-separable set yields that the dimension of a simple game is at least two. To obtain a larger lower bound, the following notion will be useful.

Definition 2

Let \( \mathcal {W}\) be a simple game with losing coalitions \( \mathcal {L}\), and let \( \mathcal {N}_1, \dots , \mathcal {N}_t \subseteq \mathcal {L}\) be non-separable with respect to \( \mathcal {W}\). A k-cover of \( (\mathcal {N}_1, \dots , \mathcal {N}_t) \) is a collection of sets \( \mathcal {L}_1,\dots ,\mathcal {L}_k \subseteq \mathcal {L}\) such that

  1. 1.

    \( \mathcal {L}_1 \cup \cdots \cup \mathcal {L}_k = \mathcal {N}_1 \cup \cdots \cup \mathcal {N}_t \) and

  2. 2.

    \( \mathcal {N}_i \nsubseteq \mathcal {L}_j \) for all \( i \in \{1,\dots ,t\} \), \( j \in \{1,\dots ,k\} \).

In order to obtain a lower bound on the dimension, we will exploit the following observation.

Lemma 1

Let \( \mathcal {W}\) be a simple game with non-separable sets \( \mathcal {N}_1, \dots , \mathcal {N}_t \). If \( \mathcal {W}\) has dimension at most k, then there exists a k-cover for \( (\mathcal {N}_1, \dots , \mathcal {N}_t) \).

Proof

If \( \mathcal {W}\) has dimension at most k, then there exist k weighted games \( \mathcal {W}_1, \dots , \mathcal {W}_k \) such that \( \bigcap _{i=1}^k \mathcal {W}_i = \mathcal {W}\). For \( i \in \{1,\dots ,k\} \) define \( \mathcal {L}_i \) as the intersection of the losing coalitions in \( \mathcal {W}_i \) and \( \mathcal {L}^* {:}{=}\mathcal {N}_1 \cup \cdots \cup \mathcal {N}_t \).

We claim that \((\mathcal {L}_1, \dots , \mathcal {L}_k)\) is a k-cover of \( (\mathcal {N}_1, \dots , \mathcal {N}_t) \). In order to show Property 1, first observe that \( \mathcal {L}_1 \cup \cdots \cup \mathcal {L}_k \subseteq \mathcal {L}^* \) holds. Now, for any \( \ell \in \mathcal {L}^* \subseteq \mathcal {L}\) we have \( \ell \notin \mathcal {W}\) and hence there is an \( i \in \{1,\dots ,k\} \) with \( \ell \notin \mathcal {W}_i \), which implies \( \ell \in \mathcal {L}_i \).

For Property 2, assume that \( \mathcal {N}_i \subseteq \mathcal {L}_j \) holds for some \( i \in \{1,\dots ,t\} \) and \( j \in \{1,\dots ,k\} \). This means that each coalition in \( \mathcal {N}_i \) is losing for \( \mathcal {W}_j \), meaning that \( \mathcal {N}_i \) and \( \mathcal {W}_j \) are disjoint. This contradicts the fact that \( \mathcal {N}_i \) is non-separable with respect to \( \mathcal {W}\) since \( \mathcal {W}_j \supseteq \mathcal {W}\) is weighted. \(\square \)

In what follows, we will consider the simple game associated with the EU council and construct a collection of non-separable losing coalitions that does not permit a 7-covering. By Lemma 1 this implies that the dimension must be at least 8.

3 Our construction

Let us give a formal definition of the simple game associated to the EU council based on the population data of 2014, as considered by Kurz and Napel [11]. In 2014, the European Union consisted of 28 members and hence we may fix \( M {:}{=}\{1,\dots ,28\} \). In the voting system of the EU council, a coalition is winning if

  1. 1.

    it contains at least \( 55\% \) of all members states and

  2. 2.

    it unites at least \( 65\% \) of the total EU population,

or

  1. 3.

    it consists of at least 25 of the 28 member states.

Denoting the weighted game associated with rule i by \(\mathcal {W}_i\) and the simple game that represents the voting system of the EU council by \(\mathcal {W}_{\mathrm{EU}}\), we thus have

$$\begin{aligned} \mathcal {W}_{\mathrm{EU}}= (\mathcal {W}_{1} \cap \mathcal {W}_{2}) \cup \mathcal {W}_{3}. \end{aligned}$$

Note that \( \mathcal {W}_{2} \) depends on the population of each member state. As in [11], we will work with the data depicted in Table 1. Out of the \(2^{28}\) possible coalitions, 30,340,718 are winning. It can be seen that the following coalitions are losing with respect to \( \mathcal {W}_{\mathrm{EU}}\).

$$\begin{aligned} L_{1}&{:}{=}M{\setminus }\left\{ 1, 4, 7, 13, 14\right\}&L_{2}&{:}{=}M{\setminus }\left\{ 2, 3, 6, 13\right\} \\ L_{3}&{:}{=}M{\setminus }\left\{ 1, 4, 5, 28\right\}&L_{4}&{:}{=}M{\setminus }\left\{ 1, 2, 10, 11, 14\right\} \\ L_{5}&{:}{=}M{\setminus }\left\{ 1, 3, 8, 11, 15\right\}&L_{6}&{:}{=}M{\setminus }\left\{ 1, 4, 8, 9, 12\right\} \\ L_{7}&{:}{=}M{\setminus }\left\{ 1, 2, 7, 17, 18\right\}&L_{8}&{:}{=}M{\setminus }\left\{ 1, 5, 6, 16, 18\right\} \\ L_{9}&{:}{=}M{\setminus }\left\{ 2, 4, 6, 15, 21\right\}&L_{10}&{:}{=}M{\setminus }\left\{ 1, 3, 9, 10, 12\right\} \\ L_{11}&{:}{=}M{\setminus }\left\{ 3, 4, 5, 20, 22\right\}&L_{12}&{:}{=}M{\setminus }\left\{ 2, 3, 7, 8, 9\right\} \\ L_{13}&{:}{=}M{\setminus }\left\{ 1, 3, 6, 26\right\}&L_{14}&{:}{=}M{\setminus }\left\{ 2, 3, 5, 19\right\} \\ L_{15}&{:}{=}M{\setminus }\left\{ 16, 17, \ldots , 28\right\} \end{aligned}$$

In fact, note that each coalition \(L_i\) contains less than 25 members. Now, \(L_1,\dots ,L_{14}\) are losing since each of them unites less than \( 65\% \) of the total EU population, and \(L_{15}\) is losing since it contains less than \( 55\% \) of all members.

Next, we construct non-separable subsets with respect to \( \mathcal {W}_{\mathrm{EU}}\) that consist of the above losing coalitions. In order to verify that these subsets are indeed non-separable, the following lemma is helpful.

Table 1 Population data of the European Union on 01.01.2014, see also [11, Table 1]
Full size table

Lemma 2

Let \( \mathcal {W}\) be a simple game and let \( \mathcal {W}^* \) and \( \mathcal {N}\) be sets of some winning and losing coalitions for \( \mathcal {W}\), respectively, such that \( |\mathcal {W}^*| \ge |\mathcal {N}| \). If

$$\begin{aligned} | \{ W \in \mathcal {W}^* : m \in W \} | \le | \{ L \in \mathcal {N}: m \in L \} | \end{aligned}$$

holds for all \( m \in M \), then \( \mathcal {N}\) is non-separable with respect to \( \mathcal {W}\).

Proof

Consider any weighted game \( \mathcal {W}' = \{ C \subseteq M : \sum _{m\in C} a_m \ge \beta \} \supseteq \mathcal {W}\) with \( a \in \mathbb {R}_{\ge 0}^M \) and \( \beta \in \mathbb {R}\). Then we have

$$\begin{aligned} \sum _{L \in \mathcal {N}} \sum _{m \in L} a_m \ge \sum _{W \in \mathcal {W}^*} \sum _{m\in W} a_m \ge \beta \left| \mathcal {W}^* \right| . \end{aligned}$$

The last inequality holds because all elements of \( \mathcal {W}^* \) are contained in \( \mathcal {W}' \). Thus, there must exist some \( L \in \mathcal {N}\), such that

$$\begin{aligned} \sum _{m \in L} a_m \ge \beta \cdot \frac{|\mathcal {W}^*|}{|\mathcal {N}|} \ge \beta . \end{aligned}$$

Therefore, we have \( L \in \mathcal {W}' \) and hence \( \mathcal {W}' \cap \mathcal {N}\ne \emptyset \). Since this holds for any weighted game \( \mathcal {W}' \supseteq \mathcal {W}\), \( \mathcal {N}\) is non-separable with respect to \( \mathcal {W}\). \(\square \)

We claim that the following 2-element subsets of the above losing coalitions are non-separable.

$$\begin{aligned}&\{ L_{1}, L_{5} \}, \{ L_{1}, L_{8} \}, \{ L_{1}, L_{9} \}, \{ L_{1},L_{10} \}, \{ L_{1},L_{11} \}, \{ L_{1},L_{13} \}, \{ L_{1},L_{14} \}, \{ L_{1},L_{15} \}, \nonumber \\&\{ L_{2}, L_{3} \}, \{ L_{2}, L_{4} \}, \{ L_{2}, L_{5} \}, \{ L_{2},L_{6} \}, \{ L_{2},L_{7} \}, \nonumber \\&\quad \{ L_{2},L_{8} \}, \{ L_{2},L_{10} \}, \{ L_{2},L_{11} \}, \{ L_{2},L_{15} \}, \nonumber \\&\{ L_{3}, L_{4} \}, \{ L_{3}, L_{5} \}, \{ L_{3}, L_{7} \}, \{ L_{3},L_{9} \}, \{ L_{3},L_{10} \}, \nonumber \\&\quad \{ L_{3},L_{12} \}, \{ L_{3},L_{13} \}, \{ L_{3},L_{14} \}, \{ L_{3},L_{15} \}, \nonumber \\&\{ L_{4}, L_{6} \}, \{ L_{4}, L_{8} \}, \{ L_{4}, L_{9} \}, \{ L_{4},L_{11} \}, \{ L_{4},L_{12} \}, \{ L_{4},L_{13} \}, \{ L_{4},L_{14} \}, \{ L_{4},L_{15} \}, \nonumber \\&\{ L_{5}, L_{7} \}, \{ L_{5}, L_{8} \}, \{ L_{5}, L_{11} \}, \{ L_{5},L_{14} \}, \{ L_{5},L_{15} \}, \nonumber \\&\{ L_{6}, L_{7} \}, \{ L_{6}, L_{8} \}, \{ L_{6}, L_{9} \}, \{ L_{6},L_{11} \}, \{ L_{6},L_{13} \}, \{ L_{6},L_{14} \}, \{ L_{6},L_{15} \}, \nonumber \\&\{ L_{7}, L_{9} \}, \{ L_{7}, L_{10} \}, \{ L_{7}, L_{11} \}, \{ L_{7},L_{13} \}, \{ L_{7},L_{14} \}, \{ L_{7},L_{15} \}, \nonumber \\&\{ L_{8}, L_{9} \}, \{ L_{8}, L_{10} \}, \{ L_{8}, L_{11} \}, \{ L_{8},L_{12} \}, \{ L_{8},L_{14} \}, \{ L_{8},L_{15} \}, \nonumber \\&\{ L_{9}, L_{10} \}, \{ L_{9}, L_{11} \}, \{ L_{9}, L_{12} \}, \{ L_{9},L_{13} \}, \{ L_{9},L_{14} \}, \{ L_{9},L_{15} \}, \nonumber \\&\{ L_{10},L_{11} \}, \{ L_{10},L_{14} \}, \{ L_{10},L_{15} \}, \nonumber \\&\{ L_{11},L_{12} \}, \{ L_{11},L_{13} \}, \{ L_{11},L_{15} \}, \nonumber \\&\{ L_{12},L_{13} \}, \{ L_{12},L_{15} \}, \nonumber \\&\{ L_{13},L_{14} \}, \{ L_{13},L_{15} \}, \nonumber \\&\{ L_{14},L_{15} \} \end{aligned}$$
(1)

To see that each above set \( \mathcal {N}{:}{=}\{L_i, L_j\} \) is non-separable, we make use of Lemma 2 as follows. If \( L_i,L_j \ne L_{15} \), we have that \( L_i \) and \( L_j \) are contained in \( \mathcal {W}_{1} {\setminus } \mathcal {W}_{2} \). Pick a set of states \( A \subseteq L_i \cup L_j {\setminus } (L_i \cap L_j) \) of minimum total population such that \( W_1 := A \cup (L_i \cap L_j) \) is contained in \( \mathcal {W}_{3} \subseteq \mathcal {W}\). For all above pairs it can be checked that \( W_2 := (L_i \cup L_j) {\setminus } A \) is contained in \( \mathcal {W}_{1} \cap \mathcal {W}_{2} \subseteq \mathcal {W}\). By construction, \( \mathcal {N}\) and \( \mathcal {W}^* {:}{=}\{W_1, W_2\} \) satisfy the assumptions of Lemma 2 and hence \( \mathcal {N}\) is indeed non-separable.

Otherwise, we may assume that \( L_j = L_{15} \). For all above pairs, exchanging the two members with the least population in \( L_i {\setminus } L_{15} \) with the member of largest population in \( L_{15} {\setminus } L_i \), results in two winning sets \( W_1, W_2 \). Again, \( \mathcal {N}\) and \( \mathcal {W}^* {:}{=}\{W_1, W_2\} \) satisfy the assumptions of Lemma 2, implying that \( \mathcal {N}\) is non-separable.

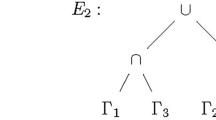
Moreover, the following 3-element subsets of losing coalitions are also non-separable.

$$\begin{aligned} \{ L_{1},L_{2}, L_{12} \}, \{ L_{1},L_{4}, L_{7} \}, \{ L_{1},L_{6}, L_{12} \}, \{ L_{4},L_{5}, L_{10} \}, \{ L_{5},L_{10},L_{12} \} \end{aligned}$$
(2)

To see that these sets are non-separable, consider the following sets of winning coalitions.

$$\begin{aligned} W_{1}&{:}{=}M{\setminus }\left\{ 3, 7, 8, 9, 10, 11, 12, 15\right\}&W_{2}&{:}{=}M{\setminus }\left\{ 1, 2, 3\right\} \\ W_{3}&{:}{=}M{\setminus }\left\{ 1, 2, 7, 14\right\}&W_{4}&{:}{=}M{\setminus }\left\{ 3, 4, 7, 8, 9\right\} \\ W_{5}&{:}{=}M{\setminus }\left\{ 1, 8, 9, 10, 11, 12, 14, 15\right\}&W_{6}&{:}{=}M{\setminus }\left\{ 1, 3, 8, 9\right\} \\ W_{7}&{:}{=}M{\setminus }\left\{ 2, 6, 7, 8, 13\right\}&W_{8}&{:}{=}M{\setminus }\left\{ 1, 7, 8, 9, 12, 13, 14\right\} \\ W_{9}&{:}{=}M{\setminus }\left\{ 1, 3, 10, 11\right\}&W_{10}&{:}{=}M{\setminus }\left\{ 1, 2, 4\right\} \\ W_{11}&{:}{=}M{\setminus }\left\{ 3, 4, 7, 9, 13, 14\right\}&W_{12}&{:}{=}M{\setminus }\left\{ 1, 7, 10, 11, 13, 14, 17, 18\right\} \end{aligned}$$

Observing that the pairs

$$\begin{aligned}&(\{ W_{2}, W_{7}, W_{11} \}, \{ L_{1}, L_{2}, L_{12} \}), \\&(\{ W_{3}, W_{10}, W_{12} \}, \{ L_{1}, L_{4}, L_{7} \}), \\&(\{ W_{4}, W_{8}, W_{10} \}, \{ L_{1}, L_{6}, L_{12} \}), \\&(\{ W_{2}, W_{5}, W_{9} \}, \{ L_{4}, L_{5}, L_{10} \}), \text { and} \\&(\{ W_{1}, W_{2}, W_{6} \}, \{ L_{5}, L_{10}, L_{12} \}) \end{aligned}$$

satisfy the assumptions of Lemma 2, we see that the sets in (2) are indeed non-separable.

In the next section, we show that the non-separable sets in (1) and (2) do not admit a 7-cover. Recall that this implies that the dimension must be at least 8 by Lemma 1.

4 Proof that no 7-Cover can exist

For the sake of contradiction, let us assume that the non-separable sets in (1) and (2) admit a 7-cover. This implies that there exist sets \( \mathcal {L}_1,\dots ,\mathcal {L}_7 \subseteq \{L_1,\dots ,L_{15}\} \) such that

  1. (i)

    each \( \mathcal {L}_j \) is an inclusion-wise maximal subset of \( \{L_1,\dots ,L_{15}\} \) that does not contain any of the sets in (1) and (2), and

  2. (ii)

    \( \mathcal {L}_1 \cup \cdots \cup \mathcal {L}_7 = \{L_1,\dots ,L_{15}\} \).

It can be easily verified that the only sets satisfying (i) are the following.

$$\begin{aligned}&\{ L_{1},L_{2} \}, \{ L_{1},L_{3} ,L_{6} \},\{ L_{1},L_{4} \}, \{ L_{1},L_{7},L_{12} \}, \{ L_{2},L_{9} \}, \{ L_{2}, L_{12},L_{14} \},\{ L_{2},L_{13} \}, \nonumber \\&\{ L_{3},L_{8} \}, \{ L_{3},L_{11} \},\{ L_{4},L_{5} \}, \{ L_{4},L_{7} \}, \{ L_{4},L_{10} \}, \{ L_{5}, L_{6} ,L_{10} \},\{ L_{5},L_{6} ,L_{12} \},\nonumber \\&\{ L_{5},L_{9} \}, \{ L_{5},L_{10},L_{13}\},\{ L_{6},L_{10},L_{12}\}, \{ L_{7},L_{8} \}, \{ L_{8},L_{13} \}, \{ L_{11},L_{14} \},\{ L_{15} \} \end{aligned}$$
(3)

In what follows, for a weight-vector \( w = (w_1,\dots ,w_{15}) \in \mathbb {R}^{15} \), let us define the weight of a set \( \mathcal {L}' \subseteq \{L_1,\dots ,L_{15}\} \) as \( w(\mathcal {L}') := \sum _{i : L_i \in \mathcal {L}'} w_i \).

Suppose first that none of the sets \( \mathcal {L}_1,\dots ,\mathcal {L}_7 \) is equal to \( \{ L_{1},L_{3} ,L_{6} \} \). In this case, consider the weight-vector

$$\begin{aligned} w = (\nicefrac {1}{2},0,1,\nicefrac {1}{2},0,1,\nicefrac {1}{2},0,1,0,0,0,1,1,1) \end{aligned}$$

and observe that the weight of each set in (3) that is distinct from \( \{ L_{1},L_{3} ,L_{6} \} \) is at most 1. Thus, the weight of each set \( \mathcal {L}_1,\dots ,\mathcal {L}_7 \) is at most 1, and we obtain

$$\begin{aligned} 7 < \tfrac{15}{2} = w(\{L_1,\dots ,L_{15}\}) = w(\mathcal {L}_1 \cup \cdots \cup \mathcal {L}_7) \le w(\mathcal {L}_1) + \cdots + w(\mathcal {L}_7) \le 7, \end{aligned}$$

a contradiction.

It remains to consider the case that one of the sets \( \mathcal {L}_1,\dots ,\mathcal {L}_7 \) is equal to \( \{ L_{1},L_{3} ,L_{6} \} \), say \( \mathcal {L}_1 \). Consider the weight-vector

$$\begin{aligned} w = (0,\nicefrac {1}{3},0,\nicefrac {2}{3},\nicefrac {1}{3},0,\nicefrac {1}{3},\nicefrac {2}{3},\nicefrac {2}{3},\nicefrac {1}{3},1,\nicefrac {2}{3},\nicefrac {1}{3},0,1) \end{aligned}$$

and observe that the weight of each set in (3) is at most 1, and that \( w(\mathcal {L}_1) = 0 \). Thus, we have

$$\begin{aligned} 6 < \tfrac{19}{3} = w(\{L_1,\dots ,L_{15}\}) = w(\mathcal {L}_1 \cup \cdots \cup \mathcal {L}_7) \le w(\mathcal {L}_2) + \cdots + w(\mathcal {L}_7) \le 6, \end{aligned}$$

another contradiction. This completes our proof.

5 Comments on the approach

As mentioned in Sect. 1, the dimension of \(\mathcal {W}_{\mathrm{EU}}\) is equal to the chromatic number of a hypergraph that is formed by all losing coalitions. Actually, it is sufficient to consider the subgraph that is induced by maximally losing coalitions. Unfortunately, this subgraph still contains 270,179 nodes and determining its chromatic number seems computationally intractable. However, in order to obtain a lower bound on the chromatic number one may consider any smaller subgraph. Natural candidates for small subgraphs with a large chromatic number are subgraphs with many hyperedges of small cardinality.

Kurz and Napel [11] considered the simple subgraph induced by \(\mathcal {L}^*\), which consists of all losing coalitions L such that \(|L| \in \{23,24\}\) or \(L = L_{15}\). Note that our losing coalitions \(L_1,\dots ,L_{15}\) all belong to \(\mathcal {L}^*\). In fact, this subgraph contains many edges: If a coalition L with \(|L| \in \{23,24\}\) is losing, then its population is below \( 65\% \) of the total EU population. For two such losing coalitions it is quite likely that exchanging a member with a high population against some members with a small population results in two winning coalitions. In this case the losing coalitions share an edge (see Lemma 2). In a similar manner, it is easy to see that \(L_{15}\) is adjacent to every other coalition in \(\mathcal {L}^*\).

As observed in [11], this subgraph contains many 7-cliques, showing that its chromatic number is at least 7. However, it is possible to find a 7-coloring for this graph. When also considering hyperedges of arbitrary size, we showed in Sect. 4 that one needs at least 8 colors. In order to provide a short combinatorial proof for the lower bound, it is not practical to work with the whole set \(\mathcal {L}^*\), which contains 950 coalitions, even when only considering maximal losing coalitions. Therefore, we iteratively reduced the size of the set, while ensuring that the bound was still intact. For the remaining set of coalitions, we analyzed the corresponding dual of the fractional coloring linear program in order to obtain the weights used in Sect. 4. y

We mention that it is possible to separate all coalitions in \(\mathcal {L}^*\) from \(\mathcal {W}_{\mathrm{EU}}\) with the help of 8 weighted games. Thus, in order to obtain an improved lower bound, it is necessary to include a broader set of losing coalitions and to find a more diverse set of blocking hyperedges. We expect some room for improvement, especially on the currently standing upper bound by Chen et al. [1], but find it hard to predict the true value of the dimension of \(\mathcal {W}_{\mathrm{EU}}\).