1 Introduction

Conflict-free routing appears in many applications where routes are constrained to the extent that vehicles may not pass each other without taking alternative routes. Previous application areas have included scheduling multiple cranes in steel logistics, transportation of containers with automated guided vehicles (AGVs), routing of taxiing aircraft and movements of trains. The motivating problem for the proposed approach is the allocation of routes to trucks in a warehouse, such routes being numbered in thousands per day. Each truck can carry multiple items that must be retrieved from various locations. Given the tight alleyways in which the trucks manoeuvre, the efficient allocation of conflict-free routes in real time is crucial. Due to width constraints, the horizontal gaps between rows are one way.

Conflict-free routing approaches allocate point-to-point routes across a graph one vehicle at a time, adding diversions and waits to avoid the paths of already-routed vehicles by considering a time-expanded version of the graph. These have proved very efficient compared to the alternative approaches that compute routes (ignoring time) and retrospectively amend the routes to avoid collisions, frequently leading to deadlocks [8].

Earlier work has proposed conflict-free routing approaches based on variations of the well-known Dijkstra’s [3, 17] and A* [4, 16, 19] shortest path algorithms. The focus in this article is on the conflict-free routing algorithm QPPTW [17], a variant of Dijkstra’s shortest path algorithm that accounts for the times of previous vehicle movements. QPPTW finds a shortest route by expanding routes from the start vertex, applying labels to each vertex that represent the shortest path to the vertex found so far. Our proposed modification adds a stack to labels, storing the required intermediate stops that have yet to be processed. When this stack is empty, the route is complete. We term this new algorithm QPPTW-m (QPPTW for multiple points).

QPPTW-m is more general than earlier works in conflict-free routing ([8, 9, 17] and others), which only considered allocation of routes with a single start and single end point with no required intermediate stopping points. Clearly, in the more general case the requirement exists to have intermediate points, visiting multiple points in a specified order. QPPTW-m is also accompanied by a metaheuristic to determine the order which to route the vehicles, and allocate jobs to the trucks. In subsequent sections, we present QPPTW-m and demonstrate its practical applicability.

2 Related work

Conflict-free routing appears in several application areas, including transportation of containers with automated guided vehicles (AGVs) [8, 9], forklift movement[19], taxiing aircraft [1, 3, 17] and rail operations [5].

Approaches to these problems can be divided into two groups [8]. The first group of approaches allocate routes then retrospectively avoid deadlocks, either as part of the objective function, or though some kind of repair operation. Examples include [13, 15], which used metaheuristics to allocate the routes. The second group of approaches (e.g. [3, 4, 16, 17, 19]) tend to use a variation of shortest path algorithms such as Dijkstra or \(A^*\), with an addition of a time element to only construct collision-avoiding routes. The closest to the proposed approach is Vivaldini et al. [19], in that it also includes a top-level heuristic to allocate jobs to trucks. However, all these approaches are for routes between single (origin,destination) pairs; the present work extends this to multi-point routes.

Several studies analysed system-level deadlocks and prevention in container terminals [6]. Many rely on the highly-constrained grid structure of the terminals, with routing being a search over predefined routes [11] or algorithms specific to the layout [14], rather than our general graph-based approach.

Aspects of the problem we address are shared with other well-known optimisation problems. The Travelling Salesman Problem (TSP) attempts to find the single most cost-effective path visiting specified vertices on a graph. An extension of TSP, the Travelling Thief Problem [2], also incorporates a Knapsack Problem, whereby the route must be chosen that also maximises the value of items collected by the travelling vehicle. The Rich Vehicle Routing Problem [12] is also arguably a generalisation of TSP, where routes are allocated to multiple vehicles. Variants of RVRP make use of time-windows, but the distinction with those mentioned in the present work is that with RVRP they are target times for each node, rather than times on which edges are free for traversal. Herein lies the major difference of the present work with TSP/RVRP: the constraint on the links, which are one-way and, crucially, one vehicle at a time.

3 Problem

We now introduce the broader application context, then describe the specific problem addressed by this paper and the model we adopt for its solution. Our partner company, PostPac, provides an outsourcing warehouse service. Customers are mail order retailers who do not wish to run their own warehouses, instead contracting PostPac to store goods and post them out on request. This means they can benefit from economies of scale, by mixing the storage of the different companies to best service all the requests, and collecting a mixture of orders for a mixture of companies, to best optimise the retrieval of goods. The issue for PostPac is how to efficiently retrieve goods in the warehouse.

3.1 Problem description

The component of the PostPac system on which we focus is the truck based retrieval. The task is one of time optimisation, gathering all the required items from the warehouse in as short a period as possible. The environment is a grid based warehouse, the basic layout of which is seen in Fig. 1. This will be developed into the directed graph model seen in Fig. 2 obeying the following conditions:

  1. 1.

    There are 7 rows, each structured in the same way (see Fig. 1).

  2. 2.

    Each row has 56 storage points, accessible on one side only. Each storage point has three levels.

  3. 3.

    Each row is split into two parts, one of 36 and one of 20 storage points, allowing trucks to change rows at the split.

  4. 4.

    Each storage point contains a collection of items of different types.

  5. 5.

    Only the 10 trucks are allowed to move inside the system, and all can move simultaneously. No personnel are ordinarily allowed in on foot.

  6. 6.

    The horizontal gaps between rows are one way, due to width constraints. The outer border and middle avenue can be considered two way.

  7. 7.

    On average, there are several thousand orders to gather per day.

  8. 8.

    On any given journey a truck can retrieve a variety of different items, thus fulfilling a number of orders.

  9. 9.

    Items are delivered by the trucks to a single collection point.

  10. 10.

    It is assumed that jobs have already been allocated to trucks ahead of time.

Fig. 1
figure 1

Warehouse layout: black are the rows, light blue is the area traversable by trucks, and orange (top-left) is the entrance/exit (color figure online)

Full size image

Two key issues cause inefficiency: (1) Trucks waiting on each other, due to the one way nature of the paths. This is a lack of coordination in their route planning. (2) Trucks retrieving a set of items travel all over the warehouse far more frequently than if the items for that trip were chosen more carefully.

We tackle (1) by applying a conflict-free routing algorithm to allocate routes to each truck. This finds the shortest route (in time) for trucks given a particular permutation of intermediate points for each truck, and a permutation of trucks in which to allocate their routes. This allows for automated planning of the routes, which also partially addresses (2). To fully tackle (2), we apply a metaheuristic search over these two permutation spaces to approximate the globally optimal set of routes for the trucks.

Fig. 2
figure 2

The directed graph model of the warehouse layout

Full size image

3.2 Model

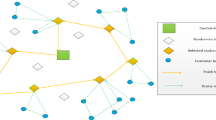
The warehouse seen in Fig. 1 is modelled as a directed graph seen in Fig. 2, to support the one way nature of many of the paths. The storage rows are seen as the yellow vertices, a truck at one of these vertices can access materials stored at that location. Blue vertices are locations that trucks can pass through while navigating the environment but do not provide direct access to storage themselves. The red vertex is the collection point which all trucks must return to with their items. Finally the black lines represent edges, and each edge can only be used one way, due to a constraint imposed by the company. Where a route is large enough to be considered two way it is modelled as two lines of blue vertices, enabling two directions of travel.

The system contains 7 access rows, each with 56 storage points. While each storage point has 3 levels, we can ignore this as all 3 can be accessed once the truck is there (this only affects the loading time at each vertex). This gives \(56 * 7 = 392\) storage points in the system. The graph, then, has 392 vertices for accessing storage, with an additional 251 vertices for the navigation around the perimeter and central alley, and 1 vertex for the entrance/exit, to give a total of 644 vertices.

4 Proposed routing algorithm

We now focus on the core of the approach, the conflict-free routing algorithm. The order in which the stopping points are visited, and in which trucks are allocated routes, is important, but we consider this to be secondary and deal with this in Sect. 4.3. The conflict-free routing algorithm we adopt extends QPPTW, first proposed by Gawrilow et al. [9] for movements at a container terminal and later adapted for aircraft taxiing [1, 3, 17]. The original QPPTW allocates routes for a single start-end pair.

4.1 The existing QPPTW

Notation in the following is summarised in Table 1. The path layout is represented as a directed graph \(G=(V,E)\) of vertices V and edges E as per Fig. 2. An edge \(e \in E\) has an associated weight \(\tau _e\), the estimated time to traverse e. Each e can only have one truck \(t_i\) on it at any one time. This limitation is enforced by each e having an associated sorted-set of time-windows\(\mathcal {F}_e\). The \(\mathcal {F}_e\) specify the times e is available for use as part of a route. A truck will only be allocated a route for which there is a chain of time-windows along its entire length, ensuring the route is conflict free. Additionally, trucks have a minimum separation equivalent to the width of one storage point at all times. This is ensured by pre-processing G to find the conflicting edges \({\text {conf}}(e)\) for each e (a conflicting edge being any edge adjacent to e, i.e. sharing a vertex with e). When a truck is routed via e, the time-windows of \({\text {conf}}(e)\) are updated to prevent other trucks conflicting with it. Long edges are divided into lengths of no more than one storage space by intermediate points to allow separation of consecutive trucks on the same path. QPPTW resembles Dijkstra’s shortest path algorithm [7], with the addition of time reservations on the edges. Vehicles are routed in sequence, with each allocated the optimal route considering already routed vehicles. By only generating routes that fit the time-windows, each route by default avoids previous routes. This means that, as long as the time-windows are updated to reflect known movements, the approach is applicable to dynamic problems. Routes can also be updated part-way through by running the routing algorithm using the current location as the starting point. However, in this article, we discuss only the static situation.

Table 1 Summary of notation
Full size table

For ease of comparison, Algorithm 1 replicates QPPTW, with our new additions highlighted in blue. In the original QPPTW, the search for a shortest route is carried out by expanding the shortest path found so far from the start vertex, represented by the label with the minimum weight removed from a heap (Line 5). Then labels are applied to the vertex reached by each outgoing edge from the present vertex (loop starting on Line 16). A label \(L=(v_L,I_L,pred_L)\) specifies the time period \(I_L=[a_L,b_L]\) within which the current truck being routed could reach vertex \(v_L\), given the previous label \(pred_L\) in the route. The time-windows on the edge are checked for the earliest time that the edge can be fully traversed for a given start time (loop starting on Line 17). The earliest time that the vertex can be reached is calculated (in the original QPPTW, this is Line 29, without the if...else block surrounding it), and a new label created for the vertex (Line 33). If the label represents a quicker way to reach a vertex (Line 34), the previous label on that vertex is replaced with the new label. As the algorithm repeats, the labels are updated to the point where they represent the shortest path, given the existing time-windows, to each vertex.

The algorithm terminates when a route \(R_i\) to the destination vertex is found. The route \(R_i\) is reconstructed by following the ancestor \(pred_L\) of each label in turn. \(R_i\) is allocated to truck \(t_i\), and the \(\mathcal {F}(e)\) are trimmed, split or deleted to reflect times that \(t_i\) is present on each e. If a complete path exists between \(v_{start}\) and \(v_{end}\) on G, QPPTW will always return a route: delay caused by conflicts with other vehicles will simply make the time of arrival at the target vertex \(v_{end}\) later. The time complexity of QPPTW is polynomial in the number of time-windows: \(O(|\mathcal {F}|^3 \log {|\mathcal {F}|})\) [18].

figure a

4.2 Additions to QPPTW

Our proposed extension is simple: the addition of a stack containing the intermediate vertices to visit. The head of the stack is used as the target vertex, and when reached, is removed so the algorithm can continue the route towards the next target. We also add “wait” periods, which extend the time periods for labels on intermediate vertices to accommodate the truck loading operation. The precise changes to the algorithm are summarised below, and highlighted in Algorithm 1. We term the extended algorithm QPPTW-m (QPPTW for multiple points).

  1. 1.

    The definition of labels is extended to include a reference to the intermediate node \(v^i_L\) that the label forms part of the path towards. The inputs to the algorithm are amended: rather than only a destination vertex \(v_{end}\), a list of vertices to visit in-order \(V_Q\) is provided. Consequently, Step 2 is amended so the first label L is created with the first vertex to visit in V.

  2. 2.

    At Step 9 a new if statement is added. The original QPPTW checks here whether the current label represents a route to the target, and if so, returns the route (Steps 7–8). We add a check to determine whether the present label represents a route to the intermediate target \(v_i\). If \(v_i\) is also the final target, we return the complete route as before. If not, we update the intermediate target to the next vertex in \(V_Q\) (Steps 10–13).

  3. 3.

    Each intermediate vertex involves a loading operation, so we update the earliest time the truck can leave \(v_i\) by adding the loading time (Step 11). Loading time is determined by the level accessed. We then create a new label \(L_{load}\) for \(v_i\) for the new times (Step 12).

  4. 4.

    There is no need to add the new label to the heap as it will just be removed at the next stage. Rather, the label that was obtained from the heap (L) is replaced with the newly created one (\(L_{load}\)) (Step 13). \(L_{load}\) will be used as the parent for any further expansion of the route.

  5. 5.

    At Steps 26–29, a new variable \(\tau _{out\_check}\) is created. \(\tau _{out}\) is the estimated exit time for the edge currently considered to expand the route. \(\tau _{out\_check}\) includes loading time if the vertex reached by the edge has a loading operation. \(\tau _{out\_check}\) is then used to check against the current time-window, so the route will only be expanded if the current edge has a time-window long enough to accommodate both loading and edge traversal. Time-windows are also updated to reflect conflicting edges so this ensures no conflicts with other trucks while the present route’s truck is loading.

  6. 6.

    At Step 35, an extra if, so the new label \(v^\prime \) is only checked for dominance against labels for the same subroute (i.e. the same intermediate target \(v^i\)).

  7. 7.

    We also propose a change to improve efficiency at Step 17. The available time-windows \(\mathcal {F}(e_L)\) for each edge \(e_L\) are stored in a sorted set, in order of ascending end time. Rather than iterating over the whole set \(\mathcal {F}(e_L)\), the tail set is used, starting with the first window to end after the current label’s start time. This way, we only consider time-windows that can be used by the truck.

4.3 Higher level search

Outside the core algorithm, there are two levels to the problem to consider. Clearly, the order in which the intermediate points are visited has an impact on collection time. This can be formulated as a search over permutations, the well-known Travelling Salesman Problem, an instance of which exists for each collection trip. Furthermore, the order in which routes are allocated to vehicles has been shown to make a small, but nevertheless notable, difference to total transit times for QPPTW [4, 17]. Simply, because the routes are reserved via the time-windows, it is possible for an earlier truck to be routed in such a way that it prevents several later trucks being routed optimally. Merely allocating the routes in a different order, without changing their start times, can avert this problem. So, we have a permutation of length n trips for which routes need allocated, and n permutations of varying lengths (one per trip).

5 In practice

We ask two questions: (Q1) Does the approach solve the problem? (Q2) Is the approach suitable for real-world use? Q1 can easily be answered. For the real-world scenario described in Sect. 3.1, with 57 truck movements (covering around 6 h), the algorithm was able to allocate conflict-free routes. Precise comparisons with the existing manual-routing approach cannot be made because the existing routes were not recorded. However, PostPac was satisfied that the automated routes were superior to manual allocation.

For Q2, a single run of QPPTW-m allocated routes within 5 s, in Java running on a standard Intel™ i7 CPU. We noted above that the approach is impacted by the order of both intermediate vertices and the order in which routes are allocated; consequently for real-time use we should consider the total run time of the high-level metaheuristic search over these permutations. To explore this, simple experimental runs were carried out with a hillclimber (HC) and simulated annealing (SA), implemented with the Haiku toolkit [10].

The representation was a set of permutations: one for the trips to route, and, for each trip, a permutation of items to collect (i.e. locations to visit). Both metaheuristics used two perturbation operators, chosen with equal probability: (1) swap trips to route; and (2) swap items for collection within a trip chosen at random. The objective to minimise was total collection time, as computed for the routes returned by QPPTW-m, assuming an average speed of 1 unit of storage space per second and loading times of 30, 180 and 300 s for items on levels 1, 2, and 3 respectively. The specific instance allocated routes for 10 trucks; more importantly these needed routes allocated for 57 trips in total. Both algorithms were run for 1000 evaluations. Item locations and requirements for each order were allocated at random, with allocations of items to specific truck trips determined by an earlier optimisation run. The problem scenario and results are available at the URL given at the end of the paper.

Table 2 Total time (s) for the routes allocated by QPPTW-m, and run times (s): for a single run of QPPTW-m using a randomly generated permutation of items and trucks; and for a run of a hillclimber and simulated annealing over 1000 evaluations each
Full size table

Table 2 shows results from both algorithms, aggregated over 30 independent runs. Also given as a reference are the results for 1000 randomly generated permutations. The results were not normally distributed, so medians and interquartile ranges are given. HC found the shortest route times for our specific scenarios, though the difference with SA was found to not be statistically significant. Both HC and SA showed a significant improvement over random permutations, of around 5% total route time. A single run of QPPTW-m for the several hours’ worth of truck movements using a randomly generated permutation takes 4–5 s. The run times for both metaheuristics are around an hour and so are indeed practical for real-world use, if planning schedules ahead of time.

This was compared to a baseline approach of running Dijkstra’s shortest path algorithm [7] to allocate the routes to each truck in turn. The results for this, using the same approaches for determining the permutations of trips to route and items to collect, are given in Table 3. It is clear that this approach finds shorter paths overall, in a much shorter time. However, as this approach did not consider conflicts, we checked how many occasions these routes would result in multiple trucks sharing an edge (a conflict). This is shown in the final column of Table 3. Conflicts occurred over 800 times during the 51 movements. The large number of conflicts to be avoided provides some explanation for the much longer route durations using QPPTW-m.

Table 3 Total time (s) for the routes allocated by Dijkstra’s algorithm, and run times (s)
Full size table

5.1 Impact of tail set

We tested the impact of changing the original QPPTW algorithm to iterate only over tail sets (Algorithm 1, Step 17). Repeating the experiment above, we generated 1000 random instances of the routing problem (that is, random permutations of trips to route and items to collect). Two variants of QPPTW-m were run for each instance: one using the tail set, and one iterating over the full set of time-windows. The count of iterations of the inner loop was then recorded. The histogram of both counts over the 1000 runs was determined to be normally-distributed. Without the use of a tail set, the loop ran a mean of 134,660,652 times; with the tail set it ran a mean of 3,584,477 times. A two-tailed t-test on these two distributions found \(p<0.001\), suggesting that the addition of tail set leads to a significant reduction in iterations of the QPPTW inner loop.

6 Conclusions

We have presented an extension of the original QPPTW conflict-free routing algorithm from [9] for routes with multiple stops. This is accompanied by a top-level metaheuristic to choose the order in which stops should be visited and the order in which to allocate routes to the vehicles. The approach was demonstrated to run in a reasonable time for a real-world application.