1 Introduction

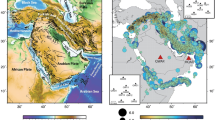
ChinArray is a large-aperture broadband seismic array deployed in continental China for understanding deep seismic structures and dynamic systems associated with Indian-Eurasian collision and Pacific-Eurasian subduction zones (Fig. 1; Ding and Wu 2013). Similar to the large-aperture USArray of the EarthScope project (http://www.usarray.org/researchers/obs/transportable), it has a two-year observation at each site and is scheduled to migrate across China over the next 15–20 years. The ChinArray Phase I, which included 350 broadband stations, was carried out in the Yunnan province and its vicinity between September 2011 and April 2013 (Li et al. 2014). Several studies using ChinArray data have focused on the subsurface seismic velocities, especially beneath SE Tibet. For example, Li et al. (2014) developed a new 3D shear-wave model beneath SE Tibet using Rayleigh waves from regional and teleseismic earthquakes. Huang et al. (2015) imaged P wave velocity in upper mantle and transition zone of the same region. However, so far no studies have evaluated the detection capability of ChinArray at a long-range distance.

Fig. 1
figure 1

Map of study region in Yunnan and its vicinity in South China. The seismic stations within ChinArray are denoted by black triangles. The inset marks the study region (black rectangle) in a larger map of Asia and Pacific. The Russian meteor event (red star) and the M W 5.8 Tonga earthquake (blue star) propagated in different directions to ChinArray. The 22 seismic stations of GSN used in Fig. 2 are denoted by black inverted triangles

Full size image

An effective way to detect weak signals in a noisy background is to enhance coherent signals and suppress incoherent noises by stacking the waveforms across a dense seismic array (e.g., Ringdal and Husebye 1982; Rost and Thomas 2002). A seismic array refers to any deployment that has more than three seismometers with the same reference time and instrument response (Rost and Garnero 2004). Using seismic arrays to detect weak events can date back to the Geneva Conference of Experts in 1958 (Mykkeltveit et al. 1990). Selby (2008) analyzed four seismic events recorded at the small-aperture ARCES array in Norway, verifying the detection capability of small-aperture array. More recently, the USArray data have been used extensively for small event detection, such as the North Korean nuclear test on October 2006 (Ammon and Lay 2007), as well as mainshock rupture processes and early aftershocks with the back-projection method (e.g., Meng et al. 2011; Yao et al. 2012; Kiser and Ishii 2013). In this paper, we evaluate the detection capability of ChinArray with array processing techniques (e.g., Vespagram and F-K analysis).

Around 03:20:00 UTC on 15 February 2013, a large meteor entered the Earth’s atmosphere over Russia. The associated bolide exploded subsequently and fragments dropped near Chelyabinsk, Russia (https://en.wikipedia.org/wiki/Chelyabinsk_meteor, last accessed 06/2016). It is the largest recorded meteor event since the 1908 Tunguska event (Ben-Menahem 1975). The equivalent yield of the explosion was about 500 kt of trinitrotoluene (TNT) (Antolik et al. 2014). Many studies focused on the trajectory and speed of the bolide (Borovička et al. 2013; Seleznev et al. 2014). They found that the bolide generated a large shock wave during the last stage of explosion. Others provided detailed observations on long-range infrasound (Le Pichon et al. 2013; de Groot-Hedlin and Hedlin 2014) and surface-wave propagation (Tauzin et al. 2013; Heimann et al. 2013). They suggested that the surface waves were generated by the ground motion coupling from the incident shock waves. Antolik et al. (2014) estimated the location of the Russian meteor event as the source of energy produced by the largest explosion, which is located ~50 km south of the Chelyabinsk. Based on Rayleigh wave observations up to 4000 km away, Tauzin et al. (2013) obtained a surface-wave magnitude of ~3.7. The epicentral distance between the Russian meteor event and ChinArray is more than 4000 km, beyond the distance of previous observations. In addition, the seismic waves from the Russian meteor were interfered by those from a magnitude 5.8 earthquake in Tonga occurred ~20 min earlier (Tauzin et al. 2013). Hence, it provides an interesting challenge for us to test the detection capability of weak signals recorded on ChinArray.

2 Data and array analysis

2.1 Data

As mentioned before, there are 350 broadband seismic stations within ChinArray deployed in Yunnan and its vicinity between 2011 and 2013 (Fig. 1). They all have a sampling rate of 100 Hz. We cut the waveforms with length of 4000 s starting from 03:00:00 UTC, February 15, 2013. Based on the Russian meteor event location by the USGS (55.15°N, 61.41°E), all vertical-component ChinArray seismograms are aligned by increasing distances from the meteor event (gray waveforms in Fig. 2b) and band-pass filtered between 0.03 and 0.05 Hz, similar to those used by Tauzin et al. (2013). We find that the signals from the Russian meteor event (dark green parallelogram in Fig. 2b) are too weak to be clearly identified because of the long-range distances and overlapping with seismic signals from the M W 5.8 Tonga event (blue parallelogram in Fig. 2b). Although different sources of bolide fragments may cause interference on waveforms, we assume that the signals recorded on ChinArray come from the main blast of the meteor due to such a long epicentral distance.

Fig. 2
figure 2

a Vertical-component seismograms combining data from GSN and 51 selected stations within ChinArray. They are band-pass filtered between 0.03 and 0.05 Hz and plotted with increasing epicentral distances with the known meteor location from USGS. b A zoom-in plot showing the vertical-component seismograms of all the stations within ChinArray (marked by gray). The 51 selected stations and corresponding waveforms are shown by red. The dark green and blue parallelograms mark the surface-wave phases from the Russian meteor event and the Tonga earthquake, respectively. For the F-K analysis of these two phases, we denote the starting points of time windows by dark green and blue arrows. The reference waveform at station 53004 (blue triangle in the inset) is marked by blue

Full size image

We note that a large number of waveforms within ChinArray are concentrated between 4500 and 4950 km (Fig. 2b). To achieve a relatively uniform distribution of waveforms across the entire distance ranges, we choose one record with signal-to-noise ratio (SNR) above 16 for every ~20 km, resulting in 51 traces for further analysis. We calculate the SNR for each ChinArray waveform with the signal energy from the Tonga earthquake (the square of the root mean square amplitude across the surface window with length of 100 s) divided by the noise energy (the average energy within the same window length before the predicted P wave arrival of the Tonga earthquake). We choose the Tonga earthquake as references for SNR calculations, mainly because it is relatively difficult to visually identify weak arrivals from the Russian meteor at all stations. To ensure high quality of selected waveforms, we set the SNR threshold to be 16, resulting in 51 waveforms for further analysis. As will be shown later, this selection process helps reduce potential impact of the surface waves from the Tonga earthquake to the surface waves from the Meteor impact.

In order to further confirm the signals from the Russian meteor event, we add 22 seismic stations of Global Seismographic Network (GSN) at distances less than 4000 km (inverted triangles in Fig. 1). Combining the vertical waveforms from GSN and 51 selected waveforms from ChinArray, we identify a clear movement from the Russian meteor event, consistent with a phase velocity v ≈ 3 km/s (Fig. 2a).

2.2 Vespagram and F-K analysis

In order to identify individual phases from a given event, we compute the vespagram, which is a contoured display of beam power with a given back azimuth (BAZ) as a function of time and slowness (Davies et al. 1971; Thomas et al. 2009). We use the code from the generic array processing (GAP) software package (Koper 2005) to generate the vespagram for the selected 51 waveforms (Fig. 3), and with station 53004 as the reference (blue waveforms in Fig. 2b). Using the BAZ of the Tonga earthquake (~110.65°) as the input, we identify a clear phase between 2900 and 3400 s on the vespagram (Fig. 3a). The measured slowness is between 24 and 37 s/deg with clear dispersions. This corresponds to a phase velocity of 3.02 and 4.65 km/s, consistent with the energy being surface waves, and the phase marked with blue parallelogram in Fig. 2b. On the other hand, using the BAZ of the Russian meteor event (~325.97°) as the input, we could identify several groups in beam power between ~2700 and ~3200 s (Fig. 3b). The first group occurred between 2700 and 2800 s, with the slowness between 28 and 36 s/deg (3.10–3.98 km/s). This is consistent with the arrival of the weak signals marked with the dark green parallelogram in Fig. 2b. The rest groups after 2800 s show multiple bands with reverse dispersions. They are likely produced by the long-period surface waves from the Tonga event with the incorrect BAZ.

Fig. 3
figure 3

a Vespagram for a given back azimuth of 110.65°, which corresponds to the propagation of the Tonga earthquake. b Vespagram for a given back azimuth of the Russian meteor event (~325.97°)

Full size image

Next, we apply the frequency-wave number (F-K) analysis with the code in the GAP software package. F-K analysis is a well-developed array processing technique to calculate the slowness and BAZ of a seismic phase within a certain time window (Rost and Thomas 2002). The starting point and length of the time window for extracting the phase are two key parameters. We note that different parameters may influence the estimation of slowness and BAZ. The starting point of the time window determines which phase to be calculated. The length of the time window may not be too long to contain other phases. For the phase marked in the blue parallelogram of Fig. 2b, we extract the phase from 3075 to 3215 s since 03:00:00, Feb 15, 2013 (03:51:15 to 03:53:35 UTC). Figure 4a shows a clear phase with the slowness of 34.82 s/deg and BAZ of 111.0°, close to the expected BAZ of the Tonga earthquake (~110.65°) based on the USGS location. We also perform the bootstrap analysis to evaluate the standard deviation of BAZ (Koper 2005). There are 51 selected traces within ChinArray for the F-K analysis. For each step of bootstrapping, we replace the trace i by selecting one trace randomly from the 51 traces (1≤ i ≤51), which means that random number of traces are replaced during one step. We perform 10 steps of bootstrapping and compute the standard deviation of BAZ for the Tonga earthquake to be 1.9°.

Fig. 4
figure 4

a F-K analysis for the phase in the blue parallelogram of Fig. 2b for the Tonga earthquake. Black star denotes the optimal estimations about slowness. Triangles represent the bootstrap solutions on the slowness grids. A 140-sec-long time window is used to extract the phase for beam power computing. All the waveforms are band-pass filtered between 0.03 and 0.05 Hz. The best-fitting back azimuth is 111.0°. F-K analysis for the phase in the dark green parallelogram of Fig. 2b for the 51-station ChinArray (b) and sub-ChinArray (c). We use the 51 selected stations for Fig. 4b and 29 ChinArray stations in a smaller region (blue rectangle in Fig. 5) for Fig. 4c, respectively. The waveforms are band-pass filtered between 0.05 and 0.07 Hz. The lengths of time window for Fig. 4b, c are both 100 s. Although the best-fitting back azimuths in Fig. 4b, c are similar (333.4° vs. 329.7°), the deviation of back azimuth in Fig. 4c is significantly smaller than Fig. 4b, due to the smaller distribution of stations

Full size image

For the phase in the dark green parallelogram of Fig. 2b, we use the same reference station and the 51 waveforms for F-K analysis. We increase the filter band to 0.05–0.07 Hz for better SNR. Based on the time window from 2770 to 2870 s since Feb 15, 2013, 03:00:00 (03:46:10 to 03:47:50 UTC), we observe the phase with the slowness of 27.95 s/deg and BAZ of 333.4° (Fig. 4b), corresponding to the Russian meteor event (BAZ ~325.97°) based on the USGS location. The BAZ discrepancy is 7.43°, much larger than that of the Tonga earthquake. We find that the beam power in Fig. 4b is not concentrated on a clear point as in Fig. 4a, which is also reflected in a large standard deviation of 142° in BAZ based on bootstrap analysis, indicating that the result is not reliable. This is likely because the Russian meteor event has a smaller magnitude and lower SNR. Hence, the coherence of the Russian meteor phases is not as good as the Tonga earthquake.

Besides the low SNR, the coherence of signals may be reduced if the array aperture is too large. In addition, the F-K analysis assumes a plane-wave, which could be violated if the array aperture is large. To test this further, we only select a small subarray of 3° × 3° within ChinArray (marked by blue rectangle in the inset of Fig. 5) for F-K analysis. We choose this subarray, mainly because the surface waves of both events are still separated, resulting in less interference. Station 53049 is used as the reference (the corresponding waveform is marked by red in Fig. 5), and all the 29 waveforms within the sub-ChinArray are band-pass filtered between 0.05 and 0.07 Hz as in Fig. 4b. With the time window from 2800 to 2900 s since Feb 15, 2013, 03:00:00 (03:46:40 to 03:48:20 UTC), we obtain a peak with slowness of 34.73 s/deg and BAZ of 329.7° (Fig. 4c). The discrepancy of BAZ with the USGS result is 3.73°, much smaller than the 7.43° in Fig. 4b. The beam power is well concentrated, and the bootstrap standard deviation of BAZ is decreased from 142.4° to 1.6°, suggesting that the result is more stable. The best-fitting slowness of 34.73 s/deg corresponds to an apparent velocity of 3.21 km/s, consistent with the move out of ~3 km/s in Fig. 2a. On the other hand, the large aperture of the 51 selected waveforms within ChinArray has less influence on the Tonga earthquake (Fig. 4a), mainly because the surface waves of the Tonga earthquake have higher SNR and longer source time durations, which contribute to the more coherent signals and the smaller deviation of BAZ.

Fig. 5
figure 5

The vertical-component seismograms used for F-K analysis in Fig. 4c (marked by blue). The corresponding stations are marked by blue triangles in the inset. We show the starting point of time window for F-K analysis in Fig. 4c by red arrow. The reference waveform at station 53049 is marked by red. The boundaries of provinces in China are shown by red lines in the inset

Full size image

As mentioned earlier, we only use a subset of the ChinArray stations for the vespagram and F-K analysis. If we use all the ~350 stations for array analysis, the result for the Tonga earthquake showed a clear evidence of surface waves with a small standard deviation of 1.6° (Fig. 6a). However, the F-K result from the Meteor impact was completely dominated by the relatively high noise level and the interference from surface waves of the Tonga earthquake (Fig. 6b), contributing to a significantly large discrepancy (~89.67° with the USGS result) and deviation (~91.7°) of BAZ. Hence, we have to use only a portion of the array for analysis, in order to suppress the interference.

Fig. 6
figure 6

a F-K analysis for the phase in the blue parallelogram of Fig. 2b. All the waveforms of ChinArray are used. The reference station, time window, and filter band are same as Fig. 4a. b F-K analysis for the phase in the dark green parallelogram of Fig. 2b for all the waveforms of ChinArray. The reference station, time window, and filter band are same as Fig. 4b

Full size image

We then stack all the waveforms within ChinArray along the best-fitting slowness and BAZ for the Russian meteor event and the Tonga earthquake, respectively (Fig. 7). The reference station is 53004 (Fig. 7a). With a linear stack, the signals from both the two events could be observed (Fig. 7b, c), but not clear due to low SNRs. If we apply the square root stack (Rost and Thomas 2002), we could reduce the noise and identify clear signals from the two events, although the waveforms are distorted due to the nonlinear stacking (Fig. 7d, e).

Fig. 7
figure 7

The vertical waveform of reference station 53004 (a), which is band-pass filtered between 0.03 and 0.05 Hz. Linear-stacked waveforms for all the waveforms within ChinArray along the best-fitting slowness and BAZ for the Russian meteor event (b) and the Tonga earthquake (c), respectively. We also test the square root stacking for all the waveforms within ChinArray along the best-fitting slowness and BAZ for the Russian meteor event (d) and the Tonga earthquake (e), respectively. The filter band between 0.03 and 0.05 Hz is also used when stacking. The waveform of station 53004 and all the stacked waveforms are normalized

Full size image

The array geometry is an important factor to affect the resolution in the F-K analysis. To quantify this further, we compute the array response function (ARF) at frequencies centered at 0.05 Hz for ChinArray (Rost and Thomas 2002). As shown in Fig. 8a, the ARF corresponding to the 51 selected stations within ChinArray has apparent side lobes, and the main lobe is elongated on the NE-SW direction (Fig. 8a). This could be due to the asymmetry of the selected stations within ChinArray in the F-K analysis as shown in Fig. 4b. However, the main lobe is relatively concentrated at the center point, because of the large aperture of the selected array configuration (Xu et al. 2009). In comparison, there are few side lobes for the ARF of the 29 selected stations within sub-ChinArray (Fig. 8b), but it has a larger main lobe due to smaller array aperture.

Fig. 8
figure 8

Array response function (ARF). The frequency of interest is 0.05 Hz. a ARF of the 51 selected stations used for F-K analysis in Fig. 4b. b ARF of the 29 stations used for F-K analysis in Fig. 4c

Full size image

2.3 Synthetic test

We also perform a synthetic test to test the robustness of F-K analysis and vespagram. Using the Preliminary Reference Earth Model (PREM) as the velocity input (Dziewonski and Anderson 1981) and the major source parameters of the Russian meteor event (Antolik et al. 2014), we generate the vertical synthetic seismograms at all stations within ChinArray using an orthonormalization method for the computation of Green’s functions (Wang 1999). As shown in Fig. 9a, the surface waves between 2500 and 3000 s could be observed clearly. We could identify this clear signal with BAZ of 326.3° and slowness of 27.04 s/deg from the F-K analysis (Fig. 9b). The best-fitting BAZ with deviation is 326.3° ± 1.2°, which includes the observed BAZ of 325.3°. Additionally, with BAZ of 326.3° as the input, the vespagram shows one clear phase between 2400 and 3200 s, with clear dispersions in the slowness range of 24 and 32 s/deg, consistent with the phase being surface waves from the Russian meteor event (Fig. 9c). No other phases are observed with reverse dispersions, suggesting that the multiple bands in Fig. 3b are more likely due to the interference of surface waves of the Tonga earthquake. Despite the incorrect BAZ, the long-period surface waves of the Tonga earthquake help increase the coherence of signals, which contributes to many separated bands of beam power on the vespagram.

Fig. 9
figure 9

a The synthetic vertical seismograms of all the stations within ChinArray. The Russian meteor event has the major source parameters of strike = 52°, dip = 24°, and rake = −14° (Antolik et al. 2014). All the waveforms are band-pass filtered between 0.03 and 0.05 Hz. b F-K analysis for the clear phase between 2500 and 3000 s of all synthetic waveforms. We also choose the station 53004 as the reference. The length of time window is 100 s. c Vespagram of all synthetic waveforms with the BAZ of 325.60°. The filter band is between 0.03 and 0.05 Hz

Full size image

3 Comparison with the F-net results

To further evaluate the robustness of the F-K results from ChinArray, we choose F-net in Japan to perform similar analysis, because it is also located between the Russian meteor event and the Tonga earthquake (Fig. 10). F-net has 71 broadband seismic stations (Okada et al. 2004) with a large aperture of ~2000 km. If we use all stations within F-net for F-K analysis, they may not satisfy the plane-wave assumption (as shown in Fig. 4b, c). We therefore select a small subarray of 5° × 3° (marked by red rectangle in the inset of Fig. 10). The 13 waveforms in the small subarray are band-pass filtered between 0.03 and 0.05 Hz. The reference station is YZK. We then extract the surface-wave phase (blue parallelogram in Fig. 10) of the Tonga earthquake with a time window from 2150 to 2290 s (03:35:50 to 03:38:10 UTC). The best-fitting BAZ is 125.0° (Fig. 11a), with a discrepancy of 5.72° compared with expected BAZ based on the USGS location (~130.72°). For the phase of the Russian meteor event (red parallelogram in Fig. 10), we also use a higher filter band between 0.05 and 0.07 Hz. With the same reference station (YZK) and the time window from 3275 to 3375 s (03:54:35 to 03:56:15 UTC), we extract the phase with BAZ of 321.3° (Fig. 11b). The beam power is also well concentrated, similar to the F-K analysis of ChinArray in the inset of Fig. 4c. The bootstrap standard deviation of the estimated BAZ is 1.5°, almost the same as ChinArray (~1.6°). The BAZ discrepancy compared with the Russian meteor event location by USGS is 4.69°, larger than ChinArray (~3.73°).

Fig. 10
figure 10

The vertical-component seismograms of all the stations within F-net. They are band-pass filtered between 0.03 and 0.05 Hz. The waveforms for F-K analysis are marked by red, corresponding to the red triangles in the inset. Other symbols are same as Fig. 2b

Full size image
Fig. 11
figure 11

a F-K analysis for the phase in the blue parallelogram of Fig. 10. The symbols are same as Fig. 4a. We use a 140-sec-long time window and a filter band between 0.03 and 0.05 Hz. The best-fitting back azimuth is 125.0°, indicating that it comes from the Tonga earthquake. b F-K analysis for the phase in the red parallelogram of Fig. 10. They are band-pass filtered between 0.05 and 0.07 Hz, and the length of time window is 100 s. The best-fitting back azimuth of 321.3° corresponds to the Russian meteor event

Full size image

4 Location and magnitude estimation

If we assume that surface waves propagate along the great circle path, we can find the source where the two ray paths defined by the BAZs overlap (Fig. 12). With the best-fitting BAZ of 329.7° on ChinArray and 321.3° on F-net for the Russian meteor event, their ray paths overlap at 58.80°N, 58.72°E, which is about 438 and 469 km away from the locations by USGS (55.15°N, 61.41°E) and Tauzin et al. (2013) (54.82°N, 61.24°E). If we use the best-fitting BAZs of 111.0° on ChinArray and 125.0° on F-net for the Tonga event, their ray paths overlap at 28.35°S, 156.98°W, which is about 2014 km away from the USGS locations (19.73°S, 174.47°W). Based on the deviation of BAZs by the F-K analysis, we mark the possible range of the Russian meteor event with ~500 km along both longitude and latitude, and the possible range of the Tonga earthquake with ~500 km along latitude and ~2000 km along longitude, respectively (Fig. 12). The USGS locations are not in the possible source regions for both events. As mentioned before, these large discrepancies are mainly due to the bending propagation path of surface waves, and the fact that we only use two BAZs for such analysis. The discrepancy of the Tonga earthquake location is much larger than the Russian meteor event, most likely because the Tonga earthquake has a larger epicentral distance so that the event location is biased more even if the discrepancy of BAZ is small. Nevertheless, with the F-K analysis, we could identify weak signals like the Russian meteor event from ChinArray and F-net when the epicentral distance is more than 4000 km.

Fig. 12
figure 12

The black great circle curves correspond to the best-fitting BAZs of F-K analysis on ChinArray and F-net, respectively. They overlap at 58.80°N, 58.72°E and 28.35°S, 156.98°W, which are marked by black stars. The Russian meteor event locations by USGS and Tauzin et al. (2013) and the Tonga earthquake location by USGS are denoted by green stars. The possible ranges of source location based on the deviation of BAZs by the F-K analysis are marked by green

Full size image

To estimate the surface-wave magnitude M S for the Russian meteor event, we apply the Praha equation M S = log(A/T) +1.66log(Δ) + 3.30 (Karnik et al. 1962), where A is the amplitude of surface-wave displacement in μm after removing the instrument responses, T is the period of the corresponding surface wave, and Δ is the epicentral distance. If we use the T = 20 s, we calculate a magnitude of M S = 3.94 ± 0.18 with the ChinArray data and 4.03 ± 0.17 for the F-net data, slightly higher than the M S ~3.7 by Tauzin et al. (2013).

5 Discussion and conclusions

In this study, we conducted a systematic detection of weak seismic signal associated with the 2013 Russian meteor event. We identified clear seismic phases with BAZ of 329.7° and slowness of 34.73 s/deg on ChinArray with F-K analysis, consistent with them being the surface waves produced by the Russian meteor event. Combing with the best-fitting BAZ of 321.3° on the Japanese F-net, we located the Russian meteor event at 58.80°N, 58.72°E, which is about 438 km away from the location by the USGS (55.15°N, 61.41°E). The surface-wave phases from the M 5.8 Tonga earthquake ~20 min earlier mixed with the surface waves of the Russian meteor event. However, with vespagram and F-K analysis, we were able to identify phases of the Tonga earthquake with BAZ of 111.0° and slowness of 34.82 s/deg on the ChinArray, and with BAZ of 125.0° and slowness of 30.52 s/deg on the F-net.

One basic assumption of array processing techniques in the GAP software package is that the incident seismic waves are coherent plane waves (Koper 2005). ChinArray has a large aperture of ~800 km, which may not satisfy this assumption. This could explain the observation that the best-fitting BAZ of F-K analysis for the Russian meteor event becomes more robust if we use a small part of ChinArray (Fig. 4c). However, there is still a discrepancy with the true event location even when we use the stations within a small subarray (Figs. 4c, 11b, 12). As discussed before, the nonhomogeneity of the subsurface velocity structure may bend the propagation path of surface wave. For example, Lebedev and van der Hilst (2008) found a low-velocity anomaly of S wave around the boundary of Eurasian and Pacific Plate at the depth of 80 km, where the F-net is located. In addition, surface waves of the Russian meteor event passed through the Tianshan orogenic belt, where a relatively fast shear-wave speed at the depth of 75 km has been observed (Sun et al. 2010). The existence of these velocity anomalies may result in a larger discrepancy of the BAZ on F-net (~4.69°) than that on ChinArray (~3.73°) for the Russian meteor event, and a larger discrepancy of BAZ on ChinArray for the Russian meteor event (~3.73°) than that for the Tonga earthquake (~0.35°).

When performing the F-K analysis, we chose a higher filter band (0.05–0.07 vs. 0.03–0.05 Hz) and a shorter time window (100 vs. 140 s) for the Russian meteor event than the Tonga earthquake. Because the Russian meteor event has a shorter epicentral distance (~4700 vs. ~10,000 km to ChinArray), higher frequency energy could be observed. In addition, the Russian meteor event has a smaller magnitude and a shorter duration of the source time function right before the surface waves from the Tonga event. Hence, a shorter time window to extract the phase could avoid contamination from later arrivals.

As mentioned before, results from the F-K analysis also depend on the choices of the starting windows. To check the stability of the results, we performed similar F-K analysis with slightly different starting times for the Russian meteor event at both ChinArray and F-net. As shown in Fig. 13, the results are generally consistent with each other if the starting time windows are within the duration of the target phase, but become unstable near both ends of the phase. This suggests that as long as we select the time window that does not have interferences with other phases, the F-K results at both arrays are relatively stable.

Fig. 13
figure 13

a The vertical waveform of the reference station 53004 within ChinArray, which is band-pass filtered between 0.03 and 0.05 Hz. The red dashed lines mark the phase from the Russian meteor. b A zoom-in plot for the phase from the Russian meteor in a. The red lines denote the different time windows for the F-K analysis. Each time window has the same length of 100 s. c The best-fitting BAZs (black circles) with the different starting windows. The black error bars mark the deviations of BAZs. We also mark the best-fitting BAZ shown in Fig. 4c as a red dashed line. d-f Similar test with different time windows for the F-K analysis on F-net recordings. The symbols and notations are the same as in a-c

Full size image

Tauzin et al. (2013) relocated the Russian meteor event source with stations of GSN and FDSN within 4000 km away from the meteor. Seleznev et al. (2014) determined the exact time of the meteor explosion using West Siberian stations within 2000 km away from the meteor. The waveforms from ChinArray have longer epicentral distances of 4100–5200 km. Due to the dense distribution of stations within ChinArray, we could select part of the waveforms to reduce the interference from the Tonga earthquake, and detect the Russian meteor event with sub-ChinArray at such distances. On the other hand, with the best-fitting BAZ and slowness, we could stack all the waveforms within ChinArray, enhance the signals from the weak Russian meteor event significantly, and identify them out of those from the stronger Tonga earthquake. Although we were unable to accurately locate their source locations based on simple back-projection of the ChinArray and F-net results, our results shown in this study clearly demonstrate the capabilities of detecting surface waves of M ~4 events at long-range distances. Further studies are needed to evaluate its detection abilities of teleseismic P waves at higher frequency ranges.