Out-of-plane (SH) soil-structure interaction: a shear wall with rigid and flexible ring foundation

Abstract

Soil-structure interaction (SSI) of a building and shear wall above a foundation in an elastic half-space has long been an important research subject for earthquake engineers and strong-motion seismologists. Numerous papers have been published since the early 1970s; however, very few of these papers have analytic closed-form solutions available. The soil-structure interaction problem is one of the most classic problems connecting the two disciplines of earthquake engineering and civil engineering. The interaction effect represents the mechanism of energy transfer and dissipation among the elements of the dynamic system, namely the soil subgrade, foundation, and superstructure. This interaction effect is important across many structure, foundation, and subgrade types but is most pronounced when a rigid superstructure is founded on a relatively soft lower foundation and subgrade. This effect may only be ignored when the subgrade is much harder than a flexible superstructure: for instance a flexible moment frame superstructure founded on a thin compacted soil layer on top of very stiff bedrock below. This paper will study the interaction effect of the subgrade and the superstructure. The analytical solution of the interaction of a shear wall, flexible-rigid foundation, and an elastic half-space is derived for incident SH waves with various angles of incidence. It found that the flexible ring (soft layer) cannot be used as an isolation mechanism to decouple a superstructure from its substructure resting on a shaking half-space.

1 Introduction

The study of soil-structure interaction (SSI) began during the late 19th century. In the early part of the 20th century, it slowly evolved and developed due to research on the design of nuclear power plants and on improvements in the safety of building structures due to significant earthquake events around the world. More recently, the sophistication of SSI modeling has grown at a fast pace due to the increasing computational ability of computer technology and in response to the demands of research in the field of non-linearity of building materials and soil media.

Reissner (1936) observed the natural effect of soil inertia and established that it lay in the inertial properties of the soil media. He also discovered that the radiation damping into the soil contributed a great deal to the response of a structure, thus marking the beginning of SSI study using the analytical method. A number of years later, Housner (1957) demonstrated that the variation of density and elasticity in the soil media caused a change in seismic wave propagation velocity that led to the reflection and refraction of incoming seismic energy. This phenomenon is understood as wave passage or kinematic interaction. Additionally, the weight of a structure generates inertial forces that impinge on the soil media when responding to seismic waves, causing additional deformation in the soil known as inertial interaction. The integration of the dynamic response of a structure and the supporting soil media causes the inertia effects. The structure deforms to dissipate the energy caused by incoming seismic waves and, in turn, the waves scatter away from the structure, increasing the soil deformation.

The topic was taken up again in 1969 by Luco (1969), who focused on the diffraction of normal incidence plane SH waves by an elastic shear wall resting on a rigid semi-circular foundation embedded in soil media. Trifunac (1972) generalized Luco’s analytical solution into cases for arbitrary oblique incidence angles of SH waves. Analytical solutions of the dynamic interaction of shear walls with circular rigid foundations embedded in the half-space were derived and evaluated. This analysis demonstrated that waves scattered from a rigid foundation contribute significantly to the surface ground motion near the shear wall and at distances at least one order of magnitude greater than the characteristic length of the foundation. Therefore, waves reflected and diffracted by the foundation must not be neglected when the Fourier amplitude ratios of accelerograms recorded in and around the building are used to study SSI. For this reason, when considering rigid shear walls founded on hard soil excited by low frequency waves (long period waves), it is possible to obtain base displacements and base shear forces which are higher when the values are computed neglecting SSI. However, when considering rigid shear walls founded on soft soil excited by higher frequency waves, the SSI has a significant effect on displacement and base shear force and should be carefully considered. In more flexible structures, the effect of interaction can vary widely for a single structure-soil couplet and must be considered as depending on the harmonic interaction of the native vibrational frequency of the superstructure with the transmitted frequency of specific seismic waves in the soil as affected by the soil’s stiffness.

In the early 1970s, Lee and Westley (1973) investigated the influence of SSI effects on the seismic response of nuclear reactors using a three-dimensional model subjected to vertical propagation of SH waves. The normal incidence SH waves used the analytical method along the two orthogonal directions and a spring-mass model for structures attached to the foundations. Luco and Contesse (1973) presented closed-form analytic solutions for the two-dimensional out-of-plane problems related to the interaction between elastic shear walls fixed on rigid circular foundations that are subjected to vertical and oblique angles of incident harmonic SH waves. Wong and Trifunac (1975) extended the analytical solutions for the incident plane SH waves to shallow or deep elliptical rigid foundations, as well as to multiple buildings and foundations. The solutions to these problems showed that buildings that are closely spaced could affect the fundamental frequencies (or period) of the neighboring buildings due to SSI.

Lee (1979) studied three-dimensional analytical solutions for the interaction of a single degree-of-freedom oscillator supported by a semi-spherical foundation for the harmonic P-, SV-, and SH waves. Kobori and Kusakabe (1980) investigated rigid rectangular and circular foundations welded to the surface of elastic half-spaces, and subjected to harmonic seismic waves. Triantafyllidis and Prange (1988) studied the dynamic interaction of two rigid circular foundations embedded in elastic half-space, and subjected to Rayleigh waves impinging at an arbitrary angle. These studies demonstrated that forces react on the foundations perpendicular to the incidence of propagation, in addition to forces in the direction of the motion. Todorovska (1993) studied the in-plane foundation-soil interaction of circular foundations embedded in elastic soil media. The research mainly focused on the influences of wave passage and the depth of the foundation below the half-space for in-plane SSI. In the same year, Hryniewicz (1993) investigated two two-dimensional trip foundations based on a semi-infinite medium embedded in a homogeneous half-space excited by anti-plane SH waves.

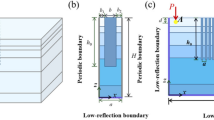
Figure 1 is the realization of the two-dimensional mathematical model in this paper presenting the interaction of an elastic shear wall (structure), flexible-rigid foundation, and the elastic half-space for incident plane SH waves. The foundation consists of a semi-circular rigid foundation which is wrapped with an elastic semi-circular flexible foundation. The lower semi-circular section can be modeled as flexible for soft soil or as rigid for hard soil—such as bedrock—which provides a more accurate mathematical model for the shear wall or structure interacting with the soil media. This accuracy is important in modeling an SSI with a stiffer layer of soil overlaying a more flexible layer. An engineer goes through a decision making process when selecting the optimum type of foundation system for soil deposits that are soft and not suitable to support the superstructure. Selecting an optimum system is based on the principle that cost-effective alternatives such as soft ground improvements must be sought first before considering relatively costly foundation alternatives (mat or pile deep foundation). Soil treatment and stabilization are techniques to enhance some aspects of soil behavior and improve the strength and bearing capacity of soft ground conditions. Through the process of soil treatment, the property of soil supporting the superstructure foundation is modified and improved in comparison to the surrounding strata. This layer of modified soil will alter the seismic wave propagating from the half-space to the superstructure foundation. The model in this paper will accurately analyze this interaction and assist in selection of optimum foundation systems.

Fig. 1

The mathematical model SSI with semi-circular flexible and rigid foundation

In this paper, the displacement of the shear wall structure and flexible/rigid foundation and the ground motion close to the subjected structure are investigated and compared the results with Luco (1969) and Trifunac (1972) which studied the interaction of a shear wall, rigid foundation, and the half-space for incident SH waves. Luo (2008) also studied this problem but the derivation and final equations here are much simplified with improved convergency and accuracy of numerical results. Moreover, the emphasis here is different, where the graphs computed here are confirmed with the results of Trifunac (1972) for only rigid foundation case, and the effect of shear wall structure response due to the flexible ring is studied. The base shear force of the wall structure is also studied with various thicknesses and stiffnesses of the flexible ring.

2 The mathematical model

2.1 The model

The model studied in this paper is a two-dimensional rectangular building resting on a semi-circular rigid foundation of radius a which is wrapped with an elastic semi-circular flexible foundation of radius $\bar{a}$ embedded in a half-space, as illustrated in Fig. 1. All materials here are assumed to be homogeneous, elastic, and isotropic. The material constants, namely shear modulus and wave speed of the half-space soil, building, and flexible foundation are denoted by $\mu ,C_{\beta }$ and $\mu_{\text{b}} ,C_{{\beta_{\text{b}} }}$, and $\mu_{\text{f}} ,C_{{\beta_{\text{f}} }}$. The contacts between the soil, foundation, and building are assumed to be fixed with no slippage between them and with the assumption that the foundation is removable.

A train of parallel harmonic incident SH waves impinge on the foundation from half-space at an incidence angle $\gamma$ with respect to the horizontal axis. The width and height of the structure are $2a$ and $H$, respectively. A Cartesian coordinate system $\left( {x,y} \right)$ and a corresponding polar coordinate system $\left( {r,\theta } \right)$ have been defined with the origin at the center of the semi-circular foundation.

2.2 The free-field waves in the half-space

The incident wave field consists of a train of plane waves of unit amplitude with harmonic frequency $\omega$, wave speed $C_{\beta }$, and wave number $k = k_{\beta } = {\omega \mathord{\left/ {\vphantom {\omega {C_{\beta } }}} \right. \kern-0pt} {C_{\beta } }}$. The incident waves can be expressed in both the rectangular and polar coordinates as follows:

$$\begin{aligned} w^{\left( {\text{i}} \right)} \left( {x,y} \right) = {\text{e}}^{{{\text{i}}\left( {k_{x} x - k_{y} y} \right)}} = {\text{e}}^{{{\text{i}}\left( {x\cos \gamma - y\sin \gamma } \right)}}, \hfill \\ w^{\left( {\text{i}} \right)} \left( {r,\theta } \right) = {\text{e}}^{{{\text{i}}kr\left( {\cos \gamma \cos \theta - \sin \gamma \sin \theta } \right)}} = {\text{e}}^{{{\text{i}}kr\cos \left( {\gamma + \theta } \right)}}, \hfill \\ \end{aligned}$$

(1)

and the reflected plane waves can be written as

$$\begin{aligned} w^{\left( {\text{r}} \right)} \left( {x,y} \right) = {\text{e}}^{{{\text{i}}\left( {k_{x} x + k_{y} y} \right)}} = {\text{e}}^{{{\text{i}}\left( {x\cos \gamma + y\sin \gamma } \right)}}, \hfill \\ w^{\left( {\text{r}} \right)} \left( {r,\theta } \right) = {\text{e}}^{{{\text{i}}kr\left( {\cos \gamma \cos \theta + \sin \gamma \sin \theta } \right)}} = {\text{e}}^{{{\text{i}}kr\cos \left( {\gamma - \theta } \right)}}. \hfill \\ \end{aligned}$$

(2)

The ${\text{e}}^{ - {\text{i}}\omega t}$ harmonic time factor is present in all wave equations, and will be understood to be omitted from all equations. Here γ is the angle of incidence or reflection with respect to the horizontal axis; $k_{x} = k\cos \gamma$ and $k_{y} = k\sin \gamma$ represent the components of the SH wave number $k$ along the x- and y-axes, respectively. Applying the Jacobi–Anger Expansion (Pao and Mow 1973),

$${\text{e}}^{ \pm {\text{i}}kr\cos \theta } = \sum\limits_{n = 0}^{\infty } {\varepsilon_{n} \left( { \pm {\text{i}}} \right)^{n} J_{n} \left( {kr} \right)\cos n\theta },$$

(3)

where ${\text{i}} = \sqrt { - 1}$ is the imaginary complex unit, and $J_{n} \left( . \right)$ is the Bessel function of the first kind with order n.

$$\begin{aligned} {\text{e}}^{{{\text{i}}kr\cos \left( {\gamma \pm \theta } \right)}} = \sum\limits_{n = 0}^{\infty } {\varepsilon_{n} {\text{i}}^{n} J_{n} \left( {kr} \right)\cos \left[ {n\left( {\gamma \pm \theta } \right)} \right]}, \hfill \\ {\text{e}}^{{{\text{i}}kr\cos \left( {\gamma \pm \theta } \right)}} = \sum\limits_{n = 0}^{\infty } {\varepsilon_{n} {\text{i}}^{n} J_{n} \left( {kr} \right)\left[ {\cos n\gamma \cos n\theta \pm \sin n\gamma \sin n\gamma } \right]}. \hfill \\ \end{aligned}$$

(4)

The two formulas in Eqs. (1) and (2) can be expanded into infinite series by using polar coordinates $\left( {r,\theta } \right)$. The free-field wave field is then given by the sum of the represented waves that are finite everywhere in the half-space for n = 0, 1, 2, 3….

$$\begin{aligned} w^{{\left( {\text{ff}} \right)}} \left( {r,\theta } \right) = {w}^{\left( {\text{i}} \right)} + w^{\left( {\text{r}} \right)} = {\text{e}}^{{{\text{i}}kr\cos \left( {\gamma + \theta } \right)}} + {\text{e}}^{{{\text{i}}kr\cos \left( {\gamma - \theta } \right)}}, \hfill \\ w^{{\left( {\text{ff}} \right)}} \left( {r,\theta } \right) = \sum\limits_{n = 0}^{\infty } {2\varepsilon_{n} {\text{i}}^{n} J_{n} \left( {kr} \right)\cos n\gamma \cos n\theta } = \sum\limits_{n = 0}^{\infty } {a_{n} J_{n} \left( {kr} \right)\cos n\theta }, \hfill \\ \end{aligned}$$

(5)

where $a_{n} = 2\varepsilon_{n} {\text{i}}^{n} \cos n\gamma$ are the coefficients of the free-field waves, and $\varepsilon_{0} = 1,\;\varepsilon_{n} = 2\;{\text{for}}\;n > 0$. The wave field in the half-space scattered from the flexible foundation is written as

$$w^{{\left( {\text{S}} \right)}} \left( {r,\theta } \right) = \sum\limits_{n = 0}^{\infty } {A_{n} {\text{H}}_{n}^{\left( 1 \right)} \left( {kr} \right)\cos \left( {n\theta } \right)} \;{\text{for}}\;n \ge a,$$

(6)

where $A_{n}$ are the unknown complex numbers to be determined by boundary conditions and the wave function, and ${\text{H}}_{n}^{\left( 1 \right)} {\text{e}}^{ - {\text{i}}\omega t}$ represents outgoing waves toward infinity satisfying Sommerfeld’s radiation condition. The expression of the wave inside the flexible foundation is

$$w^{{\left( {\text{F}} \right)}} \left( {r,\theta } \right) = \sum\limits_{n = 0}^{\infty } {\left[ {B_{n}^{\left( 1 \right)} {\text{H}}_{n}^{\left( 1 \right)} \left( {k_{\text{f}} r} \right) + B_{n}^{\left( 2 \right)} {\text{H}}_{n}^{\left( 2 \right)} \left( {k_{\text{f}} r} \right)} \right]} \cos n\theta$$

(7)

for $a \le r \le \bar{a}\;{\text{and}}\;0 \le \theta \le \uppi$ where ${\text{H}}_{n}^{\left( 1 \right)} \left( {k_{\text{f}} r} \right)$ and ${\text{H}}_{n}^{\left( 2 \right)} \left( {k_{\text{f}} r} \right)$ are the Hankel functions of the first or second kind with argument $k_{\text{f}} r$ and order $n$; $B_{n}^{\left( 1 \right)}$ and $B_{n}^{\left( 1 \right)}$ are the unknown complex numbers to be determined by boundary conditions and the wave functions.

2.3 The wave field within the structure

As pointed out by Trifunac (1972), the displacement of the shear wall, in the z-direction (out-of-plane), has the same harmonic frequency $\omega$ as the rigid foundation, and $w^{{\left( {\text{B}} \right)}}$ must satisfy the Helmholtz wave equation with $y$, the axis pointing vertically down (Fig. 1):

$$\frac{{\partial w^{{\left( {\text{B}} \right)}} }}{{\partial y^{2} }} + k_{\text{b}}^{2} w^{{\left( {\text{B}} \right)}} = 0\;{\text{for}}\; - H \le y \le 0$$

(8)

with $k_{\text{b}} = {\omega \mathord{\left/ {\vphantom {\omega {C_{{\beta_{\text{b}} }} }}} \right. \kern-0pt} {C_{{\beta_{\text{b}} }} }}$ being the building shear wave number, and $C_{{\beta_{\text{b}} }}$ the wave speed in the shear wall. The shear wall must satisfy the boundary conditions of

$$\begin{aligned} \sigma_{yz} = \mu_{b} \frac{{\partial w^{\left( {\text{B}} \right)} }}{\partial y} = 0\;{\text{at}}\;y = - H,\;{\text{at}}\;{\text{top}}\;{\text{of}}\;{\text{shear}}\;{\text{wall}}; \hfill \\ \!w^{{\left( {\text{B}} \right)}} = \Delta {\text{e}}^{ - {\text{i}}\omega t} \;{\text{at}}\;y = 0,\;{\text{at}}\;{\text{bottom}}\;{\text{of}}\;{\text{shear}}\;{\text{wall}}. \hfill \\ \end{aligned}$$

(9)

Dependence on $x$ in the shear wall is eliminated in Eq. (8) by the assumption that the foundation is rigid. The solution of Eqs. (8) and (9) is then given by

$$w^{{\left( {\text{B}} \right)}} \left( y \right) = \Delta {\text{e}}^{ - {\text{i}}\omega t} \left( {\cos k{}_{\text{b}}y - \tan k_{\text{b}} H\sin k{}_{\text{b}}y} \right).$$

(10)

The shear stress along the interface of building and foundation could be derived as

$$\left. {\tau_{yz} } \right|_{y = 0} = \left. {\mu_{\text{b}} \frac{{\partial w^{{\left( {\text{B}} \right)}} }}{\partial y}} \right|_{y = 0} = - \left( {\mu_{\text{b}} k{}_{\text{b}}\tan k_{\text{b}} H} \right)\varDelta.$$

(11)

The base shear force per unit length of the shear wall $f_{z}^{\text{b}}$ can be expressed as

$$f_{z}^{\text{b}} = - \Delta \mu_{\text{b}} k_{\text{b}} \left( {2a} \right)\tan k_{\text{b}} H = - \omega^{2} M_{\text{B}} \left( {\frac{{\tan k_{\text{b}} H}}{{k_{\text{b}} H}}} \right)\varDelta.$$

(12a)

From Eq. (12a), a dimensionless function proportional to the base shear force acting on the shear wall can be expressed as

$$\frac{{f_{z}^{\text{b}} }}{{\omega^{2} M_{\text{B}} }} = - \left( {\frac{{\tan k_{\text{b}} H}}{{k_{\text{b}} H}}} \right)\varDelta.$$

(12b)

2.4 The action of flexible foundation on the rigid foundation

The action of flexible foundation on the rigid foundation, $f_{z}^{\text{f}}$, can be expressed in term of stress as follows:

$$\begin{aligned} f_{z}^{\text{f}} = - \int_{0}^{\uppi } {\left. {\tau_{rz} } \right|_{r = a} a{\text{d}}\theta } \hfill \\ f_{z}^{\text{f}} = - \mu_{\text{f}} k_{\text{f}} a\sum\limits_{n = 0}^{\infty } {\left[ {B_{n}^{\left( 1 \right)} {\text{H}}_{n}^{\left( 1 \right){\prime }} \left( {k_{\text{f}} a} \right) + B_{n}^{\left( 2 \right)} {\text{H}}_{n}^{\left( 2 \right){\prime }} \left( {k_{\text{f}} a} \right)} \right]\times \int_{0}^{\uppi } {\cos n\theta {\text{d}}\theta } }, \hfill \\ \end{aligned}$$

(13)

where $\int_{0}^{\uppi } {\cos n\theta {\text{d}}\theta } = \left\{ {\begin{array}{*{20}c} {\uppi ,\;n = 0} \\ {0,\;n \ne 0} \\ \end{array} } \right.$. So $f_{z}^{\text{f}}$ can be rewritten as

$$f_{z}^{\text{f}} = \uppi \mu_{\text{f}} k_{\text{f}} a\left[ {B_{0}^{\left( 1 \right)} {\text{H}}_{1}^{\left( 1 \right)} \left( {k_{\text{f}} a} \right) + B_{0}^{\left( 2 \right)} {\text{H}}_{1}^{\left( 2 \right)} \left( {k_{\text{f}} a} \right)} \right].$$

(14)

3 The boundary conditions

3.1 Displacement and stress continuity

The free-stress boundary conditions of the ground surface should be satisfied by the free-field waves $w^{{\left( {\text{ff}} \right)}}$ and the scattered waves $w^{{\left( {\text{S}} \right)}}$. The displacement and stress continuity equations along the semi-circular interface at $0 \le \theta \le \uppi$ and $r = \bar{a}$, respectively are

$$\left. {w^{{\left( {\text{ff}} \right)}} + w^{{\left( {\text{S}} \right)}} } \right|_{{r = \bar{a}}} = \left. {w^{{\left( {\text{F}} \right)}} } \right|_{{r = \bar{a}}} \quad {\text{for}}\;0 \le \theta \le \uppi,$$

(15)

$$\left. {\mu \frac{\partial }{\partial r}\left( {w^{{\left( {\text{ff}} \right)}} + w^{{\left( {\text{S}} \right)}} } \right)} \right|_{{r = \bar{a}}} = \left. {\mu_{\text{f}} \frac{\partial }{\partial r}\left( {w^{{\left( {\text{F}} \right)}} } \right)} \right|_{{r = \bar{a}}} \quad{\text{for}}\;0 \le \theta \le \uppi.$$

(16)

Substitution of Eqs. (5), (6), and (7) into Eqs. (15) and (16) leads to the following two boundary condition equations, for n = 0, 1, 2, 3, …,

$$a_{n} J_{n} \left( {k\bar{a}} \right) + A_{n} {\text{H}}_{n}^{\left( 1 \right)} \left( {k\bar{a}} \right) = B_{n}^{\left( 1 \right)} {\text{H}}_{n}^{\left( 1 \right)} \left( {k_{\text{f}} \bar{a}} \right) + B_{n}^{\left( 2 \right)} {\text{H}}_{n}^{\left( 2 \right)} \left( {k_{\text{f}} \bar{a}} \right),$$

(17)

$$a_{n} J_{n}^{\prime } \left( {k\bar{a}} \right) + A_{n} {\text{H}}_{n}^{\left( 1 \right){\prime }} \left( {k\bar{a}} \right) = \kappa \left[ {B_{n}^{\left( 1 \right)} {\text{H}}_{n}^{\left( 1 \right){\prime }} \left( {k_{\text{f}} \bar{a}} \right) + B_{n}^{\left( 2 \right)} {\text{H}}_{n}^{\left( 2 \right){\prime }} \left( {k_{\text{f}} \bar{a}} \right)} \right],$$

(18)

where $\kappa = {{{\mu_{\text{f}} k_{\text{f}} }}/{\mu k}}$ is the material property ratio in the equation for the stress continuity boundary condition.The boundary condition at the interface of rigid and flexible foundations can be expressed as given below:

$$\left. {w^{{\left( {\text{F}} \right)}} } \right|_{r = a} = \left. {w^{{\left( {\text{R}} \right)}} } \right|_{r = a} = \Delta {\text{e}}^{ - {\text{i}}\omega t}$$

(19)

Substitute Eq. (7) into Eq. (19) to solve for $B_{n}^{\left( 2 \right)}$,

$$\begin{aligned} B_{0}^{\left( 1 \right)} {\text{H}}_{0}^{\left( 1 \right)} \left( {k_{\text{f}} a} \right) + B_{0}^{\left( 2 \right)} {\text{H}}_{0}^{\left( 2 \right)} \left( {k_{\text{f}} a} \right) = \Delta \;\quad {\text{for}}\;n = 0 \hfill \\ B_{n}^{\left( 1 \right)} {\text{H}}_{n}^{\left( 1 \right)} \left( {k_{\text{f}} a} \right) + B_{n}^{\left( 2 \right)} {\text{H}}_{n}^{\left( 2 \right)} \left( {k_{\text{f}} a} \right) = 0\;\quad \,{\text{for}}\;n > 0 \hfill \\ \end{aligned}$$

(20)

$B_{n}^{\left( 2 \right)}$ can be written in terms of $B_{n}^{\left( 1 \right)}$ and $\Delta$ as follows:

$$B_{n}^{\left( 2 \right)} = \left\{ {\begin{array}{*{20}c}\displaystyle {\frac{{\Delta - B_{0}^{\left( 1 \right)} {\text{H}}_{0}^{\left( 1 \right)} \left( {k_{\text{f}} a} \right)}}{{{\text{H}}_{0}^{\left( 2 \right)} \left( {k_{\text{f}} a} \right)}}\;\quad {\text{for}}\;n = 0} \\ \displaystyle { - \frac{{B_{n}^{\left( 1 \right)} {\text{H}}_{n}^{\left( 1 \right)} \left( {k_{\text{f}} a} \right)}}{{{\text{H}}_{n}^{\left( 2 \right)} \left( {k_{\text{f}} a} \right)}}\;\quad {\text{for}}\;n > 0}. \\ \end{array} } \right.$$

(21)

3.2 The dynamic equation for the rigid foundation, $w^{\text{f}} = \Delta {\text{e}}^{ - {\text{i}}\omega t}$

As pointed out by Luco (1969) and Trifunac (1972), displacement of the foundation $\Delta$ can be determined by the kinetic equation for the rigid foundation,

$$M_{\text{R}} {\ddot{w}}^{\left( {\text{R}} \right)}=-(f_z^{\text{f}}+f_z^{\text{b}}){\text{e}}^{ - {\text{i}}\omega t},$$

(22)

where ${\ddot{w}}^{\left( {\text{R}} \right)}= -\Delta \omega^{2} {\text{e}}^{ - {\text{i}}\omega t}$, $M_{\text{R}}$ is the mass of the rigid foundation per unit depth in the z-axis and $w^{{\left( {\text{R}} \right)}}$ represents the displacement function of the rigid foundation in terms of time factor t as described in Eq. (19).The foundation displacement $\Delta$ can be solved from Eqs. (12a), (14), and (22),

$$\begin{aligned} \varDelta = \left[ {\frac{{\mu_{\text{f}} k_{\text{f}} \uppi a\left( {{\text{H}}_{1}^{\left( 1 \right)} \left( {k_{\text{f}} a} \right) - \frac{{{\text{H}}_{0}^{\left( 1 \right)} \left( {k_{\text{f}} a} \right)}}{{{\text{H}}_{0}^{\left( 2 \right)} \left( {k_{\text{f}} a} \right)}}{\text{H}}_{1}^{\left( 2 \right)} \left( {k_{\text{f}} a} \right)} \right)}}{{\omega^{2} M_{\text{R}} + \mu_{\text{b}} k_{\text{b}} \left( {2a} \right)\tan k_{\text{b}} H - \mu_{\text{f}} k_{\text{f}} \uppi a\left( {\frac{{{\text{H}}_{1}^{\left( 2 \right)} \left( {k_{\text{f}} a} \right)}}{{{\rm{H}}_{0}^{\left( 2 \right)} \left( {k_{\text{f}} a} \right)}}} \right)}}} \right]B_{0}^{\left( 1 \right)}. \hfill \\ \hfill \\ \end{aligned}$$

(23)

Equation (23) can be further simplified as

$$\varDelta = \left[ {\frac{{ - \frac{4{\text{i}}}{{\uppi k_{\text{f}} a{\text{H}}_{0}^{\left( 2 \right)} \left( {k_{\text{f}} a} \right)}}}}{{\frac{{k_{\text{f}} \bar{a}}}{2a}^{2} \left( {\frac{{M_{\text{R}} }}{{M_{\text{F}} }} + \frac{{M_{\text{B}} }}{{M_{\text{F}} }}\frac{{\tan k_{\text{b}} H}}{{k_{\text{b}} H}}} \right) - \frac{{{\text{H}}_{1}^{\left( 2 \right)} \left( {k_{\text{f}} a} \right)}}{{{\text{H}}_{0}^{\left( 2 \right)} \left( {k_{\text{f}} a} \right)}}}}} \right]B_{0}^{\left( 1 \right)} = \Delta_{0} B_{0}^{\left( 1 \right)}.$$

(24)

where

$$\varDelta_{0} = \frac{{ - \frac{4{\text{i}}}{{\uppi k_{\text{f}} a{\text{H}}_{0}^{\left( 2 \right)} \left( {k_{\text{f}} a} \right)}}}}{{\frac{{k_{\text{f}} \bar{a}}}{2a}^{2} \left( {\frac{{M_{\text{R}} }}{{M_{\text{F}} }} + \frac{{M_{\text{B}} }}{{M_{\text{F}} }}\frac{{\tan k_{\text{b}} H}}{{k_{\text{b}} H}}} \right) - \frac{{{\text{H}}_{1}^{\left( 2 \right)} \left( {k_{\text{f}} a} \right)}}{{{\text{H}}_{0}^{\left( 2 \right)} \left( {k_{\text{f}} a} \right)}}}}$$

(25)

$M_{\text{B}}$, $M_{\text{R}}$, and $M_{\text{F}}$ are the masses of the building, rigid foundation, and flexible ring, respectively; $\rho_{\text{b}}$, $\rho_{\text{r}}$, $\rho_{\text{f}}$ stand for the density of those three media, sequentially; and the Wronskian $W\left[ {{\text{H}}_{n}^{\left( 1 \right)} \left( {k_{\text{f}} a} \right),{\text{H}}_{n}^{\left( 2 \right)} \left( {k_{\text{f}} a} \right)} \right] = \left[ {{\text{H}}_{n}^{{(1){\prime }}} \left( {k_{\text{f}} a} \right){\text{H}}_{n}^{\left( 2 \right)} \left( {k_{\text{f}} a} \right) - {\text{H}}_{n}^{(1)} \left( {k_{\text{f}} a} \right){\text{H}}_{n}^{{(2){\prime }}} \left( {k_{\text{f}} a} \right)} \right] = - {4{\text{i}}}/{{\uppi k_{\text{f}} a}}$. Other terms can be found in the “Appendix” section.

As pointed out by Luco (1969), the natural frequencies of a shear wall on a fixed foundation correspond to $k_{\text{b}} H = {\left( {2n + 1} \right)}{{\uppi }/{2}}$. And $\varDelta$ becomes zero at the values of $k_{\text{b}} H$ mentioned in the equation above.

Substitute Eq. (24) into Eq. (21), $B_{n}^{\left( 1 \right)}$ can be derived explicitly in terms of $B_{n}^{\left( 2 \right)}$,

$$\begin{aligned} B_{n}^{\left( 2 \right)} = \left\{ {\begin{array}{*{20}c} {\frac{{\Delta_{0} B_{0}^{\left( 1 \right)} - B_{0}^{\left( 1 \right)} {\text{H}}_{0}^{\left( 1 \right)} \left( {k_{\text{f}} a} \right)}}{{{\text{H}}_{0}^{\left( 2 \right)} \left( {k_{\text{f}} a} \right)}}\;\quad {\text{for}}\;n = 0} \\ { - \frac{{B_{n}^{\left( 1 \right)} {\text{H}}_{n}^{\left( 1 \right)} \left( {k_{\text{f}} a} \right)}}{{{\text{H}}_{n}^{\left( 2 \right)} \left( {k_{\text{f}} a} \right)}}\;\quad \quad \quad \quad {\text{for}}\;n > 0} \\ \end{array} } \right. \hfill \\ B_{n}^{\left( 2 \right)} = \left[ {\frac{{\delta_{n} \Delta_{0} - {\text{H}}_{n}^{\left( 1 \right)} \left( {k_{\text{f}} a} \right)}}{{{\text{H}}_{n}^{\left( 2 \right)} \left( {k_{\text{f}} a} \right)}}} \right]B_{n}^{\left( 1 \right)} \;\quad {\text{for}}\;n = 0,\;1,\;2,\;3,\;4 \ldots \hfill \\ \end{aligned}$$

(26)

where $\delta_{n} = \left\{ {\begin{array}{*{20}c} {1\;\quad {\text{for}}\;n = 0} \\ {0\;\quad {\text{for}}\;n > 0} \\ \end{array} } \right.$.

By substituting Eq. (26) into Eqs. (17) and (18), we can solve for wave function coefficients $A_{n} \;{\text{and}}\;B_{n}^{\left( 1 \right)}$ explicitly.

$$a_{n} J_{n} \left( {k\bar{a}} \right) + A_{n} {\text{H}}_{n}^{\left( 1 \right)} \left( {k\bar{a}} \right) = \left[ {{\text{H}}_{n}^{\left( 1 \right)} \left( {k_{\text{f}} \bar{a}} \right) + \left( {\frac{{\delta_{n} \Delta_{0} - {\text{H}}_{n}^{\left( 1 \right)} \left( {k_{\text{f}} a} \right)}}{{{\text{H}}_{n}^{\left( 2 \right)} \left( {k_{\text{f}} a} \right)}}{\text{H}}_{n}^{\left( 2 \right)} \left( {k_{\text{f}} \bar{a}} \right)} \right)} \right]B_{n}^{\left( 1 \right)},$$

(27)

$$a_{n} J_{n}^{\prime } \left( {k\bar{a}} \right) + A_{n} {\text{H}}_{n}^{\left( 1 \right){\prime }} \left( {k\bar{a}} \right) = \kappa \left[ {{\text{H}}_{n}^{\left( 1 \right){\prime }} \left( {k_{\text{f}} \bar{a}} \right) + \left( {\frac{{\delta_{n} \Delta_{0} - {\text{H}}_{n}^{\left( 1 \right)} \left( {k_{\text{f}} a} \right)}}{{{\text{H}}_{n}^{\left( 2 \right)} \left( {k_{\text{f}} a} \right)}}{\text{H}}_{n}^{\left( 2 \right){\prime }} \left( {k_{\text{f}} \bar{a}} \right)} \right)} \right]B_{n}^{\left( 1 \right)}.$$

(28)

From Eq. (27), $A_{n}$ can be derived and expressed in terms of $a_{n} \;{\text{and}}\;B_{n}^{\left( 1 \right)}$.

$$A_{n} = \left[ {\frac{{G_{n}^{\left( 1 \right)} }}{{{\text{H}}_{n}^{\left( 1 \right)} \left( {k\bar{a}} \right){\text{H}}_{n}^{\left( 2 \right)} \left( {k_{\text{f}} a} \right)}}} \right]B_{n}^{\left( 1 \right)} - \left[ {\frac{{J_{n} \left( {k\bar{a}} \right)}}{{{\text{H}}_{n}^{\left( 1 \right)} \left( {k\bar{a}} \right)}}} \right]a_{n},$$

(29)

where $G_{n}^{(1)} = {\text{H}}_{n}^{(1)} \left( {k_{\text{f}} \bar{a}} \right){\text{H}}_{n}^{(2)} \left( {k_{\text{f}} a} \right) - {\text{H}}_{n}^{(1)} \left( {k_{\text{f}} a} \right){\text{H}}_{n}^{(2)} \left( {k_{\text{f}} \bar{a}} \right) + \delta_{n} \Delta_{0} {\text{H}}_{n}^{(2)} \left( {k_{\text{f}} \bar{a}} \right)$.

Substitute Eq. (29) into Eq. (28), $B_{n}^{(1)}$ can be solved explicitly.

$$B_{n}^{\left( 1 \right)} = \frac{{\left[ {J_{n}^{{\prime }} \left( {k\bar{a}} \right){\text{H}}_{n}^{(1)} \left( {k\bar{a}} \right) - J_{n} \left( {k\bar{a}} \right){\text{H}}_{n}^{{(1){\prime }}} \left( {k\bar{a}} \right)} \right]{\text{H}}_{n}^{(2)} \left( {k_{\text{f}} a} \right)a_{n} }}{{\kappa G_{n}^{(2)} {\text{H}}_{n}^{(1)} \left( {k\bar{a}} \right) - G_{n}^{(1)} {\text{H}}_{n}^{{(1){\prime }}} \left( {k\bar{a}} \right)}},$$

(30)

where $G_{n}^{\left( 2 \right)} = {\text{H}}_{n}^{{(1){\prime }}} \left( {k_{\text{f}} \bar{a}} \right){\text{H}}_{n}^{\left( 2 \right)} \left( {k_{\text{f}} a} \right) - {\text{H}}_{n}^{\left( 1 \right)} \left( {k_{\text{f}} a} \right){\text{H}}_{n}^{{(2){\prime }}} \left( {k_{\text{f}} \bar{a}} \right) + \delta_{n} \Delta_{0} {\text{H}}_{n}^{{(2){\prime }}} \left( {k_{\text{f}} \bar{a}} \right) = - {4{\text{i}}}/{{\uppi k_{\text{f}} a}} + \delta_{n} \Delta_{0} {\text{H}}_{n}^{{(2){\prime }}} \left( {k_{\text{f}} \bar{a}} \right).$ Solve for $B_{n}^{\left( 1 \right)}$ from Eq. (30),

$$B_{n}^{\left( 1 \right)} = \left[ {\frac{{\left( {\displaystyle - \frac{2{\text{i}}}{{\uppi k\bar{a}}}} \right){\text{H}}_{n}^{\left( 2 \right)} \left( {k_{\text{f}} a} \right)}}{{ - G_{n}^{\left( 1 \right)} {\text{H}}_{n}^{\left( 1 \right){\prime }} \left( {k\bar{a}} \right) + \kappa G_{n}^{\left( 2 \right)} {\text{H}}_{n}^{\left( 1 \right)} \left( {k\bar{a}} \right)}}} \right]a_{n},$$

(31)

where Wronskian $W\left( {J_{n} \left( {k\bar{a}} \right),{\text{H}}_{n}^{\left( 1 \right)} \left( {k\bar{a}} \right)} \right) = - \left( {J_{n} \left( {k\bar{a}} \right){\text{H}}_{n}^{\left( 1 \right){\prime }} \left( {k\bar{a}} \right) - J_{n}^{\prime } \left( {k\bar{a}} \right){\text{H}}_{n}^{\left( 1 \right)} \left( {k\bar{a}} \right)} \right) = - {2{\text{i}}}/{{\uppi k\bar{a}}}$. Derive equation for $B_{0}^{\left( 1 \right)}$(n = 0) from Eq. (31),

$$B_{0}^{\left( 1 \right)} = \frac{{\left( { - \frac{2{\text{i}}}{{\uppi k\bar{a}}}} \right){\text{H}}_{0}^{\left( 2 \right)} \left( {k_{\text{f}} a} \right)a_{0} }}{{ - G_{0}^{\left( 1 \right)} {\text{H}}_{0}^{\left( 1 \right){\prime }} \left( {k\bar{a}} \right) + \kappa G_{0}^{\left( 2 \right)} {\text{H}}_{0}^{\left( 1 \right)} \left( {k\bar{a}} \right)}} = \frac{{\left( { - \frac{2{\text{i}}}{{\uppi k\bar{a}}}} \right){\text{H}}_{0}^{\left( 2 \right)} \left( {k_{\text{f}} a} \right)a_{0} }}{{G_{0}^{\left( 1 \right)} {\text{H}}_{1}^{\left( 1 \right)} \left( {k\bar{a}} \right) + \kappa G_{0}^{\left( 2 \right)} {\text{H}}_{0}^{\left( 1 \right)} \left( {k\bar{a}} \right)}}$$

(32)

By combining Eqs. (28), (29), and (31), we can derive the expressions for wave function coefficients $A_{n} \;{\text{and}}\;B_{n}^{(2)}$ as the following:

$$A_{n} = \left[ {\frac{{\left( { - \frac{2{\text{i}}}{{\uppi k\bar{a}}}} \right)\left( {\frac{{G_{n}^{\left( 1 \right)} }}{{{\text{H}}_{n}^{\left( 1 \right)} \left( {k\bar{a}} \right)}}} \right)}}{{ - G_{n}^{\left( 1 \right)} {\text{H}}_{n}^{\left( 1 \right){\prime }} \left( {k\bar{a}} \right) + \kappa G_{n}^{\left( 2 \right)} {\text{H}}_{n}^{\left( 1 \right)} \left( {k\bar{a}} \right)}} - \frac{{J_{n} \left( {k\bar{a}} \right)}}{{{\text{H}}_{n}^{\left( 1 \right)} \left( {k\bar{a}} \right)}}} \right]a_{n},$$

(33)

$$B_{n}^{\left( 2 \right)} = \left[ {\frac{{\left( { - \frac{2{\text{i}}}{{\uppi k\bar{a}}}} \right)\left[ {\delta_{n} \Delta_{0} - {\text {H}}_{n}^{\left( 1 \right)} \left( {k_{\text{f}} a} \right)} \right]}}{{ - G_{n}^{\left( 1 \right)} {\text{H}}_{n}^{\left( 1 \right){\prime }} \left( {k\bar{a}} \right) + \kappa G_{n}^{\left( 2 \right)} {\text{H}}_{n}^{\left( 1 \right)} \left( {k\bar{a}} \right)}}} \right]a_{n}.$$

(34)

4 Numerical analysis of displacement

As pointed out by Trifunac (1972), the condition for the envelope of the rigid foundation displacement, $\Delta$, corresponding to the case of which $\kappa = 1,\;\bar{a} \to a$, is given by

$$\varDelta_{\rm e} = \left[ {J_{1} \left( {ka} \right) - \frac{{J_{0} \left( {ka} \right)}}{{{\text{H}}_{0}^{\left( 1 \right)} \left( {ka} \right)}}{\text{H}}_{1}^{\left( 1 \right)} \left( {ka} \right)} \right]\left[ {\frac{{J_{0}^{2} \left( {ka} \right) + Y_{0}^{2} \left( {ka} \right)}}{{Y_{0} \left( {ka} \right)J_{1} \left( {ka} \right) - Y_{1} \left( {ka} \right)J_{0} \left( {ka} \right)}}} \right]a_{0}.$$

(35)

The backbone curve of $\varDelta$ could be understood as the displacement of the rigid foundation whose density is identical to that of the surrounding soil by setting ${{M_{\text{B}} }}/{{M_{\text{F}} }} = 0$ and ${{M_{\text{R}} }}/{{M_{\text{F}} }} = 1$.

$$\varDelta_{0} = \left[ {\frac{{ \displaystyle- \frac{4{\text{i}}}{{\uppi ka{\text{H}}_{0}^{\left( 2 \right)} \left( {ka} \right)}}}}{{\displaystyle\frac{ka}{2}\left( {\frac{{M_{\text{R}} }}{{M_{\text{F}} }}} \right) - \displaystyle\frac{{{\text{H}}_{1}^{\left( 2 \right)} \left( {ka} \right)}}{{{\text{H}}_{0}^{\left( 2 \right)} \left( {ka} \right)}}}}} \right]a_{0}$$

(36)

To characterize the problem, the dimensionless parameter is defined as $\varepsilon = {{k_{\text{b}} H}}/{{k_{\text{f}} a}} = {{\beta_{\text{f}} H}}/{{\beta_{\text{b}} a}}$. It is seen that the flexible, slender, and tall shear walls are described by large values of $\varepsilon$.

First, the correctness of the numerical results can be verified by comparing the results from the rigid semi-circular foundation case. This is done by setting $\kappa = {{\mu_{\text{f}} k_{\text{f}} }}/{\mu k} = 1,\;\bar{a} \to a$. Figure 2 represents the plots of the displacement on a Cartesian coordinate system with the x-axis being ‘wave number’ and the y-axis being ‘displacement’ and the initial conditions shown in the legends. The abscissa in these figures is the dimensionless frequency ${{\omega a} \mathord{\left/ {\vphantom {{\omega a} \beta }} \right. \kern-0pt} \beta }$ and the ordinate is the foundation displacement $\varDelta$. The displacement $\varDelta$ would be equal to one if the movement of the rigid foundation does not depend on the shear wall. This serves as a reference value which shows the influence of the interaction of structure and soil on the movement of the foundation and consequently on the base shear force. The results and plots are in line with Luco (1969) and Trifunac (1972).

Fig. 2

Effect of interaction on Δ the amplitude of foundation vibration. i ${{\bar{a}} \mathord{\left/ {\vphantom {{\bar{a}} a}} \right. \kern-0pt} a} = \text{1}$, $\kappa = \text{1}$, M _B/M _S = 1, M _F/M _S = 1, ε = 0, 2, 4. ii M _B/M _S = 1, M _F/M _S = 1, ε = 0, 2, 4 (Trifunac 1972)

Figures 3 and 4 represent the displacement curves for ${{\bar{a}} \mathord{\left/ {\vphantom {{\bar{a}} a}} \right. \kern-0pt} a} = 1.25$ and ${{\bar{a}} \mathord{\left/ {\vphantom {{\bar{a}} a}} \right. \kern-0pt} a} = 1.50$, respectively. The zeros correspond to the fixed-base natural frequencies of the shear wall. It can be seen that the thickness of the flexible ring has strong effect on the displacement amplitude of the rigid foundation. As the ratio of ${{\bar{a}} \mathord{\left/ {\vphantom {{\bar{a}} a}} \right. \kern-0pt} a}$ becomes large, peaks of the displacement amplitude increase significantly. The displacement amplitude increases greatly for low frequencies and is dependent on the amplitude of the wave in the flexible ring coefficient $B_{0}^{\left( 1 \right)}$. It is also noticed that the structure response is independent of the angle of incidence and only depending on the foundation displacement $\varDelta$.

Fig. 3

Effect of interaction on Δ the amplitude of foundation vibration. i ${{\bar{a}} \mathord{\left/ {\vphantom {{\bar{a}} a}} \right. \kern-0pt} a} = \text{1}\text{.25}$, $\kappa = 2$, M _B/M _S = 1, M _F/M _S = 1, ε = 0, 2, 4. ii ${{\bar{a}} \mathord{\left/ {\vphantom {{\bar{a}} a}} \right. \kern-0pt} a} = \text{1}\text{.25}$, $\kappa = 2$, M _B/M _S = 2, M _F/M _S = 1, ε = 0, 2, 4 iii ${{\bar{a}} \mathord{\left/ {\vphantom {{\bar{a}} a}} \right. \kern-0pt} a} = \text{1}\text{.25}$, $\kappa = 2$, M _B/M _S = 4, M _F/M _S = 1, ε = 0, 2, 4

Fig. 4

Effect of interaction on Δ the amplitude of foundation vibration. i ${{\bar{a}} \mathord{\left/ {\vphantom {{\bar{a}} a}} \right. \kern-0pt} a} = 1.50$, $\kappa = 2$, M _B/M _S = 1, M _F/M _S = 1, ε = 0, 2, 4. ii ${{\bar{a}} \mathord{\left/ {\vphantom {{\bar{a}} a}} \right. \kern-0pt} a} = 1.50$, $\kappa = 2$, M _B/M _S = 2, M _F/M _S = 1, ε = 0, 2, 4. iii ${{\bar{a}} \mathord{\left/ {\vphantom {{\bar{a}} a}} \right. \kern-0pt} a} = 1.50$, $\kappa = 2$, M _B/M _S = 4, M _F/M _S = 1, ε = 0, 2, 4

Figure 5 represents the base shear force acting on the flexible shear wall for $\varepsilon = 2$. When there is no interaction, the base shear force is infinite for the fixed-base natural frequencies of the shear wall. When the interaction is considered, the base shear force is bounded for all frequencies. It can be seen that the thickness of the flexible ring has little effect on the peaks of the base shear force.

Fig. 5

The base shear force. i $\kappa = 1$, M _B/M _S = 4, M _F/M _S = 1, ε = 2. ii $\kappa = 1.5$, M _B/M _S = 4, M _F/M _S = 1, ε = 2. iii $\kappa = 2$, M _B/M _S = 4, M _F/M _S = 1, ε = 2

Figure 6 describes the dimensionless base shear coefficient of the flexible wall structure. For the lower frequencies range which is of special importance for earthquake engineering, the peaks of the base shear forces are increased in proportion to the ratio of $\kappa = {{\mu_{\text{f}} k_{\text{f}} }}/{\mu k}$ and decreased for larger ${{\bar{a}} \mathord{\left/ {\vphantom {{\bar{a}} a}} \right. \kern-0pt} a}$. It is also indicated that the base shear force is bounded faster for higher value of material property ratio.

Fig. 6

The dimensionless base shear. i $\kappa = 1$, M _B/M _S = 4, M _F/M _S = 1, ε = 2. ii $\kappa = 1.5$, M _B/M _S = 4, M _F/M _S = 1, ε = 2. iii $\kappa = 2$, M _B/M _S = 4, M _F/M _S = 1, ε = 2

5 Conclusions

The analytical solution of the interaction of a shear wall, flexible-rigid foundation, and an elastic half-space is derived for incident SH waves with various angles of incidence. Comparison of these displacement amplitude plots and the ones in which the superstructure sits only on the rigid foundation shows that the flexible ring has the effect of diminishing the ground displacement amplitude as the building absorbs wave energy and scatters it back into the half-space that results in increased displacement amplitude of the foundation and decreased amplitude of ground displacement. This is an important phenomenon that differs from the typical SSI models in the absence of the flexible ring. It also found that the flexible ring (soft layer) cannot be used as an isolation mechanism to decouple a superstructure from its substructure resting on a shaking half-space due to the fact that waves are transmitted into and scattered from the flexible foundation.

Interesting results are shown in the graphs of displacement amplitude. The foundation displacement is zero for a rigid foundation with a fixed-base excited at the natural frequency of the shear wall. This concurs with the Luco (1969) and Trifunac (1972) results. However, for a heavy and flexible structure the peaks of displacement increase for low frequency waves as the thickness of the flexible foundation layer increases.

Base shear forces increase as the rigidity of the flexible foundation layer increases in comparison to the surrounding soil medium. Interestingly, for high frequency waves, peaks of the base shear force are the same for all ratios of ${{\bar{a}} \mathord{\left/ {\vphantom {{\bar{a}} a}} \right. \kern-0pt} a}$. For shear walls founded on soft soil and for low frequencies, the base shear forces are higher than values computed for shear walls supported on hard soil. The structure response is independent of the angle of incidence and only depending on the foundation displacement.

All of the above analytical solutions are for cases where the foundations are rigid, non-elastic movable foundations. Analytic solutions are possible because the foundation has rigid displacement characterized by only one parameter. A more realistic assumption would be to allow the foundation to be elastic. As such, analytic solutions for soil-structure interaction of a building and shear wall on an elastic foundation deserve investigation, but this, of course, is a very challenging research problem.

This paper serves as an intermediate step for such a goal. It considers the soil-structure interaction of a shear wall on a semi-elastic foundation, with the rigid semi-circular foundation being supported by an elastic ring wrapped around it as the outside layer of the foundation. However, the solution presented in this paper, though analytic, cannot be directly adapted to solutions representing a fully flexible foundation. A sequel to this paper will be to present a new model with the same foundation geometry, namely an elastic ring around a rigid foundation, with a new shape of the superstructure where the analytic solution of the SSI problems can later be more easily adapted to the SSI of a flexible foundation.

Appendix

The mass of the soil in place of foundation, $M_{\text{S}}$ per unit length is

$$M_{\text{S}} = \frac{{\rho \uppi a^{2} }}{2} = \left( {\frac{{\mu \uppi a^{2} }}{{2C^{2} }}} \right)\left( {\frac{k}{k}} \right)^{2} = \frac{{\mu \uppi a^{2} k^{2} }}{{2\omega^{2} }}.$$

(A.1)

The mass of the building, $M_{\text{B}}$ per unit length is

$$M_{\text{B}} = 2\rho_{\text{b}} aH = \left( {\frac{{2\mu_{\text{b}} aH}}{{C_{\text{b}}^{2} }}} \right)\left( {\frac{{k_{\text{b}} }}{{k_{\text{b}} }}} \right)^{2} = \frac{{2\mu_{\text{b}} k_{\text{b}}^{2} aH}}{{\omega^{2} }}$$

(A.2)

$$\frac{{\mu_{\text{b}} k_{\text{b}} R_{2} \nu \uppi }}{\mu k\uppi a} = \left( {\frac{{\mu_{\text{b}} k_{\text{b}} R_{2} \nu \uppi }}{\mu k\uppi a}} \right)\left( {\frac{{k_{\text{b}} H}}{{k_{\text{b}} H}}} \right) = \frac{{\mu_{\text{b}} k_{\text{b}}^{2} \left( {R_{2} \nu \uppi H} \right)}}{{\mu k\uppi a\left( {k_{\text{b}} H} \right)}} = \frac{{\mu_{\text{b}} k_{\text{b}}^{2} \left( {2aH} \right)}}{{\mu k\uppi a\left( {k_{\text{b}} H} \right)}}$$

(A.3)

$$\frac{{\mu_{\text{b}} k_{\text{b}} R_{2} \nu \uppi }}{\mu k\uppi a} = \frac{{\omega^{2} M_{\text{b}} }}{{\left( {\displaystyle\frac{{2\omega^{2} M_{\text{s}} }}{{\uppi k^{2} a^{2} }}} \right)\left( {k_{\text{b}} H} \right)}} = \left( {\frac{ka}{2}} \right)\left( {\frac{{M_{\text{b}} }}{{M_{\text{s}} }}} \right)\left( {\frac{1}{{k_{\text{b}} H}}} \right).$$

(A.4)

The mass of the rigid foundation, $M_{\text{R}}$ per unit length is

$$M_{\text{R}} = \frac{{\rho_{\text{r}} \uppi a^{2} }}{2}.$$

(A.5)

The mass of the flexible ring foundation, $M_{\text{F}}$ per unit length is

$$M_{\text{F}} = \frac{{\rho_{\text{f}} \uppi \bar{a}^{2} }}{2} = \left( {\frac{{\mu_{\text{f}} {{\uppi }}\bar{a}^{2} }}{{2C_{\text{f}}^{2} }}} \right)\left( {\frac{{k_{\text{f}}^{2} }}{{k_{\text{f}}^{2} }}} \right) = \frac{{\mu_{\text{f}} k_{\text{f}}^{2} \uppi \bar{a}^{2} }}{{2\omega^{2} }},$$

(A.6)

where ${\text{H}}_{0}^{{(1){\prime }}} \left( {k_{\text{f}} a} \right) = - {\text{H}}_{1}^{\left( 1 \right)} \left( {k_{\text{f}} a} \right),\,{\text{H}}_{0}^{{(2){\prime }}} \left( {k_{\text{f}} a} \right) = - {\text{H}}_{1}^{\left( 2 \right)} \left( {k_{\text{f}} a} \right),\,\mu_{\text{b}} = {{\omega^{2} M_{\text{B}} }}/{{2k_{\text{b}}^{2} aH}},\,\omega^{2} = {{\mu_{\text{f}} k_{\text{f}}^{2} \uppi \bar{a}^{2} }}/{{2M_{\text{F}} }},$ and $2a\mu_{\text{b}} k_{\text{b}} \tan k_{\text{b}} H = 2ak_{\text{b}} \left( {{{\omega^{2} M_{\text{B}} }}/{{2k_{\text{b}}^{2} aH}}} \right)\tan k_{\text{b}} H = \left( {{{\omega^{2} M_{\text{B}} }}/{{k_{\text{b}} H}}} \right)\tan k_{\text{b}} H$.