1 Introduction

The Haiyuan fault system is part of a major left-lateral fault system in the northeastern margin of the Tibetan Plateau that connects the seismically active Qilian Shan in the west to the tectonically active Liupan Shan in the east, which abuts against the relatively stable Ordos block (Molnar and Tapponnier 1975; Tapponnier and Molnar 1977; Li et al. 2009) (Fig. 1). The fault accommodates part of the deformation induced by the Indian-Asian collision, but no consensus has been reached about the best description of the widespread deformation that occurs there (Cavalié et al. 2008; Thatcher 2007). Neotectonic (Burchfiel et al. 1991; Zhang et al. 1991; Gaudemer et al. 1995; Yuan et al. 1998; Lasserre et al. 1999; He et al. 2000; Tian et al. 2001; Li et al. 2009) and geodetic studies (Meade 2007; Thatcher 2007; Cavalié et al. 2008; Wang et al. 2009; Duvall and Clark 2010; Loveless and Meade 2011; Jolivet et al. 2013; Li et al. 2013) of the Haiyuan fault estimated the Holocene and present-day slip rate, which contributes to a better understanding of the mechanisms of continental deformation and the seismic hazard of the fault. Although the crustal deformation in the northeastern Tibetan Plateau has been studied and characterized, issues still exist, e.g., the fault slip rates obtained by different methods are different from each other and the largest differences are of an order of magnitude, the near-field deformation is relatively poorly constrained by previous Global Positioning System (GPS) data and block models seldom consider non-uniform internal strain. In addition, four historical earthquakes that occurred 3500–3900 years ago suggest an average recurrence interval of approximately 1000 years, corresponding to the time elapsed since the last major event (Liu-Zeng et al. 2007). Thus the Tianzhu gap is the most probable site for the next large rupture on the fault and an assessment of its seismic hazard is an important goal (Cavalié et al. 2008).

Fig. 1
figure 1

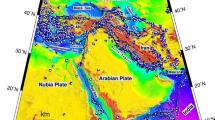
Tectonic map of the northeastern Tibetan Plateau. The inset map on the upper right shows the study area and division of the blocks. Black circles represent earthquakes with magnitude equal to or less than 5.0 and white circles correspond to earthquakes with a magnitude greater than 5.0 during the period 1920–2015 (USGS). Orange lines represent surface ruptures of the 1920 M8 and 1927 M8–8.3 earthquakes, respectively. The red line follows the Tianzhu seismic gap (Gaudemer et al. 1995). Rectangles represent segments with high seismic hazard. TLS Tuolanshan, LLL Lenglongling, JQH Jinqianghe, MMS Maomaoshan, LHS Laohushan, HYW Western Haiyan, HYM Middle Haiyuan, HYE Eastern Haiyuan, LPN Northern Liupanshan, LPS Southern Liupanshan; QL Qilian block, LZ Lanzhou block

Full size image

For this paper, we collected GPS data from Crustal Movement Observation Network of China (CMONOC I) and Continental Tectonic Environmental Monitoring Network of China (CMONOC II) from 1999–2014. Sixteen campaign-mode GPS stations in the near-field of the Haiyuan fault were established in 2013 and two of these were surveyed during 2013–2014. Moreover, 13 campaign-mode GPS stations from CMONOC were occupied two epochs in the period of 2013–2014 (Fig. 2). A denser velocity field in the northeastern Tibetan Plateau was derived. A rigid model, a uniform strain model and a linear strain model were applied to invert the deformation of the blocks. The fault slip rate, the locking depth, and the moment accumulation rate of each segment were sequentially inverted. Block deformation and its implication for tectonics in the northeastern Tibetan Plateau are discussed.

Fig. 2
figure 2

A map showing the locations of the GPS stations around the northeastern margin of the Tibetan Plateau. The black squares are CMONOC campaign stations, and the red stars are the CMONOC continuous stations. The green stars are stations we established in 2013 and monitored in 2013 and 2014, and the pink stars are stations we monitored in 2014

Full size image

2 Tectonic setting

The present-day tectonic features of the ~1000 km Haiyuan-Liupanshan fault are the result of geodynamic processes related to the India-Eurasian convergence some 50 Myr ago (Molnar and Tapponnier 1975; Tapponnier and Molnar 1977). The deformation of the Haiyuan fault is characterized by a left-lateral strike-slip movement (Gaudemer et al. 1995), while the Liupanshan fault is mainly thrusting (Li et al. 2013). The left-lateral strike-slip on the Haiyuan fault has been transformed into crustal shortening and contraction in the eastern end along the Liupanshan (Zheng et al. 2013).

Two large shocks have ruptured the Haiyuan fault during the twentieth century: the M8 Haiyuan earthquake in 1920 and the M8–8.3 Gulang thrust earthquake in 1927 (Zhang et al. 1987; Cavalié et al. 2008) (Fig. 1). Gaudemer et al. (1995) identified a 260 km-long stretch of the fault extending between those two rupture zones as a seismic gap, designated as the Tianzhu gap, which can be divided into four segments (Liu-Zeng et al. 2007) from west to east; (1) the Lenglongling segment, (2) the Jinqianghe segment, (3) the Maomaoshan segment, and (4) the Laohushan segment. The western and eastern ends of the Haiyuan-Liupanshan fault are divided into the Tuolaishan segment, the Haiyuan segment (composed of the western, middle and eastern segments), and the Liupanshan segment (consisting of northern and southern segments) (Li et al. 2009). The Haiyuan segment is the segment ruptured during the 1920 event (Fig. 1).

The Holocene slip rate of the Haiyuan fault was estimated from offset measurements and the dating of morphological markers. The slip rate decreases from 19 ± 5 mm/a along the Lenglongling segment to 12 ± 4 mm/a along the Maomaoshan-Laohushan segments (Lasserre et al. 1999), to 3.5–6.5 mm/a along the Haiyuan segment (4.5 ± 1.1 mm/a (Li et al. 2009), 5–6.5 mm/a (Tian et al. 2001), 4–6 mm/a (Zhang et al. 1991)). However, He et al. (2000) and Yuan et al. (1998) estimated the slip rate along the Lenglongling and Maomaoshan segment is only 4–5 mm/a. Slip rate estimates using block models based on GPS data suggest a 3.2–9 mm/a strike-slip rate along the Haiyuan fault (3.6–5.5 mm/a (Li et al. 2013), 4.6–4.7 mm/a (Loveless and Meade 2011), 7–9 mm/a (Meade 2007), 5–6 mm/a (Thatcher 2007), 3.4 ± 0.2 mm/a (Wang et al. 2009)), while the slip rates derived from dislocation models tend to be smaller between 1.2 and 5.5 mm/a [2–4.5 mm/a (Duvall and Clark 2010), 1.2–2.2 mm/a (Zhang et al. 2005), 1.4–4.8 mm/a (Ge et al. 2013), 2–5.5 mm/a (Zhang et al. 2011)]. Cavalié et al. (2008) obtained a 4.2–8 mm/a slip rate by modeling the fault parallel velocity profile along the Maomaoshan-Laohushan segment using ERS InSAR data and inferred the presence of creep at a shallow depth. Additionally, the slip rate of the Liupanshan fault may be less than 1.7 mm/a (Li et al. 2013; Zhang et al. 2011). The cause for the discrepancy between the short term (i.e., geodetic) and the average long-term (i.e., Quaternary) slip rates remains controversial (Jolivet et al. 2012).

3 Methodology

3.1 GPS measurement and data processing

The principal data used for this study are from the Crustal Movement Observation Network of China (CMONOC I) and the Tectonic and Environmental Observation Network of Mainland China (CMONOC II) (Gan et al. 2012) and were collected during 1999 and 2014, including 24 continuous stations, and 161 campaign-mode stations with an occupation of seven epochs over the time spanning from 1999 to 2013. Moreover, we conducted observations at 11 stations (including two newly built (2013) stations and nine pre-existing CMONOC stations) in 2013 and 29 stations (including two newly built (2013) stations, 13 pre-existing CMONOC stations and 14 newly built stations) in 2014 across the Haiyuan fault (Fig. 2).

The GPS data were processed together with 20 IGS sites around China using GAMIT/GLOBK10.4 software (Herring et al. 2010; King and Bock 2010). We processed the data in four steps (Shen et al. 2001): (1) All the observational data for a given day were processed together with the data from 20 IGS stations to solve for the daily loosely constrained station coordinates and the satellite orbits, (2) the daily solution for the local stations was combined with loosely constrained global solutions produced at the Scripps Orbital and Position Analysis Center (SOPAC, http://sopac.ucsd.edu/) using GLOBK software. Time series for the site coordinates were derived. Daily solutions with errors more than 20 mm or three sigma were deleted after removing the linearization tendency, (3) the station positions and velocities were estimated in the ITRF2008 using the GLOBK software. We imposed a frame of reference by minimizing the position and velocity deviations of 34 globally distributed IGS tracking stations with respect to the ITRF2008 while estimating the orientation, translation, and scale transformation parameters, and (4) the velocity solution was transformed into a Eurasia-fixed frame of reference using the Euler vector for Eurasia with respect to the ITRF2008 (Altamimi et al. 2012) (Fig. 3).

Fig. 3
figure 3

GPS velocities with respect to the stable Eurasian plate. Error ellipses indicate the 95 % confidence levels. Red arrows are sites used to define the self-fixed reference frame. Black rectangles indicate the velocity profiles for Fig. 5. A Tuolaishan segment, B Lenglongling segment, C Jinqianghe segment, D Maomaoshan segment, E Laohushan segment, F Haiyuan western and middle segment, G Haiyuan eastern segment, H Liupanshan northern segment, I Liupanshan southern segment

Full size image

3.2 Model

The northeastern Tibetan Plateau is divided into four blocks based on previous studies (Zhang et al. 2003; Wang et al. 2011), the Ordos block, the Alaxan block, the Qilian block and the Lanzhou block (Figs. 1, 2). The block boundaries coincide to the Haiyuan-Liupanshan fault.

The traditional theory of plate tectonics assumes that a block is a rigid body. The block kinematic can be described by the rigid model (RRM) (Li et al. 2004) using Euler’s theorem:

$$ \left[ {\begin{array}{l} {V_{\text{e}} } \\ {V_{\text{n}} } \\ \end{array} } \right] = r\left[ {\begin{array}{lll} { - \sin \varphi \cos \lambda } & { - \sin \varphi \sin \lambda } & {\cos \varphi } \\ {\sin \lambda } & { - \cos \lambda } & {\hbox{0}} \\ \end{array} } \right]\left[ {\begin{array}{l} {\omega_{x} } \\ {\omega_{y} } \\ {\omega_{z} } \\ \end{array} } \right], $$
(1)

where (λ, φ) are the longitude and latitude of a point within the block, (V e , V n) are the eastern and northern components of the velocity vector, r is the radius of the Earth, and (ω x , ω y , ω z ) is the Euler vector.

However, other studies (Li et al. 2001, 2004; Qu et al. 2014) have shown that blocks more closely resemble elastic or visco-elastic entities rather than purely rigid bodies. Deformation exists not only over the boundary zones of the blocks but also within the blocks. GPS velocities are a result of the combined effect of block rotation and internal deformation. If the deformation within a block is homogeneous, the velocity vector of a point within the block could be described using a uniform strain model (HSM) as follows:

$$ \left[ {\begin{array}{l} {V_{\text {e}} } \\ {V_{\text {n}} } \\ \end{array} } \right] = r\left[ {\begin{array}{*{20}l} { - \sin \varphi \cos \lambda } & { - \sin \varphi \sin \lambda } & {\cos \varphi } \\ {\sin \lambda } & { - \cos \lambda } & {\hbox{0}} \\ \end{array} } \right]\left[ {\begin{array}{l} {\omega_{x} } \\ {\omega_{y} } \\ {\omega_{z} } \\ \end{array} } \right] + \left[ {\begin{array}{*{20}l} {\varepsilon_{\text {e}} } & {\varepsilon_{\text {en}} } \\ {\varepsilon_{\text {ne}} } & {\varepsilon_{\text {n}} } \\ \end{array} } \right]\left[ {\begin{array}{l} x \\ y \\ \end{array} } \right], $$
(2)

where ε e , ε en , ε ne , ε n are the parameters that describe the uniform strain within a block and x = cosφ(λ–λ 0) and y = r(φ–φ 0), (λ 0 , φ 0) are the longitude and latitude of the block’s geometric center.

If strain is uneven within a block, the motion of a point within the block could be described by rigid rotation plus the non-uniform deformation of the block. The observed GPS velocity can be defined by a linear strain model (LSM) (Li et al. 2001) as shown below:

$$ \begin{gathered} \left[ {\begin{array}{*{20}l} {V_{\text {e}}} \\ {V_{\text {n}}} \\ \end{array} } \right] = r\left[ {\begin{array}{*{20}c} { - {\rm sin}\varphi {\rm cos}\lambda } & { - {\rm sin}\varphi {\rm sin}\lambda } & {{\rm cos}\varphi } \\ {{\rm sin}\lambda } & { - {\rm cos}\lambda } & 0 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\omega _{x} } \\ {\omega _{y} } \\ {\omega _{z} } \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} {\varepsilon _{\text {e}} } & {\varepsilon _{{\text {en}}} } \\ {\varepsilon _{{\text {ne}}} } & {\varepsilon _{\text {n}} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} x \\ y \\ \end{array} } \right]\; \hfill \\ \qquad \qquad+ \left[ {\begin{array}{*{20}c} {A_{0} } & {B_{0} } \\ {B_{0} } & {C_{0} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} x \\ y \\ \end{array} } \right] + \frac{1}{2}\left[ {\begin{array}{*{20}c} {A_{1} } & {B_{2} } \\ {B_{1} } & {C_{2} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {x^{2} } \\ {y^{2} } \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} {A_{2} + B_{1} } \\ {B_{2} + C_{1} } \\ \end{array} } \right]xy, \hfill \\ \end{gathered} $$
(3)

where A 0 , A 1 , A 2 , B 0 , B 1 , B 2 , C 0 , C 1 , C 2 are the strain parameters.

According to statistical theory (Tao 2007), the unbiasedness and effectiveness of a model are parameters that can be used to evaluate which model is more suitable to delineate block deformation. We used ΔV and S Δv as the criteria for unbiasedness and optimization, respectively:

$$ \Delta V = \frac{1}{2n}\left( {\sum\nolimits_{i = 1}^{n} {\Delta v_{{\text e}i} } + \sum\nolimits_{i = 1}^{n} {\Delta v_{{\text n}i} } } \right) $$
(4)
$$ S_{\Delta v} = \sqrt {\frac{1}{2n - R}\left[ {\sum\nolimits_{i = 1}^{n} {\Delta v_{{\text e}i}^{2} } + \sum\nolimits_{i = 1}^{n} {\Delta v_{{\text n}i}^{2} } } \right]}, $$
(5)

where Δv ei and Δv ni are the residual velocity components of a GPS point in the eastern and northern directions, n is the number of GPS stations and R is the number of undetermined parameters (Qu et al. 2014).

4 Results and analyses

4.1 Characteristics of GPS velocity field

The velocity field of the Tibetan Plateau relative to a stable Eurasia includes a rigid rotational component and an interior deformation component (Gan et al. 2007) (Fig. 3). In order to highlight the interior deformation of the northeastern Tibetan, we solved for the Euler vector of 16 GPS stations (Fig. 2) which are stable and evenly distributed within the region. The selection of well-behaved, evenly distributed, and stable stations follows criteria proposed by Rebischung et al. (2012) (Table 1). We also rejected sites with residuals beyond the 1.5 sigma [Eq. (1)]. The resulting Euler pole has a location and magnitude of (61.46° ± 3.12°, 99.19° ± 1.13°, 0.156° ± 0.018°/Ma). Figure 4 shows the new velocity field after taking out the rigid rotation of the northeastern Tibetan Plateau. Velocities to the south of the Haiyuan-Liupanshan fault show a clockwise rotation, while velocities to the north of the fault zone exhibit a counter-clockwise rotation. The results demonstrate that the Haiyuan-Liupanshan fault is experiencing a left-lateral striking-slip movement with a compression component, which is in agreement with previous studies (Gan et al. 2007; Ge et al. 2013; Wang et al. 2011). Figure 4 also shows that the fault movement from the Tuolaishan segment to the Laohushan segment is strike-slip with a thrusting component, the Haiyuan segment has mainly left-lateral movement and the Liupanshan segment is dominated by thrusting.

Table 1 Criteria used to select the northeastern Tibetan-fixed reference stations
Full size table
Fig. 4
figure 4

GPS velocity field in a northeastern Tibetan Plateau fixed reference frame. The thick gray solid lines indicate active faults. The gray ellipse at the tip of each velocity vector is the 95 % confidence level

Full size image

Horizontal velocities show an obvious reduction from the south to the north (about 7.0 mm/a in the south, decreasing to less than 2.0 mm/a near the Haiyuan fault), demonstrating that the crustal strain is accumulating along this deformation zone. Velocities decrease significantly from the outside to the center of the Lanzhou block (Fig. 4), suggesting that an internal strain exists within the block. Velocities also change slightly within the Alaxan and the Qilian blocks, indicating that these blocks are deformable. However, whether an internal strain exists in the Ordos block could not be ascertained from the data in Fig. 4.

4.2 Block deformation and fault slip rate

We calculated S Δv and ΔV for the RRM, HSM, and LSM, respectively (Table 2). The results suggest that the deformation of the Alaxan and the Lanzhou blocks could be described using the HSM and that of the Qilian block using the LSM. However, it is difficult to choose a deformation model to invert the Ordos block between the HSM and the LSM. The applicability of the two models for a specific block can be distinguished with an F test (Qu et al. 2014). We carried out the F test and concluded that the LSM is more suitable for the Ordos block at a significance level of 0.05.

Table 2 Statistics for models
Full size table

The directions of the residuals shown in Fig. 5 are stochastic in every block for these three block models. Meanwhile, the residuals derived from the LSM are smaller than those from the HSM in the Ordos, the Alaxan and the Lanzhou blocks but larger in the Qilian block, and residuals derived from the RRM are the largest. As a result, it is reasonable to model the Ordos, the Alaxan, and the Lanzhou blocks with the LSM and the Qilian block with the HSM. The residuals histogram conforms to the Gaussian normal distribution, indicating that the models fit the GPS velocities well without systematic errors. It should be noted that the residuals around the block boundaries have a relatively larger magnitude due to the concentration of the crustal deformation (Thatcher 2007; Wang et al. 2011). In other words, strain from interseismic coupling on block-bounding faults has significant impact on sites in the near-field, especially near block boundaries. Complicated crustal deformation around the blocks boundaries may be beyond the modeling of the current three block models.

Fig. 5
figure 5

Residuals of the GPS velocities and its histogram. The histogram consists of residuals derived from LSM within the Ordos, the Alaxan, and the Lanzhou block, and from HSM within the Qilian block

Full size image

The slip rate of each segment was estimated based on block models in terms of the relative movements of faults (Table 4). The RRM was defined as model A in order to obtain slip rates that matched long-term geological results (Zhang et al. 2007). The LSM was used to model the Ordos, the Alaxan, and the Lanzhou blocks, and the HSM was used to delineate the Qilian block. We named the mixed latter as model B (Table 3). Fault parallel and normal slip rate profiles for every segment were also mapped (Fig. 6).

Table 3 Model description
Full size table
Fig. 6
figure 6

Profiles along the fault (a) and perpendicular to the fault (b). Blue arc tangent curves are fitted velocity profiles. Red and green rectangles are used to estimate relative movement across faults and black rectangles are used to describe velocities tendency. a Tuolaishan segment, b Lenglongling segment, c Jinqianghe segment, d Maomaoshan segment, e Laohushan segment, f Haiyuan western and middle segment, g Haiyuan eastern segment, h Liupanshan northern segment, i Liupanshan southern segment

Full size image

The slip rates in Table 4 show that the overall characteristic of the Haiyuan-Liupanshan fault is dominated by a left-lateral striking-slip movement with a compression component. The slip rates derived from model A suggest that the fault activity decreases from the Tuolaishan segment to the southern Liupanshan segment with a reduction in the striking-slip rate from ~4.8 mm/a to 0.3 mm/a and in the shorting rate from ~3 mm/a to 0.7 mm/a. There is an increase in the compression component along the Liupanshan segment due to the transformation of the displacement between Haiyuan and Liupanshan (Zheng et al. 2013). Estimated slip rates from profiles (Table 4; Fig. 6) across the fault are consistent with model A. Results from model B exhibit similar trends to those from model A, with a smaller magnitude. Studies (Zhang et al. 2007; Wei et al. 2012) suggest that the slip rate obtained from the RRM and the velocity profiles probably reflects the far-field deformation of the fault, and yet the slip rate derived from the HSM and the LSM reflects the near-field crustal deformation of the fault.

Table 4 Fault slip rate and locking depth (positive is left-lateral and compression)
Full size table

Velocity gradients across the Haiyuan segment (Fig. 6a, f, g) indicate that the fault has a shallow locking depth and may still suffer from the impact of the 1920 M8.0 earthquake (Li et al. 2013; Meade and Hager 2005; Savage and Prescott 1978). Velocity gradients are also found on the western side of the Liupanshan segment (Fig. 6b, h, i). The compression component decreases from far-field (100–200 km) to near-field of the fault (50–10 km) with a slip rate from ~8 mm/a to ~6 mm/a, demonstrating that the left-lateral strike-slip on the Haiyuan fault is transforming into a thrusting component of the Liupanshan fault and crustal shortening in the region. The relative movement (Fig. 6b, h, i) is very small between the two sides (<50 km) of the Liupanshan segment, suggesting that strain might have accumulated in this area.

Our preferred slip rate for the Haiyuan fault derived from model B (from the Tuolaishan segment to the Haiyuan eastern segment) is about 2.0–3.2 mm/a, which is consistent with the estimate of Ge et al. (2013) of 1.4–3.5 mm/a. Using a finite method, Zhang et al. (2011) modeled GPS velocities in the northeastern Tibetan Plateau and obtained a value for the strike-slip of the Haiyuan fault of 2–5.5 mm/a. A similar slip rate of 2–4.5 mm/a was obtained by analyzing GPS velocities and the Quaternary fault slip of the main faults in northeastern Tibet (Duvall and Clark 2010). Moreover, the inversion of the 1683 GPS velocities within 31 blocks based on a block model by Wang et al. (2009) revealed that the strike-slip rate of the Haiyuan fault is 3.0–3.4 mm/a. Those slip rates correspond well with our results. Moreover, the slip rate of the Liupanshan fault is similar to that found in previous studies (~1.0 mm/a) (Zhang et al. 2011; Li et al. 2013), but with a smaller fault normal component. Discrepancies may arise from different models and datasets.

4.3 Locking depth and moment accumulation rate of faults

A rough estimate of relative motion of the plate across a section where the fault is locked can be obtained from a dislocation model (Savage and Burford 1973):

$$ v = \left(\frac{b}{\pi}\right) {\text{ actan }} \left({\frac{x}{D}}\right),$$
(6)

where D is the locking depth, b is the long-term slip rate of the fault, v is fault parallel velocity, and x is the distance to the fault.

The fault locking depth was estimated by a least-squares fit of the fault parallel velocities (Table 2). The locking depth in the Liupanshan segment (northern and southern Liupanshan) is none for the model and is not suitable for low-angle faults (Fig. 6a, h, i). The overall characteristic of locking depth from the Tuolaishan segment to the Haiyuan eastern segment is a decrease from 21.8 to 7.1 km, which is consistent with the decreasing trend for crustal thickness along the fault from west to east (Cui et al. 2009a, b). Cui et al. (2009a, b) gave a locking depth of 22.2 and 11.4 km for the Maomaoshan and the Laohushan segments, respectively, and 3.6–8.5 km for the Haiyuan segment based on the Smith-3D dislocation model. A locking depth of 15 km for the Jinqianghe segment is preferred by Li et al. (2013) based on GPS inversion. Our result for the locking depth is consistent with those studies. Moreover, the focal depth of the 1990 Tianzhu-Jingtai M 6.2 earthquake (the largest in decades) (Fig. 1) that occurred on the Maomaoshan is 12 km, which matches our locking depth well. The focal depth of the 1920 Haiyuan M 8 earthquake is generally believed to be between 17 and 20 km, which is different from our fitting locking depth for the Haiyuan segment. We speculate that the lower crust of the Haiyuan segment was not fully stuck until now, which may be the reason that no earthquakes with magnitude greater than 6.0 have occurred here during the past 95 years.

The seismic moment accumulation rate per unit length of the fault was also calculated. The moment accumulation rate M depends on the fault length l, the locking depth d j , the slip rate v j , and the rock shear modulus μ:

$$ {\frac {M_{j}} {l}} = \mu d_{j} v_{j} $$
(7)

An estimated locking depth was used to calculate the seismic moment accumulation rate per unit length for each segment (Table 4). As expected, the rate of moment accumulation is positively correlated with the locking depth. Those rates can be compared with the stress accumulation rate and the recurrence interval to establish the seismic hazard (Smith and Sandwell 2003). Fault segments that have a high seismic moment accumulation rate are associated with deep locking depths, while faults that have a shallow locking depth have a lower seismic moment accumulation rate and a correspondingly reduced hazard potential (Burgmann 2000). Regarding our understanding of earthquakes, all of the strain that builds up on the fault in the period between earthquakes must be released solely during large earthquakes. Tight fault coupling, high seismic moment accumulation rate, and the paucity of large seismic events over previous decades along the Tuolaishan segment and the Maomaoshan segment may imply more strain accumulation. Considering that the Tianzhu seismic gap corresponding to the time elapsed since the last major event (Liu-Zeng et al. 2007), we infer that a greater possibility of nucleation for a future event on the Tuolaishan segment and the Maomaoshan segment (lying along the Tianzhu seismic gap) exists. It should be emphasized that a complete scientific knowledge of the structure, palaeoseismic history, and dynamics of one fault are needed to our sense of security in terms of its seismic hazard (Zhang 2013).

5 Discussion

5.1 Characteristics of block deformation

GPS measurements that uniquely quantify the present-day deformation of the Tibetan Plateau can be simply and usefully described by the relative motions of the active blocks and the fault slip across the block boundaries (Meade and Hager 2005; Thatcher 2007). Our results show that the block models fit the horizontal GPS velocities well for the northeastern Tibetan Plateau. The Lanzhou block and the Qilian block can be best described by the LSM and the HSM, respectively. The Qilian block is smaller in size and has fewer secondary faults within the block than the Lanzhou block, and it deforms more uniformly. Qu et al. (2014) used regional plate kinematic models to fit GPS data in the Fenwei basin and suggested that the Ordos block deforms rigidly. On the basis of 1350 GPS velocities, Zhang et al. (2005) inferred that the Ordos block behaved as a coherent block similar to the oceanic rigid block without internal deformation. Wang et al. (2011) came to a similar conclusion for the Ordos block. In addition, Wang et al. (2009) asserted that the Ordos block and the Alaxan block are obviously rigid and the strength of these blocks is comparable to that of the lithospheric plate. However, our preferred models for the Ordos block (LSM) and the Alaxan block (LSM) are different from those in these studies because our GPS sites within the Ordos and the Alaxan blocks are primarily distributed around the block boundaries where complicated crustal deformation is concentrated (Thatcher 2007; Wang et al. 2011).

Although the relative motion located at or near the block boundaries agrees to the expectations based on the structural mapping of the active faults, the predicted slip rates are generally considerably less than those obtained by geological methods. Moreover, we should keep a rigorous attitude that these three models maybe improved more in mathematical sense than crustal block deformation.

5.2 Implication for tectonic deformation

Two alternative end-number models were proposed to describe the tectonic deformation occurring in the Tibetan and elsewhere on the continent: continuum versus block models (England and Mckenzie 1982; Avouac and Tapponnier 1993). The key divergence of the two models is whether the deformation is distributed broadly or localized on a few major faults (England and Molnar 2005). Kinematic analysis of the Haiyuan fault provides some clues. Although velocities fit block models well, attention should be paid that the low slip rates estimated by the space geodetic methods along the Haiyuan-Liupanshan fault imply that continuum models should be preferred for the northeastern Tibetan Plateau, but this is still controversial (Thatcher 2007; Cavalié et al. 2008). Zhang et at. (2005) argued that the present-day tectonic deformation of Chinese mainland can be described in terms of a coupling model of rigid block movement and continuous deformation. Meanwhile, same set of GPS data could be fitted well by microplate model (Thatcher 2007) and visco-elastic model (Cao et al. 2009). A compromise is that both the GPS data and the low fault slip rates implied are quite compatible with the block motions in the northeastern Tibetan Plateau (Zhang et al. 2005; Thatcher 2007).

6 Conclusions

On the basis of the measurements made from 185 GPS stations around the northeastern margin of the Tibetan Plateau since 1999, we derived a new velocity field, which plays a more important role in constraining the near-field crustal deformation of the Haiyuan-Liupanshan fault. After removing the rigid rotation of the northeastern Tibetan Plateau, interior deformation demonstrates quite different features bounded by the Haiyuan-Liupanshan fault. Clockwise rotation at the southern side of the fault and counter-clockwise at the northern side as indicated by the GPS velocities suggest that the Haiyuan-Liupanshan fault is undergoing a left-lateral striking-slip movement with a compression component. Block models used to invert the present-day deformation of the northeastern Tibetan Plateau show that active deformation in this region can be explained by crustal block rotation with an internal strain. The slip rates inferred from the block models vary slightly along the Haiyuan fault (2.0–3.2 mm/a) and the Liupanshan fault (0.9–1.5 mm/a), while the locking depth derived from the fault parallel velocities exhibit a large discrepancy along the Haiyuan fault (7.1–21.8 km). Compared to the adjacent area in the seismic gap, the Tuolaishan segment and the Maomaoshan segment with its high rate of moment accumulation coupled with the paucity of large earthquakes during the past ~1000 years constitute a high seismic risk in the future.