1 Introduction

Two-dimensional borehole tensor strainmeters have been well developed since the 1970s both in theory (Pan 1977; Su 1977; Gladwin and Hart 1985; Hart et al. 1996; Roeloffs 2010; Qiu et al. 2013) and in technique (Ouyang 1977; Gladwin 1984; Ishii 2001; Chi et al. 2009). Many such instruments have been deployed in countries such as China, the United States and Japan to monitor tectonic movements related to earthquakes, volcanoes, episodic tremors and slips, and other events (Linde et al. 1996; Qiu et al. 2007; Wang et al. 2008; Voight et al. 2010; Hodgkinson et al. 2010; Chardot et al. 2010; Qiu et al. 2011; Hawthorne and Rubin 2013).

Theoretically, seismic wave propagation in a continuous medium is governed by the stress–strain relationship (Timoshenko and Goodier 1951; Bullen 1963; Stein and Wysession 2003). Therefore, a tensor strainmeter may have some advantages for studying wave propagation over a conventional seismometer. To date, however, a systematic study on strain seismograph has not been carried out. A high-quality 2D strainmeter, the YRY-4 four-gauge borehole strainmeter (FGBS), has been successfully developed and deployed in China (Chi et al. 2009; Qiu et al. 2013). In the China Earthquake Administration’s observatory, FGBS data are routinely sampled at a rate of one sample per minute. In recent years, however, experiments have shown that the FGBS is capable of working at a sampling rate as high as 100 samples per second, with good signal-to-noise ratio.

2 Strain seismograms

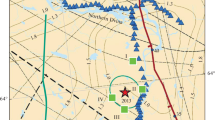
On March 17, 2008, a FGBS at the Guza site (Fig. 1) recorded a local earthquake of magnitude 3.5 in Sichuan, China, at 100 samples per second. The data from each component (Fig. 2) are high quality, with good signal-to-noise ratio.

Fig. 1
figure 1

Locations of the Guza site, and the M l3.5 earthquake. Directions of the four gauges in the FGBS are plotted

Full size image
Fig. 2
figure 2

Strain seismograms recorded at the site Guza from an M l3.5 earthquake of March 17, 2008. Dashed lines indicate the time intervals to be studied in detail for P waves and S waves

Full size image

In order to use the data of the four components to determine the strain tensor, we applied corrections based on relative in situ calibration, given in Qiu et al. (2013), to the raw time series, and the mean was removed from the data. Next, to satisfy a self-consistency criterion (Su 1977; Qiu et al. 2013), we verified equality of the sum of gauges S1 and S3 and the sum of gauges S2 and S4. As shown in Fig. 2, the seismograms of S1+S3 and S2+S4 are similar. We further examined self-consistency via plotting of S1+S3 versus S2+S4 by using the initial parts of the waveforms of the P wave and the S wave, separately (Fig. 3). The lines fitting separately from S1+S3 and S2+S4 are close (Fig. 3), which demonstrates a high degree of self-consistency of the FGBS data, even for such a high sampling rate. Some data are not very well self-consistent, especially for P wave. The reason is not yet known.

Fig. 3
figure 3

Graphs of S1+S3 versus S2+S4. a and b are for the initial parts of the P wave and S wave, as indicated by dashed lines in Fig. 2. Red stand for before correction, green after correction. Corrections in detail are given in Qiu et al. (2013)

Full size image

3 Strain pattern of P waves

Strain seismograms make it possible to plot deformation with time, while seismic waves pass through a site. When the data are self-consistent, the principal strain orientations are credible. Figure 4 shows the series of deformation patterns during the initial 0.24 s of the P wave (indicated in Fig. 2). The dotted ovals are drawn from a reference solid circle with exaggerated strains. Since the dominant period of the P wave here is nearly 0.2 s, the process plotted is a little longer than one cycle of the deformational vibration.

Fig. 4
figure 4

Illustration of the recorded deformation for multiple instants at Guza while the initial part of the P wave passes through. The time interval is indicated in Fig. 2. The dotted ovals are drawn from a reference circle with exaggerated strains

Full size image

By observing this series of plots, instant by instant, we can see that the axes of the ovals are mainly along two constant directions. One is nearly NS when the oval is larger than the reference circle; the other is nearly EW when the oval is smaller than the circle. In fact, the NS axis changes much more in length than the EW axis. This can be clearly shown in Fig. 5 as all the ovals are stacked together.

Fig. 5
figure 5

Stacked ovals of the P wave deformations plotted in Fig. 4

Full size image

Comparison of Figs. 1–5 shows that the most important feature of the P wave is that the diameter that changes most greatly coincides with the azimuth of the P wave’s ray path, which here comes from the south.

The ovals actually indicate that there are shear strains in P wave. Qiu and Chi (2013) studied the graphs of S1–S3 and S2–S4 recorded by the YRY-4 of the identical event studied in this paper. The graphs show that P wave strain contains significant shear strain components, which are obviously bigger than possible error. According to the theory of seismology, P wave has been clarified to have no rotation but volumetric strain and shear strains.

4 Strain pattern of S wave

Figures 6 and 7 show the series of deformation patterns during the initial part of the S wave (indicated in Fig. 2, total 0.24 s). Dotted ovals are drawn in the same way as those in Fig. 5. The extension directions of the ovals are obviously different from those of the P wave. In this case, there are also two nearly constant directions: one is toward the northeast when the oval is larger; the other is toward the northwest when the oval is smaller.

Fig. 6
figure 6

Illustration of the recorded deformation for multiple instants at Guza while the initial part of the S wave passes through. The time interval is indicated in Fig. 2. The dotted ovals are drawn from a reference circle with exaggerated strains

Full size image
Fig. 7
figure 7

Stacked ovals of the S wave deformations plotted in Fig. 6

Full size image

The S wave is different from the P wave in terms of strain. Unlike the strain pattern of the P wave, the strain pattern of the S wave does not indicate the location of the epicenter.

5 Comparison to conventional seismograms

A tensor strainmeter is different from a conventional seismometer in that a conventional seismometer records the rigid, translational motion of a site, whereas a tensor strain seismograph observes the internal deformation at a site. The spectra of strain seismograms and conventional seismograms should be in agreement with each other, however, because they both are governed by wave propagation. Thus, strain seismograms and conventional seismograms should be comparable in terms of waveform and frequency content.

We compared the strain seismograms, rotated into cardinal directions according to Qiu et al. (2013), with seismograms recorded by a broadband CTS-1 seismograph (flat response from 120 s to 20 Hz), co-located at the Guza site for the March 17, 2008, M l3.5 event (Fig. 1). To the first order, the records strongly resemble each other (Fig. 8), though the instruments measure different physical quantities (strain versus velocity). Distinct P and S wave arrivals are visible in the strain and seismic waveforms: impulsive P and SH phases. In addition, we observed the same pattern of P and S phase polarities in the seismic data and the rotated strain data. To elaborate, P and S phase first motions observed on the north component of the seismic data (VN) are both positive, and the first motions on the north component of the strain data are both negative. Likewise, the P and S phase first motions on the east component of the seismic data (VE) and the strain data are all positive. These observations suggest that the sense of motion correlates with the strain being either compressive or extensional.

Fig. 8
figure 8

Seismograms showing rotated nanostrain (top row) and velocity (bottom row; in counts) from the YRY-4 FGBS and the co-located CTS-1 seismograph, respectively, at station Guza. North–south nanostrain and seismic records are in the left column, and east–west records are in the right column

Full size image

We also compared the frequency content within each signal by estimating the power spectral densities (PSD) using Welch’s method (Fig. 9). The smoothed spectral density estimates show well-defined peaks in the seismic data and the north and east strain data, ε N and ε E, respectively, at 7 Hz, corresponding to the S wave. All PSDs start falling off at around 13 Hz, which corresponds to frequencies in the P wave, but show local maxima and minima at the same frequencies above 13 Hz. There is an elevated response in the strain data to frequencies below 5 Hz, compared to the seismic data. Power around 5 Hz is contained in both the P and S waves in the strain data and may reflect an increased sensitivity in the strainmeter at this frequency, perhaps a resonance.

Fig. 9
figure 9

Power spectral densities of the seismic (VN, VE) data and the rotated strain data (ε N and ε E). The units of the seismic PSDs are in counts2/Hz, whereas the strain data PSDs are in nanostrain2/Hz. PSDs are estimated using Welch’s method with 2s windows, overlapping 50 % to calculate each periodogram

Full size image

These comparisons show that, to the first order, the records strongly resemble each other and suggest that the FGBS is sensitive to seismic waves at high frequencies. Further study is needed in order to determine if the FGBS could serve as a replacement for a seismometer.

6 Conclusions

At high sampling rates (i.e., 100 samples per second), the FGBS could be used as a strain seismometer. The gauges record consistent spectra across a broadband of frequencies and are comparable to those of a conventional seismometer. The data are self-consistent, even at a high sampling rate. The FGBS strain recordings verify that a P wave can be defined as the type of seismic wave that always travels in the direction of maximum normal strain. The strain patterns of S waves are different from those of P waves. Strain seismograms might have some advantages in comparison with conventional seismograms for studying P and S waves, as well as the seismic source.

This paper presents the observation result of the YRY-4 instrument at Guza of the M l3.5 event. It provides new meaningful information about body seismic waves. Among the tens of sites in China equipped with this kind of instrument, Guza is the first where the test of 100 samples per second is carried out. More observations are needed to better understand this phenomenon.

The relation between strain records and translation records needs to be further explained. Some studies have been published concerning this issue. For instance, Bouchon and Aki (1982) simulated the time histories of strain, tilt, and rotation in the vicinity of earthquake faults in comparison to translational velocities. However, it is about near-field situation where the distance from the epicenter is less than the length of the seismic fault. Therefore, it does not fit the observation which is done 70 km away from the small event whose seismic fault should be no more than a few kilometers in size.