Advertisement

Earthquake Science

, Volume 28, Issue 2, pp 97–118 | Cite as

Stick–slip behavior of Indian gabbro as studied using a NIED large-scale biaxial friction apparatus

  • Tetsuhiro TogoEmail author
  • Toshihiko Shimamoto
  • Futoshi Yamashita
  • Eiichi Fukuyama
  • Kazuo Mizoguchi
  • Yumi Urata
Open Access
Research Paper
First Online:

Abstract

This paper reports stick–slip behaviors of Indian gabbro as studied using a new large-scale biaxial friction apparatus, built in the National Research Institute for Earth Science and Disaster Prevention (NIED), Tsukuba, Japan. The apparatus consists of the existing shaking table as the shear-loading device up to 3,600 kN, the main frame for holding two large rectangular prismatic specimens with a sliding area of 0.75 m2 and for applying normal stresses σ n up to 1.33 MPa, and a reaction force unit holding the stationary specimen to the ground. The shaking table can produce loading rates v up to 1.0 m/s, accelerations up to 9.4 m/s2, and displacements d up to 0.44 m, using four servocontrolled actuators. We report results from eight preliminary experiments conducted with room humidity on the same gabbro specimens at v = 0.1–100 mm/s and σ n = 0.66–1.33 MPa, and with d of about 0.39 m. The peak and steady-state friction coefficients were about 0.8 and 0.6, respectively, consistent with the Byerlee friction. The axial force drop or shear stress drop during an abrupt slip is linearly proportional to the amount of displacement, and the slope of this relationship determines the stiffness of the apparatus as 1.15 × 108 N/m or 153 MPa/m for the specimens we used. This low stiffness makes fault motion very unstable and the overshooting of shear stress to a negative value was recognized in some violent stick–slip events. An abrupt slip occurred in a constant rise time of 16–18 ms despite wide variation of the stress drop, and an average velocity during an abrupt slip is linearly proportional to the stress drop. The use of a large-scale shaking table has a great potential in increasing the slip rate and total displacement in biaxial friction experiments with large specimens.

Keywords

Stick–slip in gabbro Biaxial friction apparatus Shaking table Friction experiment Fault mechanics 

1 Introduction

Biaxial friction apparatuses have been widely used in experimental studies on rock friction since more than 30 years. Two biaxial apparatuses with three-block specimens built by Dieterich lead to the establishment of rate-and-state frictional constitutive law which has brought about revolution in our understanding of friction and in modeling earthquake generation (Dieterich 1972, 1978, 1979, 1981a; Ruina 1983; Tse and Rice 1986; great many papers thereafter). Biaxial friction apparatuses with similar specimen assemblies have been used in the studies of rock friction by Ohnaka (1973, 1978), Marone and Kilgore (1993), Kawamoto and Shimamoto (1998), and Noda and Shimamoto (2009, 2010). The biaxial friction apparatus built by Marone, now at Pennsylvania State University, is one of the most widely used apparatuses in the world at present (Marone 1998: Niemeijer et al. 2010; papers quoted therein). Ohnaka et al. (1987) used a two-block biaxial friction apparatus with a fault plane oriented at an angle to the loading axis, conducted very detailed experiments on dynamic rupture propagation, and established his constitutive law (see Ohnaka 2013). A large-scale biaxial apparatus was built at the USGS Menlo Park and has been used for studying rupture propagation (Dieterich 1981b; Lockner and Okubo 1983; Okubo and Dieterich 1984; Beeler et al. 2012). Xia et al. (2004) and Nielsen et al. (2010) conducted very detailed studies on dynamic rupture propagation with biaxial assemblies using transparent plastic plates with inclined faults. A biaxial friction apparatus at the Institute of Geology, China Earthquake Administration has been used for studying the effects of fault geometry on stick–slip behaviors (Ma and Ma 2003).

Those biaxial apparatuses have merits of high accuracy (no seals and no jackets are used in most cases), simplicity and easy access to the specimens for measurements, and utilization of specimens that are large enough to observe dynamic rupture propagation. However, they share a demerit of slow speed and limited displacement. Rotary-shear high-velocity friction experiments have been conducted in the last two decades and revealed dramatic weakening of faults as the slip rate approaches to a seismic slip rate on the order of 1 m/s (e.g., Di Toro et al. 2011; Ma et al. 2014; papers quoted therein). However, specimens used in rotary-shear friction apparatuses are thought to be too small to observe dynamic rupture propagation.

Thus, National Research Institute for Earth Science and Disaster Prevention (NIED) has started a project to develop a large-scale biaxial friction apparatus that is capable of producing high slip rates and larger displacements than previous biaxial apparatuses, using two blocks of large specimens (Fukuyama et al. 2012, 2014). The main purpose of building the apparatus was to study (1) the scale effect of simulated faults on their frictional properties and (2) rupture propagation during stick–slip events (a laboratory analog of earthquakes). A crucial part is the use of the Large Scale Earthquake Simulator (the existing shaking table) at NIED as the loading device that allows for the loading rates to up 1 m/s and displacements up to about 0.4 m (Minowa et al. 1989). The shaking table has been used extensively for testing the responses of houses and various structures to seismic ground motion. We designed and built a main frame for friction experiments that can be attached to the shaking table and a reaction base and a reaction bar to hold the stationary specimen to the rigid ground. The detailed design of the apparatus is reported in Fukuyama et al. (2014). Our paper reports a brief outline of the apparatus, results from eight preliminary friction experiments conducted on a pair of gabbro specimens, and stiffness properties of the apparatus determined from stick–slip events. We then discuss the advantages of using this apparatus and some improvements needed in conducting friction experiments.

2 Large-biaxial friction apparatus

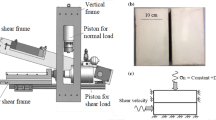
Fukuyama et al. (2014) report the details of the large-scale biaxial friction apparatus, including its design diagrams and close-up photographs of main elements. The apparatus consists of the main frame for applying normal stress to the specimens and conducting friction experiments (1; numbers in Fig. 1b, c refer to elements of the apparatus hereafter), a reaction force bar (2), and a reaction force base (3). The reaction force bar is fixed to the reaction force base with a space-adjusting device called turnbuckle (4) and a swivel (5). The main frame and the reaction force base are fixed to the shaking table (6) and to the ground with bolts, respectively. The upper specimen of 1.5 m × 0.5 m × 0.5 m in size (7) and lower specimen of 2 m × 0.5 m × 0.5 m in size (8) are placed in the center of the main frame (Fig. 1c). The lower specimen moves with the main frame as the shaking table is pushed leftward for loading with four servoactuators, whereas the upper specimen is connected with a reaction force bar to the reaction force base that is fixed to the ground, so that the upper specimen acts as a stationary block during friction experiments.
Fig. 1

A large-scale biaxial friction apparatus at the National Research Institute for Earth Science and Disaster Prevention, built by Tomoe Research & Development Co. Ltd, Tokyo, Japan. a A schematic diagram of the machine with the upper and lower rectangular prismatic specimens of 1.5 and 2.0 m in length, respectively (both width and thickness are 0.5 m). b A photograph of the entire apparatus and shaking table to which the main part of the apparatus is fixed. c A photograph showing the specimens that are set in a loading frame for applying normal stress with three hydraulic jacks. The upper specimen is connected to the ground by a reaction force bar (stationary side), and the lower specimen is fixed to the shaking table which acts as a loading device. Numbers in b, c denote elements in the apparatus as explained in the text

Normal force is applied with three hydraulic actuators (9 in Fig. 1c) with 1,000 kN in total in the loading capability, attached to a set of linear rails with ball bush (10). The actuators can move freely on the rails with the upper specimen, allowing for uniform application of the normal load to the specimens. Normal forces on each hydraulic actuator are measured with strain-gauge-based normal force gauges (9) with accuracy less than 0.5 % of the full scale. The total axial force (up to 1,000 kN) is calculated by adding up the measured forces by the three actuators. The area of sliding surface is 0.75 m2, and a normal stress up to 1.3 MPa can be applied with the main frame. We used three gas accumulators (11), which act as buffer to keep axial forces nearly constant without using a servocontrolled system during friction experiments. However, a normal force fluctuates typically by about several percentages during stick–slip events.

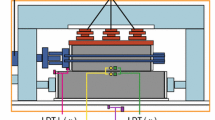
Shear force is measured using a strain-gauge-based compression/tension-type force gauge (12) with an accuracy less than 0.05 % of its full scale (1,200 kN). The shear-force gauge is bolted to the reaction bar, and they are tied with swivel (13) to the upper specimen. Swivels at 5 and 13 accommodate flexible vertical and horizontal tilting motions of the reaction force bar, respectively, thereby absorbing the misalignment of the loading column. The lower specimen with end iron plates is fixed to the lower side of the main frame by tightening the specimen-fixing screws on both sides (14) and is in frictional contact with a base plate (15). Displacement between the two iron plates, attached to the left ends of both specimens, was measured during friction experiments using a laser-displacement transducer (16: Keyence, Co. Ltd., LK-500), with the maximum stroke of 500 mm and an accuracy of 50 μm. This and two other laser-displacement transducers (Keyence, Co. Ltd., LK-150 with the maximum stroke of 150 mm) were attached to a rigid plate bolted to the iron end-plate that is fixed to the left end of the lower specimen (the lower-left side of Fig. 2a). A target bar is fixed to the iron plate at the left end of the upper specimen using the same bolts as those in the lower-middle part of Fig. 2a. Transducers XLD and YLD measure distances along white arrows marked with X and Y along the X (parallel to the fault slip) and Y (parallel to fault and normal to fault slip) directions, respectively (Fig. 2a), whereas the distance between the transducer and the target in the Z (fault-normal) direction is measured using a transducer ZLD along a white arrow with Z (Fig. 2b).
Fig. 2

Laser-displacement transducers to measure displacements in X (parallel to fault slip), Y (fault-parallel and normal to fault slip), and Z (fault-normal) directions. a Laser-displacement transducers XLD and YLD for measuring displacements in X and Y directions along arrowed lines, respectively. b Laser-displacement transducer ZLD to measure displacement in Z direction along an arrowed line (XLD and YLD are also shown in the photograph). 7 and 14 denote the lower specimen and the specimen fixing screw on the other side of that shown in the previous figure, respectively

We use the Large Scale Earthquake Simulator of NIED, Tsukuba on which a large biaxial apparatus is placed (17 in Fig. 3a), as the loading device. This simulator was built by Mitsubishi Heavy Industries, Ltd. and was installed in 1970 at the National Research Center for Disaster Prevention (NRCDP), the former organization of NIED (National Research Center for Disaster Prevention 1983). It was used extensively in earthquake resistance tests on wooden houses, oil tanks, and various structures, and was renovated in the late 1980s to extend the servocontrol and stroke capabilities (Minowa et al. 1989). The shaking table of 14.5 m × 15 m in horizontal sizes (6 in Fig. 3a) is driven with four servocontrolled hydraulic actuators (18 in Fig. 3a) which can produce a horizontal force up to 3,600 kN in total, a horizontal velocity up to 1.0 m/s, and an acceleration up to 9.4 m/s2. Two actuators are set on both sides of the shaking table, and a leftward motion for loading in our experiments is produced by compressive push with the actuators on the right and by tensile pull with the actuators on the left. The shaking table of about 1.8 × 105 kg in weight is supported by 12 hydraulic holding columns with flowing oil film (19) which reduces friction coefficient between the shaking table and the holding columns down to the order of 10−5. Rotary motion of the shaking table is prevented by using rod bearings around the table as confirmed by Yamashita et al. (2011). The shaking table, actuators, and hydraulic holding columns are set in a very rigid concrete foundation (20, 21), reinforced with iron steels and protected with sheet pile (22). The whole system is built in Quaternary sediments (23).
Fig. 3

a A schematic diagram showing the structures of the shaking table and the large biaxial friction apparatus. Reinforced concrete is used as the basement of the shaking table. b A schematic diagram showing machine elements (springs) and specimens. k m1, k m2, and k st are the stiffness values of the reaction force unit, specimen-holding part of the main frame, and shaking table, respectively. Displacement was measured at the end of the specimens which correspond to the (d 2 − d 1). Numbers in a denote machine elements and foundation (see text). Sheet pile (22) and added concrete mass (23) were installed for the reinforcement of the foundation during the renovation of the shaking table in 1989

Figure 3b exhibits a simplified constitution of our experimental system using springs, masses (heavy parts only), and frictional interface between specimens. Stiffness is defined here as a ratio of a force exerted to an elastic object to a change in its length (e.g., Jaeger and Cook 1979; Ohnaka 1973, 1978; Shimamoto et al. 1980). The stiffness can be defined in terms of the shear stress on the specimen, but this stiffness depends on specimen size (we also give this value in parenthesis using a fault area of 0.75 m2 at selected places). The stiffness of the reinforced concrete foundation is estimated to be about 2 × 1010 N/m (National Research Center for Disaster Prevention 1983). This is about two orders of magnitude greater than that of our experimental system as shown later, and we consider the foundation as a rigid reference frame. The upper specimen of 1.2 × 103 kg in mass (M 1, gabbro specimen used in our experiments) is fixed to the foundation with spring with an effective stiffness k m1 that consists of machine elements 2–5, 12, and 13 connected in series (Fig. 1b, c). The loading system is idealized as a spring with effective stiffness k st and shaking table with a huge mass M st of about 1.8 × 105 kg. The stiffness k st is determined mainly by fluid compressibility of the oil in horizontal hydraulic actuators, loading columns, and side walls of the shaking table. The lower specimen of 1.6 × 103 kg in mass (m2, gabbro specimen used in our experiments) is fixed to the bottom of the main frame, and we denote stiffness of this portion as k m2, which is determined mainly by the bending stiffness of the main frame (stiffness of the specimen-fixing screws affect k m2 slightly). The lower specimen is in frictional contact with the bottom plate of the main frame under a normal load applied to the specimen, and the behavior of the lower specimen must be complex due to this friction and bending deformation of the main frame. For simple static analysis in the next section, we consider that k m2 is an effective stiffness relating shear force acting in the system and the displacement of the left end of the lower specimen where displacement is measured, without going into the complexity of the real behaviors. The shear force is measured within the reaction force unit, very close to the upper specimen (location FG in Fig. 3b).

For displacement measurement, we take the position on the foundation where the reaction force base is fixed as a reference point with zero displacement (filled circle on the upper left side of Fig. 3b). We denote displacements of the left ends of the upper and lower specimens by d 1 and d 2, respectively (Fig. 3b). All displacements are taken positive leftward. Difference in displacements between the left ends of the specimens d is measured in our experiments (d = d 2 − d 1). Displacement d is zero before the onset of sliding of the specimens (i.e., d 1 = d 2). Suppose that an abrupt slip occurs with a force drop ΔF, the spring with a stiffness k m1 elongates by ΔF/k m1; i.e., Δd 1 = −ΔF/k m1, whereas springs with stiffness of k st and k m2 shorten by ΔF(1/k st + 1/k m2). Thus, a change in displacement Δd is given by
$$ \Updelta d = \Updelta d_{2} {-}\Updelta d_{1} = \Updelta F\left( { 1/k_{\text{st}} + { 1}/k_{m1} + { 1}/k_{m2} } \right) = \Updelta F/k $$
(1)
where k is an effective stiffness of the system:
$$ 1/k = 1/k_{\text{st}} + 1/k_{m1} + 1/k_{m2} $$
(2)

3 Frictional behavior of gabbro

Figure 4 shows results from seven friction experiments that were conducted on a pair of Indian gabbro specimens at loading rates v of 1.0–100 mm/s, at normal stresses σ n of 0.66–1.32 MPa and with displacements to around 0.39 m. Rectangular prismatic specimens were manufactured by Sekistone Co. Ltd., Gifu Prefecture, Japan, and the upper and lower sliding surfaces of 1.5 m × 0.5 m and 2.0 m × 0.5 m in area, respectively, were ground with RMS (root mean squares) surface roughness less than 18 μm (Japan Industrial Standard, JIS B 7513 level 1). Indian gabbro consists mainly of clinopyroxene (37 %), plagioclase (33 %), hornblende (11 %), hematite (5 %), biotite (4 %), and a few accessary minerals (Hirose and Shimamoto 2005; Table 1). After each experiment, specimens were removed from the main frame, the generated gouges were collected from the sliding surfaces for observation and analysis (to be reported elsewhere), and the specimens were reset for the next experiment.
Fig. 4

Shear stress/normal stress τ/σ n versus displacement d curves for tests conducted at loading rates of a 1.0 mm/s, b 10 mm/s, and c 100 mm/s. Normal stresses are given in parentheses after run numbers in each diagram. Large changes in friction coefficients are due to stick–slip that occurred throughout experiments

Table 1

Stiffness k i and mass m i of part no

No.

Parts

k i (GN/m)

k i (GN/m)

m i (kg)

(m i /3)(k m1/k i )2 (kg)

m i (k m1/k i−1)(k m1/k i ) (kg)

1

Reaction force base

2.14

2.14

600

1.1

0

2

Reaction force connector

0.88

0.624

320

3.47

6.03

3

Swivel

9.18

0.584

218

0.02

15.1

4

Turnbuckle

3.75

0.505

58

0.04

4.95

5

Reaction force bar

0.26

0.172

405

50.2

117.3

6

Shear force gauge

3.88

0.164

90

0.05

80.7

7

Swivel

4.51

0.159

218

0.09

210

8

Upper specimen

∞

0.159

1,200

0

1,200

Total effective mass M eff = 1,689 kg

55 (total)

1,634 (total)

i constituting the stationary side of the NIED friction apparatus. k i is a composite stiffness of parts 1 to i, and the sixth and the seventh columns give effective masses for dynamic deformation and for rigid-body transformation of each part, respectively. Reported masses in the design diagrams by the manufacturers are given in the table. The stiffness values k i used here were determined from the slope of the force displacement records by Fukuyama et al. (2014, Fig. 11)

Composite stiffness of the stationary side: k m1 = 0.159 GN/m

Effective stiffness k i of parts 1 to i is given by: 1/k i  = (1/k 1 +··· + 1/k i )

Rise time = π (M eff/k m1)1/2 = 0.0102 s = 10.2 ms

Shear force, normal loads, and displacements were recorded digitally with 1 MHz sampling frequency, but this paper is not focused on high-frequency processes such as rupture and seismic-wave propagations. We thus averaged 1,024 data successively to make a dataset corresponding to 0.9766 kHz sampling frequency for the analysis of frictional behaviors in this study. Figure 4a–c exhibits (shear stress)/(normal stress) τ/σ n versus displacement d curves for experiments conducted at loading rates v of 1.0, 10, and 100 mm/s, respectively, with the increasing run numbers indicating the order of experiments (LB01 in the run numbers indicate the first set of specimens and the following three digits show run numbers). Fukuyama et al. (2014) reported a table listing more than 100 runs with experimental conditions conducted using the present apparatus, including early experiments reported in this paper. The loading rates we report are average displacement rates as determined from the final displacement and the duration of a test. The shear stress τ normalized with respect to the normal stress σ n on the simulated fault gives friction coefficient μ when a fault is undergoing stable sliding, so that τ/σ n has been described as friction coefficient in many studies in the literature in rock mechanics. However, it should be kept in mind that the shear stress does not directly indicate the actual shear stress acting on the sliding surface during an abrupt slip in stick–slip, because dynamic forces to accelerate or decelerate the upper specimen block and the reaction force unit are included in the measured shear force. Stick–slip occurred in all of our experiments (Fig. 4), and we will call τ/σ n “shear stress/normal stress” or “normalized shear stress” in this paper to avoid confusion.

Violent stick–slip events occurred in all cases except for the early part of the first run (LB01-014, v = 1.0 mm/s, σ n = 0.67 MPa; the stick–slip amplitude increased from small to moderate values with the increasing displacement). The shear stress/normal stress at the onset of abrupt slip gives friction coefficient, and the maximum friction coefficient during frictional sliding, often called “frictional strength,” is 0.8–0.9 for the seven runs in Fig. 4, about the same values as those of typical rocks (Byerlee 1978). However, the peak friction coefficient μ p at the onset of abrupt slip decreased with the increasing displacement and stayed about the same at around 0.6 (Fig. 4a–c). Exceptions to this were a run LB01-014 where μ p decreased to around 0.75 (red curve in Fig. 4a), and LB01-15 in which μ p decreased down to about 0.6 at a displacement d of about 0.2 m and then increased to about 0.69 at d = 0.39 m (green curve in Fig. 4a). Overshooting of shear stress to negative values occurred during some stick–slip events at loading rates of 10 and 100 mm/s (Fig. 4b, c; the origin of the vertical axis is not zero in the figures).

Figure 5 exhibits photographs of the sliding surface of the lower specimen after three selected experiments. After a run LB01-014 (the first friction experiment on the specimens), the sliding surface is characterized by a smooth sliding surface with a very thin generated gouge and by the formation of 18 wear grooves with generated gouge powders (Fig. 5a). The lengths of the grooves range from 42 to 342 mm with an average of 250 ± 67 mm (the error being one standard deviation). The maximum length of the groove is less than the displacement of this run (387 mm), and the minimum length is greater than the amount of abrupt slip during stick–slip (typically several millimeters as we see later). Thus, the grooves formed during multiple stick–slip events. The wear grooves increase in number, and the overlapped grooves make the grooves longer and wider with the increasing number of experiments (see changes from Fig. 5a–c). Fukuyama et al. (2014) report that almost the entire sliding surface is covered with grooves and generated gouge after more than one hundred friction experiments on the same set of specimens (see a photograph in Fig. 16b of their paper).
Fig. 5

Photographs of the sliding surfaces of the lower specimen with wear grooves a after a run LB01-014 conducted at a normal stress σ n of 0.67 MPa and a loading rate v of 1.0 mm/s, b after LB01-016 at σ n = 0.67 MPa and v = 10 mm/s, and c after LB01-020 at σ n = 0.66 MPa and v = 100 mm/s. c was merged from two photographs using the Photoshop CS3. An arrow at the bottom indicates the movement direction of the facing block (upper specimen). The specimen is 2.0 m long and 0.5 m wide (a ruler in a is 175 mm long)

We now look at abrupt slip portions of stick–slip events closely, using three representative examples at loading rates of 1.0, 10, and 100 in the left diagrams of Fig. 6 which exhibit shear stress–time records (solid curves) and displacement–time records (dashed curves). The shear stress–time records are slightly smoother than the displacement–time records as can be seen in the figures because the shear stress represents a force in the stationary column (spring k m1 in Fig. 3b) that is separated from the shaking table by frictional interface. On the other hand, the displacement d is the relative motion between the two specimen blocks and is affected directly by the movements of the specimens on both sides. We thus define the onset and stop of a slip event as points of the maximum and the minimum shear stress, respectively (points A and B in Fig. 6a). The corresponding points are shown as A’ and B’ on displacement–time record in Fig. 6a and on velocity–time record in Fig. 6b. The velocity oscillates with time, but overall it tends to increase to its maximum at point C in Fig. 6b and decreases toward the point B’ where the shear stress is at its minimum. The corresponding points C’ in Fig. 6a nearly coincide with the inflection points on shear stress–time and displacement–time records in Fig. 6a. Likewise, the onset and stop of slip events and the maximum velocity are identified as points D, E, and F, and G, H and I, respectively, in the remaining figures in Fig. 6 (primed symbols denote corresponding points).
Fig. 6

Displacement–time (dashed curves) and shear stress–time (solid curves) records (left figures), and velocity–time records (right figures). a, b a run LB01-015 (loading rate v = 1.1 mm/s, normal stress σ n = 1.31 MPa), c, d LB01-019 (v = 10 mm/s, σ n = 1.32 MPa), e, f LB01-021 (v = 100 mm/s, σ n = 1.31 MPa). The displacement at the onset of slip event is 346.2, 260.8, 200.4, and 20.13 mm for (a), (c) and (e), respectively, and the locations of those events in Fig. 3 can be identified from the run number and those displacements

The stick portions of stick–slip behavior can be seen in shear force or shear stress versus displacement curves in three representative examples of two stick–slip events in Fig. 7 (run number and experimental conditions are given in each diagram). In the first example in Fig. 7a, the previous abrupt slip ended at position J which was identified conventionally as a point of minimum shear stress on a shear stress–time curve. Then a shear force (or shear stress) increased during the stick-period to L where an abrupt slip occurred to M, and another stick–slip event followed. The time durations for the loading portion (J–L) and for the slip portion (L–M) are 2,178 and 24 ms, respectively (see durations of time for J–K, K–L, and L–M at the bottom of Fig. 7a). The oscillation was initially irregular (J–K) for 62 ms, but it changed to regular decaying oscillations from K to a point slightly before point L. In an example at a faster slip rate of 10 mm/s (Fig. 7b), a slip event ended at N followed by loading with irregular oscillations from N to O in 108 ms, then with regular oscillations from O to P in 260 ms, and the next slip event occurred from P to Q in 17 ms. At even faster slip rate of 100 mm/s (Fig. 7c), the duration for loading was 52 ms, much shorter than the loading periods for the previous examples, and very irregular oscillations occurred prior to an abrupt slip from S to T in 17 ms.
Fig. 7

Three examples of stick–slip events during friction experiments. Shear load F (left vertical axis) or shear stress τ (right vertical axis) is plotted against displacement d for a representative stick–slip event a in a run LB01-015 (loading rate v = 1.0 mm/s, normal stress σ n = 1.31 MPa), b in LB01-019 (v = 10 mm/s, σ n = 1.32 MPa), and c in LB01-021 (v = 100 mm/s, σ n = 1.31 MPa). Approximate locations of those events in the records of Fig. 4 can be searched from run number and displacements on the horizontal axes of this figure

We now examine the behavior during the stick-portion more closely, using the behavior from J to L in Fig. 7a as an example. The shear force or shear stress dropped down to a level of J, slightly recovered to a level of K fairly quickly in about 62 ms, and gradually built up to a level of L where the next event initiated (Fig. 8a). A close-up of the J–K portion is shown in Fig. 8b which reveals very small oscillations overlapped on the axial force or shear stress versus time record. The displacement in the X direction fluctuated by as much as 0.8 mm near point J, but it decayed fairly rapidly from J to K, and then gradually from K to L (Fig. 8c). The next abrupt slip occurred at L, and the displacement went out of scale in the figure. Displacement in the Y direction fluctuated by about 0.7 mm initially, but it decayed monotonically toward the next event, and a similar oscillation occurred again at about the same displacement (Fig. 8e). The oscillation in the Z direction was similar to that in the Y direction, except that the amplitude of oscillation increased for about 0.25 s and then decayed monotonically in the Z direction (Fig. 8g). FFT analysis with the Octave software revealed sharp peaks at 41.5 Hz for displacements in the X and Y directions and at 54.4 Hz for that in the Z direction (Fig. 8d, f, h). Close-ups of the displacement–time records reveal that the oscillations in the Y and Z directions are simple with sharp characteristic frequencies (Figs. 9b, c, 8f, h). On the other hand, the oscillation in the X direction (slip direction) is more complex (Fig. 9a), and its frequencies seem to be variable except for the sharp peak at 41.5 Hz (Fig. 8d). We argue later that those oscillations are caused primarily by the oscillation of the target bar of the displacement transducers, rather than the fault slip.
Fig. 8

a Force or shear stress versus time curve, and b a close up of the curve for the stress drop portion (see J and K for the references). Displacement–time records in c X (slip-parallel), e Y (fault-parallel and slip-normal) and g Z (fault-normal) directions during a stick-period in a run LB01-015, corresponding J–L in Fig. 7a. d, f, h Result from fast-Fourier transform (FFT) analysis corresponding to the records on the left side. See Fig. 2 for the arrangement of displacement transducers

Fig. 9

Displacement–time records in a the X (slip-parallel), b the Y (fault-parallel and slip-normal), and c the Z (fault-normal) directions during a stick-period in a run LB01-015, just after an abrupt slip at J in Fig. 7a. The figures exhibit close-ups of the records in Fig. 8c, e and g (see J and K to correlate the two records). The displacement in a is shown in a unit of meter to correlate the location of slip event in Fig. 4a, whereas Y and Z displacements are shown in millimeters to indicate the amplitudes of oscillations

4 Stiffness of the apparatus

We identified the onset and stop of slip from seven experiments from the shear stress–time records automatically using the Matlab software (e.g., L–M, P–Q, and S–T in Fig. 7a–c), and determined the shear force drop ΔF or shear stress drop Δτ and the displacement Δd during the events. The original experimental data were filtered to cut high-frequency noises and to search for approximate locations of the onset and stop of an abrupt slip, and the initiation and stop positions of the event were determined as the points of the maximum and minimum shear stresses on the original records. Plotted results in Fig. 10a indicate that ΔF or Δτ is linearly proportional to Δd during 1,669 stick–slip events. For loading rates of 1.0 and 10 mm/s, a linear relationship between ΔF and Δd almost goes through the origin with a very small intercept of the best-fit curve (6.67 × 103 ± 5.67 × 102) N. This error is a standard error evaluated by the diagonal component of the covariance matrix during the least squares fitting with the Kaleidagraph software and is smaller than the range of ΔF by about two orders of magnitude (errors below are also standard errors during the fitting). The slope of the best-fit line gives a stiffness of the system k of (1.15 ± 0.004) × 108 N/m. For our specimens with a sliding area of 0.75 m2, the stiffness k can also be expressed as (153 ± 0.5) MPa/m. Fukuyama et al. (2014) measured the stiffness of the upper part k m1 as 1.59 × 108 N/m during static loading (see Table 4 of their paper). Then the stiffness of the lower part is 4.16 × 108 N/m which cannot be split into k st and k m2 with our data at present. We argue later, however, that the movement of the shaking table is delayed, and this stiffness is likely to be close to the value of k m2.
Fig. 10

a Force drop ΔF (left vertical axis) or shear stress drop Δτ (right vertical axis) plotted against the change in displacement Δd on the horizontal axis during 1,696 stick–slip events at normal stresses of 0.67–1.32 MPa and at loading rates of 1.0–100 mm/s (see symbols and run numbers in the diagram). Filled and open circles are for data at a loading rate of 100 mm/s (number of data is 27), and other symbols are for loading rates of 1.0 and 10 mm/s (number of data is 1,669). Data of those two groups are fit with solid lines by the least squares method (R is the correlation coefficient). b Frequency histogram of stick–slip rise times for the stick–slip events plotted in (a). Dark-gray bars are for a loading rate of 100 mm/s, and light-gray bars are for loading rates of 1.0 and 10 mm/s; their averages are given in the figure. All stick–slip events were determined by taking the points of the maximum and minimum shear stresses as the onset and stop of stick–slip events using Matlab software. Data for which an axial force dropped below 32 kN were excluded from this figure (see text for the reasons)

Stick–slip data with very large stress drops should be handled with care in determining the stiffness from data on ΔF and Δd. A calibration record of the stiffness in Fig. 10c of Fukuyama et al. (2014) clearly indicates that the apparent stiffness is very low when a shear force is less than 20–30 kN possibly due to the clearances of about 0.4 mm in total between the shear force gauge and its neighboring parts. In other words, a displacement up to this amount can take place when a shear stress drops below this level, and the datum points with such large force drops are spread to larger displacements than the linear relationship between ΔF and Δd shown in Fig. 10a. Thus, we did not plot stick–slip data for which a shear stress dropped below 32 kN in Fig. 10a to determine the stiffness well within the compressive regime and to avoid the complexity arising from loose junctions of the machine elements. In particular, a shear stress experienced overshooting to reach negative values in many stick–slip events at a slip rate of 100 mm/s (Fig. 4c), and only 27 datum points are plotted for a slip rate of 100 mm/s (open and filled circles in Fig. 10a). An interesting result is that ΔF–Δd relationship for a loading rate of 100 mm/s has a slope of (1.05 ± 0.04) × 108 N/m, similar to that at low slip rates, but it has an intercept of −(9.72 ± 1.78) × 104 N on the vertical axis. This corresponds to an intercept of 0.93 mm on the horizontal axis (Fig. 10a). Equations (1) and (2) are derived under an assumption that the load-point displacement does not change during an abrupt slip. However, this assumption does not hold for fast loading experiments. A displacement of 0.93 mm is likely to be an additional displacement due to the loading during the slip portions of stick–slip events.

On the other hand, rise time t r of stick–slip or duration of abrupt slip for the events ranges from 4 to 32 ms with an average of 17.9 ± 4.0 ms, the error being one standard deviation (see a histogram in Fig. 10b). Average rise times for data at loading rates of 1.0 and 10 mm/s and for data at 100 mm/s are 18.0 ± 4.1 and 15.8 ± 1.7 ms, respectively (light- and dark-gray columns in Fig. 10b). Thus, the rise time of abrupt slip seems to be about the same for all slip rates, as recognized in previous studies (e.g., Ohnaka 1973, 1978; Johnson and Scholz 1976; Shimamoto et al. 1980). Upon a closer look, however, the frequency histogram of the rise time for slip rates of 1 and 10 mm/s has a large peak at 17 ms and a small peak at 24 ms (Fig. 10b). We argue later that this small peak is likely to be artificial due to the oscillation of the axial load following large force drops.

Linear relationships between ΔF and Δd or between Δτ and Δd and a nearly constant rise time (Fig. 10) should lead to linear relationships between an average velocity V av during slip event and ΔF or Δτ, as recognized previously (Johnson and Scholz 1976; Ohnaka 1978; Shimamoto et al. 1980). However, the rise time of stick–slip t r was somewhat variable from one run to another run, and we plotted the results on V av, ΔF or Δτ, Δd, and t r for a slip rate of 1 mm/s in Fig. 11a–c and for slip rates of 10 and 100 mm/s in Fig. 11d–f. The average slip rate V av for an individual event was determined as Δd divided by the stick–slip rise time t r, and V av was plotted against ΔF or Δτ in Fig. 11a, d. The slope of V av–ΔF relationship appears to be slightly larger in a run LB0-014 than in LB0-015 (open and filled squares in Fig. 11a, respectively). An average rise time was 17.8 ± 8.6 and 22.2 ± 3.9 ms for LB01-014 and LB01-015, respectively (Fig. 11b). The relationship between ΔF and Δd in Fig. 10a and those t r values give V av = Δd/t r = 4.89 × 10−7 (m/sN) ΔF—0.003 (m/s) for LB01-014 and V av = 3.92 × 10−7 (m/N) ΔF—0.003 (m/s) for LB01-015. These are plotted as two solid lines in Fig. 11a, with reasonable agreement with the data. Thus, the difference in the V av–ΔF relationships between the two runs is due mainly to the difference in t r (Fig. 11b). Most stick–slip events in LB01-014 have ΔF smaller than 2 × 105 N and t r of 15–20 ms (light-gray circles in Fig. 11c), whereas ΔF ranges up to about 7 × 105 N and t r appear to have bimodal values of around 17 and 25 ms when ΔF becomes greater than about 2 × 105 N (cf. Fig. 11b, c).
Fig. 11

Average velocity V av during slip portions of stick slip events (the same events as those in the previous figure), plotted against the shear force drop (lower horizontal axis) or shear stress drop (upper horizontal axis) for the loading rated a of 1 mm/s and d of 10 and 100 mm/s. Frequency histograms of stick–slip rise time are shown for the loading rates b of 1 mm/s and e of 10 and 100 mm/s. Shear force drop ΔF is plotted against the rise time of stick–slip events for the loading rates c of 1 mm/s and f of 10 and 110 mm/s. The solid lines are the prediction from the relationships between ΔF and Δd in Fig. 10a and constant rise times given in b, e of this figure

Figure 11d exhibits V av plotted against ΔF or Δτ for slip rates of 10 and 100 mm/s, revealing two linear relationships for the two slip rates. Stick–slip rise time t r at a slip rate of 10 mm/s has an average of 18.6 ± 4.0 ms, but it has a bimodal distribution with a large peak at 17 ms and a small peak at 24 ms (Fig. 11e). The rise time t r over 21 ms was recognized when ΔF was greater than about 105 N (Fig. 11f), and this shows a similar trend to the one recognized at a slip rate of 1 mm/s (Fig. 11c). The t r of 18.6 ms and the ΔF–Δd relationship for slip rates of 1 and 10 mm/s in Fig. 10a yield V av = 4.68 × 10−7 (m/sN) ΔF—0.003 [m/s] for a slip rate of 10 mm/s which agrees reasonably well with the experimental data (lower line in Fig. 11d). On the other hand, t r has an average of 15.8 ± 1.7 ms for a slip rate of 100 mm/s and does not have a bimodal distribution (Fig. 11e, f). This t r value and the ΔF–Δd relationship for a slip rates of 100 mm/s in Fig. 10a give V av = 6.03 × 10−7 (m/sN) ΔF + 0.059 (m/s), again in good agreement with the experimental data (upper line in Fig. 11d). Thus, the average slip rate V av during stick–slip is linearly proportional to the force drop ΔF or the shear stress drop Δτ, although the relationship somewhat varies due to variation of t r. We discuss later about the variation of t r, whether it is real or not.

5 Discussion

5.1 General stick–slip behaviors

This paper reports preliminary results from a series of initial tests at loading rates of 1.0, 10, and 100 mm/s, at normal stresses to 1.32 MP, and with displacements of about 0.39 m, using a pair of ground specimens of Indian gabbro. Violent stick–slip events occurred in most experiments with shear force drops reaching 8 × 105 N. The overall stick–slip behaviors observed in our experiments exhibited the same features as recognized previously, i.e., nearly constant rise time of slip events or a constant duration of slip event (17.7 ms, Fig. 10b), and a linear relationship between the average velocity and shear force drop or shear stress drop (Fig. 11a, c; cf. Ohnaka 1973, 1978; Johnson and Scholz 1976; Shimamoto et al. 1980). Frequent stick–slip events must have been caused by rather soft loading system with stiffness of 1.15 × 108 N/m (153 MPa/m for our specimens), a value determined from a force drop ΔF and an amount of slip Δd during stick–slip events at loading rates of 1.0 and 10 mm/s (Fig. 10a). This stiffness is much smaller than the stiffness of a large-scale biaxial friction apparatus at the U. S. Geological Survey (2.6 × 109 N/m or 3.3 GPa/m; Lockner and Okubo 1983), and this is a reason for the occurrence of violent stick–slip in our experiments. Some events were so large that the shear stress went on to show negative values (Fig. 4) due to overshooting. Such overshooting of slip was suggested to have occurred during the 2011 Tohoku-Oki earthquake, resulting in the inversion from compressive stress before the earthquake to the tensile stress field over wide areas in subduction zone after the earthquake (e.g., Ide et al. 2011; Sibson 2013).

We conducted a simple analysis of a spring–slider block model with one degree of freedom assuming a constant static friction coefficient μ s (= 0.8) and a constant kinetic friction coefficient μ k in Appendix 1 (μ s was assumed to drop instantly to μ k upon the initiation of slip). The overshooting of the shear stress to a negative value begins to occur when μ k is less than 0.4 and the overall stick–slip behaviors in Fig. 4c are similar to such a behavior. Thus, μ s must have dropped to slightly less than half of μ s in violent stick–slip events in our experiments. Oscillatory slip with Coulomb damping begins to occur for μ k < 0.8/3, but such slip oscillations did not occur in our experiments.

The stick–slip amplitude appears to increase with the increasing loading rate from 1 to 100 mm/s, as seen from the results in Fig. 4. This is an opposite trend from that recognized in previous experiments (e.g., Teufel and Logan 1978, Fig. 5). In our experiments, however, the same specimens were used repeatedly, and damage accumulated on the sliding surface with the increasing number of experiments (Fig. 5a, c). Gouge was removed after each run, but the amount of generated gouge during each run was different from one run to another. Thus, the effects of loading rate and the damage/gouge accumulation cannot be separated in our experiments. The conspicuous abrasive grooves in Fig. 5 are similar to the wear grooves associated with stick–slip, described in Engelder (1974). He reported that the grooves were carrot shaped, and their lengths rarely exceeded the amount of slip during stick–slip, but the grooves were much longer than the amount of abrupt slip in our experiments. The wear grooves will be described in more detail elsewhere, along with the partition of frictional work in the gouge generation.

The observed stick–slip behaviors are complex, and we now consider how the friction apparatus behaved during stick–slip. The velocity fluctuated during and following slip events (Fig. 6b, d, f), and small oscillatory fault motion occurred during the loading or the so-called stick periods of stick–slip events (Fig. 7). Initially, we interpreted the decaying oscillatory motion during the stick periods as derived from oscillatory fault motion due to the oscillatory movement of the very heavy shaking table with low stiffness and huge mass (M st = 1.8 × 105 kg). However, Nick Beeler (personal communication) pointed out that such a Coulomb damping could not occur unless a shear stress dropped to the negative side by a large amount and suggested that the oscillations in the displacement records might have come from vibration of the sensor holder. We measured the characteristic frequencies of the target bar of the displacement transducers and confirmed that the decaying oscillations during the stick-periods in Fig. 8 are due primarily to the oscillations of the target bar, although the oscillation in the X direction (or sliding direction) is more complex than the simple oscillation of the target bar (Appendix 2).

5.2 Behavior of the friction apparatus during stick–slip

Measuring only relative displacement between the two specimens is not enough to understand the behaviors of both stationary side with upper specimen and the shaking table with lower specimen. Thus, we refer to a supplementary experiment that measured the relative displacement d at a different position with reduced vibration problem of the target bar, a displacement of the shaking table l, and the accelerations of the upper and lower specimens, a 1 and a 2, with two accelerometers (Fig. 12a; LB01-127, slip rate v = 0.1 mm/s, normal stress σ n = 1.3 MPa; to be reported elsewhere by Y. Urata and others). Table 3 of Fukuyama et al. (2014) gave the history of experiments with the specimens. The laser–displacement transducer was set to a wooden bar that was fixed to the lower moving specimen, and its target plate was glued to the middle part of the upper stationary specimen (see Fig. 12a for their positions). Integrations of a 1 and a 2 twice yield displacements of the upper and lower blocks u 1 and u 2, respectively. An inset diagram in Fig. 12b exhibits seven stick–slip events starting from 299 s after the onset of experiment (time = 0 corresponds to 299 s in the diagram), with vertical axis showing shear force F (black curve), relative displacement u 2 − u 1 (pink curve), and displacement of the shaking table l (green curve). The displacement u 2 − u 1 is the same as the displacement d = d 2 − d 1 as measured by a laser-displacement transducer in the X direction (Figs. 2, 3b), but we use different symbols because u 1 and u 2 were measured differently. Figure 12b shows temporal changes in F, d, l, –u 1, u 2, and u 2 − u 1 with different colors as shown in the diagram, for the sixth stick–slip event marked with a dashed rectangle in the inset diagram. Note that (u 2 − u 1) shown by a pink curve coincides with d in orange curve, but u 1 and u 2 in red and blue curves were plotted until the numerical integration of a 1 and a 2 was properly done (the numerical integration error accumulated, and the low-frequency response of the accelerometers was not sufficient to determine −u 1 and u 2 beyond those plotted in Fig. 12b).
Fig. 12

a Configuration of sensors during a supplementary experiment LB01-127 at a slip rate of 0.1 mm/s and a normal stress of 1.3 MPa. The position of the laser-displacement transducer was moved to the upper right side as shown by green arrow, two accelerometers were placed on the upper and lower specimens (a 1 and a 2), and the displacement of the shaking table with respect to the ground (l) was monitored. b exhibits changes in shear force F (black), fault displacement d as measured with the laser-displacement transducer (orange), displacement of shaking table l (green), displacements of the upper and lower specimens, u 1 and u 2 (red and blue), and the relative displacement (u 2 − u 1), plotted against time during a stick–slip event. The inset diagram shows seven events in a similar diagram (time t = 0 corresponds to 299 s from the start of the experiment; a dashed rectangle indicates the event in the main diagram). u 1 and u 2 were determined by double integrations of a 1 and a 2, respectively

Shear force F began to drop abruptly at time t of 16.395 s and reached a minimum value in 15 ms as shown by two dashed black lines in Fig. 12b. This time interval is plotted as the stick–slip rise time in Fig. 10b. The movement of the upper specimen stopped in 11.8 ms after the onset of shear-force drop (red curve), after which −u 1 decreased by 0.033 mm when F reached minimum (u 1 is defined positive leftward, and a decrease in (−u 1) corresponds to the movement of the upper block in the loading direction). During the same period, the displacement of the lower specimen u 2 increased by 0.037 mm (blue curve), slightly larger than the drop in (−u 1), and the relative displacement (u 2 − u 1) slightly increased as shown by the pink curve. However, this much of difference between −u 1 and u 2 can be due to the cumulative integration errors of a 1 and a 2. At about the same time, fault displacement d stopped increasing (orange curve) at around 11.8 ms, but it is unclear where exactly the fault motion stopped due to the oscillation in the d record (the oscillation was reduced with the new target plate, but was not eliminated completely). Thus, the time for the complete stop of fault motion could not be determined accurately from the current data. However, the movement of the upper block was reversed sharply at 11.8 ms from the onset of shear-force drop and after this point, the upper and lower specimens moved in the same direction by almost the same amounts as shown by −u 1 and u 2 curves. We thus consider that the 11.8 ms is the most likely time for the stop of the fault motion. Our stiffness data in Fig. 10 can be improved by conducting similar experiments as those shown in Fig. 12.

An interesting result is that a rapid movement of the shaking table started in about 12 ms after the onset of shear-force drop (green curve in Fig. 12b) and increased for 50–70 ms. The onset and stop of this rapid movement of the shaking table could not be determined clearly, but the displacement during or following an abrupt slip is seen as small steps in l–t record (green curve in the inset diagram of Fig. 12b). This displacement of the shaking table, which is in the loading direction, increased the shear force because the fault was already locked. This process corresponds to an increase in the shear force F from J to K in Fig. 8a, b. There are oscillations in l causing oscillations in F in Fig. 12b, and similar oscillations in F can be recognized in Fig. 8b as well.

The result in Fig. 12b gives an insight on the cause of the bimodal distribution of the stick–slip rise time t r in Figs. 10b, 11b and e. We determined the stop of abrupt slip during stick–slip from the point of minimum shear force F or minimum shear stress τ (e.g., dashed vertical line on the right side after 15 ms since the onset of slip in Fig. 12b). However, the fault motion is likely to have stopped after 11.8 ms from −u 1 record in this case (red vertical dashed line), as discussed above. Notable oscillation in F is overlapped on the F versus time record, and this oscillation probably caused the minimum shear force slightly after the stop of fault motion. There are 14 oscillations in a time interval of 90 ms after 16.41 s (black curve in Fig. 12b), and this gives an average duration of 6.4 ms for one oscillation. This is consistent with the time interval of 7 ms (= 24–17 ms) between the two peaks of t r in Fig. 10b, strongly suggesting that large values of t r were due to the effect of oscillation in F. A similar situation is recognized in an example shown in Fig. 7a. Shear force F or shear stress τ reached local minimums at J′ and M′, but the real minimums of F and τ were achieved at J and M which were taken as the stops of abrupt slip. In view of the results in Fig. 12b, however, J′ and M′ are probably close to the stop of fault motion. Thus, the data on t r in Figs. 10b, 11b and e are not reliable, and t r should be determined based on the improved measurements of fault displacement d and on the measurements of acceleration −u 1 of the stationary block in the future. The displacement d, used to determine Δd in Fig. 10a, remains about the same after 11.8 ms since the onset of slip, although d oscillates for several tens of ms (the orange curve in Fig. 12b). However, ΔF would have been overestimated slightly by taking the minimum point of F as the stop of fault motion, owing to the overlapped oscillation in F, and hence the stiffness k (= ΔF/Δd) determined from the data in Fig. 10a might have been overestimated slightly as well.

The supplementary experimental data in Fig. 12 clearly demonstrated that the behaviors of different parts of the apparatus behaved differently, and we now consider the apparatus behaviors in more detail. The mass is distributed in the stationary sides of the apparatus (parts 2–4, 7, 12, and 13 in Fig. 1), and we estimate an effective mass of the stationary side (M eff) following the procedures by Shimamoto et al. (1980, Eq. (20)):
$$ M^{\text{eff}} = \sum\limits_{i = 1}^{n} {\left( {\frac{{m_{i} }}{3}} \right)} \left( {\frac{{k_{m1} }}{{k_{i} }}} \right)^{2} + \sum\limits_{i = 2}^{n} {m_{j} } \left( {\frac{{k_{m1} }}{{k^{i - 1} }}} \right)\left( {\frac{{k_{m1} }}{{k^{i} }}} \right) $$
(3)
where the number of parts n is 8. We renumbered those parts and gave stiffness k i and mass m i of part i in Table 1, and the stiffness values give the bulk stiffness of the stationary side k m1 of 0.159 GN/m. Shortening or elongation of part i is given by (k m1/k i )d 1 assuming uniform force distribution, where d 1 is the displacement of the stationary side (Fig. 3b). Then the effective mass of part i during its dynamic deformation is given by (m i /3)(k m1/k i )2 (the first term in Eq. (3); Table 1, sixth column). We did not include the dynamic deformation of the upper specimen, and its stiffness is set to infinite in Table 1. On the other hand, displacement of each part has to be evaluated to estimate an effective mass of part i during its rigid-body transformation. The displacement at the bottom of the reaction force base is set to zero, and the displacement at the right end of part i is given by a sum of shortening of parts 1 to i (footnote of Table 1). Then the effective mass of the rigid-body transformation is given by the second term in Eq. (3) (Table 1, the seventh column in Table 1; part 1 is fixed, and its effective mass is zero). Note also that a displacement of each part reduces, and its effective mass becomes smaller than the real mass toward the fixed end. Thus, the total effective mass of the stationary side M eff becomes 1,689 kg if a uniform force distribution is assumed. The rise time of stick–slip of the stationary side (t m1 r ) is given by
$$ t^{r}_{m1} = \pi \left( {M^{\text{eff}} /k_{ml} } \right)^{ 1/ 2} $$
(4)
if constant static and kinetic friction coefficients, μ s and μ k , are assumed and if the friction coefficient μ is assumed to drop instantly from μ s to μ k upon the onset of slip [see Eq. (5) in Appendix 1]. Using Eq. (4), the above M eff and k m1 values give 10.2 ms for the rise time, and this is in reasonable agreement with the duration of movement of the upper specimen (11.8 ms; see red curve in Fig. 12b). The rise time of abrupt slip becomes longer when μ does not drop instantly to μ k as in the cases of real faults (e.g., Dieterich 1978), but simple analyses with constant μ s and μ k are useful to consider the overall system behaviors as first approximations.

A similar analysis with a mass of the shaking table (M st = 1.8 × 105 kg) and a stiffness of the lower part of the system (\( k_{{m2^{{\prime }} }} = k_{\text{st}} k_{m2} /(k_{\text{st}} + k_{m2} ) \) = 4.16 × 108 N/m, see Sect. 4) gives the rise time of 65 ms for the motion of the shaking table using Eq. (4). The displacement record of the shaking table indicates that the shaking table moved for 40–50 ms (green curve in Fig. 12b) which is of the same order as those estimates. Those calculations and the result in Fig. 12b raise an important question on the meaning of the data on ΔF/Δd in Fig. 10a. Our interpretations in Sect. 4 were that the slope of ΔF versus Δd relationship gives the stiffness of the whole system k and that this k and k m1 values, used above, give the stiffness of 4.16 × 108 N/m (555 MPa/m) for the lower part (k m2 and k st connected in series; Fig. 3b). However, if the shaking table did not move much before the fault motion stopped at around the minimum shear force (Fig. 12b), the stiffness given by ΔF/Δd does not include the stiffness of the shaking table k st (Fig. 3b). Then the stiffness k m2 (4.16 × 108 N/m) is more likely to give a stiffness of k m2. The mass of the lower specimen (1.6 × 103 kg) and this stiffness give a rise time of 6 ms. The displacement of the lower specimen u 2 exhibits a small peak at 4.4 ms after the onset of shear-force drop (blue curve and vertical dashed blue line in Fig. 12b). This is fairly close to the above rise time and probably the frame and holders of the lower specimen reacted immediately following the onset of slip. Subsequent displacement of the lower specimen may be due to the elastic deformation of the part of the shaking table and the displacement of the shaking table itself. A complex shape of u 2 record (blue curve in Fig. 12b) should reflect a complex behavior of the loading side with the shaking table and actuators, and should be analyzed in the future, by determining the stiffness of mass of each part.

The overall shape of the shear force F versus time t curve from a period of 16.41–16.5 s is similar to the shape of shaking-table displacement l versus t curve in Fig. 12b. This is natural if the fault is locked at around t = 16.41 s (vertical dashed red line in Fig. 12b) and the amount of displacement and an increase in displacement give a stiffness of about 1.4 × 108 N/s. This is fairly close to the stiffness (1.15 × 108 N/m) determined from the slope of ΔF–Δd line in Fig. 10a, and we conclude that the rapid increase in F following an abrupt slip (e.g., J–K in Fig. 8a, b) is due primarily to the delayed movement of the shaking table. The oscillatory changes in F have frequency of about 150 Hz (14 oscillations in 90 ms) and can be correlated with the oscillations in l although the latter appears to be more complex (Fig. 12b). We have not identified the source(s) of the oscillations yet, but any changes in l can cause changes in F when the fault is locked.

5.3 A future task for measuring friction along a fault during stick–slip

The new NIED biaxial apparatus has a merit of producing high slip rates and a large displacement on a pair of large-scale specimens by using the shaking table as the loading device, allowing us to observe dynamic rupture propagation and even to produce small-scale ruptures confined within the fault as demonstrated by Fukuyama et al. (2014). However, in order to study the evolution of friction during dynamic rupture propagation, it is essential to measure the shear stress directly along the sliding surface as conducted by Dieterich (1981b), Okubo and Dieterich (1981, 1984), Lockner and Okubo (1983), Ohnaka et al. (1987), and Beeler et al. (2012). The shear force gauge between the reaction force bar and the upper specimen (12 in Fig. 1c, FG in Fig. 3b) cannot separate the axial forces due to the friction along the sliding surface and dynamic forces to accelerate or decelerate machine elements and the upper specimen. The situation is similar to a spring–slider block system in Fig. 13a. The shear stress as calculated from the restoring force in the spring divided by the fault area is used to determine the shear stress/normal stress ratio τ/σ in Fig. 13 which varies sinusoidally, and yet the real friction along the fault during slip is constant with μ k. The situation is exactly the same as calculating the friction coefficient μ from the axial force records such as those in Fig. 4.
Fig. 13

Coulomb damping of the spring–slider block system shown in a with a stiffness K of 1.59 × 108 N/m and mass M of 1.69 × 103 kg, using their values of the stationary side in Table 1. The static friction coefficient μ s of 0.8 was assumed to solve changes in shear stress/normal stress τ/σ for a kinetic friction coefficient μ k (assumed constant) of b 0.5, c 0.3, d 0.2 and e 0.05

There are two ways to determine the friction along the simulated faults during stick–slip. One is to measure the friction directly, for instance, by using strain gauges bonded on the specimens. The other way is to restore frictional properties from observed stick–slip behaviors by modeling of the system behavior with assumed form of friction law(s). Slight deviations in behaviors from the sinusoidal behaviors for constant μ s and μ k (Fig. 13) are the source of information to determine the frictional properties, in the case of a simple spring–slider block system with one degree of freedom in Fig. 13a. It should be kept in mind that a real friction apparatus is more complex and the frictional properties cannot be restored unless the apparatus behaviors are understood properly, and this is the main reason why we conducted the present study. The behavior of the stationary side may be close to that of a spring–slider block system if the kinetic friction coefficient is constant, as discussed in the previous subsection. However, if friction depends on slip and slip-rate as in the case of rate-and-state friction (e.g., Dieterich 1979, 1981a), then the behavior of the loading side affects the fault motion, and the loading side cannot be separated from the analysis. The behavior of this side is more complex because of the huge mass of the shaking table as revealed by the slip histories of the lower moving specimen and the shaking table (Fig. 12b). We conventionally separated two springs k m2 and k st for this side in Fig. 3b, but we could not fully model the behavior of the moving side yet in this paper. Full understanding of the elastic and inertial properties of the loading side will be a key to restore the frictional properties accurately from the observed stick–slip.

6 Conclusions

This paper reports the stiffness of the first generation of the large-scale biaxial friction apparatus installed to NIED in 2012, based on the stick–slip behaviors of Indian gabbro. We conducted seven experiments at loading rates of 1.0, 10, and 100 mm/s and at normal stresses of 0.66–0.67 and 1.31–1.32 MPa, using the same set of specimens (Fig. 5). Stick–slip occurred in all tests, and some violent events were accompanied by overshooting of the shear stress to negative values. The friction coefficient at the onset of abrupt slip was about 0.8 near the peak friction and it decreased toward a steady-state friction coefficient of about 0.6 (the same level as the Byerlee friction) in about two-thirds of the runs. The stiffness of the apparatus was estimated at 1.15 × 108 N/m (153 MPa/m) from the force drop and the amount of slip during stick–slip events (Fig. 10a). As recognized for other apparatuses, abrupt slip during stick–slip occurred in nearly a constant period of time of about 18 ms (Fig. 10b), resulting in a linear relationship between an average slip rate during the abrupt slip and a shear force or shear stress drop (Fig. 11). The determination of the stick–slip rise time should be improved based on refined measurements of fault displacements and accelerations of the specimens. We used the acceleration data of the upper and lower specimens as well as the displacement of the shaking table obtained from a supplementary experiment (Fukuyama et al. 2014). The result indicates that the stationary side of the apparatus and parts of the moving side fixed to the shaking table dynamically moved in about 15 ms during stick–slip, and the above stiffness value is likely to give a combined stiffness of the stationary side and the holding parts of the moving specimen. The movement of the shaking table is delayed and is much slower that the other parts close to the specimens, and it caused a rapid increase in the shear stress following an abrupt slip. Direct measurement of shear stress along the simulated fault is a task left for the future to study the changes in friction during stick–slip.

Notes

Acknowledgments

This research was supported by the NIED research project titled “Development of the Earthquake Activity Monitoring and Forecasting,” the JSPS KAKENHI Grant No. 23340131, and by the State Key Laboratory of Earthquake Dynamics, Institute of Geology, CEA (LED2014A06). We sincerely thank two reviewers (Nick Beeler and Shengli Ma) for thorough and constructive comments. In particular, Nick Beeler pointed out our misinterpretation on the decaying oscillation in displacement records following abrupt slip events which dramatically improved our paper. We also thank Tadashi Mikoshiba, Chikahiro Minowa, Hironori Kawakata, Nana Yoshimitsu, Makoto Sato, Toshiyuki Kanesawa, Yuji Kurokawa, Toya Sato, and Yukio Sugiyama for helping us at various stages of the experiments. The present study was partly supported by the NIED research project titled “Development of the Earthquake Activity Monitoring and Forecasting.” and by the State Key Laboratory of Earthquake Dynamics, Institute of Geology, China Earthquake Administration (LED2014A06).

References

  1. Beeler N, Kilgore B, McGarr A, Fletcher J, Evans J, Baker SR (2012) Observed source parameters for dynamic rupture with non-uniform initial stress and relatively high fracture energy. J Struct Geol 38:77–89CrossRefGoogle Scholar
  2. Byerlee JD (1978) Friction of rocks. Pure Appl Geophys 116:615–626CrossRefGoogle Scholar
  3. Di Toro G, Han R, Hirose T, De Paola N, Nielsen S, Mizoguchi K, Ferri F, Cocco M, Shimamoto T (2011) Fault lubrication during earthquakes. Nature 471:494–498. doi: 10.1038/nature09838 CrossRefGoogle Scholar
  4. Dieterich JH (1972) Time-dependent friction in rocks. J Geophys Res 77:3690–3697CrossRefGoogle Scholar
  5. Dieterich JH (1978) Time-dependent friction and the mechanics of stick-slip. Pure appl Geophys 116:790–806CrossRefGoogle Scholar
  6. Dieterich JH (1979) Modeling of rock friction, 1. Experimental results and constitutive equations. J Geophys Res 84:2161–2168CrossRefGoogle Scholar
  7. Dieterich JH (1981a) Constitutive properties of faults with simulated gouge. Geophysical monograph, vol 24. American Geophysical Union, Washington DC, pp 102–120Google Scholar
  8. Dieterich JH (1981b) Potential for geophysical experiments in large scale tests. Geophys Res Lett 8:653–656CrossRefGoogle Scholar
  9. Engelder JT (1974) Microscopic wear grooves on slickensides: indicators of paleoseismicity. J Geophys Res 79:4387–4392CrossRefGoogle Scholar
  10. Fukuyama E, Mizoguchi K, Yamashita F, Togo T, Kawakata H, Yoshimitsu N, Shimamoto T, Mikoshiba T (2012). Large-scale biaxial friction experiments with an assistance of the NIED shaking table. American Geophysical Union, Fall Annual Meeting, San Francisco, S12A-04Google Scholar
  11. Fukuyama E, Mizoguchi K, Yamashita F, Togo T, Kawakata H, Yoshimitsu N, Shimamoto T, Mikoshiba T, Minowa C, Kanezawa T, Kurokawa H, Sato T (2014) Large-scale biaxial friction experiments using a NIED shaking table, Report of the National Research Institute for Earth Science and Disaster Prevention, No. 81, pp 1–21Google Scholar
  12. Hirose T, Shimamoto T (2005) Growth of molten zone as a mechanism of slip weakening of simulated faults in gabbro during frictional melting. J Geophys Res 110:B05202. doi: 10.1029/2004JB003207 Google Scholar
  13. Ide S, Baltay A, Beroza G (2011) Shallow dynamic overshoot and energetic deep rupture in the 2011 M W 9.0 Tohoku-oki earthquake. Science 332:1426–1429CrossRefGoogle Scholar
  14. Jaeger JC, Cook NGW, Zimmerman RW (2007) Fundamentals of rock mechanics, 4th edn. Blackwell, OxfordGoogle Scholar
  15. Johnson TL, Scholz CH (1976) Dynamic properties of stick–slip friction of rock. J Geophys Res 81:881–888CrossRefGoogle Scholar
  16. Kawamoto E, Shimamoto T (1998) The strength profile for bimineralic shear zones: an insight from high-temperature shearing experiments on calcite-halite mixtures. Tectonophysics 295:1–14CrossRefGoogle Scholar
  17. Lockner DA, Okubo PG (1983) Measurements of frictional heating in granite. J Geophys Res 88:4313–4320CrossRefGoogle Scholar
  18. Ma S, Ma J (2003) Recent progress in studies of experimental rock mechanics and Tectonophysics in China. Acta Seismol Sin 16:561–567CrossRefGoogle Scholar
  19. Ma S, Shimamoto T, Yao L, Togo T, Kitajima H (2014) A rotary-shear low to high-velocity friction apparatus in Beijing to study rock friction at plate to seismic slip rates. Earthq Sci 27:469–497. doi: 10.1007/s11589-014-0097-5 CrossRefGoogle Scholar
  20. Marone C (1998) Laboratory-derived friction laws and their application to seismic faulting. Annu Rev Earth Planet Sci 26:643–696CrossRefGoogle Scholar
  21. Marone C, Kilgore B (1993) Scaling of the critical slip distance for seismic faulting with shear strain in fault zones. Nature 362:619–621CrossRefGoogle Scholar
  22. Minowa C, Ogawa N, Ohtani K (1989). The report on renewal of large-scale shaking table. Technical Note of the National Research Center for Disaster Prevention, 140:1–63 (in Japanese)Google Scholar
  23. National Research Center for Disaster Prevention (1983). The short history of the large-scale shaking table in Tsukuba. Technical Note of the National Research Center for Disaster Prevention, 38:1–273 (in Japanese)Google Scholar
  24. Nielsen S, Taddeucci J, Vinciguerra S (2010) Experimental observation of stick-slip instability fronts. Geophys J Int 180:697–702CrossRefGoogle Scholar
  25. Niemeijer A, Marone C, Elsworth D (2010) Frictional strength and strain weakening in simulated fault gouge: competition between geometrical weakening and chemical strengthening. J Geophys Res 115:B10207. doi: 10.1029/2009JB000838 CrossRefGoogle Scholar
  26. Noda H, Shimamoto T (2009) Constitutive properties of clayey fault gouge from the Hanaore fault zone. J Geophys Res 114(B4409):2009. doi: 10.1029/2008JB005683 Google Scholar
  27. Noda H, Shimamoto T (2010) A rate- and state-dependent ductile flow law of polycrystalline halite under large shear and implications for transition to brittle deformation. Geophys Res Lett 37:L09310. doi: 10.1029/2010GL042512 CrossRefGoogle Scholar
  28. Ohnaka M (1973) Experimental studies of stick-slip and their application to the earthquake source mechanism. J Phys Earth 21:285–303CrossRefGoogle Scholar
  29. Ohnaka M (1978) Application of some dynamic properties of stick-slip to earthquakes. Geophys J R Astron Soc 53:311–318CrossRefGoogle Scholar
  30. Ohnaka M (2013) Physics of rock failure and earthquakes. Cambridge University Press, CambridgeCrossRefGoogle Scholar
  31. Ohnaka M, Kuwahara Y, Yamamoto K (1987) Constitutive relations between dynamic physical parameters near a tip of the propagating slip zone during stick-slip shear failure. Tectonophysics 144:109–125CrossRefGoogle Scholar
  32. Okubo PG, Dieterich JH (1981) Fracture energy of stick-slip events in a large scale biaxial experiment. Geophys Res Lett 8:887–890CrossRefGoogle Scholar
  33. Okubo PG, Dieterich JH (1984) Effects of physical fault properties on frictional instabilities produced on simulated faults. J Geophys Res 89:5817–5827CrossRefGoogle Scholar
  34. Ruina AL (1983) Slip instability and state variable friction laws. J Geophys Res 88:10359–10370CrossRefGoogle Scholar
  35. Shimamoto T, Handin JW, Logan JM (1980) Specimen-apparatus interaction during stick-slip in a triaxial compression machine: a decoupled two-degree of freedom model. Tectonophysics 67:175–205CrossRefGoogle Scholar
  36. Sibson RH (2013) Stress switching in subduction forearcs: implications for overpressure containment and strength cycling on megathrusts. Tectonophysics 600:142–152CrossRefGoogle Scholar
  37. Steidel RF Jr (1979) An introduction to mechanical vibrations, 2nd edn. Wiley, New YorkGoogle Scholar
  38. Teufel LW, Logan JM (1978) Effect of displacement rate on the real area of contact and temperatures generated during frictional sliding of Tennessee sandstone. Pure appl Geophys 116:840–965CrossRefGoogle Scholar
  39. Tse ST, Rice JR (1986) Crustal earthquake instability in relation to the depth variation of frictional properties. J Geophys Res 91:9452–9472CrossRefGoogle Scholar
  40. Xia K, Rosakis A, Kanamori H (2004) Laboratory earthquakes; the sub-Raleigh-to-supershear rupture transition. Science 303:1859–1861CrossRefGoogle Scholar
  41. Jaeger JC, Cook NGW (1979) Fundamentals of rock mechanics, 3rd edn. Chapman and Hall, LondonGoogle Scholar
  42. Yamashita F, Fukuyama E, Mizoguchi K, Togo T, Mikoshiba T, Sato M, Minowa C (2011) Quasi-static control performance of the large-scale shaking table at National Research Institute for Earth Science and Disaster Prevention (in Japanese with English abstract), vol 79. Report of the National Research Institute for Earth Science and Disaster Prevention, pp 9–23. http://dil-opac.bosai.go.jp/publication/nied_report/PDF/79/79-2yamashita.pdf)
  43. Yao L, Shimamoto T, Ma S, Han R, Mizoguchi K (2013) Rapid postseismic strength recovery of Pingxi fault gouge from the Longmenshan fault system: experiments and implications for the mechanisms of high-velocity weakening of faults. J Geophys Res 118:1–17. doi: 10.1002/jgrb.50308 Google Scholar

Copyright information

© The Author(s) 2015

Open AccessThis article is distributed under the terms of the Creative Commons Attribution License which permits any use, distribution, and reproduction in any medium, provided the original author(s) and the source are credited.

Authors and Affiliations

  • Tetsuhiro Togo
    • 1
    • 2
    Email author
  • Toshihiko Shimamoto
    • 1
  • Futoshi Yamashita
    • 3
  • Eiichi Fukuyama
    • 3
  • Kazuo Mizoguchi
    • 4
  • Yumi Urata
    • 3
  1. 1.State Key Laboratory of Earthquake Dynamics, Institute of GeologyChina Earthquake AdministrationBeijingChina
  2. 2.Geological Survey of JapanTsukubaJapan
  3. 3.National Research Institute for Earth Science and Disaster Prevention (NIED)TsukubaJapan
  4. 4.Central Research Institute of Electric Power IndustryChibaJapan

Personalised recommendations