1 Introduction

The scattering of elastic waves by the underground structure and the phenomenon of the dynamic stress concentration is an interesting and important topic in many fields, e.g., in earthquake engineering, non-destructive detection, etc. In general,the solution methods can be divided into the analytical method and numerical method. The analytical methods include the wave function expansion (Lee and Trifunac 1979; Liang et al. 2010; Li et al. 2009), earthquake coefficient method and response displacement method, etc. The numerical methods include the finite element method (Yang and Liu 1994), boundary element method (boundary integral equation method) (Du et al. 1993; Stamos and Beskos 1996; Liang et al. 2013; Chen et al. 2011) and the hybrid method (Datta et al. 1984), etc.

Note that above studies are mainly restricted to the full-space or half-space model at present. However, in practical engineering, many tunnels or underground pipes are built on sloping topography or cliffs, and then wedge space model would be more appropriate for preliminary quantitative analysis in such sites. Compared with the half-space model, more difficulties will arise for exactly satisfying the free boundary conditions of the wedge space. Achenbach (Achenbach 1970) studied the transient wave propagation problem in wedge space, considering spatially uniform shear tractions applied to one or both faces of the wedge. Knopoff (1969), Budaev and Bogy (1995) and Gautesen (2002) have investigated the wave reflection and transmission coefficients of the free field in elastic wedge space by numerical or experimental method. Moreover, Li and Gong studied the reflection and transmission of obliquely incident Rayleigh wave in two adjacent rectangular space (Li and Gong 1998).

As for the wave scattered by obstacle in wedge space, available results are rarely seen due to the complicated characteristics of wave propagation and scattering. Lee and Sherif studied the scattering of SH-waves by a canyon in wedge-shape space (Lee and Sherif 1996); Shi et al. studied the scattering solutions with a fixed circular inclusion or a hole in Cartesian space by the method of complex variable function (Shi et al. 2006, 2007). However, up to date, there is no results published for the wave scattering around a tunnel in wedge space of arbitrary angle, only Liu et al. (2009) presented some results around a cavity in wedge space. Zhang et al. (2013) studied the scattering of SH-wave by circular cavity in a right-angle plane.

This paper aims to study the scattering of SH-waves by a lined tunnel in elastic wedge space of any angle by the indirect boundary element method. It is illustrated that this method has several advantages such as reducing dimensions of problems, automatic satisfaction of radiation condition, and high calculation precision. Moreover, in this method, the virtual loads can directly act on the boundary surface, which can be recognized as a direct implementation of the Huygens’ principle.

This paper will be arranged as follows. Firstly, the numerical procedure for IBEM solution to SH-waves diffraction in wedge space is presented. Then, the accuracy of this method is verified by the comparison between the degenerated solutions and available solutions. Finally, the effects of key parameters, such as the wedge angle, excitation frequency and the incident angle on dynamic response of tunnel are investigated in detail through numerical examples, and some important conclusions have been obtained.

2 Model

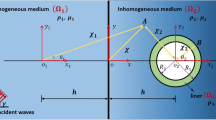
Figure 1 shows a lined tunnel of infinite length and constant cross-section located at arbitrary position of the wedge space. Define the vertex of the wedge as o, the angle between the inclined and horizontal surface as νπ, the geometric center of the lined tunnel as o′. H and D are the vertically and horizontal distance between o and o′, respectively. Assume that the material in the wedge space and lined tunnel is homogeneous and linearly elastic. Define the outer and inner surface of tunnel as Γ 1 and Γ 2, the region of the wedge space and tunnel as D 1 and D 2, the ground and wedge surface as S and B, respectively. The shear wave velocity of the wedge space is defined as \( \beta = \sqrt {\mu /\rho } \), here μ and ρ are the shear modulus and the mass density, respectively. Accordingly, β 1, μ 1, ρ 1 are corresponding parameters in the tunnel lining. Considering plane SH-waves incidence with angle α to the horizontal surface, the two dimensional anti-plane scattering problem needs to be solved. For simplicity, only the cylindrical tunnel is considered in this paper. Note that the tunnel of arbitrary shape can be treated by the IBEM.

Fig. 1
figure 1

Model for calculation

Full size image

3 Method and solution

The wave scattering problem can be solved by IBEM (Sanchez-Sesma and Campillo 1991) in the following way: based on the theory of single-layer potential, the scattered field can be formed by applying virtual uniform loads on the surface of the scatterers. Then the density of virtual loads can be solved by boundary conditions. The total wave field can be obtained by the superstition of free-wave field and scattered-wave field.

The displacement wave field u (t) in wedge-shaped space using the polar coordinate system o−θ satisfies the wave equation as follows:

$$ \frac{{\partial^{2} u^{(t)} }}{{\partial r^{2} }} + \frac{1}{r}\frac{{\partial u^{(t)} }}{\partial r} + \frac{1}{{r^{2} }}\frac{{\partial^{2} u^{(t)} }}{{\partial \theta^{2} }} = \frac{1}{{\beta^{2} }}\frac{{\partial^{2} u^{(t)} }}{{\partial t^{2} }} $$
(1)

The displacement at any location of the elastic solid, subject to a time harmonic excitation, can be written by the Somigliana integral representation:

$$ cu(\xi ) = \int\limits_{V} {G(y,\xi )f(y){\text{d}}V} + \int\limits_{S} {\left[ {G(x,\xi )t(x) - T(x,\xi )u(x)} \right]{\text{d}}S} $$
(2)

In which, u(x) and t(x) are the z-direction component of displacement and stress at arbitrary point x, respectively. f(y) is the body force, G(x,ξ) and T(x,ξ) are the corresponding displacement and stress Green’s functions, respectively.

$$ u = \int\limits_{V} {G (x ,\xi )f (\xi ) {\text{d}}V} + \int\limits_{S} {G(x,\xi )\phi (\xi ) {\text{d}}S}. $$
(3)

Similarly, the stresses can be derived according to Hooke’s law:

$$ t = \int\limits_{V} {T(x,\xi )f (\xi ) {\text{d}}V} + \int\limits_{S} {T(x,\xi )\phi (\xi ) {\text{d}}S} .$$
(4)

Equations (3) and (4) form the basis of the boundary element formulation. Numerical computation requires a discretization of the boundary surface.

3.1 Wave field construction

According to linear elastic theory, the total wave field can be decomposed into the free field and the scattered-wave field. Herein the free field is the solution of SH-waves in elastic wedge space without the lined tunnel. The scattered-wave field, based on the theory of single-layer potential, can be constructed by applying virtual uniform loads on the surface of lined tunnel and near ground surface. Then, the free field and the scattered-wave field add up to the total wave field:

$$ u_{{}}^{(t)} = u_{{}}^{(f)} + u_{{}}^{(s)} $$
(5)

3.1.1 Free field

Sanchez presented the expression for the displacement generated by plane SH-waves incidence in wedge space with wedge angle νπ (Sanchez-Sesma 1985). The resulting formulation is:

$$ u^{(f)} = u_{0} \frac{2}{\nu }\sum\limits_{n = 0}^{\infty } {\varepsilon_{n} } e^{{ - \frac{{{\text{i}}n\pi }}{2\nu }}} J_{n/\nu } (kr)\cos \frac{n\alpha }{\nu }\cos \frac{n\theta }{\nu } $$
(6)

where u 0 is the displacement amplitude, ɛ n is the Neumann factor (n = 0, ɛ n  = 1; n ≥ 1, ɛ n  = 2), α is the incident angle with the horizontal direction, and J n/ν is the Bessel function of the first kind of order n/ν.

In the polar coordinate system o–θ and the Cartesian coordinate system x–y, the stress function can be expressed by a simple derivation as follows:

$$ \tau_{rz} = - \frac{{2\mu u_{0} }}{\nu }\sum\limits_{n = 0}^{\infty } {\varepsilon_{n} e^{{\frac{in\pi }{2\nu }}} \left[ {kJ_{n/v + 1} (kr) - \frac{n}{r\nu }J_{n/v} (kr)} \right]} \cos \frac{\theta n}{\nu }\cos \frac{n\alpha }{\nu } $$
(7)
$$ \tau_{\theta z} = - \frac{{2\mu u_{0} }}{\nu }\sum\limits_{n = 0}^{\infty } {\varepsilon_{n} e^{{\frac{in\pi }{2\nu }}} \frac{n}{\nu r}J_{n/\nu } (kr)\sin \frac{n\theta }{\nu }\cos \frac{n\alpha }{\nu }}, $$
(8)
$$ \tau_{yz} = \tau_{rz} \sin \theta + \tau_{\theta z} \cos \theta ,$$
(9)
$$ \tau_{xz} = \tau_{rz} \cos \theta - \tau_{\theta z} \sin \theta .$$
(10)

Note that the tangential stress by the free field on the boundary can be written as:

$$ \tau_{nz}^{(f)} = \tau_{xz} \frac{\partial x}{\partial n} + \tau_{yz} \frac{\partial y}{\partial n} ,$$
(11)

where k = ω/β is the wave number of the SH-waves in wedge–shaped space (β is the shear wave velocity), and the time factor exp(iωt) has been omitted.

3.1.2 Scattered-wave field

According to the previous discussion, the diffracted field is given by Eqs. (3) and (4), which, in the absence of body forces, can be written as:

$$ u^{(s)} (x) = \int\limits_{S} {\phi (\xi )G(x,\xi ){\text{d}}S_{\xi } }, $$
(12)
$$ t^{(s)} (x) = \int\limits_{S} {\phi (\xi )T(x,\xi ){\text{d}}S_{\xi } }. $$
(13)

ϕ j denotes the densities of virtual uniform loads on the boundary. The anti-plane line source Green’s function in full-space can be expressed in the following form:

$$ G(x,\xi ) = - \frac{\text{i}}{4\mu }{\text{H}}_{0}^{(2)} (kr) ,$$
(14)
$$ T(x,\xi ) = - \frac{\text{i}}{4r}{\text{H}}_{1}^{(2)} (kr)(\gamma_{x} n_{x} + \gamma_{y} n_{y} ) ,$$
(15)

where \( r = \sqrt {(x - x_{0} )^{2} + (y - y_{0} )^{2} } \), γ x  = (x − x 0)/r, γ y  = (y − y 0)/r, (x, y) and (x 0, y 0) are the coordinate of the field point and source point, respectively. \( {\text{H}}_{n}^{(2)} (\bullet) \) is the Hankel function of the second kind of integer order n·(n x , n y ) denotes unit normal vector on boundary surface.

3.2 Boundary conditions and solution

The boundary conditions of this problem include the zero-traction condition on the surface of wedge space and inner surface of the tunnel, the continuity of displacements and stresses on the interface between the tunnel and the wedge space.

The zero-traction conditions are expressed as follows:

$$ \tau_{{\theta z,{\text{I}}}}^{(t)} = \mu \frac{{\partial u_{\text{I}}^{(t)} }}{r\partial r} = 0\quad (\theta = \pi_{{}} ) { } ,$$
(16)
$$ \tau_{{\theta z,{\text{I}}}}^{(t)} = \mu \frac{{\partial u_{\text{I}}^{(t)} }}{r\partial r} = 0\quad (\theta = \pi + \nu \pi ) ,$$
(17)
$$ \tau_{{r^{\prime}z,{\text{II}}}}^{(t)} = \mu \frac{{\partial u_{{{\rm I}{\rm I}}}^{(t)} }}{{\partial r^{\prime}}}{ = 0}\quad (on \, surface \, \varGamma_{2} ). $$
(18)

The continuity conditions of displacements and stresses can be written as:

$$ u_{\rm I}^{(f)} + u_{\rm I}^{(s)} = u_{{{\rm I}{\rm I}}}^{(s)} \quad (on \, surface \, \varGamma_{1} ), $$
(19)
$$ \tau_{\rm I}^{(f)} + \tau_{\rm I}^{(s)} = \tau_{{{\rm I}{\rm I}}}^{(s)} \quad (on \, surface \, \varGamma_{1} ). $$
(20)

According to the free boundary and continuity condition, integral equations can be expressed as:

$$ \int\limits_{S} {\phi_{{}}^{\rm I} (\xi )T_{{}}^{\rm I} (x,\xi ){\text{d}}S_{\xi } } = - t_{{}}^{(f)} (x) ,$$
(21)
$$ \int\limits_{S} {\phi_{{}}^{{{\rm I}{\rm I}}} (\xi )T_{{}}^{{{\rm I}{\rm I}}} (x,\xi ){\text{d}}S_{\xi } } = 0 ,$$
(22)
$$ \int\limits_{S} {\phi_{{}}^{\rm I} (\xi )G_{{}}^{\rm I} (x,\xi ){\text{d}}S_{\xi } } - \int\limits_{S} {\phi_{{}}^{{{\rm I}{\rm I}}} (\xi )G_{{}}^{{{\rm I}{\rm I}}} (x,\xi ){\text{d}}S_{\xi } } = - u_{\rm I}^{(f)} ,$$
(23)
$$ \int\limits_{S} {\phi_{{}}^{\rm I} (\xi )T_{{}}^{\rm I} (x,\xi ){\text{d}}S_{\xi } } - \int\limits_{S} {\phi_{{}}^{{{\rm I}{\rm I}}} (\xi )T_{{}}^{{{\rm I}{\rm I}}} (x,\xi ){\text{d}}S_{\xi } } = - t_{{}}^{(f)}.$$
(24)

It’s a singular Fredholm integral equation of the second kind for the boundary sources. We need to discretize the inner and outer surface of tunnel and the nearby wedge surface, then apply virtual uniform loads on each element. Due to the attenuation characteristics of the scattered-wave, the computational accuracy can easily reach to 10−3 as the discretization range of the surface of wedge space reaches to 8 times the wavelength near the tunnel. ϕ j (ξ) is assumed to be constant on each boundary element. Define the discretization numbers of the wedge surface, the outer and inner surface of tunnel are N 1, N 2, and N 3, respectively, then the linear Eqs. (21–24) can be rewritten as:

$$ \sum\limits_{l = 1}^{{N_{1} + N_{2} }} {\phi^{\rm I} (\xi_{l} )t^{\rm I} (x_{{n_{1} }} ,\xi_{l} )} = - t^{(f)} (x_{{n_{1} }} ),\quad n_{1} = 1,N_{1} , $$
(25)
$$ \sum\limits_{l = 1}^{{N_{2} + N_{3} }} {\phi^{{{\rm I}{\rm I}}} (\xi_{l} )t^{{{\rm I}{\rm I}}} (x_{{n_{3} }} ,\xi_{l} )} = 0,\quad n_{3} = 1,N_{3} , $$
(26)
$$ \sum\limits_{{l_{1} = 1}}^{{N_{1} + N_{2} }} {\phi^{\rm I} (\xi_{{l_{1} }} )g^{\rm I} (x_{{n_{2} }} ,\xi_{{l_{1} }} )} - \sum\limits_{{l_{2} = 1}}^{{N_{2} + N_{3} }} {\phi^{{{\rm I}{\rm I}}} (\xi_{{l_{2} }} )g^{{{\rm I}{\rm I}}} (x_{{n_{2} }} ,\xi_{{l_{2} }} )} = - u_{{}}^{(f)} ,\quad n_{2} = 1,N_{2} , $$
(27)
$$ \sum\limits_{{l_{1} = 1}}^{{N_{1} + N_{2} }} {\phi^{\rm I} (\xi_{{l_{1} }} )t^{\rm I} (x_{{n_{2} }} ,\xi_{{l_{1} }} )} - \sum\limits_{{l_{2} = 1}}^{{N_{2} + N_{3} }} {\phi^{{{\rm I}{\rm I}}} (\xi_{{l_{2} }} )t^{{{\rm I}{\rm I}}} (x_{{n_{2} }} ,\xi_{{l_{2} }} )} = - t^{(f)} ,\quad n_{2} = 1,N_{2}. $$
(28)

Namely, constructing matrix equation: [H] [ϕ] = [B]. ϕ(densities of virtual loads) can be solved by the equation, [ϕ] = [H]−1[B].

In which, dynamic influence functions can be expressed:

$$ t(x_{n} ,\xi_{l} ) = \int_{{\xi_{l} - \frac{\varDelta S}{2}}}^{{\xi_{l} + \frac{\varDelta S}{2}}} {T(x_{n} ,\xi ){\text{d}}S_{\xi } }, $$
(29)
$$ g(x_{n} ,\xi_{l} ) = \int_{{\xi_{l} - \frac{\varDelta S}{2}}}^{{\xi_{l} + \frac{\varDelta S}{2}}} {G(x_{n} ,\xi ){\text{d}}S_{\xi } }. $$
(30)

Equations (12) and (13) can be calculated directly by using two or three-point Gauss quadrature rules when \( x \ne \xi \). Analytical expressions can be obtained by the series expansion of Green’s functions when x is in the neighborhood of \( \xi \). It can be expressed as:

$$ t(x_{n} ,\xi_{n} ) = 0.5 ,$$
(31)
$$ g(x_{n} ,\xi_{n} ) = \int_{ - \varDelta s/2}^{\varDelta s/2} { - \frac{\text{i}}{4\mu }{\text{H}}_{0}^{(2)} (ks)} {\text{d}}s = - \frac{i\varDelta S}{4\mu }[1 + i\frac{2}{\pi }(1 - \gamma - \lg (\frac{k\varDelta S}{4})] ,$$
(32)

where γ is the Euler constant (0.5772), lg is the signs for logarithms, and ΔS is the length of element.

In summary, the introduction of Green’s function for full-space leads to extra discretization of wedge space surface, but has an advantage of analytically treating the singular integration on each element, which is fairly beneficial for improving the calculation accuracy. Then, the density of virtual loads on each element can be solved through the Eqs. (25)–(28). The total wave field is obtained by the superposition of free field and scattered-wave field. Besides, above calculations are performed in frequency domain, and the time domain solution can be obtained by Fourier transform.

4 Accuracy verification

Firstly, define non-dimensional frequency as the ratio of the equivalent diameter of scatterer to the wavelength of the incident waves:

$$ \eta = \frac{2a}{\lambda } = \frac{ka}{\pi } = \frac{\omega a}{\pi \beta } .$$
(33)

The degenerated solution in elastic wedge space can be calculated using this method. The result of displacement amplitudes by this method compared with the references (Lee and Sherif 1996) and (Lee and Trifunac 1979) are shown in Fig. 2. In Fig. 2(a), for the model of a canyon in wedge space, the following parameters are set: incident frequency η = 2.0 and wedge angle ν = 1/2. In Fig. 2(b), for the model of a tunnel in half-space, ρ 1/ρ = 1/3, μ 1/μ = 0.35, η = 0.5, 1. It shows that our results by IBEM are in good agreement with the analytical method (Lee and Trifunac 1979). Note that, the scattering of elastic wave by tunnel of arbitrary shape in elastic wedge space can be solved by present method.

Fig. 2
figure 2

Degenerated solutions compared with references (Lee and Trifunac 1979; Lee and Sherif 1996), a displacement amplitude around the surface of the canyon in wedge space, b displacement amplitude of the ground surface above the tunnel in half-space

Full size image

5 Numerical examples

In this part, detailed parameters analysis will be presented considering various wedge angles, the variety of tunnel stiffness, incident frequency and angle of incidence. For the rigid tunnel, the material parameters are: ρ 1/ρ = 5/4, β 1/β = 5/1. For the flexible tunnel, the material parameters are: ρ 1/ρ = 4/5, β 1/β = 1/3. The ratio of the inner and outer radius of tunnel is set to be r 1/r 2 = 10/11.

Figure 3 illustrates the surface displacement amplitudes in wedge space for different incident frequencies and angles. Set the angles of wedge to be 90°,120°,150°,180°, the incident frequencies η = 0.5, 1.0, 2.0, and the incident angles α = 0, π/6, π/3, π/2, respectively. The location of the lined tunnel is D = 2a,H = 2a (a is the inner radius of the tunnel). In the figure, the x-axis represents the ratio of the distance between the point on the ground surface and the vertex of the wedge to the inner radius of the tunnel (the negative axis represents the horizontal plane; the positive axis represents the inclined plane). The y-axis represents the displacement amplitude |u (t)|. Obviously, there is large difference between the results of half-space (v = 1) and that of the wedge space. Due to the multiple scattering and interface effect of SH-waves between the surfaces of the wedge and the tunnel, the response characteristic is more complicated and the amplification effect is more significant. As the wedge angle decreases, the displacement amplitude increases significantly. For an example, for ν = 1/2 (90° wedge space), the displacement amplitude can reach up to about 6.0 for η = 0.5 (which is about 5.0 in 120° wedge space, and about 3.7 in half-space). As the frequency increases, the displacement amplitude oscillates more quickly in space and the amplification effect appears to be more obvious, up to about 8.0 for η = 2.0 in 90° wedge space. Note that for horizontally incident waves, the max displacement response usually appears just above the tunnel.

Fig. 3
figure 3

Displacement amplitude around the surface of the tunnel in wedge space (v = 1/2, 2/3, 5/6, 1; rigid tunnel)

Full size image

Figures 4 and 5 illustrate the dynamic stress concentration factor (DSCF), defined as the ratio of the total shear stress to the stress of incident waves \( \tau_{{\theta^{\prime}Z}} /\tau_{0} \), at the inner and outer surface of the tunnel for different incident frequencies. The calculation parameters are the same as Fig. 3. It can be seen that as the wedge angle decreases, the wave energy centralization becomes more significant and the peak value of DSCF increases gradually. There is large difference between the 90° wedge space (v = 1/2) and the half-space (v = 1). For an example, for η = 0.5 and vertical incident waves, the DSCF at the outer surface can reach up to about 34.0 for ν = 1/2 (90° wedge space), but that is about 10.0 in half-space. Therefore, the phenomenon of the dynamic stress concentration near the tunnel in wedge space cannot be analyzed quantitatively using the model of a half-space. It can also be found that spatial characteristics of DSCF strongly depend on the incident frequency, and the stress oscillates more rapidly for high frequency. In addition, comparing Figs. 4 and 5, the peak of the DSCF at inner surface is a bit bigger than that at outer surface, but the spatial distribution characteristics are similar. From the application perspective, we should pay more attention to seismic design for the tunnel located at steep slope.

Fig. 4
figure 4

Dynamic stress concentration factor at the tunnel surface in wedge space (the outer surface of the tunnel) (η = 0.5, 1.0, 2.0; rigid tunnel)

Full size image
Fig. 5
figure 5

Dynamic stress concentration factor at the tunnel surface in wedge space (the inner surface of the tunnel) (η = 0.5, 1.0, 2.0; rigid tunnel)

Full size image

Figure 6 illustrates the effect of the location of the lined tunnel in wedge space on the displacement response, with incident frequency η = 0.5, wedge angle ν = 1/2, incident angle α = 0, and the buried depth of tunnel H = 2a. The horizontal distance from tunnel center to the vertex of wedge space takes: D = 2a, 5a, 10a and 30a, respectively. Obviously, when D = 2a, the wave interference effect between the tunnel and the wedge space is more significant. In general, as the distance D increases, the peak of displacement amplitude decrease gradually, which clearly indicates the great influence of vertical plane on wave scattering in a 90° wedge space.

Fig. 6
figure 6

The effect of the location of the tunnel in wedge space on the displacement response (D/a = 2.0, 5.0, 10, 30; rigid tunnel)

Full size image

Figures 7, 8 and 9 illustrate the displacement amplitude spectrum around the surface of the tunnel and the dynamic stress concentration factor (DSCF) spectrum on the surface of the tunnel to the incident SH-waves for different wedge angles. The incident frequency takes η∈(0,4.0), and observation points for displacement amplitude are located at x/a = −1, −2 (right above the tunnel), −4, and 4 on ground surface, respectively; for DSCF, the points take θ′ = 0°, 90°,180°, and 270° on the surface of the tunnel, respectively. It shows that as the wedge angle decreases, the peak value of the frequency spectrum increases, and the displacement amplitude can reach to 4.3 in the 90° wedge space but that is 1.8 in the half-space. In addition, compared with the half-space, the spectrum curve oscillates more rapidly in the wedge space due to the complex interference effect near the tunnel. As for DSCF spectrum curve, it shows that the dynamic stress concentration effect seems more significant for low frequency waves, and the wedge angle has large influence on the peak value of DSCF spectrum. For an example, in the 90° wedge space, the peak of the stress spectrum inner the tunnel can reach to 55 (η = 0.3) at the point θ′ = 0° (the point at the right of the tunnel). Accordingly, that are just 26 (η = 0.25) in half-space.

Fig. 7
figure 7

Displacement amplitude spectrum around the surface of the tunnel in wedge space

Full size image
Fig. 8
figure 8

Dynamic stress concentration factor spectrum of the tunnel in wedge space (the outer surface of the tunnel)

Full size image
Fig. 9
figure 9

Dynamic stress concentration factor spectrum of the tunnel in wedge space (the inner surface of the tunnel)

Full size image

Considering different material properties of the lined tunnel, Figs. 7, 8, and 9 also show the displacement amplitude and DSCF spectrum of the flexible tunnel case. Except for the material parameters, other parameters remain the same as those of the rigid tunnel. Compared with the rigid tunnel, the displacement amplitude on wedge space surface near the tunnel shows more significant amplification effect, which can reach to 7.5 at x/a = −2 (just above the tunnel), but that is 4.3 for the rigid tunnel in 90° wedge space. Additionally, the DSCF spectrums show little amplification effect inside the tunnel for the flexible case.

Figures 10, 11, and 12 show the contour pictures of the displacement amplitude both around the rigid and flexible lined tunnel in wedge space. Consider the wedge angle v = 1, 3/4, 1/2, the incident angles α = 0, π/2, and the frequencies η = 0.5, 1.0, 2.0, respectively.

Fig. 10
figure 10

Surface displacement amplitude around the tunnel in 180° wedge space (half-space) (η = 0.5, 1.0, 2.0)

Full size image
Fig. 11
figure 11

Surface displacement amplitude around the tunnel in 135° wedge space (η = 0.5, 1.0, 2.0)

Full size image
Fig. 12
figure 12

Surface displacement amplitude around the tunnel in 90° wedge space (η = 0.5, 1.0, 2.0)

Full size image

As for the rigid case, in wedge space, the displacement amplification effect becomes more significant, e.g., the displacement amplitude becomes 7.0 in 90° wedge space, and that is just 3.0 in half-space, 4.0 in 135° wedge space. It can be seen that as the frequency increases, the interference effect between the tunnel and the wedge space becomes more notable. There are more “focusing points” of wave energy for high incident frequencies. In addition, for the horizontal incident waves in half-space, due to the existence of the lined tunnel, the shielding effect on the displacement response can be seen clearly behind the tunnel, while this phenomenon is not so obvious for the 135° and 90° wedge space due to the existence of the inclined surface of wedge space.

As for the flexible tunnel, the displacement amplification effect inner the tunnel should be paid more attention. For example, when η = 1.0 and α = 0 the peak of the displacement amplitude inner the flexible tunnel can reach up to 12, while that of the rigid tunnel is about 2.5. Besides, for the flexible tunnel, in the 90° wedge space, the peak of the displacement amplitude inner the tunnel can reach up to 17.0 for η = 2.0 and α = π/2 , while that is about 6.4 for the half-space case. In general, the peak of displacement appears in the side facing the incoming waves or most close to the wedge space surfaces. Additionally, as the incident frequency increases, the amplification effect seems more significant. Hence, the seismic resistant design of the flexible tunnel should try to control the large displacement response of the tunnels.

Figure 13 shows the contour picture of dynamic stress concentration factor (DSCF) of the rigid tunnel in wedge space. It can be seen that spatial characteristics of DSCF is more complicated for high frequency, but the peak value increases gradually. Besides, as the wedge angle decreases, the peak value of DSCF increases clearly, e.g., for η = 2.0, α = π/2, the peak value can reach up to about 21.0 for ν = 1/2 (90° wedge space), but that is about 8.6 in half-space. In general, the DSCF decreases from the inner surface to the outer surface gradually.

Fig. 13
figure 13

Dynamic stress concentration factor of the tunnel in wedge space (η = 0.5, 1.0, 2.0; v = 1, 3/4, 1/2 rigid tunnel), a α = 0, v = 1, 3/4, 1/2, b α = π/2, v = 1, 3/4, 1/2

Full size image

To study the seismic response of tunnel built in cliffy mountains, Fig. 14 shows a sharply angular wedge space. Define the apex angle of the wedge as 2φ, the distance between o and o′ as L. oo′ is the bisector of the wedge space, and the incident SH-wave comes along the bisector line oo′.

Fig. 14
figure 14

Calculation model for a tunnel embedded in acute-angled wedge space

Full size image

Figure 15 illustrates the surface displacement amplitudes both for acute and obtuse angle wedge space with different incident frequencies, apex angles and the location of the lined tunnel. Set the incident frequencies to be η = 0.5, 1.0, 2.0, the apex angle of wedge 2φ = 60°, 75°, 90°, 120°, the location of the lined tunnel L = 5a, 10a, 15a, the ratio of mass density and shear wave velocity ρ 1/ρ = 5/4, β 1/β = 5/1, respectively. Obviously, when the apex angle of wedge is an acute angle, the seismic response is more significant. For example, when η = 0.5, L = 5a, the displacement amplitude can reach up to about 6.0 for 2φ = 60°, but that is about 1.4 for 2φ = 120° at the apex of wedge. Besides, as the distance L increases, the peak of displacement amplitude decreases gradually.

Fig. 15
figure 15

Displacement amplitude around the surface of the tunnel in arbitrary-angled wedge space (2φ = 60°, 75°, 90°, 120°; η = 0.5, 1.0, 2.0)

Full size image

6 Conclusions

This paper presents an indirect boundary element method (IBEM) for the scattering of plane SH-waves by a lined tunnel in elastic wedge space based on the theory of single-layer potential. Compared with the exact analytical solution, the accuracy of this method has been verified. Through detailed parameter analysis, several important conclusions can be drawn as follows:

The reflection and diffraction of elastic waves are changed substantially by the inclined surface of wedge space. The wave scattering features become more complicated, and strongly depend on the wedge angle, the angle of incidence, the incident frequency, the location of lined tunnel and material parameters. As the wedge angle decreases, the displacement amplification and dynamic stress concentration effects around the tunnel become more significant. As for the rigid tunnel in 90° wedge space, compared with the half-space case, the peak values of the displacement amplitude on ground surface and the dynamic stress concentration factor inside the tunnel increase more than 100 %. As for the flexible tunnel in wedge space, the dynamic stress concentration effect is not so significant, but the displacement amplitude of the tunnel can reach up to 17 times that of the incident waves. Therefore, the seismic or anti-explosion design of the tunnel or pipes located in slope or hillside should adopt the wedge space model to improve the accuracy.

It is worth mentioning that present method is applicable to the tunnel of arbitrary shape and in arbitrary-angle wedge space. In addition, the solution technique can also be expanded to solve the scattering of P and SV waves in elastic wedge space. The specific solution procedure will be given in another paper.