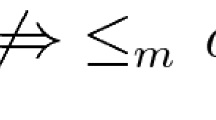1 Introduction

Let X be an absolutely continuous random variable with positive support \((0, +\infty )\), cumulative distribution function (cdf) F, probability density function (pdf) f and survival function (sf) \(\overline{F}\). In reliability theory \(F(x)=P(X\le x)\) is also known as unreliability function whereas \(\overline{F}(x)=1-F(x)=P(X>x)\) as reliability function. In this context a great importance has the hazard rate function (hr), \(r(x)=\frac{f(x)}{\overline{F}(x)}\) of X, also known as the force of mortality or the failure rate, where X is the survival model of a life or a system being studied. Hazard rate function can be interpreted as the instantaneous failure rate occurring just after the time point x, given that the unit has survived till time x. This definition will cover discrete as well as mixed survival models.

Moreover, we define cumulative hazard rate (chr), \(R(x)=\int _0^{x}r(u)\text {d}u=-\log [1-F(x)]\) (where \(\log \) denotes the natural logarithm) and the classical aging intensity (AI) function as \(L(x)=\frac{r(x)}{\frac{1}{x} R(x)}=\frac{-x\,f(x)}{[1-F(x)]\log [1-F(x)]}\) being the ratio of instantaneous hazard rate r(x) to average hazard rate \(\frac{1}{x} R(x)\) and expresses the units average aging behavior. It analyzes the aging property quantitatively, the larger the aging intensity, the stronger the tendency of aging (see [12]). For further properties and applications of the aging intensity functions see [5, 11, 14]. Recently, with the use of the multivariate conditional hazard rate functions (see, for instance, [17]), the concept of aging intensity function has been extended to the multivariate case taking into account the possibility of observing a dynamic history by the multivariate conditional aging intensity functions [7]. Let us note that \(F^{-1}(x)=-\log [1-x]\) is the quantile function of the standard exponential distribution with cdf \(F(x)=1-\exp (-x)\).

Now we recall the earlier generalization of aging intensity (see, e.g., Szymkowiak [19]) connected with the generalized Pareto distribution, with non-negative support and with the following density function

$$\begin{aligned} w_{\alpha }(x)=\left\{ \begin{array}{lll} (1-\alpha x)^{\frac{1}{\alpha }-1} &{} \text {for}&{} \left\{ \begin{array}{lll} x>0,&{}\alpha<0,\\ 0<x<\frac{1}{\alpha },&{} \alpha>0,&{} \end{array} \right. \\ \exp (-x) &{} \text {for}&{}\ \ \ \ x>0,\ \ \ \ \ \ \ \ \ \alpha =0, \end{array} \right. \end{aligned}$$

cumulative distribution function

$$\begin{aligned} W_{\alpha }(x)=\left\{ \begin{array}{lll} 1-(1-\alpha x)^{\frac{1}{\alpha }} &{} \text {for}&{} \left\{ \begin{array}{lll} x>0,&{}\alpha<0,\\ 0<x<\frac{1}{\alpha },&{} \alpha>0,&{} \end{array} \right. \\ 1-\exp (-x) &{} \text {for}&{}\ \ \ \ x>0,\ \ \ \ \ \ \ \ \ \alpha =0, \end{array} \right. \end{aligned}$$

and quantile function

$$\begin{aligned} W^{-1}_{\alpha }(x)=\left\{ \begin{array}{lll} \frac{1}{\alpha }\left[ 1-(1-x)^{\alpha }\right] &{} \text {for}&{} 0<x<1,\ \ \alpha \ne 0,\\ -\log (1-x) &{} \text {for}&{}0<x<1,\ \ \alpha = 0. \end{array} \right. \end{aligned}$$

Therefore, for distribution F with positive support \((0, +\infty )\) and density function f, we receive the following \(\alpha \)-generalized chr (see, Barlow and Zwet [3, 4])

$$\begin{aligned} R_{W_\alpha ,F}(x)= & {} (W_\alpha ^{-1}\circ F)(x)\\= & {} \left\{ \begin{array}{lll} \frac{1}{\alpha }\left[ 1-[1-F(x)]^{\alpha }\right] &{} \text {for}&{} x>0,\ \ \alpha \ne 0\\ -\log [1-F(x)] &{} \text {for}&{}x>0,\ \ \alpha = 0, \end{array} \right. \end{aligned}$$

and \(\alpha \)-generalized hr and AI functions can be defined as

$$\begin{aligned} r_{W_\alpha ,F}(x)= & {} \frac{{d }R_{W_\alpha ,F}(x)}{{d }x}=\frac{f(x)}{w_\alpha [(W_\alpha ^{-1}\circ F)(x)]}=\frac{f(x)}{[1-F(x)]^{1-\alpha }}\\ L_{W_\alpha ,F}(x)= & {} \frac{r_{W_\alpha ,F}(x)}{\frac{1}{x}R_{W_\alpha ,F}(x)}=\left\{ \begin{array}{lll} \frac{\alpha \, x\, f(x)}{\left[ 1-[1-F(x)]^{\alpha }\right] [1-F(x)]^{1-\alpha }}&{} \text {for}&{} x>0,\ \ \alpha \ne 0\\ -\frac{x f(x)}{[1-F(x)] \log [1-F(x)]} &{} \text {for}&{}x>0,\ \ \alpha = 0. \end{array} \right. \nonumber \end{aligned}$$
(1)

Obviously, for \(\alpha =0\), \(r_{W_0, F}(x)=\frac{f(x)}{1-F(x)}\), \(R_{W_0,F}(x)=\int _{0}^{x}r_{W_0, F}(u) \text {d}u\), and \(L_{W_0,F}(x)=-\frac{x f(x)}{[1-F(x)] \log [1-F(x)]}\) are classical hr, chr and AI functions, respectively.

Further on, for distribution G with non-negative support, pdf function g and quantile function \(G^{-1}\), we recall the definitions of G-generalized cumulative hazard rate (G-generalized chr), G-generalized hazard rate (G-generalized hr) and G-generalized aging intensity (G-generalized AI) functions (see also, Szymkowiak [19])

$$\begin{aligned} R_{G,F}(x)= & {} (G^{-1}\circ F)(x),\quad \text {for} \quad x>0,\nonumber \\ r_{G,F}(x)= & {} \frac{{d }R_{G,F}(x)}{{d }x}=\frac{f(x)}{g[(G^{-1}\circ F)(x)]}, \quad \text {for} \quad x>0,\nonumber \\ L_{G,F}(x)= & {} \frac{r_{G}(x)}{\frac{1}{x}R_{G}(x)}=\frac{x\,f(x)}{g[G^{-1}\circ F(x)] \left[ (G^{-1}\circ F(x)\right] },\quad \text {for} \quad x>0. \end{aligned}$$
(2)

Let us note that in the above generalizations, analogously to Barlow and Zwet generalization [3, 4], we compose the quantile function \(G^{-1}\) with non-negative support and cumulative distribution function F with positive support.

2 Previous G-generalization of reversed aging intensity

Now, we define the reversed hazard rate (rhr), \(\breve{r}(x)=\frac{f(x)}{F(x)}\) of X, that has attracted the attention of researchers and can be thought as the instantaneous failure rate occurring just before the time point x, given that the unit has not survived longer than time x. In a certain sense, it is the dual function of hr function and it bears some interesting features useful in reliability analysis (see also Block and Savits [6] and Finkelstein [10]). Further on, we recall the definition of the classical reversed cumulative hazard rate (rchr) \(\breve{R}(x)=\int _x^{\infty }\breve{r}(u)\text {d}u=~-\log F(x)\) treated as the total amount of failures accumulated after the time point x, and classical reversed aging intensity function (RAI), \(\breve{L}(x)=\frac{\breve{r}(x)}{\frac{1}{x} \breve{R}(x)}=\frac{-x\,f(x)}{F(x)\log [F(x)]}\) being the ratio of instantaneous reversed hazard rate \(\breve{r}(x)\) to its baseline value \(\frac{1}{x} \breve{R}(x)\) which is the proportion between the total amount of failures accumulated after the time point x and the time x for which the unit is still survived, see [15]. So, RAI expresses the units average aging behavior: the higher RAI (it means the higher the instantaneous reversed hazard rate, and the smaller the total amount of failures accumulated after the time point x, and the higher the time x for which the unit is still survived), the weaker the tendency of aging.

Previously, for distribution G with non-negative support, pdf and distribution F with positive support \((0,+\infty )\), Buono, Longobardi and Szymkowiak [9] defined G-generalized reversed hazard rate (G-generalized rhr), G-generalized reversed cumulative hazard rate (G-generalized rchr), and G-generalized reversed aging intensity (G-generalized RAI) functions as

$$\begin{aligned} \breve{R}_{G,F}(x)= & {} (G^{-1}\circ \overline{F})(x),\quad \text {for} \quad x>0,\nonumber \\ \breve{r}_{G,F}(x)= & {} -\frac{{d }\breve{R}_{G,F}(x)}{{d }x}=\frac{f(x)}{g\left[ (G^{-1} \circ \overline{F})(x)\right] },\quad \text {for} \quad x>0,\nonumber \\ \breve{L}_{G,F}(x)= & {} \frac{\breve{r}_{G,F}(x)}{\frac{1}{x}\breve{R}_{G,F}(x)}=\frac{x\,f(x)}{g\left[ (G^{-1} \circ \overline{F})(x)\right] \left[ (G^{-1} \circ \overline{F})(x)\right] },\quad \text {for} \quad x>0, \end{aligned}$$
(3)

where f and \(\overline{F}\) are pdf and sf of F, and \(G^{-1}\) and g are the quantile function and pdf of G, respectively. Let us note that in these generalizations we compose the quantile function \(G^{-1}\) with survival function \(\overline{F}\).

Proposition 2.1

Let G and H be cumulative distribution functions. Suppose both G and H have non-negative support. The G-generalized RAI function \(\breve{L}_{G,F}\) and the H-generalized RAI function \(\breve{L}_{H,F}\) are proportional if, and only if, there exist two non-negative constants c and K such that

$$\begin{aligned} G(x)=H\left( \left( \frac{x}{c}\right) ^K\right) . \end{aligned}$$
(4)

Proof

Let G and H be cumulative distribution functions with non-negative supports. \(\breve{L}_{G,F}\) and \(\breve{L}_{H,F}\) are proportional if, and only if, there exists \(K>0\) such that

$$\begin{aligned} g(G^{-1}(1-F(x))) G^{-1}(1-F(x))=K \ h(H^{-1}(1-F(x))) H^{-1}(1-F(x)), \ \ x>0, \end{aligned}$$

that is equivalent to

$$\begin{aligned} g(G^{-1}(x)) G^{-1}(x)=K \ h(H^{-1}(x)) H^{-1}(x), \ \ 0<x<1. \end{aligned}$$
(5)

By defining \(y(x)=G^{-1}(x)\) and \(z(x)=H^{-1}(x)\), (5) can be written as

$$\begin{aligned} \frac{y(x)}{y'(x)}=K\ \frac{z(x)}{z'(x)}, \ \ 0<x<1, \end{aligned}$$

or, equivalently,

$$\begin{aligned} \frac{y'(x)}{y(x)}=\frac{1}{K}\ \frac{z'(x)}{z(x)}, \ \ 0<x<1. \end{aligned}$$

By integrating, the above equation yields to

$$\begin{aligned} \log |y(x)|=\frac{1}{K}\log |z(x)|+ c_1, \end{aligned}$$

and then

$$\begin{aligned} |y(x)|=c|z(x)|^{\frac{1}{K}}, \end{aligned}$$
(6)

where \(c>0\) is a constant. By recalling the definitions of y and z, (6) can be written as

$$\begin{aligned} G^{-1}(x)=c(H^{-1}(x))^{\frac{1}{K}}, \end{aligned}$$
(7)

which yields to

$$\begin{aligned} G(x)=H\left( \left( \frac{x}{c}\right) ^K\right) , \end{aligned}$$

and the proof is completed.

Corollary 2.1

The only non-negative distributions which give through the generalization a RAI function proportional to the classical RAI function are the two parameters Weibull distributions.

Proof

If \(H(x)=1-\exp (-x)\), \(x>0\), i.e., the standard exponential distribution, then from (4) we deduce that the only distributions which give through the generalization a RAI function proportional to the classical RAI function are given by

$$\begin{aligned} G(x)=1-\exp \left( -\left( \frac{x}{c}\right) ^K\right) , \end{aligned}$$

that is the family of two parameters Weibull distributions.

Corollary 2.2

The only non-negative distributions which give through the generalization a RAI function proportional to the classical AI function are the inverse two parameters Weibull distributions.

Proof

If \(H(x)=\exp \left( -\frac{1}{x}\right) \), \(x>0\), i.e., the inverse standard exponential distribution, then the H-generalized RAI function is given by

$$\begin{aligned} \breve{L}_{H,F}(x)=\frac{-xf(x)}{(1- F(x))\log (1- F(x))}, \end{aligned}$$

that is the classical AI function. Hence, from (4), the only non-negative distributions which give through the generalization a RAI function proportional to the classical AI function are given by

$$\begin{aligned} G(x)=\exp \left( -\left( \frac{c}{x}\right) ^K\right) , \end{aligned}$$
(8)

that is the family of inverse two parameters Weibull distributions.

3 A stochastic order based on generalized reversed aging intensity

In [9], the generalized reversed aging intensity functions were used to define a new class of orders, namely \(\alpha \)-generalized reversed aging intensity orders. More precisely, these orders are based on the comparison between the \(\alpha \)-generalized reversed aging intensity functions of two non-negative and absolutely continuous random variables. Hence, the distribution used to obtain the generalized functions is fixed (in that case in the family of generalized Pareto distribution) and the comparison is among the variables for which the reversed aging intensity is evaluated. Here, we want to consider the problem from a different perspective. In fact, we introduce an order based on the comparison among G-generalized reversed aging intensity functions \(\breve{L}_{G,F}\) by keeping fixed F and varying the distribution G used to obtain the generalization.

Definition 1

Let \(X_1\) and \(X_2\) be non-negative and absolutely continuous random variables with cumulative distribution function \(G_1\) and \(G_2\), respectively. \(X_1\) is said to be smaller than \(X_2\) in the generalized reversed aging intensity order, \(X_1\le _{GRAI}X_2\), if \(\breve{L}_{G_1,F}(x)\le \breve{L}_{G_2,F}(x)\) for all non-negative and absolutely continuous distribution functions F and for all \(x>0\).

In the following, we prove that the above definition can be equivalently formulated in terms of a comparison based on the probability density function and the quantile function of the distributions compared in the generalized reversed aging intensity order.

Proposition 3.1

Let \(X_1\) and \(X_2\) be non-negative and absolutely continuous random variables with cumulative distribution function \(G_1\) and \(G_2\) and probability density function \(g_1\) and \(g_2\), respectively. \(X_1\) is smaller than \(X_2\) in the generalized reversed aging intensity order, \(X_1\le _{GRAI}X_2\), if and only if

$$\begin{aligned} g_1\left[ G_1^{-1}(u)\right] \cdot G_1^{-1} (u)\ge g_2\left[ G_2^{-1}(u)\right] \cdot G_2^{-1} (u), \end{aligned}$$
(9)

for \(0<u<1\).

Proof

Let F be any non-negative and absolutely continuous distribution function. From (3), the \(G_1\)-generalize reversed aging intensity function of F is expressed as

$$\begin{aligned} \breve{L}_{G_1,F}(x)=\frac{x\,f(x)}{g_1\left[ (G_1^{-1} \circ \overline{F})(x)\right] \left[ (G_1^{-1} \circ \overline{F})(x)\right] },\quad \text {for} \quad x>0. \end{aligned}$$

Hence, \(X_1\le _{GRAI}X_2\) is equivalent to

$$\begin{aligned} \frac{x\,f(x)}{g_1\left[ (G_1^{-1} \circ \overline{F})(x)\right] \left[ (G_1^{-1} \circ \overline{F})(x)\right] }\le \frac{x\,f(x)}{g_2\left[ (G_2^{-1} \circ \overline{F})(x)\right] \left[ (G_2^{-1} \circ \overline{F})(x)\right] }, \end{aligned}$$

for any F and \(x>0\). The above relation can be equivalently reformulated as

$$\begin{aligned} g_1\left[ (G_1^{-1} \circ \overline{F})(x)\right] \left[ (G_1^{-1} \circ \overline{F})(x)\right] \ge g_2\left[ (G_2^{-1} \circ \overline{F})(x)\right] \left[ (G_2^{-1} \circ \overline{F})(x)\right] , \end{aligned}$$

which, by replacing \(\overline{F}(x)\) with u, is equivalent to the condition in (9).

In the following proposition, we point out a connection between the generalized reversed aging intensity order and the concept of weighted extropy introduced in [2]. We recall that the extropy was introduced by Lad et al. [13] as a measure of uncertainty dual to the classical Shannon entropy [18]. For a non-negative and absolutely continuous random variable with pdf f, the entropy and the extropy are defined by

$$\begin{aligned} H(X)=-\int _0^{+\infty } f(x)\log f(x) dx \ \ \text{ and } \ \ J(X)=-\frac{1}{2}\int _0^{+\infty } f^2(x)dx, \end{aligned}$$

respectively. Recently, several versions of extropy have been defined in the literature (for more details see [1, 8, 20]). As remarked in [2], the extropy is position free, in the sense that X and \(X+b\), with \(b\in \mathbb R\), share the same value of uncertainty measured by the extropy. This led the authors to define the corresponding weighted version, namely the weighted extropy, which is expressed as

$$\begin{aligned} J^w(X)=-\frac{1}{2}\int _0^{+\infty } xf^2(x)dx. \end{aligned}$$

Proposition 3.2

Let \(X_1\) and \(X_2\) be non-negative and absolutely continuous random variables with cdf \(G_1\) and \(G_2\), respectively, such that \(X_1\le _{GRAI}X_2\). Then, \(J^w(X_1)\le J^w(X_2)\).

Proof

From Proposition 3.1, we know that \(X_1\le _{GRAI}X_2\) is equivalent to the condition in (9) in which both sides are non-negative. Hence, the relation in (9) is preserved by integrating with respect to u which varies from 0 to 1 obtaining

$$\begin{aligned} \int _0^1 g_1\left[ G_1^{-1}(u)\right] \cdot G_1^{-1} (u) du \ge \int _0^1 g_2\left[ G_2^{-1}(u)\right] \cdot G_2^{-1} (u) du. \end{aligned}$$

With the change of variable \(x=G_1^{-1}(u)\) in the LHS integral and \(x=G_2^{-1}(u)\) in the RHS one, the above relation leads to

$$\begin{aligned} \int _0^{+\infty } x g_1^2(x)dx \ge \int _0^{+\infty } x g_2^2(x) dx, \end{aligned}$$

which, multiplying by \(-\frac{1}{2}\) both sides, gives \(J^w(X_1)\le J^w(X_2)\).

In the following example, we consider some distributions that are ordered according to the generalized reversed aging intensity order and also give an example of distribution that are not ordered.

Example 1

Consider four families of distributions of non-negative and absolutely continuous distributions:

  1. 1.

    Exponential distribution with parameter \(\lambda >0\), \(Exp(\lambda )\), and cdf \(G_1(x)=1-\exp (-\lambda x)\);

  2. 2.

    Rayleigh distribution with parameter \(\sigma >0\), \(Rayleigh(\sigma )\), and cdf \(G_2(x)=1-\exp \left( -\frac{x^2}{2\sigma ^2}\right) \);

  3. 3.

    Log-logistic distribution with parameters \(\alpha ,\beta >0\), and cdf \(G_3(x)=\frac{1}{1+(x/\alpha )^{-\beta }}\);

  4. 4.

    Lomax distribution with parameters \(\alpha ,\lambda >0\), and cdf \(G_4(x)=1-\left[ 1+\frac{x}{\lambda }\right] ^{-\alpha }.\)

Let \(X_1\sim Exp(3)\), \(X_2\sim Rayleigh(2)\), \(X_3\sim Log-logistic(3,1)\) and \(X_4 \sim Lomax\)(3, 2). In Fig. 1 (left), we plot the functions \(g_i\left[ G_i^{-1}(u)\right] \cdot G_i^{-1} (u)\), \(i=1,2,3,4\). Hence, we note that \(X_2\le _{GRAI} X_1\le _{GRAI} X_4\le _{GRAI} X_3\). Now, we change the parameter \(\beta \) of the Log-logistic distribution and consider \(\tilde{X}_3\sim Log-logistic(3,3)\). By keeping the other distributions fixed, we plot the functions of interest for the generalized reversed aging intensity order in Fig. 1 (right). Hence, we observe that \(\tilde{X}_3\) is not comparable with respect to the generalized reversed aging intensity order with \(X_1\) and \(X_2\), while it is ordered with \(X_4\) as \(\tilde{X}_3\le _{GRAI} X_4\).

Fig. 1
figure 1

On the left, the plot of the functions \(g_i\left[ G_i^{-1}(u)\right] \cdot G_i^{-1} (u)\), \(i=1,2,3,4\) in Example 1. On the right, the case with a different choice for a parameter of the Log-logistic distribution

Full size image

In the following example, we show that the generalized reversed aging intensity order is not implied by and does not imply the usual stochastic order. We recall that \(X_1\) is said to be smaller than \(X_2\) in the usual stochastic order, \(X_1\le _{st}X_2\), if \(\bar{F}_{X_1}(x)\le \bar{F}_{X_2}(x)\) for all x. For further details on the classical stochastic orders see Shaked and Shanthikumar [16].

Example 2

Consider the four random variables \(X_1,X_2,X_3,X_4\) as in Example 1. In Fig. 2 (left), we plot the survival functions of these random variables. Hence we can observe some relations in terms of the usual stochastic order as \(X_1\le _{st}X_4\le _{st}X_3\) and \(X_1\le _{st}X_2\), while \(X_2\) is not comparable in the usual stochastic order with \(X_3\) and \(X_4\). From Example 1, we know that \(X_2\le _{GRAI} X_4\le _{GRAI} X_3\) and so the generalized reversed aging intensity order does not imply the usual stochastic order. Moreover, by considering again the random variable \(\tilde{X}_3\) as in Example 1, we obtain the survival functions plotted in Fig. 2 (right). With this choice of the parameter \(\beta \), we have \(X_2\le _{st}\tilde{X}_3\), but as remarked in Example 1 these variables are not comparable in the generalized reversed aging intensity order. Hence, the usual stochastic order does not imply the generalized reversed aging intensity order.

Fig. 2
figure 2

The survival functions of the variables \(X_1,X_2,X_3,X_4\) in Example 2 (left). The survival functions of the variables \(X_1,X_2,\tilde{X}_3,X_4\) in Example 2 (right)

Full size image

In the following proposition, we show that the usual stochastic order combined with the generalized reversed aging intensity order implies a relation on the order based on extropy.

Proposition 3.3

Let \(X_1\) and \(X_2\) be non-negative and absolutely continuous random variables with cdf \(G_1\) and \(G_2\), respectively, such that \(X_1\le _{st}X_2\) and \(X_1\le _{GRAI}X_2\). Then, \(J(X_1)\le J(X_2)\).

Proof

Note that the usual stochastic order \(X_1\le _{st}X_2\) can be equivalently formulated as \(G_1(x)\ge G_2(x)\) for \(x>0\) or \(G_1^{-1}(u)\le G_2^{-1}(u)\) for \(u\in (0,1)\). From \(X_1\le _{GRAI}X_2\), it follows

$$\begin{aligned} g_1\left[ G_1^{-1}(u)\right] \cdot G_1^{-1} (u)\ge g_2\left[ G_2^{-1}(u)\right] \cdot G_2^{-1} (u), \end{aligned}$$

for \(0<u<1\), where all the factors in LHS and RHS are non-negative. Hence, from \(X_1\le _{st}X_2\), we readily obtain

$$\begin{aligned} g_2\left[ G_2^{-1}(u)\right] \cdot G_2^{-1} (u)\ge g_2\left[ G_2^{-1}(u)\right] \cdot G_1^{-1} (u) \end{aligned}$$
(10)

and combining the previous relations

$$\begin{aligned} g_1\left[ G_1^{-1}(u)\right] \ge g_2\left[ G_2^{-1}(u)\right] , \end{aligned}$$
(11)

for \(0<u<1\). The relation in (11) is preserved by integrating with respect to u varying from 0 to 1, leading to

$$\begin{aligned} \int _0^1 g_1\left[ G_1^{-1}(u)\right] \ge \int _0^1 g_2\left[ G_2^{-1}(u)\right] . \end{aligned}$$

With a change of variable similar to that used in the proof of Proposition 3.2, we obtain

$$\begin{aligned} \int _0^{+\infty } g_1^2(x)dx \ge \int _0^{+\infty } g_2^2(x) dx, \end{aligned}$$

and so \(J(X_1)\le J(X_2)\).

As the generalized reversed aging intensity order does not imply the usual stochastic order, it does not imply all the orders that imply the usual one, as, for instance, the reversed hazard rate and the likelihood ratio orders. Nevertheless, it could be implied by some of these orders. In the following example, we show that the likelihood ratio order and the reversed hazard rate order do not imply the generalized reversed aging intensity order. We recall that \(X_1\) is said to be smaller than \(X_2\) in the likelihood ratio order, \(X_1\le _{lr}X_2\), if \(f_{X_1}(x)/f_{X_2}(x)\) is non-increasing in x, and in the reversed hazard rate order, \(X_1\le _{rh}X_2\), if \(\breve{r}_{X_1}(x)\le \breve{r}_{X_2}(x)\) for all x.

Example 3

Consider the random variables \(X_2\) and \(\tilde{X}_3\) given in Examples 1 and 2. It is easy to show that \(X_2\le _{lr}\tilde{X}_3\), and consequently \(X_2\le _{rh}\tilde{X}_3\). Hence, the likelihood ratio order and the reversed hazard rate order do not imply the generalized reversed aging rate order as these variables are not comparable in that order.

4 Modified G-generalized reversed aging intensity function

Recently, we wonder if our previous definition of G-generalized RAI function (3), where we composed quantile function \(G^{-1}\) with survival function \(\overline{F}\), can be improved, analogously to argumentation given by Barlow and Zwet [3, 4], as the composition of quantile function \(G^{-1}\) with cumulative distribution function F (see also, formula (2)).

Therefore, we propose the following modified \(\alpha \)-generalization of reversed aging intensity function using the negative generalized Pareto distribution, with negative support and with the following density function

$$\begin{aligned} v_{\alpha }(x)=\left\{ \begin{array}{lll} (1+\alpha x)^{\frac{1}{\alpha }-1} &{} \text {for}&{} \left\{ \begin{array}{lll} x<0,&{}\alpha<0,\\ -\frac{1}{\alpha }<x<0,&{} \alpha >0,&{} \end{array} \right. \\ \exp (x) &{} \text {for}&{}\ \ \ \ x<0,\ \ \ \ \ \ \ \ \ \alpha =0, \end{array} \right. \end{aligned}$$

cumulative distribution function

$$\begin{aligned} V_{\alpha }(x)=\left\{ \begin{array}{lll} (1+\alpha x)^{\frac{1}{\alpha }} &{} \text {for}&{} \left\{ \begin{array}{lll} x<0,&{}\alpha<0,\\ -\frac{1}{\alpha }<x<0,&{} \alpha >0,&{} \end{array} \right. \\ \exp (x) &{} \text {for}&{}\ \ \ \ x<0,\ \ \ \ \ \ \ \ \ \alpha =0, \end{array} \right. \end{aligned}$$

and quantile function

$$\begin{aligned} V^{-1}_{\alpha }(x)=\left\{ \begin{array}{lll} \frac{1}{\alpha }\left( x^{\alpha }-1\right) &{} \text {for}&{} 0<x<1,\ \ \alpha \ne 0,\\ \log (x) &{} \text {for}&{}0<x<1,\ \ \alpha = 0. \end{array} \right. \end{aligned}$$

Then, by analogy to formula (1), for distribution F with positive support \((0, +\infty )\) and density f, we can define \(\alpha \)-generalized rhr

$$\begin{aligned} \overset{\circ }{r}_{V_\alpha ,F}(x)= & {} \frac{f(x)}{v_\alpha [(V_\alpha ^{-1}\circ F)(x)]}\\= & {} \left\{ \begin{array}{lll} \frac{f(x)}{\left[ 1+\alpha \left[ \frac{1}{\alpha }\left( F(x)^{\alpha }-1\right) \right] \right] ^{\frac{1}{\alpha }-1}} &{} \text {for}&{}\ \ \ \ x>0,\ \ \ \ \ \ \ \ \ \alpha \ne 0 \\ \frac{f(x)}{F(x)} &{} \text {for}&{}\ \ \ \ x>0,\ \ \ \ \ \ \ \ \ \alpha =0 \end{array} \right. \nonumber \\= & {} \frac{f(x)}{[F(x)]^{1-\alpha }}\ \ \ \text {for}\ \ x>0.\nonumber \end{aligned}$$
(12)

Further on, since \((V_\alpha ^{-1}\circ F)(+\infty )=0\), \(\alpha \)-generalized crhr can be determined as

$$\begin{aligned} \overset{\circ }{R}_{V_\alpha ,F}(x)= & {} \int _{x}^{+\infty }\overset{\circ }{r}_{V_\alpha ,F}(u) \text {d}u=\int _{x}^{+\infty }\frac{f(u)}{v_\alpha [(V_\alpha ^{-1}\circ F)(u)]}\text {d}u=(V_\alpha ^{-1}\circ F)(u){\mid }^{+\infty }_x\nonumber \\{} & {} \nonumber \\= & {} (V_\alpha ^{-1}\circ F)(+\infty )-(V_\alpha ^{-1}\circ F)(x)=-(V_\alpha ^{-1}\circ F)(x)\\{} & {} \nonumber \\= & {} \left\{ \begin{array}{lll} \frac{1}{\alpha }\left[ 1-[F(x)]^{\alpha }\right] &{} \text {for}&{} x>0,\ \ \alpha \ne 0\\ -\log [F(x)] &{} \text {for}&{}x>0,\ \ \alpha = 0 \end{array} \right. \nonumber \end{aligned}$$
(13)

On the other hand, since \(\overset{\circ }{R}_{V_\alpha ,F}(+\infty )=-(V_\alpha ^{-1}\circ F)(+\infty )=0\), to determine \(\overset{\circ }{r}_{V_\alpha ,F}(x)\) given \(\overset{\circ }{R}_{V_\alpha ,F}(x)\), we can use such a formula

$$\begin{aligned} \overset{\circ }{r}_{V_\alpha ,F}(x)= & {} \frac{{d }\int _{x}^{+\infty }\overset{\circ }{r}_{V_\alpha ,F}(u) \text {d}u}{{d }x}=\frac{{d }\overset{\circ }{R}_{V_\alpha ,F}(+\infty )}{{d }x}-\frac{{d }\overset{\circ }{R}_{V_\alpha ,F}(x)}{{d }x} \\= & {} -\frac{{d }\overset{\circ }{R}_{V_\alpha ,F}(x)}{{d }x}=\frac{{d }(V_\alpha ^{-1}\circ F)(x)}{{d }x}=\frac{f(x)}{v_\alpha [(V_\alpha ^{-1}\circ F)(x)]}. \end{aligned}$$

Finally, \(\alpha \)-generalized RAI function can be defined as the ratio of the instantaneous reversed hazard rate \(\overset{\circ }{r}_{V_\alpha ,F}(x)\) to its baseline value \(\frac{1}{x}\overset{\circ }{R}_{V_\alpha ,F}(x)\)

$$\begin{aligned} \overset{\circ }{L}_{V_\alpha ,F}(x)= & {} \frac{\overset{\circ }{r}_{V_\alpha ,F}(x)}{\frac{1}{x}\overset{\circ }{R}_{V_\alpha ,F}(x)}=\left\{ \begin{array}{lll} \frac{\alpha \, x\, f(x)}{\left[ 1-[F(x)]^{\alpha }\right] [F(x)]^{1-\alpha }}&{} \text {for}&{} x>0,\ \ \alpha \ne 0\\ -\frac{x f(x)}{F(x) \log [F(x)]} &{} \text {for}&{}x>0,\ \ \alpha = 0. \end{array} \right. \end{aligned}$$

Obviously, for \(\alpha =0\), \(\overset{\circ }{r}_{V_0,F}(x)=\frac{f(x)}{P(X\le x)}\), \(\overset{\circ }{R}_{V_0,F}(x)=\int _{x}^{+\infty }\overset{\circ }{r}_{V_0,F}(u) \text {d}u\), and \(\overset{\circ }{L}_{V_0,F}(x)=-\frac{x f(x)}{F(x) \log [F(x)]}\) are classical rhr, crhr and RAI functions, respectively.

Consequently, for distribution G with non-positive support, density function g and quantile function \(G^{-1}\), and for distribution F with positive support \((0, +\infty )\) and density function f, by analogy to formula (12), we can define modified G-generalized rhr

$$\begin{aligned} \overset{\circ }{r}_{G,F}(x) =\frac{f(x)}{g[(G^{-1}\circ F)(x)]}\ \ \ \text {for}\ \ x>0. \end{aligned}$$

Further on, by analogy to formula (13), modified G-generalized crhr can be determined as

$$\begin{aligned} \overset{\circ }{R}_{G,F}(x)=-(G^{-1}\circ F)(x)\ \ \ \text {for}\ \ x>0, \end{aligned}$$

and modified G-generalized RAI function as

$$\begin{aligned} \overset{\circ }{L}_{G,F}(x)=\frac{\overset{\circ }{r}_{G,F}(x)}{\frac{1}{x}\overset{\circ }{R}_{G,F}(x)}=-\frac{x\,f(x)}{g[(G^{-1}\circ F)(x)] (G^{-1}\circ F)(x)}\ \ \ \text {for}\ \ x>0. \end{aligned}$$

Proposition 4.1

Let G and H be cumulative distribution functions. Suppose G has non-negative support and H has non-positive support. The G-generalized RAI function \(\breve{L}_{G,F}\) and the modified H-generalized RAI function \(\overset{\circ }{L}_{H,F}\) are proportional if, and only if, there exist two non-negative constants c and K such that

$$\begin{aligned} G(x)=1-H\left( -\left( \frac{x}{c}\right) ^K\right) . \end{aligned}$$
(14)

Proof

Let G and H be cumulative distribution functions with non-negative and non-positive support, respectively. The G-generalized RAI function \(\breve{L}_{G,F}\) and the modified H-generalized RAI function \(\overset{\circ }{L}_{H,F}\) are proportional if, and only if, there exists \(K>0\) such that

$$\begin{aligned} g(G^{-1}(1-F(x))) G^{-1}(1-F(x))=-K \ h(H^{-1}(F(x))) H^{-1}(F(x)), \ \ x>0, \end{aligned}$$

that is equivalent to

$$\begin{aligned} g(G^{-1}(x)) G^{-1}(x)=-K \ h(H^{-1}(1-x)) H^{-1}(1-x), \ \ 0<x<1. \end{aligned}$$
(15)

By defining \(y(x)=G^{-1}(x)\) and \(z(x)=H^{-1}(1-x)\), (15) can be written as

$$\begin{aligned} \frac{y(x)}{y'(x)}=K\ \frac{z(x)}{z'(x)}, \ \ 0<x<1, \end{aligned}$$

or, equivalently,

$$\begin{aligned} \frac{y'(x)}{y(x)}=\frac{1}{K}\ \frac{z'(x)}{z(x)}, \ \ 0<x<1. \end{aligned}$$

By integrating, the above equation yields to

$$\begin{aligned} \log |y(x)|=\frac{1}{K}\log |z(x)|+ c_1, \end{aligned}$$

and then

$$\begin{aligned} |y(x)|=c|z(x)|^{\frac{1}{K}}, \end{aligned}$$
(16)

where \(c>0\) is a constant. By recalling the definitions of y and z, (16) can be written as

$$\begin{aligned} G^{-1}(x)=c\left( -H^{-1}(1-x)\right) ^{\frac{1}{K}}, \end{aligned}$$
(17)

which yields to

$$\begin{aligned} G(x)=1-H\left( -\left( \frac{x}{c}\right) ^K\right) , \end{aligned}$$

and the proof is completed.

Corollary 4.1

Observe that for \(c=1\) and \(K=1\), (14) reduces to

$$\begin{aligned} G(x)=1-H(-x), \end{aligned}$$

i.e., if G is the cdf of a non-negative random variable Z and H the cdf of \(-Z\), then they conduce to the same generalization of the RAI function.

Proposition 4.2

Let G and H be cumulative distribution functions. Suppose both G and H have non-positive support. The modified G-generalized RAI function \(\overset{\circ }{L}_{G,F}\) and the modified H-generalized RAI function \(\overset{\circ }{L}_{H,F}\) are proportional if, and only if, there exist two non-negative constants c and K such that

$$\begin{aligned} G(x)=H\left( -\left( -\frac{x}{c}\right) ^K\right) . \end{aligned}$$
(18)

Proof

Let G and H be cumulative distribution functions with non-positive support. The modified G-generalized RAI function \(\overset{\circ }{L}_{G,F}\) and the modified H-generalized RAI function \(\overset{\circ }{L}_{H,F}\) are proportional if, and only if, there exists \(K>0\) such that

$$\begin{aligned} g[(G^{-1}\circ F)(x)] (G^{-1}\circ F)(x)= K\ h[(H^{-1}\circ F)(x)] (H^{-1}\circ F)(x), \ \ x>0 \end{aligned}$$

that is equivalent to

$$\begin{aligned} g(G^{-1}(x)) G^{-1}(x)=K \ h(H^{-1}(x)) H^{-1}(x), \ \ 0<x<1. \end{aligned}$$
(19)

By defining \(y(x)=G^{-1}(x)\) and \(z(x)=H^{-1}(x)\), (19) can be written as

$$\begin{aligned} \frac{y(x)}{y'(x)}=K\ \frac{z(x)}{z'(x)}, \ \ 0<x<1, \end{aligned}$$

or, equivalently,

$$\begin{aligned} \frac{y'(x)}{y(x)}=\frac{1}{K}\ \frac{z'(x)}{z(x)}, \ \ 0<x<1. \end{aligned}$$

By integrating, the above equation yields to

$$\begin{aligned} \log |y(x)|=\frac{1}{K}\log |z(x)|+ c_1, \end{aligned}$$

and then

$$\begin{aligned} |y(x)|=c|z(x)|^{\frac{1}{K}}, \end{aligned}$$
(20)

where \(c>0\) is a constant. By recalling the definitions of y and z, (20) can be written as

$$\begin{aligned} -G^{-1}(x)=c(-H^{-1}(x))^{\frac{1}{K}}, \end{aligned}$$
(21)

which yields to

$$\begin{aligned} G(x)=H\left( -\left( -\frac{x}{c}\right) ^K\right) , \end{aligned}$$

and the proof is completed.

Corollary 4.2

The only non-positive distributions which give through the modified generalization a RAI function proportional to the classical RAI function are the two parameters negative Weibull distributions.

Proof

If \(H(x)=\exp (x)\), \(x<0\), i.e., the standard negative exponential distribution, then from (18) we deduce that the only distributions which give through the modified generalization a RAI function proportional to the classical RAI function are given by

$$\begin{aligned} G(x)=\exp \left( -\left( -\frac{x}{c}\right) ^K\right) , \end{aligned}$$

that is the family of two parameters negative Weibull distributions.