1 Introduction

In fluid-dynamics a fundamental question is the determination of a steady state solution, called base flow, and the investigation of its stability/instability. In experiments, when turbulence is reached, one typically finds turbulent stripes that have an inclination with respect to the base flow [1]. A tentative qualitative and quantitative explanation of this phenomenon is based on finding a relation between the structure of the Fourier mode that most destabilises the base flow and the structure of the turbulent flow that arises [2, 3].

Stability analysis is typically performed using two main approaches: Lyapunov investigation for the stability, and spectral investigation for instability. Lyapunov investigation typically uses the \(L^2\) energy as Lyapunov function. In the literature a temporary increase of energy is considered indication of instability, despite the fact that the spectrum has negative real part (see for example the arguments of Reddy and others [4]). This type of investigation is so common that it is called non-modal analysis. The Reynolds number at which the energy begins to fail to be a Lyapunov function is an interesting threshold, that we investigate in this article. On the other hand, the spectral analysis of the system is often called modal analysis.

A comparison between modal and non-modal analyses is often not fruitful as one would hope. Indeed the two thresholds do not yield a threshold value above which instability arises and below which stability subsists. This creates a gap inside which the instability can possibly exist, creating a literature on subcritical instabilities (see [5]). To be more precise, it happens that the experimental threshold for instability lays below the threshold of linear instability but above the threshold for energy-Lyapunov stability. This possibly means that the energy is not the best choice of Lyapunov function, but it also means that the modal threshold only gives a sufficient condition for instability, and not the precise value for its insurgence.

Two among the most significant base flows are Couette and Poiseuille flows. It is a well known fact that laminar steady state solutions for a fluid layer with rigid moving boundaries and a non-zero pressure gradient can be a combination of Couette and Poiseuille flows, see for example Drazin and Reid [6, pag. 223]. The first investigation of linear stability of a base flow that is a combination of Couette and Poiseuille motions has been performed by Potter in [7] and Hains in [8]. The first theoretical investigation in the same setup using Lyapunov’s functions is a much more recent study of the evolution of the energy (see Bergstrom’s [9]). Experiments related to the theoretical results have been performed by Klotz and others in [10]. Such experiments lead to subcritical transition to turbulence, which is a debated argument in the field of stability of fluid flows [11].

In our manuscript we assume that the pressure gradient can have a component transverse to the direction of the moving plates, giving to the base flow a Poiseuille component also along the transverse direction, that we call spanwise to distinguish it from the direction parallel to the motion of the plates, that we call streamwise. With this addition, the articles of Potter, Hains, Bergstrom, become particular cases of our analysis, since in their work the base flow has vanishing spanwise component. Our results in this manuscript extend the cited results by assuming that the base flow is a mixture of Couette and Poiseuille flow along the streamwise direction and it possesses a Poiseuille component along the spanwise direction. The presence of cross-flow is particularly important in filtration, where the medium is porous and the Poiseuille type flow, due to a pressure gradient, is transversal (crossed) with respect to a Poiseuille–Couette flow due to the motion of a filtrating substrate [12,13,14,15]. Most modern investigations deal with this type of flows in presence of porous media, few recent articles deal with the stability of Couette–Poiseuille flow, some in relation with Sommerfeld paradox (see for example Barkley and Tuckerman [16] or the author’s [2]), some with the addition of a magnetic field [17].

The physical relevance of this investigation lays in the fact that in some natural phenomena or experiments it could happen that the pressure is not parallel to the motion of the plates. The pressure could in fact be forced by the gravitational field or by a controlled pumping, the motion of the plates by a different type of action. This article uses classical energy growth investigation and classical spectral analysis. Its originality lays in the fact that for the first time the base flow has two non-zero components. This creates an interaction between spanwise and streamwise components of the destabilising perturbation, and in this setup the most destabilising perturbation does not naturally have one wave number equal to zero. This problem is connected to the debated comparison between Orr and Joseph’s results (see [18, 19]).

Our setup generates base flow that are dependent on two parameters, that we call \(\xi \) and \(\eta \). The first parameter indicates the type of combination of Couette and Poiseuille flows along the streamwise direction, the second parameter indicates the relative strength of the Poiseuille spanwise component. To every choice of parameters \(\xi ,\eta \) there correspond a threshold value of the Reynolds number above which there exist perturbations which correspond to eigenvectors whose eigenvalue has positive real part. We call this critical value spectral-critical Reynolds number. The spectral analysis requires heavy numerical computations, for this reason we plot graphs of the energy-critical Reynolds number and its corresponding critical wave number as functions of \(\xi \) with \(\eta \) fixed to zero (retracing Potter and Hains results) and as functions of \(\eta \) with \(\xi \) fixed to zero (Couette plus a spanwise increasingly strong Poiseuille flow) and to one (Poiseuille flow of given strength along the streamwise direction plus a spanwise increasingly strong Poiseuille flow). On the other hand, for every choice of parameters \(\xi , \eta \) there correspond a threshold value of the Reynolds number above which there exist perturbations that, chosen as initial value, have increasing energy. We call this critical value energy-critical Reynolds number. We compute both critical Reynolds numbers as functions of \(\xi ,\eta \). Together with the energy-critical Reynolds number we determine the associated critical perturbation and, in particular, the energy-critical wave numbers. We will make considerations on the 3D graph of energy-critical Reynolds numbers as function of \(\xi ,\eta \), and will observe interesting features of energy-critical wave numbers.

The layout of the paper is the following: in Sect. 2 we write the equations for base flow and their perturbations in the original velocity fields and also in the stream fields, we conclude the section computing the orbital derivative of the energy. In Sect. 3 we compute the Euler–Lagrange equations for the critical values of the orbital derivative of the energy, we make an investigation of the energy-critical Reynolds number, and we compute the energy-critical wave numbers. In Sect. 4 we make a spectral investigation. A Section dedicated to discussion of the results and conclusions follows.

2 Base motions, perturbation equations, and Orr-Reynold’s energy equations

Fig. 1
figure 1

A layer of width 2d filled with a fluid. The upper boundary of the layer moves with velocity \(\alpha \textbf{i}\), the lower boundary with velocity \(-\alpha \textbf{i}\). The base flow is also influenced by a pressure gradient non parallel to \(\textbf{i}\)

Full size image

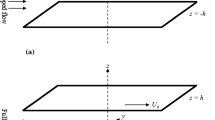
Assume to be given a layer of width 2d, filled with an incompressible fluid (see Fig. 1). The velocity field of the fluid is \({ \textbf{U}} = U(x,y,z) \, \textbf{i} + V(x,y,z) \, \textbf{j} + W(x,y,z) \, \textbf{k}\), and the equations that model such velocity are

$$\begin{aligned} {\left\{ \begin{array}{ll} \textbf{U}_t + \textbf{U}\cdot \nabla \textbf{U} = \nu \Delta \textbf{U} - \nabla Q/\rho \\ \nabla \cdot \textbf{U}= 0 \end{array}\right. }, \text { with }(x,y,z) \in \Omega = {\mathbb {R}}^2 \times [-d,d]. \end{aligned}$$
(1)

If the layer is inclined, the pressure Q incorporates also the term due to gravity [20], but in any case we can assume that some device is forcing a base pressure gradient. We also assume that the layer is subject to rigid boundary conditions, and that the upper and lower boundaries of \(\Omega \) are in constant motion one with respect to the other. Up to a uniformly translating change of coordinates, the hypotheses are equivalent to assuming that solutions \(\textbf{U}\) of Eq. (1) must satisfy the conditions

$$\begin{aligned} \textbf{U} (x,y, -d) = -\alpha \textbf{i}, \quad \textbf{U} (x,y, d) = \alpha \textbf{i}, \quad \text {for every }(x,y) \in {\mathbb {R}}^2, \quad \alpha \in {\mathbb {R}}. \end{aligned}$$
(2)

This fact creates a inhomogeneity between the direction \(\textbf{i}\), that we call streamwise and \(\textbf{j}\), that we call spanwise.

Since for steady motions the pressure is a linear function \(Q = q_x x + q_y y\) (\(q_x,q_y\) real numbers), one has that the possible steady laminar solutions to equation (1) that also satisfies the rigid boundary conditions must have the form

$$\begin{aligned} \overline{\textbf{U}} = \left( \frac{\alpha }{d} z + \frac{\beta }{d^2} (z^2 - d^2)\right) \textbf{i} + \frac{\gamma }{d^2} (z^2 - d^2) \textbf{j}, \end{aligned}$$
(3)

where \(\alpha \), \(\beta = d^2/(2 \nu \rho ) q_x\), and \(\gamma = d^2/(2 \nu \rho ) q_y\) are parameters having dimension of mt/sec (see [21]). The parameter \(\alpha \) is the relative velocity of the boundaries, and effects the solution because of the rigidity of the boundaires. The parameters \(\beta ,\gamma \) depend on the particular choice of base pressure, that is possibly due to gravity or to other physical phenomena that create a pressure gradient. We nondimensionalise the system rescaling space with d, time with \(d/(\alpha + \beta )\), denoting \(R = 2 d (\alpha + \beta )/\nu \), \(\xi = \beta /(\alpha + \beta )\), \(\eta = \gamma /(\alpha + \beta )\). Calling P the consequent rescaling of Q, the system and its with stationary laminar base flows become

$$\begin{aligned} {\left\{ \begin{array}{ll} \textbf{U}_t + \textbf{U}\cdot \nabla \textbf{U} = \frac{1}{R} \Delta \textbf{U} - \nabla P \\ \nabla \cdot \textbf{U}= 0, \end{array}\right. } \qquad {\overline{\textbf{U}}} = \begin{pmatrix} (1-\xi ) z + \xi (z^2 -1)\\ \eta (z^2-1)\\ 0 \end{pmatrix}. \end{aligned}$$
(4)

We will denote \(f(z) = (1-\xi ) z + \xi (z^2 -1)\) and \(g(z)= \eta (z^2-1)\). Observe that the parameter \(\xi \) gives the type of combination of Couette–Poiseuille in the \(\textbf{i}\) direction; with \(\xi = 0\) one has Couette flow, with \(\xi =1\) one has Poiseuille flow. Our choice of rescaling allows to include Poiseuille and Couette flows as special cases. The parameter \(\eta \) gives the intensity of transverse Poiseuille flow. The choices \(\xi = 1\) and \(\eta \in {\mathbb {R}}\) do not allow the definition of spanwise and streamwise directions, and they all correspond to Poiseuille flow along a well defined direction, depending on \(\eta \), parallel to \(\textbf{i}\) only when \(\eta = 0\), but inclined with respect to the coordinate axes when \(\eta \not = 0\) (we will return to this observation when describing Fig. 5). The base flow is typically a combination of Couette in the streamwise direction and Poiseuille along any other direction, not necessarily streamwise.

The linear equations for the perturbations \(u \, \textbf{i} + v \, \textbf{j} + w \, \textbf{k}\), p to the base flow are

$$\begin{aligned} {\left\{ \begin{array}{ll} u_t = \frac{1}{R} \Delta u - f u_x - g u_y - f' w - p_x \\ v_t = \frac{1}{R} \Delta v - f v_x - g v_y - g' w - p_y \\ w_t = \frac{1}{R} \Delta w - f w_x - g w_y - p_z \\ u_x + v_y + w_z = 0\\ u = v = w = 0 \quad \text {on the boundary}. \end{array}\right. } \end{aligned}$$
(5)

Considering w and \(\zeta = v_x - u_y\), the vorticity of (u, v, w) and performing the common reduction by means of the double curl of Eq. (5), one reduces the equations above to

$$\begin{aligned} {\left\{ \begin{array}{ll} \Delta w_t = \frac{1}{R} \Delta ^2 w - f \Delta w_x - g \Delta w_y + f'' w_x + g'' w_y\\ \zeta _t = \frac{1}{R} \Delta \zeta - f \zeta _x - g \zeta _y + f' w_y - g' w_x\\ w = w_z = \zeta = 0 \quad \text {on the boundary}. \end{array}\right. } \end{aligned}$$
(6)

The two functions \(w,\zeta \) are called stream functions, the system of Eq. (6) is deduced from (5), and it is well known that there are means of reconstructing solutions of (5) starting from solutions of (6). This can be done by taking \(w,\zeta \) solutions of (6), and solving system

$$\begin{aligned} {\left\{ \begin{array}{ll} \Delta ' u = - \zeta _y - w_{xz}\\ \Delta ' v = \zeta _x - w_{yz}\\ u = v = 0 \quad \text {on the boundary}, \end{array}\right. } \end{aligned}$$
(7)

where \(\Delta ' = \partial _x^2 + \partial _y^2\) (see [20]), with respect to the two unknown functions u, v.

In [22] is discussed the fact that the existence and uniqueness of the solutions of (7) is delicate. It is a one parametric solution (with z as parameter) of a non-homogeneous bidimentional Laplace equation with boundary conditions. The decomposition of the velocity fields in their Fourier modes resolves the problem, and Eq. (7) define a bijection between incompressible velocity fields and stream functions (see Eq. (8)).

Equation (5) can be thought as constrained equations in the space

$$\begin{aligned} {\mathcal {S}} = \{ (u,v,w) \,|\, u_x + v_y +w_z = 0, \, u(x,y,\pm 1) = v(x,y,\pm 1) = w(x,y,\pm 1) = 0\}, \end{aligned}$$

and Eq. (6) can be thought as unconstrained equation in the space

$$\begin{aligned} {\mathcal {R}} = \{ (w,\zeta ) \,|\, w(x,y,\pm 1) = 0, w_z(x,y,\pm 1) = 0, \zeta (x,y,\pm 1) = 0\}, \end{aligned}$$

where \(u,v,w,\zeta \) are regular enough. The space \({\mathcal {S}}\) can be decomposed in Fourier components \({\mathcal {S}} = \oplus _{k_x,k_y} {\mathcal {S}}_{k_x,k_y}\) where \(k_x,k_y \in {\mathbb {R}}\), \(k_x,k_y\ge 0\), \(k^2 = k_x^2 + k_y^2 > 0\) and

$$\begin{aligned} {\mathcal {S}}_{k_x,k_y}{} & {} = \Big \{\big (u(z) e^{i (k_x x + k_y y)},v(z) e^{i (k_x x + k_y y)},w(z) e^{i (k_x x + k_y y)}\big ) \,\Big |\, \\{} & {} \quad \ \Big |\, i k_x u + i k_y v + w_z = 0, \, u(\pm 1) = v(\pm 1) = w(\pm 1) = 0\Big \}. \end{aligned}$$

The same can be done for \({\mathcal {R}} = \oplus _{k_x,k_y} \mathcal R_{k_x,k_y}\), where

$$\begin{aligned} {\mathcal {R}}_{k_x,k_y} = \Big \{\big (w(z) e^{i (k_x x + k_y y)},\zeta (z) e^{i (k_x x + k_y y)}\big ) \,\Big |\, \, \zeta (\pm 1) = w(\pm 1) = w_z(\pm 1) = 0\Big \}. \end{aligned}$$

The relations between the stream functions and the original velocity fields are \(\zeta = i k_x v - i k_y u\) and

$$\begin{aligned} {\left\{ \begin{array}{ll} u = \dfrac{k_x w' + k_y \zeta }{i k^2}\\ v =\dfrac{k_y w' - k_x \zeta }{i k^2}.\\ \end{array}\right. } \end{aligned}$$
(8)

Remark

Behind this technique lays the common extension to complex-valued velocity fields and the understanding that, given a complex component of the velocity field e.g. \(w(z) e^{i (k_x x + k_y y)}\) there corresponds a real-valued physical component of the velocity field \(\Re (w(z)) \cos (k_x x + k_y y) - \Im (w(z)) \sin (k_x x + k_y y)\).

In each \({\mathcal {S}}_{k_x,k_y}\) and \({\mathcal {R}}_{k_x,k_y}\) one can define an energy

$$\begin{aligned} {\mathcal {E}}_{k_x,k_y} = \frac{1}{2} \iiint _{{\mathcal {C}}} \Big ( |u|^2 + |v|^2 + |w|^2 \Big ) dxdydz = \frac{1}{2 k^2} \iiint _{{\mathcal {C}}} \Big ( |\nabla w|^2 + |\zeta |^2 \Big ) dxdydz \end{aligned}$$

where \({{\mathcal {C}}} = [0, 2\pi /k_x] \times [0,2\pi /k_y] \times [-1,1]\) is the periodicity cell. We plan to investigate, depending on \(\xi ,\eta \), the energy-critical Reynolds number \(\overline{R}_{\xi ,\eta }\) at which the energy stops being a Lyapunov function, and the energy-critical wave numbers \((\overline{k}_x^{\xi ,\eta }, {\overline{k}}_y^{\xi ,\eta })\) of the perturbation \(({\overline{u}}^{\xi ,\eta },{\overline{v}}^{\xi ,\eta }, \overline{w}^{\xi ,\eta })\) that first violates strict monotonic decrease of the energy. The remark above is particularly important to understand the relation between \(({\overline{k}}_x^{\xi ,\eta }, \overline{k}_y^{\xi ,\eta })\), \(({\overline{u}}^{\xi ,\eta },{\overline{v}}^{\xi ,\eta }, {\overline{w}}^{\xi ,\eta })\) and the real physical perturbation of velocity that realises the critical change in monotonicity of the energy.

The problem we posed can be stated in analytic terms: on which perturbation of the velocity field the orbital derivative of the energy has its maximum, and for which R this maximum is zero? To solve this problem we numerically compute, for every \(\xi ,\eta \) the maximum \({\overline{m}}^{\xi ,\eta }\) of the functional

$$\begin{aligned} {\mathcal {G}}_{k_x,k_y}(w,\zeta ) = \frac{(f' w_x,w_z) + (g' w_y, w_z) + (f' w_y, \zeta ) - (g' w_x,\zeta )}{(\Delta w)^2 + |\nabla \zeta |^2}, \end{aligned}$$
(9)

together with the associated wave numbers \((\overline{k}_x^{\xi ,\eta }, {\overline{k}}_y^{\xi ,\eta })\) (and the functions \(({\overline{w}}^{\xi ,\eta }(z),{\overline{\zeta }}^{\xi ,\eta }(z))\) that realise such maximum). The functional \({\mathcal {G}}\) is deduced from the orbital derivative of \({\mathcal {E}}_{k_x,k_y}\) in its streamfunctions form. In fact

$$\begin{aligned} \dot{{\mathcal {E}}}_{k_x,k_y} = \Bigg [{\mathcal {G}}_{k_x,k_y}(w,\zeta ) - \frac{1}{R} \Bigg ] \Big ((\Delta w)^2 + |\nabla \zeta |^2\Big ), \end{aligned}$$
(10)

and hence \({\mathcal {E}}_{k_x,k_y}\) is strictly decreasing if and only if \(1/R > {\overline{m}}^{\xi ,\eta }\), from which it follows that the energy-critical Reynolds number \({\overline{R}}^{\xi ,\eta } = 1/{\overline{m}}^{\xi ,\eta }\), and the energy-critical wave numbers are the wave numbers \(({\overline{k}}_x^{\xi ,\eta }, \overline{k}_y^{\xi ,\eta })\) computed above.

3 Energy (non-modal) investigation of the system

The critical stream fields for the functional \({\mathcal {G}}_{k_x,k_y} (w,\zeta )\) are the solutions to the Euler–Lagrange equations

$$\begin{aligned} {\left\{ \begin{array}{ll} 2 m \Delta ^2 w= - f'' w_x - g'' w_y - 2 f' w_{xz} - 2 g' w_{yz} - f' \zeta _y + g' \zeta _x \\ 2 m \Delta \zeta = - f' w_y +g' w_x\\ w=w_z = \zeta = 0 \quad \text {on the boundary.} \end{array}\right. } \end{aligned}$$
(11)

We stress the often disregarded fact that if there exists an m such that Eq. (11) admits a non-zero solution \(({\overline{w}}_m,{\overline{\zeta }}_m)\), then m is a critical value for \({\mathcal {G}}\) and \(({\overline{w}}_m,{\overline{\zeta }}_m)\) is a critical point only if in addition \({\mathcal {G}}(\overline{w}_m,{\overline{\zeta }}_m) = m\).

Starting from Eq. (11), we use a spectral method to compute the critical values m of \({\mathcal {G}}\). We can in fact consider Eq. (11) as a generalised eigenvalue problem

$$\begin{aligned}{} & {} \left[ m \begin{pmatrix} D^4 - 2 k^2 D^2 + k^4 &{} 0 \\ 0 &{} D^2 - k^2 \end{pmatrix} -\begin{pmatrix}- i \frac{k_x f'' + k_y g''}{2} - i k_x f' D - i k_y g' D &{} \qquad -i \frac{k_y f' - k_x g'}{2} \\ - i \frac{k_y f' - k_x g'}{2} &{} \qquad 0\end{pmatrix} \right] \begin{pmatrix}w(z)\\ \zeta (z)\end{pmatrix}= 0,\nonumber \\ \end{aligned}$$
(12)

where D represents the derivative with respect to z. We use a standard Chebyshev collocation algorithm to compute the values m that admit a non-zero solution, in other words we write

$$\begin{aligned}{} & {} \left[ m \begin{pmatrix} \big (D_N^2 - k^2 {\mathbb {I}}\big )^2&{} 0 \\ 0 &{} D_N^2 - k^2 {\mathbb {I}} \end{pmatrix} + i \begin{pmatrix} \dfrac{k_x f''_N + k_y g''_N}{2} + k_x f'_N D_N + k_y g'_N D_N &{} \, \dfrac{b f'_N - k_x g'_N}{2} \\ \dfrac{k_y f'_N - k_x g'_N}{2} &{} \, 0 \end{pmatrix} \right] \begin{pmatrix} w_N \\ \zeta _N \end{pmatrix} = 0, \nonumber \\ \end{aligned}$$
(13)

where \(D_N\) is a \((N+1)\times (N+1)\) matrix \(f_N\) is a diagonal matrix that on the diagonal has the values of f on the \(N+1\) Chebyshev nodes (same for g and their derivatives), \( {\mathbb {I}}\) is the \((N+1)\times (N+1)\) identity matrix, and \(w_N,\zeta _N\) are \(n+1\) vectors whose components are the values of \(w,\zeta \) along the Chebyshev nodes. This approach allows to compute, for every \(\xi ,\eta \), the maximum \({\overline{m}}^{\xi ,\eta }\), its associated energy-critical Reynolds numbers \({\overline{R}}^{\xi ,\eta } = 1/{\overline{m}}^{\xi ,\eta }\), and the associated energy-critical wave numbers \(({\overline{k}}_x^{\xi ,\eta }, {\overline{k}}_y^{\xi ,\eta })\).

Fig. 2
figure 2

In (a) a density plot of energy-critical wave numbers: the energy-critical perturbation is only streamwise, that is \(k_x = 0\), when \((\xi ,\eta )\) belongs to the dark grey region, it is only spanwise, that is \(k_y = 0\), when \((\xi ,\eta )\) belongs to the white region, it is mixed, that is \(k_x,k_y \not = 0\), when \((\xi ,\eta )\) belongs to the light grey region. In the rectangular frames an investigation on a finer grid has been performed to have a better understanding of the interface at the meeting point of the three regions. The main plot is computed on a grid with steps of approximately 0.15 in \(\eta \), 0.05 in \(\xi \). In the two rectangles the steps have been reduced to 0.05 in \(\eta \), 0.02 in \(\xi \) and 0.005 in \(\eta \), 0.01 in \(\xi \) respectively. In b the plot of the function \(\arctan (k_x/k_y)\) to represent the same information of plot a with more quantitative detail on the transition between spanwise and streamwise (the light grey region). In c three slices of \({\overline{R}}^{\xi ,\eta }\), as \(\xi \) ranges from 0 to 3, for fixed values of \(\eta = 0\) (continuous black) \(\eta = 10\) (dashed) and \(\eta = 100\) (dotted)

Full size image

An idea of the critical wave numbers \({\overline{k}}_x^{\xi ,\eta }\) and \({\overline{k}}_y^{\xi ,\eta }\) can be given with a density plot in the plane \(\xi ,\eta \). In Fig. 2a we indicate in dark grey the region in which \({\overline{k}}_x^{\xi ,\eta } = 0\), in white the region in which \({\overline{k}}_y^{\xi ,\eta } = 0\), and in light-grey the region in which both \({\overline{k}}_x^{\xi ,\eta }\) and \(\overline{k}_y^{\xi ,\eta }\) are not zero. In Fig. 2b the same information is given with some more detail on the light-grey region, where the continuous variation of the inclination vector \((k_x,k_y)\) from spanwise to streamwise is shown.

In absence of spanwise component in the base flow (\(\eta = 0\)) the energy-critical solution is independent of x. In the literature [2, 23], this event is defined as streamwise, but this name is misleading, since it does not mean that the energy-critical solution has only streamwise component (i.e. \(v=0\)), but it only means that the solution is independent on x and hence its flow can be translated along the x-component, which typically produces rolls whose axis is along the stream direction.

When the streamwise component is Couette (\(\xi =0\)) an increase of the Poiseuille spanwise component of the base flow forces the energy-critical solution to change continuously from from streamwise to a solution that has both wave numbers non-zero (we call such perturbation “mixed”). The same happens when \(\xi \not = 0\) but small enough. When \(\xi \) exceeds a certain value, that is when the Poiseuille streamwise component is strong enough, then the change from streamwise to spanwise takes place without continuity. This is not unreasonable, and it has a possible realisation with an appropriate deformation of Figure 1 right of reference [22]. The peculiar meeting point of the three regions required a finer investigation to verify the absence of a chaotic interface. Indeed the interphase appears regular. The step-size of the coarse and finer grids are specified in the caption of Fig. 2.

Fig. 3
figure 3

Two views of the graph of \({\overline{R}}^{\xi ,\eta }\), the function that to every \(\xi ,\eta \) associates the smallest value of R at which the energy stops being a Lyapunov function. The two rectangular patches correspond to the two rectangles where a finer grid has been used to produce Fig. 2b

Full size image

The representation of the energy-critical Reynolds numbers is given in Fig. 3 as a function of \(\xi ,\eta \) and in Fig. 2c for three slices with \(\eta \) fixed and equal to 0, 10, 100. In Fig. 2c one can observe that when \(\eta =0\), that is when the spanwise component in the base flow vanishes, the energy-critical Reynolds numbers have a maximum value equal to 51.0044 when \(\xi = 0.923077\), that is on a base flow that is not Poiseuille, but it has a small Couette component, and hence it corresponds to slowly moving plates. The consequence of this fact is visible in the crossing of the surfaces computed by Giacobbe in [22] and plotted in their Figure 1 and 2. Also observe that the energy-critical Reynolds number decreases when \(\eta \) increases, and it can be numerically proven to converge to zero (see Fig. 2c). This indicates a destabilising effect of the transverse flow.

The energy-critical values \({\overline{R}}^{\xi ,\eta }\) plotted in Fig. 3 are a continuous function of \(\xi ,\eta \), but at the boundaries of the regions shaded in grey in Fig. 2 such function appears to have crests that indicate discontinuous derivative.

4 Spectral (modal) investigation of the system

Equation (6) can be recast using Fourier expansion to compute the spectrum of this system for any given base flow, that is for every choice of \(\xi ,\eta \). This can be done using a classical approach that consists in substituting to \(w(x,y,z), \zeta (x,y,z)\) in (6) the functions \(e^{\lambda t} w(z) e^{i (k_x x + k_y y)}\) and \(e^{\lambda t} \zeta (z) e^{i (k_x x + k_y y)}\) respectively. The equations can be recast into a generalised eigenvalue problem

$$\begin{aligned} {\left\{ \begin{array}{ll} \lambda (D^2 - k^2) w = ((D^2 - k^2)^2/R - f i k_x (D^2 - k^2) \\ \quad - i k_y (D^2 - k^2) + i k_x f'' w_x + i k_y g'') w\\ \lambda \zeta = ((D^2 - k^2)/R - i k_x f - i k_y g) \zeta + (i k_y f' - i k_x g') w. \end{array}\right. } \end{aligned}$$
(14)

(D indicates as usual the derivative with respect to z.) The solutions of this problem can be computed discretising the problem with a Chebyshev collocation method. We did proceed as follows: we fixed a choice of parameters \(\xi , \eta \) (this amounts to fixing the velocity profile functions f, g). For every choice of \(k_x,k_y,R\) we numerically computed the function \(\lambda _m(k_x,k_y,R)\), which is the maximal real part of the eigenvalues \(\lambda \) of (14). The equation \(\lambda _m(k_x,k_y,R) = 0\) allows to define a function \(R(k_x,k_y)\) such that \(\lambda _m(k_x,k_y,R(k_x,k_y)) = 0\). The computation of \(R(k_x,k_y)\) can be done resorting to a bisection method, which quickly converges to the solution with the accuracy needed. Since we look for the smallest Reynolds number at which there exists an eigenvalue with zero real part, we then have to minimise the function \(R(k_x,k_y)\) with respect to \(k_x,k_y\). This minimisation defines the spectrum-critical Reynolds number \(\widetilde{R}^{\xi ,\eta }\) and the spectrum-critical wave numbers \(\widetilde{k}_x^{\xi ,\eta }, {\widetilde{k}}_y^{\xi ,\eta }\) at which the minimum is attained. The determination of such critical values is very CPU consuming. To reduce this time we minimised with respect to \(k_x,k_y\) in a square of semi-side \(\delta \) around an educated guess, and then we sampled in that square with grid-step of \(\delta /5\) (which means sampling on 100 points). The educated guess can be made using the energy-critical wave numbers of neighbouring values of \(\xi ,\eta \) previously computed. The value of \(\delta \) must be slowly decreased to increase accuracy. In our computations we made various choices for \(\delta \), but mainly we ended up choosing \(\delta = 0.1\). We thus obtain an accuracy of the wave numbers up to the second digit.

Fig. 4
figure 4

In pane a the plot of \({\widetilde{R}}^{\xi ,0}\) with \(\xi \) from 0.76 to 1.06. In pane b the plot of \(\widetilde{k}_x^{\xi ,0}\) in the same range for \(\xi \)

Full size image

Let us show and comment the results: for \(\eta = 0\) the critical values have been computed implicitly in [7] and explicitly in [8], where can be found a plot identical to our Fig. 4a, plotted on a smaller \(\xi \) interval. For Couette base flow, which corresponds to our case \(\xi = 0\) and \(\eta = 0\), it is known that \({\widetilde{R}}^{0,0} = + \infty \) and hence there are no critical wave numbers. For Poiseuille base flow, which corresponds to our case \(\xi = 1\) and \(\eta = 0\), it is known that \({\widetilde{R}}^{1,0} = 5772\) and the critical wave numbers are \({\widetilde{k}}_x^{1,0} = 1.02\) and \({\widetilde{k}}_y^{1,0} = 0\).

In Fig. 4 we fix \(\eta = 0\) and plot the critical Reynolds number \({\widetilde{R}}^{\xi ,0}\) and the critical wave number \({\widetilde{k}}_x^{\xi , 0}\) for varying values of \(\xi \in [0.76,1.06]\). A plot equivalent to this can be found in Figure 2 in reference [8]. In this case it is well known that the critical wave number \({\widetilde{k}}_y^{\xi , 0}\) is always zero, for this reason only \({\widetilde{k}}_x^{\xi ,0}\) is plotted. A few peculiar facts can be listed:

  1. 1.

    the critical perturbations, where instability must occur, are independent from y. This is in opposition with what happens for the energy-critical perturbations, where “instability” first occurs on perturbations independent from x;

  2. 2.

    Poiseuille flow realises the minimal critical Reynolds number;

  3. 3.

    when \(\xi \) decreases from 1, the increase of \(\widetilde{R}^{\xi ,0}\) flattens and slightly changes monotonicity in the region [0.8, 0.9];

  4. 4.

    the critical Reynolds number does eventually tend to infinity as \(\xi \) diminishes. In our computation we have not been able to compute a critical Reynolds number for \(\xi = 0.75\), the last value of \(\xi \) for which we found a critical Reynolds number is \(\xi = 0.76\).

The first point is reasonable, the second is a known result due to Joseph, the third is unexpected, and a monotonic behaviour would appear more natural. As for the last point, an asymptote is expected, because it is well known that Couette is always spectrally stable, but it would be interesting to compute the position of the vertical asymptote (possibly \(\xi = 3/4\)) and understand if there is a reason for this.

Fig. 5
figure 5

In the two panes the plots of \(\widetilde{R}^{1,\eta }\), \({\widetilde{k}}_x^{1,\eta }\) (continuous black line) and of \({\widetilde{k}}_y^{1,\eta }\) (dashed black line) for \(\eta \) in the interval [0, 1.1]. The dotted grey graphs are their theoretical values, \({\widetilde{R}}^{1, \eta } = 5772/\sqrt{1+\eta ^2}\), \(\widetilde{k}_x^{1,\eta } = 1.02/ \sqrt{1+\eta ^2}\), \({\widetilde{k}}_y^{1,\eta } = 1.02 \eta / \sqrt{1+\eta ^2}\). when \(\eta = 1\) the Poiseuille flow is precisely along the diagonal, and the two wave numbers become equal

Full size image

In Fig. 5 we fix \(\xi = 1\), and we plot the critical Reynolds number and the critical wave numbers as \(\eta \) moves in [0, 1.05]. These plots are precisely as expected, since when \(\xi = 1\), for every \(\eta \), the base flow is a Poiseuille flow along the direction \(\textbf{i}+ \eta \, \textbf{j}\) with the nondimensionalisation done so that the maximal velocity of the fluid is \(\sqrt{1+\eta ^2}\). This implies that the Reynolds number must be \({\widetilde{R}}^{1,\eta } = 5772/\sqrt{1+\eta ^2}\) and the two wave numbers must be \(\widetilde{k}_x^{1,\eta } = 1.02/\sqrt{1+\eta ^2}\), \({\widetilde{k}}_y^{1,\eta } = 1.02 \, \eta / \sqrt{1+ \eta ^2}\).

Fig. 6
figure 6

In black, the log-log-plot of \(\widetilde{R}^{0,\eta }\) as \(\eta \) moves from 0 to 100. The grey dotdashed graph is the log-log-plot of the function \(5772/\sqrt{1+\eta ^2}\), that is the theoretical critical value of \({\widetilde{R}}^{1,\eta }\) already plotted in Fig. 5a. The grey dotted graph superimposed to the black plot is that of the function \(5772/\eta \), the Reynolds number of a Poiseuille flow nondimensionalised to have maximal velocity \(\eta \)

Full size image

In Fig. 6 some less expected features can be seen. The black continuous plot is that of the function \(\widetilde{R}^{0,\eta }\), which is the critical Reynolds number of a base flow that is Couette along the streamwise \(\textbf{i}\) direction and has an increasingly strong (with \(\eta \)) Poiseuille flow along the spanwise \(\textbf{j}\) direction. The two grey plots in Fig. 6 are those of \({\widetilde{R}}^{1,\eta }\) and of \(5774/\eta \), that corresponds to the Reynolds number of a Poiseuille base flow nondimensionalised so that the maximal velocity of the fluid is \(\eta \).

As expected, the asymptotic behaviour of all three graphs is the same as \(\eta \) grows, since the Poiseuille component is increasingly strong and hence becomes dominating. As \(\eta \) tends to zero the graph of \({\widetilde{R}}^{1,\eta }\) tends, as expected, to 5774. What is striking is that the asymptotic of \({\widetilde{R}}^{0,\eta }\) is the same as that of the function \(5774/\eta \) as \(\eta \) tends to zero. Observe that the first one is the critical Reynolds number of Couette flow plus an infinitesimal transversal Poiseuille flow, while the second one is simply an infinitesimal Poiseuille flow.

5 Discussion of the results and conclusions

In this article we made a spectral and an energy-growth analysis for a base flow that is a combination of a Couette–Poiseuille flow in the streamwise direction and of Poiseuille flow in the (crossed) spanwise direction. We did analyse in detail the effects of the Poiseuille crossflow on the monotonicity of the energy and on the spectrum of the linearisation at the base flow. In particular we did investigate the dependence of critical Reynolds number and critical wave numbers from the type of combination of Couette–Poiseuille streamwise and Poiseuille spanwise.

The most interesting result has been obtained investigating the energy-critical wave number. Smooth changes from stream (\(\overline{k}_x = 0\)) to mixed (both \({\overline{k}}_x, {\overline{k}}_y\not = 0\)) to span (\({\overline{k}}_y=0\)) can be observed when \(\xi \) is small, that is when the Couette component along the streamwise direction is dominating. When \(\xi \) is closer to 1, that is when the Poiseuille component becomes dominating, then a discontinuous change from streamwise to spanwise takes place. This abrupt changes also reflects into a discontinuity of the first derivative of the energy-critical Reynolds numbers. This numerical phenomenon becomes puzzling when \(\xi = 1\) for increasing \(\eta \). In fact it seems reasonable that the critical Reynolds number and the critical wave numbers should rescale as it happens in the modal analysis (see Fig. 5). The reason for this behaviour requires further investigation.

The modal analysis requires a heavier computational load, and we mostly obtained either confirmations of known results by Potter and Hains, or results that could be computed theoretically by considering known spectrum-critical Reynolds and wave numbers for Poiseuille flow applied to a non-normalised Poiseuille flow along a transverse direction. A new result is the observation that, if the base flow is Couette (obviously along the streamwise direction) plus a weak contribution of spanwise Poiseuille, event that is most probable in nature and is typical if one considers a small perturbation of a dominating base flow, then the spectrum-critical Reynolds number tends to infinity as it would do simply with a weak Poiseuille flow (meaning computing the Reynolds number for a Poiseuille flow nondimensionalised so that its maximal velocity equals \(\eta \) and not 1).

There is space for new investigations, as peculiar behaviours could arise. For example: a 3D plot of the spectrum-critical Reynolds number \({\widetilde{R}}\) and its corresponding critical wave numbers \({\widetilde{k}}_x, {\widetilde{k}}_y\) as functions of \(\xi ,\eta \) is missing, because computations are too heavy; a finer understanding of what happens when the energy-critical solution changes abruptly from streamwise to spanwise (the interface in \(\xi ,\eta \) space between dark grey and white regions in Fig. 2); a finer understanding of the crest in the plots of Fig. 3, that should be closely related to the previous question; a numerical simulation of the evolution of a perturbation of the base flow slightly above threshold, with initial data obtained by adding to the base flow a small multiple of the energy-critical solution.