1 Introduction

Flocking of self-propelled particles (agents) denotes a collective motion in which particles are organized into an ordered state from a disordered state only using the limited environmental information and simple rules. It appears in natural and man-made systems [1, 4, 5, 47, 49], e.g., flocking of birds, drones and robots, flocking of birds, swarming of fish and herding of sheep, etc. Despite of its ubiquitous presence, modeling and analysis for flocking were begun only several decades ago. After Reynolds’ boid model [45], Vicsek et al. [48] proposed a simple discrete planar model with a unit speed constraint. As far as the authors know, there is no rigorous convergence proof for the Vicsek model (see [37] for a convergence proof under a priori connected assumption for each instant). To circumvent this a priori connectedness assumption, Cucker and Smale introduced a second-order Newton type model [22, 23] for position and velocity which we call it as the Cucker–Smale (in short CS) model. In fact, the CS model uses a weighted sum of relative velocities as an force. For a brief introduction on CS flocking, we refer to a survey article [13]. To set up the stage, we begin with a brief discussion for the (particle) CS model.

Let \(x_i\) and \(\xi _i\) be the position and velocity of the ith CS particle on a spatial domain \(\Omega ^x (\subset {\mathbb {R}}^d)\), respectively. Then, the CS model reads as follows.

$$\begin{aligned} {\left\{ \begin{array}{ll} \displaystyle {\dot{x}}_i = \xi _i, \quad t > 0,\quad i \in [N]:= \{1,\dots ,N \}, \\ \displaystyle {{\dot{\xi }}}_i=\frac{1}{N}\sum _{j=1}^{N}\psi (x_j , x_i)(\xi _j - \xi _i), \end{array}\right. } \end{aligned}$$
(1)

where N and \(\psi \) denote the total number of particles and Lipschitz continuous communication weight function satisfying symmetry and boundedness, respectively: there exists a positive constant \(\psi _M\) such that

$$\begin{aligned} \psi (x, y) = \psi (y, x), \quad 0 < \psi (x,y) \le \psi _M, \quad \forall ~ x, y \in \Omega ^x. \end{aligned}$$
(2)

The global well-posedness for (1)–(2) is guaranteed by the standard Cauchy–Lipschitz theory. Hence, most literature for (1) are concerned with the emergence of flocking under various contexts, e.g., collision avoidance [18, 19], stochastic environment [2, 21, 25, 26, 33, 44], time-delay [27], network topologies [20, 24, 38, 39], relativistic and thermodynamic effects [32, 36], etc.

On the other hand, when the number of particles is sufficiently large (namely a mesoscopic regime), direct integration of (1) will be too expensive to describe the motion of CS ensemble with \(N \gg 1\). Hence, as an effective mean-field approximation of a large particle system (1), we can use the corresponding mean-field kinetic equation (see [34] for the mean-field limit). More precisely, let \(f = f(t, x, \xi )\) be the one-particle distribution function at position x, velocity \(\xi \) at time t. Then, the temporal-phase space evolution of f is governed by the following initial boundary value problem to the kinetic CS equation on a spatial domain \(\Omega ^x (\subset {\mathbb {R}}^d)\):

$$\begin{aligned} {\left\{ \begin{array}{ll} \partial _{t} f+\xi \cdot \nabla _{x} f+ \nabla _{\xi } \cdot (F_a(f) f)=0, \quad t > 0,~~(x, \xi ) \in \Omega ^x \times {\mathbb {R}}^d, \\ f(t, x, \xi ) \Big |_{t = 0+} = f_0(x, \xi ), \end{array}\right. } \end{aligned}$$
(3)

subject to suitable boundary conditions on \(\partial ( \Omega ^x \times {\mathbb {R}}^d)\). Here \(F_a(f)\) is a velocity alignment force whose explicit form is given as follows:

$$\begin{aligned} F_a(f)(t,x, \xi )= -\int _{\Omega ^x \times {\mathbb {R}}^d} \psi (x,x_*) (\xi -\xi _{*} ) f(t,x_*, \xi _{*}) d x_* d \xi _*. \end{aligned}$$
(4)

The global well-posedness and flocking dynamics of the Cauchy problem (3)–(4) have been extensively studied in [11, 29, 34, 35]. However due to the non-local nature of (4), numerical implementation of (3) is less investigated. Recently, structure and positivity preserving schemes are proposed for the related collective models such as the continuum Kuramoto model [8] and kinetic flocking model [46]. In particular, the latter work [46] introduces a fully discrete DG scheme for (1) and flocking model [40] in one-dimensional setting and the author also showed that his DG scheme exhibits a positivity preserving property which results in the stability in \(L^1\) under the suitable CFL type condition on time-step and mesh size. The DG method, proposed in [46], can be reduced to a classical high order finite volume method, which is proved to be positive preserving, for (3), where the transport term is neglected and the velocity alignment (4) is independent on the space variable. As long as there is no confusion, we will use the jargons “kinetic model” and “kinetic equation” interchangeably.

The main results of this paper are two-fold. First, we introduce a local discontinuous Galerkin method for the computation of the approximate solution with high order approximations in time, space and velocity (see Sect. 2.2. Indeed, the preservation of high order accuracy allows us to investigate complicate structures in space, as it has already been observed for macroscopic models. Discontinuous Galerkin methods [6, 15, 17, 30, 31] are particularly suited for transport type equations with several attractive properties, such as their easiness for adaptivity and parallel computation, and their nice stability properties. We refer to the survey paper [16] and the references therein for a discontinuous Galerkin methods. For discontinuous Galerkin methods solving kinetic type equations we refer to [3, 12]. Discontinuous Galerkin methods are particularly suitable for transport type equations with several attractive properties, such as their easiness for adaptivity and parallel computation, and their nice stability properties. Second, we study \(L^2\)-stability, consistency and convergence of numerical solutions given by the discontinuous Galerkin method for (3) and (4) (see Theorem 2.5).

The paper after this introduction is organized as follows. In Sect. 2, we study basic properties and well-posedness of the kinetic CS model, and discuss a semi discrete discontinuous Galerkin numerical approximation and main results. In Sect. 3, we study the mass conservation and \(L^2\)-stability of the numerical solutions. In Sect. 4, we provide an \(L^2\)-convergence of numerical solutions to the regular solutions to the kinetic CS model. In Sect. 5, we present several numerical implementations in one and two dimensional settings. Finally, Sect. 6 is devoted to a brief summary of our main results and some remaining issues for a future work.

Notation In what follows, we often suppress domain depencence \(\Omega ^x \times {\mathbb {R}}^d\) for Lebesgue space \(L^p(U \times {\mathbb {R}}^d)\):

$$\begin{aligned} \Vert \cdot \Vert _{L^p}:= \Vert \cdot \Vert _{L^p(\Omega ^x \times {\mathbb {R}}^d)}, \quad 1 \le p \le \infty . \end{aligned}$$

As long as there is no confusion, we use the subscript and superscript to denote the particle number and component, respectively, i.e., \(x_i^j, \xi _i^j\) are the jth spatial and velocity component of the ith particle:

$$\begin{aligned} x_i = (x_i^1, \cdots , x_i^d) \in \Omega ^x, \quad \xi _i = (\xi _i^1, \cdots , \xi _i^d) \in {{\mathbb {R}}}^d. \end{aligned}$$

2 Preliminaries and main results

In this section, we first present basic properties of the kinetic Cucker–Smale model and review the global well-posedness of the Cauchy problem to (3)–(4), and then we delineate a semi-discrete discontinuous Galerkin method and provide our main results on the \(L^2\)-stability and convergence of numerical solutions.

2.1 The kinetic CS equation on \(\Omega ^x = {\mathbb {R}}^{d}\)

Consider the Cauchy problem to the kinetic CS equation on the whole space \({\mathbb {R}}^{2d}\):

$$\begin{aligned} {\left\{ \begin{array}{ll} \displaystyle \partial _{t} f+ \nabla _{x} \cdot (\xi f) +\nabla _{\xi } \cdot (F_a(f) f )=0, \quad t > 0,~~(x,\xi ) \in {\mathbb {R}}^{2d}, \\ \displaystyle f(t, x, \xi ) \Big |_{t = 0+} = f_0(x, \xi ), \end{array}\right. } \end{aligned}$$
(5)

In what follows, we discuss the propagation of the first three velocity moments: for \(t \ge 0\),

$$\begin{aligned} m_0(t):= \int _{{\mathbb {R}}^{2d}} f(t,z) dz, \quad m_1(t):= \int _{{\mathbb {R}}^{2d}} \xi f(t,z) dz, \quad m_2(t):= \int _{{\mathbb {R}}^{2d}} |\xi |^2 f(t,z) dz, \end{aligned}$$

where \(z = (x, \xi )\) and \(dz = d\xi dx\).

Lemma 2.1

Let \(f = f(t, z)\) be a global classical solution to (5) which decays to zero sufficiently fast at infinity in the phase space. Then, velocity moments \(m_i,~i=0,1,2\) satisfy the following relations: for \(t \ge 0\),

$$\begin{aligned}{} & {} (i)~m_0(t) = m_0(0), \quad m_1(t) = m_1(0). \\{} & {} (ii)~m_2(t) = m_2(0) -\int _0^t \int _{{\mathbb {R}}^{4d}} \psi (x,x_*) |\xi -\xi _{*}|^2 f(s,z_*) f(s,z) d z_* dz ds. \end{aligned}$$

Proof

(i) The first relation directly follows from the integration of (5)\(_1\) over \({\mathbb {R}}^{2d}\) using the divergence theorem and fast decay of f at infinity. For the second relation, we multiply \(\xi \) to (5)\(_1\) to find

$$\begin{aligned} \partial _{t} (\xi f)+ \nabla _{x} \cdot (\xi \otimes \xi f) +\nabla _{\xi } \cdot ( \xi \otimes F_a(f) f )= d F_a(f) f. \end{aligned}$$

Again we integrate the above equation over \({\mathbb {R}}^{2d}\) using the symmetry property of \(\psi \), and use the divergence theorem to find the desired relation.

(ii) We use (5)\(_1\) to find

$$\begin{aligned} \begin{aligned} \partial _t (|\xi |^2 f)&= |\xi |^2 \partial _t f = - |\xi |^2 \Big ( \nabla _{x} \cdot (\xi f) +\nabla _{\xi } \cdot (F_a(f) f ) \Big ) \\&= - \nabla _{x} \cdot ( | \xi |^2 \xi f) -\nabla _{\xi } \cdot ( |\xi |^2 F_a(f) f ) + 2 ( \xi \cdot F_a(f)) f. \end{aligned} \end{aligned}$$
(6)

Now, we integrate (6) over \({\mathbb {R}}^{2d}\) and use index exchange transformation \((x, \xi ) \leftrightarrow (x_*, \xi _*)\) to get

$$\begin{aligned} \begin{aligned} \frac{d}{dt}\int _{{\mathbb {R}}^{2d}} |\xi |^2f dz&= 2 \int _{{\mathbb {R}}^{2d}} ( \xi \cdot F_a(f)) f dz\\&= -2 \int _{{\mathbb {R}}^{4d}} \psi (x,x_*) \xi \cdot (\xi -\xi _{*}) f(t,z_*) f(t,z) d z_* dz \\&= 2 \int _{{\mathbb {R}}^{4d}} \psi (x,x_|) \xi _* \cdot (\xi -\xi _{*}) f(t,z_*) f(t,z) d z_* dz \\&= - \int _{{\mathbb {R}}^{4d}} \psi (x,x_*) |\xi -\xi _{*} |^2 f(t,z_*) f(t,z) d z_* dz. \end{aligned} \end{aligned}$$

Again, we integrate the above relation in time to get the desired estimate. \(\square \)

Remark 1

Note that if we assume that initial total mass is unity, then total mass is conserved in time:

$$\begin{aligned} \int _{{\mathbb {R}}^{2d}} f(t,z) dz = 1, \quad t > 0. \end{aligned}$$

Next, we discuss the dynamics of particle trajectories (or bi-characteristics) corresponding to (5). For this, we rewrite (5)\(_1\) into a quasi-linear form:

$$\begin{aligned} \partial _{t} f+ \xi \cdot \nabla _{x} f + F_a(f) \cdot \nabla _{\xi } f = -(\nabla _{\xi } \cdot F_a(f)) f, \quad t > 0. \end{aligned}$$
(7)

Note that the coefficient \(-(\nabla _{\xi } \cdot F_a(f))\) in the R. H. S. of (7) can be rewritten as

$$\begin{aligned} -(\nabla _{\xi } \cdot F_a(f)) = d \int _{{\mathbb {R}}^{2d}} \psi (x,x_*) f(t,x_*, \xi _{*}) d x_* d \xi _*. \end{aligned}$$

This yields

$$\begin{aligned} \Vert \nabla _{\xi } \cdot F_a(f) \Vert _{L^\infty } \le d \psi _M m_0(t) = d \psi _M m_0(0). \end{aligned}$$

For \((x, \xi ) \in \text{ supp}_{(x, \xi )} f_0\), we define bi-charteristics (forward particle trajectory):

$$\begin{aligned} (x(t), \xi (t)) = (x(t; 0, x, \xi ), (\xi (t:0, x, \xi ))) \end{aligned}$$

as a solution to the following ODE system:

$$\begin{aligned} {\left\{ \begin{array}{ll} \displaystyle {\dot{x}}(t) = \xi (t), \quad t > 0, \\ \displaystyle {{\dot{\xi }}}(t) = -\int _{{\mathbb {R}}^{2d}} \psi (x(t),x_*) (\xi (t)-\xi _{*} ) f(t,x_*, \xi _{*}) d x_* d \xi _*, \\ \displaystyle (x(0), \xi (0)) = (x, \xi ). \end{array}\right. } \end{aligned}$$
(8)

Lemma 2.2

Suppose that the communication weight function \(\psi \) satisfies an extra condition together with (2): there exists positive constants \(\psi _m\) and \(\psi _M\) such that

$$\begin{aligned} 0 < \psi _m \le \psi (r) \le \psi _M, \quad \forall ~r \ge 0, \end{aligned}$$
(9)

and let \((x(t), \xi (t))\) be the particle trajectory of (5) issued from \((x, \xi ) \in \text{ supp } f_0\) at time 0. Then, the ith velocity component \(\xi _i(t)\) satisfies

$$\begin{aligned} \underline{\xi }^i (t) \le \xi ^i(t) \le \overline{\xi }^i(t), \quad t \ge 0. \end{aligned}$$

Here uniform lower and upper bounds \(\underline{\xi }^i\) and \(\overline{\xi }^i\) are defined as follows.

$$\begin{aligned} \begin{aligned} \underline{\xi }^i (t)&:= -\frac{\psi _m}{\psi _M} \sqrt{ \frac{m_2(0)}{m_0(0)} } + \Big ( \xi ^i(0) + \frac{\psi _m}{\psi _M} \sqrt{ \frac{m_2(0)}{m_0(0)} } \Big ) e^{-\psi _M m_0 t}, \quad l \in [d], \\ \overline{\xi }^i(t)&:= \frac{\psi _M}{\psi _m} \sqrt{ \frac{m_2(0)}{m_0(0)} } + \Big ( \xi ^i(0) - \frac{\psi _M}{\psi _m} \sqrt{ \frac{m_2(0)}{m_0(0)} } \Big ) e^{-\psi _m m_0 t}. \end{aligned} \end{aligned}$$
(10)

Proof

We use the same argument in [35]. For \((x, \xi ) \in \text{ supp}_{(x, \xi )} f_0\) at time 0, we set

$$\begin{aligned} x(t) = x(t; 0, x, \xi ) \quad \text{ and } \quad \xi (t) = \xi (t; 0, x, \xi ), \quad t \ge 0. \end{aligned}$$

Then, it follows from (8)\(_2\) that for \(l \in [d]\),

$$\begin{aligned} \begin{aligned} \frac{d\xi ^l(t)}{dt}&= - \int _{{\mathbb {R}}^{2d}} \psi (x^l(t), x_*) (\xi ^l(t)-\xi _{*} ) f(t,x_*, \xi _{*}) d x_* d \xi _* \\&= - \Big [ \int _{{\mathbb {R}}^{2d}} \psi (x^l(t),x_*) f(t,x_*, \xi _{*}) d x_* d \xi _* \Big ] \xi ^l(t) \\&\quad +\, \int _{{\mathbb {R}}^{2d}} \psi (x^l(t),x_*) \xi ^l_{*} f(t,x_*, \xi _{*}) d x_* d \xi _* \\&=: -\alpha _1(t) \xi ^l(t) + \alpha _2(t). \end{aligned} \end{aligned}$$
(11)

Below, we estimate \(\alpha _i,~i=1,2\) one by one.

\(\bullet \) (Estimate of \(\alpha _1\)): we apply the extra condition (9) to find

$$\begin{aligned} \psi _m m_0 \le \alpha _1(t) \le \psi _M m_0, \quad t \ge 0. \end{aligned}$$
(12)

\(\bullet \) (Estimate of \(\alpha _2\)): again, we use (9), the Cauchy-Schwarz inequality and Lemma 2.1 to obtain

$$\begin{aligned} \begin{aligned} |\alpha _2(t)|&\le \psi _M \int _{{\mathbb {R}}^{2d}} |\xi ^l_{*} | f(t,x_*, \xi _{*}) d x_* d \xi _* \\&\le \psi _M \Big ( \int _{{\mathbb {R}}^{2d}} |\xi ^l_{*} |^2 f(t,x_*, \xi _{*}) d x_* d \xi _* \Big )^{\frac{1}{2}} \cdot \Big ( \int _{{\mathbb {R}}^{2d}} f(t,x_*, \xi _{*}) d x_* d \xi _* \Big )^{\frac{1}{2}} \\&= \psi _M \sqrt{m_0(t) m_2(t)} \le \kappa \psi _M \sqrt{m_0(0) m_2(0)} . \end{aligned} \end{aligned}$$
(13)

Now, in (11) we combine all the estimates (12) and (13) to get differential inequalities:

$$\begin{aligned} - \psi _M m_0 \xi ^l(t) -\psi _M \sqrt{m_0(0) m_2(0)} \le \frac{d\xi ^l(t)}{dt} \le -\psi _m m_0 \xi ^l(t) + \psi _M \sqrt{m_0(0) m_2(0)}. \end{aligned}$$

Then, we use the Gronwall type arguments to derive the desired estimates. \(\square \)

Remark 2

Below, we briefly comment on the result of Lemma 2.2.

  1. 1.

    Note that the explicit relations (10) imply

    $$\begin{aligned} \begin{aligned}&\min \Big \{ \min _{1 \le i \le d} \xi ^i(0),~-\frac{\psi _m}{\psi _M} \sqrt{ \frac{m_2(0)}{m_0(0)} } \Big \} \le \inf _{0 \le t< \infty } \underline{\xi }^i (t), \,\, \lim _{t \rightarrow \infty } \underline{\xi }^i (t) = -\frac{\psi _m}{\psi _M} \sqrt{ \frac{m_2(0)}{m_0(0)} }, \\&\sup _{0 \le t < \infty } \overline{\xi }^i (t) \le \max \Big \{ \max _{1 \le i \le d} \xi ^i(0),~\frac{\psi _M}{\psi _m} \sqrt{ \frac{m_2(0)}{m_0(0)} } \Big \}, \,\, \lim _{t \rightarrow \infty } \overline{\xi }^i (t) = \frac{\psi _M}{\psi _m} \sqrt{ \frac{m_2(0)}{m_0(0)} }. \end{aligned} \end{aligned}$$
  2. 2.

    Suppose that communication weight and initial datum satisfy

    $$\begin{aligned} \psi \equiv 1, \quad m_0(0)< \infty , \quad |m_1(0) | < \infty . \end{aligned}$$

    Then, it follows from (11) that particle trajectory \(\xi ^i(t)\) satisfies

    $$\begin{aligned} \frac{d \xi (t)}{dt} = -m_0(0) \xi (t) + m_1(0), \quad t > 0. \end{aligned}$$

    By direct calculation, one has

    $$\begin{aligned} \begin{aligned}&\xi (t) = \frac{m_1(0)}{m_0(0)} + \Big ( \xi - \frac{m_1(0)}{m_0(0)} \Big ) e^{-m_0(0) t}, \\&x(t) = x + \frac{m_1(0)}{m_0(0)} t + \frac{1}{m_0(0)} \Big ( \xi - \frac{m_1(0)}{m_0(0)} \Big ) (1 - e^{-m_0(0) t}). \end{aligned} \end{aligned}$$

    Therefore we have

    $$\begin{aligned} \lim _{t \rightarrow \infty } \Big | \xi (t) - \frac{m_1(0)}{m_0(0)} \Big | = 0, \quad \lim _{t \rightarrow \infty } \Big | x(t) - x - \frac{m_1(0)}{m_0(0)} t - \frac{1}{m_0(0)} \Big ( \xi - \frac{m_1(0)}{m_0(0)} \Big ) \Big | = 0. \end{aligned}$$

Next, we return to the global well-posedness of (5). Then, the global well-posedness of (6) follows from a priori \(W^{k, \infty }\)-estimates along the particle trajectory.

Theorem 2.3

[35] Suppose that the initial datum \(f_0\) is compactly supported in the phase space and sufficiently regular such that

$$\begin{aligned} f_0 \in W^{k,\infty }({\mathbb {R}}^{2d}), \quad \text{ for } \text{ some } \text{ integer } k \ge 2. \end{aligned}$$

Then for any \(T \in (0, \infty )\), there exists a unique classical solution \(f(t) \in W^{k, \infty }({\mathbb {R}}^{2d})\) for \(t \in (0, T)\) and a positive constant C(T) such that

$$\begin{aligned} \sup _{0 \le t \le T} \Vert f(t) \Vert _{W^{k, \infty }} \le C(T) \Vert f_0 \Vert _{W^{k, \infty }}. \end{aligned}$$

Proof

The proof is basically based on a priori estimate on the control of \(W^{k, \infty }\)-norm for f along bi-characteristics: for \(T \in (0, \infty )\), let \((x(t), \xi (t))\) be a particle trajectory defined by (8). Then, we have

$$\begin{aligned} \frac{d}{dt} f(t, x(t), \xi (t)) \le d \psi _M m_0 f(t, x(t), \xi (t)), \quad t > 0. \end{aligned}$$

This yields

$$\begin{aligned} \Vert f(t) \Vert _{L^\infty } \le e^{d \psi _M m_0 t} \Vert f_0 \Vert _{L^\infty }, \quad t \in (0, T). \end{aligned}$$

For the higher-order \(W^{k, \infty }\)-estimate, we use the same arguments to get

$$\begin{aligned} \sup _{0 \le t \le T} \Vert f(t) \Vert _{W^{k, \infty }} \le C(T) \Vert f_0 \Vert _{W^{k, \infty }}. \end{aligned}$$
(14)

Then we combine the above a priori estimate (14) and standard local existence result to derive a global existence of classical solution for \(k \ge 2\). We refer to [35] for details. \(\square \)

Next, we discuss a global well-posedness of a measure-valued solution to the Cauchy problem (5). For the concept of measure-valued solutions, we refer to [34]. Now, we briefly recall some jargons. For the particle solution \((x_i(t),\xi _i(t))\) to (1), we introduce the associated empirical measure \(\mu ^N(t)\):

$$\begin{aligned} \mu ^N(t) = \frac{1}{N} \sum _{i=1}^N \delta _{(x_i(t), \xi _i(t))}. \end{aligned}$$

Then we can show that \(\mu ^N\) satisfies the Eq. (5) in the sense of distributions, i.e., \(\mu ^N\) is a measure-valued solution to (5).

Let \({\mathcal {M}}({\mathbb {R}}^{2d})\) be the set of positive Radon measures and we fix \(T > 0\). Then, we define the set \({{\mathcal {S}}}\) of test functions and a bounded Lipschitz distance \(d_{BL}(\mu _1,\mu _2)\) on \({{\mathcal {S}}}\) as follows:

$$\begin{aligned} \begin{aligned}&{\mathcal {S}} := \Big \{h: {\mathbb {R}}^{2d} \rightarrow {\mathbb {R}}~:~ \Vert h\Vert _{L^\infty } \le 1 \quad \text{ and } \quad \text{ Lip(h) } := \sup _{x \ne y}\frac{|h(x) - h(y)|}{\Vert x-y\Vert } \le 1 \Big \}, \\&d_{BL}(\mu _1,\mu _2) := \sup _{h \in {\mathcal {S}}} \Big \{ \Big |\int _{{\mathbb {R}}^d \times {\mathbb {R}}^d} h \,d \mu _1 - \int _{{\mathbb {R}}^d \times {\mathbb {R}}^d} h \,d\mu _2 \Big |: \quad \text{ for } \mu _1, \mu _2 \in {\mathcal {M}}({\mathbb {R}}^{2d}) \Big \}. \end{aligned} \end{aligned}$$

Theorem 2.4

[34] Suppose that the initial measure \(f_0 dx d\xi \in {\mathcal {M}}({\mathbb {R}}^{2d} )\) is compactly supported, and we take a sequence of \(\mu ^N_0\) of measures of the form \(\mu ^N_0 = \frac{1}{N} \sum _{i=1}^N \delta _{(x_i(0), \xi _i(0))}\) such that

$$\begin{aligned} \lim _{N \rightarrow \infty } d_{BL} (\mu ^N_0,f_0 d\xi dx) = 0. \end{aligned}$$

Define the empirical measure \(\mu _N(t)\) made of particle solution \((x_i, \xi _i)\) with initial data \((x_i(0), \xi _i(0))\). Then there exists a unique measure-valued solution f to (5) with the initial datum \(f_0\) such that

$$\begin{aligned} \lim _{N \rightarrow \infty }d_{BL}(\mu ^N(t),f(t) dx d\xi )=0 \quad \text{ for } \quad t \ge 0. \end{aligned}$$

2.2 A semi-discrete DG scheme

In this subsection, we describe a semi-discrete DG scheme for (5) on the spatial periodic domain \(\Omega ^x\).

Suppose that \(\psi \) and initial datum \(f_0\) are spatially periodic with the same period, and compactly supported in the velocity variable. Then, it is easy to see that the solution f is periodic in spatial variable and compactly supported in velocity variable as well. Before we describe the DG scheme, we first discuss finite-dimensional function spaces. Let \(\Omega =\Omega ^x\times \Omega ^\xi \subset {\mathbb {R}}^d\times {\mathbb {R}}^d\) be an open bounded set such that

$$\begin{aligned} \text{ supp}_{\xi } f(t,x, \cdot ) \subset \Omega ^{\xi }, \quad t > 0,~~x \in \Omega ^x, \end{aligned}$$

and we set \(\partial \Omega ^x\) and \(\partial \Omega ^\xi \) to be the boundaries of \(\Omega ^x\) and \(\Omega ^\xi \), respectively. Let \({\mathcal {P}}_h(\Omega ^x)= \left\{ \Omega ^x_h \right\} \) and \({\mathcal {P}}_h(\Omega ^\xi )= \{\Omega ^\xi _h\}\) be the partitions of \(\Omega ^x\) and \(\Omega ^\xi \) with maximal amplitude h, respectively and we define a partition of \(\Omega \) as follows:

$$\begin{aligned} {\mathcal {P}}_h(\Omega ^x\times \Omega ^\xi ):=\left\{ \Omega _h^x\times \Omega _h^\xi \subseteq \Omega ^x\times \Omega ^\xi :~~\Omega _h^x\in {\mathcal {P}}_h(\Omega _x),~\Omega _h^\xi \in {\mathcal {P}}_h(\Omega _\xi )\right\} . \end{aligned}$$

On the other hand, for a nonnegative integer k, let \(P^k(\Omega _h^x\times \Omega _h^\xi )\) be the set of polynomials of total degree at most k on \(\Omega _h^x\times \Omega _h^\xi \). We define the discrete P-type space:

$$\begin{aligned} {\mathcal {G}}^k_h=\left\{ g\in L^2(\Omega ^x\times \Omega ^\xi ) :~ g \Big |_{\Omega _h^x\times \Omega _h^\xi } \in P^k(\Omega _h^x\times \Omega _h^\xi ),~ \Omega _h^x\times \Omega _h^\xi \in {\mathcal {P}}_h(\Omega ^x\times \Omega ^\xi ) \right\} \end{aligned}$$

to be used for the approximation of the kinetic function f. We also recall that one can replace the space \({\mathcal {G}}^k_h\) by the space \(P^k(\Omega _h^x)\times P^k(\Omega _h^\xi )\). Moreover, we use the Q-type space, \(Q^k(\Omega _h^x\times \Omega _h^\xi )\) which is the set of polynomials of degree at most k in each variable in \(\Omega _h^x\times \Omega _h^\xi \), then

$$\begin{aligned} {\mathcal {H}}^k_h=\left\{ g\in L^2\left( \Omega ^x\times \Omega ^\xi \right) \,: \, g \Big |_{\Omega _h^x\times \Omega _h^\xi }\in Q^k(\Omega _h^x\times \Omega _h^\xi )\,, \Omega _h^x\times \Omega _h^\xi \in {\mathcal {P}}_h(\Omega ^x\times \Omega ^{\xi }) \right\} , \end{aligned}$$

or the space \(Q^k(\Omega _h^x)\times Q^k(\Omega _h^\xi )\). The presented results hold for each space defined above in the same manner. For the simplicity of notation, we formulate our results in the space \({\mathcal {G}}_h^k\) only, but the same arguments can be done for Q-type space. We will make this more precise in Sect. 5.

Next, we are ready to delineate a semi-discrete DG scheme for (5). For fixed k, h and \(\Omega _h^x\times \Omega _h^\xi \in {\mathcal {P}}_h(\Omega ^x\times \Omega ^\xi )\), we look for \(f_h(t,\cdot ,\cdot )\in {\mathcal {G}}^k_h\) such that

$$\begin{aligned} {\left\{ \begin{array}{ll} \displaystyle \int _{\Omega _h^{x} \times \Omega _h^{\xi }} \frac{\partial f_{h}}{\partial t} g dx d \xi -\int _{\Omega _h^{x} \times \Omega _h^{\xi }} f_{h} \xi \cdot \nabla _x g d x d \xi -\int _{\Omega _h^{x} \times \Omega ^\xi } F_a(f_{h}) f_{h} \cdot \nabla _{\xi } g d x d \xi \\ \quad \displaystyle +\,\int _{\partial \Omega _h^{x} \times \Omega _h^{\xi }} \widehat{f_{h} \xi } \cdot n_{x} g^{-} d s_{x} d \xi +\int _{\Omega _h^{x} \times \partial \Omega _h^{\xi }} \widehat{ f_{h}F_a (f_{h})} \cdot n_{\xi } g^{-} d x d s_{\xi }=0, \quad \text{ for } \text{ all } g \in {\mathcal {G}}^k_h, \\ \displaystyle F_a\left( f_{h}\right) (t,x, \xi )=-\int _{\Omega _h^{x} \times \Omega _h^{\xi }} \psi (|x-x_*|) \left( \xi - \xi _{*}\right) f_{h}\left( t, x_*, \xi _{*} \right) dx_* d \xi _{*}, \end{array}\right. } \end{aligned}$$
(15)

where \(n_{x}\) and \(n_{\xi }\) are the outward unit normal vectors of \(\partial \Omega _h^x\) and \(\partial \Omega _h^{\xi }\), resepctively and all hat functions are numerical fluxes determined by upwind condition (see upwind standard formulation [6, 12]):

$$\begin{aligned} \begin{aligned}&\widehat{f_{h} \xi } \cdot n_{x}= \xi \cdot n_{x}\left\{ f_{h}\right\} _{x}-\frac{\left| \xi \cdot n_{x}\right| }{2}\left[ f_{h}\right] _{x}\,, \\&\widehat{f_{h}F_a\left( f_{h}\right) } \cdot n_{\xi }=F_a\left( f_{h}\right) \cdot n_{\xi } \left\{ f_{h}\right\} _{\xi } - \frac{\left| F_a\left( f_{h}\right) \cdot n_{\xi }\right| }{2}\left[ f_{h}\right] _{\xi }, \end{aligned} \end{aligned}$$
(16)

where

$$\begin{aligned} \left\{ f_{h}\right\} _{x}:=\frac{f_{h}\left( t,x^{+}, \xi \right) +f_{h}\left( t,x^{-}, \xi \right) }{2} \quad \text{ and } \quad \left[ f_{h}\right] _{x}:=f_{h} \left( t,x^{+}, \xi \right) -f_{h}\left( t,x^{-}, \xi \right) \end{aligned}$$

are the average and the jump across the edge \(\Omega ^{x^{+}}_h\cap \Omega ^{x^{-}}_h\) for a piecewise functions \(f_{h}\) in x, with \(x^{+}\in \Omega ^{x^+}_h\) and \(x^{-}\in \Omega ^{x^-}_h\), respectively. The expressions \( \left\{ f_{h}\right\} _{\xi }\) and \( \left[ f_{h}\right] _{\xi }\) can be defined similarly.

2.3 Main results

Define the local mass density \(\rho _h\) as

$$\begin{aligned} \rho _{h}(t, x):= \int _{\Omega ^{\xi }} f_{h}(t,x, \xi ) d \xi . \end{aligned}$$

Now, we are ready to state our main results in the following theorem.

Theorem 2.5

Suppose that initial datum \(f_h(0,\cdot ,\cdot )\) is compactly supported and lies in the space \(W^{2,\infty }(\Omega ^x\times \Omega ^{\xi })\), and let f be a classical solution to (5) such that

$$\begin{aligned} f \in H^{k+2}((0, T) \times \Omega ^x \times \Omega ^{\xi }), \quad \text{ for }\, k\ge 0, \end{aligned}$$

and let \(f_h \in {\mathcal {G}}^k_h\) be a numerical solution given by the semi-discrete DG scheme supplemented with periodic boundary conditions in \(\Omega ^x\times \Omega ^\xi \). Then, for any \(h_0, T \in (0, \infty )\), there exists a positive constant \(C_T = C(f, T, h_0)\) such that for \(h < h_0\) and \(t \in [0, T]\), the following assertions hold:

  1. 1.

    (Mass conservation and \(L^2\)-stability):

    $$\begin{aligned} \frac{d}{dt} \int _{\Omega ^x}\rho _{h}(t,x)dx=0 \quad \text{ and } \quad \Vert f_h(t)\Vert _{L^2(\Omega )} \le C_T. \end{aligned}$$
    (17)
  2. 2.

    (\(L^2\)-convergence):

    $$\begin{aligned} \Vert f(t)-f_h(t)\Vert _{L^2(\Omega )}\le C_T h^{k+1/2}. \end{aligned}$$
    (18)

Proof

Since the proof is very lengthy, we leave its proof in Sects. 3 and 5. \(\square \)

3 Mass conservation and \(L^2\)-stability

In this section, we provide the proof of the first assertion (17) on the mass conservation and the \(L^2\)-stability of the numerical solution \(f_h\) to the semi-discrete DG scheme described in Sect. 2.2.

3.1 Mass conservation

For fixed h and k, let \(f_h \in {\mathcal {G}}_h^k\) be the numerical solution to the semi-discrete nonlinear Galerkin method for (5) supplemented with periodic boundary conditions. We choose the test function

$$\begin{aligned} g \equiv 1. \end{aligned}$$

Then, it is easy to see that

$$\begin{aligned} g \in {\mathcal {G}}_{h}^{k}, \quad \text{ for } \text{ each } k \ge 0, \quad \nabla _{x} g= 0 \quad \text{ and } \quad \nabla _{\xi } g=0. \end{aligned}$$

This and (15)\(_1\) yield

$$\begin{aligned} \frac{d}{dt}\int _{\Omega _h^x\times \Omega _h^\xi } f_h d x d \xi + \int _{\partial \Omega _h^x\times \Omega _h^{\xi }} \widehat{f_h \xi } \cdot n_x ds_x d \xi + \int _{\Omega _h^x \times \partial \Omega _h^{\xi }} \widehat{f_h F_a(f_h)} \cdot n_{\xi } d x ds_{\xi } = 0. \end{aligned}$$
(19)

We sum (19) over all the partitions using the periodic boundary condition to find the mass conservation:

$$\begin{aligned} \frac{d}{d t} \int _{\Omega ^x \times \Omega ^{\xi }} f_{h}(t,x,\xi ) d x d\xi = \frac{d}{dt} \int _{\Omega ^x}\rho _{h}(t,x)dx = 0. \end{aligned}$$

3.2 \(L^2\)-stability

Let h, k and \(T>0\) be fixed. Suppose that the initial datum \(f_h(0,\cdot ,\cdot )\in \left( C^1\cap W^{2,\infty }\right) \left( \Omega ^x\times \Omega ^\xi \right) \) and let \(f_h \in {\mathcal {G}}_h^k\) be a numerical solution to (15) with periodic boundary conditions. Then, (17)\(_2\) can be divided into two steps.

\(\bullet \) Step A (Differential inequality for \(\left\| f_{h}\right\| _{L^{2}}^{2}\)): we claim that

$$\begin{aligned} \frac{d}{d t} \sum \int _{\Omega _h^{x} \times \Omega _h^{\xi }} f_{h}^{2} \,d x d \xi +\sum \int _{\Omega _h^{x} \times \Omega _h^{\xi }} \nabla _{\xi } \cdot F_a\left( f_{h}\right) f_{h}^{2}\, d x d \xi \le 0\,, \end{aligned}$$
(20)

for each \(t>0\).

Proof of claim (20)

In (15)\(_1\), we choose \(g = f_h\) as a test function to find

$$\begin{aligned} \begin{aligned} 0&= \int _{\Omega _h^x\times \Omega _h^\xi } \frac{\partial f_h}{dt} f_h \, d x d \xi - \int _{\Omega _h^x\times \Omega _h^\xi }f_h \xi \cdot \nabla _{x} f_h \,d x d \xi - \int _{\Omega _h^x\times \Omega _h^\xi } f_h F_a(f_h)\cdot \nabla _{\xi }f_h \,d x d \xi \\&\quad +\,\int _{\partial \Omega _h^x \times \Omega _h^\xi }\widehat{f_h \xi }\cdot n_x f_h^{-}\,d s_x d \xi +\int _{\Omega _h^x \times \partial \Omega _h^\xi }\widehat{f_h F_a(f_h)}\cdot n_\xi f_h^{-} d x ds_\xi \\&=: \sum _{i=1}^{5} {{\mathcal {I}}}_{1i}. \end{aligned} \end{aligned}$$
(21)

In what follows, we estimate each term \({{\mathcal {I}}}_{1i}\) one by one. \(\square \)

\(\diamond \) Case A.1 (Estimates of \({{\mathcal {I}}}_{11}\)): by direct calculation, we have

$$\begin{aligned} \sum \int _{\Omega _h^{x} \times \Omega _h^{\xi }} \frac{\partial f_{h}}{\partial t} f_{h} d x d \xi =\frac{1}{2} \frac{d}{d t} \int _{\Omega } f_{h}^{2} d x d \xi . \end{aligned}$$
(22)

\(\diamond \) Case A.2 (Estimate of \({{\mathcal {I}}}_{12}\) and \({{\mathcal {I}}}_{13}\)): by integration by parts, we have

$$\begin{aligned} \begin{aligned}&\sum \int _{\Omega _h^x\times \Omega _h^\xi }f_h \xi \cdot \nabla _{x} f_h \,d x d \xi = \sum \frac{1}{2} \int _{\Omega _h^x\times \Omega _h^\xi } \xi \cdot \nabla _{x} f_h^2 \,d x d \xi \\&\quad =\sum \int _{\Omega _h^x\times \Omega _h^\xi } \nabla _{x} \cdot \left( \xi \frac{f_h^2}{2}\right) \,d x d \xi = - \sum \int _{\partial \Omega _h^x\times \Omega _h^\xi } n_x \cdot \xi \left( \frac{f_h^2}{2}\right) _x^{-} \,ds_x d \xi \\&\quad =- \sum \int _{\partial \Omega _h^x\times \Omega _h^\xi } n_x \cdot \xi \left\{ f_h \right\} _x \left[ f_h \right] _x \,ds_x d \xi . \end{aligned} \end{aligned}$$
(23)

Similarly, we have

$$\begin{aligned} \begin{aligned}&\sum \int _{\Omega _h^x\times \Omega _h^\xi } f_h F_a(f_h)\cdot \nabla _{\xi }f_h \,d x d \xi \\&\quad = \sum \int _{\Omega _h^x\times \Omega _h^\xi } \frac{f_h^2}{2} \nabla _{\xi } \cdot F_a(f_h) d x d \xi + \sum \int _{\Omega _h^x\times \partial \Omega _h^\xi } n_{\xi } \cdot F_a(f_h)\left\{ f_h\right\} _\xi \left[ f_h\right] _\xi d x ds_\xi . \end{aligned} \end{aligned}$$
(24)

\(\diamond \) Case A.3 (Estimate of \({{\mathcal {I}}}_{14}\) and \({{\mathcal {I}}}_{15}\)): by direct calculations, we have

$$\begin{aligned} \begin{aligned}&\sum \int _{\partial \Omega _h^x \times \Omega _h^\xi }\widehat{f_h \xi }\cdot n_x f_h^{-}\,ds_x d \xi = -\sum \int _{\partial \Omega _h^x \times \Omega _h^\xi }\widehat{f_h \xi }\cdot n_x \left[ f_h\right] _x\,ds_x d \xi , \\&\sum \int _{\Omega _h^x \times \partial \Omega _h^\xi }\widehat{f_h F_a(f_h)}\cdot n_\xi f_h^{-} \,d x ds_\xi = -\sum \int _{\Omega _h^x \times \partial \Omega _h^\xi }\widehat{f_h F_a(f_h)}\cdot n_\xi \left[ f_h\right] _\xi \,d x ds_\xi . \end{aligned} \end{aligned}$$
(25)

In (21), we combine (22), (23), (24), (25) and use (16) to get the desired estimate:

$$\begin{aligned} \begin{aligned}&\frac{1}{2} \frac{d}{d t} \int _{\Omega } f_{h}^{2} d x d \xi + \frac{1}{2} \int _{\Omega } f_{h}^{2} \nabla _{\xi } \cdot F_a\left( f_{h}\right) d \xi d x \\&\quad =\sum \int _{\partial \Omega _h^{x} \times \Omega _h^{\xi }}\left( \widehat{\xi f_{h}} \cdot n_{x}-\xi \cdot n_{x}\left\{ f_{h}\right\} _{x}\right) \left[ f_{h}\right] _{x} ds_{x} d \xi \\&\qquad +\,\sum \int _{\Omega _h^{x} \times \partial \Omega _h^{\xi }}\left( \widehat{f_{h} F_a\left( f_{h}\right) } \cdot n_{\xi }-F_a\left( f_{h}\right) \cdot n_{\xi }\left\{ f_{h}\right\} _{\xi }\right) \left[ f_{h}\right] _{\xi } d x ds_{\xi } \\&\quad =-\frac{1}{2} \sum \int _{\partial \Omega _h^{x} \times \Omega \xi }\left| \xi \cdot n_{x}\right| \left[ f_{h}\right] _{x}^{2}\, ds_{x} d x-\frac{1}{2} \sum \int _{\Omega _h^{x} \times \partial \Omega _h^{\xi }}\left| F_a\left( f_{h}\right) \right| \left[ f_{h}\right] _{\xi }^{2} d x ds_{\xi } \\&\quad \le 0, \end{aligned} \end{aligned}$$

where we used (16) in the last equality.

\(\bullet \) Step B (A bound for \(\left\| f_{h}\right\| _{L^{2}}^{2}\)): it follows from (20) that

$$\begin{aligned} \frac{d}{d t} \left\| f_{h}\right\| _{L^{2}}^{2} \le \left\| \nabla _{\xi } \cdot F_a\left( f_{h}\right) \right\| _{L^{\infty }} \left\| f_{h}\right\| _{L^{2}}^{2} \le d \psi _M \Vert f_h(0) \Vert _{L^1} \left\| f_{h}\right\| _{L^{2}}^{2}, \end{aligned}$$
(26)

where we used (2), (15)\(_2\) and conservation of mass to find

$$\begin{aligned} \left\| \nabla _{\xi } \cdot F_a\left( f_{h}\right) \right\| _{L^{\infty }(\Omega ^x\times \Omega ^\xi \times [0,T])}\le d \psi _M \Vert f_h(0) \Vert _{L^1}. \end{aligned}$$

Then, we apply Gronwall’s lemma for (26) to obtain, for \(t \in [0,T]\),

$$\begin{aligned} \left\| f_{h}(\cdot ,\cdot ,t)\right\| _{L^{2}}^{2} \le \left\| f_h(\cdot ,\cdot ,0)\right\| _{L^{2}}^{2} e^{d \psi _M \Vert f_h(0) \Vert _{L^1} t} \le \left\| f_h(\cdot ,\cdot ,0)\right\| _{L^{2}}^{2} e^{d \psi _M \Vert f_h(0) \Vert _{L^1} T}. \end{aligned}$$

Now we set

$$\begin{aligned} C_T:= e^{\frac{d\psi _M \Vert f_h(0) \Vert _{L^1} T}{2}} \end{aligned}$$

to get the desired \(L^2\)-stability estimate:

$$\begin{aligned} \sup _{0 \le t < T} \left\| f_{h}(t)\right\| _{L^{2}(\Omega ^x\times \Omega ^\xi )} \le C_T. \end{aligned}$$

4 Preparatory lemmas for convergence analysis

In this section, we study several preparatory estimates to be used in the \(L^2\)-convergence of the numerical solution \(f_h\) for (15) to the classical solution f for (5).

4.1 Error functional

Let f an g be piecewise \(C^1\) functions in each partition box \(\Omega ^x_h\) and \(\Omega _h^\xi \), and we also assume that f has integrable first time-derivative. Then, we set

$$\begin{aligned} \begin{aligned} {\mathcal {E}}(f, g)&:= \sum \int _{\Omega _h^x\times \Omega _h^\xi }\frac{\partial f}{\partial t} g d x d \xi - \sum \int _{\Omega _h^x\times \Omega _h^\xi } f \xi \cdot \nabla _{x} g d x d \xi \\&\quad -\,\sum \int _{\Omega _h^x\times \Omega _h^\xi } f F_a(f) \cdot \nabla _{\xi } g d x d \xi \\&\quad +\, \sum \int _{\partial \Omega _h^x\times \Omega _h^\xi } \widehat{ f \xi } \cdot n_{x} g^{-} \, d s_x d \xi + \sum \int _{\Omega _h^x\times \partial \Omega _h^\xi } \widehat{f F_a(f)} \cdot \xi g^{-} d x ds_\xi . \end{aligned} \end{aligned}$$

For a classical solution f and semi-disctete DG solution \(f_h\), one has

$$\begin{aligned} {\mathcal {E}}(f, g)=0; \quad {\mathcal {E}}\left( f_{h}, g\right) =0, \quad \forall ~g\in {\mathcal {G}}^k_h. \end{aligned}$$

Note that

$$\begin{aligned} {\mathcal {E}}:= & {} {\mathcal {E}}(f, g)-{\mathcal {E}}\left( f_{h}, g\right) \nonumber \\= & {} \underbrace{\sum \int _{\Omega _h^x\times \Omega _h^\xi }\frac{\partial }{\partial t} (f-f_h) g d x d \xi - \sum \int _{\Omega _h^x\times \Omega _h^\xi } (f - f_h) \xi \cdot \nabla _{x} g d x d \xi } \nonumber \\{} & {} +\, \underbrace{\sum \int _{\partial \Omega _h^x\times \Omega _h^\xi } \widehat{ (f - f_h) \xi } \cdot n_{x} g^{-} \, d s_x d \xi }_{=: {{\mathcal {L}}}(f-f_h, g)} \nonumber \\{} & {} \underbrace{-\sum \int _{\Omega _h^x\times \Omega _h^\xi } f F_a(f) \cdot \nabla _{\xi } g d x d \xi + \sum \int _{\Omega _h^x\times \partial \Omega _h^\xi } \widehat{f F_a(f)} \cdot \xi g^{-} d x ds_\xi }_{=:{{\mathcal {N}}}(f,g)} \nonumber \\{} & {} -\, \Big [ \underbrace{-\sum \int _{\Omega _h^x\times \Omega _h^\xi } f_h F_a(f_h) \cdot \nabla _{\xi } g d x d \xi + \sum \int _{\Omega _h^x\times \partial \Omega _h^\xi } \widehat{f_h F_a(f_h)} \cdot \xi g^{-} d x ds_\xi }_{=: {{\mathcal {N}}}(f_h, g)} \Big ] \nonumber \\=: & {} {{\mathcal {L}}}(f-f_h, g) + {{\mathcal {N}}}(f, g) - {{\mathcal {N}}}(f_h, g), \end{aligned}$$
(27)

where \({\mathcal {L}}\) is the linear part of \({\mathcal {E}}\), while the terms \({\mathcal {N}}\) and \({\mathcal {N}}_{h}\) are nonlinear.

4.2 Estimates for \({{\mathcal {L}}}\) and \({{\mathcal {N}}}\)

In this subsection, we study reduced expressions for the linear and nonlinear functionals introduced in (27). We denote the \(L^2\)-projection onto \({\mathcal {G}}_h^k\) by \({{\mathbb {P}}}_h\), and we set

$$\begin{aligned} \sigma _{h} :=f- {{\mathbb {P}}}_{h} f, \quad \delta _{h} := {{\mathbb {P}}}_{h}( f-f_{h}), \quad \varepsilon _h := \sigma _h+\delta _h=f-f_h~:~\text{ total } \text{ error }. \end{aligned}$$
(28)

Lemma 4.1

The linear functional \({{\mathcal {L}}}\) defined in (27) satisfies

$$\begin{aligned} {\mathcal {L}}\left( f-f_{h}, \delta _{h}\right) = \frac{1}{2} \frac{d}{d t} \sum \int _{\Omega _h^{x} \times \Omega _h^{\xi }} |\delta _{h}|^{2} d x d \xi +\frac{1}{2} \sum \int _{\partial \Omega _h^{x} \times \Omega _h^{\xi }}\left| \xi \cdot n_{x}\right| \left[ \delta _{h}\right] _{x}^{2} ds_{x} d \xi +{\mathcal {K}}, \end{aligned}$$
(29)

where \({{\mathcal {K}}}\) is given by

$$\begin{aligned} \begin{aligned} {\mathcal {K}}&= \sum \int _{\Omega _h^x\times \Omega _h^\xi } \frac{\partial \sigma _h}{\partial t} \delta _h d x d \xi -\sum \int _{\Omega _h^x\times \Omega _h^\xi } \sigma _h \xi \cdot \nabla _{x} \delta _h dx d\xi \\&\quad +\, \sum \int _{\partial \Omega _h^x\times \Omega _h^\xi } \widehat{\sigma _h \xi }\cdot n_x \left[ \delta _h\right] _x \,ds_x d\xi \,. \end{aligned} \end{aligned}$$
(30)

Proof

It follows from (28) that

$$\begin{aligned} f-f_{h}=\sigma _{h}+\delta _{h}. \end{aligned}$$
(31)

Then, we use (31) to get

$$\begin{aligned} \begin{aligned} {\mathcal {L}}\left( f-f_{h}, \delta _{h}\right)&={\mathcal {L}}\left( \sigma _{h}, \delta _{h}\right) +{\mathcal {L}}\left( \delta _{h}, \delta _{h}\right) \\&= \sum \int _{\Omega _h^{x} \times \Omega _h^{\xi }} \frac{\partial \sigma _h}{\partial t} \delta _{h}\, d x d \xi - \sum \int _{ \Omega _h^{x} \times \Omega _h^{\xi }}\sigma _h\xi \cdot \nabla _{x}\delta _{h} d x d \xi \\&\quad +\, \sum \int _{ \partial \Omega _h^{x} \times \Omega _h^{\xi }}\widehat{\sigma _h\xi } \cdot n_{x}\delta _{h}^{-} ds_x d \xi \\&\quad +\, \sum \int _{\Omega _h^{x} \times \Omega _h^{\xi }} \frac{\partial \delta _h}{\partial t}\delta _{h} d x d \xi - \sum \int _{ \Omega _h^{x} \times \Omega _h^{\xi }}\delta _h\xi \cdot \nabla _{x}\delta _{h} d x d \xi \\&\quad +\, \sum \int _{ \partial \Omega _h^{x} \times \Omega _h^{\xi }}\widehat{\delta _h\xi } \cdot n_{x}\delta _{h}^{-} ds_x d \xi \\&= \sum \int _{\Omega _h^{x} \times \Omega _h^{\xi }} \left( \frac{\partial \sigma _h}{\partial t} +\frac{\partial \delta _h}{\partial t}\right) \delta _{h} d x d \xi \\&\quad +\,\frac{1}{2} \sum \int _{ \partial \Omega _h^{x} \times \Omega _h^{\xi }}\left| \xi \cdot n_x\right| \left[ \delta _{h}\right] ^{2}_x ds_x d \xi \\&\quad -\,\sum \int _{ \Omega _h^{x} \times \Omega _h^{\xi }}\sigma _h\xi \cdot \nabla _{x}\delta _{h} d x d \xi + \sum \int _{ \partial \Omega _h^{x} \times \Omega _h^{\xi }}\widehat{\sigma _h\xi } \cdot n_{x}\delta _{h}^{-} ds_x d \xi \\&= \sum \int _{\Omega _h^{x} \times \Omega _h^{\xi }} \left( \frac{\partial \sigma _h}{\partial t} +\frac{\partial \delta _h}{\partial t}\right) \delta _{h} d x d \xi \\&\quad +\,\frac{1}{2} \sum \int _{ \partial \Omega _h^{x} \times \Omega _h^{\xi }}\left| \xi \cdot n_x\right| \left[ \delta _{h}\right] ^{2}_x ds_x d \xi \\&\quad -\,\sum \int _{ \Omega _h^{x} \times \Omega _h^{\xi }}\sigma _h\xi \cdot \nabla _{x}\delta _{h} d x d \xi + \sum \int _{ \partial \Omega _h^{x} \times \Omega _h^{\xi }}\widehat{\sigma _h\xi } \cdot n_{x} \left[ \delta _{h}\right] _{x} ds_x d \xi \\&=: \sum \int _{\Omega _h^{x} \times \Omega _h^{\xi }} \frac{\partial \delta _h}{\partial t}\delta _{h} d x d \xi +\frac{1}{2} \sum \int _{ \partial \Omega _h^{x} \times \Omega _h^{\xi }}\left| \xi \cdot n_x\right| \left[ \delta _{h}\right] ^{2}_x ds_x d \xi +{\mathcal {K}}, \end{aligned} \end{aligned}$$

where \({\mathcal {K}}\) is given by (30). \(\square \)

Lemma 4.2

The functional \({{\mathcal {N}}}\) defined in (27) satisfies

$$\begin{aligned} \begin{aligned}&{\mathcal {N}}(f, \delta _h)-{\mathcal {N}}_h(f_h, \delta _h) \\&\quad =\sum \int _{\Omega _h^x\times \Omega _h^\xi } \nabla _{\xi }\cdot \left( F_a(f-f_h)\,f \right) \delta _h d x d \xi \\&\qquad +\,\frac{1}{2}\sum \int _{\Omega _h^x\times \partial \Omega _h^\xi } \left| F_a(f_h)\right| \, \left[ \delta _h\right] ^2 d x ds_\xi + {\mathcal {H}}, \end{aligned} \end{aligned}$$
(32)

where \({{\mathcal {H}}}\) is given by

$$\begin{aligned} \begin{aligned} {\mathcal {H}}&=-\sum \int _{\Omega _h^x\times \Omega _h^\xi } F_a(f_h)\,\sigma _h\, \cdot \nabla _{\xi } \delta _h \, d x d \xi \\&\quad +\,\sum \int _{\Omega _h^x\times \partial \Omega _h^\xi } \left( \widehat{\sigma _h F_a(f_h)}\right) \cdot n_{\xi } \left[ \delta _h\right] dx ds_\xi . \end{aligned} \end{aligned}$$
(33)

Proof

Recall that

$$\begin{aligned} \begin{aligned} {\mathcal {N}}(f, \delta _h)&=- \sum \int _{\Omega _h^x\times \Omega _h^\xi } fF_a(f) \cdot \nabla _{\xi } \delta _h d x d \xi \\&\quad +\, \sum \int _{\Omega _h^x\times \partial \Omega _h^\xi } \widehat{f F_a(f)} \cdot n_{\xi } \delta _h^{-} d x ds_\xi , \\ {\mathcal {N}}_h(f_h, \delta _h)&=- \sum \int _{\Omega _h^x\times \Omega _h^\xi } f_hF_a(f_h) \cdot \nabla _{\xi } \delta _h d x d \xi \\&\quad +\, \sum \int _{\Omega _h^x\times \partial \Omega _h^\xi } \widehat{f_h F_a(f_h)} \cdot n_{\xi } \delta _h^{-} d x ds_\xi . \end{aligned} \end{aligned}$$

Then, these yield

$$\begin{aligned} \begin{aligned}&{\mathcal {N}}(f, \delta _h)-{\mathcal {N}}_h(f_h, \delta _h) \\&\quad = -\sum \int _{\Omega _h^x\times \Omega _h^\xi } \left[ fF_a(f)-f_hF_a(f_h)\right] \cdot \nabla _{\xi } \delta _h d x d \xi \\&\qquad +\,\sum \int _{\Omega _h^x\times \partial \Omega _h^\xi } \left( \widehat{f F_a(f)} - \widehat{f_h F_a(f_h)}\right) \cdot n_{\xi } \delta _h^{-} \, dx ds_\xi \\&\quad = {{\mathcal {I}}}_{21} + {{\mathcal {I}}}_{22}. \end{aligned} \end{aligned}$$

Next, we estimate the term \({{\mathcal {I}}}_{2i}\) one by one.

\(\bullet \) (Estimate of \({{\mathcal {I}}}_{21}\)): note that

$$\begin{aligned} - {{\mathcal {I}}}_{21}= & {} \sum \int _{\Omega _h^x\times \Omega _h^\xi } \left[ fF_a(f)-f_hF_a(f_h)\right] \cdot \nabla _{\xi } \delta _h d x d \xi \nonumber \\= & {} \sum \int _{\Omega _h^x\times \Omega _h^\xi } \left( F_a(f)-F_a(f_h)\right) \,f \cdot \nabla _{\xi } \delta _h d x d \xi \nonumber \\{} & {} +\,\sum \int _{\Omega _h^x\times \Omega _h^\xi } F_a(f_h)\,\left( f-f_h\right) \, \cdot \nabla _{\xi } \delta _h d x d \xi \nonumber \\= & {} \sum \int _{\Omega _h^x\times \Omega _h^\xi } \left( F_a(f)-F_a(f_h)\right) \,f \cdot \nabla _{\xi } \delta _h d x d \xi \nonumber \\{} & {} +\,\sum \int _{\Omega _h^x\times \Omega _h^\xi } F_a(f_h)\,\left( \sigma _h+\delta _h\right) \, \cdot \nabla _{\xi } \delta _h d x d \xi \nonumber \\= & {} \sum \int _{\Omega _h^x\times \Omega _h^\xi } \left( F_a(f-f_h)\right) \,f \cdot \nabla _{\xi } \delta _h d x d \xi \nonumber \\{} & {} +\,\sum \int _{\Omega _h^x\times \Omega _h^\xi } F_a(f_h)\sigma _h \cdot \nabla _{\xi } \delta _h d x d \xi \nonumber \\{} & {} + \,\sum \int _{\Omega _h^x\times \Omega _h^\xi } F_a(f_h)\,\delta _h\, \cdot \nabla _{\xi } \delta _h d x d \xi \nonumber \\= & {} -( {{\mathcal {I}}}_{211} + {{\mathcal {I}}}_{212} + {{\mathcal {I}}}_{213}). \end{aligned}$$
(34)

Below, we estimate the term \({{\mathcal {I}}}_{21i},~i=1,2,3\) one by one.

\(\diamond \) (Estimate of \(-{{\mathcal {I}}}_{211}\) and \(-{{\mathcal {I}}}_{213}\)): note that

$$\begin{aligned} \begin{aligned} -{{\mathcal {I}}}_{211}&= -\sum \int _{\Omega _h^x\times \Omega _h^\xi } \nabla _{\xi }\cdot \left( F_a(f-f_h)\,f \right) \delta _h d x d \xi \\&\quad +\,\sum \int _{\Omega _h^x\times \partial \Omega _h^\xi } \widehat{\left( F_a(f-f_h)\,f\right) } \cdot n_\xi \delta _h^{-} d x d s_\xi \\&\quad -\,\sum \int _{\Omega _h^x\times \Omega _h^\xi } \nabla _{\xi }\cdot \left( F_a(f-f_h)\,f \right) \delta _h \, d x d \xi \\&\quad +\,\sum \int _{\Omega _h^x\times \partial \Omega _h^\xi } \widehat{\left( F_a(f-f_h)\,f\right) } \cdot n_\xi \left[ \delta _h\right] d x d s_\xi , \end{aligned} \end{aligned}$$
(35)

and

$$\begin{aligned} \begin{aligned} -{{\mathcal {I}}}_{213}&=-\sum \int _{\Omega _h^x\times \partial \Omega _h^\xi } F_a(f_h)\, \cdot n_\xi \left( \frac{\delta _h^2}{2}\right) ^{-} d x d s_\xi \\&=-\frac{1}{2}\sum \int _{\Omega _h^x\times \partial \Omega _h^\xi } \widehat{F_a(f_h)}\, \cdot n_\xi \left[ \delta _h^2\right] d x d s_\xi . \end{aligned} \end{aligned}$$
(36)

\(\bullet \) (Estimate of \({{\mathcal {I}}}_{22}\)): by direct estimate, we have

$$\begin{aligned} \begin{aligned} {{\mathcal {I}}}_{22}&=\sum \int _{\Omega _h^x\times \partial \Omega _h^\xi } \left( \widehat{f F_a(f)} - \widehat{f F_a(f_h)}\right) \cdot n_{\xi } \delta _h^{-} d x ds_\xi \\&\quad +\,\sum \int _{\Omega _h^x\times \partial \Omega _h^\xi } \left( \widehat{(f-f_h) F_a(f_h)}\right) \cdot n_{\xi } \delta _h^{-} d x ds_\xi \\&=\sum \int _{\Omega _h^x\times \partial \Omega _h^\xi } \left( \widehat{f F_a(f)}- \widehat{f F_a(f_h)}\right) \cdot n_{\xi } \left[ \delta _h\right] d x ds_\xi \\&\quad +\,\sum \int _{\Omega _h^x\times \partial \Omega _h^\xi } \left( \widehat{(f-f_h) F_a(f_h)}\right) \cdot n_{\xi } \left[ \delta _h\right] d x ds_\xi \\&=\sum \int _{\Omega _h^x\times \partial \Omega _h^\xi } \left( \widehat{f F_a(f)}- \widehat{f F_a(f_h)}\right) \cdot n_{\xi } \left[ \delta _h\right] d x d s_\xi \\&\quad +\,\sum \int _{\Omega _h^x\times \partial \Omega _h^\xi } \left( \widehat{\sigma _h F_a(f_h)}\right) \cdot n_{\xi } \left[ \delta _h\right] d x ds_\xi \\&\quad -\,\sum \int _{\Omega _h^x\times \partial \Omega _h^\xi } \left( \widehat{\delta _h F_a(f_h)}\right) \cdot n_{\xi } \left[ \delta _h\right] d x ds_\xi . \end{aligned} \end{aligned}$$
(37)

Finally, we combine all the estimates (34), (35), (36) and (37) to obtain

$$\begin{aligned} \begin{aligned}&{\mathcal {N}}(f, \delta _h)-{\mathcal {N}}_h(f_h, \delta _h) \\&\quad = \sum \int _{\Omega _h^x\times \Omega _h^\xi } \nabla _{\xi } \cdot \left( F_a(f-f_h)\,f \right) \delta _h d x d \xi \\&\qquad -\,\sum \int _{\Omega _h^x\times \partial \Omega _h^\xi } \widehat{\left( F_a(f-f_h)\,f\right) } \cdot n_\xi \left[ \delta _h\right] d x d s_\xi \\&\qquad -\,\sum \int _{\Omega _h^x\times \Omega _h^\xi } F_a(f_h)\,\sigma _h\, \cdot \nabla _{\xi } \delta _h dx d \xi -\frac{1}{2}\sum \int _{\Omega _h^x\times \partial \Omega _h^\xi } \widehat{F_a(f_h)}\, \cdot n_\xi \left[ \delta _h^2\right] dx ds_\xi \\&\qquad +\,\sum \int _{\Omega _h^x\times \partial \Omega _h^\xi } \left( \widehat{f F_a(f)}- \widehat{f F_a(f_h)}\right) \cdot n_{\xi } \left[ \delta _h\right] d x ds_\xi \\&\qquad +\,\sum \int _{\Omega _h^x\times \partial \Omega _h^\xi } \left( \widehat{\sigma _h F_a(f_h)}\right) \cdot n_{\xi } \left[ \delta _h\right] dx ds_\xi \ \\&\qquad -\,\sum \int _{\Omega _h^x\times \partial \Omega _h^\xi } \left( \widehat{\delta _h F_a(f_h)}\right) \cdot n_{\xi } \left[ \delta _h\right] dx ds_\xi \\&\quad = \sum \int _{\Omega _h^x\times \Omega _h^\xi } \nabla _{\xi } \cdot \left( F_a(f-f_h)\,f \right) \delta _h d x d \xi -\sum \int _{\Omega _h^x\times \Omega _h^\xi } F_a(f_h)\,\sigma _h\, \cdot \nabla _{\xi } \delta _h d x d \xi \\&\qquad -\,\frac{1}{2}\sum \int _{\Omega _h^x\times \partial \Omega _h^\xi } \widehat{F_a(f_h)}\, \cdot n_\xi \left[ \delta _h^2\right] d x d s_\xi +\sum \int _{\Omega _h^x\times \partial \Omega _h^\xi } \left( \widehat{\sigma _h F_a(f_h)}\right) \cdot n_{\xi } \left[ \delta _h\right] d x ds_\xi \\&\qquad -\,\sum \int _{\Omega _h^x\times \partial \Omega _h^\xi } \left( \widehat{\delta _h F_a(f_h)}\right) \cdot n_{\xi } \left[ \delta _h\right] dx ds_\xi , \end{aligned} \end{aligned}$$
(38)

where we used

$$\begin{aligned} \widehat{\left( F_a(f-f_h)\,f\right) } =\left( \widehat{f F_a(f)}- \widehat{f F_a(f_h)}\right) . \end{aligned}$$

Moreover, we have

$$\begin{aligned}{} & {} -\frac{1}{2}\sum \int _{\Omega _h^x\times \partial \Omega _h^\xi } \widehat{F_a(f_h)}\, \cdot n_\xi \left[ \delta _h^2\right] d x d s_\xi \,+\sum \int _{\Omega _h^x\times \partial \Omega _h^\xi } \left( \widehat{\delta _h F_a(f_h)}\right) \cdot n_{\xi } \left[ \delta _h\right] dx ds_\xi \nonumber \\{} & {} \quad =\frac{1}{2}\sum \int _{\Omega _h^x\times \partial \Omega _h^\xi } \left| F_a(f_h) \right| \, \left[ \delta _h\right] ^2 d x d s_\xi . \end{aligned}$$
(39)

We combine (38) and (39) to obtain

$$\begin{aligned} \begin{aligned}&{\mathcal {N}}(f, \delta _h)-{\mathcal {N}}_h(f_h, \delta _h) \\&\quad = \sum \int _{\Omega _h^x\times \Omega _h^\xi } \nabla _{\xi }\cdot \left( F_a(f-f_h)\,f \right) \delta _h d x d \xi -\sum \int _{\Omega _h^x\times \Omega _h^\xi } F_a(f_h)\,\sigma _h\, \cdot \nabla _{\xi } \delta _h d x d \xi \\&\qquad +\,\sum \int _{\Omega _h^x\times \partial \Omega _h^\xi } \left( \widehat{\sigma _h F_a(f_h)} \right) \cdot n_{\xi } \left[ \delta _h\right] d x ds_\xi +\frac{1}{2}\sum \int _{\Omega _h^x\times \partial \Omega _h^\xi } \left| F_a(f_h)\right| \, \left[ \delta _h\right] ^2 dx ds_\xi . \end{aligned} \end{aligned}$$
(40)

\(\square \)

4.3 \(L^{\infty }\)-estimates for \({{\mathcal {K}}}\) and \({{\mathcal {H}}}\)

In this subsection, we study uniform bound estimate for functionals defined in (30) and (33). For this, we first recall a lemma regarding approximation and Poincare type inequality. We set

$$\begin{aligned} \Omega := \Omega ^x\times \Omega ^{\xi }, \qquad \Omega _h:=\Omega _h^x\times \Omega _h^\xi \in {\mathcal {P}}_h(\Omega ). \end{aligned}$$

Lemma 4.3

[15] Let k and h be a nonnegative integer and positive real number, respectively, and let \(\Omega = \Omega ^{x} \times \Omega ^{\xi }\) be a periodic domain in x and \(\xi \)-variables. We denote the \(L^2\)-projection onto \({\mathcal {G}}_h^k\) by \({{\mathbb {P}}}_h\). Then, there exists a positive constant \(C = C(k, \Omega ) > 0\) independent of h such that the following assertions hold.

  1. 1.

    (Approximation properties): for any \(g\in H^{k+1}(\Omega )\) and \(\Omega _h \in {\mathcal {P}}_h(\Omega )\),

    $$\begin{aligned} \Vert g- {{\mathbb {P}}}_h g\Vert _{L^2(\Omega _h)}+h^{1/2} \Vert g- {{\mathbb {P}}}_h g\Vert _{L^2(\partial \Omega _h)}\le C h^{k+1}\Vert g\Vert _{H^{k+1}(\Omega )}, \end{aligned}$$
    (41)
  2. 2.

    (Poincare type inequality): for any \(g \in P^k(\Omega _h)\) with \(\Omega _h \in {\mathcal {P}}_h(\Omega )\),

    $$\begin{aligned} \Vert \nabla _{x} g\Vert _{L^2(\Omega _h)}\le \frac{C}{h}\Vert g\Vert _{L^2(\Omega _h)}, \quad \Vert \nabla _{\xi } g\Vert _{L^2(\Omega _h)}\le \frac{C}{h}\Vert g\Vert _{L^2(\Omega _h)}. \end{aligned}$$
    (42)

Now, we are ready to provide \(L^\infty \)-estimates for \({\mathcal {K}}\) and \({\mathcal {H}}\) in the following two lemmas.

Lemma 4.4

For a positive constant \(h_0 \), if \(h \le h_0\), there exits a positive constant \(C = C(k, \Omega )\) independent of the mesh sizes h such that

$$\begin{aligned} \begin{aligned} \Vert {\mathcal {K}} \Vert _{L^{\infty }}&\le C \Big ( h^{2k+2}\left\| \frac{\partial f}{\partial t}\right\| _{H^{k+1}}+ h^{2k+2} \Vert f\Vert ^2_{H^{k+1}}+ \left\| \delta _{h}\right\| ^2_{L^{2}} \Big ) \\&\quad +\,\frac{1}{2} \sum \int _{\partial \Omega _h^{x} \times \Omega _h^{\xi }}\left| \xi \cdot n_{x}\right| \left[ \delta _{h}\right] _{x}^{2} ds_{x} d \xi . \end{aligned} \end{aligned}$$
(43)

Proof

Note that

$$\begin{aligned} \begin{aligned} {\mathcal {K}}&=\sum \int _{\Omega _h^x\times \Omega _h^\xi } \frac{\partial \sigma _h}{\partial t} \delta _h\, d x d \xi -\sum \int _{\Omega _h^x\times \Omega _h^\xi } \sigma _h \xi \cdot \nabla _{x} \delta _h dx d\xi \\&\quad +\, \sum \int _{\partial \Omega _h^x\times \Omega _h^\xi } \widehat{\sigma _h \xi }\cdot n_x \left[ \delta _h\right] _x \,ds_x d\xi \\&=: {{\mathcal {I}}}_{31} + {{\mathcal {I}}}_{32} + {{\mathcal {I}}}_{33}. \end{aligned} \end{aligned}$$
(44)

Below, we estimate the term \({{\mathcal {I}}}_{3i},~i=1,2,3\) one by one.

\(\bullet \) (Estimate of \({{\mathcal {I}}}_{31}\)): now, we use (41) and Young’s inequality to get

$$\begin{aligned} \left| \sum \int _{\Omega _h^{x} \times \Omega _h^{\xi }} \frac{\partial \sigma _{h}}{\partial t} \delta _{h} d x d \xi \right| \le \frac{1}{2}\left\| \frac{\partial \sigma _{h}}{\partial t}\right\| ^2_{L^{2}}+\frac{1}{2}\left\| \delta _{h}\right\| ^2_{L^{2}} \le \frac{C}{2} h^{2k+2}\left\| \frac{\partial f}{\partial t}\right\| _{H^{k+1}}+\frac{1}{2}\left\| \delta _{h}\right\| ^2_{L^{2}}. \end{aligned}$$
(45)

\(\bullet \) (Estimate of \({{\mathcal {I}}}_{32}\)): let \(\xi _{0}\) be the \(L^{2}\) projection of \(\xi \) onto the piecewise constant space with respect to \({\mathcal {P}}_h(\Omega )\). Then, we have

$$\begin{aligned} \begin{aligned} \sum \int _{\Omega _h^{x} \times \Omega _h^{\xi }} \sigma _{h} \xi \cdot \nabla _{x} \delta _{h} d x d \xi&= \sum \int _{\Omega _h^{x} \times \Omega _{h}^{\xi }} \sigma _{h} \left( \xi -\xi _0\right) \cdot \nabla _{x} \delta _{h} d x d \xi \\&\quad +\,\sum \int _{\Omega _h^{x} \times \Omega _h^{\xi }} \sigma _{h} \xi _0 \cdot \nabla _{x} \delta _{h} d x d \xi . \end{aligned} \end{aligned}$$
(46)

By definition of \(\sigma _{h}\) in (28), it follows from [28] that

$$\begin{aligned} \sum \int _{\Omega _h^{x} \times \Omega _h^{\xi }} \sigma _{h} \xi _0 \cdot \nabla _{x} \delta _{h} d x d \xi = 0. \end{aligned}$$
(47)

Then, we use (41), (42), (46) and (47) to find

$$\begin{aligned} \begin{aligned}&\left| \sum \int _{\Omega _h^{x} \times \Omega _h^{\xi }} \sigma _{h} \xi \cdot \nabla _{x} \delta _{h} d x d \xi \right| =\left| \sum _{\Omega _h^{x} \times \Omega _h^{\xi }} \sigma _{h}\left( \xi -\xi _{0}\right) \cdot \nabla x \delta _{h} d x d \xi \right| \\&\quad \le \left\| \xi -\xi _{0}\right\| _{L^{\infty }}\left\| \sigma _{h}\right\| _{L^{2}}\left\| \nabla _{x} \delta _{h}\right\| _{L^{2}} \le Ch^{k +1}\Vert f\Vert _{H^{k+1}}\left\| \delta _{h}\right\| _{L^{2}} \\&\quad \le \frac{1}{2}C\left( h^{2k+2}\Vert f\Vert ^2_{H^{k+1}}+\left\| \delta _{h}\right\| ^2_{L^{2}}\right) , \end{aligned} \end{aligned}$$
(48)

where we used \(\left\| \xi -\xi _{0}\right\| _{L^{\infty }} \le C h\) in [28].

\(\bullet \) (Estimate of \({{\mathcal {I}}}_{33}\)): we use (40) to find

$$\begin{aligned} \begin{aligned}&\left| \sum \int _{\partial \Omega _h^x\times \Omega _h^\xi } \widehat{\sigma _h \xi }\cdot n_x \left[ \delta _h\right] _x \,d s_x d\xi \right| \le \sum \int _{\partial \Omega _h^x\times \Omega _h^\xi } \left| \sigma _h\right| \left| \xi \cdot n_x\right| \left| \left[ \delta _h\right] _x\right| \,ds_x d\xi \\&\quad \le \frac{1}{2}\sum \int _{\partial \Omega _h^x\times \Omega _h^\xi } \left| \xi \cdot n_x\right| \sigma _h^2 \,ds_x d\xi +\frac{1}{2}\sum \int _{\partial \Omega _h^x\times \Omega _h^\xi } \left| \xi \cdot n_x\right| \left[ \delta _h\right] _x^2 \,ds_x d\xi \\&\quad \le C \left\| f\right\| ^2_{H^{k+1}}\,h^{2h+1} + \frac{1}{2}\sum \int _{\partial \Omega _h^x\times \Omega _h^\xi } \left| \xi \cdot n_x\right| \left[ \delta _h\right] _x^2 \,ds_x d\xi . \end{aligned} \end{aligned}$$
(49)

In (44), we combine all the estimates (45), (48) and (49) to find the desired estimate. \(\square \)

Recall that the quantity \(\left\| F_a(f_h)\right\| _{\infty }\) is bounded for each time \(t\in [0,T]\) as \(f_h\in {\mathcal {P}}_h^k(\Omega )\).

Lemma 4.5

For \(h_0 > 0\), if \(h \le h_0\), there exits a positive constant \(C = C(k, \Omega )\) independent of the mesh sizes h such that

$$\begin{aligned} \begin{aligned} \left\| {\mathcal {H}}\right\| _{L^{\infty }}&\le C \Big ( h^{k} \left\| F_a(f_h)\right\| _{\infty } \Vert f\Vert _{H^{k+1}} \left\| \delta _h \right\| _{L^2} + \left\| f\right\| ^2_{H^{2k+1}}h^{2k+1} \Big ) \\&\quad +\,\frac{1}{2}\sum \int _{\Omega _h^x\times \partial \Omega _h^\xi } \left| F_a(f_h) \cdot n_{\xi }\right| \,\left[ \delta _h\right] ^2 \, dx ds_\xi . \end{aligned} \end{aligned}$$
(50)

Proof

It follows from (33) that

$$\begin{aligned} \begin{aligned} \left| {\mathcal {H}} \right|&\le \left| \sum \int _{\Omega _h^x\times \Omega _h^\xi } F_a(f_h)\, \sigma _h\, \cdot \nabla _{\xi } \delta _h d x d \xi \,\right| \\&\quad +\,\left| \sum \int _{\Omega _h^x\times \partial \Omega _h^\xi } \left( \widehat{\sigma _h F_a(f_h)}\right) \cdot n_{\xi } \left[ \delta _h\right] \, d x d s_\xi \,\right| \\&=: {{\mathcal {I}}}_{41} + {{\mathcal {I}}}_{42}. \end{aligned} \end{aligned}$$
(51)

Below, we estimate the term \({{\mathcal {I}}}_{4i}\) one by one.

\(\bullet \) (Estimate of \( {{\mathcal {I}}}_{42}\)): we use (40) and (41) to obtain

$$\begin{aligned} \begin{aligned} {{\mathcal {I}}}_{42}&\le \sum \int _{\Omega _h^x\times \partial \Omega _h^\xi } \left| F_a(f_h)\cdot n_{\xi }\right| \, |\sigma _h|\, \left| \left[ \delta _h\right] \right| \, d x d s_\xi \\&\le \frac{1}{2}\sum \int _{\Omega _h^x\times \partial \Omega _h^\xi } \left| F_a(f_h)\cdot n_{\xi }\right| \, |\sigma _h|^2\, d x d s_\xi \,\\&\quad +\,\frac{1}{2}\sum \int _{\Omega _h^x\times \partial \Omega _h^\xi } \left| F_a(f_h)\cdot n_{\xi }\right| \,\left[ \delta _h\right] ^2 \, d x d s_\xi \\&\le C\left\| f\right\| ^2_{H^{2k+1}}h^{2k+1}+\frac{1}{2}\sum \int _{\Omega _h^x\times \partial \Omega _h^\xi } \left| F_a(f_h)\cdot n_{\xi }\right| \,\left[ \delta _h\right] ^2 \, d x d s_\xi . \end{aligned} \end{aligned}$$
(52)

\(\bullet \) (Estimate of \( {{\mathcal {I}}}_{41}\)): similarly, one has

$$\begin{aligned} {{\mathcal {I}}}_{41} \le \left\| F_a(f_h)\right\| _{\infty } \left\| \sigma _h \right\| _{L^2} \left\| \nabla _{\xi } \delta _h \right\| _{L^2} \le C h^{k} \left\| F_a(f_h)\right\| _{\infty } \Vert f\Vert _{H^{k+1}} \left\| \delta _h \right\| _{L^2}. \end{aligned}$$
(53)

In (51), we combine (52) and (53) to get the desired estimate. \(\square \)

In the following lemma, we give an \(L^2\)-estimate of the velocity divergence of the interaction term:

Lemma 4.6

For \(h_0 > 0\), if \(h \le h_0\), there exits a positive constant \(C = C(k, \Omega )\) independent of the mesh sizes h such that

$$\begin{aligned} \Vert \nabla _{\xi }\cdot \left( F_a(f-f_h)\right) \Vert _{L^2}^2\le C \Big ( h^{2k+2}\Vert f\Vert ^2_{H^{k+1}}+ \Vert \delta _h\Vert _{L^2}^2 \Big ). \end{aligned}$$
(54)

Proof

We use (41) and (42) to find the desired estimate:

$$\begin{aligned} \begin{aligned}&\Vert \nabla _{\xi }\cdot \left( F_a(f-f_h)\right) \Vert _{L^2}^2 \\&\quad \le \kappa d\,\int _{\Omega ^x\times \Omega ^\xi } \int _{\Omega ^x\times \Omega ^\xi } \psi (|x-x_*|)^2 |(f - f_h) (t, x_*, \xi _{*}|^2\ d\xi _* d x_* d \xi dx \\&\quad \le C \Big ( \Vert \sigma _h\Vert _{L^2}^2+\Vert \delta _h\Vert _{L^2}^2 \Big ) \le C \Big ( h^{2k+2}\Vert f\Vert ^2_{H^{k+1}}+ \Vert \delta _h\Vert _{L^2}^2 \Big ). \end{aligned} \end{aligned}$$

\(\square \)

5 \(L^2\)-convergence

In this section, we provide the proof of the second part in Theorem 2.3 on \(L^2\)-convergence. Suppose that the initial data \(f_h(0)\) lies in \((C^1 \cap W^{k,\infty })(\Omega ^x\times \Omega ^\xi ),~k \ge 2\) and f is the corresponding classical solution to (3)–(4) satisfying the regularity assumption:

$$\begin{aligned} f\in H^{k + 2}\left( [0, T) \times \Omega ^x\times \Omega ^\xi \right) , \quad \text{ for }\, k \ge 0. \end{aligned}$$

Let \(f_h \in {\mathcal {G}}^k_h\) be the numerical solution given by the semi-discrete DG scheme supplemented with periodic boundary conditions in \(\Omega ^x\times \Omega ^\xi \). Then, we claim that for any \(h_0 > 0\), there exists a positive constant \(C_T = C(f, T, h_0) > 0\) such that for \(h < h_0\)

$$\begin{aligned} \Vert f(t)-f_h(t)\Vert _{L^2} \le C_T h^{k+1/2}, \quad t \in [0, T]. \end{aligned}$$
(55)

In what follows, we provide a derivation of (55). For this, we use (29), (32) and

$$\begin{aligned} {\mathcal {E}}={\mathcal {L}}\left( f-f_{h}, g\right) +{\mathcal {N}}(f, g)-{\mathcal {N}}\left( f_{h}, g\right) \end{aligned}$$

to find

$$\begin{aligned} \begin{aligned}&\frac{1}{2} \frac{d}{d t} \sum \int _{\Omega _h^{x} \times \Omega _h^{\xi }} \delta _{h}^{2} d x d \xi +\frac{1}{2} \sum \int _{\partial \Omega _h^{x} \times \Omega _h^{\xi }}\left| \xi \cdot n_{x}\right| \left[ \delta _{h}\right] _{x}^{2} d s_{x} d \xi +{\mathcal {K}} \\&\quad +\,\sum \int _{\Omega _h^x\times \Omega _h^\xi } \nabla _{\xi }\cdot \left( F_a(f-f_h)\,f \right) \delta _h \, d x d \xi \\&\quad +\,\frac{1}{2}\sum \int _{\Omega _h^x\times \partial \Omega _h^\xi } \left| F_a(f_h)\right| \, \left[ \delta _h\right] ^2 \, d x d s_\xi \,+ {\mathcal {H}} =0, \end{aligned} \end{aligned}$$
(56)

where \({\mathcal {K}}\) and \({\mathcal {H}}\) are given in (30) and (33), respectively. We use (43), (50) and (54) to rewrite (56) as

$$\begin{aligned} \begin{aligned}&\frac{1}{2} \frac{d}{d t} \sum \int _{\Omega _h^{x} \times \Omega _h^{\xi }} \delta _{h}^{2} d x d \xi \\&\qquad +\,\frac{1}{2} \sum \int _{\partial \Omega _h^{x} \times \Omega _h^{\xi }}\left| \xi \cdot n_{x}\right| \left[ \delta _{h}\right] _{x}^{2} d s_{x} d \xi +\frac{1}{2}\sum \int _{\Omega _h^x\times \partial \Omega _h^\xi } \left| F_a(f_h)\right| \, \left[ \delta _h\right] ^2 \, d x d s_\xi \\&\quad \le \Vert f\Vert _{L^\infty } \sum \int _{\Omega _h^x\times \Omega _h^\xi } \left| \nabla _{\xi } \cdot \left( F_a(f-f_h) \right) \right| \left| \delta _h\right| \, d x d \xi \, +\left| {\mathcal {K}}\right| + \left| {\mathcal {H}}\right| \\&\quad \le \frac{1}{2}\Vert f\Vert _{L^\infty } \left( \left\| \nabla _{\xi }\cdot \left( F_a(f-f_h) \right) \right\| _{L^2}^2+ \Vert \delta _h\Vert _{L^2}^2\right) +C h^{2k+2}\left\| \frac{\partial f}{\partial t}\right\| _{H^{k+1}} \\&\qquad +\,Ch^{2k+2} \Vert f\Vert ^2_{H^{k+1}}+C\left\| \delta _{h}\right\| ^2_{L^{2}} +\frac{1}{2} \sum \int _{\partial \Omega _h^{x} \times \Omega _h^{\xi }}\left| \xi \cdot n_{x}\right| \left[ \delta _{h}\right] _{x}^{2} d s_{x} d \xi \\&\qquad +\,h^{k} \left\| F_a(f_h)\right\| _{L^\infty }\Vert f\Vert _{H^{k+1}} \left\| \delta _h \right\| _{L^2}\,+ C\left\| f\right\| ^2_{H^{2k+1}}h^{2k+1} \\&\qquad +\,\frac{1}{2}\sum \int _{\Omega _h^x\times \partial \Omega _h^\xi } \left| F_a(f_h)\cdot n_{\xi }\right| \,\left[ \delta _h\right] ^2 \, d x d s_\xi \\&\quad \le C \frac{1}{2} \Vert f\Vert _{L^\infty } h^{2k+2} \Vert f \Vert _{H^{k+1}}^2 + C \Vert f\Vert _{L^\infty } \Vert \delta _h\Vert _{L^2}^2 +C h^{2k+2}\left\| \frac{\partial f}{\partial t}\right\| _{H^{k+1}} \\&\qquad +\,Ch^{2k+2} \Vert f\Vert ^2_{H^{k+1}}+C\left\| \delta _{h}\right\| ^2_{L^{2}} +\frac{1}{2} \sum \int _{\partial \Omega _h^{x} \times \Omega _h^{\xi }}\left| \xi \cdot n_{x}\right| \left[ \delta _{h}\right] _{x}^{2} d s_{x} d \xi \\&\qquad +\,h^{k} \Vert F_a(f_h) \Vert _{L^\infty } \Vert f\Vert _{H^{k+1}} \Vert \delta _h \Vert _{L^2} \\&\qquad +\, C\left\| f\right\| ^2_{H^{2k+1}}h^{2k+1}+\frac{1}{2}\sum \int _{\Omega _h^x\times \partial \Omega _h^\xi } \left| F_a(f_h)\cdot n_{\xi }\right| \,\left[ \delta _h\right] ^2 \, d x d s_\xi . \end{aligned} \end{aligned}$$

This yields

$$\begin{aligned} \begin{aligned} \frac{1}{2} \frac{d}{d t} \Vert \delta _{h}\Vert _{L^2}^{2}&\le \frac{1}{2}\Vert f\Vert _{L^\infty } C h^{2k+2} \left\| f \right\| _{H^{k+1}}^2+ \Vert f\Vert _{L^\infty } C\Vert \delta _h\Vert _{L^2}^2 +C h^{2k+2} \left\| \frac{\partial f}{\partial t}\right\| _{H^{k+1}} \\&\quad +\,Ch^{2k+2} \Vert f\Vert ^2_{H^{k+1}}+C\left\| \delta _{h}\right\| ^2_{L^{2}} +h^{k} \left\| F_a(f_h) \right\| _{L^\infty } \Vert f\Vert _{H^{k+1}} \left\| \delta _h \right\| _{L^2} \\&\quad +\, C\left\| f\right\| ^2_{H^{2k+1}} h^{2k+1}. \end{aligned} \end{aligned}$$
(57)

Now, we estimate \(\left\| F_a(f_h)\right\| _{\infty }\) as follows.

$$\begin{aligned} \begin{aligned} \left| F_a(f_h)\right|&\le \int _{\Omega ^x\times \Omega ^\xi } \left| \psi (|x-x_*|)\right| \left| \xi -\xi _{*}\right| \left| f_h\left( t, x_*, \xi _{*} \right) \right| \, dx_* d \xi _{*} \\&\le h\, \left\| f_h\right\| _{L^1}\, \le \kappa h\, \left( \left\| \delta _h\right\| _{L^1} +\left\| \sigma _h\right\| _{L^1}+\left\| f\right\| _{L^1}\right) \\&\le C h \left( \left\| \delta _h\right\| _{L^2}+\left\| \sigma _h\right\| _{L^2}+\left\| f\right\| _{L^1}\right) \\&\le C \Big ( h \left\| \delta _h\right\| _{L^2}+ h^{k+2}\left\| f\right\| _{H^{k+1}}+ h\left\| f\right\| _{L^1} \Big ). \end{aligned} \end{aligned}$$

Since \(h<h_0\), we can chose a positive constant C such that one can rewrite (57) as

$$\begin{aligned} \begin{aligned}&\frac{1}{2} \frac{d}{d t} \Vert \delta _{h}\Vert _{L^2}^{2} \\&\quad \le \frac{1}{2}\Vert f\Vert _{L^\infty } C h^{2k+2}\left\| f \right\| _{H^{k+1}}^2 + \Vert f\Vert _{L^\infty } C\Vert \delta _h\Vert _{L^2}^2 +C h^{2k+2}\left\| \frac{\partial f}{\partial t}\right\| _{H^{k+1}} \\&\qquad +\,Ch^{2k+2} \Vert f\Vert ^2_{H^{k+1}}+C\left\| \delta _{h}\right\| ^2_{L^{2}} +Ch^{k+1} \Vert f\Vert _{H^{k+1}}\left\| \delta _h\right\| _{L^2}^2 +C h^{2k+2}\left\| f\right\| ^2_{H^{k+1}}\left\| \delta _h\right\| _{L^2} \\&\qquad +\,Ch^{h+1}\left\| f\right\| _{L^1}\Vert f\Vert _{H^{k+1}} \left\| \delta _h \right\| _{L^2}\, + C\left\| f\right\| ^2_{H^{2k+1}}h^{2k+1} \\&\quad \le \left( C\Vert f\Vert _{L^\infty } +C +Ch^{k+1} \Vert f\Vert _{H^{k+1}}+\frac{1}{2}C h^{2k+2} +\frac{1}{2}\right) \Vert \delta _h\Vert _{L^2}^2 \\&\qquad +\, \frac{1}{2}\Vert f\Vert _{L^\infty } C h^{2k+2}\left\| f \right\| _{H^{k+1}}^2 + C h^{2k+2}\left\| \frac{\partial f}{\partial t}\right\| _{H^{k+1}}+Ch^{2k+2} \Vert f\Vert ^2_{H^{k+1}} \\&\qquad +\,\frac{C}{2} h^{2k+2}\left\| f\right\| ^4_{H^{k+1}}+\frac{C}{2}h^{2h+2} \left\| f\right\| ^2_{L^1}\Vert f\Vert ^2_{H^{k+1}}\,+ C\left\| f\right\| ^2_{H^{2k+1}}h^{2k+1}. \end{aligned} \end{aligned}$$

Again, this yields

$$\begin{aligned} \frac{1}{2} \frac{d}{d t} \Vert \delta _{h}\Vert _{L^2}^{2} \le C \Vert \delta _{h}\Vert _{L^2}^{2} + C h^{2k+1}. \end{aligned}$$
(58)

Finally, we apply Gronwall’s lemma to (58) and use the projection inequality (41) to find

$$\begin{aligned} \Vert f-f_h\Vert _{L^2}^{2} \le \Vert \delta _{h}\Vert _{L^2}^{2} +\Vert \delta _{h}\Vert _{L^2}^{2} +\Vert \sigma _{h}\Vert _{L^2}^{2} \le C h^{2k+1}. \end{aligned}$$

This completes the proof.

In the sequel, we provide a corollary which improves the \(L^2\)-stability estimate and the \(L^\infty \) bound of the interaction function in term of h, and the \(L^2\)-norm of the classical solution.

Corollary 5.1

Suppose that the same assumptions in Theorem 2.5 hold, and let f and \(f_h \in {\mathcal {G}}^k_h\) be a classical solution to (5) and a numerical solution given by the semi-discrete DG scheme supplemented with periodic boundary conditions in \(\Omega ^x\times \Omega ^\xi \). Then, we have the following estimates:

$$\begin{aligned} \begin{aligned}&(i)~\Vert f_h\Vert _{L^2}\le C h^{k+1/2}+\Vert f\Vert _{L^2}. \\&(ii)~\Vert F_a(f_h)\Vert _{L^\infty }\le Ch\left( h^{k+1/2}+\Vert f\Vert _{L^2}\right) . \\&(iii)~\Vert \nabla _{\xi }\cdot F_a(f_h)\Vert _{L^\infty }\le C\left( h^{k+1/2}+\Vert f\Vert _{L^2}\right) . \end{aligned} \end{aligned}$$

Proof

(i) Note that

$$\begin{aligned} \Vert f_h\Vert _{L^2}\le \Vert f-f_h\Vert _{L^2}+\Vert f\Vert _{L^2}. \end{aligned}$$

Then, we use the above relation and (18) to get the desired estimate.

(ii) We use the result (i) and the relation

$$\begin{aligned} \left| F_a(f_h)\right| \le Ch\Vert f_h\Vert _{L^1}\le Ch\Vert f_h\Vert _{L^2} \le Ch \Big ( C h^{k+1/2}+\Vert f\Vert _{L^2} \Big ). \end{aligned}$$

The third estimate can be treated analogously. \(\square \)

6 Numerical simulations

In this section, we present several numerical results. Let \(\phi _j\), for \(j=1,\dots ,N_k\) be the \(N_k\)-polynomials of k almost degree in the box \(\Omega _h^{x} \times \Omega _h^{\xi }\) (for example Lagrange interpolant polynomials or Legendre polynomial expansion). Then, we set

$$\begin{aligned} f_h(t,x,\xi )=\sum _{j=1}^{N_k} f_h^j(t) \phi _j(x,\xi ), \quad \textbf{f}_h=(f_h^1,\dots ,f_h^{N_k}). \end{aligned}$$

On each box of the partition, we have the following system of ODEs:

$$\begin{aligned} {\mathcal {M}} \frac{d \textbf{f}_h}{dt} = {\mathcal {S}}( \textbf{f}_h), \end{aligned}$$

where the square matrices \({\mathcal {M}} = ({\mathcal {M}}_{ij}), {{\mathcal {S}}}^1 = ({{\mathcal {S}}}^1_{ij})\) and a vector \( {\mathcal {S}}^2(\textbf{f}_h) \) are defined as follows.

$$\begin{aligned} {\left\{ \begin{array}{ll} \displaystyle {\mathcal {M}}_{ij} =\int _{\Omega _h^{x}\times \Omega _h^{\xi }}\phi _i(x,\xi ) \phi _j(x,\xi )dx d \xi , \quad {\mathcal {S}}(\textbf{f}_h)_i ={\mathcal {S}}^1 \textbf{f}_h +{\mathcal {S}}^2(\textbf{f}_h), \\ \displaystyle {\mathcal {S}}^1_{ij} =\int _{\Omega _h^x\times \Omega _h^\xi } \phi _i(x,\xi ) \xi \cdot \nabla _{x} \phi _j(x,\xi ) d x d \xi + \int _{\partial \Omega _h^x\times \Omega _h^\xi } \widehat{\phi _j \xi } \cdot n_{x} \phi _i^{-} ds_x d \xi , \\ \displaystyle {\mathcal {S}}^2( \textbf{f}_h)_i =\sum _{j =1} ^{N_k} \left( \int _{\Omega _h^x \times \Omega _h^\xi } \phi _j F_a(f_h) \cdot \nabla _{\xi } \phi _i dx d \xi \right) f_h^j \\ \qquad \qquad +\,\sum _{j=1}^{N_k} \left( \int _{\Omega _h^x\times \partial \Omega _h^\xi } \widehat{\phi _j F_a(f_h)} \cdot n_{\xi } \phi _i^{-} dx ds_\xi \,\right) f_h^j, \end{array}\right. } \end{aligned}$$

and the integral in the interaction term \(F_a(f_h)\) is computed by the Cavalieri-Simpson rule on a grid which ensures the \(h^{2k}\) convergence. To solve the method of lines ODE resulting from the semi-discrete DG scheme (\({\mathcal {M}}\) is invertible and \({\mathcal {R}}={\mathcal {M}}^{-1}{\mathcal {S}}\)):

$$\begin{aligned} \frac{d \textbf{f}_h}{dt}= {\mathcal {R}}(\textbf{f}_h), \end{aligned}$$

we use the total variation diminishing third order Runge–Kutta method (see [30, 31]):

$$\begin{aligned} {\left\{ \begin{array}{ll} \displaystyle \textbf{f}^{(1)}_h= \textbf{f}_h^n + \Delta t {\mathcal {R}}(\textbf{f}_h^n), \\ \displaystyle \textbf{f}^{(2)}_h=\frac{1}{4}\left( 3 \textbf{f}_h^n + \textbf{f}_h^{(1)} + \Delta t {\mathcal {R}}( \textbf{f}_h^{(1)}) \right) , \\ \displaystyle \textbf{f}^{n+1}_h=\frac{1}{3}\left( \textbf{f}_h^n +2 \textbf{f}_h^{(2)} + 2\Delta t {\mathcal {R}}(\textbf{f}_h^{(2)}) \right) , \end{array}\right. } \end{aligned}$$

where \(\textbf{f}^n_h\) represents a numerical approximation of the solution at discrete time \(t^n\). Such time stepping methods are the convex combinations of the Euler forward time discretization. We now present a numerical experiment.

Consider the domain

$$\begin{aligned} \Omega ^x\times \Omega ^\xi =[-\pi ,\pi ]\times [-2,2] \end{aligned}$$

with boundary condition in the x domain and zero at the boundary of the velocity domain. The region is divided into N rectangles, and we choose Lagrange polynomial of degree less then 2 (\(N_2=6\)), on each rectangle. Consider the following initial datum:

$$\begin{aligned} \begin{aligned} f_0(x, \xi )&= 0.1\,e^{-20\left[ (x+1.5)^2+(\xi +0.2)^2\right] }+ 0.05\,e^{-15\left[ (x+0.1)^2+(\xi +0.5)^2\right] } \\&\quad +\,0.3\,e^{-50\left[ (x+0.7)^2+(\xi +0.4)^2\right] }. \end{aligned} \end{aligned}$$

As the initial datum is rapidly decaying, it is almost zero at the boundaries of the computational domain considered. So that we can assume that it is periodic in x and with compact support in \(\xi \). As a communication weight function, we consider

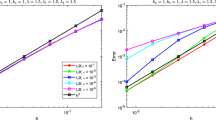
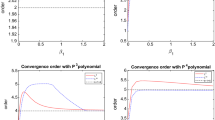
$$\begin{aligned} \psi (|x - y|) =\frac{1}{(1 + (x - y)^2)^\frac{\beta }{2}}, \end{aligned}$$

with \(\beta =2\) (see [13]). The numerical computation is performed up to a time such that the numerical solution is compactly supported in the \(\xi \) variable. In our case this time is \(t\approx 2.5\). The order of accuracy of the method is summarized in the table below, where the errors and the orders are computed at time \(t=1\):

 

N

\(L^2\) error

Order

\(L^\infty \) error

Order

\(k=2\)

16

0.113

1.98

0.0855

2.73

64

0.0381

2.22

0.0253

2.94

256

0.0142

2.48

0.0105

3.01

In Fig. 1, we show the temporal evolution of the mass density function

$$\begin{aligned} \rho _h(t,x)=\int _{[-2,2]} f_h(t,x,\xi )d\xi \end{aligned}$$

and the evolution in time of the total mass \(\int _{[-\pi ,\pi ]}\rho _h(t,x)dx,\) which is shown to be constant up to fifth digit order.

Fig. 1
figure 1

Temporal evolutions of \(\rho _h\) and \(\Vert \rho _h \Vert _{L^1}\)

Full size image

7 Conclusion

In this paper, we have presented a semi-discrete DG scheme tor the kinetic Cucker–Smale equation. The kinetic Cucker–Smale equation is a dissipative Vlasov type equation whose total energy is non-increasing along the solution. This is a contrasted difference with the classical Vlasov equation. From the viewpoint of numerics, due to the non-local nature of velocity alignment forcing, its numerical studies are vary few, compared to extensive analytical studies. We showed that our proposed semi-discrete DG scheme exhibits three crucial properties such as the total mass conservation, \(L^2\)-stability estimate and \(L^2\)-convergence of the numerical solution to the corresponding classical solution to the kinetic CS equation. Moreover, we showed that the convergence is at most \(k + \frac{1}{2}\), as long as the target classical solution lies in \(H^{k+ 2}\). In this paper, we assume that the communication weight function is bounded. However, there are several analytical studies [7, 9, 10, 14, 41,42,43] for the particle and kinetic CS models with singular communication weights. Thus, it would be interesting to extend current DG method to the setting with a singular communication weight. We leave this interesting problem for a future work.