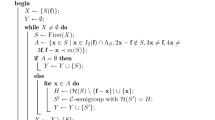Characterizing affine ${\mathcal {C}}$-semigroups

Abstract

Let ${\mathcal {C}} \subset {\mathbb {N}}^p$ be a finitely generated integer cone and $S\subset {\mathcal {C}}$ be an affine semigroup such that the real cones generated by ${\mathcal {C}}$ and by S are equal. The semigroup S is called ${\mathcal {C}}$-semigroup if ${\mathcal {C}}\setminus S$ is a finite set. In this paper, we characterize the ${\mathcal {C}}$-semigroups from their minimal generating sets, and we give an algorithm to check if S is a ${\mathcal {C}}$-semigroup and to compute its set of gaps. We also study the embedding dimension of ${\mathcal {C}}$-semigroups obtaining a lower bound for it, and introduce some families of ${\mathcal {C}}$-semigroups whose embedding dimension reaches our bound. In the last section, we present a method to obtain a decomposition of a ${\mathcal {C}}$-semigroup into irreducible ${\mathcal {C}}$-semigroups.

1 Introduction

An affine semigroup $S\subset {\mathbb {N}}^p$ is called ${\mathcal {C}}_S$-semigroup if ${\mathcal {C}}_S\setminus S$ is a finite set where ${\mathcal {C}}_S\subset {\mathbb {N}}^p$ is the minimal integer cone containing it. These semigroups are a natural generalization of numerical semigroups, and several of their invariants can be generalized. For a given numerical semigroup G, it is well-known that ${\mathbb {N}}\setminus G$ is finite; in fact, $G\subset {\mathbb {N}}$ is a numerical semigroup if it is a submonoid of ${\mathbb {N}}$ and ${\mathbb {N}}\setminus G$ is finite (for topics related with numerical semigroups see [13] and the references therein). In general, it does not happen for affine semigroups.

${\mathcal {C}}$-semigroups are introduced in [8], where the authors study several properties about them (for example, an extended Wilf’s conjecture for ${\mathcal {C}}$-semigroups is given). These semigroups appear in different contexts: when the integer points in an infinite family of some homothetic convex bodies in ${\mathbb {R}}^p_{\ge }$ are considered (see, for instance, [9, 10] and the references therein), or when the non-negative integer solutions of some modular Diophantine inequality are studied (see [5]), et cetera. In case the cone ${\mathcal {C}}$ is ${\mathbb {N}}^p$, ${\mathbb {N}}^p$-semigroups are called generalized numerical semigroups and they were introduced in [6]. Recently, in [11] it is proved that the minimal free resolution of the associated algebra to any ${\mathcal {C}}$-semigroup has maximal projective dimension possible.

In this context, ${\mathbb {N}}^p$-semigroups are characterized in [3], but the general problem was opened, given any affine semigroup S, how to detect if Sis or not a ${\mathcal {C}}_S$-semigroup? The primary goal of this work is to determine the conditions that any affine semigroup given by its minimal set of generators has to verify to be a ${\mathcal {C}}_S$-semigroup. We solve this problem in Theorem 9, and in Algorithm 1 we provide a computational way to check it.

Another open problem is to compute the set of gaps of any ${\mathcal {C}}$-semigroup defined by its minimal generating set. We solve this problem by means of setting a finite subset of ${\mathcal {C}}$ containing all the gaps of a given ${\mathcal {C}}$-semigroup. Algorithm 2 computes the set of gaps of the given ${\mathcal {C}}$-semigroup.

In this paper, we also go in-depth to study the embedding dimension of ${\mathcal {C}}$-semigroups. In [8, Theorem 11], a lower bound of the embedding dimension of ${\mathbb {N}}^p$-semigroups is provided, and some families of ${\mathbb {N}}^p$-semigroups reaching this bound are given. Besides, in [8, Conjecture 12], it is proposed a conjecture about a lower bound for the embedding dimension of any ${\mathcal {C}}$-semigroup. In Sect. 5, we introduce a lower bound of the embedding dimension of any ${\mathcal {C}}$-semigroup, and some families of ${\mathcal {C}}$-semigroups whose embedding dimension is equal to this new bound.

An important problem in Semigroup Theory is to determine some decomposition of a semigroup into irreducible semigroups (for example, see [13, Chapter 3] for numerical semigroups, or its generalization for ${\mathbb {N}}^p$-semigroups in [2]). We propose an algorithm to compute a decomposition of any ${\mathcal {C}}$-semigroup into irreducible ${\mathcal {C}}$-semigroups.

The results of this work are illustrated with several examples. To this aim, we have used third-party software, such as Normaliz [4], and the libraries CharacterizingAffineCSemigroup and Irreducible [7] developed by the authors in Python [12].

The content of this work is organized as follows. Section 2 introduces the initial definitions and notations used throughout the paper, mainly related to finitely generated cones. In Sect. 3, a characterization of ${\mathcal {C}}$-semigroups is provided, and an algorithm to check if an affine semigroup is a ${\mathcal {C}}$-semigroup. Section 4 is devoted to give an algorithm to compute the set of gaps of a ${\mathcal {C}}$-semigroup. Section 5 makes a study of the minimal generating sets of ${\mathcal {C}}$-semigroups formulating explicitly a lower bound for their embedding dimensions. Finally, in Sect. 6 an algorithm for computing a decomposition of a ${\mathcal {C}}$-semigroup into irreducible ${\mathcal {C}}$-semigroups is presented.

2 Preliminaries

The sets of real numbers, rational numbers, integer numbers and the non-negative integer numbers are denoted by ${\mathbb {R}}$, ${\mathbb {Q}}$, ${\mathbb {Z}}$ and ${\mathbb {N}}$, respectively. Given a subset A of ${\mathbb {R}}$, $A_\ge$ is the set of elements in A greater than or equal to zero. For any $n\in {\mathbb {N}}$, [n] denotes the set $\{1,\ldots n\}$. Given an element x in ${\mathbb {R}}^n$, $||x||_1$ denotes the sum of the absolute value of its entries, that is, its 1-norm. In this paper we assume the set $\{{\mathbf {e}}_1,\ldots , {\mathbf {e}}_p\}$ is the canonical basis of ${\mathbb {R}}^p$.

For a non empty subset B of ${\mathbb {R}}_\ge ^p$, we define the cone generated by B:

$$\begin{aligned} L(B){:}{=} \left\{ \sum _{i=1}^n \lambda _i {\mathbf {b}}_i \mid n\in {\mathbb {N}}, \{{\mathbf {b}}_1,\ldots ,{\mathbf {b}}_n\}\subset B,\text { and } \lambda _i \in {\mathbb {R}}_{\ge }, \forall i \in [n] \right\} . \end{aligned}$$

Given a real cone ${\mathcal {C}}\subset {\mathbb {R}}^p_\ge$, it is well-known that ${\mathcal {C}}\cap {\mathbb {N}}^p$ is finitely generated if and only if there exists a rational point in each extremal ray of ${\mathcal {C}}$. Moreover, any subsemigroup of ${\mathcal {C}}$ is finitely generated if and only if there exists an element in the semigroup in each extremal ray of ${\mathcal {C}}$. A good monograph about rational cones and affine monoids is [1]. From now on, we assume that the integer cones considered in this work are finitely generated.

Definition 1

Given an integer cone ${\mathcal {C}}\subset {\mathbb {N}}^p$, an affine semigroup $S\subset {\mathcal {C}}$ is said to be a ${\mathcal {C}}$-semigroup if ${\mathcal {C}}\setminus S$ is a finite set. If the cone ${\mathcal {C}}={\mathbb {N}}^p$, a ${\mathcal {C}}$-semigroup is called ${\mathbb {N}}^p$-semigroup.

Fix a finitely generated semigroup $S\subset {\mathbb {N}}^p$, we denote by ${\mathcal {C}}_S$ the integer cone $L(S)\cap {\mathbb {N}}^p$. Note that, if S is a ${\mathcal {C}}$-semigroup, the cone ${\mathcal {C}}$ is ${\mathcal {C}}_S$. Obviously, a unique cone corresponds to infinite different semigroups.

The cone L(S) is a polyhedron and we denote by $\{h_1(x)=0,\ldots , h_t(x)=0\}$ the set of its supported hyperplanes. We suppose $L(S)=\{ x\in {\mathbb {R}}_\ge ^d \mid h_1(x)\ge 0, \ldots , h_t(x)\ge 0\}$. Unless otherwise stated, the considered coefficients of each $h_i(x)$ are integers and relatively primes.

Assume L(S) has q extremal rays denoted by $\tau _1,\ldots ,\tau _q$. Then, each $\tau _i$ is determined by the set of linear equations $H_i{:}{=}\{h_{j^{(i)}_1}(x)=0,\ldots , h_{j^{(i)}_{p-1}}(x)=0\}$ where $J_i{:}{=}\{j^{(i)}_1<\cdots <j^{(i)}_{p-1}\}\subset [t]$ is the index set of the supported hyperplanes containing $\tau _i$. So, for each $i\in [q]$, there exists the minimal non-negative integer vector ${\mathbf {a}}_i$ such that $\tau _i=\{\lambda {\mathbf {a}}_i\mid \lambda \in {\mathbb {R}}_\ge \}$. The set $\{{\mathbf {a}}_1,\ldots , {\mathbf {a}}_q\}$ is a generating set of L(S).

Note that a necessary condition for S to be a ${\mathcal {C}}_S$-semigroup is the set $\tau _i \cap ({\mathcal {C}}_S\setminus S)$ is finite for all $i\in [q]$.

From each extremal ray $\tau _i$ of L(S), we define $\upsilon _{i}(\alpha )$ as the parallel line to $\tau _i$ given by the solutions of the linear equations $\bigcup _{j\in J_i} \{h_j(x)=\alpha _j\}$ where $\alpha =(\alpha _{j_1},\ldots ,\alpha _{j_{p-1}})\in {\mathbb {Z}}^{p-1}$. For every integer point $P\in {\mathbb {Z}}^p$ and $i\in [q]$, there exists $\alpha \in {\mathbb {Z}}^{p-1}$ such that P belongs to $\upsilon _{i}(\alpha )$; if $P\in {\mathcal {C}}_S$, $\alpha \in {\mathbb {N}}^{p-1}$. We denote by $\Upsilon _i(P)$ the element $(h_{j^{(i)}_1}(P),\ldots , h_{j^{(i)}_{p-1}}(P))\in {\mathbb {N}}^{p-1}$ with $J_i=\{j^{(i)}_1<\cdots <j^{(i)}_{p-1}\}$, $P\in {\mathcal {C}}_S$ and $i\in [q]$. Note that for any $P\in {\mathcal {C}}_S$, $P\in \upsilon _i(\alpha )$ if and only if $\alpha =\Upsilon _i(P)$.

Since all the semigroups appearing in this work are finitely generated, from now on, we omit the term affine when affine semigroups are considered.

3 An algorithm to detect if a semigroup is a ${\mathcal {C}}$-semigroup

In this section, we study the conditions that a semigroup has to satisfy to be a ${\mathcal {C}}$-semigroup. This characterization depends on the minimal set of generators of the given semigroup.

Let $S\subset {\mathbb {N}}^p$ be the affine semigroup minimally generated by $\Lambda _S=\{{\mathbf {s}}_1,\ldots , {\mathbf {s}}_q,{\mathbf {s}}_{q+1}, \ldots , {\mathbf {s}}_n\}$ and $\tau _1,\ldots ,\tau _q$ be the extremal rays of L(S). Assume that for every $i\in [q]$, $\tau _i \cap ({\mathcal {C}}_S\setminus S)$ is finite and ${\mathbf {s}}_i$ is the minimum (respect to the natural order) element in $\Lambda _S$ belonging to $\tau _i$. We denote by ${\mathbf {f}}_i$ the maximal element in $\tau _i \cap ({\mathcal {C}}_S\setminus S)$ with respect to the natural order in ${\mathbb {N}}^p$. Recall that ${\mathbf {a}}_i$ is the minimal non-negative integer vector defining $\tau _i$, and let ${\mathbf {c}}_i\in S$ be the element ${\mathbf {f}}_i+{\mathbf {a}}_i$. In case $\tau _i \cap ({\mathcal {C}}_S\setminus S)=\emptyset$, we fix ${\mathbf {f}}_i=-{\mathbf {a}}_i$. The elements ${\mathbf {f}}_i$ and ${\mathbf {c}}_i$ are a generalization on the semigroup $\tau _i \cap S$ of the concepts Frobenius number and conductor of a numerical semigroup; for numerical semigroups, the Frobenius number is the maximal natural number that is not in the semigroup, and the conductor is Frobenius number plus one (see [13, Chapter 1]). Hence, we call Frobenius element and conductor of the semigroup $\tau _i\cap S$ the elements ${\mathbf {f}}_i$ and ${\mathbf {c}}_i$, respectively. One easy but important property of S is for every $P\in S$, $P+{\mathbf {c}}_i+\lambda {\mathbf {a}}_i\in S$ for any $i\in [q]$ and $\lambda \in {\mathbb {N}}$.

Note that $\tau _i\cap {\mathbb {N}}^p$ is equal to $\{\lambda {\mathbf {a}}_i\mid \lambda \in {\mathbb {N}}\}$. So, there exists $S_i\subset {\mathbb {N}}$ such that $\tau _i\cap S=\{\lambda {\mathbf {a}}_i\mid \lambda \in S_i \}$. If we assume that $\tau _i \cap ({\mathcal {C}}_S\setminus S)$ is finite, it is easy to prove that $S_i$ is a numerical semigroup.

Lemma 2

The $\tau _i$-semigroup $\tau _i \cap S$ is isomorphic to the semigroup $S_i=\{\lambda \in {\mathbb {N}}\mid \lambda {\mathbf {a}}_i\in S\}$. Moreover $\tau _i\cap ({\mathcal {C}}_S\setminus S)$ is finite if and only if $S_i$ is a numerical semigroup.

Proof

Consider the isomorphism $\varphi :\tau _i \cap S\rightarrow S_i$ with $\varphi ({\mathbf {w}}){:}{=}\lambda$ such that ${\mathbf {w}}=\lambda {\mathbf {a}}_i$. The second statement holds since $\tau _i\cap ({\mathcal {C}}_S\setminus S)=\{\lambda {\mathbf {a}}_i\in {\mathbb {N}}\mid \lambda {\mathbf {a}}_i\not \in S,\lambda \in {\mathbb {N}}\}$. $\square$

Corollary 3

Given the semigroup $\tau _i \cap S$, ${\mathbf {f}}_i$ is equal to $f{\mathbf {a}}_i$ and ${\mathbf {c}}_i=c\,{\mathbf {a}}_i$ where f and c are the Frobenius number and the conductor of the numerical semigroup $S_i$, respectively.

To test whether $\tau _i \cap ({\mathcal {C}}_S\setminus S)$ is finite, the following result can be used.

Lemma 4

Let $S\subset {\mathbb {N}}^p$ be a semigroup and $\tau$ be an extremal ray of L(S) satisfying $\tau \cap {\mathbb {N}}^p=\{\lambda {\mathbf {a}}\mid \lambda \in {\mathbb {N}}\}$ with ${\mathbf {a}}\in {\mathbb {N}}^p$. Then, $\tau \cap ({\mathcal {C}}_S\setminus S)$ is finite if and only if $\gcd (\{\lambda \mid \lambda {\mathbf {a}}\in \tau \cap \Lambda _S \})=1$.

Proof

Assume that $\tau \cap ({\mathcal {C}}_S\setminus S)$ is finite and suppose that $\gcd (\{\lambda \mid \lambda {\mathbf {a}}\in \tau \cap \Lambda _S \})=n\ne 1$. Hence, every element $\lambda {\mathbf {a}}$ with $\gcd (n,\lambda )=1$ does not belong to S, and then $\tau \cap ({\mathcal {C}}_S\setminus S)$ is not finite.

Conversely if $\gcd (\{\lambda \mid \lambda {\mathbf {a}}\in \tau \cap \Lambda _S \})=1$, then the semigroup $S'=\{\lambda \in {\mathbb {N}}\mid \lambda {\mathbf {a}}\in S\}$ is a numerical semigroup. From the proof of Lemma 2, $S'$ is isomorphic to $\tau \cap S$. Therefore, $\tau \cap ({\mathcal {C}}_S\setminus S)$ is finite. $\square$

To introduce the announced characterization, we need to define some subsets of L(S) and prove some of their properties. Associated to the integer cone ${\mathcal {C}}_S$, consider the sets ${\mathcal {A}}{:}{=}\{ \sum _{i\in [q]} \lambda _i{\mathbf {a}}_i \mid 0\le \lambda _i\le 1\}\cap {\mathbb {N}}^p$ and ${\mathcal {D}}{:}{=}\{ \sum _{i\in [q]} \lambda _i{\mathbf {s}}_i \mid 0\le \lambda _i\le 1\}\cap {\mathbb {N}}^p$.

Lemma 5

Given $P\in {\mathcal {C}}_S$, there exist $Q\in {\mathcal {A}}$ and $\beta \in {\mathbb {N}}^q$ such that $P=Q+\sum _{i\in [q]} \beta _i{\mathbf {a}}_i$. Moreover, $\Upsilon _j(P)=\Upsilon _j(Q)+\sum _{i\in [q]}\beta _i \Upsilon _j(\mathbf {a_i})$ for every $j\in [q]$.

Proof

Since $P\in {\mathcal {C}}_S$, $P=\sum _{i\in [q]}\mu _i{\mathbf {a}}_i$ with $\mu _i\in {\mathbb {Q}}_\ge$. For each $\mu _i$ there exists $\lambda _i\in [0,1)$ satisfying $\mu _i=\lfloor \mu _i\rfloor +\lambda _i$. Hence, $P=Q +\sum _{i\in [q]}\lfloor \mu _i\rfloor {\mathbf {a}}_i$ where $Q=\sum _{i\in [q]}\lambda _i{\mathbf {a}}_i=P-\sum _{i\in [q]}\lfloor \mu _i\rfloor {\mathbf {a}}_i\in {\mathcal {A}}$. Trivially, $\Upsilon _j(P)$ is equal to $\Upsilon _j(Q)+\sum _{i\in [q]}\beta _i \Upsilon _j({\mathbf {a}}_i)$ for every $j\in [q]$. $\square$

For every $i\in [q]$, consider $T_i\subset {\mathbb {N}}^{p-1}$ the semigroup generated by the finite set $\{\Upsilon _i(Q)\mid Q\in {\mathcal {A}}\}$ and let $\Gamma _i$ be its minimal generating set. Note that the sets ${\mathcal {A}}$, $T_i$ and $\Gamma _i$ only depend on the cone ${\mathcal {C}}_S$, and $0\in T_i$, since ${\mathbf {a}}_i\in {\mathcal {A}}$. The relationships between the elements in ${\mathcal {C}}_S$ and S, and the elements belonging to $T_i$ and $\Gamma _i$ are explicitly determined in the following results for each $i\in [q]$.

Lemma 6

Let P be an element in ${\mathcal {C}}_S$ such that $P\in \upsilon _i(\alpha )$ for some $\alpha \in {\mathbb {N}}^{p-1}$, then $\alpha \in T_i$.

Proof

By definition, $P\in \upsilon _i(\alpha )$ means that $\alpha =\Upsilon _i(P)$. Using Lemma 5, $P=Q+\sum _{j\in [q]} \beta _j{\mathbf {a}}_j$ with $Q,{\mathbf {a}}_1,\ldots ,{\mathbf {a}}_q\in {\mathcal {A}}$ and $\beta _1,\ldots ,\beta _q\in {\mathbb {N}}$. Therefore, $\Upsilon _i (P)=\Upsilon _i(Q)+\sum _{j\in [q]}\beta _j \Upsilon _i({\mathbf {a}}_j)\in T_i$. $\square$

Corollary 7

For every $\alpha \in T_i$, ${\mathcal {C}}_S\cap \upsilon _i(\alpha )\ne \emptyset$ if and only if ${\mathcal {C}}_S\cap \upsilon _i(\beta )\ne \emptyset$ for all $\beta \in \Gamma _i$.

Proof

Since $\Gamma _i\subset T_i$, if for all $\alpha \in T_i$, ${\mathcal {C}}_S\cap \upsilon _i(\alpha )\ne \emptyset$ then ${\mathcal {C}}_S\cap \upsilon _i(\beta )\ne \emptyset$ for all $\beta \in \Gamma _i$.

Assume that ${\mathcal {C}}_S\cap \upsilon _i(\beta )\ne \emptyset$ for all $\beta \in \Gamma _i$ and let $\alpha$ be an element in $T_i$. Then, there exist $\beta _1,\ldots ,\beta _k\in \Gamma _i$, $\mu _1,\ldots ,\mu _k\in {\mathbb {N}}$ and $Q_1,\ldots ,Q_k\in {\mathcal {A}}$ such that $\alpha =\sum _{j\in [k]}\mu _j\beta _j$ and $\Upsilon _i(Q_j)=\beta _j$ for $j\in [k]$. Note that $P=\sum _{j\in [k]}\mu _jQ_j\in {\mathcal {C}}_S$ belongs to $\upsilon _i(\alpha )$. $\square$

Corollary 8

For every $\alpha \in T_i$, $S\cap \upsilon _i(\alpha )\ne \emptyset$ if and only if $S\cap \upsilon _i(\beta )\ne \emptyset$ for all $\beta \in \Gamma _i$.

Proof

Since $S\cap \upsilon _i(\beta )\ne \emptyset$ for all $\beta$, then there exists $Q_1,\ldots ,Q_k\in {\mathcal {A}}$ such that $\Upsilon _i(Q_j)=\beta _j$ for $j\in [k]$. Thus, the proof of this corollary is analogous to the proof of Corollary 7. $\square$

Note that if $P\in S\cap \upsilon _i(\alpha )$ for some $\alpha \in {\mathbb {N}}^{p-1}$ and $i\in [q]$, then $P+{\mathbf {c}}_i+\lambda {\mathbf {a}}_i\in S$ and $\Upsilon _i(P+{\mathbf {c}}_i+\lambda {\mathbf {a}}_i)=\alpha$ for all $\lambda \in {\mathbb {N}}$.

Now, we introduce a characterization of ${\mathcal {C}}$-semigroups. This characterization depends on the minimal generating set of the given semigroup. Besides, from its proof, we provide an algorithm for checking if a semigroup is a ${\mathcal {C}}$-semigroup (Algorithm 1). Note that most of the parts of Algorithm 1 can be parallelized at least in q stand-alone processes.

Theorem 9

A semigroup S minimally generated by $\Lambda _S=\{{\mathbf {s}}_1,\ldots ,{\mathbf {s}}_n\}$ is a ${\mathcal {C}}_S$-semigroup if and only if:

• 1. $\tau _i \cap ({\mathcal {C}}_S\setminus S)$ is finite for all $i\in [q]$.

• 2. $\Lambda _S\cap \upsilon _i(\alpha )\ne \emptyset$ for all $\alpha \in \Gamma _i$ and $i\in [q]$.

Proof

Let S be a ${\mathcal {C}}_S$-semigroup. Trivially, $\tau _i \cap ({\mathcal {C}}_S\setminus S)$ is finite for all $i\in [q]$. Now let $i\in [q]$ and $\alpha \in \Gamma _i$, we probe that $\Lambda _S\cap \upsilon _i(\alpha )\ne \emptyset$. Since $\alpha \in \Gamma _i$, there exists $Q\in {\mathcal {A}}$ such that $\alpha =\Upsilon _i(Q)$. Besides, $Q+\lambda {\mathbf {a}}_i\in {\mathcal {C}}_S$ and $\Upsilon _i(Q+\lambda {\mathbf {a}}_i)=\alpha$ for all $\lambda \in {\mathbb {N}}$. For some $\lambda \in {\mathbb {N}}$, $Q+\lambda {\mathbf {a}}_i$ has to be in S (S is ${\mathcal {C}}_S$-semigroup), that is to say, $Q+\lambda {\mathbf {a}}_i=\sum _{j\in [n]} \mu _j {\mathbf {s}}_j$ with $\mu _1,\ldots ,\mu _n\in {\mathbb {N}}$. Therefore, $\alpha =\Upsilon _i (Q+\lambda {\mathbf {a}}_i)= \sum _{j\in [n]} \mu _j \Upsilon _i({\mathbf {s}}_j)$. By Lemma 5, for all $j\in [n]$, ${\mathbf {s}}_j=Q_j+\sum _{k\in [q]} \beta _{jk}{\mathbf {a}}_k$ for some $Q_j\in {\mathcal {A}}$ and $\beta _{j1},\ldots ,\beta _{jq}\in {\mathbb {N}}$. So, $\alpha = \sum _{j\in [n]} \mu _j \Upsilon _i(Q_j+\sum _{k\in [q]} \beta _{jk}{\mathbf {a}}_k)= \sum _{j\in [n]} \mu _j \Upsilon _i(Q_j) +\sum _{j\in [n]} \sum _{k\in [q]} \mu _j \beta _{jk}\Upsilon _i( {\mathbf {a}}_k)$. Since $\alpha$ is a minimal generator of $T_i$, $\sum _{j\in [n]} \mu _j +\sum _{j\in [n]} \sum _{k\in [q]\setminus \{i\}} \mu _j \beta _{jk}=1$. So $\beta _{jk}=0$ for all $j\in [n]$ and for all $k\in [q]\setminus \{i\}$, and there exists $l\in [n]$ such that $\mu _l=1$ and $\mu _j=0$ for all $j\in [n]\setminus \{l\}$. Hence, there exists ${\mathbf {s}}\in \Lambda _S$ such that $\Upsilon _i({\mathbf {s}})=\alpha$ and then $\Lambda _S\cap \upsilon _i(\alpha )\ne \emptyset$.

Conversely, we assume that $\forall i\in [q]$ and $\forall \alpha \in \Gamma _i$, $\tau _i \cap ({\mathcal {C}}_S\setminus S)$ is finite and $\Lambda _S\cap \upsilon _i(\alpha )\ne \emptyset$ (recall that ${\mathbf {c}}_i={\mathbf {f}}_i+{\mathbf {a}}_i$). Let Q be an element in ${\mathcal {D}}$. By Lemmas 5 and 6, $Q\in \alpha _i(\Upsilon _i(Q))$ and $\Upsilon _i(Q) \in T_i$. If $Q\in \tau _i$ for some $i\in [q]$, then $v_i(\Upsilon _i(Q))=\tau _i$ and, by the first condition, $S\cap v_i(\Upsilon _i(Q))\ne \emptyset$. If Q is not in any ray, by the second condition and Corollary 8, $S\cap v_i(\Upsilon _i(Q))\ne \emptyset$. Therefore, for every $Q\in {\mathcal {D}}$, the line $\upsilon _i(\Upsilon _i(Q))$ includes a unique non zero minimum (respect 1-norm) point belonging to S. Denote by $\{{\mathbf {m}}_{i1},\ldots , {\mathbf {m}}_{id_i}\}$ the set obtained from the union of above points for the different elements in ${\mathcal {D}}$ (some of these elements belong to $\Lambda _S$). Note that ${\mathbf {m}}_{ij}+{\mathbf {c}}_i+\lambda {\mathbf {a}}_i\in S$ for all $j\in [d_i]$ and $\lambda \in {\mathbb {N}}$. Consider $n_i{:}{=}\max \{||{\mathbf {m}}_{i1}+{\mathbf {c}}_i||_1,\ldots , ||{\mathbf {m}}_{id_i}+{\mathbf {c}}_i ||_1\}$, and ${\mathbf {x}}_i$ the minimum element (respect to the 1-norm) in $\tau _i\cap S$ such that $||{\mathbf {x}}_i||_1$ is greater than or equal to $n_i$. The set ${\mathcal {D}}_i{:}{=}{\mathcal {D}}+{\mathbf {x}}_i$ satisfies that ${\mathcal {D}}_i \cap S={\mathcal {D}}_i \cap {\mathcal {C}}_S={\mathcal {D}}_i$. Consider ${\mathbf {a}}\in {\mathbf {x}}_i+{\mathcal {C}}_S$, proceeding as in the proof of Lemma 5, ${\mathbf {a}} = {\mathbf {x}}_i + P + \sum _{j\in [q]} \beta _j {\mathbf {s}}_j$ for some $P\in {\mathcal {D}}$ and $\beta _1,\ldots ,\beta _q\in {\mathbb {N}}$, and hence, ${\mathbf {x}}_i+{\mathcal {C}}_S\subset S$. We define the bounded set ${\mathcal {X}}{:}{=} \{\sum _{i\in [q]}\lambda _i{\mathbf {x}}_i \mid 0\le \lambda _i\le 1 \}$. Since ${\mathbf {x}}_i+{\mathcal {C}}_S\subset S$ for every $i\in [q]$ and $L({\mathcal {C}}_S)=\{ \sum _{i\in [q]} \lambda _i {\mathbf {x}}_i | \lambda _i\in {\mathbb {R}}_\ge \}$, ${\mathcal {C}}_S\setminus S\subset {\mathcal {X}}$. Therefore, S is a ${\mathcal {C}}_S$-semigroup. $\square$

Example 10 illustrates Theorem 9 and Algorithm 1.

Example 10

Let $S\subset {\mathbb {N}}^3$ be the semigroup minimally generated by

$$\begin{aligned} \Lambda _S=\{ (2, 0, 0), (4, 2, 4), (0, 1, 0), (3, 0, 0), (6, 3, 6), (3, 1, 1), (4, 1, 1),\\ (3, 1, 2), (1, 1, 0), (3, 2, 3), (1, 2, 1) \}. \end{aligned}$$

The cone L(S) is $\langle (1,0,0),(2,1,2),(0,1,0) \rangle _{{\mathbb {R}}_\ge }$ and its supported hyperplanes are $h_1(x,y,z)\equiv 2y-z =0$, $h_2(x,y,z)\equiv x-z =0$ and $h_3(x,y,z)\equiv z=0$. Recall ${\mathcal {C}}_S=L(S)\cap {\mathbb {N}}^3$. By ${\mathbf {a}}_1$, ${\mathbf {a}}_2$ and ${\mathbf {a}}_3$ we denote the vectors (1, 0, 0), (2, 1, 2) and (0, 1, 0) respectively, and $\tau _1$, $\tau _2$ and $\tau _3$ are the extremal rays with sets of defining equations $\{h_1(x,y,z)=0,h_3(x,y,z)=0\}$, $\{h_1(x,y,z)=0,h_2(x,y,z)=0\}$ and $\{h_2(x,y,z)=0,h_3(x,y,z)=0\}$, respectively. Hence, $S_1=(\tau _1\setminus \{(1,0,0)\})\cap {\mathbb {N}}^3$, $S_2=\tau _2\setminus \{(2,1,2)\}\cap {\mathbb {N}}^3$ and $S_3=\tau _3\cap {\mathbb {N}}^3$, and the first condition in Theorem 9 holds.

The set ${\mathcal {A}}$ is equal to

$$\begin{aligned} \{(0, 0, 0), (0, 1, 0), (1, 0, 0), (1, 1, 0), (1, 1, 1), (2, 1, 1), (2,1, 2),\nonumber \\ (2, 2, 2), (3, 1, 2), (3, 2, 2)\}, \end{aligned}$$

(1)

and

$$\begin{aligned} \Upsilon _1({\mathcal {A}})&=\{(0, 0), (0, 2), (1, 1), (2, 0), (2, 2)\}, \\ \Upsilon _2({\mathcal {A}})&=\{(0, 0), (0, 1), (1, 0), (1, 1), (2, 0), (2, 1)\}, \\ \Upsilon _3({\mathcal {A}})&=\{(0, 0), (0, 1), (0, 2), (1, 0), (1, 1), (1, 2) \}. \end{aligned}$$

Therefore, $\Gamma _1=\{(0,2),(1,1),(2,0)\}$ and $\Gamma _2=\Gamma _3=\{(0,1),(1,0)\}$.

Since $\Upsilon _1(\{(3,1,1),(3,1,2),(1,1,0)\})=\Gamma _1$, $\Upsilon _2(\{(3,1,2),(3,2,3)\})=\Gamma _2$, and $\Upsilon _3(\{(1,1,0),(1,2,1)\})=\Gamma _3$, S satisfies the second condition in Theorem 9. Hence, S is a ${\mathcal {C}}_S$-semigroup.

By using our implementation of Algorithm 1, we can confirm that S is a ${\mathcal {C}}_S$-semigroup,

To finish this section, it should be pointed out that there exist some special cases of semigroups where Theorem 9 can be simplified: ${\mathbb {N}}^p$-semigroups and two-dimensional case.

Note that, if the integer cone ${\mathcal {C}}_S$ is ${\mathbb {N}}^p$, its supported hyperplanes are $\{x_1=0,\ldots ,x_p=0\}$. Moreover, since its extremal rays are the axes, $\tau _i\equiv \{\lambda {\mathbf {e}}_i\mid \lambda \in {\mathbb {Q}}_\ge \}$ is determined by the equations $\cup _{j\in [p]\setminus \{i\}}\{x_{j}=0\}$, and for any canonical generator ${\mathbf {e}}$ of ${\mathbb {N}}^{p-1}$, there exists P in ${\mathbb {N}}^p$ such that $\Upsilon _i(P)={\mathbf {e}}$. Furthermore, $\cup _{j\in [p]\setminus \{i\}} \{\Upsilon _i({\mathbf {e}}_j)\}$ is the canonical basis of ${\mathbb {N}}^{p-1}$. Hence, $\Gamma _1=\cdots =\Gamma _p$ is the canonical basis of ${\mathbb {N}}^{p-1}$. From previous considerations, the same characterization of ${\mathbb {N}}^p$-semigroups in [3, Theorem 2.8] is obtained from Theorem 9.

Corollary 11

A semigroup S minimally generated by $\Lambda _S$ is an ${\mathbb {N}}^p$-semigroup if and only if:

• 1. for all $i\in [p]$, the non null entries of the elements in $\tau _i \cap \Lambda _S$ are coprime, or ${\mathbf {s}}_i={\mathbf {e}}_i$.

• 2. for all $i,j\in [p]$ with $i\ne j$, ${\mathbf {e}}_i+\lambda _j{\mathbf {e}}_j\in \Lambda _S$ for some $\lambda _j\in {\mathbb {N}}$.

Focus on two dimensional case, note that the extremal rays and the supported hyperplanes of a cone are equal. Since for each extremal ray the coefficients of its defining linear equation are relatively primes, the linear equations $h_1(x,y)=1$ and $h_2(x,y)=1$ always have non-negative integer solutions. So, any semigroup $S\subset {\mathbb {N}}^2$ is a ${\mathcal {C}}_S$-semigroup if and only if $\tau _i \cap ({\mathcal {C}}_S\setminus S)$ is finite for $i=1,2$, and both sets $\Lambda _S\cap \{h_1(x,y)=1\}$ and $\Lambda _S\cap \{h_2(x,y)=1\}$ are non empty.

4 Set of gaps of ${\mathcal {C}}$-semigroups

This section gives an algorithm to compute the set of gaps of a ${\mathcal {C}}$-semigroup, i.e. the set ${\mathcal {H}}(S)={\mathcal {C}}_S\setminus S$. This algorithm is obtained from Theorem 9. To introduce such an algorithm, let us start by redefining some objects used to prove that theorem.

Given S a ${\mathcal {C}}_S$-semigroup with q extremal rays, for any $i\in [q]$, let ${\mathbf {c}}_i$ be the conductor of the semigroup $\tau _i\cap S$. By Corollary 8, for any $\alpha \in \Upsilon _i({\mathcal {D}})$ the intersection $\upsilon _i(\alpha )\cap S$ is not empty. Hence, set ${\mathbf {m}}^{(i)}_\alpha$ the element in $\upsilon _i(\alpha )\cap S$ with minimal 1-norm and $\alpha \in \Upsilon _i({\mathcal {D}})\setminus \{0\}$. Note that ${\mathbf {m}}^{(i)}_\alpha + {\mathbf {c}}_i+\lambda {\mathbf {a}}_i\in S$ for all $\lambda \in {\mathbb {N}}$. Let $n_i{:}{=}||{\mathbf {c}}_i ||_1+ \max \big (\{||{\mathbf {m}}^{(i)}_\alpha ||_1\mid \alpha \in \Upsilon _i({\mathcal {D}}) \setminus \{0\} \}\big )$, and ${\mathbf {x}}_i$ the minimal element in $\tau _i\cap S$ such that $||{\mathbf {x}}_i||_1$ is greater than or equal to $n_i$. The vector ${\mathbf {x}}_i$ can be computed as follows: let Q be the non-negative rational solution of the systems of linear equations $\{x_1+\cdots +x_p=n_i, h_{j^{(i)}_1}(x)=0,\ldots , h_{j^{(i)}_{p-1}}(x)=0\}$ (recall that $h_{j^{(i)}_1}(x)=0,\ldots , h_{j^{(i)}_{p-1}}(x)=0$ are the equations defining $\tau _i$), then ${\mathbf {x}}_i= \Big \lceil \frac{||Q||_1}{||{\mathbf {a}}_i||_1}\Big \rceil {\mathbf {a}}_i$.

By the proof of Theorem 9, ${\mathcal {C}}_S\setminus S\subset {\mathcal {X}}$, with ${\mathcal {X}}= \{\sum _{i\in [q]}\lambda _i{\mathbf {x}}_i \mid 0\le \lambda _i\le 1 \}$. Algorithm 2 shows the process to computed the set of gaps of S. Note that several of its steps can be computed in a parallel way.

We illustrate Algorithm 2 in the following example. Besides, we confirm our handmade computations by using our free software [7].

Example 12

Consider the ${\mathcal {C}}_S$-semigroup S defined in example 10. So, ${\mathbf {s}}_1={\mathbf {c}}_1= (2,0,0)$, ${\mathbf {s}}_2={\mathbf {c}}_2= (4,2,4)$, ${\mathbf {s}}_3= (0,1,0)$ and ${\mathbf {c}}_3= (0,0,0)$. The set ${\mathcal {D}}$ is

$$\begin{aligned} \{ (0, 0, 0), (0, 1, 0), (1, 0, 0), (1, 1, 0), (1, 1, 1), (2, 0, 0), (2, 1, 0), (2, 1, 1),\\ (2, 1, 2), (2, 2, 2), (3, 1, 1), (3, 1, 2), (3, 2, 2), (3, 2, 3), (4, 1, 2), (4, 2, 2),\\ (4, 2, 3), (4, 2, 4), (4, 3, 4), (5, 2, 3), (5, 2, 4), (5, 3, 4), (6, 2, 4), (6, 3, 4) \}. \end{aligned}$$

For example, for the extremal ray $\tau _1$, $\Upsilon _1({\mathcal {D}})$ is the set

$$\begin{aligned} \{(0, 0), (0, 2), (0, 4), (1, 1), (1, 3), (2, 0), (2, 2), (2, 4)\}, \end{aligned}$$

and $\cup _{\alpha \in \Upsilon _1({\mathcal {D}}) \setminus \{0\}} \{{\mathbf {m}}^{(1)}_\alpha \}$ is

$$\begin{aligned} \{ (0, 1, 0), (3, 1, 1), (3, 1, 2), (3, 2, 2), (3, 2, 3), (4, 2, 4), (4, 3, 4) \} \end{aligned}$$

For $\tau _2$ and $\tau _3$,

$$\begin{aligned} \cup _{\alpha \in \Upsilon _2({\mathcal {D}})\setminus \{0\}} \{{\mathbf {m}}^{(2)}_\alpha \}= \{(0, 1, 0), (3, 1, 2), (1, 1, 0), (3, 2, 3), (2, 0, 0),\\ (2, 1, 0), (6, 3, 5), (3, 1, 1)\} \\ \cup _{\alpha \in \Upsilon _3({\mathcal {D}})\setminus \{0\}} \{{\mathbf {m}}^{(3)}_\alpha \}= \{ (1, 1, 0), (1, 2, 1), (2, 0, 0), (2, 3, 1), (2, 4, 2),\\ (3, 1, 1), (3, 1, 2), (3, 2, 3), (4, 2, 2), (4, 3, 3), (4, 2, 4), (5, 3, 4), (6, 2, 4) \} \end{aligned}$$

Then $n_1=13$, $n_2=24$ and $n_3=12$, and ${\mathbf {x}}_1= (14,0,0)$, ${\mathbf {x}}_2= (10,5,10)$ and ${\mathbf {x}}_3= (0,13,0)$. Therefore, the set of gaps of S is,

$$\begin{aligned} \{ (1,0,0), (1,1,1), (2,1,1), (2,1,2), (2,2,1), (2,2,2), (2,3,2),\\ (4,1,2), (4,2,3), (5,2,4), (5,3,5), (8,4,7) \}. \end{aligned}$$

By using our implementation of Algorithm 2, we obtain the same gaps:

5 Embedding dimension of ${\mathcal {C}}$-semigroups

In [8], it is proved that the embedding dimension of an ${\mathbb {N}}^p$-semigroup is greater than or equal to 2p, and this bound holds. Furthermore, a conjecture about a lower bound of embedding dimension of any ${\mathcal {C}}$-semigroup is proposed. In this section, we determine a lower bound of the embedding dimension e(S) of a given ${\mathcal {C}}$-semigroup S by studying its elements belonging to ${\mathcal {A}}$.

As in previous sections, let ${\mathcal {C}}\subset {\mathbb {N}}^p$ be a finitely generated cone and $\tau _1,\ldots ,\tau _q$ its extremal rays. For any $i\in [q]$, ${\mathbf {a}}_i$ is the generator of $\tau _i\cap {\mathbb {N}}^p$, ${\mathcal {A}}$ is the finite set $\{ \sum _{i\in [q]} \lambda _i{\mathbf {a}}_i \mid 0\le \lambda _i\le 1\}\cap {\mathbb {N}}^p$ and $\Gamma _i$ denotes the minimal generating set of the semigroup $T_i\subset {\mathbb {N}}^{p-1}$ generated by $\Upsilon _i({\mathcal {A}})$. Given a ${\mathcal {C}}$-semigroup S, consider $\Lambda '_S{:}{=}\{{\mathbf {s}}_{t_1},\ldots ,{\mathbf {s}}_{t_k}\}$ the set of minimal generators of S belonging to ${\mathcal {A}}{\setminus \cup _{i\in [q]}\tau _i}$, and $M_l{:}{=}\{i\in [q] \mid \Upsilon _{i}({\mathbf {s}}_{t_l})\in \Gamma _i\}$ for $l\in [k]$.

The following result provides us with a lower bound for the embedding dimension of any ${\mathcal {C}}$-semigroup.

Proposition 13

Given a ${\mathcal {C}}$-semigroup $S\subset {\mathbb {N}}^p$, then

$$\begin{aligned} \mathrm {e}(S)\ge \sum _{i\in [q]} (\mathrm {e}(S_i)+\mathrm {e}(T_i))+k-\sum _{i\in [k]}\sharp (M_i). \end{aligned}$$

(2)

Proof

From Theorem 9, for any $i\in [q]$, there exist $\mathrm {e}(S_i)$ minimal generators of S in $\tau _i$. Moreover, for each element $\gamma \in \Gamma _i$, there is at least an element of $\Lambda _S$ in $\upsilon _i(\gamma )$. Note that, for every ${\mathbf {s}}\in \Lambda _S\setminus {\mathcal {A}}$, there is no $\gamma \in \Gamma _i$ and $\gamma '\in \Gamma _j$ such that ${\mathbf {s}}\in \upsilon _i(\gamma ) \cap \upsilon _j(\gamma ')$, since for any $i,j\in [q]$, $\gamma \in \Gamma _i$ and $\gamma '\in \Gamma _j$, the intersection $\upsilon _i(\gamma ) \cap \upsilon _j(\gamma ')$ is empty or belongs to ${\mathcal {A}}$. However, if ${\mathbf {s}}\in \Lambda '_S$, then it is possible that ${\mathbf {s}}$ belongs to two (or more) different lines $\upsilon _i(\gamma )$ and $\upsilon _j(\gamma ')$ with $\gamma \in \Gamma _i$ and $\gamma '\in \Gamma _j$ (in that case, $\upsilon _i(\gamma )\cap \upsilon _j(\gamma ')=\{{\mathbf {s}}\}$). Thus, the value of $\sharp (M_l)$ indicates the number of different lines $v_i(\gamma _i)$ with $\gamma _i\in \Gamma _i$ to which ${\mathbf {s}}_{t_l}\in \Lambda _S'$ belongs. So, counting the minimal amount of elements needed to have at least one minimal generator in each line $\upsilon _i(\gamma )$ for each $\gamma \in \Gamma _i$ and $i\in [q]$, we have that the embedding dimension of S is greater than or equal to $\sum _{i\in [q]} (\mathrm {e}(S_i)+\mathrm {e}(T_i))+k-\sum _{i\in [k]}\sharp (M_i).$ $\square$

Example 14

Consider the ${\mathcal {C}}_S$-semigroup S given in example 10. In that case, $\Lambda '_S=\{(3,1,2),(1,1,0)\}$, $\sharp (M_1)=2$ (i.e. $\Upsilon _i(3,1,2)\in \Gamma _i$ for $i=1,2$), and $\sharp (M_2)=2$ ($\Upsilon _1 (1,1,0) \in \Gamma _1$ and $\Upsilon _2 (1,1,0) \in \Gamma _3$). So, $\sum _{i\in [q]} (\mathrm {e}(S_i)+\mathrm {e}(T_i))+k-\sum _{i\in [k]}\sharp (M_i)= 5 + 7 +{2} - 2-2= {10}$ that is smaller than $\mathrm {e}(S)=11$.

Given any bound, the first interesting question about it is if the bound is reached for some ${\mathcal {C}}$-semigroup. The answer is affirmative for (2), and this fact is formulated as follows.

Lemma 15

Let ${\mathcal {C}}\subset {\mathbb {N}}^p$ be an integer cone generated by $\{{\mathbf {a}}_1,\ldots ,{\mathbf {a}}_q\}$ and let $S_1,\ldots ,S_q$ be the non proper numerical semigroups minimally generated by $\{n_1^{(i)},\ldots ,n_{\mathrm {e}(S_i)}^{(i)}\}$ for each $i\in [q]$. Let $\Lambda ''\subset {\mathcal {C}}\setminus \cup _{i\in [q]}\tau _i$ be a finite set satisfying:

• for every $\gamma \in \Gamma _i$ and $i\in [q]$, there exists a unique ${\mathbf {d}}\in \Lambda ''$ such that $\Upsilon _i({\mathbf {d}})=\gamma$,

• for every ${\mathbf {d}}\in \Lambda ''$, $\Upsilon _i({\mathbf {d}})\in \Gamma _i$ for some $i\in [q]$.

Then, the embedding dimension of the ${\mathcal {C}}$-semigroup S generated by

$$\begin{aligned} \Lambda '' \cup \bigcup _{i\in [q]} \{n_1^{(i)}{\mathbf {a}}_i,\ldots ,n_{\mathrm {e}(S_i)}^{(i)}{\mathbf {a}}_i\} \end{aligned}$$

is

$$\begin{aligned} \sum _{i\in [q]} (\mathrm {e}(S_i)+\mathrm {e}(T_i))+k-\sum _{i\in [k]}\sharp (M_i), \end{aligned}$$

where k is the cardinality of $\Lambda '_S=\{{\mathbf {s}}_{1},\ldots ,{\mathbf {s}}_{k}\}$, the set of minimal generators of S belonging to ${\mathcal {A}}\setminus \cup _{i\in [q]}\tau _i$, and $M_l=\{i\in [q] \mid \Upsilon _{i}({\mathbf {s}}_{l})\in \Gamma _i \}$ for $l\in [k]$.

Proof

By the hypothesis, there are exactly $\sum _{i\in [q]} \mathrm {e}(T_i)+k-\sum _{i\in [k]}\sharp (M_i)$ minimal generators of S outside its extremal rays, and $\sum _{i\in [q]} \mathrm {e}(S_i)$ belonging to its extremal rays. $\square$

Example 16

Let $S\subset {\mathbb {N}}^3$ be the semigroup minimally generated by

$$\begin{aligned} \Lambda _S=\{ (2, 0, 0), (4, 2, 4), (0, 2, 0), (3, 0, 0), (6, 3, 6), (0, 3, 0), (3, 1, 1),\\ (3, 1, 2), (1, 1, 0), (3, 2, 3), (1, 2, 1) \}. \end{aligned}$$

Note that the cone ${\mathcal {C}}_S$ is the same as the cone in example 10. So, ${\mathcal {A}}$, $\Gamma _1$, $\Gamma _2$ and $\Gamma _3$ are the sets given in that example. For the semigroup S, $\Upsilon _1(\{(3,1,1),(3,1,2),(1,1,0)\})=\Gamma _1$, $\Upsilon _2(\{(3,1,2),(3,2,3)\})=\Gamma _2$ and $\Upsilon _3(\{(1,1,0),(1,2,1)\})=\Gamma _3$. Since $(1,1,0),(3,1,2)\in {\mathcal {A}}$, $\mathrm {e}(S)= 11= 6+7+2-2-2 = \sum _{i\in [3]} (\mathrm {e}(S_i)+\mathrm {e}(T_i))+2-\sum _{i\in [2]}\sharp (M_i)$.

Fix a cone ${\mathcal {C}}$, studying the different possibilities to select sets of points $K\subset {\mathcal {C}}$ such that $\cup _{i\in [q]}\Gamma _i$ is the union of the minimal generating set of the semigroup given by $\cup _{Q\in K}\Upsilon _i(Q)$ (for i from 1 to q), we can state results like the following:

Corollary 17

Let $S_1,\ldots ,S_q$ be the non proper numerical semigroups minimally generated by $\{n_1^{(i)},\ldots ,n_{\mathrm {e}(S_i)}^{(i)}\}$ for each $i\in [q]$, and $\Lambda ''\subset {\mathcal {C}}$ satisfying the hypothesis of Lemma 15. Thus, if $\Lambda ''\subset {\mathcal {C}}\setminus {\mathcal {A}}$, then the embedding dimension of the ${\mathcal {C}}$-semigroup generated by $\Lambda '' \cup \bigcup _{i\in [q]} \{n_1^{(i)}{\mathbf {a}}_i,\ldots ,n_{\mathrm {e}(S_i)}^{(i)}{\mathbf {a}}_i\}$ is $\sum _{i\in [q]} (\mathrm {e}(S_i) + \mathrm {e}(T_i))$.

Finally, we illustrate the above result with an example.

Example 18

Let $S\subset {\mathbb {N}}^3$ be the semigroup minimally generated by

$$\begin{aligned} \Lambda _S=\{(2, 0, 0), (4, 2, 4), (0, 2, 0), (3, 0, 0), (6, 3, 6), (0, 3, 0), (3, 1, 1),\\ (4, 1, 2), (5, 2, 4), (2, 1, 0), (1, 2, 0), (3, 2, 3), (1, 2, 1) \}. \end{aligned}$$

Again, the cone ${\mathcal {C}}_S$ is the cone appearing in example 10. Note that the elements (2, 0, 0) and (3, 0, 0) are in $S_1$, (4, 2, 4) and (6, 3, 6) belong to $S_2$, and (0, 2, 0) and (0, 3, 0) are in $S_3$. Moreover, $\Upsilon _1(\{ (3, 1, 1), (4, 1, 2), (2, 1, 0) \})=\Gamma _1$, $\Upsilon _2(\{(5, 2, 4), (3, 2, 3)\})=\Gamma _2$, $\Upsilon _3(\{(1, 2, 0),(1, 2, 1)\})=\Gamma _3$, and $\Lambda _S\setminus { \cup _{i\in [q]} \tau _i}\subset {\mathcal {C}}_S\setminus {\mathcal {A}}$. As previous corollary asserts, $\mathrm {e}(S)=13 = 6 + 7 = \sum _{i\in [3]} (\mathrm {e}(S_i) + \mathrm {e}(T_i))$.

6 On the decomposition of a ${\mathcal {C}}$-semigroup in terms of irreducible ${\mathcal {C}}$-semigroups

We define the set of pseudo-Frobenius of a ${\mathcal {C}}$-semigroup S as $\text {PF}(S)=\{{\mathbf {a}}\in {\mathcal {H}}(S)\mid {\mathbf {a}}+(S\setminus \{0\})\subset S\}$ (recall that ${\mathcal {H}}(S)={\mathcal {C}}\setminus S$), and the set of special gaps of S as $\text {SG}(S)=\{{\mathbf {a}}\in \text {PF}(S)\mid 2{\mathbf {a}}\in S\}$. Note that the elements ${\mathbf {a}}$ of $\text {SG}(S)$ are those elements in ${\mathcal {C}}\setminus S$ such that $S\cup \{{\mathbf {a}}\}$ is again a ${\mathcal {C}}$-semigroup.

A ${\mathcal {C}}$-semigroup is ${\mathcal {C}}$-reducible (simplifying reducible) if it can be expressed as an intersection of two ${\mathcal {C}}$-semigroups containing it properly (see [11]). Equivalently, S is ${\mathcal {C}}$-irreducible (simplifying irreducible) if and only if $|\text {SG}(S)|\le 1$. A decomposition of a ${\mathcal {C}}$-semigroup S in terms of irreducible ${\mathcal {C}}$-semigroups is to express S as intersection of irreducible ${\mathcal {C}}$-semigroups. This definition generalizes the definitions of irreducible numerical semigroups (see [13]) and irreducible ${\mathbb {N}}^p$-semigroups (see [2]).

Our decomposition method into irreducible is based on adding to a ${\mathcal {C}}$-semigroup elements of $\text {SG}(S)$. If we repeat this operation, we always reach an irreducible ${\mathcal {C}}$-semigroup or the cone ${\mathcal {C}}$. Since the set of gaps ${\mathcal {H}}(S)$ is finite, this process can be performed only a finite number of times. This allows us to state the following algorithm inspired by [13, Algorithm 4.49].

By definition, the set $\text {SG}(S)$ is obtained from $\text {PF}(S)$. If S is determined by its minimal generating set, then $\text {PF}(S)$ can be computed from the set ${\mathcal {H}}(S)$ obtained with Algorithm 2, or using the two different ways given in [11, Corollary 9 and Example 10].

Example 19

Consider the ${\mathcal {C}}$-semigroup S given in examples 10 and 12. It is minimally generated by

$$\begin{aligned} \Lambda _S=\{ (2, 0, 0), (4, 2, 4), (0, 1, 0), (3, 0, 0), (6, 3, 6), (3, 1, 1), (4, 1, 1),\\ (3, 1, 2), (1, 1, 0), (3, 2, 3), (1, 2, 1) \}, \end{aligned}$$

with

$$\begin{aligned} {\mathcal {H}}(S)=\{ (1,0,0), (1,1,1), (2,1,1), (2,1,2), (2,2,1), (2,2,2), (2,3,2),\\ (4,1,2), (4,2,3), (5,2,4), (5,3,5), (8,4,7) \}. \end{aligned}$$

Hence, $\text {PF}(S)=\{(2, 2, 1), (2, 3, 2), (4, 1, 2), (8, 4, 7)\}$, and $\text {SG}(S)$ is equal to $\text {PF}(S)$.

Applying Algorithm 3 to S, we obtain the decomposition into six irreducible ${\mathcal {C}}$-semigroups, $S=S_1\cap \cdots \cap S_{6}$ where

• $S_1=\langle (3, 0, 0), (2, 0, 0), (1, 1, 0), (0, 1, 0), (4, 1, 1), (3, 1, 1), (3, 1, 2),(4, 1, 2)$, $(1, 2, 1), (2, 2, 1), (2, 2, 2), (3, 2, 3), (4, 2, 4), (6, 3, 6) \rangle$;

• $S_2=\langle (3, 0, 0), (2, 0, 0), (1, 1, 0), (0, 1, 0), (4, 1, 1), (3, 1, 1), (2, 1, 2),(3, 1, 2)$, $(1, 2, 1), (2, 2, 1), (3, 2, 3) \rangle$;

• $S_3=\langle (1, 0, 0), (0, 1, 0), (2, 1, 1), (3, 1, 2), (1, 2, 1), (3, 2, 3), (4, 2, 4),(5, 3, 5)$, $(6, 3, 6) \rangle$;

• $S_4=\langle (3, 0, 0), (2, 0, 0), (1, 1, 0), (0, 1, 0), (2, 1, 1), (1, 1, 1), (3, 1, 2),(4, 1, 2)$, $(3, 2, 3), (4, 2, 4), (6, 3, 6) \rangle$;

• $S_5=\langle (3, 0, 0), (2, 0, 0), (1, 1, 0), (0, 1, 0), (2, 1, 1), (1, 1, 1), (3, 1, 2),(3, 2, 3)$, $(4, 2, 4), (5, 2, 4), (6, 3, 6) \rangle$;

• $S_6=\langle (3, 0, 0), (2, 0, 0), (1, 1, 0), (0, 1, 0), (4, 1, 1), (3, 1, 1), (2, 1, 2),(3, 1, 2)$, $(1, 2, 1), (3, 2, 3), (4, 2, 3) \rangle$;

To get these semigroups we have used our implementation in [7] by typing the following