A graph associated to a lattice

Abstract

In this paper, we associate a simple graph to a lattice $\mathcal L$, in which the vertex set is being the set of all elements of $\mathcal L$, and two distinct vertices $x$ and $y$ are adjacent if $x\vee y\in S$, when $S$ is a multiplicatively closed subset of $\mathcal L$. We denote this graph by $\Gamma _S(\mathcal L )$. We study some properties of $\Gamma _S(\mathcal L )$. Moreover, we investigate the planarity of $\Gamma _S(\mathcal L )$, whenever $S$ is a saturated multiplicatively closed subset of $\mathcal L$.

1 Introduction

The study of algebraic structures, using the properties of graph theory, tends to an exciting research topic in the last decade. There are many papers on assigning a graph to a ring, see for example [2–4, 6]. One of these graphs is the total graph. Let $R$ be a commutative ring. The total graph of $R$ is a simple graph with vertex set $R$, and two distinct vertices $a$ and $b$ are adjacent if $a+b$ is a zero divisor of $R$ (see for example [1, 2]). By using this idea, for a multiplicatively closed subset $S$ of $R$, in [5], the authors defined a graph on $R$, denoted by $\Gamma _S(R)$, with vertices as elements of $R$, and two distinct vertices $a$ and $b$ are adjacent if and only if $a+b\in S$. In this paper, we generalize the concept of $\Gamma _S(R)$ for a lattice. Recall that a lattice is an algebra $\mathcal{L }=( L,\vee ,\wedge )$ satisfying the following conditions: for all $a,b,c\in L$,

• 1. $a\wedge a=a$, $a\vee a=a$,

• 2. $a\wedge b= b\wedge a$, $a\vee b= b\vee a$,

• 3. $(a\wedge b)\wedge c= a\wedge (b \wedge c)$, $(a\vee b)\vee c= a\vee (b \vee c)$, and

• 4. $a\vee (a\wedge b)= a\wedge (a \vee b)=a$.

There is an equivalent definition for a lattice (see for example [8, Theorem 2.1]). To do this, for a lattice $\mathcal L$, one can define an order $\leqslant$ on $\mathcal L$ as follows: For any $a,b\in \mathcal{L }$, we set $a\le b$ if and only if $a\wedge b=a$. Then $(\mathcal{L }, \le )$ is an ordered set in which every pairs of elements has a greatest lower bound (g.l.b.) and a least upper bound (l.u.b.). Conversely, let $P$ be an ordered set such that, for every pair $a,b\in P$, ${\mathrm{g.l.b.}}(a,b)\in P$ and ${\mathrm{l.u.b.}}(a,b)\in P$. For each $a$ and $b$ in $P$, we define $a\wedge b:={\mathrm{g.l.b.}}(a,b)$ and $a\vee b:= {\mathrm{l.u.b.}} (a,b)$. Clearly $(P,\wedge , \vee )$ is a lattice.

The lattice $\mathcal L$ is said to be bounded if there are elements $0$ and $1$ such that

$$\begin{aligned} 0\wedge x=0 \quad {\mathrm{and}} \quad x\vee 1=1 \end{aligned}$$

for all $x\in \mathcal L$. Let $S$ be a nonempty subset of $\mathcal L$. We say that $S$ is a multiplicatively closed subset of $\mathcal L$ if $x\wedge y\in S$, for all $x$ and $y$ of $S$. Also, we say that a subset $S$ of $\mathcal L$ is saturated if $x\wedge y\in S$ if and only if $x,y\in S$.

For a multiplicatively closed subset of $\mathcal L$, we define $\Gamma _S(\mathcal L )$ as a simple graph, with vertex-set $\mathcal L$ and two distinct vertices $x$ and $y$ being adjacent if and only if $x\vee y \in S$.

In the second section, we study some basic properties of the graph $\Gamma _S(\mathcal{L })$ such as connectivity, diameter and completeness whenever $\mathcal{L }$ is a bounded lattice. In the third section, for bounded lattices, we investigate $\Gamma _S(\mathcal L )$, whenever $S$ is a saturated multiplicatively closed subset of $\mathcal L$ and, in the final section, we study the planarity of $\Gamma _S(\mathcal L )$ where $\mathcal L$ is a bounded lattice.

Now, we start to remind a belief necessary background of lattice theory from [8]. Let $x$ and $y$ be two distinct elements of $\mathcal L$. Whenever $x \leqslant y$ and there is no element $z$ in $\mathcal L$ such that $x \leqslant z \leqslant y$, we say $y$ covers $x$. An element $a\in \mathcal{L }$ is an atom of lattice $\mathcal L$ if it covers $0$. Also, an element $m\in \mathcal L$ is a coatom of lattice $\mathcal L$ if $1$ covers it. We denote the set of all coatoms of $\mathcal L$ by Coatom $(\mathcal L )$ and the set of atoms of $\mathcal L$ by Atom $(\mathcal L )$. An ideal $I$ of $\mathcal L$ is a non-empty subset of $\mathcal L$ such that

• (i) for all $a$ and $b$ of $I$, $a\vee b\in I$, and

• (ii) for any $a\in I$ and $b\in \mathcal L$ , $a\wedge b \in I$.

An ideal $I$ of $\mathcal L$ is maximal if $I$ is proper ($I\ne \mathcal L$) and the only ideal having $I$, as a proper subset, is $\mathcal L$. We use the notation J$(\mathcal L )$ for the jacobson radical of $\mathcal L$ which is the intersection of all maximal ideals of $\mathcal L$. Given a lattice $\mathcal L$ and $A\subseteq \mathcal L$. An element $x \in \mathcal L$ is a lower bound of $A$ if $x \le a$ for all $a\in A$. An upper bound is defined in a dual mannar. The set of all lower bounds of $A$ is denoted by $A^\ell$ and the set of all upper bounds by $A^u$, where

$$\begin{aligned} A^\ell :=\left\{ x\in \mathcal{L };\, x \le a\,\, {\mathrm{for\,all}}\,\, a\in A\right\} \end{aligned}$$

and

$$\begin{aligned} A^u:=\left\{ x\in \mathcal{L }; \ a \le x\,\, {\mathrm{for\,all}}\,\, a\in A\right\} . \end{aligned}$$

Now, we recall some definitions of graph theory from [7] which are needed in this paper. The degree of a vertex $v$ in the graph $X$ is the number of edges of $X$ incident with $v$ and denoted by ${\mathrm{deg}}(v)$. In a graph $X$ with vertex-set $V(X)$, the distance between two distinct vertices $a$ and $b$, denoted by ${\mathrm{d}}(a,b)$, is the length of a shortest path connecting $a$ and $b$, if such a path exists; otherwise, we set ${\mathrm{d}}(a,b):=\infty$. The diameter of a graph $X$ is ${\mathrm{diam}}(X)={\mathrm{sup}}\{{\mathrm{d}}(a,b)$ : $a$ and $b$ are distinct vertices of $X\}$. For two distinct vertices $a$ and $b$ in $X$, the notation $a-b$ means that $a$ and $b$ are adjacent. Also the girth of a graph $X$, denoted by ${\mathrm{gr}}(X)$, is the length of a shortest cycle in $X$ if $X$ has a cycle; otherwise, we set $\mathrm{{gr}}(X):=\infty$. A graph $X$ is said to be connected if there exists a path between any two distinct vertices, and it is complete if it is connected with diameter one. We use $K_n$ to denote the complete graph with $n$ vertices. Also, we say that $X$ is totally disconnected if no two vertices of $X$ are adjacent. A clique of a graph is a complete subgraph of $X$ and the number of vertices in a largest clique of $G$ is called the clique number of $G$ and is denoted by $\omega (G)$.

2 Basic properties of $\Gamma _S(\mathcal L )$

Form now on $\mathcal L$ is a bounded lattice. In this section $S$ is a multiplicatively closed subset of $\mathcal L$. We begin with the following lemma.

Lemma 2.1

If $0\notin S$, then $|S\cap \mathrm{{Atom}}(\mathcal{L })|\le 1$.

Proof

Assume in contrary that $|S\cap \mathrm{{Atom}}(\mathcal{L })|\ge 2$. Let $a_1$ and $a_2$ be two distinct elements in $S\cap \mathrm{{Atom}}(\mathcal{L })$. Since $S$ is a multiplicatively closed subset of $\mathcal L$, we have $a_1\wedge a_2\in S$ which implies that $0\in S$. This is a required contradiction. Hence $|S\cap \mathrm{{Atom}}(\mathcal L )|\le 1$. $\square$

Lemma 2.2

The following statements hold.

• (i) If $0\in S$, then $\mathrm{{deg(0)}}=|S|-1$. Otherwise, $\mathrm{{deg(0)}}=|S|$.

• (ii) If $1\in S$, then $\mathrm{{deg(1)}}=|\mathcal{L }|-1$. Otherwise, $\mathrm{{deg(1)}}=0$.

Proof

Since $0\vee x=x$ and $1\vee x=1$, for all $x\in \mathcal{L }$, the statements (i) and (ii) hold.

$\square$

In the following theorem, we study the connectivity of $\Gamma _S(\mathcal L )$.

Theorem 2.3

$\Gamma _S(\mathcal L )$ is connected if and only if $1\in S$. Moreover, if $\Gamma _S(\mathcal L )$ is connected, then $\mathrm{{diam}}(\Gamma _S(\mathcal L ))\le 2$.

Proof

Suppose that $1\in S$. By part (ii) of Lemma 2.2, $\mathrm{{deg(1)}}=|\mathcal L |-1$ which implies that $\Gamma _S(\mathcal L )$ is connected.

Conversely, if $\Gamma _S(\mathcal L )$ is connected, then $\mathrm{{deg(1)}}\ne 0$. Now, by part (ii) of Lemma , we have $1\in S$.

The last statement is clear. $\square$

Proposition 2.4

$\Gamma _S(\mathcal L )$ is complete if and only if $S=\mathcal L$ or $S=\mathcal L \setminus \{0\}$.

Proof

Assume that $\Gamma _S(\mathcal L )$ is complete. So $\mathrm{{deg(0)}}=|\mathcal L |-1$. By part (i) of Lemma , we have $|S|=|\mathcal L |-1$ or $|S|-1=|\mathcal L |-1$. Hence $S=\mathcal L$ or $S=\mathcal L \setminus \{x\}$, for some $x\in \mathcal L$. We claim that $x=0$. Assume in contrary that $x\ne 0$. Since $0\vee x=x$, the vertex $0$ is not adjacent to $x$, which is impossible. So $x=0$, and thus $S=\mathcal L$ or $S=\mathcal L \setminus \{0\}$.

The converse statement follows easily. $\square$

Theorem 2.5

The following statements hold.

• (i) The graph $\Gamma _S(\mathcal L )$ is regular if and only if it is either complete or totally disconnected.

• (ii) $\Gamma _S(\mathcal L )$ is a star graph if and only if $S=\{1\}$ or $S=\{1,0\}$ and $|\mathrm{{Coatom}}(\mathcal L )|=1$.

Proof

(i) Suppose that $\Gamma _S(\mathcal L )$ is regular and that is not totally disconnected. By part (ii) of Lemma , we have $1\in S$. Then $\mathrm{{deg}}(1)=|\mathcal L |-1$. Since $\Gamma _S(\mathcal L )$ is regular, $\mathrm{{deg}}(x)=|\mathcal L |-1$, for all $x\in \mathcal L$. Hence $\Gamma _S(\mathcal L )$ is complete.

The converse statement is clear.

(ii) Suppose that $\Gamma _S(\mathcal L )$ is a star graph. Since $\Gamma _S(\mathcal L )$ is connected, we have $1\in S$, and so $\mathrm{{deg(1)}}=|\mathcal L |-1$. Hence $1$ is the center of $\Gamma _S(\mathcal L )$. On the other hand, since $0$ is adjacent to all element of $S$, we have $S=\{1\}$ or $S=\{1,0\}$. Assume in contrary that $|\mathrm{{Coatom}}(\mathcal L )|\ge 2$. Thus there exists distinct vertices $m$ and $m^{\prime }$ in $\mathrm{{Coatom}}(\mathcal L )$ which are adjacent in $\Gamma _S(\mathcal L )$. This is impossible. Hence $|\mathrm{{Coatom}}(\mathcal L )|=1$.

The converse statement is clear. $\square$

Proposition 2.6

Assume that $1\in S$. Then $\mathrm{{gr}}(\Gamma _S(\mathcal{L }))\in \{3,\infty \}$.

Proof

Suppose that $|\mathrm{{Coatom}}(\mathcal L )|\ge 2$ and consider the cycle $1-m-m^{\prime }-1$ in $\Gamma _S(\mathcal L )$, where $m,m^{\prime }\in \mathrm{{Coatom}}(\mathcal L )$, to deduce that $\mathrm{{gr}}(\Gamma _S(\mathcal L ))=3$. Otherwise, $|\mathrm{{Coatom}}(\mathcal L )|=1$. Now we have the following cases:

• (i) Suppose that $|S|=1$. Then $S=\{1\}$ and so, by Proposition 2.5, the graph $\Gamma _S(\mathcal L )$ is a star graph. Thus $\mathrm{{gr}}(\Gamma _S(\mathcal L ))=\infty$.

• (ii) Suppose that $|S|=2$. If $S=\{0,1\}$, then, by Proposition 2.5, $\Gamma _S(\mathcal L )$ is a star graph and so $\mathrm{{gr}}(\Gamma _S(\mathcal L ))=\infty$. Otherwise, $S=\{1,s\}$ where $s\ne 0$. Now, the cycle $1-s-0-1$ is the shortest cycle in the graph $\Gamma _S(\mathcal L )$ which implies that $\mathrm{{gr}}(\Gamma _S(\mathcal L ))=3$.

• (iii) Suppose that $|S|\ge 2$. Thus there is $s\in S$ such that $s\ne 0,1$. Now, the cycle $1-s-0-1$ is the shortest cycle in the graph $\Gamma _S(\mathcal L )$ . So $\mathrm{{gr}}(\Gamma _S(\mathcal L ))=3$.

$\square$

Let $\mathcal A$ be a chain in $S$. Since $x\vee y\in S$ for all $x,y\in \mathcal{A }$, we have the following proposition.

Proposition 2.7

$\omega (\Gamma _S(\mathcal{L }))\ge \mathrm{max} \{ |\mathcal{A }|; \mathcal{A }\,\mathrm{is\,a\,chain\,in}\,S\}$.

3 Basic properties of $\Gamma _S(\mathcal L )$ where $S$ is a saturated subset of the lattice $\mathcal L$

Throughout this section, $S$ is a saturated subset of the lattice $\mathcal L$. It is easy to see that if $x\in S$, then $\{x\}^u\subseteq S$, and so we always have $1\in S$. Hence, by Proposition 2.3, one can conclude that $\Gamma _S(\mathcal L )$ is connect with diameter less than three.

Proposition 3.1

For all $s\in S$, we have that $\mathrm{{deg(s)}}=|\mathcal L |-1$.

Proof

Let $s$ be an arbitrary element in $S$. Since $s\wedge (s\vee x)=s$ for all $x\in \mathcal L$, we have that $s\wedge (s\vee x)\in S$. Therefore $\mathrm{{deg(s)}}=|\mathcal L |-1$ for all $s\in S$. $\square$

In the following proposition, we present a lower bound for the clique number of $\Gamma _S(\mathcal L )$.

Proposition 3.2

In the graph $\Gamma _S(\mathcal L )$ we have the following inequality.

$$\begin{aligned} \omega (\Gamma _S(\mathcal{L })) \ge \mathrm{{max}}\{|S|, |\mathrm{{Coatom}}(\mathcal{L })|\}+1 \end{aligned}$$

Proof

Since $m\vee m^{\prime }=1$ for all $m$ and $m^{\prime }$ in $\mathrm{{Coatom}}(\mathcal L )$, the set $\mathrm{{Coatom}}(\mathcal L )\cup \{1\}$ forms a clique in $\Gamma _S(\mathcal L )$. Also, by Proposition 3.1, $S\cup \{0\}$ is a clique in $\Gamma _S(\mathcal L )$. This implies that $\omega (\Gamma _S(\mathcal L ))\ge \mathrm{{max}}\{|S|, |\mathrm{{Coatom}}(\mathcal L )|\}+1$. $\square$

Lemma 3.3

Assume that $0\in S$. Then $\Gamma _S(\mathcal L )$ is complete.

Proof

Since $0\in S$, we have that $\{0\}^u \subseteq S$. Hence $S=\mathcal L$. Now, by Proposition 2.4, the graph $\Gamma _S(\mathcal L )$ is complete. $\square$

From now on, we assume that $0\notin S$. So, by Lemma 2.1, we have $|S\cap \mathrm{{Atom}}(\mathcal L )|\le 1$.

Proposition 3.4

If $S\cap \mathrm{{Atom}}(\mathcal L )= \{a\}$, then $S=\{a\}^u$.

Proof

Clearly $\{a\}^u \subseteq S$. Now, assume in contrary that there exists $b\in S\setminus \{a\}^u$. Since $S$ is a multiplicatively closed subset of $\mathcal L$, we have $0=a\wedge b\in S$, which is impossible. Thus $S=\{a\}^u$. $\square$

Proposition 3.5

Suppose that $|\mathcal L |\ge 3$.

• (i) If $|S|\ge 2$, then every vertex of the graph $\Gamma _S(\mathcal L )$ lies in a cycle of length 3, and so $\mathrm{{gr}}(\Gamma _S(\mathcal L ))=3.$

• (ii) If $|S|=1$, then $\mathrm{{gr}}(\Gamma _S(\mathcal L ))\in \{3, \infty \}.$

Proof

(i) Since $|S|\ge 2$, we can choose $s\ne 1$ in $S$. Now, let $x$ be an arbitrary element in $\mathcal L$. Then we have the cycle $1-x-s-1$, and so each vertex of the graph $\Gamma _S(\mathcal L )$ lies in a cycle of length 3 and $\mathrm{{gr}}(\Gamma _S(\mathcal L ))=3$.

(ii) Since $|S|=1$, we have that $S=\{1\}$. The result now follows from Proposition 2.6.$\square$

Proposition 3.6

If $|S|=1$, then $\mathrm{{deg}}(x)=1$, for all $x\in J(\mathcal L )$.

Proof

Since $|S|=1$, we have that $S=\{1\}$. If $|\mathrm{{Coatom}}(\mathcal L )|=1$, then, by Proposition 2.5, $\Gamma _S(\mathcal L )$ is a star graph with center $1$. Since $1\notin J(\mathcal L )$, every vertex in $\mathrm{{J}}(\mathcal L )$ has degree one. Otherwise, $|\mathrm{{Coatom}}(\mathcal L )|\ge 2$. Let $x$ be an arbitrary vertex in $J(\mathcal L )$. Clearly $1$ is adjacent to every vertex in $\Gamma _S(\mathcal L )$ which implies that $\mathrm{{deg}}(x)\ge 1$. Assume in contrary that $\mathrm{{deg}}(x)\ge 2$. So there is $y\ne 1$ in $\mathcal L$ such that $x$ and $y$ are adjacent, and so $x\vee y=1$. If $y\in \mathrm{{Coatom}}(\mathcal L )$, then $x\vee y=y$, which is impossible. Hence $y\notin \mathrm{{Coatom}}(\mathcal L )$, but there is $m\in \mathrm{{Coatom}}(\mathcal L )$ such that $y\in \{m\}^{\ell }$. Since $x\in \cap _{m\in \mathrm{{Coatom}}(\mathcal L )} \{m\}^{\ell }$, we have that $x\vee y\le m$, which is impossible. So $\mathrm{{deg}}(x)=1$, for all $x\in J(\mathcal L )$. $\square$

Proposition 3.7

If $|S|=1$ and $|\mathrm{{Coatom}}(\mathcal L )|\ge 2$, then every vertex in graph $\Gamma _S(\mathcal L \setminus \mathrm{J}(\mathcal L ))$ lies in a cycle of length 3.

Proof

Since $|S|=1$, we have that $S=\{1\}$. Let $y$ be an arbitrary element in $\mathcal L \setminus J(\mathcal L )$. We need to show that $y$ lies in a cycle of length 3 in $\Gamma _S(\mathcal L \setminus J(\mathcal L ))$. If $y\in \mathrm{Coatom}(\mathcal L )$, since $|\mathrm{Coatom}(\mathcal L )|\ge 2$, there exists $m$ with $m\ne y$ in $\mathrm{Coatom}(\mathcal L )$. Thus, we can consider the cycle $y-m-1-y$ in $\Gamma _S(\mathcal L \setminus J(\mathcal L ))$. Otherwise $y\notin \mathrm{Coatom}(\mathcal L )$. Since $y\notin J(\mathcal L )$, there exists $m\in \mathrm{Coatom}(\mathcal L )$ such that $y\notin \{m\}^{\ell }$. Therefore $y\vee m=1$, which implies that $y$ and $m$ are adjacent in $\Gamma _S(\mathcal L \setminus J(\mathcal L ))$. So we can consider the cycle $y-m-1-y$ and the result follows. $\square$

4 Planarity of $\Gamma _S(\mathcal L )$ when $S$ is a saturated subset of $\mathcal L$

In this section, we characterize all planar graphs $\Gamma _S(\mathcal L )$, where $S$ is a saturated subset of $\mathcal L$. Recall that a planar graph is a graph that can be embedded on the plane, that is, it can be drawn on the plane in such a way that it’s edges intersect only at their endpoints. Kuratowski provided a nice characterization of planar graphs, which now is known as Kuratowski’s Theorem:

A finite graph is planar if and only if it does not contain a subdivision of $K_5$ or $K_{3,3}$.

Proposition 4.1

If $0\in S$, then $\Gamma _S(\mathcal L )$ is planar if and only if $|\mathcal L |\le 4$.

Proof

If $0\in S$, then $S=\mathcal L$. Hence $\Gamma _S(\mathcal L )$ is a complete graph, and so the result follows from Kuratowski’s Theorem. $\square$

Proposition 3.2 in conjunction with Kuratowski’s Theorem implies the following lemma.

Lemma 4.2

If $|\mathrm{Coatom}(\mathcal L )|\ge 4$ or $|S|\ge 4$, then $\Gamma _S(\mathcal L )$ is not planar.

In view of Lemma 4.2, we investigate to study the planarity of $\Gamma _S(\mathcal L )$, in the case that $|S|\leqslant 3$ and $|\mathrm{Coatom}(\mathcal L )|\leqslant 3$. We start with the following proposition.

Proposition 4.3

Suppose that $|S|=3$. Then $\Gamma _S(\mathcal L )$ is planar if and only if $|\mathcal L |\le 5$.

Proof

Suppose that $\Gamma _S(\mathcal L )$ is planar. Assume in contrary that $|\mathcal L |\ge 6$. Now, put $V_1:= S$ and $V_2:=\{x_1,x_2,x_3\}\subseteq \mathcal L \setminus S$. Clearly one can find a copy of $K_{3,3}$ in $\Gamma _S(\mathcal L )$. Therefore, by Kuratowski’s Theorem, $\Gamma _S(\mathcal L )$ is not planar, which is impossible. Hence $|\mathcal L |\le 5$.

Conversely, assume that $|\mathcal L |\le 5$. It is clear that if $|\mathcal L |\le 4$, then $\Gamma _S(\mathcal L )$ is planar. Also, if $|\mathcal L |=5$, then, in view of Proposition 2.4, $\Gamma _S(\mathcal L )$ is not $K_5$. So $\Gamma _S(\mathcal L )$ is planar. $\square$

Note that, if $|S|=2$, then $S=\{1,m\}$ for some $m\in \mathrm{Coatom}(\mathcal L )$. Also, if $|S|=1$, then $S=\{1\}$.

For the rest of the paper, we need the following definition.

Definition 4.4

Let $x$ be an arbitrary element in $\mathcal L$. We define the lower neighbors of $x$ as the set $B_{\ell }(x):=\{y\in \mathcal L ; \ x\ covers \ y\}$. Also, for every subsets $A$ and $B$ of $\mathcal L$, we put $L_{A}^{B}:=\{B\}^{\ell }\setminus \{A\}^{\ell }$. Moreover, for $x\in \mathcal L$, we denote the sets $L_{A}^{\{x\}}$ and $L_{\{x\}}^{B}$, by $L_{A}^{x}$ and $L_{x}^{B}$, respectively.

Lemma 4.5

Assume that $S=\{1,m\}$, where $m\in \mathrm{Coatom}(\mathcal L )$. If $|B_{\ell }(m)|\ge 3$, then $\Gamma _S(\mathcal L )$ is not planar.

Proof

Since $|B_{\ell }(m)|\ge 3$, we can choose the subset $A=\{x_1,x_2,x_3\}$ of the set $B_{\ell }(m)$. It is clear that $x_i\vee x_j=m$ for all $1\le i\ne j\le 3$. So, the induced subgraph of $\Gamma _S(\mathcal L )$ on $A\cup S$ is isomorphic to $K_5$. Thus, by Kuratowski’s Theorem, $\Gamma _S(\mathcal L )$ is not planar. $\square$

Proposition 4.6

Let $S=\{1,m\}$, where $m\in \mathrm{Coatom}(\mathcal L )$. If $\Gamma _S(\mathcal L )$ is planar, then one of the following statements holds:

• (i) $|B_{\ell }(m)|=1$,

• (ii) $|B_{\ell }(m)|=2$, and $|L_{x}^{y}|\le 2$, for all $x,y\in B_{\ell }(m)$, and if $|L_{x}^{y}|= 2$, then $|L_{y}^{x}|=1$, and if $|L_{y}^{x}|= 2$, then $|L_{x}^{y}| =1$.

Proof

Since $\Gamma _S(\mathcal L )$ is planar, by Lemma 4.5, $|B_{\ell }(m)|\le 2$. Suppose that $|B_{\ell }(m)|\ne 1$. Thus, we have that $|B_{\ell }(m)|=2$. Set $B_{\ell }(m):=\{x,y\}$. If $|L_{y}^{x}|\ge 3$ or $|L_{x}^{y}|\ge 3$, then it is easy to see that $\Gamma _S(\mathcal L )$ has a subgraph which is isomorphic to $K_{3,3}$, and so $\Gamma _S(\mathcal L )$ is not planar, which is impossible. Hence $|L_{y}^{x}|\le 2$ and $|L_{x}^{y}|\le 2$.

Now, suppose that $|L_{x}^{y}|= 2$ and $|L_{y}^{x}|= 2$. Set $V_1:=L_{x}^{y}\cup \{m\}$ and $V_2:=L_{y}^{x} \cup \{1\}$. It is easy to see that $\Gamma _S(\mathcal L )$ has a subgraph isomorphic to $K_{3,3}$ with parts $V_1$ and $V_2$, which is impossible. So if $|L_{x}^{y}|= 2$, then $|L_{y}^{x}|=1$. Also, if $|L_{y}^{x}|= 2$, then $|L_{x}^{y}| =1$.

$\square$

Assume that $S=\{1,m\}$, where $m\in \mathrm{Coatom}(\mathcal L )$. By Lemma 4.2, we have $|\mathrm{Coatom}(\mathcal L )|\le 3$. In the following proposition, we present a necessary and sufficient condition for planarity of $\Gamma _S(\mathcal L )$ whenever $|\mathrm{Coatom}(\mathcal L )|=1$.

Theroem 4.7

Let $S=\{1,m\}$ and $\mathrm{Coatom}(\mathcal L )=\{m\}$. Then the graph $\Gamma _S(\mathcal L )$ is planar if and only if one of the conditions (i) or (ii) in Proposition 4.6 holds.

Proof

Let $\Gamma _S(\mathcal L )$ is planar. Then, by Proposition 4.6, we are done.

Conversly, we show that if one of the conditions (i) or (ii) in Proposition 4.6 occurs, then $\Gamma _S(\mathcal L )$ is planar. One can easily check that, if $|B_{\ell }(m)|=1$, then $\Gamma _S(\mathcal L )$ is isomorphic to $K_{1,1, |\mathcal L |-2}$, and so $\Gamma _S(\mathcal L )$ is planar. Also, if condition (ii) in Proposition 4.6 occurs, then it is not hard to see that $\Gamma _S(\mathcal L )$ is planar. $\square$

In the next theorem, we provide a necessary and sufficient condition for planarity of $\Gamma _S(\mathcal L )$ whenever $|\mathrm{Coatom}(\mathcal L )|=2$.

Theroem 4.8

Suppose that $S=\{1,m\}$ and $\mathrm{Coatom}(\mathcal L )=\{m , m^{\prime }\}$. Then the graph $\Gamma _S(\mathcal L )$ is planar if and only if $\mathcal L$ is one of the following lattices:

• (i) $\mathcal L =S \cup L_{m^{\prime }}^{x} \cup \mathrm{J}(\mathcal L )$, where $B_{\ell }(m)=\{x\}$ such that $x\in \{m^{\prime }\}^{\ell }$.

• (ii) $\mathcal L =S \cup L_{x}^{m^{\prime }} \cup L_{m^{\prime }}^{x} \cup \mathrm{J}(\mathcal L )$, where $B_{\ell }(m)=\{x\}$ such that

  • (a) $x\notin \{m^{\prime }\}^{\ell }$.

  • (b) The numbers $| L_{x}^{m^{\prime }} |$ and $| L_{m^{\prime }}^{x}|$ are less than 3, and if $| L_{x}^{m^{\prime }} |=2$, then $| L_{m^{\prime }}^{x}|=1$, and if $| L_{m^{\prime }}^{x} |=2$, then $| L_{x}^{m^{\prime }}|=1$.

• (iii) $\mathcal L =S \cup \{m^{\prime }\} \cup B_{\ell }(m) \cup \mathrm{J}(\mathcal L )$, where $|B_{\ell }(m)|=2$ and $|B_{\ell }(m)\setminus \{m^{\prime }\}^{\ell }|= 1$.

Proof

Assume that $\Gamma _S(\mathcal L )$ is a planar graph. Then, by Lemma 4.6, $|B_{\ell }(m)\setminus \{m^{\prime }\}^{\ell }|\le 2$. Now, suppose that $|B_{\ell }(m)\setminus \{m^{\prime }\}^{\ell }|=2$, and set $B_{\ell }(m)\setminus \{m'\}^{\ell }:=\{x,y\}$. Since the induced subgraph of $\Gamma _S(\mathcal L )$ on $\{1,m,m^{\prime },x,y\}$ is isomorphic to $K_5$, by Kuratowski’s Theorem, $\Gamma _S(\mathcal L )$ is not planar, which is impossible. Thus $|B_{\ell }(m)\setminus \{m^{\prime }\}^{\ell }|\le 1$. Also, by Proposition 4.6, one of the conditions (i) or (ii) in Proposition 4.6 must holds. So we have the following cases:

Case 1. Suppose that the condition (i) in Proposition 4.6 holds and put $B_{\ell }(m):=\{x\}$. At first note that $\mathcal L =S \cup L_{x}^{m^{\prime }} \cup L_{m^{\prime }}^{x} \cup \mathrm{J}(\mathcal L )$. Now, assume that $|B_{\ell }(m)\setminus \{m^{\prime }\}^{\ell }|= 1$. Thus $B_{\ell }(m)\setminus \{m^{\prime }\}^{\ell }=\{x\}$. If $|L_{x}^{m^{\prime }}|\ge 3$, then it is easy to see that the graph $\Gamma _S(\mathcal L )$ has a copy of $K_{3,3}$, which is impossible. Therefore $|L_{m}^{m^{\prime }}|\le 2$. Similarly $|L_{m^{\prime }}^{x}|\le 2$. Now, if $|L_{x}^{m^{\prime }}|=|L_{m^{\prime }}^{x}|= 2$, then consider the sets $V_1:= L_{x}^{m^{\prime }} \cup \{1\}$ and $V_2:= L_{m^{\prime }}^{x} \cup \{m\}$, to deduce that $\Gamma _S(\mathcal L )$ has a copy of $K_{3,3}$, which is impossible. Therefore, if $|L_{x}^{m^{\prime }}|=2$, then $|L_{m^{\prime }}^{x}|=1$. Similarly, if $|L_{m^{\prime }}^{x}|=2$, then $|L_{x}^{m^{\prime }}|=1$. So $\mathcal L =S \cup L_{x}^{m^{\prime }} \cup L_{m^{\prime }}^{x} \cup \mathrm{J}(\mathcal L )$, where $B_{\ell }(m)=\{x\}$ and $| L_{x}^{m^{\prime }} |$, and $| L_{m^{\prime }}^{x}|$ are less than 3, and if $| L_{x}^{m^{\prime }} |=2$, then $| L_{m^{\prime }}^{x}|=1$, and also, if $| L_{x}^{m^{\prime }} |=2$, then $| L_{m^{\prime }}^{x}|=1$.

Now, let $|B_{\ell }(m)\setminus \{m^{\prime }\}^{\ell }|= 0$. Since $|B_{\ell }(m)\setminus \{m^{\prime }\}^{\ell }|= 0$, we have that $L_{m^{\prime }}^{x}=\emptyset$. So $\mathcal L =S \cup L_{x}^{m^{\prime }} \cup \mathrm{J}(\mathcal L )$.

Case 2. Suppose that the condition (ii) in Proposition 4.6 holds. Set $B_{\ell }(m):=\{x,y\}$. Note that in this case, we have that

$$\begin{aligned} \mathcal L =S \cup L_{\{x,y\}}^{m^{\prime }} \cup L_{\{m^{\prime },y\}}^{x} \cup L_{\{m^{\prime },x\}}^{y} \cup L_{y}^{\{m^{\prime },x\}} \cup L_{x}^{\{m^{\prime },y\}}\cup L_{m^{\prime }}^{\{x,y\}}\cup \mathrm{J}(\mathcal L ). \end{aligned}$$

Since $\mathcal L$ is a lattice, we have that $|B_{\ell }(m)\setminus \{m^{\prime }\}^{\ell }|= 1$. Without loss of generality, we may assume that $B_{\ell }(m)\setminus \{m^{\prime }\}^{\ell }=\{y\}$. If $|L_{\{x,y\}}^{m^{\prime }}|\ge 2$, then, by setting $V_1:= L_{\{x,y\}}^{m^{\prime }} \cup \{y\}$ and $V_2:= \{1, m, x\}$, one can find a copy of $K_{3,3}$ in the graph $\Gamma _S(\mathcal L )$, which is impossible. Hence $L_{\{x,y\}}^{m^{\prime }}=\{m^{\prime }\}$. Since $x\in \{m^{\prime }\}^{\ell }$, we have that $L_{\{y,m^{\prime }\}}^{x}=\emptyset$. Also, if $|L_{\{x,m^{\prime }\}}^{y}|\ge 2$, then one can easily to find a copy of $K_{3,3}$, which is impossible. So $L_{\{x,m^{\prime }\}}^{y}=\{y\}$. On the other hand, since $x\in \{m^{\prime }\}^{\ell }$, $L_{m^{\prime }}^{\{x,y\}}=\emptyset$. Thus $\mathcal L =S \cup \{m^{\prime }\} \cup B_{\ell }(m) \cup \mathrm{J}(\mathcal L )$.

The converse statment is clear. $\square$

In the following, we investigate the planarity of the graph $\Gamma _S(\mathcal L )$ whenever $|S|=2$ and $\mathrm{Coatom}(\mathcal L )=\{m, m^{\prime }, m^{\prime \prime }\}$.

Proposition 4.9

Suppose that $S=\{1,m\}$, $\mathrm{Coatom}(\mathcal L )=\{m, m^{\prime }, m^{\prime \prime }\}$ and that the graph $\Gamma _S(\mathcal L )$ is planar. Then the following statements hold.

• (i) $L_{\{m^{\prime },m^{\prime \prime }\}}^{m} =\{m\}$,

• (ii) $|L_{\{m,m^{\prime \prime }\}}^{m^{\prime }}|\le 2$ and $|L_{\{m,m^{\prime }\}}^{m^{\prime \prime }}|\le 2$, and if $|L_{\{m,m^{\prime \prime }\}}^{m^{\prime }}|= 2$ then $|L_{\{m,m^{\prime }\}}^{m^{\prime \prime }}|=1$, and if $|L_{\{m,m^{\prime }\}}^{m^{\prime \prime }}|= 2$, then $|L_{\{m,m^{\prime \prime }\}}^{m^{\prime }}|=1$

Proof

(i) Suppose that $\Gamma _S(\mathcal L )$ is planar. Assume in contrary that $|L_{\{m^{\prime },m^{\prime \prime }\}}^{m}|\ge 2$. Note that, for every element $x\in L_{\{m^{\prime },m^{\prime \prime }\}}^{m}$, we have $x\vee m^{\prime }=1$ and $x\vee m^{\prime \prime }=1$. So the graph $\Gamma _S(\mathcal L )$ has a copy of $K_5$, which is impossible. Thus $L_{\{m^{\prime },m^{\prime \prime }\}}^{m} =\{m\}$.

(ii) Assume in contrary that $|L_{\{m,m^{\prime \prime }\}}^{m^{\prime }} |\ge 3$ or $|L_{\{m,m^{\prime }\}}^{m^{\prime \prime }}|\ge 3$. One can easily see that the graph $\Gamma _S(\mathcal L )$ has a subgraph isomorphic to $K_{3,3}$, and so $\Gamma _S(\mathcal L )$ is not planar, which is impossible. Therefore $|L_{\{m,m^{\prime \prime }\}}^{m^{\prime }}|\le 2$ and $|L_{\{m,m^{\prime }\}}^{m^{\prime \prime }}|\le 2$. Now, if $| L_{\{m,m^{\prime \prime }\}}^{m^{\prime }}|=2$ and $|L_{\{m,m^{\prime }\}}^{m^{\prime \prime }}|=2$, then, by setting $V_1:= L_{\{m,m^{\prime }\}}^{m^{\prime \prime }}\cup \{1\}$ and $V_2:=L_{\{m,m^{\prime \prime }\}}^{m^{\prime }} \cup \{m\}$, we can find a copy of $K_{3,3}$ in the graph $\Gamma _S(\mathcal L )$, which is impossible. Hence if $|L_{\{m,m^{\prime \prime }\}}^{m^{\prime }}|= 2$, then $|L_{\{m,m^{\prime }\}}^{m^{\prime \prime }}|=1$. Similarly if $|L_{\{m,m^{\prime }\}}^{m^{\prime \prime }}|= 2$, then $|L_{\{m,m^{\prime \prime }\}}^{m^{\prime }}|=1$. $\square$

Theroem 4.10

Let $S=\{1,m\}$ and $\mathrm{Coatom}(\mathcal L )=\{m , m^{\prime }, m^{\prime \prime }\}$. Then the graph $\Gamma _S(\mathcal L )$ is planar if and only if $\mathcal L$ is one of the following lattices:

• (i) $\mathcal L =\{1,m,m^{\prime },m^{\prime \prime },x\}\cup L_{x}^{\{m^{\prime },m^{\prime \prime }\}}\cup \mathrm{J}(\mathcal L )$, where $B_{\ell }(m)=\{x\}$ and $x\in \{m^{\prime }\}^{\ell }{\setminus } \{m^{\prime \prime }\}^{\ell }$ or $x\in \{m^{\prime \prime }\}^{\ell }{\setminus } \{m^{\prime }\}^{\ell }$.

• (ii) $\mathcal L =\{1,m,x\}\cup L_{\{x,m^{\prime \prime }\}}^{m^{\prime }}\cup L_{\{x,m^{\prime \prime }\}}^{m^{\prime }} \cup L_{x}^{\{m^{\prime },m^{\prime \prime }\}}\cup \mathrm{J}(\mathcal L )$, where $B_{\ell }(m)=\{x\}$ and

  • (a) $x\in \{m^{\prime }\}^{\ell } \cap \{m^{\prime \prime }\}^{\ell }$,

  • (b) $|L_{\{x,m^{\prime \prime }\}}^{m^{\prime }}|\le 2$ and $|L_{\{x,m^{\prime \prime }\}}^{m^{\prime }}|\le 2$, and if $|L_{\{x,m^{\prime \prime }\}}^{m^{\prime }}|= 2$, then $|L_{\{x,m^{\prime }\}}^{m^{\prime \prime }}|=1$, and if $|L_{\{x,m^{\prime }\}}^{m^{\prime \prime }}|= 2$, then $|L_{\{x,m^{\prime \prime }\}}^{m^{\prime }}|=1$

Proof

Suppose that $\Gamma _S(\mathcal L )$ is planar. Firstly, by Proposition 4.9 , we have $L_{\{m^{\prime },m^{\prime \prime }\}}^{m} =\{m\}$ which implies that $|B_{\ell }(m)\setminus \{m^{\prime },m^{\prime \prime }\}^{\ell }|=0$. Now, by Proposition 4.6, we have the following cases:

Case 1. Suppose that the condition (i) of Proposition 4.6 holds. Then set $B_{\ell }(m):=\{x\}$. Since $|B_{\ell }(m){\setminus } \{m^{\prime },m^{\prime \prime }\}^{\ell }|=0$ , we have the following subcases:

• (a) $B_{\ell }(m){\setminus } \{m^{\prime }\}^{\ell }= \{x\}$ and $B_{\ell }(m){\setminus } \{m^{\prime \prime }\}^{\ell }= \emptyset$. In this case, if $|L_{\{x ,m^{\prime \prime }\}}^{m^{\prime }} |\ge 2$, then one can easily find a copy of $K_{3,3}$, which is impossible. So $|L_ {\{x ,m^{\prime \prime }\}}^{m^{\prime }} |=1$. Similarly $| L_ {\{x ,m^{\prime }\}}^{m^{\prime \prime }}|=1$. Also $L_ {\{m^{\prime } ,m^{\prime \prime }\}}^{x}$, $L_{m^{\prime \prime }}^{\{x,m^{\prime }\}}$ and $L_{m^{\prime }}^{\{x,m^{\prime \prime }\}}$ are empty sets, because $x\in \{m^{\prime }\}^{\ell }$. So

  $$\begin{aligned} \mathcal{L }=\{1,m,m^{\prime },m^{\prime \prime },x\}\cup L_{x}^{\{m^{\prime },m^{\prime \prime }\}}\cup \mathrm{J}(\mathcal L ). \end{aligned}$$

• (b) $B_{\ell }(m){\setminus } \{m^{\prime \prime }\}^{\ell }= \{x\}$ and $B_{\ell }(m){\setminus } \{m^{\prime }\}^{\ell }= \emptyset$. It is similar to (a).

• (c) $B_{\ell }(m){\setminus } \{m^{\prime \prime }\}^{\ell }= \emptyset$ and $B_{\ell }(m){\setminus } \{m^{\prime }\}^{\ell }= \emptyset$. In this case, by Proposition 4.9, we have that $|L_{\{x,m^{\prime \prime }\}}^{m^{\prime }}|\le 2$ and $|L_{\{x,m^{\prime \prime }\}}^{m^{\prime }}|\le 2$, and if $|L_{\{x,m^{\prime \prime }\}}^{m^{\prime }}|= 2$, then $|L_{\{x,m^{\prime }\}}^{m^{\prime \prime }}|=1$ and vis versa. Also, since $x\in \{m^{\prime }\}^{\ell }$ and $x\in \{m^{\prime \prime }\}^{\ell }$, the sets $L_ {\{m^{\prime } ,m^{\prime \prime }\}}^{x}$, $L_{m^{\prime \prime }}^{\{x,m^{\prime }\}}$ and $L_{m^{\prime }}^{\{x,m^{\prime }\}}$ are empty. Thus $\mathcal L =\{1,m,x\}\cup L_{\{x,m^{\prime \prime }\}}^{m^{\prime }}\cup L_{\{x,m^{\prime \prime }\}}^{m^{\prime }} \cup L_{x}^{\{m^{\prime },m^{\prime \prime }\}}\cup \mathrm{J}(\mathcal L )$, where $|L_{\{x,m^{\prime \prime }\}}^{m^{\prime }}|\le 2$ and $|L_{\{x,m^{\prime \prime }\}}^{m^{\prime }}|\le 2$, and if $|L_{\{x,m^{\prime \prime }\}}^{m^{\prime }}|= 2$ and $|L_{\{x,m^{\prime }\}}^{m^{\prime \prime }}|=1$ and if $|L_{\{x,m^{\prime }\}}^{m^{\prime \prime }}|= 2$ and $|L_{\{x,m^{\prime \prime }\}}^{m^{\prime }}|=1$

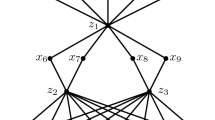
Case 2. Suppose that the condition (ii) of Proposition 4.6 holds. Set $B_{\ell }(m):=\{x,y\}$. Since $\mathcal L$ is a lattice and $|B_{\ell }(m)\setminus \{m',m''\}^{\ell }|=0$, one can conclude that $|B_{\ell }(m)\setminus \{m'\}^{\ell }|=1$ and $|B_{\ell }(m)\setminus \{m''\}^{\ell }|=1$. So, without loss the generality, we may assume that $x\in L_{m''}^{m'}$ and $y\in L_{m'}^{m''}$. Now if we set $V_1:=\{1,m',x\}$ and $V_1:=\{m,m'',y\}$, then one can find a subgraph isomorphic to $K_{3,3}$ in $\Gamma _S(\mathcal L )$ which is impossile. So this case never happens.

The converse statment is clear. $\square$

Now, the only remaining case is that $|S|=1$. The following lemmas are useful.

Lemma 4.11

Assume that $|S|=1$. Then the graph $\Gamma _S(\mathcal L )$ is planar if and only if $\Gamma _S(\mathcal L \setminus J(\mathcal L ))$ is planar.

Proof

By Proposition 3.6 we have that $\mathrm{{deg}}(x)=1$, for all $x\in J(\mathcal L )$. So, the result holds. $\square$

Lemma 4.12

Let $|S|=1$ and $|\mathrm{{Coatom}}(\mathcal L )|\ge 2$. If $| L_{\mathrm{{Coatom}}(\mathcal L )\setminus \{m\}}^{m}|\ge 3$ and $|L_{m}^{m'}|\ge 2$, for some distinct $m, m' \in \mathrm{{Coatom}}(\mathcal L )$, then $\Gamma _S(\mathcal L )$ is not planar.

Proof

Since $| L_{\mathrm{Coatom}(\mathcal L )\setminus \{m\}}^{m}|\ge 3$, we set $V_1:=\{m,x_1,x_2\} \subseteq L_{\mathrm{Coatom}(\mathcal L )\setminus \{m\}}^{m}$. Also, since $|L_{m}^{m'}|\ge 2$, we set $V_2:=\{1,m', y_1\}$ where $y_1\in L_{m}^{m'}$. It is easy to see that the subgraph of $\Gamma _S(\mathcal L )$ on $V_1\cup V_2$ is isomorphic to $K_{3,3}$. Thus, by Kuratowski’s Theorem, $\Gamma _S(\mathcal L )$ is not planar. $\square$

In the next theorem, we provide a necessary and sufficient condition for planarity of $\Gamma _S(\mathcal L )$ when $|S|=1$.

Theroem 4.13

Suppose that $|S|=1$. Then the graph $\Gamma _S(\mathcal L )$ is planar if and only if one of the following statements holds:

• (i) $|\mathrm{Coatom}(\mathcal L )|=1$,

• (ii) $|\mathrm{Coatom}(\mathcal L )|=2$ and if there is an element $m\in \mathrm{Coatom}(\mathcal L )$ such that $| L_{\mathrm{Coatom}(\mathcal L )\setminus \{m\}}^{m}| \ge 3$, then $|L_{m}^{\mathrm{Coatom}(\mathcal L )\setminus \{m\}}|=1$

• (iii) $|\mathrm{Coatom}(\mathcal L )|=3$, and

  • (a) For all $m\in \mathrm{Coatom}(\mathcal L )$, $|L_{\mathrm{Coatom}(\mathcal L )\setminus \{m\}}^{m}|\le 2$ and there is at most one element $m$ in $\mathrm{Coatom}(\mathcal L )$ such that $|L_{\mathrm{Coatom}(\mathcal L )\setminus \{m\}}^{m}|=2$.

  • (b) If there is $m\in \mathrm{Coatom}(\mathcal L )$ such that $|L_{\mathrm{Coatom}(\mathcal L )\setminus \{m\}}^{m}|=2$, then $|L_{m}^{\mathrm{Coatom}(\mathcal L )\setminus \{m\}}|=0$.

Proof

Assume that the graph $\Gamma _S(\mathcal L )$ is planar. Then, by Proposition 3.2, $|\mathrm{Coatom}(\mathcal L )| \le 3$. Suppose that $|\mathrm{Coatom}(\mathcal L )|\ne 1$. So, we have the following cases:

Case 1. Suppose that $|\mathrm{Coatom}(\mathcal L )|= 2$ and put $\mathrm{Coatom}(\mathcal L )=\{m,m'\}$. If there is one element $c\in \mathrm{Coatom}(\mathcal L )$ such that $|L_{\mathrm{Coatom}(\mathcal L )\setminus \{c\}}^{c}| \ge 3$, then we show that $|L_{c}^{\mathrm{Coatom}(\mathcal L )\setminus \{c\}}|=1$. Without loss the generality, we may assume that $c=m$. Assume in contrary that $|L_{m}^{m'}|\ge 2$. Then, by setting $V_1:=\{1,m',x\}$ and $V_2:=\{m,y_1,y_2\}$, where $x\in L_{m}^{m'}$ and $y_1, y_2\in L_{\mathrm{Coatom}(\mathcal L )\setminus \{m\}}^{m}$, one can find a copy of $K_{3,3}$ in $\Gamma _S(\mathcal L )$, which is impossible. Therefore if there is one element $m\in \mathrm{Coatom}(\mathcal L )$ such that $| L_{\mathrm{Coatom}(\mathcal L )\setminus \{m\}}^{m}| \ge 3$, then $L_{m}^{m'}=\{m'\}$.

Case 2. Suppose that $|\mathrm{Coatom}(\mathcal L )|=3$ and put $\mathrm{Coatom}(\mathcal L )=\{m,m',m''\}$. It is easy to see that if $| L_{\mathrm{Coatom}(\mathcal L )\setminus \{m\}}^{m} | \ge 3$, then the graph $\Gamma _S(\mathcal L )$ is not planar, which is impossible. So $| L_{\mathrm{Coatom}(\mathcal L )\setminus \{m\}}^{m}| \le 2$ for all $m\in \mathrm{Coatom}(\mathcal L )$. Now, Assume in contrary that $| L_{\mathrm{Coatom}(\mathcal L )\setminus \{c\}}^{c}| = 2$ and $|L_{\mathrm{Coatom}(\mathcal L )\setminus \{c'\}}^{c'} |= 2$ for some $c$ and $c'$ in $\mathrm{Coatom}(\mathcal L )$. Without loss of generality, we may assume that $c=m$ and $c'=m'$. Put $V_1:=\{1,m,x\}$ and $V_2:=\{m',m'',y\}$, where $x\in L_{\{m',m''\}}^{m}$ and $y\in L_{\{m,m''\}}^{m'}$. Then one can find a subgraph of $\Gamma _S(\mathcal L )$ which is isomorphic to $K_{3,3}$, which is impossible. So, there is at most one element $c$ in $\mathrm{Coatom}(\mathcal L )$ such that $|L_{\mathrm{Coatom}(\mathcal L )\setminus \{c\}}^{c}|=2$. Now, assume that $|L_{\mathrm{Coatom}(\mathcal L )\setminus \{m\}}^{m}|=2$, and assume in contrary that $|L_{m}^{\{m',m''\}}|\ge 1$. Then, by setting $V_1:=\{1\}\cup L_{\mathrm{Coatom}(\mathcal L )\setminus \{m\}}^{m}$ and $V_2:=\{m',m'',y\}$ where $y\in L_{m}^{\{m',m''\}}$, we can find a subgraph in the graph $\Gamma _S(\mathcal L )$ which is isomorphic to $K_{3,3}$, which is impossible. So, $|L_{m}^{\{m',m''\}}|=0$.

Conversely, if $|\mathrm{Coatom}(\mathcal L )|=1$, then, by part (ii) of Proposition 2.5, $\Gamma _S(\mathcal L )$ is a star graph, and so it is planar.

Now, assume that $|\mathrm{Coatom}(\mathcal L )|=2$ and that there is one element $m\in \mathrm{Coatom}(\mathcal L )$ such that $|L_{\mathrm{Coatom}(\mathcal L )\setminus \{m\}}^{m}| \ge 3$. Then $|L_{m}^{\mathrm{Coatom}(\mathcal L )\setminus \{m\}}|=1$. It is not hard to see that $\Gamma _S(\mathcal L\setminus J(\mathcal L\mathcal ))$ is a complete 3-partite graph such that at least two parts of it has exactly one element. Therefore $\Gamma _S(\mathcal L\setminus J(\mathcal L\mathcal ))$ is planar. Now, by Proposition 4.11, $\Gamma _S(\mathcal L )$ is planar.

Now, suppose that $|\mathrm{Coatom}(\mathcal L )|=3$ and put $\mathrm{Coatom}(\mathcal L )=\{m,m',m''\}$. Also, assume that the conditions (a) and (b) hold. It is easy to see that the subgraph $\Gamma _S(\mathcal L\setminus J(\mathcal L\mathcal ))$ on $\{1\}\cup L_{\{m',m''\}}^{m}\cup L_{\{m,m''\}}^{m'}\cup L_{\{m,m'\}}^{m''}$ is a complete 4-partite graph such that at least three parts of it has exactly one element. Now, by condition (b), it is easy to see that $\Gamma _S(\mathcal L\setminus J(\mathcal L\mathcal ))$ is planar. Hence, by Proposition 4.11, $\Gamma _S(\mathcal L )$ is planar.

$\square$