Introduction

The search for efficient solid-state iodide ion conductors is vital not only for the development of dye sensitized solar cells but for many other applications as well [1, 2]. In particular, chemically and physically stable solid electrolytes are favourable for many such applications compared to their liquid counterpart [1–3]. Owing to the recent extensive research aimed at developing lithium ion batteries, etc., the field of cation-conducting solid polymer electrolytes has gained a rapid development [3, 4]. In contrary, the solid polymer anionic conductors have not been studied in greater detail and as a result, reports on dielectric analysis of such anion conductors are rare to find, and the present work is intended to fill that gap.

The solid-state iodide ion conductors can be used to enhance the dye-sensitized solar cell (DSSC) performances with wider operating temperature range and longer operating life due to the better chemical and physical stability of such solid polymer electrolytes compared to liquid electrolytes [5–10]. For instance, the chemical inertness of the host polymers used in these polymer electrolytes minimizes the possibility of side reactions and limits the redox reactions to the proximity of electrode–electrolyte interfaces, which in turn improve the stability of the cell [11, 12].

Literature review reveals that solid polymer electrolytes have been widely studied as cation, mostly lithium ion, conductors with intention of applying as secondary batteries; however their utilization as anionic conductors is rather unexplored [5–7, 13–16]. Anionic conductors are important not only for DSSCs but also for other electrochemical applications such as electrochromic devices and separation processes, which are also less studied [15, 17]. Further, anion-conducting solid polymer electrolytes are suitable for super-capacitors as well [18].

There are large numbers of host polymers suitable for fabricating solid or gel polymer electrolytes. Some examples are polyethylene oxide (PEO), polypropylene oxide (PPO) polyacrylonitrile (PAN), polymethyl methacrylate (PMMA) and polyvinylidene fluoride (PVdF) [8, 9, 19, 20]. PEO is one of the widely studied host polymers used for solid-state polymer electrolytes. Solid polymer electrolytes, based on high molecular weight PEO, appeared to be the most appropriate electrolytes for such applications [21, 22]. However, the nature of PEO-based polymer electrolytes is rather complex due to the coexistence of semi-crystalline phases and an amorphous eutectic elastomeric phase in which most of the ionic conduction is taking place [23–25].

The structural morphology of the PEO-based electrolytes depends on many factors such as method of fabrication, thermal history, concentration and the type of the salt along with other additives in the electrolytes like ceramic fillers and plasticizers [26, 27]. The electrolytes with high molecular weight PEO have shown higher conductivities above their crystallite melting temperature. Many attempts have been made to control the crystallinity by decreasing the melting temperature below 60 °C in order to improve the conductivity [11, 21, 27].

One of the popular methods to increase the conductivity is the addition of plasticizers or co-solvents to the electrolyte complex [5, 10, 13, 14]. Those plasticizers take part in enhancing the mobility of ions by lowering the local viscosity and thus increasing the segmental flexibility of polymer chains. In addition, plasticizers with relatively high dielectric constants improve salt solvation [28]. In a study, Ito et al. observed that the ionic conductivity raised as the amount of plasticizer increased, but it was a setback for the interfacial properties due to the presence of hydroxyl end-groups [29]. Further, most of the plasticizers used in general, are inflammable, toxic and volatile. Even though the incorporation of plasticizers improves the conductivity, at the same time, it lowers the mechanical strength of electrolytes, making it difficult to accomplish the real advantages expected from the replacement of liquid electrolytes by solid-state electrolytes.

On the other hand, ceramic fillers improve the ionic conductivity without degrading mechanical and interfacial properties [20, 21]. The inorganic fillers can also be dispersed in host polymer in order to fabricate composite solid polymer electrolytes. However, the role of the filler in enhancing the ionic conductivity is still not clearly resolved [21, 30–32]. The inorganic fillers such as nano-sized, Al2O3, TiO2, SiO2 and BaTiO3 contribute to the ionic conductivity by enhancing the stability of highly conductive amorphous phase, which in turn improved the electrode–electrolyte interfacial contacts by providing conducting pathways for ionic spices [30, 33, 34].

Further, it is rare to find studies on anionic conductivity behaviour in composite polymer electrolytes and especially the analysis of dielectric behaviour in high-frequency region (close to GHz). Therefore, the investigation of iodide ion-conducting composite solid-state polymer electrolytes is worthwhile, particularly for the field of DSSCs to understand both the conductivity mechanism and the characteristics of the fillers.

During the last decade, DSSCs have attained a considerable progress [5, 8, 14, 35]. Numerous reports on DSSCs with liquid type electrolytes and gel polymer electrolytes can be found in literature. However, very few reports have been published on all-solid-state solar cells. A study of electrochemically compatible and highly conductive iodide ion-conducting solid-state electrolyte is important to further develop applications such as dye-sensitized solar cells. This effort is focused on improving the iodide ion conductivity in PEO-based solid-state electrolytes without degrading mechanical strength of the electrolyte. In addition, the study was broadened to analyse the electrical and dielectric behaviour of such systems.

Experimental

Polyethylene oxide (Mw 4 × 106), tetrapropylammonium iodide, neutral alumina powder (pore size 5.8 nm, 150 mesh), iodine chips (I 2) and ethylene carbonate (EC) were purchased from Sigma-Aldrich. For the electrolyte preparation, fixed weights of PEO (0.630 g), Pr4N+I− (0.065 g), I 2 (0.005 g) and EC (0.700 g) were used. The mass fraction of alumina in the electrolyte was varied according to Table 1. The weight percentage of alumina with respect to the PEO weight is also given in Table 1.

Table 1 The alumina filler composition in electrolyte samples
Full size table

The relevant weights of the raw materials were dissolved in about 25 ml of anhydrous acetonitrile solvent and were magnetically stirred at room temperature for 24 h. The resulted slurry was cast on to a Teflon plate and kept in a fume box for 24 h to evaporate the solvent. Then, the film was vacuum dried for 12 h in order to obtain solvent free solid-state electrolyte sample.

The room temperature morphologies of polymer and electrolyte samples were studied by scanning electron microscopy (SEM) using Zeiss Evo LS15. Differential scanning calorimetry (DSC) of samples was performed using a Mettler Toledo DSC 30 differential scanning calorimeter at a heating rate of 10 °C min−1 between −120 and 120 °C. The melting enthalpy of the samples was calculated using the data obtained from the 2nd heating cycle in order to get similar thermal history for all the samples.

Complex impedance measurements were taken using a high-frequency HP 4291 A RF impedance analyser in the frequency range of 1 MHz–1.8 GHz. For the measurements, sample cells were prepared by sandwiching thin electrolyte films of 5 mm diameter and 0.1–0.5 mm thickness between two stainless steel electrodes. The temperature of the sample was varied from about 30 °C to about 0 °C at approximately 6 °C intervals. The temperature of the sample was allowed to stabilize at each measuring temperature for about 30 min. A flow of nitrogen gas was purged over the sample holder to prevent contact with atmospheric moisture, and samples were heated to 70 °C before taking the data in order to get unique thermal history for all the samples.

Results and discussion

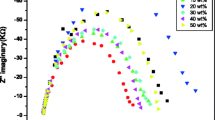
The complex impedance analysis in the high-frequency region (1 MHz–1 GHz) was employed to each sample for electrical and dielectric analysis. Figure 1 shows the Nyquist plot (impedance in complex plane) obtained for sample a which is without alumina, for an example. All the alumina added samples also have exhibited similar behaviour and showed only the semi-circular in the part of the Nyquist plot. Thus, in order to extract the bulk resistance (R b) of electrolyte samples, the measured data were fitted to a circle which is also shown in Fig. 1. This procedure was repeated for all the samples (from a to i) to determine the bulk direct current (DC) resistance and consequently to determine the conductivity.

Fig. 1
figure 1

Nyquist plot for the sample a (sample without alumina). A fitted circle is also shown (dashed line)

Full size image

Figure 2 shows the conductivity, calculated using Nyquist plots, as a function of 1000/T (where T is absolute temperature). The room temperature conductivities of PEO-based polymer electrolytes without additives are in the range of 10−6 to 10−8 S cm−1; this is as a result of low effective carrier mobility below the crystalline melting temperature [21]. However, the measured samples showed relatively higher conductivities possibly due to added limited amount of ethylene carbonate. For all the electrolyte samples, a controlled amount of EC was incorporated in order to improve salt dissociation and polymer flexibility. EC is a non-volatile solvent; however, below 30 °C, it is in solid phase since its melting temperature is about 36 °C (according to manufacturer’s specifications). It is well known that relatively high dielectric constant of solvents favours the salt dissociation and the solvation [10, 36]. Hence, the electrolyte without alumina (0% alumina, sample a) exhibited the conductivities of about 1.55 × 10−4, 2.13 × 10−4 and 3.28 × 10−4 S cm−1 at 0, 12 and 24 °C, respectively.

Fig. 2
figure 2

Conductivity as a function of 1000/T for electrolytes containing different alumina contents (from 0 to 25 wt.%)

Full size image

However, the contribution to conductivity by added inert filler particles is clearly visible in the conductivity plots in Fig. 2. The highest conductivity is exhibited by sample d, which is with 5% alumina indicating that the optimum filler content is 5 wt.%. For the measured temperature range, the conductivities of 2.4 × 10−4, 3.3 × 10−4 and 4.2 × 10−4 S cm−1 at 0, 12 and 24 °C, respectively, are shown in the Fig. 2. In comparison, 5 wt.% Al2O3 filler containing electrolyte (sample d) has shown conductivity enchantments which are about 54.3, 56.9 and 29.5% at 0, 12 and 24 °C, respectively, compared to that of the filler free sample.

The logarithm of conductivity varies more or less linearly with 1000/T within the measured temperature range as shown in Fig. 3. Hence, the experimental data can be fitted to Arrhenius equation (Eq. (1)) in order to calculate conductivity activation energies. The fitted lines are also shown in Fig. 3.

$$ \sigma T= A \exp \left[\raisebox{1ex}{$-{E}_{\mathrm{a}}$}\!\left/ \!\raisebox{-1ex}{${k}_{\mathrm{B}} T$}\right.\right] $$
(1)
Fig. 3
figure 3

Variation of ln (σT) versus 1/1000 T for the nine different alumina compositions in solid-state PEO-based electrolyte. The fitted solid lines to Arrhenius equation are also shown

Full size image

where A is a constant, E a is the activation energy and k B is the Boltzmann constant.

The values obtained for activation energy (E a,σ ) utilizing the graphs of ln (σT) against 1/1000 T are given in Fig. 4 for the electrolytes with different alumina compositions. Samples with higher conductivities have shown lower activation energies. For example, the activation energy for the 5% alumina composition is the lowest. In addition, samples without alumina and with 15% alumina have shown higher conductivities and their activation energies are also lower. Consequently, the samples with higher activation energies have shown lower conductivities. For instance, sample with 10 and 20% alumina showed low conductivities. This behaviour is expected since conductivity is energized due to a combined effect of activation of the mobility and the charge carrier density.

Fig. 4
figure 4

Conductivity activation energy (E a,σ ) and activation energy (E a,fm) values calculated using peak frequency in complex dielectric loss for electrolytes with different alumina contents (0 to 20%)

Full size image

For the polyethylene oxide-based composite Li+ ion conductors, the nano-fillers contributed to conductivity enhancement in two mechanisms. Major contribution is resulted in the creation of favourable conducting paths through Lewis acid–base type surface interactions of ionic species with O/OH groups in the filler surface [31, 32]. It has been revealed that the highest conductivity enhancement for a PEO-based Li-conducting electrolyte is given for the filler particles with acidic groups followed by basic, neutral and weakly acidic [30]. The other contribution to the conductivity enhancement comes from the reduction of crystallinity due to the added filler. It is evident from the increase of the conductivity in the amorphous phase in PEO-based electrolytes [30, 31].

Figure 5 shows the variation of conductivity with alumina content at 0, 6, 12 and 18 °C. With the addition of small amount of alumina, the conductivity initially shows a dip at ∼1% alumina content. This initial drop is possibly due to dilution effect caused by the addition of inert alumina grains. The isolated alumina particles cannot affect the conductivity, but it can enforce some stiffness to PEO chains [37]. In Fig. 5, the conductivity then starts to increase and the maximum conductivity is for the sample containing about 5% alumina. Since many reports have indicated that the ionic conductivity increases with added alumina, this observed increase is not difficult to understand [5–7, 21, 28, 30–32]. The observed increase can be ascribed to the formation of additional high conducting pathways through Lewis acid-base type interactions as reported by others for ion-conducting polymer electrolytes [32, 38]. According to Fig. 5, when the alumina concentration is further increased, the conductivity is dropped. This drop can be due to the “blocking effect” imposed by more prevalent alumina grains. The decrease in conductivity can also be attributed to immobilization of the host polymer by geometric constrictions of non-conducting ceramic fillers [30, 37]. The small bump shown in Fig. 5 around 12 to 15% alumina content can be attributed to the formation of high conducting pathways for ionic species by interconnected alumina particles [31]. A reasonable number of ionic charge carriers in this region can travel along and between these interconnected high conducting pathways. However, the conductivity increase is not as high as in the case showed at 5% alumna content, and this could be due to the limitation of number of high conducting pathways.

Fig. 5
figure 5

Conductivity isotherms for plasticized electrolyte membranes containing different filler contents

Full size image

Figure 6 shows microstructures of polymer and selected electrolyte samples. SEM images of solvent casted (a) pure PEO films, (b) PEO with salt Pr4NI, (c) PEO with salt Pr4NI and 5% alumina (sample d) and (d) PEO with salt Pr4NI and 15% alumina (sample h) are shown in Fig. 6. The corresponding variation in ionic conductivity and its activation energy changes with their compositions could be understood by analysing SEM images [39]. It has been suggested that morphological changes observed in SEM represent the changes in conductivity of the samples [39]. As seen in Fig. 6a, there are some spherulites with diameter about 200 μm formed by lamellar eutectics in pure PEO samples. However, when the salt, Pr4NI, is added to pure PEO, the spherulite structure was completely suppressed (Fig. 6b). This can be attributed to the random distribution of salt in PEO causing altered morphology in the electrolyte. However, spherulites can be restructured and formed when EC and alumina are present in the samples. For example, scattered spherulites with ∼200 μm diameter are visible in sample d (Fig. 6c) which contains 5% alumina. On the other hand, when the alumina content is increased to 15% (sample h), the structure is dominated by compacted spherulites as can be seen in Fig. 6d. Clearly, more surface area is covered by spherulites in sample h compared to sample d. This is an evidence for the high crystallinity in sample h compared to that in sample d since spherulites represent crystalline phase of PEO [40]. It seems that spherulite formation has been activated by added alumina. Further, small pores visible in sample h, which lie between spherulites, may be formed due to high crystallinity of the sample.

Fig. 6
figure 6

SEM images of solvent casted a pure PEO films, b PEO with salt Pr4NI, c PEO with salt Pr4NI and 5% alumina (sample d) and d PEO with salt Pr4NI and 15% alumina (sample h)

Full size image

In order to get an idea about relative crystallinity of the electrolyte samples, the melting enthalpy of electrolytes extracted using DSC measurements is given in the Table 2. The mass normalized enthalpy (corrected for the alumina weight in the electrolyte) of melting is also shown in Table 2.

Table 2 Melting enthalpy of electrolyte samples
Full size table

In order to understand polarization effects of material, analysis of dielectric constant is important. Besides, the dielectric constant values are complex and depend on the frequency of applied electromagnetic radiation. Therefore, instead of dielectric constant, “dielectric function” is used in this work. Complex dielectric function has two limiting values, namely static dielectric constant and high-frequency dielectric constant. The difference between static and high-frequency dielectric constants is a measure of the polarization constituents in the material. Dielectric analysis of all the samples was performed using the real (ε′) and imaginary (ε″) parts of the dielectric function extracted from high-frequency impedance data [30, 31]. Real and imaginary parts of the dielectric function are calculated using the following Eqs. (2) and (3).

$$ {\varepsilon}_r^{\prime }=\frac{-{Z}^{{\prime\prime} }}{\omega {C}_0\left({Z^{\prime}}^2+{Z^{{\prime\prime}}}^2\right)} $$
(2)
$$ {\varepsilon}_r^{{\prime\prime} }=\frac{Z^{\prime }}{\omega {C}_0\left({Z^{\prime}}^2+{Z^{{\prime\prime}}}^2\right)} $$
(3)

where ω, Z ′and Z ″are angular frequency and real and imaginary parts of the dielectric function, respectively. The C 0 is geometrical capacitance of the cell (capacitor which does not contain any medium between two plates) and is given by equation

$$ {C}_0={\varepsilon}_0 A/ d $$
(4)

where A is surface area of the active electrode and d is the thickness of the electrolyte.

The aim is to detect any possible dielectric relaxations caused by polymer chains or ion–ion interactions. Dielectric relaxations are difficult to identify in these measured samples by using calculated imaginary and real parts of the dielectric function. For instance, calculated real and imaginary parts of the dielectric function are shown in Figs. 7 and 8 for sample a. The values of real part of the dielectric function are very high at low frequencies. This can be attributed to effects of space charge polarization and electrode polarization resulted by high ionic condition in the electrolyte. Values of real part of the dielectric function decrease with increasing frequency due to ionic and dipole relaxation. As seen by Fig. 7, the values of dielectric function increase with increasing temperature within the measured frequency window, and this trend is shown by the other samples as well. Thus, evidently, the polarizability of all the electrolytes increases with increasing temperature. Considering the respective frequencies for different relaxations, the rapid drop of low frequency values of dielectric function may be attributed to ionic relaxation (interfacial and space charge relaxation). Consequently, the sudden drop visible in the high-frequency region may be related to dipole relaxation. Though a plateau is visible around 108 Hz, the measurement frequency window needs to be elaborated to Gigahertz region in order to catch high-frequency limiting values. However, relaxation peaks are still unseen due to the dominated contribution by the bulk DC conductivity of the dielectric function. Thus, the contribution by DC conductivity should be removed from the imaginary part of the dielectric constant in order to clearly see the relaxation effects. Accordingly, the corrected dielectric loss was determined by subtracting bulk DC conductivity contribution σ dc/ε0 ω from the calculated ε″ [41]. The frequency dependent of the corrected dielectric loss is shown in Fig. 9 for electrolyte samples a, b, c, d, e, f, g and h.

Fig. 7
figure 7

Real part of the dielectric function, ε′, versus frequency for electrolyte sample a at different temperatures

Full size image
Fig. 8
figure 8

Imaginary part of the dielectric function, ε″, versus frequency for the electrolyte sample a at different temperatures

Full size image
Fig. 9
figure 9

The\( {\varepsilon}_{\mathrm{corr}}^{{\prime\prime} } \)versus frequency for electrolyte samples a, b, c, d, e, f, g and h (given in Table 1) at different temperatures

Full size image

The inverse of dielectric relaxation time corresponds to the frequency (f m) at peak dielectric loss. Therefore, the frequency is related to maximum (peak) corrected dielectric loss (f m) and is associated with the polymer chain segmental flexibility. Further, it is inversely proportional to local viscosity and finally to the mobility of the charge carriers [42, 43]. Therefore, the conductivity and the f m, are interrelated. The peak frequency values extracted from the corrected dielectric loss curves in Fig. 9 are shown in Fig. 10. The activation energies (E a,fm) calculated from the peak frequency of the corrected dielectric loss versus 1/1000 T plots are also shown in Fig. 4. The correlation between conductivity and f m values can be seen by scrutinizing the activation energy data in Fig. 3.

Fig. 10
figure 10

The frequency values correspond to maximum corrected dielectric loss extracted using the different corrected dielectric loss curves in Fig. 9

Full size image

As seen from the Fig. 4, the conductivity activation energies are larger than those of corresponding peak frequency maxima. The trend can be understood since conductivity is activated by both the mobility and the charge carrier density. The relaxation time decreases for relatively fast motion of segments which coupled with mobile ion enhancement resulting in increasing transport properties in the polymer electrolytes [43]. Therefore, the E a,fm, which relates to the mobility, exhibited lower activation energies than that of conductivity. As expected, lower activation energies are exhibited by high conducting samples.

Conclusions

In electrical and dielectric behaviours in composite electrolytes based on PEO, tetrapropylammonium iodide was modified by incorporating various amounts of Al2O3 nano-filler. The conductivity variation with temperature shows Arrhenius behaviour. The electrolyte without alumina exhibited the conductivities of about 1.55 × 10−4, 2.13 × 10−4 and 3.28 × 10−4 S cm−1 at 0, 12 and 24 °C, respectively.

The incorporation of nano-fillers could modify conductivity of electrolyte samples. The highest conductivity is exhibited by sample with 5% alumina indicating that the optimum filler content is 5 wt.% with a conductivity of 2.4 × 10−4, 3.3 × 10−4 and 4.2 × 10−4 S cm−1 at 0, 12 and 24 °C, respectively. Al2O3 filler (5 wt.%) containing samples have shown conductivity enchantments of about 54.3, 56.9 and 29.5% at 0, 12 and 24 °C, respectively, compared to that of filler-free sample. The room temperature morphologies of polymer and selected electrolyte samples were studied using SEMs. PEO spherulite formation has been altered by the introduction of salt, but the addition of alumina restructured PEO spherulite with smaller size. Higher crystallinity in 15% alumina sample could be inferred compared to that in 5% sample by activating the formation of spherulites with added alumina.

The dielectric polarization effects of electrolytes were understood using the behaviour of complex dielectric function in the high-frequency region for different alumina contents at different temperatures. Dielectric analysis of all the samples revealed the increase in the values of the real (ε′) and imaginary (ε″) parts of the dielectric function. The relaxation behaviour is clearly visible after dielectric function is corrected for the conductivity contribution.

The conductivity activation energy values are 0.23, 0.20 and 0.29 eV for electrolytes containing 0, 5 and 15% alumina while the corresponding activation energy values from dielectric measurements are 0.19, 0.19 and 0.24 eV. The conductivity activation energy (E a,σ) and the activation energy (E a,fm) values calculated using peak frequency in complex dielectric loss have shown similar behaviour for electrolytes with different alumina contents. As expected, activation energies are lower for the sample with higher conductivity.