Introduction

The structure of apatite Ca10(PO4)6A2 A = F, OH, Cl apatite in the space group P63/m allows a wide range of cation and anion substitutions [1–16]. In fact, the two Ca positions have distinct stereochemistries (Ca(1), equipoint 4f, CaO9 polyhedron, Ca(2), equipoint 6 h, CaO6 (A polyhedron)) are able to accommodate a variety of univalent, divalent, and trivalent cations as substituents. Concerning the substitution of the trivalent samarium (rare earth elements), it is charge compensated in various ways as in the following example:

$$ 2{\mathrm{Ca}}^{2+}\kern0.5em =\kern0.5em {\mathrm{Na}}^{+}\kern0.5em +\kern0.5em {\mathrm{Sm}}^{3+};\kern0.5em {\mathrm{Ca}}_{10\hbox{--} 2\mathrm{y}}{\mathrm{Na}}_{\mathrm{y}}{\mathrm{Sm}}_{\mathrm{y}}{\left({\mathrm{PO}}_4\right)}_6{\mathrm{A}}_2. $$

What is worthwhile to note is that the structure role of rare earth in apatite is currently unclear. Actually, minor amounts appear to replace Ca on the smaller Ca(2) position. Moreover, lanthanum, which is a synthetic Ca4La6(SiO4)6(OH)2, is reported to be randomly distributed on both Ca positions [10]. In NaY9(SiO4)6O2, while Y is ordered in the 6 h position [Ca(2)], it is disordered with Na in 4f [Ca(1)] [12].

The structure of Nd-substituted fluorapatite showed that 80 % of the Nd was partitioned into Ca2, in general agreement with Hughes [13, 14].

The preference of individual rare earth among multiple Ca positions in minerals (site occupancy) has not been extensively studied because of the inability of conventional diffraction methods to distinguish among individual elements on multiple occupied sites. We have reproduced the rare earth contents of the natural apatites studied to emphasize the extent of this problem for natural samples.

In order to understand the charge carrier diffusion processes occurring in apatite, investigations on calcium apatite substituted by samarium and sodium were performed. This work aims to determine the effects of the substitution of monovalent and trivalent ions for lead on the ionic conduction and the structural behavior.

In order to get a better understanding of these puzzling effects, we undertook a systematic study of the apatite containing rare earth. This paper is devoted to the case of a compound based on samarium. The objective is the examination of vibrational Raman and infrared spectroscopy of Na0.11Ca9.6Sm0.23(PO4)6F2.

Experimental methods

The Na0.11Ca9.64Sm0.23(PO4)6F2 compound was obtained by the solid-state reaction of Sm2O3, Ca3(PO4)2 (Cerac, 99.95 %), CaF2, Na2CO3, and (NH4)2HPO4 (Merck, 99 %). After grinding, the mixture was heated at 300 °C for 6 h to eliminate ammoniac. The resultant powder was subsequently heated at 700 °C for 12 h and then at 840 °C for 24 h with intermittent grinding.

$$ \begin{array}{c}\hfill 0.055\ {\mathrm{Na}}_2{\mathrm{CO}}_3+0.115\ {\mathrm{Sm}}_2{\mathrm{O}}_3+{\mathrm{Ca}\mathrm{F}}_2+3.88\ {\mathrm{Ca}}_3{\left({\mathrm{PO}}_4\right)}_2+0.24{\left({\mathrm{NH}}_4\right)}_2{\mathrm{HPO}}_4\to \kern9em \hfill \\ {}\hfill \kern10em {\mathrm{Na}}_{0.11}{\mathrm{Ca}}_{9.64}{\mathrm{Sm}}_{0.23}{\left({\mathrm{PO}}_4\right)}_6{\mathrm{F}}_2+{\mathrm{Ca}}_3{\left({\mathrm{PO}}_4\right)}_2+0.055{\mathrm{CO}}_2+0.48{\mathrm{NH}}_3\hfill \end{array} $$

X-ray powder diffraction (XRD) pattern was determined by means of a PANalytical X’Pert PRO MPD diffractometer equipped with a detector X’cellerator operating with a secondary monochromator and using a CuKα radiation source (Kα1 = 0.15406 nm and Kα2 = 0.15444 nm). The diffraction pattern was recorded under ambient atmosphere over an angular range of 5°–80° (2θ), with a step length of 0.033° (2θ).

The Fourier transform infrared (FT-IR) measurements were performed at room temperature, on a Perkin-Elmer FT-IR Paragon 1000 PC spectrometer over the 400– 4,000-cm−1 region, in a KBr pellet. Furthermore, Raman spectra were measured with a LABRAM HR800 triple monochromator at room temperature under a × 50 LF objective microscope. An He–Ne ion laser operating at about 20 mW was used (on the sample) as an excitation source (514.5 nm), with a spectral steps of 3 cm−1.

Electrical conductivity measurements of apatite materials were undertaken using the impedance method on an HP 4194A impedance meter between 200 and 600 °C with the signal frequency ranging from 5 Hz to 13 MHz. An applied voltage was fixed at 100 mV. Powder was pressed under 5 t/cm2. Electrodes were prepared by painting platinum paste on both sides of the sintered pellet surfaces, which were then heated at 600 °C to ensure a good electrical contact.

Results and discussion

Refinement of the structure

The structures of the compounds in the solid are closely related to those of the common phosphate apatite, which have been frequently described in the literature [17]. They have been commonly determined by XRD using the Rietveld method refinement stating from the isostructural phase Ca9.66Na0.17Sm0.17(PO4)6Cl2 [18].

The final results of this refinement are presented in Table 1 (for the structure parameters and the R factors) and in Table 2 (for the atomic positions, selected bond lengths, and angles). Besides, Fig. 1 shows the observed, calculated, and different X-ray profiles of the powder diffraction of these apatite phosphates.

Table 1 Refined structure parameters and R factors from powder X-ray Rietveld analysis in P63/m space group of Na0.11Ca9.64Sm0.23(PO4)6F2
Full size table
Table 2 Bond lengths (Å) and selected angles (°) of Na0.11Ca9.64Sm0.23(PO4)6F2
Full size table
Fig. 1
figure 1

The final Rietveld refinement plot of the Na0.11Ca9.64Sm0.23(PO4)6F2. Points correspond to the experimental values and the continuous lines; the calculated pattern and vertical bars indicate the positions of Bragg peaks. The bottom trace depicts the difference between the experimental and the calculated intensity values

Full size image

Discussion

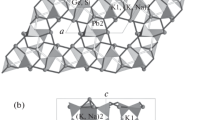
The analysis of the tetrahedrons has revealed that the average P–O distance (1.506 (5) Å) is slightly shorter than the average values observed in fluorapatite (1.535 Å) [19]. The angles O–P–O are, on the other hand, seen to vary between 106.2° and 116.7°, with an average value (109.76°), which is very close to the one of a uniform tetrahedron (109.47°) (Fig. 2).

Fig. 2
figure 2

Perspective view of Na0.11Ca9.64Sm0.23(PO4)6F2

Full size image

There are two symmetrically nonequivalent M(1) and M(2) in the structure of Na0.11Ca9.64Sm0.23(PO4)6F2. The cations M(1) are coordinated to nine oxygen anions belonging to six distinct tetrahedrons. Each polyhedron is linked to four PO4 tetrahedrons via corners and two other tetrahedrons via edges. The M(2) cations are inserted into fivefold sites that constitute the walls of the tunnels. Each polyhedron is linked to three PO4 tetrahedrons via corners.

In the case of the M(1)–O distances, the nine distances have an average value of 2.409 (5) Å, which is quite similar to fluorapatite (2.56 (20) Å) (Fig. 3) [20]. In the case of the M(2)–O distances, on the other hand, the distance average value is 2.288 (4) Å, which is slightly smaller than the one observed in calcium fluorapatite 2.44 (13) Å (Fig. 4).

Fig. 3
figure 3

Coordination of the metal in site (4f)

Full size image
Fig. 4
figure 4

Coordination of the metal in site (6 h)

Full size image

Therefore, the analysis of the final adjustments carried out for the observed and calculated diagrams indicates that there are three nonindexed lines that could be identified as minor impurities β-Ca3(PO4)2.

Spectroscopy analysis

The IR and Raman spectra are shown in Figs. 5 and 6, respectively. The spectral data and proposed vibrational assignment are listed in Tables 3 and 4.

Fig. 5
figure 5

Raman spectrum of Na0.11Ca9.64Sm0.23(PO4)6F2

Full size image
Fig. 6
figure 6

Infrared spectrum of Na0.11Ca9.64Sm0.23(PO4)6F2

Full size image
Table 3 Experimental wave number (cm−1) of the PO4 3− tetrahedron vibration of Na0.11Ca9.64Sm0.23(PO4)6F2
Full size table
Table 4 The external modes Raman of Na0.11Ca9.64Sm0.23(PO4)6F2 (ANCSPF), flourapatite (FAP), and Ca6Sm2 Na2(PO4)6F2 (CSPF)
Full size table

As shown in the Raman spectrum presented in Fig. 5, one strong band at 962 cm−1 was observed, which can be attributed to ν1 (PO4). The position of the band at 960 cm−1 is similar to the one previously reported by A. Hadrich [21].

The weaker peaks observed at 1,000 and 1,027 cm−1 and those recorded at 548, 558, and 575 can be accredited to the asymmetric stretching ν3 and the asymmetric bending modes ν4 of PO4 groups, respectively. The bands assigned to ν3 (PO4) vibrations are reported at 1,000 cm−1, whereas those assigned to ν4 (PO4), vibrations are described at 610 and 615 cm−1 for fluorapatites [21]. Regarding the weak lines observed at 421, 440, and 447 cm−1, they could be assigned to the symmetric bending ν2 mode.

With respect to the IR spectrum of the compound shown in Fig. 6, it is similar to that of fluorapatites. While the bands corresponding to the asymmetric stretching ν3 (PO4) are located at 1,045 and 1,003 cm−1, the symmetric stretching ν1 (PO4) mode is observed at 943 cm−1, such a mode was previously reported at 947 cm−1 in NaPb9(PO4)6F(H2O)0.33 [22] and 930 cm−1 in Pb10(PO4)6F2 [23].

With regard to the two strong lines located at 563 and 600 cm−1 and observed at 575/600 and at 545/575 cm−1 in Pb10(PO4)6F2 and Ca10(PO4)6F2 [23], respectively, they are attributed to the asymmetric bending (ν4) modes of PO4 groups. Concerning the very weak line observed at 453 cm−1, it could be attributed to the symmetric bending ν2 mode.

The most interesting feature is the existence of few lines with much weaker frequencies than that in Ca10 (PO4)6F2. This can be attributed to the presence of much mass heavier ions. Actually, with regard to the huge mass of samarium with respect to the other components, several vibrations are presumably weakly coupled, and some modes can involve this ion alone. This is probably the case for two modes in the vicinity of 94 and 104 cm−1 since, with regard to the mass effect, they would correspond a vibration in the vicinity of 98 cm−1 in fluorapatite. The fact is that these modes appear with regard to the polarizability of the rare earth.

Conductivity data

The complex AC impedance responses of Na0.11Ca9.64Sm0.23(PO4)6F2 at different temperatures shown in Fig. 7 indicated the presence of two regions for measuring frequency. The high-frequency region might be due to the ionic conduction of mobile ions, including bulk and grain boundary, which collapse in the same semicircle. The low-frequency region, on the other hand, exhibited a conduction mechanism that could be related to the contribution of the electrode interface. The bulk and grain boundary semicircle that appeared at a high frequency was noted to get remarkably smaller at 600 °C. The sample impedance was generally observed to decrease with the increase in temperature.

Fig. 7
figure 7

Complex impedance diagrams of Na0.11Ca9.64Sm0.23(PO4)6F2 measured at various temperatures

Full size image

The conductivity (σ) of Na0.11Ca9.64Sm0.23(PO4)6F2 was calculated using the following equation: σ = (e/S) × (1/R), where e, S, and R refer to the thickness, area, and resistance, respectively. The conductivity variation revealed an increase of conductivity with the rise in temperature, with a typical Arrhenius-type that indicated a semiconductor-like behavior having a linear dependence of electrical conductivity logarithm log (σT) on the inverse of temperature 103/T K−1 (Fig. 8). This temperature dependence of conductivity indicated that the electrical conduction in the material was a thermally activated process. It can be elucidated through the following expression: σ = σ0exp(−ΔEa/kT), where σ, σ0, ΔEa, k, and T refer to conductivity, pre-exponential factor, activation energy, Boltzmann constant, and absolute temperature, respectively.

Fig. 8
figure 8

Arrhenius plot log (σT) = f (103/T) of ionic conductivity for Na0.11Ca9.64Sm0.23(PO4)6F2

Full size image

The total activation energy was obtained as Et = 0.6 eV for ionic hopping of mobile ions (Na+ and F−) along the c axis, including the bulk and grain boundary [24].

The conductivity of Na0.11Ca9.64Sm0.23(PO4)6 F2 ( 2.3 × 10−5 S cm−1 at 475 °C) was relatively important than that of Pb10 (PO4)6(OH)2 (2.05 × 10−7 S cm−1 at 500 °C ) (Table 5) [25].

Table 5 Comparison of electrical properties between fluorapatite and hydroxyapatite materials in relation with physical characteristics of M2+ ions
Full size table

The break of Arrhenius lines at T = 475 °C for the Na0.11Ca9.64Sm0.23(PO4)6F2 apatite is related to the pseudo ionic bond, which needs a high energy to romp this bound and to liberate the mobile ion (Na+ or F−; Fig. 8) [25–28].

The conduction mechanism is related to the translational hopping of sodium ions along the c axis of the unit cell from ordinary lattice sites in interstitial sites and back again, which are the only candidates for such a condition process.

Conclusions

The results from X-ray refinement have shown that the formula assigned to the new Sm-substituted Ca apatite was Na0.11Ca9.64Sm0.23(PO4)6F2. The analysis of data from vibrational spectroscopy has also provided support for the high symmetry P63/m space group. This apatite contained channels where samarium ions are located in two different sites. Accordingly, further investigations that employed complex impedance were used to explore the possibility of cation conduction along these channels. The highest overall conductivity values were found at σ475 °C = 2.3 × 10−5 S cm−1 and Ea = 0.60 eV.