Introduction

The prospect of creating new functional materials with tunable properties gives a strong motivation on the research of organic–inorganic hybrids [1, 2]. Interest in these compounds has grown due to their remarkable structural and physical properties like ferro-electricity, ferro-elasticity, and low-dimensional magnetism [3–5]. The synthesis of low-dimensional mixed organic–inorganic materials enables both inorganic and organic components on the molecular scale to be optimized and thus to exhibit specific properties, such as electronic, catalytic, optical, and second-order non-linear optical [6–9] ones. On the other hand, the compounds crystallized with aliphatic tetra-ammonium cations with the general formula (CnH2n+1)4N+, such as (CH3)4N+, (C2H5)4N+, and (C3H7)4N+, undergo many structural phase transitions governed by the reorientational dynamics of the tetra-alkyl-ammonium groups [10]. That is why we are interested, in our laboratory, in the investigation of the physical properties of hybrid materials with quaternary ammonium cation with the general formula (CnH2n+1)4 N+. Such properties related to cation with n = 1 and 2 were well stabilized [11, 12]. In the case of a long chain (n > 2), only [N(C3H7)4]2Cu2Cl6, [N(C3H7)4]2Cd2Cl6, [N(C3H7)4]2Hg2Cl6, and [N(C4H9)4]2Cu2Cl6 structure are reported [11, 13–15].

The present work reports the synthesis, crystal structure, thermal analysis, vibrational study, and electrical properties of the bis tetrapropylammonium hexachloro-dizincate.

Experimental section

Synthesis

ZnCl2 (purity 98 %; FLUKA) and [N(C3H7)4]Cl (purity 97 %; FLUKA) were dissolved in a HCl (1 M) aqueous solution in a molar ratio of 1:1. Colorless prismatic monocrystals of [N(C3H7)4]2Zn2Cl6 compound were obtained by slow evaporation at room temperature. The single crystal was selected by using a microscope. After that, it has been washed by absolute ethanol and dried in vacuum desiccators 2 days before the measurements.

The reactions sequence for the synthesis is shown in the following equation:

$$ 2\left[\mathrm{N}{\left({\mathrm{C}}_3{\mathrm{H}}_7\right)}_4\right]\mathrm{Cl}+{2\mathrm{ZnCl}}_2\overset{\mathrm{H}\mathrm{Cl}\left(1\mathrm{M}\right)}{\to }{\left[{\left({\mathrm{C}}_3{\mathrm{H}}_7\right)}_4\mathrm{N}\right]}_2{\mathrm{Zn}}_2{\mathrm{C}\mathrm{l}}_6 $$

Crystal structure

X-ray data were collected at 298 K on colorless prismatic crystal of dimensions 0.35 × 0.23 × 0.06 mm3 using a Bruker AXS CCD area detector diffractometer, with MoKα radiation (λ = 0.71073 Å), in φ and ω scans mode. For unit cell refinement, 20,522 reflections with θ ranging from 1.3° to 30.5° were used. The crystal structure adopts a triclinic system with \( P\overline{1} \) space group (Z = 4). Absorption corrections were based on multiple and symmetry-equivalent reflections in the data set using the SADABS program [16]. The structure was solved by Patterson methods using SHELXS 97 [17] and refined by least squares techniques with Crystals 2003 [18]. Anisotropic thermal parameters were employed for non-hydrogen atoms. With regard to the hydrogen atoms attached to carbon atoms, they were positioned geometrically, and initially refined with soft restraints on the bond lengths and angles to regularize their geometry, C–H in the range of 0.93–0.98 Å. Diamond computer program [19] was used to prepare drawings. The crystal data, collected reflections, and parameters of the final refinement are reported in Table 1. Interatomic bond distances and angles schemes are listed in Tables 2 and 3. It is worthwhile to mention that atomic coordinates anisotropic displacement parameters, tables for all bond distances, and angles have been deposited at the Cambridge Crystallographic Data Center (deposition number CCDC 861352).

Table 1 Crystal data and structure refinement for [N(C3H7)4]2Zn2Cl6
Full size table
Table 2 Principal intermolecular distances (Å) and angles (°) for anionic part [Zn2Cl6]2−
Full size table
Table 3 Principal intermolecular distances (Å) and angles (°) for cationic part [N(C3H7)4]+
Full size table

Characterization

With respect to the calorimetric measurements, they were performed on Perkin Elmer DSC-7 from 293 up to 473 K at an average heating of 5 °C/min with 12 mg sample weight.

The infrared spectrum was obtained using a Perkin-Elmer FT-IR 1000 spectrometer with a sample pressed in KBr pellet in the 400–4,000 cm−1 region. The Raman spectra of the sample were obtained under microscope with a T-64000 Raman spectrometer (ISA, Jobin Yvon) with nitrogen-cooled CCD detector. The spectra were registered in triple subtractive mode with 1,800 tr/mm grating from 50 to 3,500 cm−1.

Electrical measurements

The electrical measurements were performed using a two-electrode configuration. In fact, the [(C3H7)4N]2Zn2Cl6 sample was pressed into pellets of 8 mm in diameter and 1.1 mm in thickness using 3 t/cm2 uniaxial pressures. The ac impedance data, |Z|, and phase angle were obtained in the frequency range 209 Hz–5 MHz using TEGAM 3550 impedance analyzer over the temperature range 303–403 K.

Results and discussion

Structure description

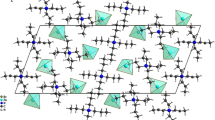
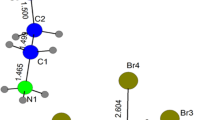
The crystallographic analysis of this compound reveals that the crystal structure of [(C3H7)4N]2Zn2Cl6 consists of one and two half of [Zn2Cl6]2− un-equivalent dimers and four [N(C3H7)4]+ cations. A view of the asymmetric unit of the structure showing the thermal ellipsoid atoms mean square displacements of non-hydrogen is depicted in Fig. 1. The structural arrangement of the title compound can be described as an alternation of organic and inorganic layers parallel to the (001) plan, made up of [N(C3H7)4]+ groups and [Zn2Cl6]2− dimers, respectively (Fig. 2). This figure shows that cations are stacked in a regularly cross form and orient their ramifications toward ZnCl4 tetrahedra of four adjacent dimers localized in two successive inorganic sheets. The compound crystallizes in the centrosymmetric triclinic space group \( P\overline{1} \). Regarding the organic layers, they are formed by two alternating infinite chains parallel to the b direction. Each chain is made up of two alternative unequivalent cations; one is in trans or the other in gauche configurations (Fig. 3).

Fig. 1
figure 1

ORTEP representation of asymmetric unit with 50 % probability of the thermal ellipsoid of non-hydrogen atoms of [N(C3H7)4]2Zn2Cl6

Full size image
Fig. 2
figure 2

[0 0 1] view showing alternation of organic and inorganic sheets of [N(C3H7)4]2Zn2Cl6

Full size image
Fig. 3
figure 3

View of an organic layer showing the alternating of two infinite organic chains parallel to b direction of [N(C3H7)4]2Zn2Cl6

Full size image

The atoms of all organic cations occupy general positions with C1 point group symmetry. In the fourth cations, C–C–C, C–N–C, and N–C–C angles and C–C and C–N distances (Table 3) are commonly observed [20]. Two inorganic layers are observed at z = 0 and z = 1/2, the first of which is made up of two un-equivalent Zn2Cl6 dimers. Not only is each anion built up by two ZnCl4 tetrahedra generated by inversion center but also shares one bridging chlorine atom (ClL3 and ClL4). In both anions, bridging chlorine and zinc atoms (Zn3, Zn4) are planar. As for the second layer, it is composed of one Zn2Cl6 dimers built up by two ZnCl4 tetrahedra sharing two bridging chlorine atoms (ClL1 and ClL2), whereas in the latter dimers, bridging chlorine and zinc atoms (Zn1, Zn2) are pseudo-planar with distortion angle equal to 3.87(3)°. The Zn2Cl6 dimers can be described as two strongly distorted ZnCl4 tetrahedra, commonly observed in M2X6 groups [11, 13]. Two types of ligands are usually mentioned, XE (external) and XL (linkage). Moreover, bibliographic investigations show that M–X distances and X–M–X angles verify (M–XL > M–XE) (I) and (XL–M–XE, and XE–M–XE are generally bigger than XL–M–XL) (II) [21]. The geometry of Zn2Cl6 dimers verifies the reported relations (Table 2). For all Zn2Cl6 anions, ClL–Zn–ClL–Zn are pseudo-square with a weak out-of-plan distortion in dimers observed in the second inorganic sheets. These results are in agreement with the above comparison (I and II). Taking into account the geometrical characteristics of the entities and considering the calculated average values of the Baur distortion indices (DI) [22]

$$ \operatorname{ID}\left( Zn-\operatorname{Cl}\right)={\displaystyle \sum_{i=1}^4\frac{\left| Zn-{\operatorname{Cl}}_i- Zn-{\operatorname{Cl}}_m\right|}{4\kern0.5em \left( Zn-{\operatorname{Cl}}_m\right)}}\kern0.5em ;\kern0.5em \operatorname{ID}\left(\operatorname{ClZnCl}\right)={\displaystyle \sum_{i=1}^6\frac{\left|{\operatorname{ClZnCl}}_i-{\operatorname{ClZnCl}}_m\right|}{6\left(\operatorname{Cl}\kern0.5em Zn\kern0.5em C{l}_m\right)}} $$

where m signifies the mean value for the polyhedron.

{ID Zn(1)–Cl = 0.031, ID Zn(2)–Cl = 0.032, ID Zn(3)–Cl = 0.033, and ID Zn(4)–Cl = 0.030}, we can deduce that the ZnCl4 tetrahedra are more distorted in the Zn2Cl6 observed in the second inorganic sheets in the dimers formed by Zn(3)Cl4 tetrahedron than in Zn2Cl6 made up of Zn(4)Cl4.

Calorimetric study

The order of the phase transition (first or second order) may be determined by analyzing the shape of the heat anomaly and value of the temperature hysteresis in the calorimetric measurements. The values of the thermal hysteresis in our experiment were estimated from linear extrapolation to the scanning rate. On the other hand, the character of the phase transition (order–disorder or displacive) is classified on the basis of the value of the entropy effect.

Figure 4a and b shows the DSC runs for [N(C3H7)4]2Zn2Cl6 upon the heating and cooling of 5 °C/min. An overview of the results unambiguously illustrates the existence of three endothermic solid–solid phase transitions that define four successive phases on heating, denoted by I, II, III, and IV, respectively. The parameters characterizing these phase transitions are summarized in Table 4.

Fig. 4
figure 4

Differential scanning calorimetry analysis of [N(C3H7)4]2Zn2Cl6 compound

Full size image
Table 4 Phase transitions in [N(C3H7)4]2Zn2Cl6
Full size table

Figure 4b clearly shows that slightly above room temperature, the compound undergoes two reversible phase transitions (PT). Extrapolated to zero scanning rate, the transition between phase I and phase II occurs at T 1 = 327/324 K (heating/cooling cycle) and its significant temperature hysteresis (ΔT = 3 K). In phase II–phase III, the transition appears at T 2 = 347/343 K and its significant temperature hysteresis (ΔT = 4 K). Therefore, the transitions at T 1 and T 2 are typical for the first-order phase transition.

The entropy of the I → II and II → III phase transition at heating and cooling cycle is quite small (ΔS = 0.07 J g−1 K−1 at T 1 and ΔS = 0.0146 J g−1 K−1 at T 2), and does not indicate the pure “order disorder” mechanism of this transition. This implies, from DSC results, that both order–disorder and displacive mechanism are expected for the phase transition. The mechanism experimentally observed in transition entropy can be interpreted in terms of Boltzmann’s principle ΔS = R Ln(Ω) [23], where Ω is the rapport number of distinguishable orientations allowed in the high- and the low-temperature phases. The observed values of Ω 1 at T 1 and Ω 2 at T 2 ∼1 (Ω 1, 2 < 2) therefore do not indicate the pure “order disorder”. As regards the DSC diagrams obtained from single crystals, they also show a weak peak (Fig. 4a) in the vicinity of 429 K (T 3) prior to the melting temperature at 451 K (T melting). At this T 3 transition (from phase III to phase IV), the single crystals break and lose their transparency to become a white powder. This transition is not well shaped since it is too close to the melting point.

Infrared and Raman spectra

To gain more information on the crystal structure, we have undertaken a vibrational study using infrared spectroscopy and Raman scattering. The infrared and Raman spectra of the studied compound at room temperature are shown in Figs. 5 and 6. The assignments of the observed bands are realized by comparison with similar compounds [5, 13, 14, 24–27]. Besides, the wavenumbers of the observed peaks are quoted in Table 5.

Fig. 5
figure 5

Infrared spectrum of the [N(C3H7)4]2Zn2Cl6 compound at room temperature in the 4,000–400 cm–1 range

Full size image
Fig. 6
figure 6

Raman spectrum of [N(C3H7)4]2Zn2Cl6 at room temperature in the 50–3,500 cm−1 spectral region

Full size image
Table 5 Assignments of observed in infrared and Raman spectra of [N(C3H7)4]2Zn2Cl6
Full size table

While the principal bands are assigned to the internal modes of organic cation, the bands observed at 2,992, 2,973, and 2,986 cm−1 in IR and Raman, respectively, are accredited to the asymmetric νas(CH3), νas(CH2) stretching mode. Concerning the CH stretching vibrations νs(CH2) + νs(CH3), they are observed at 2,883 and 2,881 cm−1 in IR and Raman, respectively. The band which appears at 1,371 and 1,389 cm−1 in IR is related to the symmetric deformation δs(CH3), whereas the bands observed at 1,470 cm−1 in IR and at 1,459 cm−1 in Raman can be assigned to the asymmetric deformation δas(CH3). Two sharp bands are observed at 1,310 and 1,330 cm−1 in IR, which are assigned to the ω(CH2) wagging modes. The frequencies observed at 1,174 and 1,318, 1,139 cm−1 in infrared and Raman spectra, respectively, are related to the rocking ρr(CH3) vibration modes. Another band, assigned to the rocking ρr(CH2), is observed near 845 and 1,039 cm−1 in infrared and Raman, respectively. With respect to the bands observed at 943, 973 cm−1 in IR and 937 cm−1 in Raman, they are assigned to ν1(NC4) stretching modes. The deformation mode ν3(NC4) appears at 757 and 776 cm−1 in IR and Raman spectra, respectively. The splitting bending mode νs(CCCN) are observed at 1,103 cm−1 in infrared and Raman spectra. This mode may correspond to different conformers of the organic chains [νs(NCC) + νs(CCC)]. Moreover, the weak peak in infrared spectrum at 1,042 cm−1 is related to the bending mode [νs(C–C–N)].

The Raman and IR active bands involving mainly the Zn2Cl6 vibration were proposed in comparison with Ga2Cl6 and Cd2Cl6. The isolated inorganic entities exhibit D2h symmetry with 18 normal modes. Among the Zn2Cl6 Raman active modes, the 474, 333, and 93 cm−1 lines can be assigned to the 3Ag (ν1, ν2, and ν4) and one band at 268 cm−1 attributed to the B1g(ν6) mode. Two modes 2B2g (ν11, ν12) occur at 519 and 134 cm−1, respectively. The band observed at 377 cm−1 should be attributed to B3g (ν18) mode at the Raman spectra. The ν1 and ν11 vibrations due to the Zn2Cl6 stretching motions and their frequencies are higher than those of ν2, ν6, and ν13, which are mainly due to the vibrations of the bridging Zn2Cl6 groups.

Electrical conductivity

The complex impedance spectra of the [N(C3H7)4]2Zn2Cl6 compound recorded at different temperatures are shown in Fig. 7a and b. The well-defined semicircles either passing through or close to the origin were obtained at 303 K ≤ T ≤ 403 K. As temperature increases, the radius of the arc corresponding to the bulk resistance of the sample decreases, indicating an activated thermal conduction mechanism. The depressed semicircles have their centers on a line below the real axis, which indicates the departure from the ideal Debye behavior [28].

Fig. 7
figure 7

The Cole–Cole plots at different temperature of the [N(C3H7)4]2Zn2Cl6 compound

Full size image

The electrical conductivity σ = e/RS (S is the electrolyte–electrode contact area and e is the thickness of the sample) increases with the increase in temperature. In order to understand the conduction phenomena, we used the Arrhenius modeling equation [11]: σT = A  exp(−E a/kT), where E a is the activation energy, A is the pre-exponential factor, k is the Boltzmann constant, and T is the temperature. The thermal evolution of the specific conductivity [Ln(σT) vs. 1,000/T] of bis tetrapropylammonium hexachloro-dizincate compound is shown in Fig. 8, indicating an Arrhenius-type behavior. In the 303–403 K temperature range, the conductivity plot exhibits one anomaly at 327 ± (5)K. In comparison with the studied [N(C3H7)4]2Cd2Cl6 compounds [13], this anomaly probably corresponds to the orientation and/or reorientation of molecular groups as [N(C3H7)4]+. The obtained activation energy is E a1 = 0.69 eV in phase I and E a2 = 0.96 eV in phase II. The differences can be due to the high displacement of the ammonium proton caused by the cell deformation introduced with the establishment of a non-polar phase, that is to say, the existence of a paraelectric phase at room temperature in the compound [29]. The anomaly is characterized by a sharp increase in the conductivity values, so the conductivity increases from σ = 2.2610−7 (Ω cm)−1 at 303 K to σ = 1.6510−6 (Ω cm)−1 at 327 K for the first region, and from σ = 2.6010−6 (Ω cm)−1 at 333 K to σ = 1.3910−4 (Ω cm)−1 at 403 K for the second one. The sudden conductivity variation at 327 ± (5)K marks the transitions, first to a more disordered state, which might be correlated with changes in the orientation of molecular groups as [N(C3H7)4]+. The variation of conductivity at various temperatures confirms the occurrence of the phase transition at 327 K detected by the thermal analysis.

Fig. 8
figure 8

Temperature dependence of Ln(σT) versus reciprocal temperature for [N(C3H7)4]2Zn2Cl6

Full size image

Figure 9a and b shows the variation of real part Z′ of the impedance at different temperatures. It is observed that all the curves merge in high-frequency region (>106 Hz), and then Z′ becomes independent of frequency. Indeed, the magnitude of Z′ decreases with the increase in both frequency and temperature indicating an increase in ac conductivity of the material. This result may be related to the release of space charge emanating from the reduction in the barrier properties of material with the rise in temperature [30].

Fig. 9
figure 9

Variation of Z′ with angular frequency for [N(C3H7)4]2Zn2Cl6 compound

Full size image

The angular frequency dependence of the imaginary part Z″ of complex impedance of [N(C3H7)4]2Zn2Cl6 at various temperatures is shown in Fig. 10a and b. The Z″ increases with the increase in frequency at all the temperatures, covered in the present study, and exhibits a maximum before it starts decreasing rapidly. The magnitude of Z″ maxima decreases gradually with the increase in both frequency and temperature, and it merges finally in the high-frequency region. This may possibly be an indication of the accumulation of space charge polarization effects in the material at lower frequency and at higher temperature [31].

Fig. 10
figure 10

Plots of the imaginary part of impedance at several temperatures

Full size image

Ac conductivity

The variation of alternating current (ac) conductivity as a function of frequency at different temperatures for the [N(C3H7)4]2Zn2Cl6 is shown in Fig. 11. It is clear from the plot that the conductivity increases with the increase in frequency. From the previously mentioned figure, it is also evident that the dc contribution is important at low frequencies and high temperatures, yet in the low-frequency region, the conductivity depends on temperature. Such dependence may be described by the variable range hopping mechanism [32], which is frequency independent and only weakly dependent temperature compared with band theory. This model is important for the electrical conduction mechanism. The phenomenon of the conductivity dispersion is generally analyzed using Jonscher’s law [33, 34]

Fig. 11
figure 11

Frequency dependence of the ac conductivity at various temperatures of the [N(C3H7)4]2Zn2Cl6 compound

Full size image
$$ {\sigma}_{\mathrm{ac}}\left(\omega \right)={\sigma}_{\mathrm{dc}}+A{\omega}^n $$

where σ dc is the direct current conductivity of the sample, n is the frequency exponent with 0 < n < 1, and A is the temperature dependent pre-exponential factor. This suggests that electrical conduction in [N(C3H7)4]2Zn2Cl6 is a thermally activated process.

Dc conductivity data are plotted in Arrhenius format as Ln(σ dc T) versus (103/T) (Fig. 12). Following the Arrhenius law, the obtained activation energy of the samples are E a = 0.68 eV in region I (T < 327 K) and 0.90 eV in region II (T > 333 K). Those values are similar to the activation energy determined by impedance, suggesting that the near values of activation energies confirm that the transport is probably due to a hopping mechanism. The conduction is explained by the thermally activated mechanism. A change in the slope of the curve was observed at around T = 327 ± (5)K which is close to the temperature of the transition detected by DSC and electric measurement. The ionic conductivity here is considered to be induced by the reorientation of the tetra-ammonium alkyl chains [29]

Fig. 12
figure 12

Dependence of Ln(σ dc T) on temperature of [N(C3H7)4]2Zn2Cl6 compound

Full size image

Conclusion

The crystal structure of bis tetrapropylammonium hexachloro-dizincate compound is built up of [N(C3H7)4]+ cation groups and bi-tetrahedral [Zn2Cl6]-2 dimers connected to each other via electrostatic interaction. The compound is crystallized at room temperature in the triclinic system (space group \( P\overline{1} \)). In crystal structure, the inorganic layer, built up by Zn2Cl6 dimers, is connected to the organic ones through van der Waals interaction in order to build cation–anion–cation cohesion. The thermal investigation of the title crystal indicates the presence of four endothermic peaks at 327, 347, and 429. Two solid–solid reversible phase transitions of first order at 327/324 and 347/343 K (heating/cooling) have been observed. The infrared and Raman studies confirm the presence of organic and inorganic groups.

The Cole–Cole plots of impedance complex measurements have been performed in the electric analysis. Besides, Z′ and Z″ curves which merge above 106 Hz at different temperatures reveal the reduced space charge polarization and contribution from grain. The ac conductivity spectrum was found to obey Jonscher’s universal power law, whereas dc conductivity shows a typical Arrhenius type of electrical conductivity. The near values of activation energies obtained from the impedance and dc conductivity spectra confirm that the transport is probably due to a hopping mechanism.