Is Kyle’s equilibrium model stable?

Abstract

In the dynamic discrete-time trading setting of Kyle (Econometrica 53:1315–1336, 1985), we prove that Kyle’s equilibrium model is stable when there are one or two trading times. For three or more trading times, we prove that Kyle’s equilibrium is not stable. These theoretical results are proven to hold irrespectively of all Kyle’s input parameters.

1 Introduction

Kyle [13] is a cornerstone model in today’s market microstructure theory. Its relevance is long established; see, e.g., the textbook discussions in Back [1]. We consider the discrete-time formulation where an informed trader, noise traders, and market makers dynamically trade the stock at $N\in \mathbb N$ time points. After observing the aggregate order flow, the market makers set the stock price to clear the stock market. Kyle [13] proves existence of a unique linear equilibrium, and we study its stability properties. We prove that the number of trading time points $N\in \mathbb N$ determines all stability properties of Kyle’s equilibrium. Specifically, irrespectively of all other input parameters, we prove that Kyle’s equilibrium is stable for $N\in \{1,2\}$ and not stable for $N\ge 3$.

Hadamard [9] deems a model well-posed if existence, uniqueness, and stability hold. Kyle [13] gives existence and uniqueness of a linear equilibrium, and we use the convergence of policy iterations to determine if Kyle’s linear equilibrium is stable.¹ We start the policy iterations from a marginal perturbation away from the insider’s equilibrium orders. Then, we iteratively create a sequence of insider orders by considering the market makers’ best response to the insider’s perturbed orders and the subsequent best response by the insider and so on. Kyle’s equilibrium is deemed stable if this iteratively constructed sequence of insider orders converges to Kyle’s equilibrium orders whenever the initial orders are only marginally different from Kyle’s equilibrium orders. This definition of fixed-point stability in terms of iterations of a marginal perturbation away from the fixed point itself is standard in numerical analysis; see, e.g., Definition 1.3 in the textbook [15].²

Defining stability in terms of the convergence of policy iterations is natural in the context of a financial market equilibrium because policy iterations can be viewed as the best responses of rational agents given the current state of the market. Thus, a stable equilibrium has the property that if the agents find themselves in the equilibrium’s vicinity, their actions draw the economy closer to equilibrium.³

To the best of our knowledge, stability of Kyle’s dynamic equilibrium model has not been studied in the literature. The closest study to our paper is Boulatov and Bernhardt [6], who proves a robustness property for Kyle’s equilibrium when $N=1$. We study stability of Kyle’s discrete-time model for arbitrary $N\in \mathbb N$ trading times. In the economics literature, stability of equilibria is typically considered within the context of multiple equilibria and is used as a refinement to discard repellent equilibria. However, as we also demonstrate in this paper, uniqueness of equilibrium does not imply its stability. Indeed, Kyle’s unique linear equilibrium is not stable for $N\ge 3$.

The main part of our analysis uses marginal perturbations of the insider’s equilibrium orders that are linear. For such perturbations, there is an operator T, which produces the next iteration of insider orders as a function of her previous orders. Naturally, the insider’s equilibrium orders are a fixed point for T. However, because T is nonlinear, T has multiple fixed points of which only one fixed point corresponds to Kyle’s equilibrium. We note that such marginal perturbations may arise in practice as a result of measurement or precision errors in model parameters. Thus, in addition to being of theoretical interest, our interest in stability comes from a numerical perspective. Numerics related to Kyle’s equilibrium have become more and more relevant as algorithmic market makers have become an important part of asset pricing; see, e.g., [7].

We prove two theoretical results. First, when $N\in \{1,2\}$, we prove that Kyle’s equilibrium is always stable. Our proof establishes that the policy iterations are locally contracting near Kyle’s equilibrium. Even stronger, for $N=1$, we show that Kyle’s equilibrium is a super-attractive fixed point in the sense that local convergence is strictly faster than linear. Second, when $N\ge 3$, we prove that Kyle’s equilibrium is always not stable. Table 1 summarizes our theoretical results.

Table 1 Key results

To provide some intuition for our results, we illustrate numerically the non-stability of Kyle’s equilibrium when $N=3$. Our numerics are based on a 5th digit perturbation where we illustrate that the policy iterations converge, however, not to Kyle’s equilibrium. Mathematically speaking, this happens because the eigenvalue of the Jacobian of the policy iteration operator evaluated at Kyle’s equilibrium is strictly bigger than one (in absolute value), which implies non-stability. However, there are other non-equilibrium attractive fixed points and we illustrate that the policy iterations can converge numerically to such a fixed point.

While the main part of the paper is about policy iterations in the insider’s control (i.e., informed stock orders), we consider an alternative in Appendix A, where we iterate the market makers’ control (i.e., the pricing rule). This variation leads to the same stability conclusions in that Kyle’s equilibrium is stable for $N\in \{1,2\}$ and not stable for $N\ge 3$.

All proofs are in Appendix B. Our proofs rely on a new characterization of Kyle’s equilibrium in terms of a one-dimensional fully autonomous recursion, which is independent of all model inputs.

Throughout the text, we use the symbol $^{\prime }$ to transpose vectors. For example, $\vec {x} = (x_1,\ldots ,x_N)'$ denotes a column vector in $\mathbb {R}^N$. For numbers, we use... to indicate that we have excluded remaining decimals. For example, we have $\pi = 3.14159\ldots$.

2 Kyle’s discrete-time model

This section briefly recalls the discrete-time model in Kyle [13] with $N\in \mathbb N$ trading times. The noise traders’ orders $\Delta u_n$ at trading time $n\in \{1,\ldots ,N\}$ are Gaussian random variables with mean zero and variance $\sigma _u^2 \Delta$, where $\Delta >0$ is the time step. The stock’s liquidating value is denoted by $\tilde{v}$, which is assumed Gaussian with mean zero and variance $\Sigma _0:= \mathbb {V}[\tilde{v}]>0$. These exogenous random variables $(\tilde{v},\Delta u_1,\ldots ,\Delta u_N)$ are assumed mutually independent.

At time $n=1$, the insider submits orders $\Delta x_1$ to the market makers. The orders $\Delta x_1$ are required to be measurable with respect to $\sigma (\tilde{v})$. At later times $n\in \{2,\ldots ,N\}$, the insider submits orders $\Delta x_n$, which are required to be measurable with respect to $\sigma (\tilde{v},\Delta u_1,\ldots ,\Delta u_{n-1})$. The aggregate orders are defined as

$$\begin{aligned} \Delta y_n := \Delta u_n + \Delta x_n,\quad n\in \{1,\ldots ,N\}. \end{aligned}$$

(2.1)

For a given pricing rule $p_n = p_n(\Delta y_1,\ldots , \Delta y_n)$, the insider seeks orders $(\Delta x_1,\ldots ,\Delta x_n)$ that maximize her expected profit given by

$$\begin{aligned} \sum _{n=1}^N \mathbb {E}\big [(\tilde{v}-p_n)\Delta x_n\big | \tilde{v}\big ]. \end{aligned}$$

(2.2)

The market makers set prices $p_n$ in the following sense. At time $n\in \{1,\ldots ,N\}$, the market makers observe the aggregate orders $\Delta y_n$ from (2.1) before setting the stock price as

$$\begin{aligned} p_n = \mathbb {E}[\tilde{v}| \Delta y_1,\ldots ,\Delta y_n ],\quad n\in \{1,\ldots ,N\}. \end{aligned}$$

(2.3)

The next result (due to [13]) gives existence of a linear Kyle equilibrium in the sense that items 2. and 3. in Theorem 2.1 hold.

Theorem 2.1

[13]

• 1. For $\Delta>0, \sigma _u>0, \Sigma _0:=\mathbb {V}[\tilde{v}] >0$, and $\alpha _N:=0$, there exist unique solutions $({\hat{\lambda }}_n,{\hat{\Sigma }}_n,{\hat{\alpha }}_n,{\hat{\beta }}_n)$, $n=1,\ldots ,N$, of

  $$\begin{aligned} \lambda _n&= \frac{\beta _n\Sigma _{n-1}}{\beta _n^2\Sigma _{n-1}\Delta +\sigma _u^2},\quad \Sigma _n = \frac{\Sigma _{n-1}\sigma _u^2}{\beta _n^2\Sigma _{n-1}\Delta +\sigma _u^2},\nonumber \\ \alpha _{n-1}&= \frac{1}{4\lambda _n(1-\alpha _n\lambda _n)},\quad \beta _n = \frac{1-2\alpha _n\lambda _n}{\Delta 2\lambda _n(1-\alpha _n\lambda _n)},\quad n=1,\ldots ,N, \end{aligned}$$

  (2.4)

  such that the second-order condition $\lambda _n(1-\lambda _n\alpha _n) >0$ holds.

• 2. For the pricing rule

  $$\begin{aligned} \Delta p_n := {\hat{\lambda }}_n \big (\Delta u_n + \Delta x_n\big ),\quad p_0 := 0, \end{aligned}$$

  (2.5)

  the insider’s optimal orders are

  $$\begin{aligned} {\left\{ \begin{array}{ll} \Delta {\hat{x}}_n = {\hat{\beta }}_n(\tilde{v}- {\hat{p}}_{n-1})\Delta ,\\ \Delta {\hat{p}}_n = {\hat{\lambda }}_n \big (\Delta u_n + \Delta {\hat{x}}_n\big ),\quad {\hat{p}}_0=0. \end{array}\right. } \end{aligned}$$

  (2.6)

• 3. For the orders (2.6), the stock price (2.5) is efficient in the sense that (2.3) holds.

In what follows, we will refer to $\vec {\hat{\beta }}$ as the insider’s equilibrium trading intensity as $\vec {\hat{\beta }}$ determines how aggressively the insider trades when the market price differs from her own valuation.

3 Policy iterations and stability

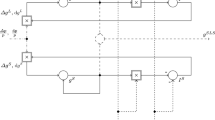
In (3.9) below, we construct the best response operator T for which Kyle’s equilibrium is a fixed point. One iteration takes as input linear insider orders and produces as output updated linear insider orders (Appendix A presents an alternative where we iterate the pricing rule). For given input orders, market makers’ respond by creating a pricing rule based on computing conditional expectations of $\tilde{v}$ given aggregate orders. Given this pricing rule, the insider computes her optimal orders, which gives the outcome of one policy iteration.

To iteratively create a sequence of insider orders, we start with some vector $\vec {\beta }^{(0)}=(\beta _1^{(0)},\ldots ,\beta _N^{(0)})'\in (0,\infty )^N$, which differs only marginally from Kyle’s equilibrium $\vec {{\hat{\beta }}}$ from Theorem 2.1. Kyle’s lambda $\vec {\lambda }^{(0)}=(\lambda _1^{(0)},\ldots ,\lambda _N^{(0)})'\in \mathbb {R}^N$ is defined similarly to (2.4) by $\Sigma ^{(0)}_0:=\mathbb {V}[\tilde{v}]>0$ and

$$\begin{aligned} \lambda ^{(0)}_n := \frac{\beta ^{(0)}_n\Sigma ^{(0)}_{n-1}}{\big (\beta _n^{(0)}\big )^2\Sigma ^{(0)}_{n-1}\Delta +\sigma _u^2},\quad \Sigma ^{(0)}_n := \frac{\Sigma ^{(0)}_{n-1}\sigma _u^2}{\big (\beta ^{(0)}_n\big )^2\Sigma ^{(0)}_{n-1}\Delta +\sigma _u^2},\quad n=1,\ldots ,N. \end{aligned}$$

(3.1)

The initial pricing rule is defined by

$$\begin{aligned} \Delta p^{(0)}_n := \lambda ^{(0)}_n \big (\Delta u_n + \Delta x_n\big ),\quad p^{(0)}_0 := 0, \end{aligned}$$

(3.2)

where ($\Delta x_1,\ldots ,\Delta x_N)$ denote arbitrary insider orders. When she faces the pricing rule (3.2), the insider’s optimal orders that maximize (2.2) are similar to (2.6), and given by

$$\begin{aligned} {\left\{ \begin{array}{ll} \Delta x^{(1)}_n := \beta ^{(1)}_n(\tilde{v}- \hat{p}^{(0)}_{n-1})\Delta ,\\ \Delta \hat{p}^{(0)}_n := \lambda ^{(0)}_n \big (\Delta u_n + \Delta x^{(1)}_n\big ),\quad {\hat{p}}^{(0)}_0 := 0. \end{array}\right. } \end{aligned}$$

(3.3)

In (3.3), the next policy iteration $\vec {\beta }^{(1)}:=(\beta _1^{(1)},\ldots ,\beta _N^{(1)})'$ is computed by $\alpha ^{(1)}_N:=0$ and

$$\begin{aligned} \beta ^{(1)}_n := \frac{1-2\alpha ^{(1)}_n\lambda ^{(0)}_n}{\Delta 2\lambda ^{(0)}_n(1-\alpha ^{(1)}_n\lambda ^{(0)}_n)},\quad \alpha ^{(1)}_{n-1} := \frac{1}{4\lambda ^{(0)}_n(1-\alpha ^{(1)}_n\lambda ^{(0)}_n)},\quad n=N,\ldots ,1. \end{aligned}$$

(3.4)

Given the pricing rule (3.2), the orders (3.3) maximize (2.2) provided that the second-order condition $\alpha ^{(1)}_n\lambda ^{(0)}_n < 1$ holds. However, because Kyle’s equilibrium coefficients from Theorem 2.1 satisfy ${\hat{\alpha }}_n{\hat{\lambda }}_n < 1$, a continuity argument gives that $\alpha ^{(1)}_n\lambda ^{(0)}_n < 1$ provided that $|\vec {\beta }^{(0)}-\vec {{\hat{\beta }}}|<\epsilon$ for some $\epsilon >0$ sufficiently small. Here, $|\vec {\beta }|$ denotes the standard Euclidean norm of $\vec {\beta }\in \mathbb {R}^N$ given by $|\vec {\beta }|:= \sqrt{\sum _{n=1}^N \beta _n^2}$.

We write the above policy iteration step compactly as

$$\begin{aligned} \vec {\beta }^{(1)} = T(\vec {\beta }^{(0)}), \end{aligned}$$

(3.5)

for a non-linear smooth function $T:\mathbb {R}^N\rightarrow \mathbb {R}^N$ with domain dom$(T)\subset \mathbb {R}^N$. For $\vec {\beta } \notin \text {dom}(T)$, we set $T(\vec {\beta }):= (\infty ,\ldots ,\infty )'$. Of course, Kyle’s equilibrium coefficients $\vec {{\hat{\beta }}} = ({\hat{\beta }}_1,\ldots ,{\hat{\beta }}_N)'$ from Theorem 2.1 satisfy the fixed-point property

$$\begin{aligned} \vec {{\hat{\beta }}}=T(\vec {{\hat{\beta }}}), \end{aligned}$$

(3.6)

but there are several other solutions to (3.6). Because Kyle’s linear equilibrium is unique, exactly one of T’s fixed points produces an equilibrium (T’s other fixed points violate the insider’s second-order condition). The n’th coordinate of the function T in (3.5) is given as a ratio of polynomial functions (i.e., T is a rational function). Because the general expression for T is long and not needed in our stability analysis for $N\ge 3$, we only give T for $N\in \{1,2\}$.

Example 3.1

• 1. For $N=1$, the function T in (3.5) is given by

  $$\begin{aligned} T(\beta ) := \frac{\beta ^2\Sigma _0\Delta +\sigma _u^2}{2\Delta \beta \Sigma _0}. \end{aligned}$$

  (3.7)

  The domain of T is given by

  $$\begin{aligned} \text {dom}(T)= \{ \beta \in \mathbb {R}: \beta \ne 0\}. \end{aligned}$$

• 2. For $N=2$, the function T in (3.5) is given by

  $$\begin{aligned} T \begin{pmatrix} \beta _1\\ \beta _2 \end{pmatrix}&= \begin{pmatrix} \frac{\left( \beta _1^2 \Delta \Sigma _0+\sigma _u^2\right) \left( \beta _1 \Delta \Sigma _0 (\beta _1-\beta _2)^2+\sigma _u^2 (\beta _1-2 \beta _2)\right) }{\beta _1 \Delta \Sigma _0 \left( \beta _1 \Delta \Sigma _0 \left( \beta _1^2-4 \beta _1 \beta _2+\beta _2^2\right) +\sigma _u^2 (\beta _1-4 \beta _2)\right) }\\ \frac{\Delta \Sigma _0 \left( \beta _1^2+\beta _2^2\right) +\sigma _u^2}{2 \beta _2 \Delta \Sigma _0} \end{pmatrix}. \end{aligned}$$

  (3.8)

  The domain of T is given by

  $$\begin{aligned} \text {dom}(T)&= \{ (\beta _1,\beta _2)'\in \mathbb {R}^2 : \\&\quad \beta _1 \left( \beta _1 \Delta \Sigma _0 \left( \beta _1^2-4 \beta _1 \beta _2+\beta _2^2\right) +\sigma _u^2 (\beta _1-4 \beta _2)\right) \ne 0, \beta _2\ne 0\}. \end{aligned}$$

$\diamondsuit$

Based on $\vec {\beta }^{(1)}$ from (3.5), we use forward recursion to iteratively construct the sequence $\vec {\beta }^{(2)}, \vec {\beta }^{(3)},\ldots$. More specifically, given the m’th policy iteration $\vec {\beta }^{(m)}\in \mathbb {R}^N$, the next policy iteration is defined as

$$\begin{aligned} \vec {\beta }^{(m+1)}:= T(\vec {\beta }^{(m)}),\quad m\in \{0,1,\ldots \}. \end{aligned}$$

(3.9)

We use the following definition of stability, which is based on Definition 1.3 in Süli and Mayers [15].

Definition 3.2

Kyle’s equilibrium is locally stable with respect to policy iterations for the insider if there exists $\epsilon >0$ such that all initial policies $\vec {\beta }^{(0)}\in \text {dom}(T)$ with $0<|\vec {\beta }^{(0)} -\vec {{\hat{\beta }}} |<\epsilon$ satisfy

$$\begin{aligned} \lim _{m\rightarrow \infty } \vec {\beta }^{(m)} = \vec {{\hat{\beta }}}, \end{aligned}$$

(3.10)

where the sequence $\vec {\beta }^{(m)}$ is defined recursively by (3.9). $\diamondsuit$

In Definition 3.2, the term locally refers to the smallness condition $|\vec {\beta }^{(0)} -\vec {{\hat{\beta }}} |<\epsilon$. Definition 5.2 below allows for more general policy iterations.

Figure 1 depicts a fictitious operator $T:\mathbb {R}\rightarrow \mathbb {R}$ with two fixed points. The dashed line is the 45-degree line and the intersections of the two lines correspond to T’s two fixed points. The fixed point to the left is not stable because policy iterations starting from a vicinity of this point moves away from this fixed point. This is called a repellent fixed point. At the left fixed point, the graph of T intersects the 45-degree line from below at this point indicating that T’s derivative is larger than 1. On the other hand, the fixed point to the right is stable and T’s derivative at this point is smaller than 1. This is called an attractive fixed point.

Fig. 1

Two fixed points of a fictitious operator $T:\mathbb {R}\rightarrow \mathbb {R}$. The left fixed point is not stable and the right fixed point is stable

To gain some intuition of local stability, we consider a first-order Taylor approximation around a point ${\tilde{\beta }} \in \text {dom}(T) \subseteq \mathbb {R}$ given by

$$\begin{aligned} T(\beta ) = {\tilde{\beta }} + T'({\tilde{\beta }})(\beta - {\tilde{\beta }}) + R(\beta -{\tilde{\beta }}),\quad \beta \in \text {dom}({\tilde{T}}), \end{aligned}$$

where R is the reminder function, which satisfies $R(\beta ) = o(|\beta |)$ as $|\beta | \rightarrow 0$. When we heuristically replace (3.9) with the linear iterations

$$\begin{aligned} \beta ^{(m+1)}:= {\tilde{\beta }} + T'({\tilde{\beta }})(\beta ^{(m)} - {\tilde{\beta }}), \end{aligned}$$

(3.11)

we see that

$$\begin{aligned} \beta ^{(m+1)} - {\tilde{\beta }} = T'({\tilde{\beta }})(\beta ^{(m)} - {\tilde{\beta }}) =\cdots = T'({\tilde{\beta }})^{m+1}(\beta ^{(0)} - {\tilde{\beta }}). \end{aligned}$$

(3.12)

If ${\tilde{\beta }} \in \mathbb {R}$ is the left fixed point in Fig. 1, we have $|T'({\tilde{\beta }})|>1$ and so the iterations in (3.12) diverge as soon as $\beta ^{(0)} \ne {\tilde{\beta }}$. On the other hand, if ${\tilde{\beta }} \in \mathbb {R}$ is the right fixed point in Fig. 1, we have $| T'({\tilde{\beta }})|<1$ and so the iterations in (3.11) converge to ${\tilde{\beta }}$.

In the subsequent sections, we prove that the derivative of the policy iteration operator T in (3.5) evaluated at Kyle’s equilibrium $\vec {{\hat{\beta }}}$ has a norm less than one when $N\in \{1,2\}$, and a norm larger than 1 when $N\ge 3$. In view of the above discussion, these norms indicate that Kyle’s equilibrium is stable if and only if $N\in \{1,2\}$.

4 One or two trading times

Let T be defined in (3.7) for $N=1$ or (3.8) for $N=2$. In the next result, $\nabla T(\vec {\beta })\in \mathbb {R}^{N\times N}$ denotes the Jacobian matrix of T’s derivatives evaluated at $\vec {\beta }\in \text {dom}(T)$.

Theorem 4.1

For $\Delta>0,\,\sigma _u>0$, and $\Sigma _0>0$, we have:

• 1. For $N:=2$, the Jacobian matrix of T’s derivative satisfies

  $$\begin{aligned} \nabla T (\vec {{\hat{\beta }}})= \begin{pmatrix} -0.981214\ldots &{}\quad 0\\ 0.554958\ldots &{}\quad 0 \end{pmatrix}. \end{aligned}$$

  (4.1)

• 2. For $N\in \{1,2\}$, Kyle’s equilibrium is locally stable with respect to policy iterations for the insider in the sense of Definition 3.2.

Our proof of Theorem 4.1 shows that T defined in (3.7) or (3.8) is a local contraction for $\vec {\beta }$ near Kyle’s equilibrium $\vec {{\hat{\beta }}}$ when $\mathbb {R}^N$ is equipped with the norm $|\vec {\beta }|_\infty := \max \{|\beta _1|,\ldots ,|\beta _N|\}$ and when $N\in \{1,2\}$. For $N=1$, the proof gives the stronger property $T'({\hat{\beta }})=0$, which implies that Kyle’s equilibrium is a super-attractive fixed point. Hubbard and Papadopol [11] has details about super-attractive fixed-points. A similar observation is in Boulatov and Bernhardt [6].

5 Three or more trading times

Before rigorously proving that the policy iterations are not stable, we consider a numerical illustration.

5.1 Numerical example for $N=3$

This section considers numerical experiments corresponding to the parameters

$$\begin{aligned} N=3,\quad \sigma _u := \Delta := \mathbb {V}[\tilde{v}]:=1. \end{aligned}$$

(5.1)

The terminal variance $\Sigma _N = 0.26830307$ produces $\Sigma _0 = 1.000000047\ldots$, which agrees with $\mathbb {V}[\tilde{v}]=1$ up to 7 digits. Kyle’s corresponding equilibrium is given by

$$\begin{aligned} \vec {{\hat{\beta }}} := \begin{pmatrix} 0.538169580578541\ldots \\ 0.757586803229793\ldots \\ 1.365124248887518\ldots \end{pmatrix}. \end{aligned}$$

(5.2)

In this case, there are 18 solutions of (3.6) valued in $\mathbb {C}^3$ of which 8 are valued in $\mathbb {R}^3$ with (5.2) being the only solution valued in $(0,\infty )^3$. Except for (5.2), the other 7 real-valued solutions of (3.6) violate the second-order condition (because some of the corresponding $\vec {\lambda }$ values are negative).

Based on the parameters in (5.1), the policy iteration operator in (3.5) is given by

$$\begin{aligned} T \begin{pmatrix} \beta _1\\ \beta _2\\ \beta _3 \end{pmatrix}= \begin{pmatrix} \frac{\left( \beta _1^2+1\right) \left( \left( \beta _1^2+1\right) \beta _2^2 \beta _3^2+2 \beta _3 \left( \beta _1 (\beta _1-\beta _2)^2+\beta _1-2 \beta _2\right) \left( \beta _1^2+\beta _2^2+1\right) +\left( \beta _1^2+1\right) \beta _2^2 \left( \beta _1^2+\beta _2^2+1\right) \right) }{2 \beta _1 \left( \left( \beta _1^2+1\right) \beta _2^2 \beta _3^2+\beta _3 \left( \beta _1^2+\beta _2^2+1\right) \left( \beta _1 \left( \beta _1^2-4 \beta _1 \beta _2+\beta _2^2+1\right) -4 \beta _2\right) +\left( \beta _1^2+1\right) \beta _2^2 \left( \beta _1^2+\beta _2^2+1\right) \right) }\\ \frac{\left( \beta _1^2+\beta _2^2+1\right) \left( -2 \beta _3 \left( \beta _1^2+\beta _2^2+1\right) +\beta _2 \left( \beta _1^2+\beta _2^2+1\right) +\beta _2 \beta _3^2\right) }{\beta _2 \left( -4 \beta _3 \left( \beta _1^2+\beta _2^2+1\right) +\beta _2 \left( \beta _1^2+\beta _2^2+1\right) +\beta _2 \beta _3^2\right) }\\ \frac{\beta _1^2+\beta _2^2+\beta _3^2+1}{2 \beta _3} \end{pmatrix}. \end{aligned}$$

To illustrate the model’s non-stability, we start the policy iterations from a 5 digit perturbation defined by⁴

$$\begin{aligned} \vec {\beta }^{(0)} := \vec {{\hat{\beta }}} + \begin{pmatrix} 0.00001\\ 0 \\ 0 \end{pmatrix}. \end{aligned}$$

(5.3)

Numerically, the non-linear policy iterating scheme (3.9) starting from $\vec {\beta }^{(0)}$ in (5.3) converges to

$$\begin{aligned} \vec {\beta }^{(\infty )} := \begin{pmatrix} &{}1.2582536009629393\ldots \\ &{}-2.157491457005712\ldots \\ &{}2.6903478420808034\ldots \end{pmatrix}\ne \vec {\hat{\beta }}. \end{aligned}$$

Table 2 reports two sets of eigenvalues of the Jacobian matrix of T’s derivatives $\nabla T(\cdot )\in \mathbb {R}^{N\times N}$.

Table 2 Eigenvalues for $\sigma _u = \mathbb {V}[\tilde{v}] =\Delta =1$ and $N=3$

By replacing $T'({\tilde{\beta }})$ with the eigenvalues of T’s derivatives, the discussion following Fig. 1 gives some intuition for why $\vec {\beta }^{(m+1)} = T(\vec {\beta }^{(m)})=T\big (\cdots T(\vec {\beta }^{(0)})\big )$ converges to $\vec {\beta }^{(\infty )}$ instead of converging to Kyle’s equilibrium $\vec {\hat{\beta }}$. Indeed, for an induced matrix norm $||\cdot ||$, the value $||\nabla T(\vec {\hat{\beta }}) ||$ dominates (in absolute value) all of $\nabla T(\vec {\hat{\beta }})$’s eigenvalues. Therefore, the second row in Table 2 shows that $||\nabla T(\vec {\hat{\beta }}) ||>1$, which indicates that Kyle’s equilibrium is not stable. On the other hand, the eigenvalues for $\nabla T(\vec {\beta }^{(\infty )})$ in the first row in Table 2 are smaller than one and therefore do not contradict local stability. To build an analogy with Fig. 1, $\vec {\hat{\beta }}$ (resp. $\vec {\beta }^{(\infty )}$) can be associated with the non-stable left fixed point (resp. the stable right fixed point) at which the operator has a derivative bigger (resp. less) than 1. Mathematically speaking, for $N =3$, Kyle’s equilibrium $\vec {{\hat{\beta }}}$ is a repelling fixed point for the policy iteration operator T whereas the fixed point $\vec {\beta }^{(\infty )}$ is an attractive fixed point for T.

5.2 Theory for $N\ge 3$

To rigorously disprove local stability when $N\ge 3$, we iterate only in the third-to-last variable $\beta _{N-2}$ whereas all other coefficients are set equal to Kyle’s equilibrium values. Then, we show that the resulting policy iterations diverge, and, consequently, there is no $\epsilon >0$ such that (3.10) holds. To this end, we let T be from (3.5) and define the scalar function ${\tilde{T}}:\mathbb {R}\rightarrow \mathbb {R}$ as T’s $(N-2)$’th coordinate

$$\begin{aligned} {\tilde{T}}(\beta ^{(m)}_{N-2} ) := T\begin{pmatrix} {\hat{\beta }}_1 \\ {\hat{\beta }}_2 \\ \vdots \\ {\hat{\beta }}_{N-3} \\ \beta ^{(m)}_{N-2} \\ {\hat{\beta }}_{N-1} \\ {\hat{\beta }}_N \end{pmatrix}_{N-2}, \end{aligned}$$

(5.4)

where $({\hat{\beta }}_1,\ldots ,{\hat{\beta _N}})$ are Kyle’s equilibrium coefficients from Theorem 2.1 and $\beta ^{(m)}_{N-2}\in \mathbb {R}$ is the variable we iterate in. When $\beta ^{(m)}_{N-2}\in \mathbb {R}$ is such that $({\hat{\beta }}_1,\ldots ,{\hat{\beta }}_{N-3},\beta ^{(m)}_{N-2},{\hat{\beta }}_{N-1},{\hat{\beta }}_N)' \notin$ dom(T), we set ${\tilde{T}}(\beta ^{(m)}_{N-2} ):=\infty$.

Theorem 5.1

Let $N\ge 3$. For $\Delta>0,\,\sigma _u>0$, and $\Sigma _0>0$, we have:

• 1. For any starting value $\beta ^{(0)}_{N-2} \in \mathbb {R}$ with $\beta ^{(0)}_{N-2} \ne {\hat{\beta }}_{N-2}$, the recursively defined sequence

  $$\begin{aligned} \beta ^{(m+1)}_{N-2} := {\hat{\beta }}_{N-2}+{\tilde{T}}'( {\hat{\beta }}_{N-2})\big (\beta ^{(m)}_{N-2} - {\hat{\beta }}_{N-2}\big ),\quad m=0,1,\ldots , \end{aligned}$$

  (5.5)

  diverges in the sense $\lim _{m\rightarrow \infty } |\beta ^{(m)}_{N-2}| =\infty$.

• 2. Kyle’s equilibrium is not locally stable with respect to policy iterations for the insider in the sense of Definition 3.2.

Theorem 5.1 implies that policy iterations based on more general starting policies are also not locally stable in the following sense. We say stock holdings $\vec {x} = (x_0,x_1,\ldots ,x_N)'\in \mathcal {L}^2$ if the random variables $\Delta x_n:=x_n-x_{n-1}$ satisfy $||\vec {x}||:= \sqrt{\sum _{n=1}^N \mathbb {E}\big [(\Delta x_n)^2\big ]}<\infty$. An extension $T^\circ$ of T has dom$(T)\subseteq$ dom$(T^\circ )\subseteq \mathcal {L}^2$ and is said to be consistent with T if $T^\circ (\vec {x})=T(\vec {x})$ for all $\vec {x}\in$ dom(T).

Definition 5.2

Let $T^\circ$ be a consistent extension of T. Kyle’s equilibrium is locally stable with respect to generalized policy iterations for the insider if there exists $\epsilon >0$ such that all starting policies $\vec {x}^{(0)}\in \text {dom}(T^\circ )$ with $0< || \vec {x}^{(0)} - \vec {{\hat{x}}}|| <\epsilon$ satisfy

$$\begin{aligned} \lim _{m\rightarrow \infty } \vec {x}^{(m)} = \vec {{\hat{x}}},\quad \vec {x}^{(m+1)} := T^\circ (\vec {x}^{(m)}), \end{aligned}$$

(5.6)

where $T^\circ (\vec {x}):= (\infty ,\ldots ,\infty )'$ whenever $x\notin \text {dom}(T^\circ )$. $\diamondsuit$

The following by-product is an immediate consequence of Theorem 5.1.

Corollary 5.3

Let $N\ge 3$ and let $T^\circ$ be a consistent extension of T. Then, for $\Delta>0,\,\sigma _u>0$, and $\Sigma _0>0$, Kyle’s equilibrium is not locally stable with respect to generalized policy iterations for the insider in the sense of Definition 5.2.

We conclude this section by considering the related definition of an unstable equilibrium. This definition can be found in, e.g., Definition 1.3 in Süli and Mayers [15] and differs from non locally stable equilibria (i.e., unstable and non-stable are different mathematical concepts).

Definition 5.4

If $\vec {\beta }^{(0)}= \vec {{\hat{\beta }}}$ is the only starting policy for which (3.10) holds, we say that Kyle’s equilibrium is unstable with respect to policy iterations for the insider. $\diamondsuit$

By comparing Definitions 3.2 and 5.4, we see that an unstable fixed point is always also not stable. However, Exercise 1.2 in Süli and Mayers [15] shows that a non-stable fixed point can fail to be unstable. For $N\ge 3$, our next and last theoretical result shows that while Kyle’s equilibrium is not stable, it is also not unstable.

Theorem 5.5

Let $N\ge 3$. For $\Delta>0,\,\sigma _u>0$, and $\Sigma _0>0$, Kyle’s equilibrium is not unstable with respect to policy iterations for the insider in the sense of Definition 5.4.

In our proof of Theorem 5.5, we marginally perturb the last equilibrium coordinate by setting $\beta ^{(0)}_N:={\hat{\beta }}_N+\delta$ for a small $\delta >0$ and $\beta ^{(0)}_n:={\hat{\beta }}_n$ for $n\in \{1,\ldots ,N-1\}$. Then, we show the corresponding policy iterations converge to $\vec {{\hat{\beta }}}$. Alternatively, the iterations also converge to $\vec {{\hat{\beta }}}$ when we set $\beta ^{(0)}_{N-1}:={\hat{\beta }}_{N-1}+\delta$ and $\beta ^{(0)}_n:={\hat{\beta }}_n$ for $n\in \{1,\ldots ,N-2,N\}$. However, no matter how small a perturbation, as soon as we perturb one of the first $N-2$ coordinates of $\vec {{\hat{\beta }}}$, the policy iterations do not converge to $\vec {{\hat{\beta }}}$.

6 Conclusion

Based on a standard notion of stability used widely in both numerical analysis and financial economics, we proved that the dynamic equilibrium model of informed trading in Kyle [13] is stable when $N\in \{1,2\}$ and not stable when $N\ge 3$. To investigate further the severity of non-stability, we proved that Kyle’s equilibrium is not unstable when $N\ge 3$. We numerically illustrated that policy iterations can converge to fixed points, which are not equilibria.

Appendices

Policy iterations for the market markers

We outline how to perform policy iterations in the market makers’ control (i.e., how to iterate the pricing rule). Because this alternative policy iteration scheme produces the same conclusions as iterating the insider’s orders, we keep the presentation brief.

Given $\vec {\lambda }^{(m)}=(\lambda _1^{(m)},\ldots ,\lambda _N^{(m)})'\in \mathbb {R}^N$, we define $\vec {\lambda }^{(m+1)}=(\lambda _1^{(m+1)},\ldots ,\lambda _N^{(m+1)})'\in \mathbb {R}^N$ recursively as follows. We define the insider’s response by starting from $n=N$ and going to $n=1$ by setting $\alpha ^{(m)}_N:=0$ and

$$\begin{aligned} \beta ^{(m)}_n = \frac{1-2\alpha ^{(m)}_n\lambda ^{(m)}_n}{\Delta 2\lambda ^{(m)}_n(1-\alpha ^{(m)}_n\lambda ^{(m)}_n)},\quad \alpha ^{(m)}_{n-1}&= \frac{1}{4\lambda ^{(m)}_n(1-\alpha ^{(m)}_n\lambda ^{(m)}_n)},\quad n=N,\ldots ,1. \end{aligned}$$

To update the markets makers’ response, we start with $n=1$ and go to $n=N$ by defining $\Sigma _0^{(m+1)}:=\mathbb {V}[\tilde{v}]>0$ and

$$\begin{aligned} \lambda ^{(m+1)}_n := \frac{\beta ^{(m)}_n\Sigma ^{(m+1)}_{n-1}}{\big (\beta _n^{(m)}\big )^2\Sigma ^{(m+1)}_{n-1}\Delta +\sigma _u^2},\quad \Sigma ^{(m+1)}_n := \frac{\Sigma ^{(m+1)}_{n-1}\sigma _u^2}{\big (\beta ^{(m)}_n\big )^2\Sigma ^{(m+1)}_{n-1}\Delta +\sigma _u^2},\quad n=1,\ldots ,N. \end{aligned}$$

Similar to (3.9), we write this iteration compactly as

$$\begin{aligned} \vec {\lambda }^{(m+1)} = S(\vec {\lambda }^{(m)}), \end{aligned}$$

(A.1)

for a non-linear but smooth function $S:\mathbb {R}^N\rightarrow \mathbb {R}^N$.

By replacing T and $T(\vec {\beta }^{(m)})$ with S and $S(\vec \lambda ^{(m)})$ in Definitions 3.2, 5.2, and 5.4, we obtain the precise mathematical meaning of stability and instability with respect to policy iterations for the market makers.

Theorem A.1

For $\Delta>0,\,\sigma _u>0$, and $\Sigma _0>0$, we have:

• 1. For $N\in \{1,2\}$, Kyle’s equilibrium is locally stable with respect to policy iterations for the market makers.

• 2. For $N\ge 3$, Kyle’s equilibrium is not locally stable with respect to policy iterations for the market makers.

• 3. For $N\ge 3$, Kyle’s equilibrium is not unstable with respect to policy iterations for the market makers.

We omit the proofs because they are similar to the proofs of Theorems 4.1, 5.1, and 5.5.

Proofs

1.1 Autonomous recursion

We start by providing an autonomous recursion, which will be used in our proofs. A related recursion appears in Proposition 2 in Holden and Subrahmanyan [10]. Instead of Kyle’s equilibrium coefficients $({\hat{\beta }}_1,\ldots ,{\hat{\beta _N}})$, we will use the coefficients $({\hat{b}}_1,..,{\hat{b}}_N)$ in the next lemma. We prefer $({\hat{b}}_1,..,{\hat{b}}_N)$ because they are independent of the model input parameters $(\Delta , \sigma _u, \mathbb {V}[\tilde{v}])$.

Lemma B.1

• 1. There exist unique coefficients $({\hat{b}}_n)_{n=1}^{N-1}\subset (0,1)$ given by the backward recursion

  $$\begin{aligned} {\hat{b}}_N=1,\quad {\hat{b}}_{n}^2 = \frac{{\hat{b}}_{n-1}^2}{(1-{\hat{b}}_{n-1}^2)^2(1+{\hat{b}}_{n-1}^2)},\quad n=N,N-1,\ldots ,1. \end{aligned}$$

  (B.1)

• 2. Kyle’s equilibrium coefficients (2.4) can be expressed as

  $$\begin{aligned} {\hat{\beta }}_n=\frac{{\hat{b}}_n\sigma _u}{\sqrt{{\hat{\Sigma }}_{n-1}\Delta }},\quad {\hat{\Sigma _n}} = \frac{{\hat{\Sigma }}_{n-1}}{1+{\hat{b}}_n^2},\quad {\hat{\Sigma }}_0 :=\mathbb {V}[\tilde{v}]>0,\quad n=1,2,\ldots ,N. \end{aligned}$$

  (B.2)

Proof

1. We proceed by backward induction and assume ${\hat{b}}_n\in (0,1]$. The transformation $a:= {\hat{b}}_{n-1}^2$ produces the third-degree polynomial

$$\begin{aligned} {\hat{b}}_{n}^2 = \frac{a}{(1-a)^2(1+a)}. \end{aligned}$$

(B.3)

For ${\hat{b}}_n\in (0,1]$, the polynomial (B.3) has exactly one root $a\in (0,1)$.

2. Inserting ${\hat{\beta }}_n=\frac{{\hat{b}}_n\sigma _u}{\sqrt{{\hat{\Sigma }}_{n-1}\Delta }}$ into the formula for $\Sigma _n$ in (2.4) gives ${\hat{\Sigma _n}} = \frac{{\hat{\Sigma }}_{n-1}}{1+{\hat{b}}_n^2}$. Solving for $\alpha _n$ in the formula for $\beta _n$ in (2.4) produces

$$\begin{aligned} {\hat{\alpha }}_n = \frac{2{\hat{\beta }}_n\Delta {\hat{\lambda _n}}-1}{2{\hat{\lambda _n}}({\hat{\beta _n\Delta }} {\hat{\lambda _n}}-1)}=\frac{\sqrt{({\hat{b}}_n^2+1) \Delta {\hat{\Sigma _n}}}-2 {\hat{b}}_n \Delta {\hat{\lambda _n\sigma _u}}}{2 {\hat{\lambda }}_n \sqrt{({\hat{b}}_n^2+1) \Delta {\hat{\Sigma _n}}}-2 {\hat{b}}_n \Delta {\hat{\lambda _n}}^2\sigma _u}. \end{aligned}$$

(B.4)

From Eq. (3.18) in Kyle [13], we have ${\hat{\lambda _n}}=\frac{{\hat{\beta _n}} {\hat{\Sigma _n}}}{\sigma _u^2}$. Then, the recursion for $\alpha _n$ in (2.4) becomes the recursion in (B.1).

Finally, the terminal condition ${\hat{b}}_N=1$ in (B.1) comes from ${\hat{\alpha _N}}=0$. This is because (B.4) for $n=N$ gives the requirement

$$\begin{aligned} 1= 2{\hat{\beta }}_N\Delta {\hat{\lambda _N}} = \frac{2{\hat{b}}_N^2}{1+{\hat{b}}_N^2}, \end{aligned}$$

which has ${\hat{b}}_N=1$ as its only positive solution. $\diamondsuit$

1.2 Mathematical proofs

For a matrix $A\in \mathbb {R}^{N\times N}$, we recall the matrix norm $||A||_\infty := \max _{i\in \{1,\ldots ,N\}} \sum _{j=1}^N |A_{ij}|$. The matrix norm $||\cdot ||_\infty$ is induced by the vector norm $|\vec {\beta }|_\infty := \max \{|\beta _1|,\ldots ,|\beta _N|\}$ and therefore the inequality $|A\vec {\beta }|_\infty \le ||A||_\infty |\vec {\beta }|_\infty$ holds. The second part of the following proof is standard and can be found in, e.g., the proof of Theorem 4.2 in Süli and Mayers [15].

Proof of Theorem 4.1

1. We consider the parametrization

$$\begin{aligned} \beta _1:= \frac{b_1\sigma _u}{\sqrt{\Sigma _0 \Delta }},\quad \beta _2:= \frac{b_2\sigma _u}{\sqrt{\Sigma _1 \Delta }},\quad b_1,b_2\in \mathbb {R}. \end{aligned}$$

Lemma B.1 ensures $(b_1,b_2):= ({\hat{b}}_1,{\hat{b}}_2)$ produces Kyle’s equilibrium. Furthermore, we can use (3.8) to calculate $\nabla T (\vec {\beta })$ for $\vec {\beta } = (\beta _1,\beta _2)'$. Inserting Kyle’s equilibrium $\vec {{\hat{\beta }}}$ into $\nabla T$ gives (4.1).

2. First, we consider $N=1$. The policy iteration function T in (3.5) is given in (3.7). Our argument is based on the second-order Taylor expansion around Kyle’s equilibrium ${\hat{\beta }}:=\frac{\sigma _u}{\sqrt{\Delta \Sigma _0}}$ given by

$$\begin{aligned} T(\beta )&= T({\hat{\beta }})+ T'({\hat{\beta }})\big (\beta -{\hat{\beta }}\big )+ \frac{1}{2}T''(\gamma )\big (\beta -{\hat{\beta }}\big )^2\nonumber \\&= {\hat{\beta }}+ \frac{1}{2}\frac{\sigma _u^2}{\gamma ^3\Delta \Sigma _0}\big (\beta -{\hat{\beta }}\big )^2, \end{aligned}$$

(B.5)

where $\gamma$ is a point between $\beta$ and ${\hat{\beta }}$. The second equality in (B.5) follows from $T'({\hat{\beta }})= 0$.⁵

Let $\epsilon \in (0,1)$ be such that (i) $\epsilon <{\hat{\beta }}$ and (ii) $\frac{\epsilon \sigma _u^2}{({\hat{\beta }} -\epsilon )^3\Delta \Sigma _0}<2$. Let $\beta ^{(0)}>0$ with $0<|\beta ^{(0)}-{\hat{\beta }}|<\epsilon$ be arbitrary. By combining the expressions in (3.9) and (B.5), we get

$$\begin{aligned} \big |\beta ^{(1)}-{\hat{\beta }}\big |&\le \frac{1}{2}\frac{\sigma _u^2}{({\hat{\beta }} -\epsilon )^3\Delta \Sigma _0}\big (\beta ^{(0)} -{\hat{\beta }}\big )^2\\&\le \frac{1}{2}\frac{\epsilon \sigma _u^2}{({\hat{\beta }} -\epsilon )^3\Delta \Sigma _0}\big |\beta ^{(0)} -{\hat{\beta }}\big |. \end{aligned}$$

Iterating this inequality forward gives

$$\begin{aligned} \big |\beta ^{(m+1)}-{\hat{\beta }}\big |\le \left( \frac{1}{2}\frac{\epsilon \sigma _u^2}{({\hat{\beta }} -\epsilon )^3\Delta \Sigma _0}\right) ^{m+1}\big |\beta ^{(0)} -{\hat{\beta }}\big |,\quad m\in \mathbb N, \end{aligned}$$

which converges to zero as $m\rightarrow \infty$.

Second, we consider $N=2$. Based on (4.1), we have $||\nabla T(\vec {{\hat{\beta }}})||_\infty =0.981214\ldots$. Because the function $\text {dom}(T)\ni \vec {\beta } \rightarrow \nabla T(\vec {\beta })_{ij}$ is continuous for each matrix entry $i,j \in \{1,\ldots ,N\}$, we have continuity of $\text {dom}(T)\ni \vec {\beta } \rightarrow ||\nabla T(\vec {\beta })||_\infty$. Therefore, there exists an $\epsilon >0$ such that

$$\begin{aligned} || \nabla T(\vec {\beta })||_\infty<0.99,\quad \text {whenever}\quad |\vec {\beta } -\vec {{\hat{\beta }}}|_\infty <\epsilon . \end{aligned}$$

For $|\vec {\beta }^{(m)} -\vec {{\hat{\beta }}}|_\infty <\epsilon$ and $t\in [0,1]$, we have

$$\begin{aligned} \big |\big (\vec {\beta }^{(m)} +t(\vec {{\hat{\beta }}}-\vec {\beta }^{(m)})\big )-\vec {{\hat{\beta }}}\big |_\infty = (1-t)|\vec {\beta }^{(m)}-\vec {{\hat{\beta }}}|_\infty <\epsilon , \end{aligned}$$

and therefore $|| \nabla T\big (\vec {\beta }^{(m)} +t(\vec {{\hat{\beta }}}-\vec {\beta }^{(m)})\big )||_\infty <0.99$. The fundamental theorem for line integrals gives the representation

$$\begin{aligned} \vec {{\hat{\beta }}} -\vec {\beta }^{(m+1)}&= T(\vec {{\hat{\beta }}}) -T(\vec {\beta }^{(m)}) \\&= \int _0^1 \nabla T\big (\vec {\beta }^{(m)} +t(\vec {{\hat{\beta }}}-\vec {\beta }^{(m)})\big )(\vec {{\hat{\beta }}}-\vec {\beta }^{(m)})dt. \end{aligned}$$

Applying $|\cdot |_\infty$ produces the inequality

$$\begin{aligned} |\vec {{\hat{\beta }}} -\vec {\beta }^{(m+1)}|_\infty&\le \int _0^1 || \nabla T\big (\vec {\beta }^{(m)} +t(\vec {{\hat{\beta }}}-\vec {\beta }^{(m)})\big )||_\infty |\vec {{\hat{\beta }}}-\vec {\beta }^{(m)}|_\infty dt\\&\le 0.99|\vec {{\hat{\beta }}}-\vec {\beta }^{(m)}|_\infty . \end{aligned}$$

By iterating this inequality forward, we see that

$$\begin{aligned} |\vec {{\hat{\beta }}} -\vec {\beta }^{(m+1)}|_\infty \le 0.99^{m+1}|\vec {{\hat{\beta }}}-\vec {\beta }^{(0)}|_\infty ,\quad m\in \mathbb N, \end{aligned}$$

which converges to zero as $m\rightarrow \infty$. $\diamondsuit$

Proof of Theorem 5.1

1. Step 1/4: We start by rewriting (5.4) as

$$\begin{aligned} {\tilde{T}}(\beta _{N-2}) = \frac{f(\vec {B})}{g(\vec {B})},\quad \vec {B} := ({\hat{\beta }}_1,\ldots ,{\hat{\beta }}_{N-3},\beta _{N-2},{\hat{\beta }}_{N-1}, {\hat{\beta }}_N )' , \end{aligned}$$

(B.6)

for $\beta _{N-2}\in \mathbb {R}$ such that $\vec {B} \in \text {dom}(T) = \{ \vec {\beta }\in \mathbb {R}^N: g(\vec {\beta } )\ne 0\}$. In (B.6), the polynomials $f,g:\mathbb {R}^N \rightarrow \mathbb {R}$ are defined as

$$\begin{aligned} f(\vec {\beta })&:= \big (\Delta \Sigma _0(\beta _1^2+\cdots +\beta _{N-2}^2)+\sigma ^2\big )\nonumber \\&\quad \times \Big (\beta _{N-1}^2 \big (\Delta \Sigma _0(\beta _1^2+\cdots +\beta _{N-2}^2)+\sigma ^2\big )\nonumber \\&\quad \times \big (\Delta \Sigma _0\left( \beta _1^2+\cdots +\beta _{N-2}^2+4\beta _{N-2}\beta _N+\beta _{N}^2\right) +\sigma ^2\big )\nonumber \\&\quad +\beta _{N-1}^4 \Delta \Sigma _0\big (\Delta \Sigma _0(\beta _1^2+\cdots +\beta _{N-2}^2+2\beta _{N-2}\beta _N)+\sigma ^2\big )\nonumber \\&\quad -4\beta _{N-1}^3\beta _N \Delta \Sigma _0\big (\Delta \Sigma _0(\beta _1^2+\cdots +\beta _{N-2}^2)+\sigma ^2\big )\nonumber \\&\quad -4\beta _{N-1}\beta _N \big (\Delta \Sigma _0(\beta _1^2+\cdots +\beta _{N-2}^2)+\sigma ^2\big )^2\nonumber \\&\quad +2\beta _{N-2}\beta _N \big (\Delta \Sigma _0(\beta _1^2+\cdots +\beta _{N-2}^2)+\sigma ^2\big )^2\Big ),\nonumber \\ g(\vec {\beta })&:= 2 \beta _{N-2} \Delta \Sigma _0 \bigg (-4 \beta _{N-1}^3 \beta _{N} \Delta \Sigma _0 \big (\Delta \Sigma _0(\beta _1^2+\cdots +\beta _{N-2}^2)+\sigma ^2\big )\nonumber \\&\quad +\beta _{N-1}^2 \big (\Delta \Sigma _0 (\beta _1^2+\cdots +\beta _{N-2}^2)+\sigma ^2\big )\nonumber \\&\quad \times \Big (\Delta \Sigma _0 \big (\beta _1^2+\cdots +\beta _{N-3}^2+(\beta _{N-2}+\beta _{N})^2\big )+\sigma ^2\Big )\nonumber \\&\quad -4 \beta _{N-1} \beta _{N} \big (\Delta \Sigma _0 (\beta _1^2+\cdots +\beta _{N-2}^2)+\sigma ^2\big )^2\nonumber \\&\quad +\beta _{N-2} \beta _{N} \big (\Delta \Sigma _0 (\beta _1^2+\cdots +\beta _{N-2}^2)+\sigma ^2\big )^2\nonumber \\&\quad +\beta _{N-1}^4 \Delta \Sigma _0 \Big (\Delta \Sigma _0 \big (\beta _1^2+\cdots +\beta _{N-3}^2+\beta _{N-2} (\beta _{N-2}+\beta _{N})\big )+\sigma ^2\Big )\bigg ), \end{aligned}$$

(B.7)

for $\vec {\beta } = (\beta _1,\ldots ,\beta _N)'\in \mathbb {R}^N$. As functions of $\beta _{N-2}\in \mathbb {R}$ alone, f is a polynomial of degree 7 and g is a polynomial of degree 6.

Step 2/4: By substituting ${\hat{\beta _n}}$ from (B.2) for $n\ne N-2$, and $\beta _{N-2}= \frac{z \sigma _u}{\sqrt{\Delta \Sigma _0}}$ for $z>0$, we can find polynomials $\tilde{f},{\tilde{g}}:\mathbb {R}\rightarrow \mathbb {R}$ that are independent of $(\Delta , \sigma _u, \Sigma _0)$ such that (B.6) becomes

$$\begin{aligned} {\tilde{T}}(\beta _{N-2}) = {\tilde{T}}\left( \frac{z \sigma _u}{\sqrt{\Delta \Sigma _0}}\right) = \frac{\frac{\sigma ^8}{\Delta \Sigma _0} {\tilde{f}}(z)}{\frac{\sigma ^7}{\sqrt{\Delta \Sigma _0}}{\tilde{g}}(z)}. \end{aligned}$$

The chain rule gives the derivative

$$\begin{aligned} {\tilde{T}}'(\beta _{N-2}) = \frac{\sqrt{\Delta \Sigma _0}}{\sigma _u}\frac{\partial }{\partial z}{\tilde{T}}\left( \frac{z \sigma _u}{\sqrt{\Delta \Sigma _0}}\right) = \frac{\partial }{\partial z}\frac{ {\tilde{f}}(z)}{{\tilde{g}}(z)}. \end{aligned}$$

Step 3/4: Based on the previous step, we can assume $\Delta = \sigma _u= \Sigma _0=1$ without loss of generality. In this step, we eliminate the dependence on N by reversing indices in (B.1). That is, we let ${\tilde{b}}_n \in (0,1)$ be uniquely given by the forward recursion

$$\begin{aligned} {\tilde{b}}_1=1,\quad {\tilde{b}}_{n-1}^2 = \frac{{\tilde{b}}_{n}^2}{(1-{\tilde{b}}_{n}^2)^2(1+{\tilde{b}}_{n}^2)},\quad n=2,\ldots \end{aligned}$$

(B.8)

Unlike $({\hat{b}}_1,{\hat{b}}_2,\ldots )$ from (B.1), the values $({\tilde{b}}_1,{\tilde{b}}_2,\ldots )$ in (B.8) do not depend on $N\ge 3$.

We augment $\vec {{\hat{\beta }}}$ and write $\vec {{\hat{\beta }}}_N=\big ({\hat{\beta }}_{N,1},\ldots ,{\hat{\beta }}_{N,N}\big )'\in \mathbb {R}^N$ to highlight its dependence on N. Similarly, we augment notation and write $({\tilde{T}}_N, f_N, g_N)$ instead of $({\tilde{T}},f,g)$. We use (B.2) to write $\vec {{\hat{\beta }}}_N$ as

$$\begin{aligned} {\hat{\beta }}_{N,1}&= \tilde{b}_N,\quad {\hat{\beta }}_{N,2} = \tilde{b}_{N-1}\sqrt{1+ \tilde{b}_N^2},\quad {\hat{\beta }}_{N,3} = \tilde{b}_{N-2}\sqrt{1+ \tilde{b}_N^2}\sqrt{1+ \tilde{b}_{N-1}^2},\ldots ,\\ {\hat{\beta }}_{N,N}&= \tilde{b}_{1}\sqrt{1+ \tilde{b}_N^2}\ldots \sqrt{1+ \tilde{b}_2^2}. \end{aligned}$$

We insert these expressions for ${\hat{\beta }}_{N,1},\ldots ,{\hat{\beta }}_{N,N}$ into (B.7) and use

$$\begin{aligned} {\tilde{T}}_N'({\hat{\beta }}_{N,N-2})&= \frac{f_N'({\hat{\beta }}_{N,N-2})g_N({\hat{\beta }}_{N,N-2})-f_N({\hat{\beta }}_{N,N-2})g'_N({\hat{\beta }}_{N,N-2})}{g_N({\hat{\beta }}_{N,N-2})^2},\\ {\tilde{T}}_{N-1}'({\hat{\beta }}_{N-1,N-3})&= \frac{f_{N-1}'({\hat{\beta }}_{N-1,N-3})g_{N-1}({\hat{\beta }}_{N-1,N-3})-f_{N-1}({\hat{\beta }}_{N-1,N-3})g'_{N-1}({\hat{\beta }}_{N-1,N-3})}{g_{N-1}({\hat{\beta }}_{N-1,N-3})^2}, \end{aligned}$$

to see that

$$\begin{aligned} {\tilde{T}}_N'({\hat{\beta }}_{N,N-2}) ={\tilde{T}}_{N-1}'({\hat{\beta }}_{N-1,N-3}), \quad N\ge 4. \end{aligned}$$

Consequently, ${\tilde{T}}_N'({\hat{\beta }}_{N,N-2})$ does not depend on N for $N\ge 3$ and it suffices to consider $N=3$. For $N=3$, the common value is explicitly given as

$$\begin{aligned} {\tilde{T}}_3'( {\hat{\beta }}_{3,1}) = -2.07611\ldots \end{aligned}$$

(B.9)

Step 4/4: To prove that $\beta ^{(m)}_{N-2}$ defined in (5.5) diverges, we iteratively use (5.5) to produce

$$\begin{aligned} \beta ^{(m+1)}_{N-2} -{\hat{\beta }}_{N-2}&= {\tilde{T}}'( {\hat{\beta }}_{N-2})\big (\beta ^{(m)}_{N-2} - {\hat{\beta }}_{N-2}\big )\\&= {\tilde{T}}'( {\hat{\beta }}_{N-2})^2\big (\beta ^{(m-1)}_{N-2} - {\hat{\beta }}_{N-2}\big )\\&=\cdots \\&= {\tilde{T}}'( {\hat{\beta }}_{N-2})^{m+1}\big (\beta ^{(0)}_{N-2} - {\hat{\beta }}_{N-2}\big ). \end{aligned}$$

Because $\beta ^{(0)}_{N-2} \ne {\hat{\beta }}_{N-2}$ and $|{\tilde{T}}'( {\hat{\beta }}_{N-2})|>1$, we see that $\beta ^{(m+1)}_{N-2}$ diverges as $m\rightarrow \infty$.

2. To see that divergence in coordinate $N-2$ suffices to rule out local stability, we use a first-order Taylor expansion around Kyle’s equilibrium $\vec {{\hat{\beta }}}\in \mathbb {R}^N$. For $\vec {\beta } \in \text {dom}(T)$, we have

$$\begin{aligned} T(\vec {\beta }) = T(\vec {{\hat{\beta }}}) + \nabla T(\vec {{\hat{\beta }}})( \vec {\beta } -\vec {{\hat{\beta }}}) + R( \vec {\beta } -\vec {{\hat{\beta }}}), \end{aligned}$$

(B.10)

where R is the reminder function, which satisfies $R( \vec {\beta } ) = o(| \vec {\beta } |)$ as $|\vec {\beta }| \rightarrow 0$. Inserting $\vec {B}$ from (B.6) into (B.10) and using (5.4) give us

$$\begin{aligned} {\tilde{T}}(\beta _{N-2}) = {\hat{\beta }}_{N-2} + {\tilde{T}}'({\hat{\beta }}_{N-2})\big ( \beta _{N-2} -{\hat{\beta }}_{N-2}\big ) + R(\vec {B}-\vec {{\hat{\beta }}})_{N-2}. \end{aligned}$$

(B.11)

To complete the proof, we argue by contradiction and assume that the sequence $\vec {\beta }^{(m)}$ defined in (3.9) converges to $\vec {{\hat{\beta }}}$. We set $\vec {B}^{(m)}:= ({\hat{\beta }}_1,\ldots ,{\hat{\beta }}_{N-3},\beta ^{(m)}_{N-2},{\hat{\beta }}_{N-1}, {\hat{\beta }}_N )'$. For m sufficiently big, (B.9) and $R(\vec {\beta } ) = o(| \vec {\beta } |)$ as $|\vec {\beta }| \rightarrow 0$ give the lower bound

$$\begin{aligned} \left| {\tilde{T}}'({\hat{\beta }}_{N-2})+\frac{R(\vec {B}^{(m)} -\vec {{\hat{\beta }}})_{N-2}}{(\beta ^{(m)} _{N-2} -{\hat{\beta }}_{N-2})} \right| > 2. \end{aligned}$$

(B.12)

From (B.11), we have

$$\begin{aligned} \beta ^{(m+1)}_{N-2}- {\hat{\beta }}_{N-2}&= {\tilde{T}}'({\hat{\beta }}_{N-2})\big ( \beta ^{(m)}_{N-2} -{\hat{\beta }}_{N-2}\big ) + R(\vec {B}^{(m)}-\vec {{\hat{\beta }}})_{N-2}\nonumber \\&= \left( {\tilde{T}}'({\hat{\beta }}_{N-2})+\frac{R(\vec {B}^{(m)}-\vec {{\hat{\beta }}})_{N-2}}{(\beta ^{(m)}_{N-2} -{\hat{\beta }}_{N-2})} \right) \big ( \beta ^{(m)}_{N-2} -{\hat{\beta }}_{N-2}\big ). \end{aligned}$$

(B.13)

This gives a contradiction because the iterations (B.13) diverge by (B.12). $\diamondsuit$

Proof of Theorem 5.5

Instead of using the $(N-2)$’th coordinate, we redefine ${\tilde{T}}$ in (5.4) to be the N’th coordinate. That is, we define

$$\begin{aligned} {\tilde{T}}(\beta ^{(m)}_N) := T\begin{pmatrix} {\hat{\beta }}_1 \\ \vdots \\ {\hat{\beta }}_{N-1} \\ \beta ^{(m)}_{N} \\ \end{pmatrix}_{N}, \end{aligned}$$

(B.14)

where $({\hat{\beta }}_1,\ldots ,{\hat{\beta _N}})$ are Kyle’s equilibrium coefficients from Theorem 2.1 and $\beta ^{(m)}_{N}\in \mathbb {R}$ is the variable we iterate in. Proceeding as in the proof of Theorem 5.1, we see that $\tilde{T}'({\hat{\beta }}_N)=0$ for all $N\ge 3$. Consequently, as in the first part of Theorem 4.1, the equilibrium value ${\hat{\beta }}_N$ is a super-attracting fixed point for ${\tilde{T}}$. Proceeding as in the proof of the first part of Theorem 4.1, we see that for a starting value $\beta ^{(0)}_N$ sufficiently close to ${\hat{\beta }}_{N}$ with $\beta ^{(0)}_N \ne {\hat{\beta }}_N$, the initial policy

$$\begin{aligned} \vec {B}^{(0)}:= ({\hat{\beta }}_1,\ldots ,{\hat{\beta }}_{N-1},\beta ^{(0)}_N)', \end{aligned}$$

produces a sequence $\vec {B}^{(m+1)} = T(\vec {B}^{(m)})=T\big (\cdots T(\vec {B}^{(0)})\big )$ which converges to $\vec {{\hat{\beta }}}$. Because $\vec {B}^{(0)} \ne \vec {{\hat{\beta }}}$, Kyle’s equilibrium is not unstable in the sense of Definition 5.4. $\diamondsuit$